
On the Efficient Graph Representation of Collinear Relation in the Shape
Grammars
Kamila Kotulska and Leszek Kotulski
AGH University of Science and Technology, Mickiewicza 30, 30-059 Krakow, Poland
Keywords:
Shape Grammars, Graph Representation, Computational Model(s), Grammar, Computer-aided Conceptual
Design.
Abstract:
Shape grammars are a powerful, generative approach to description, interpretation and evaluation of many
designs. However, their practical implementation has problems related to computational and spatial efficiency.
Because of that, successful examples are restricted to small graphs or those with reduced numbers of rules and
shapes. While executing a project inspired by Antonio Gaudi’s designs, we found those limitations critical and
initiated a series of research tasks to improve of the efficiency of their implementation. The most important
task consists in developing an efficient graph representation of the collinear segments. The proposed solution,
based on a classical application of shape grammars – Stiny’s Chinese lattice design – has been compared with
two most popular existing representations.
1 INTRODUCTION
Shape Grammars have been introduced in 1971 by
Stiny (Stiny and Gips, 1971) and further developed
by himself. Stiny defined them as a “set of rules of
transformation applied recursively to an initial form,
generating new forms” (Stiny, 1980). Since then, they
have been used as a powerful generative approach to
description, interpretation and evaluation of many de-
signs. For over 45 years, the notation of the formalism
has been significantly changed and developed. De-
spite that, shape grammars were used constantly as a
rule-based system for describing and generating de-
signs (Knight, 1999), (Stiny, 2006).
Shape Grammars are used for creating and un-
derstanding designs directly, by performing compu-
tations with shapes. They have been applied to tackle
a variety of design tasks from analysis to synthesis.
Basing on a classification by Terry Knight and George
Stiny (Knight, 2015), which distinguishes seven areas
of application of shape grammars, the following rep-
resentatives can be pointed out in each area.
Painting is an area where shape grammars are used
to analyse transformations of the style of a painting.
Terry Knight (Knight, 1989) has developed her re-
search on transformations of De Stijl Art: The Paint-
ings of Georges Vantongerloo and Fritz Glarner. She
used the formalism to describe stylistic changes in de-
sign.
Shape grammars can be also used for product de-
sign. Jay P. McCormack, Jonathan Cagan and Craig
M. Vogel (Jay P McCormack, 2004) used them to
explore brand identity and showed that they might
have an important role in studio work, engineering
and marketing.
Terry Knight and George Stiny also mentioned the
area of craft. In his work, Rizal Muslimin (Mus-
limin, 2010) restructured weaving performance in ar-
chitecture. He has analysed the tacit knowledge of
traditional weavers through perceptual study and con-
verted it into explicit rules in computational design.
Mechanical design is another area where shape
grammar-based methods have been developed. Agar-
wal, Cagan and Stiny (Agarwal et al., 2000) have
shown that they are capable of generating coupled
forms, by means of so-called function shape gram-
mars. They have achieved that by satisfying the mini-
mal required functionality and then modifying the de-
vice to obtain the desired specifications.
Stiny and Mitchell (Stiny and Mitchell, 1980) also
used shape grammars for landscape design. They
used parametric shape grammars to design Mughal
gardens.
Jos Pinto Duarte (Duarte, 2005) researched shape
grammars in the area of architecture. He has de-
scribed an interactive computer system for design of
customised mass housing. The role of shape gram-
mars in such a system is to systematise the design
Kotulska K. and Kotulski L.
On the Efficient Graph Representation of Collinear Relation in the Shape Grammars.
DOI: 10.5220/0006503800600066
In Proceedings of the International Conference on Computer-Human Interaction Research and Applications (CHIRA 2017), pages 60-66
ISBN: 978-989-758-267-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

rules.
One of the most developed area of shape grammar
application is urban design. Jos Nuno Beiro (Beirao,
2012) defined all the aspects of using shape gram-
mars in this field and successfully applied his theses
in practice. Although he mentioned that rules had be
hidden from the designer, he gave the designer some
freedom by using discernible names for the moves
and their parameters.
Analysis of the mentioned examples leads us to
the conclusion that Shape Grammars can be success-
fully applied in many fields. However, the graph
structures, which formally represent problems, are
based on small graphs or have limited numbers of
rules.
During our work on the project inspired by Anto-
nio Gaudi’s designs we have noticed a serious prob-
lem with graph processing efficiency. We work on
different types of structures, which are described by
large numbers of nodes. The project requires rep-
resentation of thousands or even millions of edges,
nodes and shapes which are not represented by lines.
Even the most advanced among the exiting meth-
ods are incapable to process such vast collections
data. Real-life application of shape grammars de-
mands their efficient implementation for shapes con-
sisting of thousands of elements.
Translation of shapes into graph grammars re-
quires many problems to be solved, including:
• Complexity reduction of designation of the left-
hand side of transformation rules: In a general
case, it is an NP-complete problem, just like sub-
graph isomorphism. But with some restrictions on
the application rule form and the generated graph
structure, it can be solved in a polynomial time
(cf. (Flasinski, 1990)).
• Introduction of a mechanism of parallel applica-
tion of the transformation rules with implicit syn-
chronization; cf. (Kotulski and Sedziwy, 2010).
However, the most basic and yet still open prob-
lem is proper representation of the shape elements.
The shape graph presented in Figure 1 consists of
two overlapping squares (basic elements). In this ex-
ample, the line segment (a, b) has been split into three
collinear segments (the other line segments also have
been split). The representation of relations among
them and segment (a,b) has a strong influence on the
implementation of the shape grammar.
This problem has been outlined by Grasl and
Economou (Grasl and Economou, 2011), the authors
of one of the best shape graph interpreters called
GRAPE. The efficiency of the line segment represen-
tation, with each line consisting of several segments,
will be considered here. The representation proposed
b
a
Figure 1: Collinearity problem in Shape Grammars.
in the following part of the paper has been compared
with two others – Grasl (Grasl and Economou, 2011)
and Kelles et al. (Keles et al., 2010) – based on the
classical Stiny shape grammar application for Chi-
nese ice-ray lattice design (Stiny, 1977).
2 COLLINEAR SEGMENTS
IMPLEMENTATION
One of the most important problems associated with
graph representation of shapes is the representation
of collinear shapes in a way that allows their use it
for the analogical relations for Bezir curve elements.
The maximum line segments are a set of lines created
by combining all collinear line segments that touch
or overlap. The most straightforward approach is to
map points to the nodes and segments to the edges. In
such a representation, if a line is divided into several
segments by a crossing line, it is difficult to designate
the other collinear segments. Note that two or more
connected collinear segments can appear in the trans-
formation rule as one segment.
To overcome this problem, Keles et al. (Keles
et al., 2010) join all node pairs in such lines. Unfor-
tunately, this approach results in creation of too many
edges. For n points along the line, n ·(n − 1)/2 edges
have to be created. Thus, even for a small grid of
lines (over a dozen intersecting lines), like the one
in Stiny’s ice-ray (Stiny, 1977), a large number of
edges is generated: 1653 edges for Chengtu Szee-
hwan, 1825 AD and 1392 edges for Hanchow, Szech-
wan 1875 AD. The mentioned examples of Chinese
lattice design creates a good background for evalua-
tion of the efficiency of the considered methods.
Grasl and Economou analyse 7 other representa-

Figure 2: Keles’s long line representation.
Figure 3: GRAPE long line representation.
tions and finally introduce the representation in which
both points and segment lines are represented as
nodes (points as a black nodes and lines as a white
nodes). The collinear 5-segment line in both ap-
proaches is presented in Figure 3 and Figure 2. This
representation is efficient for collinear lines, but we
have to analyse it in the entire context of the generated
shapes. Thus, an intermediate solution has to be con-
sidered and two such approaches are presented here.
3 CHINESE LATTICE DESIGN
Stine (Stiny, 1977) analyses several examples of Chi-
nese lattice design to show the expressiveness and ca-
pabilities of shape grammars. In this paper we will
Figure 4: Chinese Lattice design - Chengtu, Szechwan 1800
AD.
consider the Chengtu Szeehwan, from 1800 AD (see
Figure 4) and from 1825 AD (see Figure 5), as well
as Hanchow, Szechwan from 1875 AD (see Figure 6).
Table 1 shows number of lines consisting from n
collinear nodes in the designs from 1800, 1825 and
1875 years.
Table 1: Number of collinear nodes in the design.
NCN 1800 AD 1825 AD 1875 AD
2 262 42 0
3 0 84 24
4 0 0 4
5 0 0 6
7 0 0 4
9 0 0 3
11 0 0 2
13 0 8 5
15 0 7 0
17 0 0 4

Figure 5: Chinese Lattice design - Chengtu, Szechwan 1825
AD.
Figure 6: Chinese Lattice design - Hanchow, Szechwan
1875 AD.
4 SHAPE GRAPH
REPRESENTATION
During definition of a shape grammar, we have to de-
fine what kinds of the basic elements can be used as
building blocks for shapes generated by the grammar.
In the Virtual Gaudi project we assume that we will
describe the shape as Bezir curves (linear, quadratic,
cubic or higher order) connected by common nodes.
Such a curve will be denoted by S
A
n
(x,y), where x
and y are the nodes representing end points, and A
n
is
a set of other (n − 2) attributes defining the Bezier
curve of the order n. For two curves, we denote
S
A
n
(x,y) ⊂ S
A
n
(w,z) if all points of the first curve be-
long to the second one. For a given n and a set of
attributes A
n
, we will say that two shapes, are co-n-
bezier shapes (denoted ↔) as if the following condi-
tions are met: for any nodes x,y, u,w,v,z:
• S
A
n
(x,y) ↔ S
A
n
(u,z) if S
A
n
(x,y) ⊂ S
A
n
(u,z)
• ↔ relation is closed under symmetry i.e.
S
A
n
(x,y) ↔ S
A
n
(u,z) ⇒ S
A
n
(u,z) ↔ S
A
n
(x,y)
• ↔ relation is closed under transitivity i.e.
S
A
n
(x,y) ↔ S
A
n
(u,w) and S
A
n
(u,w) ↔ S
A
n
(v,z)
⇒ S
A
n
(x,y) ↔ S
A
n
(v,z)
The S
A
n
(x,y) that does not contain any curves ↔ re-
lated with them will be called minimal and its end
nodes will be connected with direct edges.
The shapes grammars use hybrid notation:
• for the presentation layer, the mentioned basic
shapes are used to express the designed item,
• for efficient generation of this item, a more com-
plex graph-based representation (based on graph
transformation rules) is used.
Here, we compare the efficiency of several graph
representations according to the number of source
items (nodes and edges). There is a necessity to re-
member the information about the generated shapes;
the number of nodes and edges in the graph are the
basic parameters while considering the computational
complexity of graph-based algorithms.
Let us note that in S
A
n
(x,y) representation of the
Bezier curves we separate the notation of end nodes
and A attributes. Thus, in the graph representation we
will represent only these end nodes, while the A at-
tributes will be remembered either as attributes of the
edge representing shapes (in case of Keles’ approach)
or as attributes of the node representing shapes (ac-
cording to Grasl). The advantage of such a represen-
tation is that it is the same for all orders of Bezier
curves. For the simplicity of presentation, we will
illustrate the mentioned representation based on the
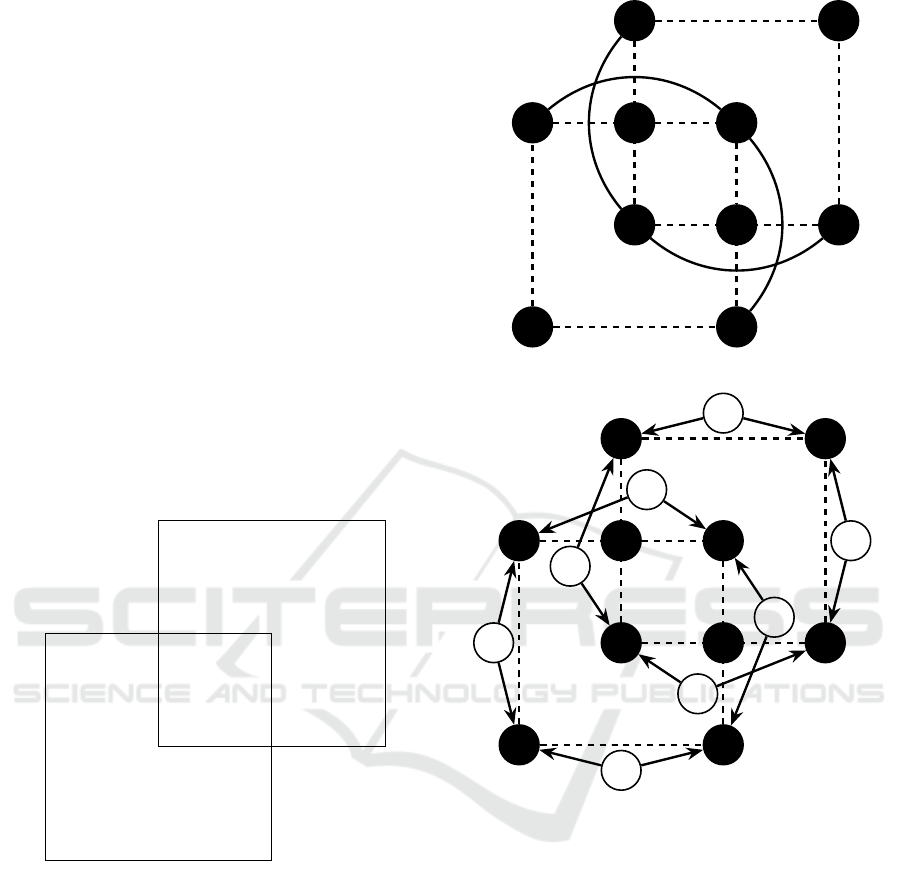
co-1-bezier shape called line segments (shortened to
S(x,y)) and collinear shape relation.
As already mentioned, two opposite graph repre-
sentations of the collinearity problem have been con-
sidered in literature. The first one has been pro-
posed by Keles (Keles et al., 2010). He mentioned
that shape nodes are represented as graph nodes and
shapes are represented as edges (A attributes are
also remembered in edges). The representation of
collinear segments defiend using 5 nodes is illustrated
in Figure 2. We will have 10 collinear segments and
the same number of edges. A more compact represen-
tation suggested by Grasl and Economu (Grasl and
Economou, 2011) introduces white nodes for repre-
sentation of the shape edges. The representation of
collinear segments defined by 5 nodes is illustrated
in Figure 3. The A attributes will be remembered in
white nodes. Two segments are collinear if their end
nodes are connected with the same white node.
The advantage of the Grasl representation is not
obvious in the case of more complex shapes, such as
the one presented in Figure 7.
Figure 7: Complex shape.
Keles’s representation of the shapes presented in
Figure 7 is presented in Figure 8.
Grasl’s representation of the same shape presented
in Figure 9 is not that simple. The shape is now rep-
resented using 18 nodes and 28 edges, while in Ke-
les’s approach, the same shape is represented using
10 nodes and 16 edges.
4.1 Virtual Gaudi Project
The Virtual Gaudi Project, developed in our depart-
ment, is inspired by the art of Antonio Gaudi. The
general idea is to formally describe the existing works
of Antonio Gaudi, analyse them using various AI sys-
tems and finally start to generate a new design in the
1
2
3
4
5
6
7
8
9
0
Figure 8: Keles’s two-square representation.
1
2
3
4
5
6
7
8
9
0
Figure 9: Grasl’s two square representation.
“Gaudi style”. It is obvious that composed artworks
consist of millions of details. Because of that, effi-
cient graph representation is a principal requirement
for this idea. In contrast to human perception, which
prefers one consistent representation of the problem,
the graph grammar formal notation has no problem
in describing the same concept in two or more ways,
depending on some parameters e.g. the size of the rep-
resented elements. This fact is the basis for the pro-
posed solution.
We Will Merge Both Presented Representations.
For the two (alternatively three) collinear segments,
we will use direct inline edges (as in Keles’s solution)
and if there are more segments, Grasl’s representation
will be used.
We analyse these four approaches on the Chinese

lattice designs.
In Chengtu, Szechwan 1800 AD design we have
167 (black) nodes and 262 direct (dashed) edges. The
(white) nodes, additional edges and the overall num-
ber of the given method of representation are pre-
sented in Table 2.
Table 2: Comparision of representation for 1800 AD.
represen- Extra Extra Together
tation nodes edges
Keles’2 0 0 429 100,00%
Grasl’s 262 524 1215 238,22%
VG-2 0 0 429 100,00%
VG-3 0 0 429 100,00%
In Chengtu, Szechwan 1825 AD design we have
237 (black) nodes and 262 direct (dashed) edges. The
(white) nodes, additional edges and the overall num-
ber of the given method of representation are pre-
sented in Table 3.
Table 3: Comparision of representation for 1825 AD.
represen- Extra Extra Together
tation nodes edges
Keles’2 0 1249 1890 100,00%
Grasl’s 141 545 1327 70,21%
VG-2 15 293 949 50,21%
VG-3 15 293 949 50,21%
In Hanchow, Szechwan 1875 AD design we have
165 (black) nodes and 276 direct (dashed) edges. The
(white) nodes, additional edges and the overall num-
ber of the given method of representation are pre-
sented in Table 4.
Table 4: Comparision of representation for 1875 AD.
represen- Extra Extra Together
tation nodes edges
Keles’2 0 1116 1557 100,00%
Grasl’s 52 328 821 52,73%
VG-2 28 280 749 48,11%
VG-3 24 276 741 47,59%
5 APPLICATION OF VG-X
NOTATION TO SHAPE
TRANSFORMATION RULES
The analysed examples show that the introduced VG-
2 and VG-3 representations have the same or bet-
ter expressiveness in comparison with Keles’s ap-
proach; their advantage grows when longer collinear
Figure 10: Online conversion of Keles’s to Grasl’s repre-
sentations - inline edge.
segments appear in the shape. They are always bet-
ter than Grasl’s approach. The VG-3 representation
seems to be slightly better, but the implementation of
splitting one of the collinear segments becomes more
complex. Thus, we will sketch the solution for VG-2.
As mentioned above, there is no problem for graph
transformation rules to use the both representations of
collinearity in the same system. The left side of the
transformation rule lhs will use the Grasl’s collinear-
ity representation. While searching the subgraph of
the entire graph G that is isomorphic to lhs, we will
convert:
• Keles’s in-line edge (black line) and the (only)
node connected with the in-line endnodes with
direct edges (dashed one) — into four nodes in
Grasl’s representation (see Figure 10),
• direct edges that are not considered in the previ-
ous in-line relation — into three nodes in Grasl’s
representation (see Figure 11).
The opposite transformation will be performed af-
ter the application of the transformation rule – all the
white nodes that participate in this rule and do not
point to at least three black nodes are converted to the
Grasl’s notation.
In the real life the final project consist of many
different styles and shapes. we can present such a sit-
uation by summing up Chengtu, Szechwan 1800 AD,
1825 AD and Hanchow, Szechwan 1875 AD. That
proves that introduced VG-2 and VG-3 representa-
tions are the most efficient ones (see table 5).

Figure 11: Online conversion of Keles’s to Grasl’s repre-
sentations - direct edge.
Table 5: Comparision of representation for the sum.
represen- Extra Extra Together
tation nodes edges
Keles’2 0 2365 3876 100,00%
Grasl’s 455 1397 3363 86,73%
VG-2 43 573 2127 54,88%
VG-3 39 569 2119 54,67%
6 CONCLUSIONS
The more compact graph representation of the shapes
generated by shape grammars is very important, as
the efficiency of graph transformation algorithms de-
pends on the graph size (number of nodes and edges).
In this context, efficient representation of the collinear
segments is proposed. The definition of transfor-
mation rule application, extended by the conversion
mechanisms, allows us to combine two different rep-
resentations of the collinear segments. It should also
be noted that the mentioned approach can be extended
to representation of co-n-bezier shapes (defined in
section 4), which is important in real-world appli-
cation of shape grammars. For example, in Antoni
Gaudi’s Sagrada Familia, line nearly do not appear.
ACKNOWLEDGEMENTS
This work has been partially supported by AGH UST
research project 11.11.120.859
REFERENCES
Agarwal, M., Cagan, J., and Stiny, G. (2000). A micro lan-
guage: Generating mems resonators by using a cou-
pled form — function shape grammar. Environment
and Planning B: Planning and Design, 27(4):615–
626.
Beirao (2012). Citymaker designing grammars for urban
design. Architecture and the Built Environment.
Duarte, J. P. (2005). Towards the mass customization of
housing: The grammar of siza’s houses at malagueira.
Environment and Planning B: Planning and Design,
32(3):347–380.
Flasinski, M. (1990). Distorted pattern analysis with the
help of node label controlled graph languages. Pattern
Recognition, 23(7):765–774.
Grasl, T. and Economou, A. (2011). Grape: Using graph
grammars to implement shape grammars. In Proceed-
ings of the 2011 Symposium on Simulation for Ar-
chitecture and Urban Design, Boston, Massachusetts,
2011, pp. 21-28. SCITEPRESS.
Jay P McCormack, Jonathan Cagan, C. M. V. (2004).
Speaking the buick language: capturing, understand-
ing, and exploring brand identity with shape gram-
mars. Elsevier Ltd, 25.
Keles, H. Y.,
¨
Ozkar, M., and Tari, S. (2010). Embedding
shapes without predefined parts. Environment and
Planning B: Planning and Design, 37(4):664–681.
Knight, T., S. G. (2015). Making grammars: From com-
puting with shapes to computing with things. Elsevier
Ltd.
Knight, T. (1999). Shape grammars in education and prac-
tice: Histrory and prospects. International Journal of
Design Computing 2.
Knight, T. W. (1989). Transformations of de stijl art: The
paintings of georges vantongerloo and fritz glarner.
Environment and Planning B: Planning and Design,
16(1):51–98.
Kotulski, L. and Sedziwy, A. (2010). GRADIS - the mul-
tiagent environment supported by graph transforma-
tions. Simulation Modelling Practice and Theory,
18(10):1515–1525.
Muslimin, R. (2010). Interweaving grammar: Reconfig-
uring vernacular structure through parametric shape
grammar. International Journal of Architectural Com-
puting, 8(2):93–110.
Stiny (2006). Shape: Talking about seeing and doing. The
MIT Press.
Stiny, G. (1977). Ice-ray: A note on the generation of chi-
nese lattice designs. Environment and Planning B,
4:89–98.
Stiny, G. (1980). Introduction to shape and shape grammars.
Environment and Planning B Planning and Design 7,
7:343–351.
Stiny, G. and Gips, J. (1971). Shape grammars and the gen-
erative specification of painting and sculpture. In IFIP
Congress (2), pages 1460–1465.
Stiny, G. and Mitchell, W. J. (1980). The grammar of par-
adise: On the generation of mughul gardens. En-
vironment and Planning B: Planning and Design,
7(2):209–226.
