
Parallel Markov-based Clustering Strategy for Large-scale
Ontology Partitioning
Imadeddine Mountasser
1
, Brahim Ouhbi
1
and Bouchra Frikh
2
1
LM2I Laboratory, ENSAM, Moulay Ismaïl University, Marjane II, B.P.4024 Meknès, Morocco
2
LTTI Laboratory, ESTF, Sidi Mohamed Ben Abdellah University, B.P.1796 Atlas, Fès, Morocco
Keywords: Knowledge-based Systems, Big Data Integration, Parallel Large-Scale Ontology Partitioning, Markov
Clustering, Distributed Architecture.
Abstract: Actually, huge amounts of data are generated at distributed heterogeneous sources, to create and to share
information on several domains. Thus, data scientists need to develop appropriate and efficient management
strategies to cope with the heterogeneity and the interoperability issues of data sources. In fact, ontology as
schema-less graph model and ontology matching as dynamic real-time large-scale data integration enabler
are addressed to design and develop advanced management mechanisms. However, given the large-scale
context, we adopt ontology partitioning strategies, which split ontologies into a set of disjoint partitions, as a
crucial part to reduce the computational complexity and to improve the performance of the ontology
matching process. To this end, this paper proposes a novel approach for large-scale ontology partitioning
through parallel Markov-based clustering strategy using Spark framework. This latter offers the ability to
run in-memory computations to provide faster and expressive partitioning and to increase the speed of the
matching system. The results drawn by our strategy over real-world ontologies demonstrate significant
performance which makes it suitable to be incorporated in our large-scale ontology matching system.
1 INTRODUCTION
Nowadays, the proliferation and the adoption of
emerging technologies have spawned new research
disciplines. Every day, enormous amounts of data
are generated in several sectors (Manufacturing,
health, social life etc.) resulting in what-is now
called Big Data (Bello-orgaz et al., 2016; Jin, 2015).
Therefore, appropriate processing and harnessing of
this data could reveal sound knowledge and valuable
insights and could herald new impetus potentials to
sustain productivity growth.
Given the fact that Big Data reside at distributed,
heterogeneous sources, we argue that the design and
development of advanced Big Data management
techniques and technologies requires effective
integration mechanisms (cleaning, matching and
transforming) and effective analytical exploitations.
However, there are many challenges that encumber
managing Big Data ranging from those caused by
the features of Big Data, as well as, those related to
the current data processing strategies (Chen et al.,
2013; Chen et al., 2014).
Hence, to build efficient Knowledge-based
systems, we address Big Data aspects from data
management perspectives by proposing a Big Data
management system based on semantic data models
as a data integration enabler to cope with Big Data
challenges (Mountasser et al., 2015). The integration
strategy aims to aggregate various heterogeneous
data sources to discover valuable insights in a wide
array of domains. As a schema-less graph model,
ontologies can describe the knowledge aspects of
any domain and can be suitable to resolve data
heterogeneity and interoperability issues of
overlapped domains.
From this regard, we have already proposed a
dynamic large-scale ontology matching approach in
conjunction with Big Data features that discover
correspondences among resultant ontologies from
each data sources (Mountasser et al., 2016).
Moreover, we focus on decomposing large and
complex ontologies into simpler subsets with
performance and scalability-friendly data structures
that contribute on the reduction of computational
complexity and improve the performance of our
system. However, in large scale context, massive
Mountasser I., Ouhbi B. and Frikh B.
Parallel Markov-based Clustering Strategy for Large-scale Ontology Partitioning.
DOI: 10.5220/0006504001950202
In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KEOD 2017), pages 195-202
ISBN: 978-989-758-272-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

amount of ontologies entities can cause performance
impediments during the ontology matching process
which negatively impacts the system scalability.
Therefore, to proceed matching of large-scale
ontologies, ontology partitioning strategies must be
adopted to split ontologies into a set of disjoint
partitions to increase matching accuracy and to
improve memory consumption.
The objective of ontology partitioning
approaches is to partition the entities of ontology
into several disjoint clusters, so that, the
cohesiveness among the entities in a cluster is high
while the coupling crossing different clusters is low.
For that, this paper presents a novel approach for
large-scale ontology partitioning through parallel
Markov-based clustering strategy over distributed
architecture using Spark framework.
The rest of the paper is structured as follows. In
section 2, we describe the related work in the field of
graph-based ontology partitioning in the large-scale
context. Section 3 describes our proposed
methodology and the implementation details.
Section 4 provides a comprehensive evaluation of
our system on real-world ontologies of various
domains and sizes over distributed platform.
2 RELATED WORK
Hu et al., (2008) develop a structure-based
partitioning algorithm that firstly, partitions the
entities of each ontology into a set of clusters based
on their structural proximities, then, they construct
blocks using RDF sentences assignment to those
clusters.
Similarly to the latter, Algergawy et al., (2011)
propose a hierarchical clustering-based approach
that represents ontologies as direct acyclic graph.
The approach represents each node its own single
element cluster, then, the algorithm iteratively
merges clusters in descending order of structural
similarity. Algergawy et al., (2015) introduce a
seeding-based clustering technique that identifies the
seeds of clusters using a distribution condition, then;
the remaining entities are placed into clusters based
on a membership function.
Unfortunately, these works perform ontology
partitioning, far afield from the available
opportunities of parallel platforms. In other words,
using better computational resources can improve
memory consumption and achieve faster results. For
this reason, using the Hadoop distributed platform,
Mountasser et al., (2016) propose parallel entity-
assignment clustering system that aims to partition
large-scale ontologies by parallelizing and
distributing clustering tasks over available
computational resources. First, the algorithm parses
and splits ontologies into smaller and simpler
resource-based subsets. Using these latter, the
system create clusters centroid through the
combination of several metrics based on the node
importance philosophy. Then, it assigns remaining
nodes to their proper clusters based on several
similarity metrics.
3 IMPROVED MARKOV
CLUSTERING
Let us assume that all the ontologies used by this
approach are in the OWL form. Ontologies in this
form can be organized as a Directed Acyclic Graph
with its nodes describing entities of ontology and the
edges between nodes describing the relations
(taxonomic and non-taxonomic) between entities.
Our goal of ontology clustering is dividing
ontology into a set of clusters with related entities
based on a graph structure. To the best of our
knowledge, there is no study relating the large scale
ontology partitioning using Markov clustering
models. Consequently, this paper introduced a novel
approach for parallel large-scale ontology
partitioning using Markov clustering strategy.
3.1 Preliminaries
In this section, we highlight some pertinent
definitions and concepts concerning graph
description and Markov clustering strategies, used
throughout this approach.
3.1.1 Ontology Parsing
Our approach builds a finite ergodic Markov chain
model of ontology by mapping ontology classes to
states in the Markov chain and by mapping all
relations between classes to state transitions. Hence,
ontology is modelled as a directed acyclic graph by
considering concepts as a finite set of nodes and
including taxonomic and non-taxonomic
relationships between classes as a finite set of
directed edges.
3.1.2 Notations
Throughout this paper, we assume that G = (V, E) is
a directed acyclic graph with V and E represent the
node set and edge set respectively. Let A be the
adjacency matrix corresponding to the graph G, with
A(i, j) denoting the weight of the edge between the
vertex v
i
and the vertex v
j
. If the graph is non-
weighted, which is the case of ontologies, then, the
weight on each edge is fixed to 1.
A column stochastic matrix M associated to a
graph G can be interpreted as the matrix of the
transition probabilities of a random walk defined on
the graph, e.g. the i
th
column of M represents the
transition probabilities out of the vertex v
i
. The most
appropriate way of deriving a column stochastic
transition matrix M for a graph G is to simply
normalize the columns of the adjacency matrix to
sum to 1. Moreover, we define the canonical
transition matrix by M
G
= AD
−1
, where D is the
diagonal degree matrix of the graph G.
3.2 Markov Clustering Approaches
The Markov clustering algorithm is a commonly
used graph-based clustering strategy that
incorporated the structure of the graphs to reveal the
clusters structure.
Markov clustering algorithm (MCL) has been
adopted in a wide range of applications (Enright et
al., 2002; Wong et al., 2008). The algorithm allows
the search for structurally homogeneous subsets by
considering a random walk on the graph based on
the paradigm that a “random walk that visits a dense
cluster will likely not leave the cluster until many of
its vertices have been visited.”. Rather than
simulating random walks, MCL iteratively
transforms the stochastic flow matrix associated
with the graph. It offers various advantages. It is
significantly tolerant to noise and behaves robustly
(Chen and Ji, 2010).
3.2.1 Markov Clustering
MCL algorithm is an iterative process that applies
three operators- expansion, inflation and pruning- to
the stochastic matrix until convergence. The
stochastic matrix M associated with a graph G is
defined by normalizing all columns of the adjacency
matrix of G. These operators are mapping the space
of the stochastic matrix to itself (Satuluri and
Parthasarathy, 2009).
Expand operation: simulates a random walk on
the graph (i.e. normal matrix squaring). Thus, it
increases the flow between existing nodes.
Expand (M) = M * M
(1)
Inflate operation: regulates the flow in the graph,
strengthens the strong flows and weakens the weak
ones. Each element of the matrix is raised to the
power of inflation parameter r, then, matrix
normalization is performed so that columns sum to
1.
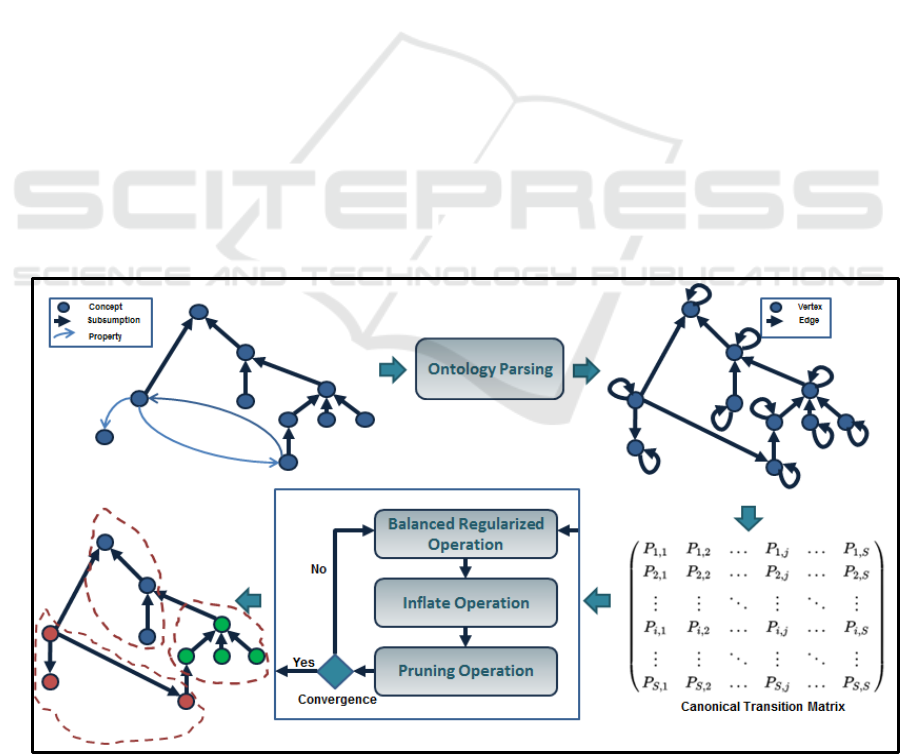
Figure 1: The improved parallel balanced regularized Markov clustering process.

The parameter r can control the outcome of the
algorithm by determining the granularity of the
obtained clusters, in such a way that, larger
parameter (r) can produce finer granularity, and
more clusters.
(2)
Pruning operation: In each column, entries’
having values less than some threshold (heuristically
computed) is removed, and the remaining entries are
normalized to make the column sum to 1. This step
aims to reduce the non-zero value in the matrix and
hence reduces memory consumption, which helps to
accelerate the convergence of the process. Finally,
the iteration is interrupted upon reaching a matrix
that is invariant under k expansions and inflations.
However, in spite of its advantages, MCL has
drawn several limitations; MCL lacks scalability and
suffers from fragmentation issue (large clusters and
singleton cluster) which is not ideal in large-scale
cases.
3.2.2 Regularized Markov Clustering
To retain the strengths of MCL and reduce its
limitations Satuluri and Parthasarathy, (2010)
proposed a regularized variant of MCL that
improves the accuracy and the scalability of the
clustering process. Regularized MCL was proposed
as a variant of MCL to produce more accurate
results and typically more compact clusters than
MCL. The RMCL algorithm resolves the output
fragmentation issues through regularizing the
distribution flow out of the node on conjunction to
its neighbours (Satuluri, 2012). Therefore, the
Expand operator in MCL algorithm is replaced by
the regularize operator which updates the flow
distribution of each node.
Regularize (M) = M * M
G
(3)
where M
G
is the canonical flow matrix of the graph
G.
Essentially, the impact of the regularize operator
consists on setting the out-flow distribution of a
node to be the weighted average of the out-flow
distributions of its neighbours (Ginanjar et al.,
2016). This operator ensures the permanent
influence of the original topology of the graph on
clustering process beyond the first iteration.
3.2.3 Balanced Regularized Markov
Clustering
The BRMCL is a balanced variant that preserves the
native features of R-MCL. Instead of using M
G
as
the weight matrix, we construct a new regularization
M
R
using both the current flow matrix M and the
canonical flow matrix M
G
. For that, given a flow
matrix M associated with the graph, the following
concepts must be defined:
Node mass: Defined as the sum total of the
flows into the node, in such a way that, nodes
with higher mass attract more nodes in the
graph towards them.
(4)
Node propensity: Defined as the weighted
average of the masses of the nodes that flows
into this node.
(5)
The distribution of masses of the “Attractor”
nodes is a proto-indicator of the distribution of final
cluster sizes (i.e. nodes imbalanced clusters reflects
imbalanced masses distribution). The aim is to push
more nodes towards attractors having lower mass,
thus requires that weight of each neighbour of a
given node in the regularization matrix M
G
must be
in inverse proportion to the propensity of the
neighbour. This means that at each iteration step, we
need to construct a new regularization matrix M
R
while maintaining the rest of R-MCL unchanged.
The new regularization matrix M
R
is given by:
M
R
= normalize (M
G
* P
-b
)
(6)
where P is the diagonal matrix with the propensity
vector p along the diagonal.
The normalize operation rescales each column so
that each column sums to 1. We notice that, the
balance parameter b specifies the extent to which
higher-propensity neighbours are to be penalized, in
such a way that higher the value of b is the greater
the penalty on high-propensity neighbours.
3.3 Improved Parallel Markov
Clustering
Given the introduced approaches, there are still
some critical limiting factors in working with
Markov clustering especially for large scale graphs,
since the performance of the ontology clustering

(partitioning) process can be a critical part of the
upcoming ontology matching process performance.
Regularized Markov Clustering still suffers from
the scalability and storage issues, resulting from
high time and space complexity of the clustering
process (Bustamam et al., 2012). At the core of the
Regularized variants of Markov clustering, we can
notice that its complexity is dominated by the
iteratively sparse matrix-matrix multiplication and
normalization steps, which is an intensive and time-
consuming component. Thus, for scalability and
performance-gain reasons, we need to develop
computationally efficient algorithm that performs
parallel sparse matrix-matrix computations and
parallel sparse Markov matrix normalizations in
order to improve the MCL performance.
To overcome the above MCL’s issues, we
propose a parallel Markov clustering approach that
tries to improve the performance of the Markov
Clustering by implementing parallel tasks for
expansion, inflation and pruning operators using
Spark framework (See Figure 1), which is a fast and
general-purpose cluster computing system.
3.3.1 Apache Spark Framework
Apache Spark is a unified programming
environment that provides computing framework
designed for scheduling, distributing, and
monitoring applications that consist of many
computational tasks across many commodity worker
machines (computing cluster) (Shanahan and Dai,
2015).
The computational engine Spark Core provides
the basic functionality of Spark, including
components for memory management, task
scheduling and fault recovery mechanisms,
interacting with storage systems. Furthermore, it
offers the ability to run in-memory computations to
provide faster and expressive processing and
increase the speed of system. In-memory processing
is faster since no time is spent in moving the data
and processes, in and out of the hard disk.
Accordingly, Spark caches much of the input data on
memory for further explorations leading to more
performance iterative algorithms that access the
same data repeatedly.
3.3.2 Our Implementation
In order to improve the MCL performance, the
parallel implementation of the Regularized Markov
Clustering algorithm constitutes an important
challenge. Thereby, we introduce a very fast Markov
clustering algorithm using Spark framework to
perform parallel sparse matrix-matrix computations
operations, which are at the heart of Markov
clustering.
First of all, the resulting graphs from large scale
ontology are generally sparse; thus, Markov
clustering storage issues can be resolved using
distributed sparse matrix data structures offered by
the resilient distributed datasets (RDD) (Bosagh et
al., 2016), which are partitioned collections of
objects spread across many compute nodes that can
be manipulated in parallel. These matrices are
distributed across computational nodes by entries
using CoordinateMatrix implementation, by rows
via RowMatrix or via blocks by implementing
BlockMatrix.
Moreover, the distributed sparse matrices offered
by Spark ignore the large amount of zero entries,
found in the initial stochastic matrices of Markov
clustering algorithms. Hence, the distributed
matrices can reduce the computational load by
avoiding the additions and multiplications with null
entries, since the zero values do not influence any of
the Markov clustering operations. Furthermore,
Spark comes with a library containing common
computational functionality (Spark MLlib) (Meng et
al., 2016), especially for matrix-matrix
computations. These properties are the primary
source of acceleration of our system.
Besides, Spark provides a way to parallelize our
Markov clustering strategy across clusters, while
hiding the complexity of distributed clustering
programming, network communication, and fault
tolerance in order to ensure the effective and reliable
use of cache memory and the process balanced load.
These latter is enhanced by dividing data according
to performance and scalability-friendly data
structures, aiming to dynamically adapt the system
to fine-grained allocation of both resources and
computations based on the workload. The pseudo-
code for our parallel Markov Clustering
implementation is given in the following:
Input: An ontology O, Balance
parameter b, Inflation rate r
Output: Clusters Set C={C
1
,C
2
,…,C
n
}
{//Phase 1: Ontology Parsing}
//get ontology concepts
Nodes:= Concepts(O)
//taxonomic and non-taxonomix
Edges:= Relations(O)
//create associated graph
G := CreateGraph(Nodes,Edges);
//Graph adjacency matrix
A := Adjacency(G)
{//Phase 2: Markov Clustering}
A := A + I // Add self-loops
//Initialize M as the canonical
flow matrix
M := M
G
:= A*D
−1
repeat
// Compute mass vector
mass(i)=∑
j
M(j,i)
// Compute propensity vector
p(i)=∑
j
M(j,i)*mass(j)
P := diag(p)
// Compute regularized matrix
//Normalize MR so that each column
sums to 1.
M
R
:= M
G
*P
−b
M := M
reg
:= M*M
R
M := M
inf
:= Inflate(M, r)
M := Prune(M)
until M converges
Interpret M as clustering Sets
4 EXPERIMENTAL
EVALUATION
In order to evaluate the performance of our approach
and the execution time, we conducted a set of
experiments using a distributed architecture. We
implemented our system in Java; ontologies were
parsed using Jena Apache. All processes are
elaborated within Apache Spark Framework as
programming environment that provides computing
framework designed for scheduling distributing
computational tasks across many computing nodes.
4.1 Data Sets
The Performance of our approach is evaluated over
the anatomy data set that contains two large
ontologies of human and mouse anatomy which
contains 3306 and 2746 concepts respectively, and
the DBpedia ontology release DBpedia_2015_10.
4.2 Experimental Architecture
All the experiments were carried out using the
Apache Spark which is an open source, in-memory
analytics computing framework. For this
experimentation, we use a cluster of 10 slave
machines and one master machine. Each node is
equipped with 3.4 GHz Intel(R) Core i3(R) with 4
GB memory, Java 1.8 and Ubuntu 14.04 LTS.
4.3 Experimental Results
In order to incorporate the Markov clustering
approach in our large-scale ontology matching
system, we must evaluate the scalability of the
clustering approach. In our implementation, we
attempt to validate the performance and the
effectiveness of the proposed approach via a set of
experiments on real world ontologies.
The simulation ran by using default expansion
parameter (square), parameters of inflation r= 1.5; 2
and 2.5, balanced parameter b= 0, 1.5, and 2 and
pruning threshold ϵ=0.000001. The simulation is
performed several times with different parameters of
inflation to look at the speed and the number of
formed clusters.
The number of resulting clusters from the
improved BRMCL simulation using the inflation
rates 1.5, 2 and 2.5 vary from 1523 to 2136 clusters
for Human ontology, from 1622 to 1968 clusters for
Mouse ontology and from 519 to 533 clusters for
DBpedia ontology. We can notice that varying the
inflation parameter can result in clustering of
different granularities, in such a way that, if the
inflation parameter gets higher, the clustering
algorithm predicts more clusters with smaller size.
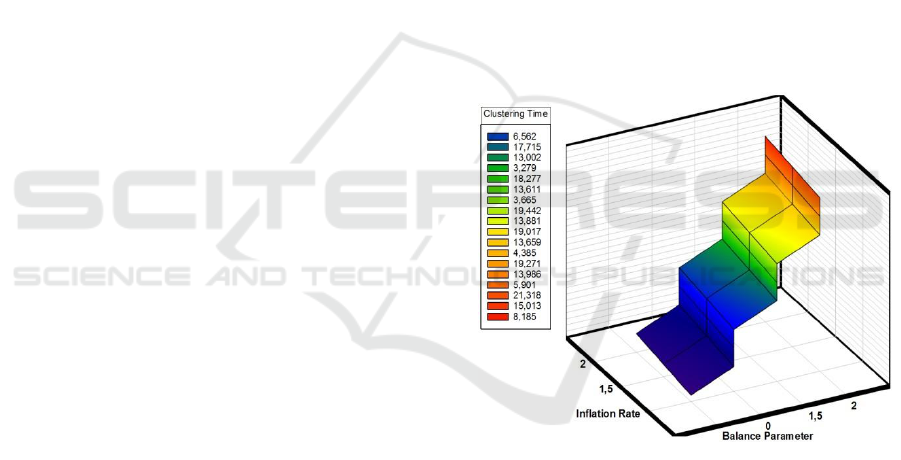
Figure 2: Clustering Time related to the inflation rate and
the balance parameter.
As shown in Figure 2, we clearly notice that the
runtime of our clustering implementation is related
to the inflation rate and the balance parameter. Thus,
having more balanced clusters can be achieved by
increasing the balance parameter, for the reason that
higher values of this latter lead to more severe down
weighting of nodes with high propensity values,
which consequently, provoke more iteration
operations and lead to a slower convergence for the
clustering process. By contrast, the incorporation of
the balanced strategy improves the clustering quality
by allowing the discovery of balanced clusters (See
Table 1, Table 2 and Table 3).
Despite these impediments, our parallel Markov-
Based clustering implementation demonstrates
significant performance and provides faster and
expressive partitioning of the large-scale ontologies.
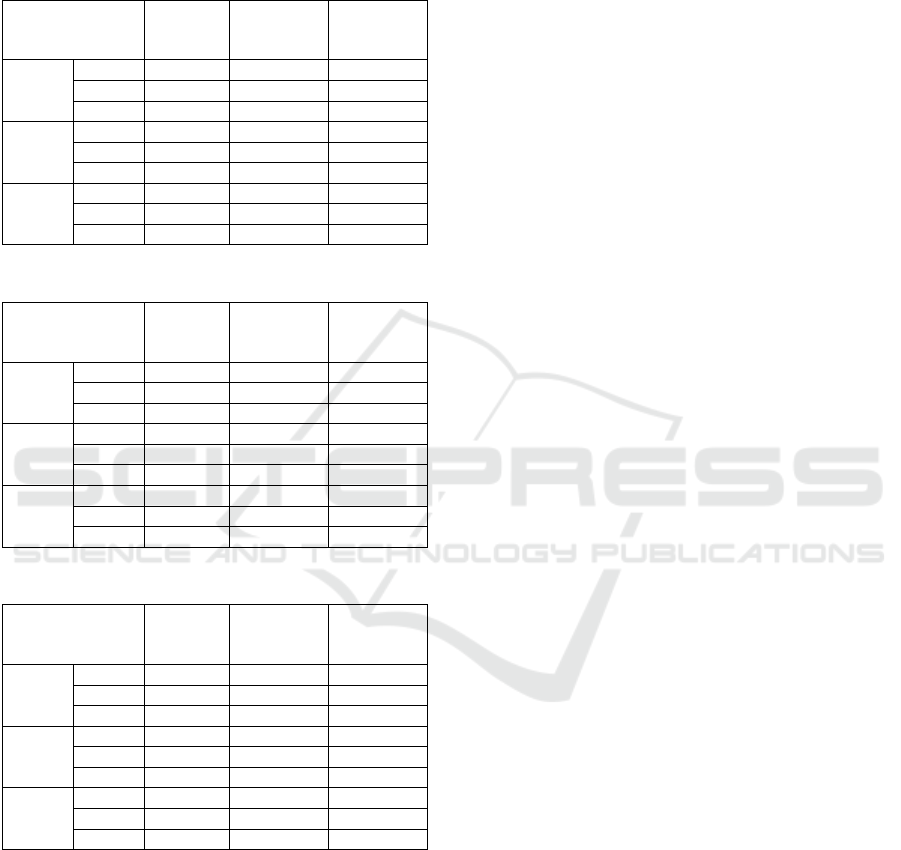
Table 1: Clustering results for the Human ontology.
Clusters
Number
Clustering
Time
% of
Balanced
Clusters
b = 0
r = 1.5
1523
16,492 s
11%
r = 2
1785
17,032 s
27%
r= 2.5
2136
17,336 s
33%
b = 1.5
r = 1.5
1523
17,715 s
21%
r = 2
1785
18,277 s
28%
r= 2.5
2136
19,442 s
33%
b = 2
r = 1.5
1523
19,017 s
28%
r = 2
1785
19,271 s
35%
r= 2.5
2136
21,318 s
46%
Table 2: Clustering results for the Mouse ontology.
Clusters
Number
Clustering
Time
% of
Balanced
Clusters
b = 0
r = 1.5
1622
12,853 s
15%
r = 2
1787
13,071 s
17%
r= 2.5
1968
13,473 s
22%
b = 1.5
r = 1.5
1622
13,002 s
35%
r = 2
1787
13,611 s
46%
r= 2.5
1968
13,881 s
51%
b = 2
r = 1.5
1622
13,659 s
41%
r = 2
1787
13,986 s
58%
r= 2.5
1968
15,013 s
63%
Table 3: Clustering results for the DBpedia ontology.
Clusters
Number
Clustering
Time
% of
Balanced
Clusters
b = 0
r = 1.5
519
3,112 s
44%
r = 2
527
4,016 s
51%
r= 2.5
533
6,562 s
53%
b = 1.5
r = 1.5
519
3,279 s
47%
r = 2
527
3,665 s
59%
r= 2.5
533
4,279 s
68%
b = 2
r = 1.5
519
4,385 s
47%
r = 2
527
5,901 s
61%
r= 2.5
533
8,185 s
70%
5 CONCLUSIONS
In this paper, we presented our parallel Markov-
based partitioning strategy considered as a crucial
part of the large-scale ontology matching process,
which aims to cope with the velocity issues and to
increase the performance of the matching system.
Our strategy provides faster and expressive
partitioning through dynamic, real-time in-memory
computations based on the Spark distributed
programming environment.
From the results drawn by our strategy over real-
world ontologies, it is apparent that our parallel
Markov-based partitioning approach presents
significant performance results for partitioning large
ontologies, which consequently make the approach
suitable to be incorporated in our large-scale
ontology matching system.
REFERENCES
Algergawy, A., Babalou, S., Kargar, M.J. and
Davarpanah, S.H., 2015, September. Seecont: A new
seeding-based clustering approach for ontology
matching. In East European Conference on Advances
in Databases and Information Systems (pp. 245-258).
Springer International Publishing.
Algergawy, A., Massmann, S. and Rahm, E., 2011,
September. A clustering-based approach for large-
scale ontology matching. In East European
Conference on Advances in Databases and
Information Systems (pp. 415-428). Springer Berlin
Heidelberg.
Bello-Orgaz, G., Jung, J.J. and Camacho, D., 2016. Social
big data: Recent achievements and new challenges.
Information Fusion, 28, pp.45-59.
Bosagh Zadeh, R., Meng, X., Ulanov, A., Yavuz, B., Pu,
L., Venkataraman, S., Sparks, E., Staple, A. and
Zaharia, M., 2016, August. Matrix computations and
optimization in apache spark. In Proceedings of the
22nd ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining (pp. 31-38).
ACM.
Bustamam, A., Burrage, K. and Hamilton, N.A., 2012.
Fast parallel Markov clustering in bioinformatics
using massively parallel computing on GPU with
CUDA and ELLPACK-R sparse format. IEEE/ACM
Transactions on Computational Biology and
Bioinformatics (TCBB), 9(3), pp.679-692.
Chen, C.P. and Zhang, C.Y., 2014. Data-intensive
applications, challenges, techniques and technologies:
A survey on Big Data. Information Sciences, 275,
pp.314-347.
Chen, J., Chen, Y., Du, X., Li, C., Lu, J., Zhao, S. and
Zhou, X., 2013. Big data challenge: a data
management perspective. Frontiers of Computer
Science, 7(2), pp.157-164.
Chen, Z. and Ji, H., 2010, July. Graph-based clustering for
computational linguistics: A survey. In Proceedings of
the 2010 workshop on Graph-based Methods for
Natural Language Processing (pp. 1-9). Association
for Computational Linguistics.
Enright, A.J., Van Dongen, S. and Ouzounis, C.A., 2002.
An efficient algorithm for large-scale detection of

protein families. Nucleic acids research, 30(7),
pp.1575-1584.
Ginanjar, R., Bustamam, A. and Tasman, H., 2016,
October. Implementation of regularized Markov
clustering algorithm on protein interaction networks of
schizophrenia's risk factor candidate genes. In
Advanced Computer Science and Information Systems
(ICACSIS), 2016 International Conference on (pp.
297-302). IEEE.
Hu, W., Qu, Y. and Cheng, G., 2008. Matching large
ontologies: A divide-and-conquer approach. Data &
Knowledge Engineering, 67(1), pp.140-160.
Jin, X., Wah, B.W., Cheng, X. and Wang, Y., 2015.
Significance and challenges of big data research. Big
Data Research, 2(2), pp.59-64.
Meng, X., Bradley, J., Yavuz, B., Sparks, E.,
Venkataraman, S., Liu, D., Freeman, J., Tsai, D.B.,
Amde, M., Owen, S. and Xin, D., 2016. Mllib:
Machine learning in apache spark. Journal of Machine
Learning Research, 17(34), pp.1-7.
Mountasser, I., Ouhbi, B. and Frikh, B., 2015, December.
From data to wisdom: A new multi-layer prototype for
Big Data management process. In Intelligent Systems
Design and Applications (ISDA), 2015 15th
International Conference on (pp. 104-109). IEEE.
Mountasser, I., Ouhbi, B. and Frikh, B., 2016, November.
Hybrid large-scale ontology matching strategy on big
data environment. In Proceedings of the 18th
International Conference on Information Integration
and Web-based Applications and Services (pp. 282-
287). ACM.
Satuluri, V.M., 2012. Scalable clustering of modern
networks (Doctoral dissertation, The Ohio State
University).
Satuluri, V. and Parthasarathy, S., 2009, June. Scalable
graph clustering using stochastic flows: applications to
community discovery. In Proceedings of the 15th
ACM SIGKDD international conference on
Knowledge discovery and data mining (pp. 737-746).
ACM.
Satuluri, V., Parthasarathy, S. and Ucar, D., 2010, August.
Markov clustering of protein interaction networks with
improved balance and scalability. In Proceedings of
the First ACM International Conference on
Bioinformatics and Computational Biology (pp. 247-
256). ACM.
Shanahan, J.G. and Dai, L., 2015, August. Large scale
distributed data science using apache spark. In
Proceedings of the 21th ACM SIGKDD International
Conference on Knowledge Discovery and Data
Mining (pp. 2323-2324). ACM.
Wong, S. and Ragan, M.A., 2008. MACHOS: Markov
clusters of homologous subsequences. Bioinformatics,
24(13), pp.i77-i85.
