
Deep Associative Semantic Neural Graphs for Knowledge
Representation and Fast Data Exploration
Adrian Horzyk
Department of Automatics and Biomedical Engineering, AGH University of Science and Technology in Krakow,
Mickiewicza Av. 30, 30-059 Krakow, Poland
Keywords: Active Knowledge-based Neural Structures, Semantic Neural Structures, Representation of Complex Entities,
Knowledge-based Inference, Deep Neural Network Architectures, Associative Graph Data Structures, Big
Data, Associative Database Normalization, Database Transformation, Data Mining, Knowledge Exploration.
Abstract: This paper presents new deep associative neural networks that can semantically associate any data, represent
their complex relations of various kinds, and be used for fast information search, data mining, and knowledge
exploration. They allow to store various horizontal and vertical relations between data and significantly
broaden and accelerate various search operations. Many relations which must be searched in the relational
databases are immediately available using the presented associative data model based on a new special kind
of associative spiking neurons and sensors used for the construction of these networks. The inference
operations are also performed using the reactive abilities of these spiking neurons. The paper describes the
transformation of any relational database to this kind of networks. All related data and their combinations
representing various objects are contextually connected with different strengths reproducing various
similarities, proximities, successions, orders, inclusions, rarities, or frequencies of these data. The
computational complexity of the described operations is usually constant and less than operations used in the
databases. The theory is illustrated by a few examples and used for inference on this kind of neural networks.
1 INTRODUCTION
Efficient and safe collecting, storage, retrieval,
processing, mining, and exploration of big data are
the most important tasks of contemporary computer
science (Apiletti et al., 2017), (Han and Kamber,
2000), (Piatetsky-Shapiro and Frawley, 1991),
(Fayyad, 1996), (Jin et al., 2015), (Linoff and Berry,
2011), (Pääkkönen and Pakkala, 2015). To get
benefits from various big data collections, we need to
use smart and very fast methods for data search,
mining, and knowledge exploration. It is not an easy
task because data are typically stored in relational
databases which relate data and entities only
horizontally. Data must be sorted, indexed, or joined,
and vertical relations must often be found and
processed in many time-consuming nested loops.
This paper introduces new deep associative
semantic neuronal graphs (DASNG) which allow for
storing data where the data are automatically
horizontally and vertically associated and ordered
according to all attributes without any substantial
computational or memory costs. Moreover, these
relations can be easily supplemented by any further
relations or related objects that can be added to this
structure or stored in a result of data exploration using
extra neurons and connections. Vertical data
associations describe many useful relations like
similarity, proximity, order, or succession in space or
time. They can also easily determine minima,
maxima, medians, average numbers, and data ranges.
Data mining and knowledge exploration methods
usually try to find interesting groups of similar,
different, frequent, or infrequent patterns for a given
minimum support and minimum confidence to define
associative rules, cluster objects or draw some useful
conclusions about objects or their groups (Agrawal et
al., 1993), (Apiletti et al., 2017). The introduced
model of the data representation and storage in the
DASNG structure supplies us with an ability to
directly or indirectly connect related data. This
strategy excludes computationally expensive loops
and reduces the computational complexity of
operations on the related data. All minima and
maxima are available in constant time. All other
values of each attribute are organized using the
Horzyk A.
Deep Associative Semantic Neural Graphs for Knowledge Representation and Fast Data Exploration.
DOI: 10.5220/0006504100670079
In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KEOD 2017), pages 67-79
ISBN: 978-989-758-272-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

introduced aggregated values B-trees which
automatically aggregate and count duplicated values
and order them linearly during their construction
process. This strategy reduces the computational
complexity of many operations.
The introduced DASNGs consist of a special kind
of spiking neurons introduced in this paper and
referring to the earlier models presented in (Horzyk,
2014), (Horzyk et al., 2016), (Horzyk, 2017). Spiking
neurons are reactive and use a time approach for
computations (Gerstner and Kistler, 2002), so data
exploration routines can be triggered in these graphs
automatically by stimulation of neurons representing
any search context. It is very useful because some
frequently performed operations are built-in this
neural system and do not need to be implemented in
the form of typical algorithmic procedures. The
connection network between neurons allows us to
quickly find associated data, objects, and patterns
accordingly to their frequency, similarity, or vicinity
in raw data. Furthermore, all important findings can
be almost costless converted into new neuronal
substructures that will store them in the same graph
for any further use and inference.
The way, in which the DASNGs work, classify
them as emergent cognitive neuronal systems. They
have a few similar features to semantic networks and
other emergent cognitive systems (Duch and Dobosz,
2011), (Nuxoll and Laird, 2004), (Parisia et al., 2017),
(Starzyk, 2007), (Starzyk, 2015). The semantic
networks represent semantic relations between
concepts that are linked together (Sowa, 1991), while
in the introduced DASNGs, neurons can represent
any sets of elementary or complex sub-combinations
of input data and directly or indirectly related objects
for defining differing contexts affecting the neurons
with different strength. Semantic networks are
browsed through using various search routines
operating on graph structures, while the presented
associative graphs are equipped with special reactive
spiking neurons that can automatically perform some
search operations by stimulating them. It will be
shown how neurons process such search operations
and how this neural graph works on exemplary data
in section 6.
2 RELATIONAL DATABASE
MODEL DRAWBACKS
In computer science, we used to store data in
relational databases, consisting of tables, which use
primary and foreign keys to represent related entities.
In relational databases, we use entity-relational model
(ER model) that describes interrelated things of
interest in a specific domain of knowledge (Bagui and
Earp, 2011), (Chen, 2002). The above-mentioned ER
model is composed of entity types which classify the
things of interests and specifies various horizontal
relationships that can exist between instances of those
entity types. This model is also an abstract data model
that defines a data structure that can be implemented
as a relational database. The ER modeling was
developed for database design by Peter Chen (Chen,
2002). However, the ER model can also be used in the
specification of domain-specific ontologies.
Entities may be characterized not only by
relationships but also by additional properties
(attributes), which include special identifies called
primary keys. In the databases, each row of a table
represents one instance of an entity type, and each
field represents an attribute type, where a relationship
between entities is implemented by storing a primary
key of one entity as foreign keys in other entities of
other tables (Fig. 1).
Figure 1: A sample of the small database with typically
repeated attribute values and relations to the same objects
of another table represented by the primary keys.
In the relational database model, features are
grouped in rows defining entities (records, tuples,
objects) collected in tables. The rows of different
tables can be horizontally linked together using
primary and foreign keys. This kind of row linking
allows defining more complex objects by other
already represented objects in other tables. Keys are
unique, sorted, and usually quite quickly available
using B-trees, B+trees, hash-tables, or other methods
typically in logarithmic time (Cormen et al., 2001),
(Hellerstein et al., 2007).
All modern databases use a Cost Based
Optimization (CBO) to optimize queries and to create
and an individual execution plan for each query.
Usually, there are many possibilities, which
dependently on row numbers and created indices can
differ computational cost and complexity of various
execution plans. Execution plans can comprise

dynamically created temporal indices for the current
query if it improves the cost of the execution plan.
Many times, heuristic or greedy algorithms are also
used to quickly find out a “good” enough execution
plan without brute force search (Hellerstein et al.,
2007).
Moreover, we distinguish various join operations
as nested loop join, hash join, and merge join which
can be more efficient in some specific situations. The
join operations are frequently executed on every
database, so their optimization is crucial. The nested
loop join takes O(N*M) time, the hash join is
processed in O(N+M) time, and the merge join in
O(N+M) or O(N*log N + M*log M) dependently on
working on the sorted or unsorted data, where N and
M are the numbers of merged records of two joined
tables (Hellerstein et al., 2007).
Statistics are also very useful and help to estimate
the disk I/O and CPU operations and memory usage
to find a “good” enough execution plan, however,
there is a certain cost of updating statistics as well.
The I/O disk data access for reading and writing
operations are bottlenecks of databases, especially
when a database is huge and do not fit into memory
because disk operations are typically at least hundreds
of times slower than operations executed in the RAM.
Despite the many advantages of such a solution,
we also come across many difficulties and
bottlenecks, where the ER data model is not effective
enough (Hellerstein et al., 2007), e.g. the time
necessary to update statistics and indices, sorting
operations, cope with hundred times slower I/O disk
operations, quick finding a good enough execution
plan for each query, or the necessity to frequently
search for various vertical relations between entities
of the same table. One of the main drawbacks of the
relational database model, which is addressed in this
paper, is in the limited way of binding data and
objects vertically. Vertical relations between entities
and their defining values stored in columns are not
represented (Fig. 1). This lack forces database
management systems (DBMS) to search for vertical
relations in many loops using SQL operations if the
information about such relations is required. The SQL
search operations (SELECT) in relational databases
are typically the most frequent operations, so
inefficiency of them costs a lot of time which is most
annoying and very expensive when managing huge
data collections.
Moreover, the objects can be naturally ordered
only after a single selected attribute in each table. If it
is necessary to have data sorted after several attributes
simultaneously, indices must be used. The indices
typically use B+trees or hash tables to sort and
organize data to make them available in logarithmic
time. The main drawbacks of using indices are the
relevant additional memory cost and the slowdown of
addition, updating, and removal operations. In result,
it is not recommended to add indices for data
attributes which data are not frequently used in search
operations. This paper presents how to overcome
these drawbacks and organize data in such a way that
both horizontal and vertical relations are represented
in the proposed associative neuronal graph data
structure described in the following sections.
3 AVB-TREES
In this section, a new self-ordering and self-balancing
tree structure is proposed to efficiently organize input
elements of the further introduced associative neural
structures and get a very fast access to all stored
features and objects. This structure, called AVB-tree
(Aggregated-Values B-tree), is similar to the well-
known B-tree structure, but it automatically
aggregates and counts all duplicates (Fig. 2). Thus,
the AVB-trees store only unique values of each
attribute defining stored objects. Despite the
aggregation of duplicates, this operation does not
diminish the information about the stored objects.
The neurons representing these unique attribute
values can have many connections to neurons
representing objects. Hence, AVB-trees are usually
much smaller than B-trees or B+trees constructed for
the same data, where duplicates are not aggregated.
The aggregation of the same values also saves the
memory and accelerates the access to the stored
objects, especially to the related objects which are on
the top of interests and usually searched by queries.
The counting of duplicates makes possible to remove
data from this structure correctly.
Figure 2: Construction of an exemplary AVB-tree.
The AVB-trees are constructed in a very similar
way as the B-trees, however, several important chan-

ges must be implemented in it:
The insertion of the next key to the AVB-tree is
processed as follows (Fig. 3):
1. Start from the root and go recursively down along
the edges to the descendants until the leaf is not
achieved after the following rules:
if one of the keys stored in the node equals to
the inserted key, increment the counter of this
key, and finish this operation,
else go to the left child node if the inserted key
is less than the leftmost key in the node,
else go to the right child node if the inserted
key is greater than the rightmost key in the
node,
else go to the middle child node.
2. When the leaf is achieved:
and if the inserted key is equal to one of the
keys in this leaf, increment the counter of this
key, and finish this operation,
else insert the inserted key to the keys stored
in this leaf in the increasing order, initialize its
counter to one, and go to step 3.
3. If the number of all keys stored in this leaf is
greater than two, divide this leaf into two leaves
in the following way:
let the divided leaf represent the leftmost
(least) key together with its counter;
create a new leaf and let it to represent the
rightmost (greatest) key together with its
counter;
and the middle key together with its counter
and the pointer to the new leaf representing the
rightmost key pass to the parent node if it
exists, and go to step 4;
if the parent node does not exist, create it (a
new root of the AVB-tree) and let it represent
this middle key together with its counter, and
create new edges to the divided leaf
representing the leftmost key and to the leaf
pointed by the passed pointer to the new leaf
representing the rightmost key (Fig. 2). Next,
finish this operation.
4. Insert the passed key together with its counter to
the key(s) stored in this node in the increasing
order after the following rules:
if the key comes from the left branch, insert it
on the left side of the key(s);
if the key comes from the right branch, insert
it on the right side of the key(s);
if the key comes from the middle branch,
insert it between the existing keys.
5. Create a new edge to the new leaf or node pointed
by the passed pointer and insert this pointer to the
child list of pointers immediately after the pointer
representing the edge to the divided leaf or node.
6. If the number of all keys stored in this node is
greater than two, divide this node into two nodes
in the following way:
let the existing node represent the leftmost
(least) key together with its counter;
create a new node and let it represent the
rightmost (greatest) key together with its
counter;
the middle key together with its counter and
the pointer to the new node representing the
rightmost key pass to the parent node if it
exists and go back to step 4 (Fig. 2);
if the parent node does not exist, create it (a
new root of the AVB tree) and let it represent
this middle key together with its counter, and
create new edges to the divided node
representing the leftmost key and to the node
pointed by the passed pointer to the new node
representing the rightmost key (Fig. 2). Next,
finish this operation.
The removal of the key from the AVB-tree is
processed very similarly as for B-trees with respect to
the counters of individual keys that must be gradually
decreased to zero for each removed object before
removing a given countered key from this structure.
During this operation, the AVB-tree is self-balanced
in the same way as is proceeded for B-trees (Cormen
et al., 2001).
Figure 3: The intermediate steps of passing the middle key
to the parent node after the division of a leaf or a node.
The search operation in the AVB-tree is
processed as follows:
1. Start from the root and go recursively down along
the edges to the descendants until the searched key
or the leaf is not achieved after the following
rules:
If one of the keys stored in the node equals to
the searched key, return the pointer to this key.
else go to the left child node if the searched
key is less than the leftmost key in this node.
else go to the right child node if the searched
key is greater than the rightmost key in this
node.
else go to the middle child node.

2. If the leaf is achieved and no stored key in it
equals the searched key, return the null pointer.
The search operation for any key in the above-
introduced AVB-trees is very efficient because the
maximum number of search steps is equal to the
logarithm of the number unique keys stored in them,
i.e.
, where
is the number of the
unique keys of the attribute
. Considering that the
attribute values are typically many times repeated in
the database table rows, the number of all entities
in the table is usually much bigger than the number of
unique values
of each attribute
(≫
).
Hence, the logarithm computed for the usually
constant number of unique values
for AVB-trees
is usually smaller than the logarithm of the number of
all entities (rows) used in the search operations
using B-trees or B+trees in relational databases, i.e.
≅
1
. The
computational complexity of the insertion, removal,
and update operations in AVB-trees is the same as for
the search operation. It is typically constant
independently of the size of data tables thanks to the
aggregation property of AVB-trees.
Each key element in the AVB-tree structure
represents a sensor which is most sensitive to the
value represented by the key. The sensors stimulate
connected value neurons which can be connected to
any number of object neurons representing objects.
4 SENSORS AND ASSOCIATIVE
SPIKING NEURONS
The presented associative neural graph structures in
the next section will use special kinds of sensors and
associative spiking neurons (ASN), which enable fast
inference using various combinations of stimuli of the
network elements. These graphs consist mainly of
numerical and symbolic sensors, value neurons, and
object neurons to represent tabular data.
In these associative neural graphs, all non-key
database table attributes
,…,
are transformed
into sensory input fields
,…,
and all attribute
values are represented by sensors
,…,
which
are organized using the introduced AVB-trees.
Sensors aggregate all duplicates of each attribute
separately. Each sensor
represents all duplicates
of the value
, so for large data collections, we
usually achieve high memory savings without any
loss of information. It is possible because each value
represented by the sensor
and subsequently
by a connected value neuron
can be repeatedly
connected to various object neurons that represents
various entities which contains this value. While
attribute values can define entities in database tables,
here sensors together with value neurons representing
values can define object neurons representing entities.
Each sensor
is connected to a value neuron
which is stimulated by this sensor with a constant
stimulus
computed after:
1
0
0
(1)
Value neurons
and
representing numerical
neighbor values
and
of the same attribute
are additionally mutually connected, and their
weights are computed after the formula:
,
,
1
(2)
where
is the range of all already
represented values of the attribute
, and
and
are the minimum and maximum values of this
attribute appropriately. The range is automatically
updated by each sensory input field
when a new
minimum
or maximum
is introduced.
Each numerical attribute
is additionally
equipped with special extreme sensors
and
sensitive for existing and new minima and
maxima. These sensors compute their output values
using the following formulas:
0
1
0
(3)
0
1
0
(4)
The output values of sensors define the strength of
stimulation of the connected extreme neurons
and
which continuously stimulated achieve their
spiking thresholds after the certain periods of time:
1
0
∞
0
(5)

1
0
∞
0
(6)
The extreme sensor
or
stimulate the
extreme neurons
and
with strength equal
to one only if the current minimum or maximum
value is presented on the
. The stimulation
or
is stronger than one only if there is presented a
new minimum or maximum value which causes the
achievement of the spiking threshold of the
or
neuron in time
1 or
1. Such a
strong stimulation of the extreme neuron starts a
conditional plasticity routine that brakes the existing
connection from extreme neuron
or
to the
connected value neuron
, and a new connection to
the new created value neuron representing a new
extreme value is established, and its weight is set to
one. It updates the minimum value
or maximum
value
and range
appropriately. In other
cases, the extreme sensors stimulate the connected
neurons with strength less than one, so the neurons
fire later (5) or (6) according to the distance of the
presented value to the extreme ones.
Each sensor
is connected to its value neuron
which is stimulated and charged by this sensor
as long as the input value
is presented on the
sensory input field
. All value neurons used for
the associative transformation of databases into the
DASNG neuronal systems have their activation
thresholds equal to one (
1). According to this
fact, each stimulated value neuron
solely by its
connected sensor
achieves its spiking threshold
after the time
calculated after:
1
0
∞
(7)
In the next step of the associative transformation,
there are created object neurons
,…,
for each
table
that does not contain foreign keys. These
neurons represent entities, so they are connected to
the adequate value neurons representing attribute
values which define these entities. The weights of the
connections from these value neurons to the object
neurons should reproduce rarity of the values
represented by value neurons in the defining various
object neurons, so they are defined as the reciprocal
of the numbers of all connections that come from the
given value neuron
to all connected object
neurons
representing the entities of the table
:
,
1
:
(8)
These weights can be easily updated when a new
entity is added, or an existing one is removed. These
weights do not even need to be stored in a neural
network structure because they can be locally and
very fast calculated before each neuronal spike.
Next, there are created object neurons
for the
tables
which contain not only attributes but also
some foreign keys for which the object neurons
representing primary keys have been already created
in the previous steps. The connection weights that
come from the object neurons
representing
primary keys to the object neurons
containing
adequate foreign keys are computed as the reciprocal
of the numbers of connections that comes from the
given object neurons
to all connected object
neurons
representing the entities of the table
:
,
1
:
(9)
The weights (8) and (9) allow for the stimulation of
the postsynaptic object neurons with the strength
reflecting the rarity of the values or the entities
represented by the presynaptic neurons. It means that
frequent values and entities have a smaller impact on
the postsynaptic object neurons, while rare values and
entities have a bigger impact and can faster charge
postsynaptic neurons to their spiking thresholds. Each
unique value and entity which primary key is used
only once as a foreign key in another table
(representing the relation 1:1) have the biggest
possible impact because its connection weight is
equal to one, and such a connection can solely charge
the postsynaptic object neuron to its spiking
threshold. The interpretation is quite intuitive because
such features or entities exclusively identify objects
that should also be automatically recognized in any
natural or artificial cognitive neural system.
The spiking threshold of each object neuron must
be achieved ultimately when all defining inputs start
to charge it. However, it can be achieved earlier when
any sub-combination of enough rare inputs happens.
All defining inputs of each object neuron can achieve
the following maximum strength of stimulation:

,
,
(10)
The object neuron’s spiking threshold is defined as:
1
0
0
(11)
The associative spiking neurons used for modeling of
the value and objects neurons incorporate the concept
of time and implement charging, discharging,
relaxation, and absolute and relative refraction
processes (Fig. 4) (Kalat, 2012). They can also be in
resting state when not stimulated for a longer time.
All internal neuronal processes are modeled using
linear functions that can be easily added, subtracted,
or combined for charging, discharging, or
overlapping stimuli (Fig. 4). All external stimuli
influence on internal neuronal processes which
change states of neurons (Fig. 4-5).
Figure 4: Overlapping charging and discharging external
stimuli influencing the state changes and internal neuronal
processes of associative spiking neurons.
Figure 5: The illustration of the operation that combines the
new stimulus S
3
with the processes P
0
and P
1
in the IPQ
created for previous stimuli S
1
and S
2
where d
i
determines
the duration of the stimulus S
i
, and s
i
is its strength.
The ASNs work parallel and combine the external
input stimuli that can appear at any time. To simulate
them on a sequential CPU, they use an internal
process queue (IPQ) to manage and switch internal
processes P
k
and update neuronal states at the right
time (Fig. 5), and a global event queue (GEQ) to order
and execute these internal processes of all neurons at
an appropriate moment and sequence. The GEQ
watches out the time when processes finish to start
updating neurons at the right time. The expected
moments of achievement of spiking thresholds (11)
of individual neurons are always calculated in
advance and watched out. Different than in the
artificial neural networks of the second generation
(Haykin, 2009), which answers are produced by
various values of the output neurons, ASN answers
are produced based on their frequencies of spikes and
the elapsed time from a given external stimulation
moment to the moments when these neurons start
spiking. Hence, the most frequently spiking neurons
represent the answer that can be read from connected
neurons representing the associated objects and
values.
5 DASNG - DEEP ASSOCIATIVE
SEMANTIC NEURAL GRAPHS
Brains consist of many complex and very deep graph
structures of connected neurons of various kinds
(Longstaff, 2011), which use thousands of
connections to represent our knowledge and make our
intelligence work smartly, quickly, and context-
sensitively (Kalat, 2012).
In this section, new deep associative semantic
neural graphs (DASNG) will be introduced to
demonstrate how relational databases can be
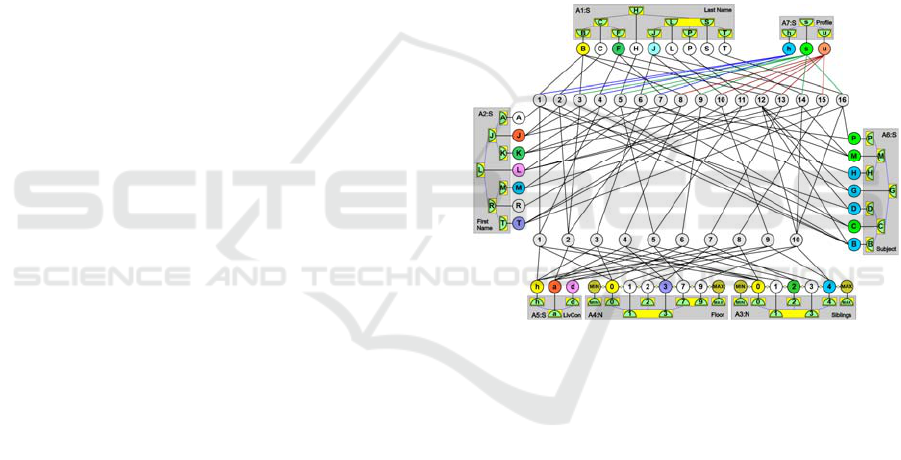
transformed into these graphs. Figure 6 illustrates a
neuronal DASNG structure that represents all data
and their relations from the sample database
presented in Fig. 1. This neuronal structure does not
reduce any information so that it can always be
transformed back into the original database. The
DASNG can be constructed for any database storing
related records. In any formal database or cognitive
model, we can distinguish individual data which are
related in different ways. Some groups of related data
model objects (represented by e.g. entities) that can
also be related between themselves in various ways
(e.g. using primary and foreign keys), which describe
semantic relations between them. Such relations can
reproduce similarity, proximity, inclusion, sequence,
actions etc. Such relations can group objects and
define their classes based on similar features. Such
kinds of tasks should be solved in computational
intelligence and knowledge engineering because our
intelligence is based on the ability to discover various
relations and find interesting groups among other
things. To find such relations, the algorithms use
various conditions, limitations, search routines, and
operations which compare or group objects to satisfy
defined requirements or achieve given goals.
The introduced DASNG model can naturally
reproduce data, entities, and all relations that are
represented by the primary-foreign key relational
model. Classes of objects can be defined based on the
similarity between objects which some subsets of
attribute values are the same or close. In the DASNG
model, all the same values are aggregated and all
similar attribute values are directly or indirectly
connected. Consequently, all related objects are fast
accessible thanks to these aggregations and
connections between neurons representing similar
values. The similarity between objects can be
defined as any subset of close attribute values
(features) that relates the group of objects. Thus, all
possible clusters coming from similarity are naturally
included in the DASNG model. In consequence, any
class of objects can be quickly found in the DASNG
network because the stimulation of a subgroup of
sensors representing selected features will gradually
induce activation of connected neurons representing
objects (entities) which the most meet the given
limitations defined by these features as will be
described in the following section.
The DASNG model can also represent other
relations that usually come from object vicinity in
time or space. Vicinity can be defined as an attribute
of time or space where the two compared objects
occur in the close time interval, or their coordinates
are not too far away. Therefore, the vicinity is a
distance in space or time in which objects can interact
with each other or can be perceived as being
neighboring or subsequent by somebody. Close
objects in space or time cannot be similar at all, so we
do not include vicinity as an attribute that groups
objects into classes, but we talk about object
neighborhood or succession. Thus, vicinity can relate
objects independently of their similarity or
differences. Therefore, we can define any sequence of
objects or actions, and elaborate various procedures
and algorithms that come from our intelligence and
knowledge about objects, their features, and
usefulness. Moreover, not only directly subsequent
objects but also more distant ones in any sequence or
neighborhood can be connected and these
connections appropriately weighted to emphasize the
right contexts of their occurrences which exclude
ambiguity. This feature is very important in view of
storing various complex sequences, procedures, or
algorithms that can be applied only in some specific
situations, contexts, constraints, or circumstances, in
which our brains make us undertake a specific
strategy or action selected from the portfolio of the
possible ones that are available to us.
In the DASNG model, objects represented by
neurons are connected to other neurons that represent
other objects or specific features. Each connection is
appropriately weighted to reproduce the strength of
the similarity, vicinity, or defining relations between
them. In comparison to the non-weighted primary-
foreign key binding mechanism used in databases, we
achieve more precise information about the relation
strengths of related objects when representing them in
the DASNG model, so we can conclude about the
represented relations easier and more accurately.
Summarizing, the DASNG model enriches the
horizontal relations used in the databases with
additional vertical relations between objects thanks to
aggregations of the same values and connections
between neighbor values. The use of reactive sensors
and neurons instead of passive database records
allows for fast automatic exploration of information
according to the context given by the stimulation of
any selected subset of sensors and/or neurons.
Figure 6: A deep associative semantic neural graph
(DASNG) constructed for the database presented in Fig. 1
without any loss of information, where first letters represent
appropriate words from the database tables.
In the relational database model, we can
distinguish one-to-one, one-to-many, and many-to-
many relationships between related entities. The one-
to-many relationship is represented by a primary key
in one entity (e.g. in table E in Fig. 1) which is related
to many foreign keys of other entities (e.g. in table A
in Fig. 1). The many-to-many relationship defines
multiple relations between various objects from two
tables, so we typically use an additional link table
which binds together primary keys of these tables
(e.g. the table D relates entities of the tables A and C
in Fig. 1). The link tables are unnecessary in the
DASNG networks because we can directly represent
many-to-many relations using direct connections
between objects represented by neurons (Fig. 6). This
is also true for one-to-many relations where objects
are directly connected in the same way. Hence, we do

not need to distinguish between various cardinalities
of relations as in relational databases.
Each attribute is represented by a separate sensory
input field
which consists of sensors representing
aggregated attribute values, i.e. various features of
objects. All sensors of each field
are organized
using a separate AVB-tree (Fig. 2). Such a structure
makes all values quickly available, usually in
constant time, however, the sub-linearithmic access
time may also happen for rarely frequent features.
Moreover, numerical value neurons connect in order,
so there is no need to sort data later (Fig. 2).
In the relational databases, modeled objects are
stored in separate or connected table entities
(records), while in the DASNG model, each object
can be represented by a single neuron connected to
other neurons defining features and included objects
in it. If more than one database record contains the
same set of attribute values and foreign keys, these
records can be aggregated and represented by the
same object neuron that counts the number of
aggregated records. This aggregation does not
eliminate diversity because the aggregating neuron
can be further connected to various other neurons
representing differing features for various aggregated
objects. However, during such an aggregation, we
lose the unique identity of the aggregated objects
represented by the primary keys that diversify such
records, e.g. two people with the same first and last
name. When the diversity of records (objects) is
necessary, the primary key must be treated as an
attribute feature that cannot be reduced in the
aggregation process. In result, such objects will not
be aggregated and do not lose their identity and
separateness fixed by their primary keys. On the other
hand, the aggregation is many times beneficial, and
we do not need to store the separate identities of all
objects, e.g. it is usually unimportant to store the
information about which exact entities of the same
products have been sold by which the seller. It is
possible to automatically distinguish between tables
that represent objects that cannot lose their identity
and other tables where we can do aggregations. The
primary keys that are directly used by SQL queries to
search for records are non-reducible and should be
treated as other attributes that store important data.
On the other hand, when the primary keys are used
only to join records from the related tables, such keys
are reducible and can be converted to connections
between neurons. Hence, we need to analyze a
possibly large subset of real SQL queries that have
been processed on the given database in the past to
automatically and correctly distinguish between
reducible and non-reducible primary keys. In case,
when we get a collection of empirical data records,
where some records are identical (e.g. a few samples
in the Iris data set from ML Repository), they can also
be aggregated and represented by the same neurons.
Concluding, aggregations are very important in view
of generalization, knowledge formation, and drawing
conclusions about objects, so we should not always
trend to store identities of all objects if not necessary.
Another benefit of direct connections between
neurons representing objects is that we do not need to
browse primary and foreign keys to join records from
various tables and waste time. In the DASNG
network, we simply go along the connections to
associated information in constant time.
Figure 7: Various kinds of sensory stimuli and interactions
with sensors in the sensory input fields (SIFs).
During the construction process, there is created a
sensory input field
for each attribute
(the grey
fields in Figs. 6, 8-10). The sensory input fields (SIFs)
can be of various types alike the senses in a human
body. These fields constitute input interfaces for the
remaining part of the neural structure (Fig. 6). The
SIFs contain sensors that are sensitive for some
values, their ranges, or subsets (Fig. 7). The sensors
can be differently sensitive to various values
presented to their SIF. They are no sensitive to the
values presented to the other SIFs. The way the
sensors work can be described by suitable
mathematical functions introduced in section 4.
The structure presented in Fig. 6 represents not
only horizontal relations between objects but also
vertical relations between data of each attribute.
These data are ordered, and all duplicated values of
each attribute are removed. Despite this reduction,
there is no loss of information because the duplicated
values have been replaced by connections to various
neurons representing various objects in Fig. 1.
Moreover, the aggregation of duplicates and their
joined representation allow for very fast access to any
data. Databases use B-trees or B+trees to achieve a
logarithmic time of search operations while DASNGs
use AVB-trees which for a constant set of stored
unique attribute values usually work in constant time.
Hence, we also do not waste so much time during
insertion or delete operations like when using indexes
in databases. We do not need to sort data or add
indices to this structure because data are always
automatically sorted simultaneously for all attributes.
Furthermore, the transformation of the table structure
to the presented graph structure automatically
extracts additional relations of their order, similarity,
minima, maxima, ranges from the data, which are
available on demand in constant time. Thanks to the
aggregation and joined representation of duplicates
we have direct access to all objects (records) that have
some given value which we want to explore. We also
have indirect but very fast access to all similar objects
which are defined by similar attribute values. Thus,
we can also define various clusters of similar objects
or recognize their defined classes represented by
neurons very fast for any criteria. The stimulation of
any subset of features, their ranges, or any subset of
objects induces gradual activations of the associated
objects neurons, which can be clustered on this basis.
The object class can be retrieved based on the first or
most frequently activated class neuron. Every such
stimulation of DASNG takes constant time, so it is
fast in comparison to many other methods.
The use of ASNs in the DASNG network makes
possible to develop a reactive graph structure that can
execute some operations on the represented data fully
automatically. Such operations let us draw useful
conclusions about objects and their features
represented in this neural network.
6 NEURONAL INFERENCE
After the transformation of the database tables into
the DASNG neural network presented in Fig. 6, this
network can be used for inference about represented
objects to find similar objects quickly, various classes
of objects, identify shared features, filter or sort
objects after various criteria, attributes, or draw some
useful conclusions about selected groups of objects.
Figures 8, 9, and 10 present exemplary inference
processes that can be performed in this DASNG
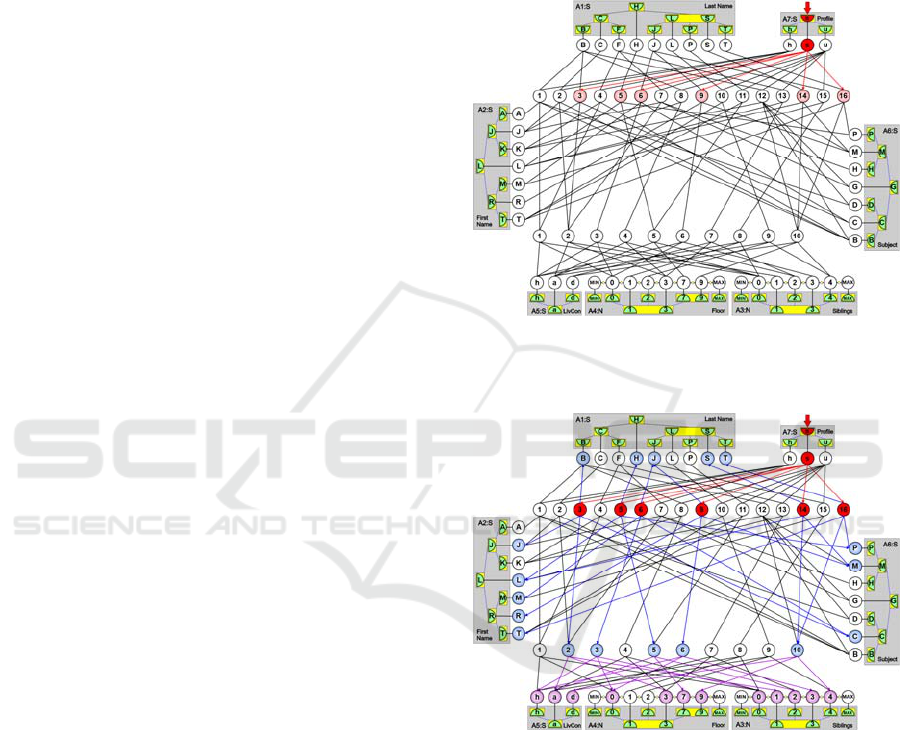
network. To filter out objects including some features
or other objects, it is enough to stimulate these
features or objects via sensors or neurons representing
them in the DASNG network and wait for spikes of
neurons representing answers (Fig. 8). In such a
network, it works like associative reminding in a
human brain when recalled information together with
the previous calling context create a new context for
recalling of the next memories associated with the
information represented by the recently activated
neurons. Therefore, the further stimulation of the
initial context (here: the sensor representing
“science”) induce the gradual activations of the next
connected neurons representing associated
information about previously recalled objects (Fig.
9). Thus, we can automatically find out what are the
names of pupils who like science, what subjects they
like at most, and what are their living conditions. We
can conclude about them as far as the created
structure contains such information and as long as the
sensor “science” is stimulated providing subsequent
spikes of the directly or indirectly connected neurons.
If the network works parallel, then we always get all
this information in constant time.
Figure 8: Direct connections from the stimulated value
neuron representing “science” let us quickly filter out pupils
who are interested in science.
Figure 9: The next stimulation lets us find out what subjects
do these pupils like and what are their living conditions.
The inference processes in the DASNG neural
network are based on measuring the time when the
ASN neurons representing the desirable answer(s)
start spiking and on counting the numbers of their
spikes (Fig. 10). Neurons representing the answer
spike most frequently and typically start to spike at
first. The less frequently or later spiking neurons
usually represent other weaker alternatives, i.e.
objects that only partially satisfy the input conditions
or the associated features of the objects representing
the answer. On this basis, we can conclude that pupils
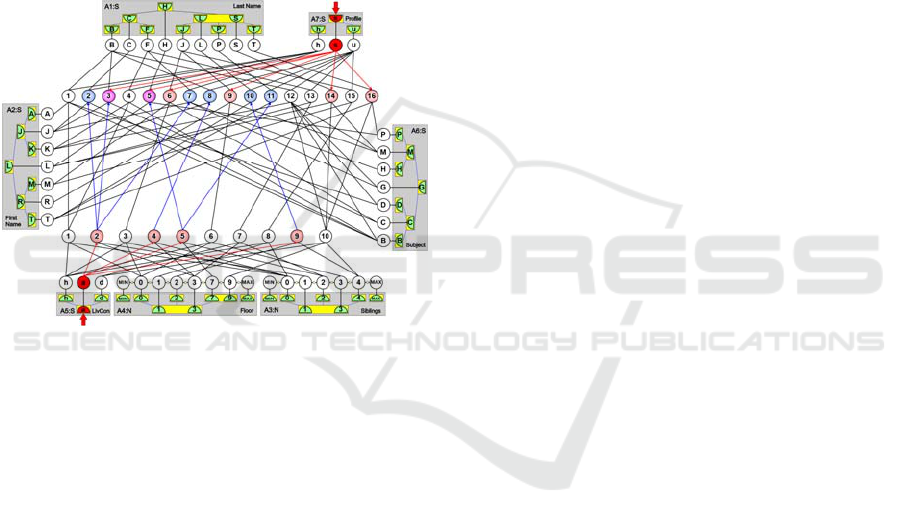
represented by the most frequently spiking neurons 3
(Jack Brown) and 5 (Luke Hanks) are interested in
science and live in the apartments. The other pupil
neurons 2, 6, 7, 8, 9, 10, 11, 14, and 16, which spike
less frequently, represent the pupils who like science
or live in apartments. The pupil neurons 1, 4, 12, 13,
and 15, which do not spike at all, represent pupils with
the other interests and those, who do not live in
apartments. The chronology of activations of
individual neurons automatically sorts the objects or
features represented by these neurons. These kinds of
neuronal structures do not only represent data
transformed from the database but also have the built-
in inference routines available thanks to associations
represented by the connections between ASNs.
Figure 10: Neurons representing the conjunction of the
stimulated features spike the most frequently and usually
also at first (the violet pupil neurons 3 and 5), while neurons
representing the other alternatives spike less frequently and
usually start spiking later (the red and blue pupil neurons).
Each database table which represents only a single
attribute is transformed into a single SIF, sensors, and
value neurons, while database tables containing more
attributes and foreign keys are represented by
separate layers of object neurons. Hence, such an
associative graph can have many appropriately
connected layers dependently on the size and
complexity of the transformed database.
The construction and inference processes in the
DASNG networks are parallel in their nature, so there
can be used many processors and many cores of
processors to accelerate such computations and make
them even faster in comparison to sequential methods
often used in many relational DBMS systems.
Today, the main limitation of DASNG networks
is in the capacity of RAM memory installed on the
server because the efficiency of operations proceeded
on these kinds of networks can be significantly
reduced by the disc operations. Therefore, it is
recommended to keep the whole DASNG network in
the RAM memory during its work like the biological
neurons in brains which are still ready to use in a
human brain (Kalat, 2012). Despite this limitation,
thanks to the possible aggregations of duplicates,
even large databases can be successfully transformed
into the DASNG networks, fit into the RAM, and can
benefit from the very fast operations on them and
automatic inference about represented objects.
7 CONCLUSIONS
This paper presented new complex deep associative
semantic neuronal graph structures consisting of the
special kind of spiking neurons which let us associate
data and objects in various ways and run fast
inference in constant time. It was also investigated
that such networks produce answers based on speed
and frequency of spikes of neurons which represent
the most associated values or objects in the DASNG
network. This paper also provides the information
about the possible interpretation of how biological
and spiking neurons represent information using
frequencies of spikes and the time of being activated
that had elapsed from the input stimulations that had
a real influence on these spikes (Kalat, 2012).
It was presented how this network can represent
horizontal and vertical relations between data and
objects, expanding possibilities of the relational
model used in relational databases (Hellerstein et al.,
2007). It was also explained why the most frequent
operations of this model are typically processed in
constant time thanks to its automatic ordering
mechanism which works for all attributes
simultaneously. The presented AVB-trees manage
attribute data and allow for very fast access to them
in comparison to other popular algorithms used in
relational databases due to the aggregations of
duplicates and connections of successive values. The
presented associative spiking neurons can be used to
create complex neuronal structures which represent
related objects defined by attributes and other objects.
The DASNG abilities were demonstrated on
several examples which showed how these networks
could be used for inference and searching for related
information according to some initial contexts,
including filtering, conjunction, and alternative. Due
to the aggregation properties of the DASNG
networks, they could be used for mining and finding
frequent itemsets for Big Data (Apiletti et al., 2017)
and be applied to overcome new challenges (Jin et al.,

2015) thanks to their built-in self-organizing neural
network mechanisms (Parisia, 2015).
The future works include further studies on deep
architectures consisting of the associative spiking
neurons and possible ways of complex inference
using various kinds of associations. The presented
model will be developed to represent and use
sequential patterns, ranges, clusters, and classes to
allow for deeper inference, mining, and appropriate
generalization during classification. The future
studies will strive to create a self-developing graph
structure to store and reinforce the gained conclusions
and build neural knowledge-based cognitive systems.
However, this paper is not a complete solution for
solving all difficulties and inefficiencies of databases,
but it has shown how neurons and DASNG networks
could help to solve some of the problems mentioned
above, and make the computations on big data more
efficient in the future. The associative spiking
neurons used in the DASNG networks as well as
biological neurons do not calculate output values
directly but using time-based approaches and
frequencies of spikes. They represent and associate
various data combinations in many ways to recall
these associations in the future when the similar
ignition contexts will happen again. They can also
generalize about associated data, especially when
new input contexts are used. It is planned to construct
intelligent associative knowledge-based cognitive
systems on their basis in the future. Finally, deep
associative spiking neural models can be an
interesting alternative to databases not only to store
data but also to supply us with conclusions and enable
very fast access to various pieces of information that
can be drawn from the collected and associated data.
The presented neural networks can support the future
big data mining and knowledge exploration systems.
ACKNOWLEDGEMENTS
This work was supported by AGH 11.11.120.612 and
a grant from the National Science Centre DEC-
2016/21/B/ST7/02220.
REFERENCES
Apiletti, D., Baralis, E., Cerquitelli, T., Garza, P.,
Pulvirenti, F., Venturini, L., 2017. Frequent Itemsets
Mining for Big Data: A Comparative Analysis, Big
Data Research, Elsevier, https://doi.org/10.1016/
j.bdr.2017.06.006.
Agrawal, R., Imielinski, T., Swami, A., 1993. Mining
association rules between sets of items in large
databases, ACM SIGMOND Conf. Management of
Data, 207-216.
Bagui, S., Earp, R., 2011. Database Design Using Entity-
Relationship Diagrams, 2nd ed., CRC Press.
Chen, P., 2002. Entity-Relationship Modeling: Historical
Events, Future Trends, and Lessons Learned. Software
pioneers. Springer-Verlag, pp. 296-310.
Cormen, T., Leiserson, Ch., Rivest, R., Stein, C., 2001.
Introduction to Algorithms, 2nd ed., MIT Press and
McGraw-Hill, 434-454.
Duch, W., Dobosz, K., 2011. Visualization for
Understanding of Neurodynamical Systems, Cognitive
Neurodynamics 5(2), 145-160.
Fayyad, U. P.-S., 1996. From Data Mining to Knowledge
Discovery in Databases. Advances in Knowledge
Discovery and Data Mining. Vol. 17, MIT Press, 37-54.
Gerstner, W., Kistler, W., 2002. Spiking Neuron Models:
Single Neurons, Populations, Plasticity. New York NY:
Cambridge University Press.
Han, J., Kamber, M., 2000. Data Mining: Concepts and
Techniques, Morgan Kaufmann.
Haykin, S.O., 2009. Neural Networks and Learning
Machines, 3 ed., Upper Saddle River, NJ: Prentice Hall.
Hellerstein, J.M., Stonebraker, M., Hamilton, J., 2007.
Architecture of a Database System, Foundations and
Trends in Databases, vol. 1, no. 2, 141-259.
Horzyk, A., 2014. How Does Generalization and Creativity
Come into Being in Neural Associative Systems and
How Does It Form Human-Like Knowledge?,
Neurocomputing, vol. 144, 238-257, DOI:
10.1016/j.neucom.2014.04.046.
Horzyk, A., Starzyk, J. A., and Basawaraj, 2016. Emergent
creativity in declarative memories, IEEE Xplore, In:
2016 IEEE SSCI, Curran Associates, Inc. 57
Morehouse Lane Red Hook, NY 12571 USA, 2016, 1-
8, DOI: 10.1109/SSCI.2016.7850029.
Horzyk, A., 2017. “Neurons Can Sort Data Efficiently”,
Proc. of ICAISC 2017, Springer Verlag, LNAI 9119,
64-74, DOI: 10.1007/978-3-319-59063-9_6.
Jin, X., Wah, B.W., Cheng, X., Wang, Y., 2015.
Significance and Challenges of Big Data Research, Big
Data Research, Elsevier, vol. 2, issue 2, 59-64.
Kalat, J.W., 2012. Biological Psychology, Belmont, CA:
Wadsworth Publishing.
Linoff, G.S., Berry, M.A., 2011. Data Mining Techniques:
For Marketing, Sales, and Customer Relationship
Management, 3rd ed.
Longstaff, A., 2011. BIOS Instant Notes in Neuroscience,
New York, NY: Garland Science.
Nuxoll, A., Laird, J. E., 2004. A Cognitive Model of
Episodic Memory Integrated With a General Cognitive
Architecture, Int. Conf. on Cognitive Model., 220-225.
Pääkkönen, P., Pakkala, D., 2015. Reference Architecture
and Classification of Technologies, Products and
Services for Big Data Systems, Big Data Research,
Elsevier, vol. 2, issue 4, 166-186.
Parisia, G.I., Tanib, J., Webera, C., Wermter, S., 2017.
Emergence of multimodal action representations from

neural network self-organization, Cognitive Systems
Research, vol. 43, 208-221.
Piatetsky-Shapiro, G., Frawley, W.J., 1991. Knowledge
Discovery in Databases, AAAI, MIT Press.
Sowa, J.F., 1991. Principles of Semantic Networks:
Explorations in the Representation of Knowledge, San
Mateo, CA: Morgan Kaufmann.
Starzyk, J.A., He, H., 2007. Anticipation-based temporal
sequences learning in hierarchical structure, IEEE
Trans. on Neural Networks, vol. 18, no. 2, 344-358.
Starzyk, J.A., Graham, J., 2015. MLECOG - Motivated
Learning Embodied Cognitive Architecture, IEEE
Systems Journal, vol. PP , no. 99, 1-12.
