Analysis of a Batch Strategy for a Master-Worker Adaptive Selection

Algorithm Framework

Christopher Jankee

, S

ebastien Verel

, Bilel Derbel

and Cyril Fonlupt

Universit

e du Littoral C

ote d’Opale, LISIC, France

Universit

e Lille 1, LIFL – CNRS – INRIA Lille, France

Keywords:

Master-Worker Architecture, Adaptive Selection Strategy.

Abstract:

We look into the design of a parallel adaptive algorithm embedded in a master-slave scheme. The adaptive

algorithm under study selects online and in parallel for each slave-node one algorithm from a portfolio. In-

deed, many open questions still arise when designing an online distributed strategy that attributes optimally

algorithms to distribute resources. We suggest to analyze the relevance of existing sequential adaptive strate-

gies related to multi-armed bandits to the master-slave distributed framework. In particular, the comprehensive

experimental study focuses on the gain of computing power, the adaptive ability of selection strategies, and the

communication cost of the parallel system. In fact, we propose an adaptive batch mode in which a sequence

of algorithms is submitted to each slave computing node to face a possibly high communication cost.

1 INTRODUCTION

In this work, we target black-box optimization prob-

lems for which no information can be known before-

hand. There is no explicit hypothesis on these prob-

lems such as an explicit analytic expression of the

ﬁtness function, regularity, gradient properties, etc.

This wide range of problems include optimization

scenarios that require extensive numerical simulation.

For example, some engineering design problems use a

simulator of the physic to optimize criteria of interest

for the designed system (Muniglia et al., 2016) (Ar-

mas et al., 2016). From a practical, as well as from a

theoretical, point of view, in a black-box optimization

scenario, the choice of the relevant algorithmic com-

ponents according to the problem to solve is an open

issue, and an active domain of research (Baudi

s and

ık, 2014). Moreover, when a large scale parallel

compute environment is available, an optimization al-

gorithm implies additional design challenges to make

an effective cooperation between parallel resources.

Thus, the paper investigates the online selection of al-

gorithmic components in a master-worker framework

in order to take full beneﬁts from the compute power

in a black-box optimization scenario.

From the early works of Grefenstette (Grefen-

stette, 1986) to recent works (Kotthoff, 0 30) and

many other researchers (Kunanusont et al., 2017),

the parameters setting or the algorithm selection, is

a recurrent topic in evolutionary computation due to

its crucial importance in practice. In this work, we

are interested in adaptive algorithm selection; which

consists in the online choice, among a number of

alternatives stored beforehand in a portfolio, of an

appropriate algorithm to execute next according to

the current state of the search. Unlike the off-line

tuning of parameters (Eiben et al., 2007) which se-

lects an effective set of parameters (that is algorithmic

components) before the execution of the optimization

method, the online setting, also called control con-

tinuously selects an algorithm all along the optimiza-

tion process using the feedback from the optimiza-

tion algorithm being executed (Fialho et al., 2010;

Baudi

s and Po

ık, 2014). Hence, online algorithm se-

lection can be viewed as an adaptive optimization al-

gorithm which follows the multi-armed bandit frame-

work where the arms are the algorithms of the portfo-

lio (DaCosta et al., 2008). The adaptive selection is

then performed as follows. A reward is computed ac-

cording to the performance observed when previously

executing an algorithm.

As previously noticed, numerous black-box real

world optimization problems, such as in engineer-

ing design, are computationally expensive, e.g., one

ﬁtness function evaluation can take several min-

utes (Muniglia et al., 2016). Thus, such problems

can take beneﬁt of the new compute facilities of-

fered by large scale parallel platforms (clouds, pay-

as-you-go, etc.). At the same time, it opens new re-

search perspectives to develop original and more ro-

bust optimization methods. Several models of paral-

lel evolutionary algorithms have been investigated for

Jankee C., Verel S., Derbel B. and Fonlupt C.

Analysis of a Batch Strategy for a Master-Worker Adaptive Selection Algorithm Framework.

DOI: 10.5220/0006504203130320

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 313-320

ISBN: 978-989-758-274-5

parallel compute platform: from ﬁne-grained (cellu-

lar model) to coarse grain (island) model (Tomassini,

2005). The centralized Master-Worker (M/W) archi-

tecture is the general research context of this work.

Each worker computes a batch of actions scheduled

by the master (i.e. mainly the evaluation of candi-

dates solutions), and the master collects the local re-

sults from the workers, again mainly the ﬁtness value

of the best local solution, and coordinates the next ac-

tions to send to each worker. It is worth-noticing that

this framework is often adopted in practice, not only

due to the simplicity of deploying it over a real test

bed, but also due to its high accuracy when dealing

with computationally expensive optimization prob-

lems (Dasgupta and Michalewicz, 2013; Harada and

Takadama, 2017).

In this context, we argue that an adaptive selection

method of algorithms in a master-worker approach re-

quires speciﬁc mechanisms in order to achieve opti-

mal performances. In a sequential approach, the re-

ward of each possible algorithm in the portfolio is up-

dated according to the performance of the algorithm

executed previously in the last iteration by one single

process. In an M/W approach, the reward can be up-

dated using the set of performances observed by the

set of distributed workers. Nevertheless, two careful

design components of the reward method has to be

taken into account. First, if a batch of algorithms is

executed by each worker node at each round, an ac-

curate function to compute the local reward has to be

deﬁned. In addition, a global reward function is also

required to aggregate the set of local rewards and to

assign a reward of each algorithm from the portfo-

lio. Besides, we can differentiate two types of parallel

adaptive strategy: when adopting a homogenous strat-

egy, all workers will execute the same algorithm at

each round, or when adopting a heterogeneous strat-

egy, the workers can execute different algorithms even

in the case where a batch of algorithms is executed at

each round by each worker. Several existing machine

learning schemes have been used and studied previ-

ously in the sequential setting (Fialho et al., 2010),

as well as in the decentralized island model (Derbel

and Verel, 2011; Jankee et al., 2015). However, to

our best knowledge, the analysis of online selection

strategies have not been investigated within an M/W

framework. Indeed, the M/W framework is more suit-

able to understand the tradeoff between an optimal

global selection at the parallel system level and an op-

timal local selection of the most accurate algorithms

at the worker level. In an M/W framework, the master

node has a global view of the system which enables to

deﬁne a global reward function and a global selection

approach. This allows us to focus on the important

selection strategy at the master level; and to propose

new dedicated selection mechanisms. For instance,

we deeply analyze a batch strategy which submits a

sequence of actions to each worker (e.g. several ﬁt-

ness evaluation obtained by a set of algorithms). Such

framework provides a way to deal with the tradeoff

between communication and computation costs (ﬁt-

ness evaluation) as well as the adaptive efﬁciency of

such strategy.

To summarize, we introduce a M/W algorithm se-

lection framework contributing to the solving of the

following questions:

(i) How to extend a selection strategy in a batch-

oriented distributed framework ?

(ii) What is the impact of a batch framework on the

performance of selection strategies ?

(iii) How does the batch framework affects the cost of

communication?

Our M/W framework is evaluated using a tun-

able benchmark family and a simulation-based ex-

perimental procedure in order to abstract away the

technical implementation issues, and instead provide

a fundamental and comprehensive analysis of the ex-

pected empirical parallel performance of the underly-

ing adaptive algorithm selection.

The rest of the paper is organized as follows. In

Section 2, we review some related works.

In Section 3, the design components of our M/W

adaptive framework is described in detail. In Sec-

tion 4, we report our main experimental ﬁndings. In

Section 5, we conclude the paper and discuss future

research directions.

2 RELATED WORKS

In the following, we provide an overview of related

studies on the algorithm selection problem in the se-

quential and distributed setting, as well as a brief sum-

mary of exiting optimization benchmark problems de-

signed at the aim of evaluating their dynamics and be-

havior.

2.1 Sequential Adaptive Algorithm

Selection

In the sequential setting, a number of reinforcement

machine learning schemes have been proposed for the

online and adaptive selection of algorithms from a

given portfolio. Back to the early works of Grefen-

stette (Grefenstette, 1986), one standard technique

consists in predicting the performance of a set of oper-

ators using a simple linear regression and the current

average ﬁtness of the population, which then allows

to select the best operator to be chosen according to

the prediction given by the regression. However, re-

cent works embed this selection problem into a multi-

armed bandit framework dealing more explicitly with

the tradeoff between the exploitation of the best so

far identiﬁed algorithm, and the exploration of the re-

maining potentially underestimated algorithms.

A simple strategy is the so-called ε-greedy strat-

egy which consists in selecting the algorithm with the

best estimated performance at the rate (1 − ε), and a

random one at rate ε.

The Upper Conﬁdence Bound (UCB) strat-

egy (Auer et al., 2002) is a state-of-the-art framework

in machine-learning which consists in estimating the

upper conﬁdence bound of the expected reward of

each arm by ˆµ

+C · e

; where ˆµ

is the estimated (em-

pirical) mean reward, and e

is the standard error of

the prediction. It then selects the algorithms with the

higher bound (for maximization problem). The pa-

rameter C allows to tune the exploitation/exploration

trade-off. In the context of algorithm selection (Fialho

et al., 2010) where the arms could be neither indepen-

dent nor stationary, the estimation of the expected re-

ward is reﬁned using a sliding window where only the

W previous performance observations are considered.

The Adaptive Pursuit (AP) strategy (Thierens,

2005) is another technique using an exponential re-

cency weighted average to estimate the expected re-

ward with a parameter α to tune the adaptation rate

of the estimation. This is used to deﬁne the probabil-

ity p

of selecting every algorithm from the portfolio.

At each iteration, these probability values are updated

according to a learning rate β, which basically allows

to increase the selection probability for the best algo-

rithm, and to decrease it for the other ones.

One key aspect to design a successful adaptive se-

lection strategy is the estimation of the quality of an

algorithm based on the observed rewards. Some au-

thors showed that the maximum reward over a sliding

window improves the performance compared to the

means on some combinatorial problems (Fialho et al.,

2010; Candan et al., 2013); but no fundamental analy-

sis of this result was given. In genetic algorithms, the

reward can be computed not only based on the quality

but also on the diversity of the population (Maturana

et al., 2009). In the context of parallel adaptive al-

gorithm selection, the estimation of quality of each

available algorithm is also a difﬁcult question since

not only one but many algorithms instances could be

executed in each iteration.

2.2 Parallel Adaptive Algorithm

Selection

The Master-Worker (M/W) architecture has been ex-

tensively studied in evolutionary computation (e.g.,

see (Dubreuil et al., 2006)). It is in fact simple to im-

plement, and does not require sophisticated parallel

operations.

Two communication modes are usually consid-

ered. In the synchronous mode, the distributed enti-

ties operate in rounds, where in each round the master

communicates actions to the workers and then waits

until receiving a response from every worker before

starting a new round, and so on. In the asynchronous

mode, the master does not need to wait for all work-

ers; but instead can initiate a new communication with

a worker, typically when that worker has terminated

executing the previous action and is idle. When the

evaluation time of the ﬁtness function can vary sub-

stantially during the course of execution, the asyn-

chronous mode is generally preferred (Yagoubi and

Schoenauer, 2012) since it can substantially improve

parallel efﬁciency. However, the synchronous mode

can allow to have a more global view of the dis-

tributed system which can be crucially important to

better coordinate the workers (Wessing et al., 2016).

Adaptive selection approaches designed to oper-

ate in a distributed setting are not new. The island

model, which is considered as inherently distributed,

has been investigated in the past. The ﬁrst studies con-

ducted in this context demonstrate that the dynamics

of an optimal parallel selection method can be funda-

mentally different at the ﬁrst sight from its sequential

counterpart. For instance, because of the stochasticity

of evolutionary operators, it has been noted that a set

of heterogeneous nodes can outperform a set of nodes

executing in parallel the same sequence of algorithms

computed according to a sequential algorithm selec-

tion oracle (Derbel and Verel, 2011). To cite a few,

in (Tanabe and Fukunaga, 2013; Garc

ıa-Valdez et al.,

2014), it is also well known that a random setting

the parameters at each iteration in a heterogeneous

manner can outperform static homogeneous parame-

ter settings. Nonetheless, embedding a reinforcement

machine learning technique instead of random selec-

tion can improve the performance of the adaptive dis-

tributed system.

In (Derbel and Verel, 2011; Jankee et al., 2015),

a distributed adaptive metaheuristic selection frame-

work is proposed which can be viewed as a natural

extension of the island model that was speciﬁcally de-

signed to ﬁt the distributed nature of the target com-

pute platforms.

The adaptive selection is performed locally by

selecting the best rewarded metaheuristic from the

neighboring nodes (islands) or a random one with

small probability like in ε-greedy strategy. Notice,

however, that we are not aware of any in-depth anal-

ysis addressing the design principles underlying an

M/W adaptive algorithm selection approach. In this

work, we propose and empirically analyze the behav-

ior of such an approach in an attempt to ﬁll the gap

between the existing sequential algorithm selection

methods and the possibility to deploy them in a paral-

lel compute environment using a simple, yet effective,

parallel scheme like the M/W one.

2.3 Benchmarks: The Fitness Cloud

Model

The understanding of the dynamics of a selection

strategy according to the problem at hand is a difﬁcult

issue. A number of artiﬁcial combinatorial problems

have been designed and used in the literature. We

can distinguish between two main benchmark classes.

In the ﬁrst one, a well-known combinatorial problem

in evolutionary algorithm is used, such as oneMax or

long-path problems, with basic operators, such as bit-

ﬂip, embedded in a (1+λ)-EA (DaCosta et al., 2008).

This, however, can only highlight the search behavior

according to few and problem-speciﬁc properties. In

the second class of benchmarks, the problem and the

stochastic operators are abstracted. The performance

of each available operator is then deﬁned according to

the state of the search (Thierens, 2005; Fialho et al.,

2010; Go

effon et al., 2016; Jankee et al., 2016). This

allows to study important black box (problem inde-

pendent) features such as the number of operators, the

frequency of change of the best operators, the quality

difference between operators, etc.

In this work, we use a tunable benchmark, called

the Fitness Cloud Model (FCM), introduced recently

in (Jankee et al., 2016). The FCM is a benchmark

from the second class where the state of the search is

given by the ﬁtness of the solution. The ﬁtness of

a solution after applying a search operator is mod-

eled by a random variable for which the probability

distribution depends on the ﬁtness of the current so-

lution. A normal distribution with tunable parame-

ters is typically used. More speciﬁcally, given the

ﬁtness z = f (x) of the current solution x, the prob-

ability distribution of the ﬁtness f (y) of one solu-

tion obtained by a speciﬁc operator is deﬁned by:

Pr( f (y) = z

| f (x) = z) ∼ N (µ(z), σ

(z)) where µ(z)

and σ

(z) are respectively the mean and the variance

of the normal distribution. In (Jankee et al., 2016),

a simple scenario with two operators is studied. The

mean and variance of the conditional normal distri-

bution are deﬁned as follows: µ

(z) = z + K

and

(z) = K

for each operator i ∈ {1, 2}. Parameters

and K

are different constant numbers. An adap-

tive algorithm is assumed to start with a search state

where the ﬁtness value is 0, and stops when a ﬁtness

value of 1 is reached. The expected running time of

(1 +1)-EA is then proved to be the inverse of the best

expected improvement of among the considered oper-

ators, which can be analytically computed assuming a

normal distribution. Notice that in the FCM, one can

control the average quality and the variance of each

operator as well the relative difference between the

considered operators.

3 DESIGN BATCH ADAPTIVE

MASTER-WORKER

ALGORITHM

The global architecture of the proposed adaptive M/W

framework is summarized in Algorithm 1. 2 depicts

the high level code executed by the master. Algo-

rithm 3 presents the high level code executed in par-

allel by each worker. The overall algorithm operates

in different parallel rounds. At each round, the master

sends the best solution x

and a batch of operator iden-

tiﬁers Θ to be executed by each worker node i. After

getting the batch, each worker executes iteratively its

assigned operators starting from x

as an initial solu-

tion and computes a new local best solution. The mas-

ter waits for all best local solutions to be computed in

parallel by the workers, and updates the x

to be con-

sidered in the next round. The workers also inform

back the master of the performance observed when

executing the batch of operators. Note that when the

size of the batch of operators is one, each worker ex-

ecutes only one ﬁtness evaluation; which is basically

the same as a synchronous parallel (1+ λ)-EA with λ

equals to the number of workers n.

In our algorithm selection setting, a portfolio of k

(local search) operators is assumed to be given, and

no a priori knowledge is assumed on the behavior of

the operators. The adaptive part of our framework

is mainly handled at the master level. In fact, af-

ter collecting the rewards computed locally by each

worker, the master executes the main function Selec-

tion Strategy (line 12 of Algo. 1) which allows him to

compute the new set of batches Θ

to be sent again to

each worker i. Before going into further details, it is

important to emphasize that the batch Θ

is simply an

ordered list of operators to be executed consecutively

in a row by the corresponding worker i following the

general framework of a (1+1)-EA as depicted in Al-

Algorithm 1: Adaptive M/W algorithm for the master node.

1: (Θ

, Θ

, ..., Θ

) ←Selection Strategy Initialization()

2: x

← Solution Initialization() ; f

← f (x

)

3: repeat

4: for each worker i do

5: Send Msg(Θ

, x

, f

) to worker i

6: end for

7: Wait until all messages are received from all work-

ers

8: for each worker i do

9: (r

, x

, f

) ← Receive Msg() from worker i

10: end for

11: x

← x

; f

← f

s.t. f

= max{ f

, f

, . . . , f

}

12: (Θ

, Θ

, ..., Θ

) ← Selection Strategy(r

, ..., r

)

13: until stopping criterion is true

Algorithm 2: Adaptive algorithm selection strategy.

1: function SELECTION STRATEGY(r

, ..., r

)

2: for each operator j do

3: R

← Global Reward Aggregation(r

, ..., r

)

4: end for

5: (Θ

, Θ

, ..., Θ

) ←Decision Strategy(R

, R

, ..., R

)

6: return (Θ

, Θ

, ..., Θ

)

7: end function

Algorithm 3 : Adaptive M/W algorithm for each worker

node.

1: (Θ, x

, f

) ← Receive Msg() from master

2: for each index b of operators batch Θ do

3: x

← Apply operator Θ

on x

4: f

← Evaluate ﬁtness of x

5: δ

← max(0, f

− f

)

6: if f (x

) < f (x

) then

7: x

← x

; f

← f

8: end if

9: end for

10: for each operator j do

11: r

← Local Reward Aggregation(δ)

12: end for

13: Send Msg((r

, r

, . . . , r

), x

∗

, f

∗

) to master

gorithm 3.

More precisely, the number of search iterations

executed by each worker is the size of the batch, and

the search operator applied at each iteration corre-

spond to the order given in the same batch. At each

iteration, the ﬁtness improvement δ

of each operator

is evaluated (the positive ﬁtness difference between

solutions before and after applying the operator). The

ﬁtness improvement (Fialho et al., 2009) will allow

each worker to compute a local reward for every exe-

cuted operator. The Local Reward Aggregation func-

tion (line 11 of Algo. 3) allows each worker to com-

pute a local reward r

for each operator (if included in

the batch) according to the observed improvements δ.

The main function Selection Strategy executed at

the master level is responsible for : (i) aggregating

Table 1: Parameter use for the selection strategies.

Selection strategies Parameter

UCB c = 0.005, w = 700

AP α = 0.2, β = 0.2

ε-Greedy ε = 0.05, w = 4500

δ-Greedy Inc = 10

Operators µ (×10

−4

) σ (×10

−4

)

-1 1

-10 5

the local rewards sent by the worker and (ii) accord-

ingly select the new set of operators batches. This is

described in next subsection.

We also designed a simple heterogeneous selec-

tion strategy, called ∆-greedy. In the very ﬁrst round,

the operators are randomly assigned to workers just

like for any other strategies. In the subsequent rounds,

the number of workers associated with the best opera-

tor is increased by ∆, where ∆ is an integer parameter;

and the number of workers associated with the worst

operator is decreased by ∆. The best (resp. worst) op-

erator is computed as the one which attains the high-

est (resp. lowest) local reward in the previous round.

In order to avoid side effects, the number of workers

associated with each operator is bounded by a min-

imal number n

min

which is the second parameter of

this strategy. For each worker, the batch of operators

remains, however, homogeneous for this strategy, i.e.,

a worker executes the same operator which is possibly

different from the one executed by a different worker.

4 EXPERIMENTAL ANALYSIS

In this section, we analysis by experiments on the ﬁt-

ness cloud benchmark which deﬁnes a relevant sce-

nario for M/S framework using a batch of opera-

tors the adaptive performance of difference selection

strategies, and the parallel efﬁciency of using a batch

of algorithms to execute on each worker according to

the communication cost relatively to the computation

cost of the ﬁtness function.

4.1 Experimental Setup

In order to examine different possible parallel ar-

chitecture, we choose a simulation-based approach

where we count the number of round and the amount

of communication performed by the master until

reaching the optimal ﬁtness value. In that way, we are

able to discuss on the communication cost indepen-

dently to a speciﬁc architecture. Following the Fit-

ness Cloud Model (Jankee et al., 2016), we consider

a portfolio with two operators, both follows a normal

distribution of ﬁtness value as discussed in the section

2.3. The mean value of the ﬁrst operator op

is cho-

sen to be higher than the second operator op

, but the

variance of op

is smaller than the second operator.

This scenario is one of the most relevant for a parallel

system. Indeed, when one solution is created by an

operator, the expected improvement of the ﬁrst oper-

ator op

is higher than the one of the operators op

In that way, the ﬁrst operator would be preferred in a

sequential algorithm producing iteratively new solu-

tions. On the contrary, when a number of solutions

are created at the same time by an operator, the gain

of the second operator op

is larger than the ﬁrst op-

erator, i.e. the longest tail of the ﬁtness distribution of

the second operator op

is more likely to produce a

better solution. This scenario allows us to accurately

analyze the impact of the number of workers and the

size of the batch of algorithms send to each worker.

The Table 1 gives the values of the parameters of the

normal distribution used in this work.

In this work, the sequential selection strategies,

AP, UCB, and ε-Greedy, (see Sect. 2.1) are tailored

to a M/W framework. There are two main differences

with the original versions. First, instead of one reward

value, a set of reward values are used to update the

quality of each operator. To this goal, the local and the

global aggregation functions (see Algo. 1 and 3) com-

pute the maximum of ﬁtness improvements given, re-

spectively, by the batch of operators and by the set of

workers. Second, each selection strategy selects a set

of operators instead of a single operator at each round.

For UCB strategy which selects the operator with the

highest score, the set of selected operators is homo-

geneous: for any workers and any operators from the

batch of operators, the same operator (with the high-

est score) is selected. The other selection strategies

(AP, ε-greedy, and δ-Greedy) deﬁnes a probability of

selection of each operator. Then, for any operator in

the batch of any worker, the operator is selected ac-

cording to these probabilities. Those set of operators

is heterogenous at the workers level and at the batch

level.

The parameter set of the different selection strate-

gies is given in Table 1. We follow the robust param-

eters proposed in (Jankee et al., 2016; Jankee et al.,

2015). For all following experiments, the algorithm

is repeated independently 32 times, and the average

value of performance (number of rounds, or compu-

tation effort) are computed.

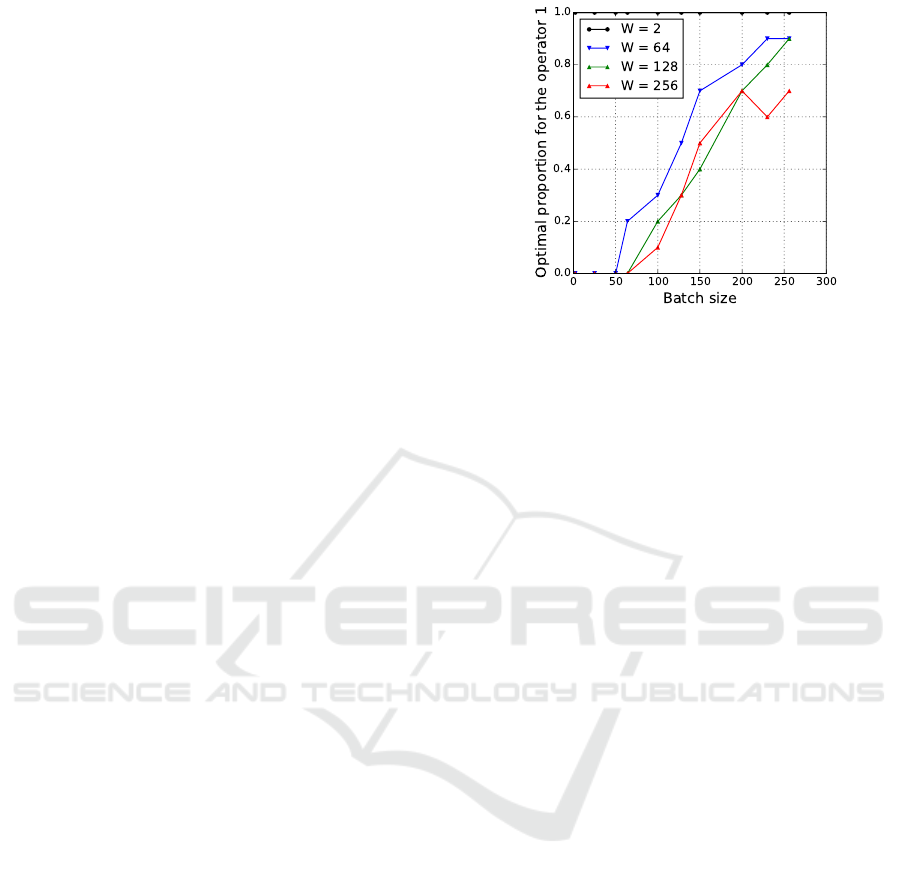
Figure 1: Random strategies in function the batch size and

windows size, we observe the proportion to use the operator

2 that is to say the operator having long tail.

4.2 Baseline Selection Strategy

The operator op

and op

of the benchmark are static

in the sense that the parameters of the ﬁtness distri-

bution does not change the optimization process ac-

cording to the state of the search. In this case, a bias

random selection of operators can be considered as a

baseline strategy: with a rate p between 0 and 1, the

operator op

is selected, and the with the rate 1 − p

the operator op

is selected. This baseline strategy

helps to understand the tradeoff between a selection

that promotes the worker level or that promotes the

master level according to the operator batch size and

the number of workers.

Figure 1 shows the value of p which ob-

tains the best performance. This best value is

computed off-line by experiments from the set

{0, 0.2,0.4, 0.6, 0.8, 1}, and we denote by p

this

value. When the batch size is small, i.e. the number

of operators in the batch send to each worker, except

when the number of workers is very small (such as 2

workers), the optimal rate p

is 0, and a bias random

selection strategy always selects the second operator.

In this case, the operator op

with the lowest average

but longest tail is the most interesting one. On the

contrary, the optimal rate p

increases with the batch

size. When the number of workers is equal to the size

of batch, both equal to 128, the optimal bias random

selection selects the operator 2 (with long tails) with

rates 70% and therefore the operator 1 with rate 30%

(with the highest average). The optimal p

is larger

than 80% when the batch size is large with respect to

the number of workers (the batch size is the double of

the number of workers). With lower amounts of infor-

mation exchange between workers, an efﬁcient search

converges toward to sequential process where the ﬁrst

operator with highest expected gain with one trial is

preferred. In that case, a sequential setting in favor

of the operator with a small improvement but with a

high probability is promoted.

4.3 Adaptive Performance with a Batch

Scheduling Technique

In Master/Worker framework, a batch scheduling

technique can be used to reduce the communication

to the computation cost. In this section, the goal is not

to analyze the performance of such a technique from

a purely parallel perspective, but instead, to highlight

the accuracy of an adaptive strategy to select the rele-

vant operators in the batch, which is a challenging is-

sue per se. Instead of analyzing the number of rounds

to optimum, we hence study the number of evalua-

tions executed in parallel by all the workers. Since the

range of the number of evaluations can be huge as a

function of the number of workers and the batch size,

we consider to normalize it by the average number

of evaluations of the unbiased heterogeneous random

strategy with p = 0.5 considered as a baseline. Due

to lack of space, only a representative set of results is

shown in Fig. 2, providing an overview of the relative

behavior of the adaptive strategies with respect to the

baseline one.

Notice that a strategy with a normalized value be-

low 1 in Fig. 2 is better than the unbiased random one,

and inversely. For completeness, we include the static

strategies that would always select the same pre-ﬁxed

operator in all rounds.

For all adaptive strategies, the relative normal-

ized performance decreases with the size of the batch

scheduling. The adaptive strategies are in fact found

to be relatively better than the random one for a small

size batch, but, they become worse for a large size

batch. On the contrary, the relative normalized perfor-

mance of adaptive strategies increases with the num-

ber of workers. UCB and ε-greedy are not able to

select the optimal operator in each round when the

number of workers is lower than 50 (and batch size

128). In this case, the heterogeneous AP outperforms

the other strategies, and can be better than an opti-

mal homogeneous strategy. Actually, when the size of

the batch is large with respect to the number of work-

ers, the adaptive strategies fail to perform accurately.

In this case, we hypothesize that alternative selection

mechanism based on the local reward of each worker

would be better than a selection based on the estima-

tion of the global reward.

0 50 100 150 200 250 300

Number of workers

0.8

0.9

1.0

1.1

1.2

1.3

Normalized average number of evaluations

Static(op1)

Static(op2)

Rand p*

UCBw

-Greedy

δ-Greedy

Figure 2: Normalized average number of evaluations as a

function of batch size using 128 workers (top), and as a

function of the number of workers using a batch size 128

(bottom). The values are normalized by the average number

of evaluations of the heterogeneous random strategy with

p = 0.5. The lower the better.

5 CONCLUSIONS

An efﬁcient Master/Worker framework should deal

with the tradeoff between the communication and the

computation costs. Independently of the adaptive

properties of the optimization method, a batch strat-

egy can be used to reduce the communication cost but

possibly decrease the performance of the optimization

process. In this paper, we deeply analyze the adaptive

method according to the number of workers as well of

the size of the batch of operators sent to each worker.

We show that another tradeoff is also required from

an adaptive point of view, and the heterogeneous se-

lection strategy outperforms homogeneous ones when

the batch size is large with respect to the number of

workers.

We proposed a naive batch strategy, the master de-

termines an operator list to be executed on the slave

according to this knowledge. It would be interesting

to have two selection strategies on the master, another

on the worker. The master could send the parameters

to the worker selection policy instead of pre-setting

an operator list because we know that the operator to

use is not necessarily the same according to the stage

of the search state of a worker.

In another perspective, an asynchronous architec-

ture would make it possible to improve the time of

use of the slave processors, especially when the com-

putation time of the ﬁtness varies according to the

state of the search. Moreover, the batch does not im-

prove the synchronization between the different com-

pute nodes. An asynchronous architecture makes it

possible to better exploit the network resources.

REFERENCES

Armas, R., Aguirre, H., Zapotecas-Mart

ınez, S., and

Tanaka, K. (2016). Trafﬁc signal optimization: Mini-

mizing travel time and fuel consumption. In EA 2015,

pages 29–43. Springer.

Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-

time analysis of the multiarmed bandit problem. Ma-

chine learning, 47(2-3):235–256.

Baudi

s, P. and Po

ık, P. (2014). Online black-box algorithm

portfolios for continuous optimization. In PPSN XIII,

pages 40–49. Springer.

Candan, C., Go

effon, A., Lardeux, F., and Saubion, F.

(2013). Non stationary operator selection with island

models. In GECCO, pages 1509–1516.

DaCosta, L., Fialho, A., Schoenauer, M., and Sebag, M.

(2008). Adaptive operator selection with dynamic

multi-armed bandits. In GECCO, page 913. ACM

Press.

Dasgupta, D. and Michalewicz, Z. (2013). Evolutionary

algorithms in engineering applications. Springer Sci-

ence & Business Media.

Derbel, B. and Verel, S. (2011). DAMS: distributed adap-

tive metaheuristic selection. In GECCO, pages 1955–

1962. ACM Press.

Dubreuil, M., Gagne, C., and Parizeau, M. (2006). Analy-

sis of a master-slave architecture for distributed evolu-

tionary computations. IEEE T. on Systems, Man, and

Cybernetics: Part B, 36:229–235.

Eiben, A. E., Michalewicz, Z., Schoenauer, M., and Smith,

J. E. (2007). Parameter control in evolutionary algo-

rithms. In Parameter Setting in Evolutionary Algo-

rithms, pages 19–46. Springer.

Fialho, A., Da Costa, L., Schoenauer, M., and Sebag, M.

(2009). Dynamic multi-armed bandits and extreme

value-based rewards for adaptive operator selection in

evolutionary algorithms. In LION’09, volume 5851,

pages 176–190. Springer.

Fialho, A., Da Costa, L., Schoenauer, M., and Sebag, M.

(2010). Analyzing bandit-based adaptive operator se-

lection mechanisms. Annals of Mathematics and Arti-

ﬁcial Intelligence, 60:25–64.

Garc

ıa-Valdez, M., Trujillo, L., Merelo-Gu

ervos, J. J., and

Fern

andez-de Vega, F. (2014). Randomized parame-

ter settings for heterogeneous workers in a pool-based

evolutionary algorithm. In PPSN XIII, pages 702–710.

Springer.

effon, A., Lardeux, F., and Saubion, F. (2016). Simu-

lating non-stationary operators in search algorithms.

Appl. Soft Comput., 38:257–268.

Grefenstette, J. J. (1986). Optimization of control parame-

ters for genetic algorithms. Systems, Man and Cyber-

netics, IEEE Transactions on, 16(1):122–128.

Harada, T. and Takadama, K. (2017). Performance compar-

ison of parallel asynchronous multi-objective evolu-

tionary algorithm with different asynchrony. In CEC.

Jankee, C., Verel, S., Derbel, B., and Fonlupt, C. (2015).

Distributed Adaptive Metaheuristic Selection: Com-

parisons of Selection Strategies. In EA 2015, pages

83–96.

Jankee, C., Verel, S., Derbel, B., and Fonlupt, C. (2016). A

ﬁtness cloud model for adaptive metaheuristic selec-

tion methods. In PPSN 2016, pages 80–90. Springer.

Kotthoff, L. (2012-10-30). Algorithm selection for com-

binatorial search problems: A survey. AI Magazine,

pages 48–60.

Kunanusont, K., Gaina, R. D., Liu, J., Perez-Liebana, D.,

and Lucas, S. M. (2017). The n-tuple bandit evolu-

tionary algorithm for automatic game improvement.

In CEC.

Maturana, J., Fialho,

A., Saubion, F., Schoenauer, M., and

Sebag, M. (2009). Extreme compass and dynamic

multi-armed bandits for adaptive operator selection.

In CEC, pages 365–372. IEEE.

Muniglia, M., Do, J.-M., Jean-Charles, L. P., Grard, H.,

Verel, S., and David, S. (2016). A Multi-Physics PWR

Model for the Load Following. In ICAPP.

Tanabe, R. and Fukunaga, A. (2013). Evaluation of a ran-

domized parameter setting strategy for island-model

evolutionary algorithms. In CEC 2013, pages 1263–

1270.

Thierens, D. (2005). An adaptive pursuit strategy for al-

locating operator probabilities. In GECCO’05, pages

1539–1546.

Tomassini, M. (2005). Spatially Structured Evolutionary

Algorithms: Artiﬁcial Evolution in Space and Time

(Natural Computing Series). Springer-Verlag New

York, Inc., Secaucus, NJ, USA.

Wessing, S., Rudolph, G., and Menges, D. A. (2016). Com-

paring asynchronous and synchronous parallelization

of the sms-emoa. In PPSN XIV, pages 558–567,

Cham. Springer.

Yagoubi, M. and Schoenauer, M. (2012). Asynchronous

master/slave moeas and heterogeneous evaluation

costs. In GECCO, pages 1007–1014.