Mining Hot Research Topics based on Complex Network Analysis
A Case Study on Regenerative Medicine
Rong-Qiang Zeng
1,2
, Hong-Shen Pang
3
, Xiao-Chu Qin
4
, Yi-Bing Song
4
, Yi Wen
1
, Zheng-Yin Hu
1
,
Nin Yang
1
, Hong-Mei Guo
5
and Qian Li
5
1
Chengdu Documentation and Information Center, Chinese Academy of Sciences, Chengdu, Sichuan 610041, P. R. China
2
School of Mathematics, Southwest Jiaotong University, Chengdu, Sichuan 610031, P. R. China
3
Shenzhen University, Shenzhen, Guangdong 518060, P. R. China
4
Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences,
Guangzhou, Guangdong 510530, P. R. China
5
National Science Library, Chinese Academy of Sciences, Beijing 100190, P. R. China
Keywords:
Hot Research Topics, Modularity Function, Regenerative Medicine, Community Detection, Hypervolume
Indicator.
Abstract:
In order to mine the hot research topics of a certain field, we propose a hypervolume-based selection algorithm
based on the complex network analysis, which employs a hypervolume indicator to select the hot research
topics from the network in the considered field. We carry out the experiments in the field of regenerative
medicine, and the experimental results indicate that our proposed method can effectively find the hot research
topics in this field. The performance analysis sheds lights on the ways to further improvements.
1 INTRODUCTION
The relations among the literatures in a certain field
can be usually represented as networks, where the
nodes denote the objects and the edges denote the
interactions among these objects. Many researchers
have tried to use the quantitative methods to study the
complex networks, in order to recognize the knowl-
edge structure of the considered field. Based on the
complex works, mining the hot research topics is very
important for the researchers to analyze the trends of
scientific research and provide some directions of re-
search mainstream in the certain field.
In this paper, we propose the hypervolume-based
selection algorithm to analyze the bibliometric net-
work, in order to mine the hot research topics of a
certain field. Based on the relation between the lit-
eratures and the key words, we realize the commu-
nity detection for the bibliometric network and select
the hot research topics according to two objectives:
the frequency of the key words and the number of the
key words. The experimental results indicate that the
proposed method can effectively recognize the hot re-
search topics. The performance analysis explains the
behavior of our proposed method and sheds lights on
the ways to further improvements.
The remaining part of this paper is organized as
follows. In the next section, we briefly review the pre-
vious works related to the bibliometric studies based
on the complex network analysis. In Section 3, we
present the ingredients of hypervolume-based selec-
tion algorithm for mining the hot research topics. Sec-
tion 4 shows the experimental results and analysis in
the field of regenerative medicine. The conclusions
are provided in the last section.
2 LITERATURE REVIEWS
In this section, we present the literature reviews con-
centrating on the bibliometrics network analysis.
In (Zhu and Guan, 2013), the authors applied the
small world complex network theory to analyze sci-
entific research in the field of service innovation, and
discover its research focuses. Their study considered
the key words and subject categories of the publica-
tions as actors to map keyword co-occurrence net-
work and subject category co-occurrence network,
and compare them with their corresponding random
Zeng R., Pang H., Qin X., Song Y., Wen Y., Hu Z., Yang N., Guo H. and Li Q.
Mining Hot Research Topics based on Complex Network Analysis - A Case Study on Regenerative Medicine.
DOI: 10.5220/0006504802630268
In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KDIR 2017), pages 263-268
ISBN: 978-989-758-271-4
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

binary networks to judge whether these complex net-
works have the characteristics of small world net-
work, in order to find the hot issues in the field by
the small world network analysis. The experimen-
tal results through analyzing 437 papers from Web of
Science database over the period 1992 to 2011 show
the dynamic development of the research focuses in
recent 10 years.
In (Lipizzi et al., 2016), the authors have pre-
sented a methodology to assess moviegoers’ early re-
actions to movies’ premieres through the extraction of
analytics from Twitter conversations that take place in
the weekend in which a movie is released. They ap-
plied data mining techniques to a sample of 22 movies
to identify models able to predict box-office sales in
the first weekend. Their findings confirmed that the
importance of commonly used buzz-metrics is proba-
bly overstated, and the analysis of conversational dy-
namics can help to understand the interplay between
collectivegeneration and diffusion of content in social
networks as well as to obtain the insights on whether
information diffusion influences off-line behavior.
In (Zhang et al., 2016), the authors focused on the
NSF data and constructed a K-Means-based cluster-
ing methodology with high accuracy in a local K-
value interval, where an optimized K value would
be determined automatically. Then, they introduced
a similarity measure function for topic relationship
identification to explore the interaction among TRM
components quantitatively and predict possible future
trends. The experimental results are carried forward
to present the mechanisms that forecast prospective
developmentsusing Technology Road mapping, com-
bining qualitative and quantitative methodologies.
3 METHODOLOGY
In our work, we propose the hypervolume-based se-
lection procedureto analyze the bibliometric network,
in order to detect the key structure and select the hot
research topics in a certain field. First, we give an
introduction to the basic notations and definitions of
the network. Then, we present the method of detect-
ing the community in the network. Afterwards, we
describe the main ingredients of hypervolume-based
selection algorithm.
3.1 Network Construction
Generally, given a simple undirected graph G =
(V,E), where V is the set of vertices and E is the set
of undirected edges. Suppose the vertices are divided
into two sets: one is composed of the literatures, and
another one is composed of the key words.
Then, these exists the edges between the literature
and the key word, if and only if the key word belongs
to the considered literature. Actually, there is no edge
among the literatures or the key words. That’s to say,
it is indeed a bipartite graph.
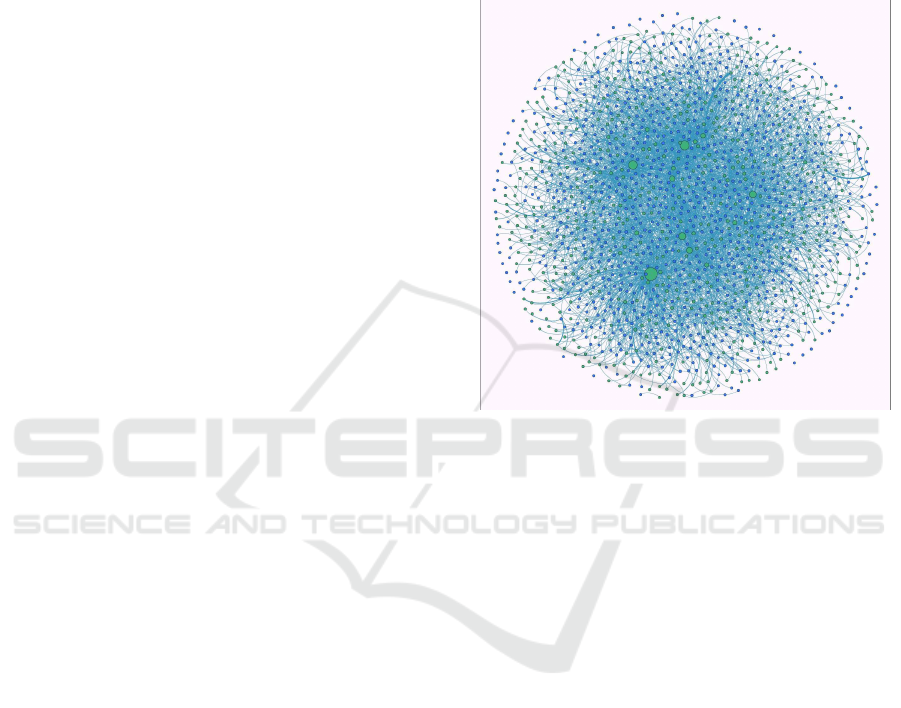
Figure 1: An example of the bibliometric network.
An example is illustrated in Fig. 1, which con-
sists of thousands of vertices and edges. In this fig-
ure, a green circle denotes one key word and a blue
circle denotes one literature. Usually, one literature
consists of hundreds of key words, which makes the
whole network very complicated. Therefore, it is very
difficult for the experts to recognize the hot research
topics from the network.
3.2 Community Detection
In order to clearly recognize the hot research topics
from the network, it is essential to detect the commu-
nity structure, which is one of the most relevant fea-
tures of the networks. In fact, the community struc-
ture plays an important role in understanding the in-
trinsic properties of networks.
One of the most popular quality functions is
the modularity proposed by Newman and Girvan in
(Newman and Girvan, 2004), which is based on the
idea that a random network is not expected to have a
community structure. Now, the modularity is widely
accepted by the scientific community. Suppose the
vertices are divided into the communities such that
vertex v belongs to community C denoted by C
v
, the
modularity is defined as follows (Newman and Gir-
van, 2004):

Q =
1
2m
∑
vw
[A
vw
−
k
v
k
w
2m
]δ(C
v
,C
w
), (1)
where A is the adjacency matrix of graphG. A
vw
= 1 if
one node v is connected to another node w, otherwise
A
vw
= 0. The δ function δ(i, j) is equal to 1 if i = j and
0 otherwise. The degree k
v
of a vertex v is defined to
be k
v
=
∑
v
A
wv
, and the number of edges in the graph
is m =
∑
wv
A
wv
/2.
Furthermore, the modularity function can be rep-
resented in a simple way, which is formulated below
(Newman and Girvan, 2004):
Q =
∑
i
(e
ii
− a
2
i
), (2)
where i runs over all communities in graph, e
ij
and
a
2
i
are respectively defined as follows (Newman and
Girvan, 2004):
e
ij
=
1
2m
∑
vw
A
vw
δ(C
v
,i)δ(C
w
, j), (3)
which is the fraction of edges that join vertices in
community i to vertices in community j, and
a
i
=
1
2m
∑
v
k
v
δ(C
v
,i), (4)
which is the fraction of the ends of edges that are at-
tached to vertices in community i. Actually, the mod-
ularity has been proven to be NP-hard in (Brandes
et al., 2006).
In order to find the community structure effec-
tively, we employ the local search procedure to
achieve the aim, and the main steps are presented
in the Algorithm 1. In this algorithm, we divide
the whole network into two communities, and each
smaller community is further divided into two com-
munities. This process is repeated until the modular-
ity can not be improved as done in (L¨u and Huang,
2009).
Algorithm 1: Community Detection Algorithm.
1: Input: network adjacency matrix A
2: Output: the best value of the modularity function
3: P = {x
1
,..., x
p
} ← Random
Initialization (P)
4: repeat
5: x
i
← Local
Search (x
i
)
6: until a stop criterion is met
Generally, one community C
k
is divided into two
communitiesC
i
and C
j
, and all the vertices belonging
to C
k
are randomly assigned to C
i
and C
j
.
After the initialization, we introduce a special data
structure named
move value used in (L¨u and Huang,
2009) to compute the incremental value of the modu-
larity function for each possible move of the current
solution. Let C
i
and C
j
are two communities, w be a
vertex from C
i
or C
j
. We assume that w ∈ C
i
and the
corresponding change by moving vertex w from C
i
to
C
j
can be computed as follows (L¨u and Huang, 2009):
∆Q(w,C
i
,C
j
) =
k
j
w
− k
i
w
m
+
k
w
(a
i
− a
j
)
m
−
k
2
w
2m
2
, (5)
where k
i
w
and k
j
w
are respectively the number of edges
connecting vertex w and the other vertices in commu-
nities C
i
and C
j
.
On the other hand, for any vertex v in commu-
nity C
i
, we can also obtain the updated ∆Q value
∆Q
′
(v,C
i
,C
j
) with the formula below (L¨u and Huang,
2009):
∆Q
′
(v,C
i
,C
j
) = ∆Q(v,C
i
,C
j
) − (
k
2
w
m
2
−
2A
wv
m
). (6)
Correspondingly, for any vertex v in community C
j
,
there are two possible cases for the updated ∆Q value
∆Q(v,C
j
,C
i
). When considering the same vertex v
(v = w), ∆Q(v,C
j
,C
i
) is updated as follows (L¨u and
Huang, 2009):
∆Q
′
(v,C
j
,C
i
) = −∆Q(v,C
i
,C
j
). (7)
When considering two different vertices v and w
(v 6= w), ∆Q(v,C
j
,C
i
) is updated as follows (L¨u and
Huang, 2009):
∆Q
′
(v,C
j
,C
i
) = ∆Q(v,C
j
,C
i
) + (
k
2
w
m
2
−
2A
wv
m
). (8)
According to Eqs. (5), (6), (7) and (8), the local
search procedure chooses the best move in the current
neighborhood at each step until the modularity does
not improve any more. Then, we obtain the commu-
nities of the considered network.
3.3 Hypervolume-Based Selection
After finding the communities in the network, we pre-
fer to select a certain number of the potential hot re-
search topics from each community. Since there are
a large number of literatures in each community, it is
not necessary to select all of them, but to select the
most important ones.
Actually, we evaluate the importance of the hot
research topics by defining two objectives: the fre-
quency of the key words (f
1
) and the number of key
words (f
2
), which are computed by the formulas be-
low:
f
1
= weight(x
i
) (9)
f
2
= degree(x
i
) (10)

Specifically, the objective f
1
represents the fre-
quency of one key word emerging in a literature,
which corresponds the weight of the edge, and the
objective f
2
represents the number of the key words
belonging to a literature, which corresponds the de-
gree of a vertex denoting a literature in the network.
According these two objectives, we evaluate the
importance of one hot research topic in each com-
munity. In order to achieve this goal, we propose a
hypervolume-basedselection algorithm, which is pre-
sented in Algorithm 2 below (Basseur et al., 2012).
Algorithm 2: Hypervolume-Based Selection Algorithm.
Steps:
1) calculate two objective function values of x
i
2) calculate the fitness value of x
i
with the HC indicator
3) select n l
i
based on the fitness values
In this algorithm, x
i
denotes the i
th
literature in
each community. First, we calculate the two objective
values of x
i
. Then, we calculate the fitness value of x
i
with the HC indicator, which is defined as follows:
HC(x
1
) = ( f
1
(y
1
) − f
1
(x)) × ( f
2
(y
0
) − f
2
(x)) (11)
f
x
1
f
2
Z
ref
y
1
y
0
Figure 2: An example of fitness computation.
As is shown in Fig. 2, the fitness value of x cor-
responds to the size of the green area, where y
0
and
y
1
are the neighbors of x. Thus, we can select a des-
ignated number of literatures with high fitness values,
which refer to the hot research topics in this commu-
nity.
4 CASE STUDY
In this section, we present the experimental results of
our method in the field of regenerative medicine. All
the algorithms are programmed in C++ and compiled
using Dev-C++ 5.0 compiler on a PC running Win-
dows 7 with Core 2.50 GHz CPU and 4 GB RAM.
4.1 Data Information
In order to conduct the experiments with our meth-
ods, we generate the data from the PubMed Database
by inputting the key words ”regenerative medicine”
from 2000 to 2014. Then, we select the literatures re-
trieved by the Semantic Medline Database, the type
of literature is ”Journal Article”.
1
The information of
literature is given below:
Table 1: The number of literatures.
Year Number of Literatures
2000 ∼ 2004 950
2005 ∼ 2009 3914
2010 ∼ 2014 11392
On the other hand, we have to select the key words
from the literature by setting the frequency T
f
. If is
smaller than , we delete these key words. Besides,
the general words are also deleted from the literature,
such ”cell”, ”disease”, etc. The information of key
words is given in Table 2 below.
Table 2: The number of key words.
Year Number of Key Words T
f
Values
2000 ∼ 2004 589 5
2005 ∼ 2009 759 10
2010 ∼ 2014 941 20
4.2 Experimental Results
In this subsection, we present the experimental results
in the field of regenerative medicine based on three
periods, which are the first period from 2000 to 2004,
the second period from 2005 to 2009 and the third
period from 2010 to 2014. The computational results
are summarized in Table 3.
In Table 3, the numbers represent the literatures
of the hot research topics in the field of regenerative
medicine. From this table, we can observe that there
are three hot research topics during the periods from
2000 to 2014. In each community, there are five liter-
atures of the hot research topics based on the complex
networks.
1
More information about the PubMed database can
be found on this website: https://www.ncbi.nlm.nih.gov/
pubmed.

Table 3: The hot research topics during periods from 2000 to 2014.
Year Community Hot Research Topics
2000 ∼ 2004 Community 1 11970903, 14648870, 11584365, 15083202, 15277237
Community 2 15086545, 15028134, 11850444, 11340065, 11077425
Community 3 11641084, 12963221, 15271696, 14745326, 14992357
2005 ∼ 2009 Community 1 16596286, 18047416, 19755676, 15808690, 17273778
Community 2 17635045, 18804048, 19198070, 19507174, 20042793
Community 3 20058201, 17882886, 17473528, 17510916, 19101095
2010 ∼ 2014 Community 1 20137136, 20507271, 23209652, 24799420, 24573178
Community 2 22008910, 24200501, 23554141, 22876135, 23916701
Community 3 21873605, 24895283, 24551049, 21464334, 23659910
Figure 3: An example of the hot research topics.
An example of the hot research topics is illustrated
in Fig. 3, In this figure, the blue circles with the num-
ber denote the literatures, and the green circles with
words denote the key words. The size of the green
circles represent the frequency of the key words.
5 CONCLUSIONS
In this paper, we have presented the community de-
tection algorithm based on local search procedure and
the hypervolume-based selection algorithm for rec-
ognizing and selecting the hot research topics. For
this purpose, we have carried out the experiments in
the field of regenerative medicine. The experimental
results indicate that our proposed method can effec-
tively find the hot research topics in the complex net-
works.
ACKNOWLEDGEMENTS
The work in this paper was supported by the Guang-
dong Science and Technology Program ”Integrated
Information Service for Regenerative Medicine and
Tissue Engineering” (Grant No. 2016A040403098),
supported by the West Light Foundation of Chinese
Academy of Science (Grant No. Y4C0011001), sup-
ported by the Fundamental Research Funds for the
Central Universities (Grant No. A0920502051722-
53) and supported by the ISTIC-EBSCO Joint Lab-
oratory Foundation Program of Literature Big Data
Discovery Service ”Research on Text Subject Recog-
nition Method Based on Clique Subgroup Cluster-
ing”.
REFERENCES
Basseur, M., Zeng, R.-Q., and Hao, J.-K. (2012).
Hypervolume-based multi-objective local search.
Neural Computing and Applications, 21(8):1917–
1929.
Brandes, U., Delling, D., Gaertler, M., G¨orke, R., Hoefer,
M., Nikoloski, Z., and Wagner, D. (2006). Maximiz-
ing modularity is hard. arXiv:physics, page 0608255.
Lipizzi, C., Iandoli, L., Emmanuel, J., and Marquez, R.
(2016). Combining structure, content and mean-
ing in online social networks: The analysis of
public’s early reaction in social media to newly

launched movies. Technological Forecasting and So-
cial Change, 109:35–49.
L¨u, Z. P. and Huang, W. Q. (2009). Iterated tabu search
for identifying community structure in complex net-
works. Physical Review E, 80:026130.
Newman, M. E. J. and Girvan, M. (2004). Finding and eval-
uating community structure in networks. Physical Re-
view E, 69(2):026113.
Zhang, Y., Zhang, G., Chen, H., Porter, A. L., Zhu, D., and
Lua, J. (2016). Topic analysis and forecasting for sci-
ence, technology and innovation: Methodology with a
case study focusing on big data research. Technologi-
cal Forecasting and Social Change, 105:179–191.
Zhu, W. and Guan, J. (2013). A bbibliometric study of ser-
vice innovation research: Based on complex network
analysis. Scientometrics, 94:1195–1216.