Enhanced Symbolic Regression Through Local Variable Transformations

ı Kubal

ık

, Erik Derner

1,2

and Robert Babu

ska

1,3

Czech Institute of Informatics, Robotics, and Cybernetics, Czech Technical University in Prague, Prague, Czech Republic

Department of Control Engineering, Faculty of Electrical Engineering, Czech Technical University in Prague,

Prague, Czech Republic

Cognitive Robotics, Faculty of 3mE, Delft University of Technology, Delft, The Netherlands

Keywords:

Symbolic Regression, Single Node Genetic Programming, Nonlinear Regression, Data-driven Modeling.

Abstract:

Genetic programming (GP) is a technique widely used in a range of symbolic regression problems, in particular

when there is no prior knowledge about the symbolic function sought. In this paper, we present a GP extension

introducing a new concept of local transformed variables, based on a locally applied afﬁne transformation of

the original variables. This approach facilitates ﬁnding accurate parsimonious models. We have evaluated the

proposed extension in the context of the Single Node Genetic Programming (SNGP) algorithm on synthetic as

well as real-problem datasets. The results conﬁrm our hypothesis that the transformed variables signiﬁcantly

improve the performance of the standard SNGP algorithm.

1 INTRODUCTION

Symbolic regression (SR) is a regression analysis

method formulated as an inductive learning task. The

main principle is to search in a predeﬁned space of

mathematical expressions for a model that ﬁts the

given data as accurately as possible. SR has been

successfully used in nonlinear data-driven model-

ing or data mining, often with quite impressive re-

sults (Schmidt and Lipson, 2009; Vladislavleva et al.,

2013; Staelens et al., 2013; Brauer, 2012). The main

advantage of SR is that it generates parsimonious and

human-understandable models. This is in contrast to

other widely used nature-inspired algorithms, such as

artiﬁcial neural networks, which are black box and do

not offer any insight or interpretation of the underly-

ing model.

Symbolic regression is usually solved by means

of genetic programming (GP). On the one hand, this

approach is suitable as there is generally no prior

knowledge on the structure and shape of the sym-

bolic function sought. On the other hand, the search

space in SR is huge so when a pure GP is applied

to a SR task, it needs a long time to ﬁnd an ac-

ceptable solution. Besides the standard Koza’s tree-

based GP (Koza, 1992), many other variants have

been proposed such as Grammatical Evolution, Gene

Expression Programming, Cartesian GP or Single

Node Genetic Programming. Grammatical Evolution

(Ryan et al., 1998) evolves programs whose syntax

is deﬁned by a user-speciﬁed grammar. Gene Ex-

pression Programming (Ferreira, 2001) evolves lin-

ear chromosomes that are expressed as tree struc-

tures through a genotype-phenotype mapping. Carte-

sian GP (CGP) (Miller and Thomson, 2000) uses the

genotype-phenotype mapping to express linear chro-

mosomes as programs in the form of a directed graph.

Single Node Genetic Programming (SNGP) (Jackson,

2012a; Jackson, 2012b) is a GP technique evolving a

population organized as an ordered linear array of in-

terlinked individuals, each representing a single pro-

gram node.

It has been widely reported in the literature that

evolutionary algorithms work much better when hy-

bridized with local search techniques or other means

of ﬁnal solution optimization. An example is the

memetic algorithm (Hart et al., 2005), where the lo-

cal search is used to ﬁne-tune the candidate solu-

tions along the whole evolution process. A simi-

lar approach can be used to develop efﬁcient GP-

based methods for symbolic regression. Recently,

several evolutionary SR methods emerged that explic-

itly restrict the class of generated models to gener-

alized linear models, i.e., models formed as a lin-

ear combination of non-linear basis functions, also

called features. Examples of these methods are Evo-

lutionary Feature Synthesis (EFS) (Arnaldo et al.,

2015), Multi-Gene Genetic Programming (MGGP)

(Hinchliffe et al., 1996; Searson et al., 2010), Fast

Function Extraction (FFX) (McConaghy, 2011), and

KubalÃ k J., Derner E. and BabuÅ ˛aka R.

Enhanced Symbolic Regression Through Local Variable Transformations.

DOI: 10.5220/0006505200910100

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 91-100

ISBN: 978-989-758-274-5

Single-Run SNGP with LASSO (s-SNGPL) (Kubal

ık

et al., 2016). Candidate basis functions are generated

through a standard evolutionary process, while the co-

efﬁcients of the basis functions are found by using a

multiple regression technique. In this way, accurate

linear-in-parameters nonlinear models can efﬁciently

be evolved.

In this paper, we go one step further towards ro-

bust GP methods for SR. We introduce local trans-

formed variables, which are coordinate transforma-

tions introduced in the individual nonlinear functions.

The motivation for using transformed variables is that

in many cases a good symbolic model is hard to pro-

duce with features in the original coordinate system.

The search process for an acceptable model can be

much more efﬁcient if some of its components use

transformed variables.

We chose a variant of Single Node Genetic Pro-

gramming (Jackson, 2012a; Jackson, 2012b) for a

proof-of-concept implementation of the transformed

variables into GP. It has been shown in (Kubal

ık et al.,

2016) that SNGP is good at solving the SR problem.

The concept of transformed variables is general and

can be implemented with other types of GP as well.

In order to facilitate operations with constants, which

is crucial for a proper functioning of the transformed

variables, we used the concept of partitioned popula-

tion, similar to the one introduced in (Alibekov et al.,

2016). The partitioned population is organized so that

it contains a continuous segment of nodes producing

only constant output. These constant-output nodes are

used in and evolved simultaneously with other expres-

sions in the population.

We evaluated the proposed extension on synthetic

as well as real-problem datasets with the number of

dimensions ranging from 2 to 4.

The paper is organized as follows. Section 2 de-

scribes the standard Single Node Genetic Program-

ming algorithm. The novel concept of transformed

variables is introduced in Section 3. Section 4

presents the experiments performed in order to com-

pare the algorithm variants. Finally, the achieved im-

provement of the proposed algorithm extension is dis-

cussed in Section 5.

2 STANDARD SNGP

Single Node Genetic Programming is a graph-based

GP technique that evolves a population organized as

an ordered linear array of individuals, each represent-

ing a single program node. Program nodes can be

of various types depending on the particular problem

solved. In the context of SR the program node can

either be a terminal, i.e. a constant or a variable, or

some operator or function chosen from a set of func-

tions deﬁned for the problem at hand. The individuals

are interconnected in the left-to-right manner, mean-

ing that an individual can act as an input operand

only of those individuals which are positioned to the

right of it in the population. Thus, the whole popu-

lation represents a graph structure similar to that of

the CGP with multiple expressions rooted in individ-

ual nodes. The population is evolved through a ﬁrst-

improvement local search procedure using a single re-

versible mutation operator.

Formally, the SNGP population is a set M =

,... ,m

L−1

} of L individuals, with each indi-

vidual m

being a single node represented by the tuple

= he

,Succ

,Pred

, f

i, where

• e

∈ T ∪F is either an element chosen from a func-

tion set F or a terminal set T deﬁned for the prob-

lem;

• Succ

is a set of successors of this node, i.e. the

nodes whose output serves as the input to this

node;

• Pred

is a set of predecessors of this node, i.e. the

nodes that use this node as an input operand;

• o

is a vector of its outputs;

• f

is the individual’s ﬁtness.

The population is organized as shown in Figure 1,

starting with constants and variables, followed by

function nodes.

Figure 1: Structure of the standard SNGP population.

Links between the nodes in the population must

satisfy the condition that any function node can use as

its successor (i.e. the operand) only nodes that are po-

sitioned lower down in the population. Similarly, pre-

decessors of individual i must occupy higher positions

in the population. Note that each function node is in

fact a root of an expression that can be constructed by

recursively traversing its successors towards the leaf

terminal nodes.

The ﬁtness of each individual (i.e. of each expres-

sion) is for SR problems typically calculated as the

root mean squared error observed on the set of train-

ing samples.

A simple evolutionary operator called successor

mutation (smut) is used to modify the population. It

picks one individual of the population at random and

then replaces one of its successors by a reference to

another individual chosen among all individuals posi-

tioned to the left of it in the population.

The population is evolved using a local search pro-

cedure. In each iteration, a new population is derived

from the current one by the smut operator. The new

population is then accepted for the next iteration if it

satisﬁes the chosen acceptance rule (typically, if its

performance is not worse than the performance of the

original population). Otherwise the original popula-

tion remains for the next iteration.

The baseline SNGP implementation used in this

work differs from the one described in (Jackson,

2012a; Jackson, 2012b) in several aspects described

in the following paragraphs.

Form of Regression Models. A hybrid SNGP de-

noted as the Single-Run SNGP with LASSO proposed

in (Kubal

ık et al., 2016) is used in this work. It pro-

duces generalized linear regression models. In par-

ticular, candidate features, i.e. expressions rooted in

individual nodes, are combined into generalized lin-

ear regression model using some multiple regression

technique. In this way, precise linear-in-parameters

nonlinear regression models can efﬁciently be pro-

duced.

Original s-SNGPL uses the Least Absolute

Shrinkage and Selection (LASSO) regression tech-

nique to generate models of limited complexity, i.e.

models composed of a limited number of features. In

particular, all features in the population with a non-

constant output are eligible candidates for the ﬁnal

model. Though, only some of the candidate features

are used in the ﬁnal model returned by the LASSO

procedure in the end. An advantage of this LASSO

approach is that a suitable subset of features used in

the model is chosen automatically. On the other hand,

the LASSO procedure is more computationally ex-

pensive than a simple least squares regression. Here,

instead of the LASSO regression operating with large

set of features, we use the simple least squares re-

gression explicitly operating on a ﬁxed number of

features. The complexity of the resulting regression

models is controlled by (i) the maximum depth of fea-

tures evolved in the population, d, and (ii) the maxi-

mum number of features the models can be composed

of, n

In order to have a possibility to identify the nodes

to be used as features in the linear regression model, a

special type of node called identity node is introduced.

This node has a single successor (i.e. an input), which

is a link to another node in the population. The iden-

tity node then returns outputs of the node it refers

to. The identity nodes are positioned at the end of

the population, see Figure 1. The number of identity

nodes n

is equal to the maximum number of features

to be used in the generated models. By changing the

successors of the identity nodes, the set of features for

the generated regression models can be altered. This

is realized in two ways. The ﬁrst one is by the stan-

dard mutation operator during the evolution. The sec-

ond one is through a local search procedure at line 21

in Algorithm 1. It is launched in the end of each epoch

and runs for a predeﬁned number of iterations, l

. In

each iteration, one identity node is randomly chosen

and its successor reference is changed to a new node

randomly chosen from the set of tail partition nodes.

Such a modiﬁed population is evaluated, meaning its

linear regression model is constructed using the mod-

iﬁed set of identity nodes (i.e. the features). If the

new model’s ﬁtness is not worse than the ﬁtness of

the original population model, the modiﬁcation made

to the identity node is accepted. Otherwise, the orig-

inal setting of the identity node remains for the next

iteration.

Fitness. Here, the ﬁtness represents a quality of the

whole generalized linear regression model calculated

as the root mean squared error observed on the set of

training samples. In addition, we also assess a quality

of each single node in the population. This is denoted

as the node’s utility and it is calculated as the Pearson

product-moment correlation coefﬁcient between the

node’s output and the desired output over the set of

training samples.

paragraphSelection Strategy. In the original

SNGP, nodes to be mutated are selected purely at ran-

dom. Here we use a variant of tournament selection

(see line 12 in Algorithm 1). It operates with util-

ity values assigned to the nodes during the population

evaluation step at line 3 and 15, respectively. When

selecting the node to be mutated, t candidate individ-

uals are randomly picked from the population at ﬁrst.

Then, out of the candidates the one that is involved

in the best-performing expression with respect to the

root node utility value is chosen. In this way, not only

nodes that have high utility values themselves are be-

ing favoured. Instead, all nodes at least contributing

to high-quality expressions are preferred to the ones

not playing an important role in the population (i.e.

the nodes not involved in any well-performing expres-

sion).

Evolutionary Model. The process of evolving the

population is carried out in epochs. In each epoch,

multiple independent parallel threads are run for a

predeﬁned number of generations, all of them start-

ing from the same population, which is the best ﬁnal

population out of the previous epoch threads. This re-

duces the chance of getting stuck in a local optimum.

The model is parameterized by the number of threads

, the epoch length l

, and the number of epochs n

3 PROPOSED EXTENSIONS

In this section, we describe the concept of trans-

formed variables, introduced in order to make the

SNGP algorithm more efﬁcient at solving the SR

problem.

3.1 Transformed Variables

The transformed variables are obtained by local afﬁne

transformations of the coordinate system. Assume n-

dimensional input space X ⊂ R

. Each transformed

variable v is represented by the tuple

v = hw

,. .. ,w

where c

is a pointer to a constant-valued node in the

population, w

∈ R is a real-valued constant, x

is the

jth original variable, with x

= 1 corresponding to

the offset of the transformation. The constant-valued

nodes referred to by the c

pointers are either basic

constant nodes (i.e. nodes from the ﬁrst section of the

partitioned population in Figure 2) or head partition

nodes. The value of the transformed variable v is cal-

culated as

v =

∑

j=0

where b

= w

with o

the output of the node refer-

enced by c

. The weighting coefﬁcients are formed as

= w

in order to allow for both global and local

tuning of their values. In particular, changing the ref-

erence c

to a different constant-valued node is likely

to lead to a signiﬁcant change of the corresponding

. On the contrary, ﬁne-tuning of the coefﬁcient b

can be achieved by applying small changes to w

. The

values of w

are initialized to 1. The links c

are tuned

by means of the standard mutation operator.

Both c

and w

can further be tuned through a lo-

cal search procedure, see line 22 in Algorithm 1. It

is launched in the end of each epoch and runs for

a predeﬁned number of iterations, l

. In each itera-

tion, one transformed variable v

is randomly chosen

and either its reference to the constant-valued node c

or the value of w

is changed with equal probability.

The value of w

is modiﬁed by adding a random value

drawn from a normal distribution as follows:

= w

+ N(0,1).

The population with the modiﬁed node v

is evalu-

ated and if its ﬁtness is not worse than the ﬁtness of

the original population, the modiﬁcation made to the

node v

is accepted. Otherwise, the original setting

of the transformed variable node remains for the next

iteration.

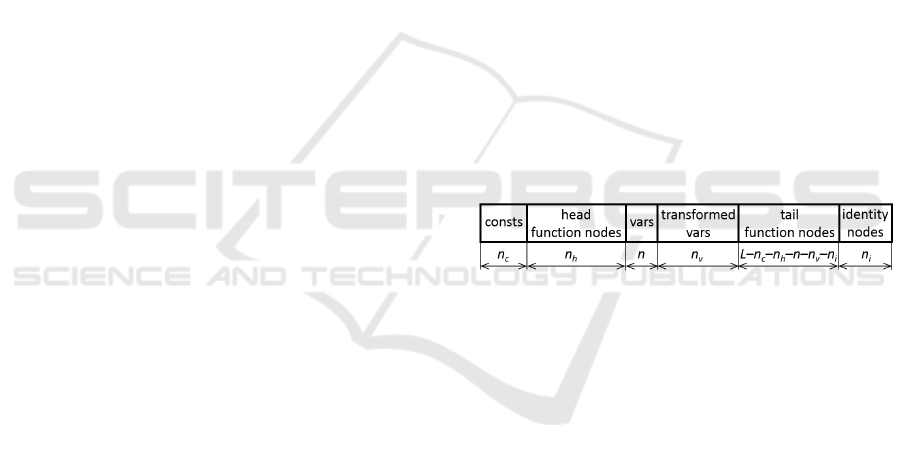
3.2 Partitioned Population

To support the concept of transformed variables, the

population is organized so that the function nodes

are further divided into two continuous segments, the

head and tail partitions as introduced in (Alibekov

et al., 2016). The head partition nodes are allowed

to represent root nodes of expressions producing only

constant output. The tail nodes can be roots of both

the constant-output as well as variable-output expres-

sions. The head partition therefore represents a pool

of constants that are used in and evolved simultane-

ously with other features in the population.

The number of transformed variables n

and the

number of head partition nodes n

are user-deﬁned

parameters. Note that besides the transformed vari-

ables the population always contains also all the orig-

inal variables x ∈ {x

,. .. ,x

}. The structure of the

partitioned population is shown in Figure 2.

Figure 2: Structure of partitioned population.

3.3 Algorithm SNGP-TV

The whole algorithm, denoted here as SNGP with

transformed variables (SNGP-TV), is outlined in Al-

gorithm 1. It iteratively evolves current best popula-

tion of individuals P and the corresponding model M.

The main loop, lines 5–29, iterates through epochs.

In each epoch, multiple independent threads are run,

lines 7–24, all of them started with the same popula-

tion P, line 8. Each thread runs for a predeﬁned num-

ber of generations, lines 11–20. In the end of each

thread, the identity nodes and transformed variables

are tuned for a speciﬁed number of trials, lines 21–

22. The best ﬁnal population and its model are saved

in P and M, lines 25–27, and P becomes the starting

population for next epoch. Finally, the last version of

model M is returned as the solution.

Algorithm 1: SNGP with transformed vari-

ables.

Input: training data set, L, n

, n

, n, n

, n

, d,

, l

, n

1 initialize population P

2 build regression model M using P

3 evaluate M

4 e ← 0

5 do

6 t ← 0

7 do

8 P

← P

9 M

← M

10 generation ← 0

11 do

12 s ← selectNode(P

)

13 P

← mutate(P

,s)

14 build model M

using P

15 evaluate M

16 if (M

is not worse than M

)

17 P

← P

18 M

← M

19 generation ← generation +1

20 while (generation < l

)

21 [P

] ← optIdentityNodes(P

)

22 [P

] ← optTrans fVars(P

)

23 t ← t + 1

24 while (t < n

)

25 b ← argbest

t=1,...,n

)

26 P ← P

27 M ← M

28 e ← e +1

29 while (e < n

)

30 return M

Output: symbolic model M

4 EXPERIMENTS

4.1 Test Datasets

For the proof-of-concept experiments we used thir-

teen datasets, featuring both synthetic and real data,

with the number of dimensions ranging from 2 to

4. Figure 3 shows mesh plots of all 2-dimensional

datasets used.

To demonstrate how the transformed variables fa-

cilitate ﬁnding models of functions in a transformed

space, we used the synthetic datasets sig0, sigπ/8

and sigπ/4 shown in Figures 3(a) through 3(c). The

dataset sig0 was calculated using a sigmoid-like func-

tion, deﬁned by Equation 1, sampled on a regular grid

of 31 × 31 points for x

∈ [−10,10].

(x) = 0.1x

1 + e

−x

(1)

Note that x

is not used in the equation and there-

fore, the values of the function do not change along

the x

dimension. The function was then rotated by

π/8 rad (dataset sigπ/8) and π/4 rad (dataset sigπ/4)

in the counterclockwise direction in order to simulate

the transformation of the coordinate system.

Other two synthetic datasets f2 and f3 (Figures

3(d) and 3(e)) were generated using the following

functions:

(x) = x

cos(10x

− 15x

), (2)

(x) =(x

− 1)

cos(10(x

− 1) − 15(x

− 1)) (3)

−(x

− 1)

sin(10(x

− 1) + 15(x

− 1)),

sampled on a regular grid of 31 × 31 points in the in-

terval x

∈ [0,1].

The following datasets come from the domain of

reinforcement learning applications.

The 1dof dir dataset (Figure 3(f)) consists of sam-

ples of the value function approximator for a 1-DOF

inverted pendulum swingup (Adam et al., 2012). The

pendulum moves in a state space deﬁned by variables

α ∈ [−π, π],

α ∈ [−40, 40], where α denotes the an-

gle and

α is the angular velocity of the pendulum.

The pendulum is pointing up for α = 0. The 961 data

points were sampled on a regular grid with 31 samples

in each dimension. The 1dof inv dataset (Figure 3(g))

is a variant of the 1-DOF swingup problem, which

differs in the interpretation of the angle α. The pen-

dulum is pointing down for α = 0, whereas both for

α = −π and α = π, the pendulum is pointing up.

The magman dataset (Figure 3(h)) is based on a

magnetic manipulation (Hur

ak and Zem

anek, 2012)

problem. The magnetic manipulation setup consists

of two electromagnets in a line positioned at a = 0 m

and a = 0.025 m. The dataset is represented by sam-

ples of the value function approximator on the domain

∈ [0,0.05], x

∈ [−0.4,0.4], where x

= a is the po-

sition and x

= ˙a is the velocity. The data are sampled

on a regular grid of 31 × 31 points.

The policy dataset represents samples of the pol-

icy function for the direct inverted pendulum task,

described above. The policy function was sampled

on the range x

∈ [−π,π], x

∈ [−40,40]. From the

whole state space, only the samples in the transition

region were used and the plateaus were removed from

the dataset, see Figure 3(i). In order to retain the num-

ber of training data points comparable with the rest of

the datasets used in the experiments, these data were

sampled on a regular grid with a higher resolution of

61 × 61 points. The policy dataset comprises 313 data

points.

The last dataset related to the reinforcement learn-

ing, denoted 2dof, is derived from the value function

for an inverted pendulum with two links. It is a 4-

dimensional problem with the angle α

and angular

velocity

describing the state of each link i ∈ {1,2}.

The dataset consists of 6561 data points sampled on

a regular grid with nine samples evenly distributed in

each dimension.

4.2 Experiment Setup

We experimentally evaluated the proposed SNGP-TV

algorithm and compared it to two other variants of

SNGP – namely the SNGP with simple population

(see Figure 1) denoted as SNGP-SP and the SNGP

with partitioned population (see Figure 2) but not us-

ing the transformed variables, denoted as SNGP-PP.

Note, both the variants can be described by the Algo-

rithm 1 if the population type and control parameters

are set accordingly. The SNGP-SP and SNGP-PP dif-

fer in the population type while none of them uses

the transformed variables, so n

= 0 and l

= 0. The

SNGP-TV was tested with the number of transformed

variables being equal to the number of the original

variables, i.e. n

= n.

Other control parameters were set as follows:

• population size: L = 500

• total number of ﬁtness evaluations: 20.000

• epochs: n

= 20, n

= 2

• trivial constants: C = {0,0.5,1,2,3,4}, n

= 6

• original variables: n = 2

• maximum tree depth: d = 7

• basic functions:

= {∗,+,−,square,cube,BentIdentity

= {∗,+,−,square,cube,Sigmoid}

• maximum number of features: n

= 10, n

= 3

• SNGP-SP: l

= 650, l

= 150

• SNGP-PP: l

= 650, l

= 150, n

= 121

• SNGP-TV: l

= 500, l

= 150, l

= 150, n

= 120

We carried out three experiment series:

1. experiment-1 – all compared algorithms were run

on all datasets with function set F

and the maxi-

mum number of features n

= 10.

Bent identity is a non-linear, unbounded, monotonic

function that approximates identity near the origin, see

http://www.wow.com/wiki/Activation function.

2. experiment-2 – all compared algorithms were run

on all datasets with function set F

and the maxi-

mum number of features n

= 3.

3. experiment-3 – algorithms SNGP-PP and SNGP-

TV were run on synthetic datasets sigπ0, sigπ/8,

and sigπ/4 with function set F

and the maximum

number of features n

= 3.

The ﬁrst two experiments were run to support our hy-

pothesis that the use of the transformed variables in

GP can be beneﬁcial. The two experiments differ

in the complexity of the evolved general regression

models. Our hypothesis is that when more complex

models (in terms of the maximum number of evolved

features combined in the linear regression models) are

allowed, then even less effective algorithms (i.e. the

ones not using the transformed variables) can be able

to construct a good model. On the other hand, when

less complex models are allowed, the advantage of us-

ing the transformed variables should prove more sig-

niﬁcant. Experiment-3 is proposed to illustrate that

when the population contains some feature or its part

that might well describe the data if its input was prop-

erly transformed, then this can efﬁciently be achieved

with the transformed variables. In this case the key

element of the model sought is the sigmoid function

that was added to the set of basic functions in place of

the BentIdentity function.

Each experiment was replicated 30 times with the

root mean squared error (RMSE) calculated for each

single run. The median RMSE over the 30 runs is

used as the performance measure in the tables with

results. The Wilcoxon rank sum test (also known as

the Mann-Whitney U-test) was used to evaluate sta-

tistical signiﬁcance of the difference in performance

between two algorithms.

Besides the RMSE, the complexity of the pro-

duced models was analyzed as well. In general, the

complexity of a model was calculated as the total

number of nodes in the model. More precisely, the

model complexity equals the sum of the complexi-

ties of the features that the model is composed of,

plus the operators and weights that are used to join

the features into one expression (the whole regres-

sion model). The following assumptions were made

for the calculation of a complexity of the SNGP-PP

and SNGP-TV models. In the case of SNGP-PP and

SNGP-TV, each constant-valued tree rooted in a head

partition node was treated as a single constant-valued

node. Thus, if some tail partition function node takes

a head partition node as its input, then this head par-

tition node is counted as a single node, even though

it is effectively represented by a more complex tree

structure. The rationale behind this assumption is that

the head partition was introduced into the population

(a) (b) (c)

(d) (e) (f)

(g) (h) (i)

Figure 3: Mesh plots of the datasets. The intersections of the grid represent the data used as the input for the SNGP algorithm

and its variants. The following datasets were used in the experiments: from (a) to (c) – synthetic sigmoid-like function

described by Equation 1, rotated by (a) 0 rad, (b) π/8 rad and (c) π/4 rad; (d), (e) – synthetic functions described by Equation

2 and 3, respectively; (f), (g) – variants of inverted pendulum, (h) – magnetic manipulation; (i) – policy function for inverted

pendulum (transition region only).

in order to facilitate a production of constant-valued

expressions that act as single constants in the ﬁnal

models. Similarly, each transformed variable node in

SNGP-TV is treated as a single variable node, even

though it is effectively represented by a more com-

plex structure, see Section 3.1.

Note, we restrict our experiments to compare only

the SNGP variants – SNGP with and without the

transformed variables. We do not include any other

GP method into the analysis since we simply want

to demonstrate that if the transformed variables are

used in some GP method for solving the symbolic re-

gression problem, then it leads to an improved perfor-

mance of that method. We did not tune control param-

eters of the compared SNGP algorithms either since

the purpose of the experiments was not to present

the best possible performance of the algorithms on

the test data sets. Again, we just wanted to show

the difference between using and not using the trans-

formed variables with the other control parameters set

the same for both variants. It is very likely that if we

tuned the control parameters of the SNGP, the perfor-

mance of the compared variants, both the one with

and the one without the transformed variables, would

improve.

4.3 Results

Results for experiment-1 are summarized in Table 1,

Table 2 and Table 3. Table 1 presents the median

RMSE values. Table 2 shows which algorithms out-

perform the other algorithms. A given algorithm out-

performs another algorithm on a given dataset if both

of the following two conditions are met:

Table 1: Medians of RMSE for all tested algorithms and

datasets in experiment-1.

Dataset

SNGP variant

Scale

SP PP TV

sig0 8.75 8.51 6.98 ×10

−4

sigπ/8 5.42 5.45 0.46 ×10

−2

sigπ/4 1.64 2.85 0.26 ×10

−2

f2 2.76 2.64 1.59 ×10

−1

f3 4.06 4.00 3.26 ×10

−1

1dof dir 2.82 2.82 1.34 ×10

1dof inv 2.50 2.20 2.22 ×10

magman 8.54 7.51 3.55 ×10

−3

policy 1.88 1.88 1.84 ×10

2dof 5.24 5.24 4.66 ×10

Table 2: Comparison of performance of algorithms in

experiment-1. The table shows which algorithms are out-

performed by the algorithm in the column heading for each

dataset. The performance is compared using the Wilcoxon

rank sum test with a signiﬁcance level of 1 %. The entry

with an asterisk would be included if the signiﬁcance level

was increased to 5 %.

Dataset

SNGP variant

SP PP TV

sig0

sigπ/8 SP, PP

sigπ/4 SP, PP

f2 SP, PP

f3 SP, PP

1dof dir SP, PP

1dof inv SP SP

magman SP SP, PP

policy SP, PP*

2dof SP, PP

• its RMSE median is smaller than the RMSE me-

dian of the compared algorithm,

• the Wilcoxon rank sum test rejects the null hy-

pothesis that the RMS errors in the 30 runs for

each of the two algorithms are samples from dis-

tributions with equal medians, at the statistical

signiﬁcance level of 1 % and 5 %, respectively.

In the case of 1 % signiﬁcance level, the null hypothe-

sis for the pair of SNGP-PP and SNGP-TV algorithms

was not rejected on 3 datasets. When the signiﬁ-

cance level was increased to 5 %, the null hypothesis

was not rejected on 2 datasets. Table 3 presents the

median complexity of models produced by the three

compared variants. It shows that the complexity of

SNGP-TV models, as deﬁned in Section 4.2, is in

most cases less than the complexity of the SNGP-SP

and SNGP-PP models.

Table 3: Medians of complexity for all tested algorithms

and datasets in experiment-1.

Dataset

SNGP variant

SP PP TV

sig0 108 106 100

sigπ/8 119 121 104

sigπ/4 119 117 102

f2 137 144 125

f3 128 133 119

1dof dir 122 122 106

1dof inv 126 119 112

magman 132 144 122

policy 118 118 119

2dof 103 106 106

Table 4: Medians of RMSE obtained with SNGP-PP and

SNGP-TV in experiment-2.

Dataset

SNGP variant

Scale

PP TV

sig0

4.07 2.41

×10

−2

sigπ/8

1.43 0.72

×10

−1

sigπ/4

1.45 0.42

×10

−1

2.98 2.74

×10

−1

4.31 4.17

×10

−1

1dof dir

5.20 4.03

×10

1dof inv

5.00 4.31

×10

magman

1.04 0.73

×10

−2

policy

3.21 2.92

×10

2dof

8.40 7.01

×10

Results for the experiment-2 are summarized in

Table 4. Here, the null hypothesis was rejected at the

1 % signiﬁcance level for all datasets with the excep-

tion for the policy dataset. When the signiﬁcance level

was increased to 5 %, the null hypothesis was rejected

for all datasets. Thus, the improvement provided

by the transformed variables is even more signiﬁcant

when smaller models are evolved as demonstrated by

the increased number of datasets on which SNGP-TV

proved to be signiﬁcantly better than SNGP-PP com-

pared to the results observed in experiment-1. Simi-

larly as in the experiment-1, the complexity of SNGP-

TV models is in most cases less than the complexity

of the SNGP-PP models, see Table 5.

Results for the experiment-3 are summarized in

Table 6. Both SNGP-PP and SNGP-TV variants per-

form equally well on the unrotated dataset sig0 as the

null hypothesis was rejected neither at the 1 % nor 5 %

signiﬁcance level. This is in accordance with our ex-

pectation that this dataset is easy for the algorithms

since they only need to generate and combine sim-

ple linear and sigmoid features with a single input x

Table 5: Medians of complexity obtained with SNGP-PP

and SNGP-TV in experiment-2.

Dataset

SNGP variant

PP TV

sig0

32 32

sigπ/8

32 37

sigπ/4

37 35

57 47

49 49

1dof dir

40 36

1dof inv

40 35

magman

53 42

policy

41 39

2dof

39 38

Table 6: Medians of RMSE obtained with SNGP-PP and

SNGP-TV in experiment-3.

Dataset

SNGP variant

Scale

PP TV

sig0

6.26 6.75

×10

−10

sigπ/8

9.61 0.17

×10

−2

sigπ/4

3.72 0.13

×10

−2

Table 7: Medians of complexity obtained with SNGP-PP

and SNGP-TV in experiment-3.

Dataset

SNGP variant

PP TV

sig0

24 22

sigπ/8

38 25

sigπ/4

33 29

On dataset sigπ/4, a signiﬁcant difference in perfor-

mance between SNGP-PP and SNGP-TV can already

be observed. However, even SNGP-PP was able to

ﬁnd a solution with RMSE lower than 6.5 × 10

−10

10 out of 30 runs. These results correspond to models

that employ a sigmoid feature with a simple argument

). A similar trend of SNGP-TV outperforming

SNGP-PP was observed on the sigπ/8 dataset where

SNGP-TV achieves by more than one order of mag-

nitude better RMSE than SNGP-PP. Moreover, the

best solution obtained with SNGP-PP had an RMSE

of 7.7 × 10

−5

, while SNGP-TV generated ﬁve solu-

tions with RMSE lower than 6.5 × 10

−10

. Again,

the complexity of SNGP-TV models is lower than

the complexity of the SNGP-PP models, see Table 7.

The most signiﬁcant difference being observed on the

sigπ/8 dataset, which is the one with the most ”difﬁ-

cult” transformation of the input space.

5 CONCLUSIONS

The concept of local transformed variables for sym-

bolic regression was introduced, so that the genetic

programming search for an accurate model is more ef-

ﬁcient. We have integrated transformed variables into

the Single Node Genetic Programming algorithm, us-

ing a partitioned population with certain nodes ex-

plicitly devoted to producing constant-output expres-

sions.

The experimental results show that the proposed

SNGP with transformed variables outperforms the

baseline SNGP algorithm on the majority of test

datasets. We found that the transformed variables

are especially useful when parsimonious models are

sought.

Our future research will focus on incorporating

model complexity control into the algorithm, which

may further boost the performance of the approach.

ACKNOWLEDGMENT

This research was supported by the Grant Agency

of the Czech Republic (GA

CR) with the grant

no. 15-22731S titled “Symbolic Regression for Re-

inforcement Learning in Continuous Spaces” and

by the European Regional Development Fund un-

der the project Robotics 4 Industry 4.0 (reg. no.

CZ.02.1.01/0.0/0.0/15 003/0000470).

REFERENCES

Adam, S., Bus¸oniu, L., and Babu

ska, R. (2012). Experi-

ence replay for real-time reinforcement learning con-

trol. IEEE Transactions on Systems, Man, and Cyber-

netics. Part C: Applications and Reviews, 42(2):201–

212.

Alibekov, E., Kubal

ık, J., and Babu

ska, R. (2016). Sym-

bolic method for deriving policy in reinforcement

learning. In Proceedings of the 55th IEEE Conference

on Decision and Control (CDC), pages 2789–2795,

Las Vegas, USA.

Arnaldo, I., O’Reilly, U.-M., and Veeramachaneni, K.

(2015). Building predictive models via feature syn-

thesis. In Proceedings of the 2015 Annual Conference

on Genetic and Evolutionary Computation, GECCO

’15, pages 983–990, New York, NY, USA. ACM.

Brauer, C. (2012). Using Eureqa in a Stock Day-Trading

Application. Cypress Point Technologies, LLC.

Ferreira, C. (2001). Gene expression programming: a new

adaptive algorithm for solving problems. Complex

Systems, 13(2):87–129.

Hart, W. E., Smith, J. E., and Natalio, K. (2005). Recent

Advances in Memetic Algorithms. Springer, Berlin,

Heidelberg.

Hinchliffe, M., Hiden, H., McKay, B., Willis, M., Tham,

M., and Barton, G. (1996). Modelling chemical pro-

cess systems using a multi-gene genetic programming

algorithm. In Koza, J. R., editor, Late Breaking Papers

at the Genetic Programming 1996 Conference Stan-

ford University July 28-31, 1996, pages 56–65, Stan-

ford University, CA, USA. Stanford Bookstore.

Hur

ak, Z. and Zem

anek, J. (2012). Feedback lineariza-

tion approach to distributed feedback manipulation. In

American control conference, pages 991–996, Mon-

treal, Canada.

Jackson, D. (2012a). A new, node-focused model for ge-

netic programming. In Moraglio, A., Silva, S., Kraw-

iec, K., Machado, P., and Cotta, C., editors, Genetic

Programming: 15th European Conference, EuroGP

2012, M

alaga, Spain, April 11-13, 2012. Proceedings,

pages 49–60. Springer, Berlin, Heidelberg.

Jackson, D. (2012b). Single node genetic programming

on problems with side effects. In Coello, C. A. C.,

Cutello, V., Deb, K., Forrest, S., Nicosia, G., and

Pavone, M., editors, Parallel Problem Solving from

Nature - PPSN XII: 12th International Conference,

Taormina, Italy, September 1-5, 2012, Proceedings,

Part I, pages 327–336. Springer, Berlin, Heidelberg.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion (Complex Adaptive Systems). MIT Press Ltd.

Kubal

ık, J., Alibekov, E.,

Zegklitz, J., and Babu

ska, R.

(2016). Hybrid single node genetic programming for

symbolic regression. In Nguyen, N. T., Kowalczyk,

R., and Filipe, J., editors, Transactions on Compu-

tational Collective Intelligence XXIV, pages 61–82.

Springer, Berlin, Heidelberg.

McConaghy, T. (2011). FFX: Fast, scalable, determin-

istic symbolic regression technology. In Riolo, R.,

Vladislavleva, E., and Moore, J. H., editors, Genetic

Programming Theory and Practice IX, pages 235–

260. Springer New York, New York, NY.

Miller, J. F. and Thomson, P. (2000). Cartesian genetic pro-

gramming. In Poli, R., Banzhaf, W., Langdon, W. B.,

Miller, J., Nordin, P., and Fogarty, T. C., editors, Ge-

netic Programming: European Conference, EuroGP

2000, Edinburgh, Scotland, UK, April 15-16, 2000.

Proceedings, pages 121–132. Springer, Berlin, Hei-

delberg.

Ryan, C., Collins, J., and Neill, M. O. (1998). Gram-

matical evolution: Evolving programs for an arbi-

trary language. In Banzhaf, W., Poli, R., Schoenauer,

M., and Fogarty, T. C., editors, Genetic Program-

ming: First European Workshop, EuroGP’98 Paris,

France, April 14–15, 1998 Proceedings, pages 83–96.

Springer, Berlin, Heidelberg.

Schmidt, M. and Lipson, H. (2009). Distilling free-

form natural laws from experimental data. Science,

324(5923):81–85.

Searson, D. P., Leahy, D. E., and Willis, M. J. (2010). GP-

TIPS : An open source genetic programming toolbox

for multigene symbolic regression. In Proceedings

of the International Multiconference of Engineers and

Computer Scientists 2010 (IMECS 2010), volume 1,

pages 77–80, Hong Kong.

Staelens, N., Deschrijver, D., Vladislavleva, E., Vermeulen,

B., Dhaene, T., and Demeester, P. (2013). Construct-

ing a no-reference H.264/AVC bitstream-based video

quality metric using genetic programming-based sym-

bolic regression. IEEE Transactions on Circuits and

Systems for Video Technology, 23(8):1322–1333.

Vladislavleva, E., Friedrich, T., Neumann, F., and Wagner,

M. (2013). Predicting the energy output of wind farms

based on weather data: Important variables and their

correlation. Renewable Energy, 50:236–243.