
Influence of Selection of Release Angle and Speed on Success Rates of
Jump Shots in Basketball
Yuki Inaba, Noriko Hakamada and Munenori Murata
Department of Sports Science, Japan Institute of Sports Science, 3-15-1 Nishigaoka, Kita-ku, Tokyo, Japan
Keywords: Jump Shots, Basketball, Margin for Error, Release Angle, Release Speed.
Abstract: Enhancing the successful jump-shot percentages in basketball is critical for winning a game. A selection of
release parameters and variability can influence the success rate, but the actual selection of the release
parameters and variabilities in those during jump shots and the influence of this selection on success rate
have not been investigated and are not understood well. Thus, the purpose of this study was to investigate
the influences of the selection of release angle, release speed and spin rate, and variability on the success
rate of jump-shots in basketball. Ten male collegiate basketball players participated in the study and actual
ball trajectories for the jump-shots from the free-throw (FT) and three-point (3P) lines were recorded by the
three-dimensional motion analysis system. The experimental data was compared with the theoretical
optimal release parameters. We found that the players with higher success rate in FT shots had a higher
release position, a lower release velocity, and a larger margin for error for the release speed. On the other
hand, for the 3P shots, the player with a larger margin for error for the combination of the release speed and
angle had higher success rate. Variability in release parameters did not have significant correlation with the
success rate. Thus, it can be said that selecting the release parameters that allow greater margin for error was
important for increasing the success rate. Also, depending on the required release speed or the shooting
distance, the strategies for the selection of the release parameters must be adjusted to increase the success
rate in jump-shots.
1 INTRODUCTION
Shooting is the only way to score in basketball, and
needless to say, it is very important skill in a
basketball game. In particular, it has been reported
that jump shots are effective and one of the most
frequently used styles of shots in a basketball game
(Knudson, 1993). Thus, enhancing the successful
jump-shot percentages is critical for winning a game.
A ball trajectory with higher success rate can be
considered from the number or range of possible
successful trajectories from a certain release position.
Since the size of the basketball ring (diameter: 0.45
m) is about the twice the size of the basketball
(diameter: 0.25 m), the range for a successful paths
for a ball passing through the basket is not limited to
one, but there is a margin for error for the
trajectories (Brancazio, 1981). Thus, the selection of
the conditions that increase this margin for error is
one factor that enhances the shooting success rate.
The range of successful paths is influenced by
the entry angle of the ball into the basket ring. This
is because a higher entry angle (closer to
perpendicular) provides a larger area for the
successful paths of a ball passing through the basket.
Since the trajectory of the ball after it is released
from the hand of a player can be regarded as
parabolic motion, the release parameters such as the
release speed, release angle, and release height are
the main factors that influence the trajectory and
arrival position of the ball. In particular, influences
of selection of release angle and speed with a fixed
release height have been investigated. As for the
release angle, since it affects the entry angle into the
basket ring (Brancazio,1981; Miller and Bartlett,
1996) and a greater release angle provides a larger
area for the ball to pass through the ring, a higher
release angle can be regarded as advantageous. That
is, the range of speed for a successful trajectory
becomes larger for a higher release angle. The range
of release speeds at a selected release angle is called
the margin for error for the speed. Thus, it can be
assumed that it is advantageous to increase the
release angle in order to achieve a larger margin for
error for the speed.
Inaba Y., Hakamada N. and Murata M.
Influence of Selection of Release Angle and Speed on Success Rates of Jump Shots in Basketball.
DOI: 10.5220/0006505500480055
In Proceedings of the 5th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2017), pages 48-55
ISBN: 978-989-758-269-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

However, if the release angle is increased, a
higher release speed is required, which can
negatively affect the consistency and accuracy of the
movement (Knudson, 1993). This is because a low
release velocity accompanies a decreased movement
variability and results in a lower variability in
release velocity (Darling & Cooke, 1987). Thus,
increase in the release angle that is higher than
necessary can be disadvantageous for enhancing the
shooting success rate. At the same time, a margin
for error for the angle also exists for a certain release
speed; thus, maximization of this margin for error
should also be taken into consideration.
Considering this trade-off between the release
angle and the release speed, Brancazio(1981)
introduced the existence of the “minimum-speed
angle”. The ratio of the margin for error for the
speed to the release speed is very small compared to
the release angle. Also, releasing a ball at the
minimum speed requires minimum force. Thus,
minimizing the release speed was used as the criteria
to choose the optimal combination of the release
angle and speed. There exists a release angle that
causes the ball to arrive at the center of the ring at
minimum speed, which was referred to “minimum-
speed angle.” Thus, theoretically, the minimum-
speed angle was regarded as the optimal release
angle that maximise the margin for error and
achieves movement consistency.
Though theoretically established, the actual
selection of the release parameters by players during
jump shots and the influence of this selection on
success rate have not been investigated and are not
understood well. In addition, the variability in the
release parameters has not been investigated
thoroughly with a combination of the optimal
selection. It is possible that the variabilities in the
release angle and speed influence the success rate.
Thus, the purpose of this study was to investigate the
influences of the selection of the release parameters
(the release angle and the release speed) and
variability on the success rate by comparing the
calculated theoretical optimal release parameters.
In addition to the release angle and release speed,
the spin rate possibly influences the trajectory and
success rate. It has been reported by numerical
analysis that having back spin and increasing the
spin rate to about 3 Hz increase the possibility that
free-throw shots are made (Hamilton and
Reinschmidt, 1997; Silverberg et al., 2003; Okubo
and Hubbard, 2006; Tran and Silverberg, 2008). In
these studies, the main influence of back spin was
not on the trajectory in air, but rather the behavior of
the ball upon collision with the ring or backboard. In
fact, these studies neglected the influences of the
drag force and lift force in air, and some studies
reported that the air resistance is negligible and does
not have a significant effect on the trajectory of a
ball (Okazaki and Rodacki, 2012). However,
Brancazio (1981) mentioned that air resistance does
have an effect on the trajectory though it is almost
neligible. Therefore, in our study, effects of spin and
aire resistance on the ball trajectory was examined
by analyzing the entire trajectory of the ball from
release to arrival at the basket since the selection of
the release parameters can be influenced if they
affect the trajectories. Thus, the influences of the
spin rate on the trajectory and the combination of the
release angle and release speed were also
investigated by simulating the ball trajectory at
different ball spin rates.
By investigating the actual selection of and
variability in the release parameters (the release
angle, speed, and spin rate) for basketball jump shots
and the influence on the success rate, we believe that
the results will provide reference for selecting
release parameters during coaching or training of
jump shots.
2 METHODS
2.1 Participants
Ten male collegiate basketball players (height: 1.86
±0.07 m, body mass: 82.1±7.4 kg, age: 22±1
years-old, years of experience in basketball: 13±3
years, mean±standard deviation (SD)) who belong
to a collegiate basketball team in the Japanese Kanto
College Basketball Division 1 League participated in
this study. Three players were selected to Japanese
National Basketball Teams for the Universiade (or
World University Games). Written informed consent
to participate in the study was obtained from all
participants after informing them of the purpose of
this study and explaining the procedure and possible
risks of the study. The study protocol was approved
by the Human Subjects Committee of the Japan
Institute of Sports Sciences.
2.2 Experimental Procedure
After a sufficient warm-up period, the participants
attempted 100 jump shots. Fifty shots were from the
three-point line (6.75 m away from the center of the
ring in the horizontal direction: 3P), and another 50
shots were from the free-throw line (4.23 m away

from the center of the ring in the horizontal
direction: FT). Shots were attempted after receiving
a pass from an experienced basketball player
positioned under the basketball goal ring.
Participants were instructed to “shoot as you do in
the game,” or a quick shot released at high position.
Participants took a short break after each set of 25
shots.
2.3 Data Collection
Forty-eight reflective markers were attached to the
participants, and 9-11 reflective marks were
randomly attached to the surface of the basketball.
The positions of these markers and the marks during
shooting motion were obtained using a three-
dimensional motion analysis system using 20
cameras operating at 500 Hz (VICON MX series,
Vicon Motion Systems Ltd., Oxford, UK).
2.4 Data Processing
The ball trajectories and spin rate were computed
using the obtained markers attached to the ball’s
surface. To take the possible influences due to air
drag and lift force into consideration, the
coefficients of drag and lift, the release speed, the
release angle, and the position of the ball at the
height of ring were estimated by optimization. A
successful combinations of a release angle and
release speed from a mean release height and
horizontal distance from the ring center, and spin
rate was calculated by solving the equation of
motion for the ball including the drag and lift forces.
The margins for error for the release angle and speed
were calculated and theoretically optimal parameters
were compared with those that the participants
actually selected. The ball trajectories were also
simulated at a higher spin rate to investigate the
influence of the increased spin rate on shot success
possibility.
2.4.1 Ball Trajectory
The trajectories of the ball center
,
,
)
were computed using the positional data of the
marks attached to the surface of the basketball
,
,
). The relation between
and the
positional data of the ball surface marks are
expressed as equation of sphere (1).
1
2
(1)
Thus, the position of center of the ball
was
determined through optimization to minimize the
least-squares deviation.
where
is the diameter of the basketball (0.245 m).
2.4.2 Computation of the Drag and Lift
Coefficients and Release Parameters
Since the raw ball trajectory data was different from
the calculated trajectory from the initial velocity by
a significant amount, it was assumed that there were
significant influences due to drag and lift forces on
the ball. The equation of motion for the ball in air
was formulated as follows (Yasuda, 2014):
(2)
where
is the acceleration of the ball,
is the
acceleration by drag force,
is the acceleration by
lift force, and
is the gravitational acceleration.
Here,
was computed from equation (3):
(3)
where m is the mass of the ball, q is the speed of the
ball, is the velocity vector, and k is calculated by
the following equation (4):
1
2
(4)
where is the air density, S is the cross sectional
area of the ball,
is the coefficient of drag force.
was calculated by the following equation (5):
(5)
where
is the unit vector of the axis of rotation of
the ball, and l is calculated by the equation (6):
1
2
(6)
where
is the coefficient of lift force. The release
position, the release speed, the coefficient of drag
force, and the coefficient of lift force were
determined through optimization by a genetic
algorithm to minimize the least-squares deviation
between the calculated and actual (raw) trajectories.
2.4.3 Computation of Successful
Combination of Release Angle and
Release Speed
The ball trajectories were recalculated for various
combinations of the release angle and the release
speed with the mean release height, horizontal
distance from the ring center, spin rate, and

coefficients of drag and lift of fifty shots of each
player by solving the equation of motion using a
fourth order Runge–Kutta algorithm. The position of
the ball when it reached the height of the goal ring
was calculated (arrival position). A shot was
regarded as successful if the arrival position was
within the successful region (x < ∆ and y < ∆,Fig.
1) where it could go through the ring without
touching the rim (swish) or barely touching the rim
(swish ± 50 mm region), which were calculated by
the following equations:
∆
1
2
sin
(7)
where
is the diameter of the ring (0.45 m) and
is the entry angle calculated by equation (8) as
reported in Brancazio (1981) :
arctantan
2
(8)
where
is release angle, is the vertical distance
between release height and basket height (3.05 m).
Also, the mediolateral boundary was calculated as
equation (9):
∆
1
2
(9)
where is the anteroposterior distance between
center of the ring and the arrival position of the ball.
Figure 1: Calculation of successful region of arrival
position of the ball.
2.4.4 Margin for Error for Release Angle
and Release Speed
The margin for error for the release angle at the
selected release speed and the margin for error for
the release speed at the selected release angle were
calculated at mean release height, horizontal
distance from the ring center, and spin rate. In
particular, the margin for error for the release angle
and release speed at the mean release speed and
release angle of each player were calculated and
compared with the release speed and release angle
that maximize the margin for error to evaluate the
selection of the release parameters.
2.4.5 Influence of Spin Rate on the
Successful Shot Possibility
The influence of the spin rate on the successful
combination of the release angle and the release
speed for the 3P shot was investigated by simulating
the ball trajectory with an increased spin rate and the
corresponding lift and drag coefficients for one
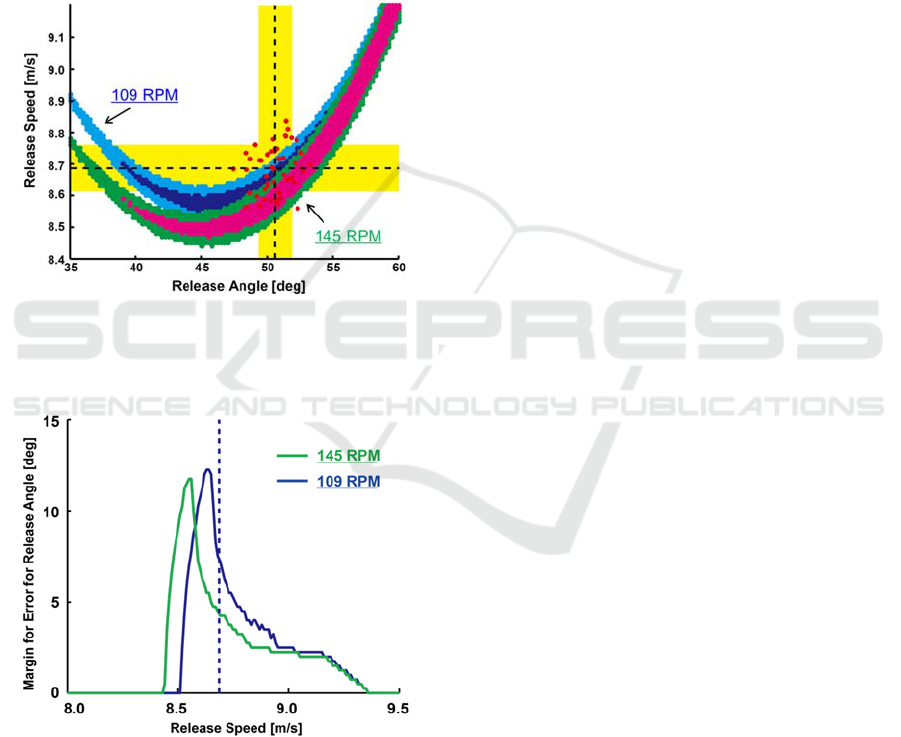
subject. The original spin rate for this subject was
109 rotations per minute (RPM) and was altered to
145 RPM which was equal to the highest spin rate of
all players.
2.4.6 Statistics
A Pearson correlation coefficient was used to
establish relationships between the success rate and
the horizontal distance from the ring center, release
angles, speed, and margins for errors. The level of
significance was set at P < 0.05.
3 RESULTS
3.1 Successful Shot Percentages and
the Arrival Position of the Ball
The number of shots made and the mean and SD of
the distance from the ring center for FT and 3P shots
for all participants are listed in Table 1 and Table 2.
The successful shot percentages were lower for 3P
than FT shots and there were differences in the
percentages between the players. A significant
correlation between the successful shot percentage
and the SD of the anteroposterior distance of arrival
position of the ball from the ring center for 50 FT
shots in FT (r = -0.68, p < 0.05) was observed but
not for 3P shots. For instance, for 3P shots, player 4
whose shot percentage was the lowest among all
players had larger mean anteroposterior and
mediolateral distances from the ring center but the
SDs were not the largest among all players.

Table 1: Percentages of shots made for each player and
arrival positions in FT shots.
FT
# of
shots
made
Distance from ring center for 50 shots [cm]
Anteroposterior Mediolateral
ID Mean SD Mean SD
1 47 2.3 7.4 1.3 5.3
2 45 0.2 7.8 4.2 6.1
3 44 11.4 9.2 2.8 5.0
4 42 5.7 9.4 3.9 6.4
5 32 12.5 12.0 -1.3 6.9
6 46 6.1 11.1 1.3 5.8
7 41 4.3 8.7 -2.4 6.1
8 42 -0.1 9.0 -2.2 6.2
9 46 7.6 7.6 -1.7 7.4
10 39 5.2 9.7 0.9 8.4
Mean
42
(84%)
5.5 9.2 0.7 6.4
SD 4.5 4.2 1.5 2.5 1.0
Table 2: Percentages of shots made for each player and
arrival positions in 3P shots.
3P
# of
shots
made
Distance from ring center for 50 shots [cm]
Anteroposterior Mediolateral
ID Mean SD Mean SD
1 36 4.2 7.8 3.1 10.5
2 33 -1.9 9.1 0.1 9.2
3 36 6.7 11.7 3.8 6.4
4 17 18.9 11.4 7.7 10.7
5 27 7.1 9.3 -1.4 12.1
6 34 7.4 12.7 -3.1 10.4
7 26 4.0 10.1 -5.4 9.9
8 31 -2.2 10.0 -2.9 8.1
9 36 5.7 11.1 1.0 9.1
10 35 1.9 9.4 2.6 8.7
Mean
31
(62%)
5.2 10.3 0.6 9.5
SD 6.2 5.9 1.5 3.9 1.6
3.2 Comparison of the Selected Release
Parameters and the Theoretical
Optimal Combination
For FT shots, significant correlations between the
success rate and the release height (r = 0.82,
p < 0.05) and release speed (r = -0.64, p < 0.05)
were observed. The release angle and its variability,
and the variability in the release speed did not have
significant correlation with the success rate.
Moreover, players with a larger margin for error for
the release speed at his mean release angle had a
higher success rate (r = 0.64, p < 0.05). For player 9
with a higher FT success rate (92%), the mean
release angle (50.4°) was higher than the minimum-
speed angle (47.6°), and the mean release speed
(6.90 m/s) was close to the release speed that
maximizes the margin for error for the release angle
(6.86 m/s) (Figs.2 and 3). For player 5 with the
lowest FT success rate (64%), the mean release
angle (46.6°) was lower than the minimum-speed
angle (49.6°), and the mean release speed (6.97 m/s)
was close to the release speed that maximizes the
margin for error for the release angle (6.93 m/s)
(Figs.2 and 3).
Figure 2: Theoretical successful combination of the
release angle and release speed (dark blue: swish, light
blue: swish±50 mm) and the experimental data (red) for
player 9, whose successful rate was high (top), and for
player 5, whose successful rate was the lowest (bottom) in
FT shots.
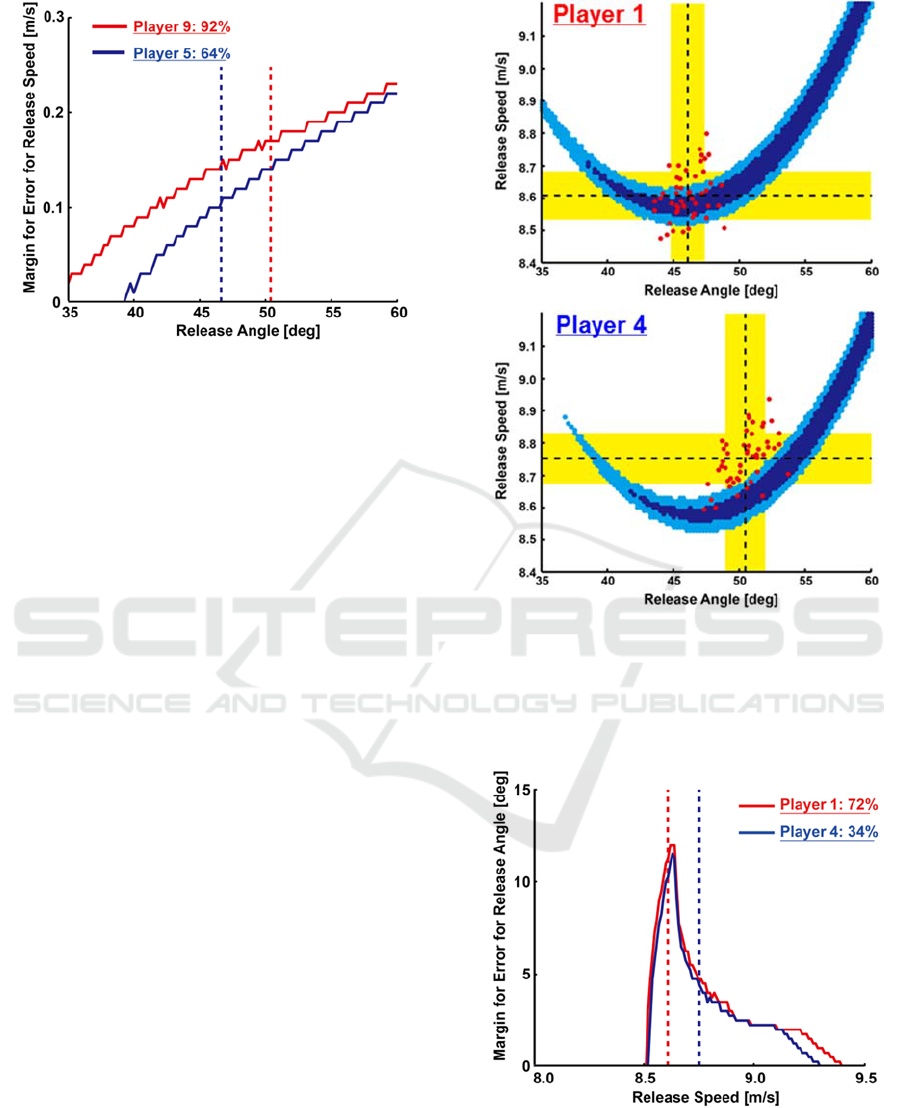
Figure 3: Margin for error for the release speed for player
9 (red) and player 5 (blue) in FT shots. The dashed lines
show the mean release angle for each player and the solid
lines show the computed margin for error for the release
speed at the selected release angle.
For 3P shots, no significant correlation was
observed for the release parameters and those
variabilities, and success rate. No significant
correlations between the margins for error for the
release speed and the release angle, and success rate
were observed. However, considering the combined
margin for error for both the release speed and
release angle were computed (margin for error for
the speed × margin for error for the angle), a
significant correlation (r = 0.70, p < 0.05) was
observed. For player 1 with the highest success rate
for 3P shots (72%), the mean release angle (46.1°)
was close to the minimum-speed angle (47.0°), and
the mean release speed (8.61 m/s) was close to the
release speed that maximizes the margin for error for
the release angle (8.62 m/s). For player 4 with the
lowest success rate for FT shots (34%), the mean
release angle (50.4°) was higher than the minimum-
speed angle (48.4°), and the mean release speed
(8.75 m/s) was also higher than the release speed
that maximizes the margin for error for the release
angle (8.63 m/s). For player 4, the actual
combination of release parameters was different than
the theoretical successful combination (Figs 4 and 5).
Figure 4: Theoretical successful combination of the
release angle and release speed (dark blue: swish, light
blue: swish±50 mm) and the experimental data (red) for
player 1, whose successful rate was one of the highest
(top), and for player 4, whose successful rate was the
lowest (bottom) in 3P shots.
Figure 5: Margins for error for the release angle for player
1 (red) and player 4 (blue). The dashed lines show the
mean release speed for each player, and solid lines show
the computed margin of error for the release angle at the
selected release speed.
3.3 Influence of Spin Rate on the
Theoretical Optimal Combination
Noticeable changes in the successful combination of
release angle and speed were observed when the ball
trajectories were simulated with different spin rate
(Figs. 6 and 7). For the selected release angles, the
corresponding release speeds resulting in successful
trajectories were lower for the higher spin rate
condition. Also, the region of release speed resulting
in successful shot was greater when the spin rate was
higher.
Figure 6: Theoretical successful combination of the
release angle and release speed with different spin rate
(dark blue and light blue: original spin rate 109 RPM,
green and pink: increased spin rate 145 RPM).
Figure 7: Margins for error for the release angle simulated
at original spin rate (blue) and increased spin rate (green)
for 3P shot.
4 DISCUSSION
The purpose of this study was to investigate the
influences of the selection of release angle, release
speed and spin rate and variability on the success
rate of jump-shots in basketball by comparing the
theoretical and actual release parameters. The
greater influence of selection of the release angle
and release speed than those variabilities on the
success rate during jump shots from different
distances was revealed in this study. For FT shots,
players with a higher release position, a lower
release speed, and a larger margin for error for the
release speed had higher success rate. For 3P shots,
player with a larger margin for error for the
combination of the release speed and angle had
higher success rate. However, the variabilities in
release speed and angle did not have significant
correlations with the success rate. Thus, it can be
said that selecting the release parameters that allow
greater margin for error was important for increasing
the success rate.
For FT shots, players who selected the release
angle with larger margin for error for the release
speed had higher success rate. It must be noted that
this accompanied lower release speed and higher
release height, which are assumed to have played a
role in minimizing the variability in release speed as
reported by Knudson(1993).On the other hand, for
shots from a larger distance, it is difficult to
maintain a low variability in the release speed since
the amplitude is higher. If release angle was
increased in addition to the increased release speed,
it would negatively affect the variability. Therefore,
it is expected that the players with a higher success
rate did not simply increase the release angle to
increase the margin for error for the release speed,
but selected the region that can maximize the
margins for error for both release angle and speed.
In fact, there was one player who selected high
release angle yet had higher success rate (Fig. 8).
Though this player selected relatively high release
angle, the selection of release speed was adjusted
according to the release angle. Also, since the
selected combinations of release angle and speed
were almost within the successful region, he could
achieve high success rate.
Thus, for shots from a larger distance, it is not
recommended to increase the release angle to
increase the margin for error for the release speed
unless the player can keep the variability low with
the increased release angle. On the other hand, for
shots from a close distance, the variability is not
negatively affected by increasing the release angle
since the release speed required is smaller. Therefore,
it is recommended to increase the release angle to
the extent that does not affect the variability.
However, it must be noted that the trend in changes

in variability depending on the shot distance varies
with the levels of players. Also, this study did not
assume indirect shots (interaction with the
backboard and ring), which can also influence the
success rate. In addition, the mean body height of
the participants was relatively high, which could
contribute to reduce the variability of the shots since
smaller release speed and angle are required for the
shots with higher release point.
Figure 8: Theoretical successful combination of the
release angle and release speed (dark blue: swish, light
blue: swish±50 mm) and the experimental data (red) for
player 9, whose successful rate was one of the highest.
The spin rate also had a significant effect on the
successful combination of the release speed and
angle. At the higher spin rate, the required speed at
the selected release angle was reduced (Fig. 6). Also,
the release speed that maximizes the margin for
error for release angle was lower for the increased
spin rate. It is assumed that by increasing the spin
rate, the ball experienced greater lift force, which
resulted in the trajectory with higher arch even when
the ball was released at lower release speed. Thus, in
addition to the reported positive influence of back
spin at the interaction with the backboard and ring
(Hamilton and Reinschmidt, 1997; Silverberg et al.,
2003; Okubo and Hubbard, 2006; Tran and
Silverberg, 2008), our results added an insight that
the trajectory is altered by the spin rate during the
ball is in air. When a player is relatively shorter it is
difficult to increase the release height as taller
players do. In that case, increasing the spin rate can
be another option for them to decrease the release
speed with respect to the same release angles.
5 CONCLUSIONS
The results of this study permit us to make the
following recommendations for increasing the
success rate in jump-shots: (1) The player should
increase the release height to decrease the required
release speed and variability in the closer shots
possibly by increasing their jump height or altering
their arm angle. (2) The player should increase the
release angle for shots from a closer distance since it
increases the margin for error for the release speed.
(3) The player should not increase the release angle
higher than necessary if it negatively affects the
variability of release speed especially in longer shots
such as the three-point shot. (4) Increasing spin rate
will help maintain the successful release speeds
lower for a given release angle and thereby
maintaining the variability in release speed low.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number 15K16482.
REFERENCES
Brancazio, P.J., 1981. Physics of basketball. American
Journal of Physics, 49, 356-365.
Knudson, D., 1993. Biomechanics of the basketball jump
shot- six key teaching points. Journal of physical
Education, Recreation, and Dance, 64, 67-73.
Yasuda, K., Tsuboi, K., Tanaka, K., Miyazaki, T., 2014.
Estimation of aerodynamic coefficients for aball by
using characteristics of trajectory. Transactions of the
JSME, 80 (814), 1-10.
Miller, S.A., Bartlett, R.M., 1996. The effects of increased
shooting distance in the basketball jump shot. Journal
of Sports Sciences, 11, 286-293.
Darling, W.G., Cooke, J.D., 1987. Movement related
EMGs become more variabl during learning of fast
accurate movements. Journal of Motor Behavior, 19,
311-331.
Hamilton, G.R., and Reinschmidt, C., 1997. Optimal
trajectory for the basketball free throw. Journal of
Sports Sciences, 15, 491-504.
Silverberg, L., Tran, C., Adcock, K., 2003. Numerical
analysis of the basketball shot. Journal of Dynamic
Systems, Measyrenebt, and Control, 125, 531-540.
Okubo, H., Hubbard, M., 2006. Dynamics of the
basketball shot with application to the free throw.
Journal of Sports Sciences, 24(12), 1303-1314.
Tran, C.M., Silverberg, L.M., 2008. Optimal release
conditions for the free throw in men’s basketball.
Journal of Sports Sciences, 26(11), 1147-1155.
Okazaki, V.H.A., Rodacki, A.L.F., 2012. Increased
distance of shooting on basketball jump shot. Journal
of Sport Science and Medicine, 11, 231-237.
