A Hybrid Feedback Control Model

for a Gesture-based Pointing Interface System

Kazuaki Kondo, Genki Mizuno and Yuichi Nakamura

Academic Center for Computing and Media Studies, Kyoto University, Yoshida Honmachi, Kyoto, Japan

Keywords:

Human-in-the-loop System, Pointing Behavior, Feedback Control Theory.

Abstract:

This study proposes a mathematical model of a pointing interface system that includes indicator behaviors

and pointer visualization based on the measurement of pointing postures. The key idea for simulating point-

ing behaviors under measurement noise involves constructing a hybrid feedback control model. It switches a

target value follow-up phase to a noise compensate phase at a speciﬁc elapsed time. We evaluated its perfor-

mance in terms of a simulation error with given step inputs as target values and random-walk noise sequences.

The results indicate that the proposed hybrid model simulates the actual pointing trajectories within several

centimeter errors.

1 INTRODUCTION

In daily communication, “pointing pose” is typically

used as an intuitive way to indicate target objects, lo-

cations, directions, and areas. However, the point-

ing pose could be potentially ambiguous for audience

such as when a questioner at a distance from a wide

screen points out a speciﬁc location on it. In these

type of cases, a pointing stick or a laser pointer is gen-

erally used to clearly indicate the target. The purpose

of our study is constructing a pointing support inter-

face as opposed to the additional equipments. Figure

1 illustrates an example of a construction that uses

visual sensing. It recognizes an indicator’s pointing

posture, estimates a target location on the screen, and

shows a visual pointer at the estimated location.

This study proposes a mathematical model of the

pointing interface system based on feedback control

theory including sensors, computers, visual devices,

and an indicator. It allow us simulation-based per-

formance evaluation and interface design. Once a

mathematical model of a target pointing interface sys-

tem is established, its behaviors under various point-

ing situations can be simulated and then its usability

is also evaluated. It aids in designing the interface

by employing a trial-and-error strategy without any

experimental evaluations in the real world. This ad-

vantage is extremely important for human inclusive

system because many real evaluations with partici-

pants require immense effort and involve difﬁculties

in conﬁguring the same experimental conditions. Fur-

thermore, repeatability of human behavior is not very

high, and thus each participant must constantly repeat

pointing under the same conditions to collect a sufﬁ-

cient number of samples from which general and es-

sential analysis/evaluations are obtained.

A key idea for modeling involves assuming that an

indicator switches a pointing strategy from approach-

ing to the target location to attempting to maintain a

pointer in its neighborhood. These behaviors are for-

mulated with two feedback control phases, namely a

target value follow-up phase and a noise compensate

phase. The characteristics of the two phases are rep-

resented with different parameter sets in the same for-

mulation with an assumption that the essential body

control schemes in those phases are same. This type

of hybrid framework is a ﬁrst trial in modeling point-

ing interface systems that were investigated. Thus in

this paper, we evaluate the performance of the pro-

posed model in accuracy of pointing trajectory simu-

lation.

2 RELATED WORKS

Easy-to-use interfaces should suit human perception

and behaviors. Speciﬁcally, transient behaviors from

the beginning to end of pointing were analyzed by

several extant studies. Woodworth et. al. proposed

a pointing action model by using a combination of

feed-forward motions for a rapid approach to a tar-

get position, and subsequent feedback adjustments

Kondo K., Mizuno G. and Nakamura Y.

A Hybrid Feedback Control Model for a Gesture-based Pointing Interface System.

DOI: 10.5220/0006506501340141

In Proceedings of the International Conference on Computer-Human Interaction Research and Applications (CHIRA 2017), pages 134-141

ISBN: 978-989-758-267-7

Indicator

Audience

Visual sensing

Visualization

Figure 1: An overview of a vision-based pointing interface.

The vision sensor measures indicator’s pointing posture and

estimates the indicated location to show a pointer.

(R.S.Woodworth, 1899). Fitts et. al. reported that

pointing duration depends on a distance and a tar-

get size(Fitts, 1954). This fact is known as “Fitts’s

law”, which has been used in many studies because

of its accurate approximation in various conditions.

McGufﬁn and Balakrishnan proposed zooming the re-

gion around a pointer (McGufﬁn and Balakrishnan,

2005). This gives a perceptual illusion that the tar-

get size and its distance from a pointer appear larger

than the actual amounts in neighborhood of a destina-

tion. In order to obtain a similar effect, several pre-

vious studies also controlled pointer size and/or its

speed (Worden et al., 1997; Grossman and Balakr-

ishnan, 2005; Blanch et al., 2004). However, those

conventional methods were designed for mouse inter-

faces and visualization on laptop monitors. Hence,

it is necessary to apply those scheme with respect to

the design of gesture-based pointing interfaces for a

distant and/or large screen.

A particular problem of the present gesture-based

pointing interface system is difﬁculty in estimating

the location that an indicator wants to point. One rea-

son is accuracy of pointing pose measurement. In

the pointing interface system, signiﬁcant measure-

ment accuracy is required especially for a target at

a distance from an indicator because even extremely

small errors on body coordinates are ampliﬁed on a

screen. Although various type of motion capture tech-

niques developed with acceleration sensors (Slyper

and Hodgins, 2008), magnetic sensors (O’Brien et al.,

2000), or visual markers (Loper et al., 2014) could

satisfy the accuracy requirement, they are not appro-

priate in daily pointing situations. Several previous

studies proposed markerless methods based on visual

sensing that do not interfere with an indicator’s be-

havior (Shotton et al., 2011; Yoshimoto and Naka-

mura, 2015; Nickel and Stiefelhagen, 2003). How-

ever the performance of these methods does not sat-

isfy the requirement because visual sensing basically

corresponds to semi-2D measurement, and thus it is

weak in terms of self-occlusion and non-rigid defor-

mation by clothing.

Another problem in estimating pointed position is

body pose ambiguity. It corresponds to inconsistency

between 3D pose structure and a pointed location in

indicator’s intent. Although previous studies investi-

gated the relationship between a pointing posture and

an indicated position, it still be uncertain and inﬂu-

enced substantially by pointing conditions. Addition-

ally each person possesses individual characteristics

in a pointing pose. Initially, Fukumoto et. al. re-

ported that a target position is placed on an indicat-

ing vector deﬁned by a ﬁngertip and a reference point

inside an indicator’s body (Fukumoto et al., 1994).

The reference point moves according to the pointing

pose. It is placed on an eye position when an indica-

tor’s arm is straight while resting on an elbow when

it is bent. Kondo et. al. reported on selecting a suit-

able model for intermediate poses with slightly bent

elbows (Kondo et al., 2016). Ueno et. al. indicated

that despite a straight arm, an intended location does

not stay on the indication vector. Although calibrating

the amount of the disparity as horizontal and vertical

offsets for targets at various locations (Ueno et al.,

2014), they did not propose its general model.

Extant studies do not discuss the mathematical

model that assumes estimation errors on pointed loca-

tions caused by the above problems. Although Kondo

et. al. proposed a feedback control model for point-

ing interface system (Kondo et al., 2015), it focused

on pure step responses under no or sufﬁciently small

noises.

3 CONTROL MODEL OF

POINTING INTERFACE

SYSTEM

3.1 Fundamental Formulation

With a vision-based pointing interface system as

shwon in Fig. 1, a pointing procedure is modeled as

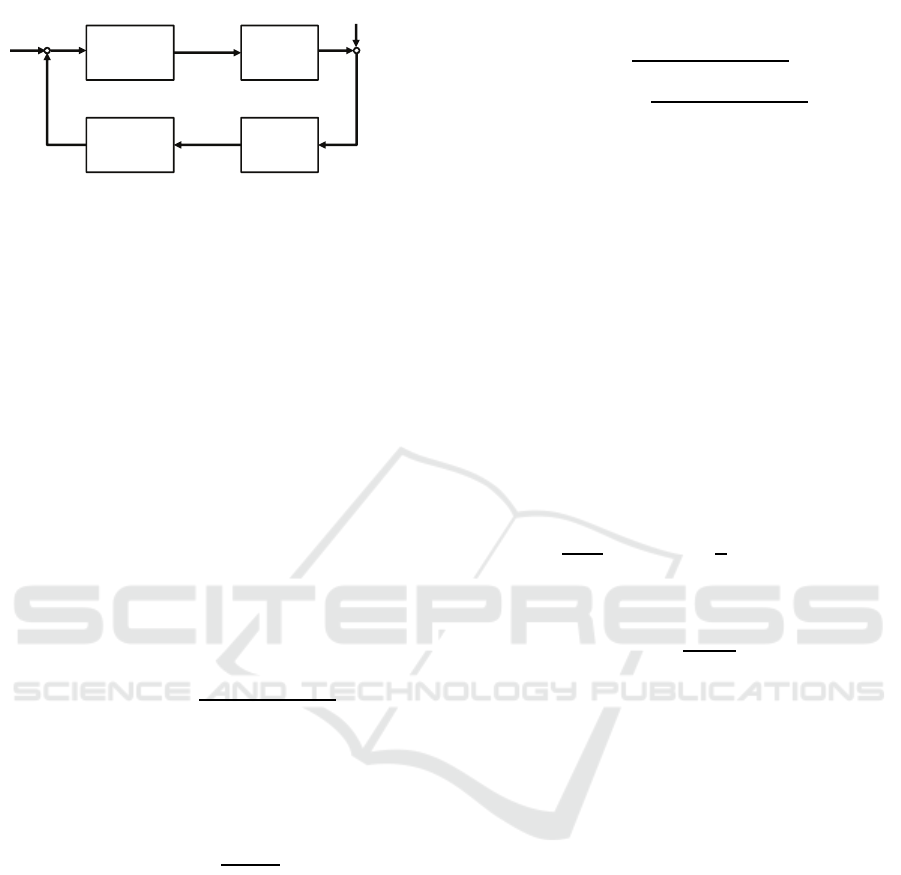
a feedback loop as shown in Fig. 2. Based on classi-

cal control theory, Kondo et. al. formulated it with

four transfer functions H

, H

and H

to denote

indicator’s body dynamics, visual perception catch-

ing a pointer location, computer estimating pointed

position, and visualization ﬁlter, respectively (Kondo

et al., 2015). However they did not consider the esti-

mation error caused by the visual sensing accuracy

and the pointing posture ambiguity. Our study as-

sumes that H

correctly estimates the pointed position

Indicator’s

pointing

gesture H

Visual

sensing H

Visualizatio

n H

Indicator’s

visual

perception H

Target

position p

Estimated

position p

Visualized

position p

Perceived

position p

Estimation error d

Figure 2: The feedback loop scheme of the vision-based

pointing interface system. The modules H

, H

, and

describe the indicator’s body dynamics, visual percep-

tion, estimation of the pointing location, and pointer visu-

alization. Additionally d

refers to disturbance given to the

pointed position estimation.

and its estimation error is inserted as unexpected in-

coming noise d

. Additionally no visualization ﬁlter

is assumed to model a simple pointing interface sys-

tem. Therefore the transfer functions H

and H

con-

sisting of the pointing interface side are formulated as

follows :

(s) = e

−τ

(s) = e

−τ

(1)

where τ

and τ

denote the latencies for the pointed

position estimation, and the pointer visualization, re-

spectively.

The pointing dynamics H

is assumed as a second-

order lag element

(s) = e

−τ

+ 2ζT

s+ 1

. (2)

based on the preliminary analysis of pure step re-

sponses, where τ

denotes the dead time to begin a

pointing action. The human visual perception H

simply formulated as a ﬁrst-order lag element

(s) =

s+ 1

(3)

to simulate a cognitive delay.

3.2 Hybrid Feedback Model

Let the output of H

be a control value denoted as p

because an indicator can not know amount of incom-

ing noise and thus tries to make p

closer to p

Given four transfer functions and input signals

(t),d

(t), the control value p

consists of two terms

of a target value response and a noise response:

(s) = P

(s)G

(s) + D

(s)G

(s) (4)

with an assumption of their linear independency.

(s), P

(s), and D

(s) correspond frequency domain

descriptions of p

(t), p

(t), d

(t), respectively, with

Laplace transform. G

(s) and G

(s) are described

(s) =

(s)H

(s)

1+H

(s)H

(s)

(s) = −

(s)H

(s)

1+H

(s)H

(s)

(5)

based on a closed loop theorem.

Pointing behaviors is also inﬂuenced by values

of the parameters K

, T

, ζ, τ

, τ

and τ

. These

should be conﬁgured so that Eq. (4) well simulate

actual pointing behaviors. We have an important con-

straint for the parameter conﬁguration. With enough

small or ignorable noise, a trajectory of pointed po-

sitions generally converges to a target position after

sufﬁcient time goes. Additionally p

can be given

as a step signal because an indicator usually conﬁg-

ures a target position at a distant from the initial po-

sition and it remains for a certain duration. Thus the

convergence behavior corresponds to a mathematical

constraint that stationary error e(t) = p

(t) − p

(t) at

t = inf must be 0 under the condition of p

(t) being a

step signal and d

= 0. This can be formulated as

(t)

t= ∞

= lim

s→0

s·

(s) = 1 (6)

based on the ﬁnal-value theorem. It results in

− 1

(7)

where K

corresponds to the gain of H

. Here K

should not be extremely high when considering hu-

man body dynamics. Speciﬁcally, the previous study

reported that estimated values of K

are slightly ex-

ceed 1 (Kondo et al., 2015). This fact and Eq. (7)

lead to a signiﬁcantly small feedback gain K

. Thus a

feedback effect to compensate noise inﬂuence is also

small. Essentially, it is difﬁcult for a simple feedback

model to simultaneously satisfy precise tracking to a

target value and compensating noise inﬂuence. Thus

a more advanced scheme is necessary to construct a

compatible model.

In order to solve this issue, this study focuses

on a transition of control strategy as reported in

(R.S.Woodworth, 1899) ; namely human pointing be-

havior switches from a rapid approach at the begin-

ning to a subsequent adjustment. Similarly the pro-

posed model switches the control model from a target

value follow-up phase to a noise compensation phase

at a speciﬁc time T. Given this hybrid framework, the

control value p

(t) is formulated as



−1

(s)G

(s)) t < T

−1

(s)G

(s))|

t= T

+ L

−1

(s)G

(s)) t ≥ T

(8)

and the control strategy G

(s) for a target value

input and G

(s) for an incoming noise sig-

nal are obtained from the same feedback scheme

shown in Fig. 2 but with individual pa-

rameter sets φ

= [K

, T

, ζ

, τ

], φ

, K

, T

, ζ

, τ

], respectively. Because

even the different pointing strategy appears to follow

the same body control scheme and visual perception

rule. K

is automatically determined from the values

of K

by using Eq. (7) while it is not applied to φ

The reason is that the incoming noise is a probabilis-

tic sequence and thus it is less meaningful to discuss

convergence to that. τ

and τ

are assumed as com-

mon because the parameters of artiﬁcial components

do not depend on the human pointing strategy.

4 EXPERIMENTS

4.1 System Implementation

A pointing interface system was implemented as

shown in Fig. 3 for experimental evaluation of the

proposed method. The 1280pixel × 800pixel visual

contents are projected on a screen (white wall in

the ﬁgure) approximately corresponding to 2m × 1m

by using a short focal length projector RICOH PJ

WX4141. Subjects stand at a distance of approxi-

mately 2.5m from the screen. For natural pointing,

a contactless visual sensing should be used. A Kinect

v2 sensor is placed close to the screen at the left of the

subjects. However in the following experiments, the

magnetic ﬁeld-based 3D pose sensor POLHEMUS

Liberty is used to accurately measure pointing pos-

tures. The magnetic sensors are attached on ﬁnger

tips of subject’s right hands and temples. Although

this implementation is not allowed in practical use, it

can be accepted for analyzing human pointing behav-

iors.

The subjects are requested to straighten their arms

during pointing behaviors. Therefore the indicated lo-

cation is estimated as where the indicating vector that

connects the center of the temples coordinates and the

ﬁnger tip across to the screen, based on a previous re-

port (Fukumoto et al., 1994). This corresponds to the

processing of H

. Then an approximately 1cm circu-

lar pointer that is assumed as a “point” for the subjects

is drawn at the estimated position on the screen.

4.2 Model Calibration

It is necessary to determine the parameters used in

each pointing phase prior to evaluating performance

Kinect sensor

Screen for display

Magnetic field-based

3D sensor

Figure 3: The experimental environment.

of the proposed model. In order to simplify a cali-

bration, we assumed that both of the parameter sets

and φ

are independent for each other and do not

change. It allows to individually calibrate them be-

forehand.

The latency parameters τ

and τ

included in

, H

, respectively, are assumed as inherent and sta-

ble features. Thus they are estimated in advance from

directly measured durations of sensing, calculation

and display. The remaining parameters are estimated

via a non-linear optimization that minimizes residuals

between

(t) from the model and the actually mea-

sured p

(t).

4.2.1 Target Value Follow-up Phase

A step input signal and its response are used to cal-

ibrate G

that describes the target follow-up phase.

They correspond to the pointing target that suddenly

arises at a distance from the initial location and the

transient trajectory till an indicator complete pointing

the target, respectively. Given this consideration, the

experimental procedures for step response measure-

ment are conﬁgured as follows.

1. The measurement starts when a subject indicates

an initial target visualized on the screen and the

pointer remains in that location.

2. The initial target suddenly disappears. Simultane-

ously, a new target pops up at a distance of ap-

proximately 70 cm from the initial target. The

subject changes his or her posture to move the

pointer onto the new target.

3. The measurement stops when the subject calls the

ﬁnish of the pointing action.

A sufﬁciently small noise d

(t) = 0 was expected be-

cause of the measurement accuracy of the magnetic

sensor and the straight arm condition. Thus it was as-

sumed the estimated values of pointed positions cor-

responded to p

(t). The subjects include three univer-

time(sec)

0 1 2 3

response(cm)

100

time(sec)

0 1 2 3

response(cm)

100

time(sec)

0 1 2 3

response(cm)

100

Subject #1 Subject #2 Subject #3

Figure 4: The calibration results of G

. The horizontal and vertical axes denote the elapsed time from when the new pointing

target appears and the distance from the initial location, respectively. (black) the measured step response trajectories. (red)

the trajectories simulated by G

with the optimized parameter sets φ

shown in Table 1.

Table 1: The optimized parameter set φ

for each subject.

Subject K

#1 1.02 0.37 0.12 0.02 0.12 0.81

#2 1.04 0.45 0.36 0.03 0.10 0.79

#3 1.08 0.39 0.26 0.07 0.12 0.49

sity students. Each of them conducted N = 20 trials

under the same conditions.

The parameter optimization for the calibration is

formulated as

= argmin

∑



(t) − L

−1



(s, φ

)



(9)

that means minimizing sum of squared errors with re-

gard to the response trajectory. A trust region non-

linear optimization method is applied to solve Eq. (9).

The upper and lower limits of the parameters were

conﬁgured as 1 < K

≤ 2, 1 ≤ T

≤ 10

, 0 < ζ ≤ 50,

300 ≤ τ

≤ 700, 0 ≤ T

≤ 10

by considering of hu-

man body dynamics and visual perception. The opti-

mal parameter set that minimizes Eq. (9) is selected

from the results of multiple optimizations beginning

with various initial values so that at least few of them

reached the global minimum. With this procedure, an

optimal parameter set φ

(i, j) for each pointing trial

i of each subject j is determined. After that, the ﬁ-

nal parameter set for each subject is estimated as their

average values

∑

(i, j). A direct optimization of

the common parameter set for all trials is simpler than

the above two step calibration. However it estimates a

parameter set that averages dispersed pointing trajec-

tories in a real domain but not in a frequency domain.

The two step calibration averages the parameter sets

that reﬂect the system behaviors in both the real and

frequency domains, and thus it appears to maintain

essential characteristics.

The black and red curves in each ﬁgures in Fig. 4

show the trajectories of each subject’s 20 pointing tri-

als and their simulated trajectories with the calibrated

Table 2: The optimized parameter set φ

for each subject.

Subject K

#1 1.73 400 14.5 1.69 317 3.22

#2 1.73 403 18.3 1.63 296 14.2

#3 1.73 403 14.2 1.69 288 2.32

parameter sets as shown in Table 1, respectively. Even

the 20 samples under the same experimental condition

had certain diversity because of unconscious pointing

posture perturbation. The calibrated models approxi-

mated almost the center of the diversities. The amount

of the diversity depends on the subject. The pointing

trajectories of subjects #1 and #3 appear to be ade-

quately simulated while those of subject #2 are not so

much.

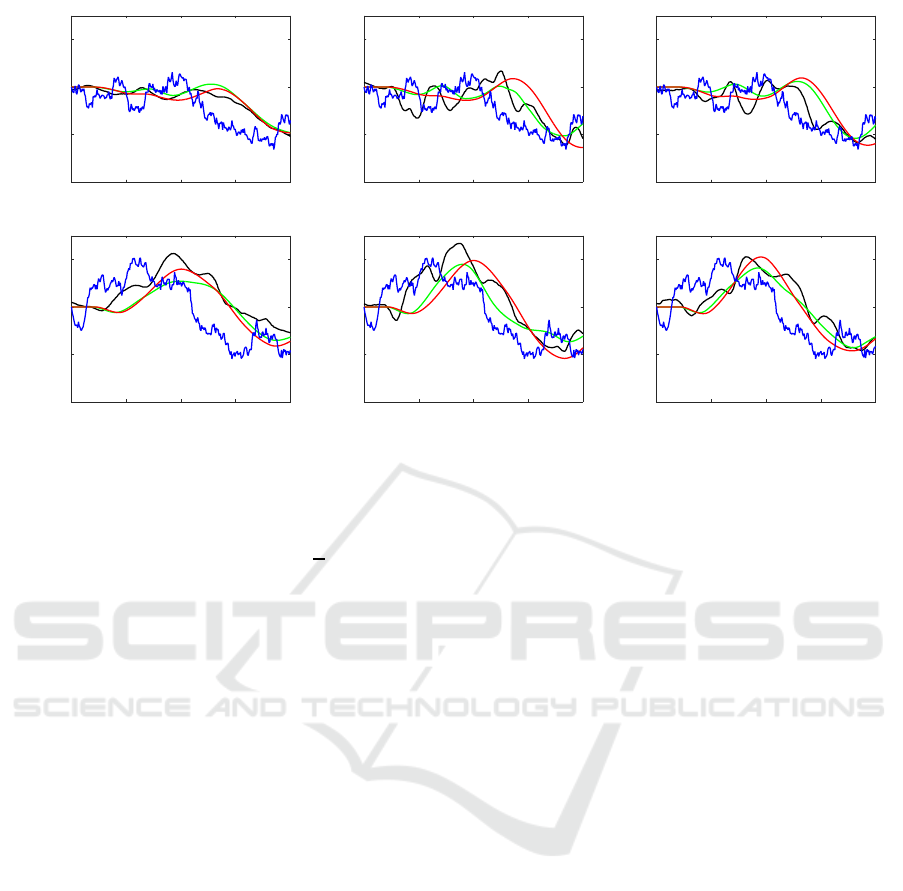
4.2.2 Noise Compensation Phase

Similarly the parameter set φ

of G

for the noise

compensation phase is estimated by using the pointer

location stabilizing behaviors against to given noises.

The experimental procedures for the measurement are

conﬁgured as follows :

1. The measurement begins when a subject indicates

a stable target visualized on the screen and the

pointer stays at that location.

2. A noise sequence is added to the measured point-

ing location p

(t). The subject changes its own

pointing posture to maintain the pointer on the sta-

ble target.

3. The measurement stops after a certain experimen-

tal duration T

= 4.0 seconds.

The pointing target does not move, and thus only the

responses to given noises are appeared. A vision-

based pose measurement usually searches a neighbor-

hood of that in the previous frame. It corresponds to

that the estimation error is accumulated. Thus in this

experiment a random walk sequence is assumed as the

given noise. It is formulated as

time(sec)

0 1 2 3 4

response(cm)

-20

-10

time(sec)

0 1 2 3 4

response(cm)

-20

-10

time(sec)

0 1 2 3 4

response(cm)

-20

-10

time(sec)

0 1 2 3 4

response(cm)

-20

-10

time(sec)

0 1 2 3 4

response(cm)

-20

-10

time(sec)

0 1 2 3 4

response(cm)

-20

-10

Subject #1 Subject #2 Subject #3

Figure 5: The calibration results of G

. The ﬁgures in each column correspond to results with respect to two representative

trials of each subject. (blue) given random-walk noise sequences. (black) the measured noise compensation trajectories.

(green) the trajectories simulated by G

with the optimized parameter sets φ

(i, j) for each pointing trial i and subject j. (red)

those with the ﬁnal parameter sets φ

(j) =

∑

(i, j) shown in Table 2.

(t + 1) = n

(t) + sx, x ∼ N (0, 1) (10)

with an update factor x that follows an indepen-

dent and identical standard normal distribution where

(0) = 0, t < T

, and s = 2.0 cm were conﬁgured. In

the experiment, 20 different random walk sequences

(t)} were given to each subject. The manner to ac-

quire an optimal parameter set is the same as that in

the previous calibration experiment.

Figure 5 shows the calibration results of each sub-

ject. The blue, black, green, and red curves in the ﬁg-

ures denote the given random-walk noises, response

trajectories, simulated trajectories with the individu-

ally optimized parameter sets for each trial, and those

with the ﬁnal parameter sets as the results of the two

step estimation, respectively. A high frequency com-

ponent ﬁltering with particular latency appears in a

translation from the given noise trajectories to their

responses. Simultaneously we can see that small dis-

parities remain between the given noise sequences

and their compensation response. Our hypothesis is

that human pointing dynamics is not so fast to follow

high frequent changes. Thus too much trial to do so

may result in worse. In stead of that, the subjects ap-

peared to allow the certain amount of remaining gap

between the shown pointer and the target position.

This non-linear characteristic is a possible reason of

not so good approximation performance shown as the

inconsistency in the black and green (or red) curves in

Fig. 5.

While the proposed G

roughly simulate the

noise responses, it does not adequately explain rel-

atively high frequent components. The proposed

model consists of a tamdemly connected 2nd-order

and 1st-order lag elements, and thus it is difﬁcult to

explain the non-linear characteristics. A visual per-

ception component that is insensible to small position

disparities be necessary.

4.3 Model Evaluation

The performance of the proposed hybrid model was

evaluated in the situations such as when an indicator

attempts to move a pointer under a certain noise. A

method to evaluate is analyzing how it approximates

actual pointing trajectories.

In a manner similar to the calibration experiments,

(t) and d

(t) given to the subjects were conﬁg-

ured as step inputs and random-walk sequences. The

way to measure the response trajectories p

(t) as

ground truth was almost same as that shown in sec-

tion 4.2.1 with the exception of random-walk noises

being added during pointing. Their simulated trajec-

tories p

prop

(t) were generated by the proposed hybrid

feedback model Eq. (8) by using G

, G

calibrated

in the previous two experiments and the same p

(t)

and d

(t) given to the subjects. The model switch-

ing time T was manually conﬁgured to 1.2 seconds

(just after the overshoot in most cases). The reference

time(sec)

0 1 2 3 4

response(cm)

100

time(sec)

0 1 2 3 4

response(cm)

100

time(sec)

0 1 2 3 4

response(cm)

100

time(sec)

0 1 2 3 4

response(cm)

100

time(sec)

0 1 2 3 4

response(cm)

100

time(sec)

0 1 2 3 4

response(cm)

100

Subject #1 Subject #2 Subject #3

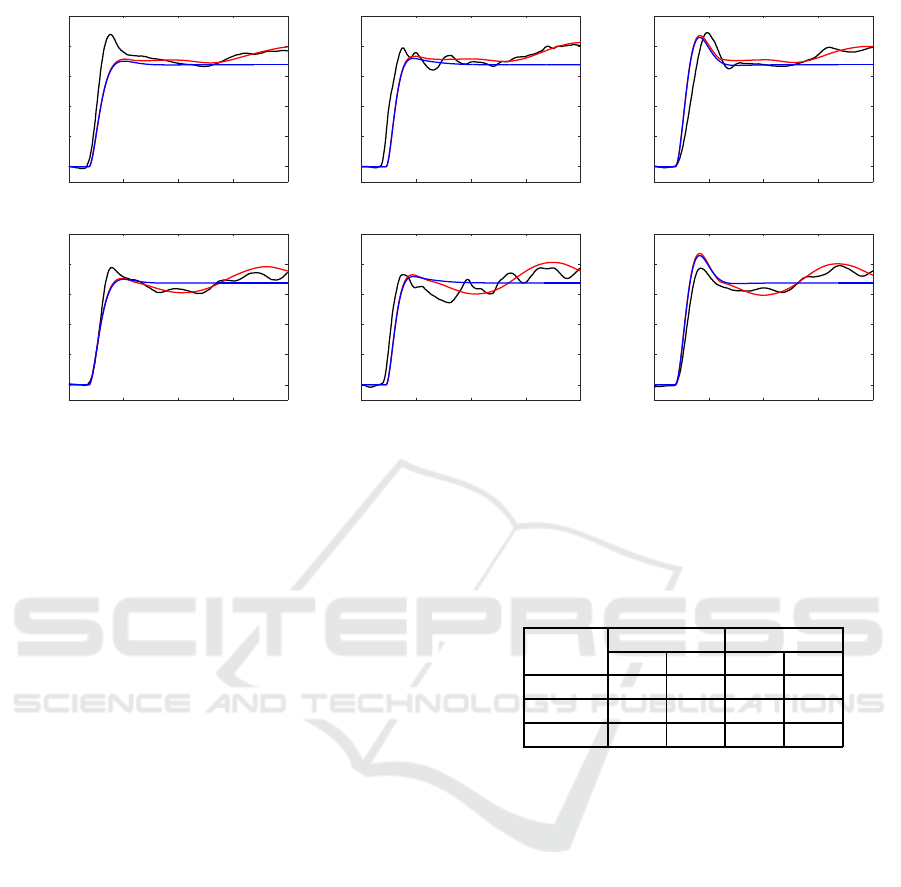
Figure 6: The predicted pointing trajectory by simulation. The ﬁgures in each column correspond to results with respect to two

representative trials of each subject. The given random-walk noise sequences are different from those used in the calibration

phase. (black) the ground-truth trajectories p

(t). (red) the simulated trajectories p

prop

(t) by using the hybrid model. (blue)

those by using reference model.

trajectories p

ref

(t) for comparison were generated by

using the common parameter set φ

for both of G

and G

. This assumed the conventional non-hybrid

model that does not consider the inﬂuence of the esti-

mation error.

The predction results by simulation of each sub-

ject are shown in Fig. 6. The proposed hybrid model

begins to compensate for the noise inﬂuence after

t = T, and thus the trajectories p

prop

(t) more ade-

quately approximate the ground truth p

(t). How-

ever the fact that the noise compensation behaviors

can not be well approximated as shown in the calibra-

tion results appeared also in this evaluation situation.

Another reason for the remaining errors corresponds

to the inﬂuence of the phase switching time T. In this

moment, a method to determine T is a quite naive way

and it should be automatically conﬁgured based on

model parameters and input signals. Thus the inﬂu-

ence of T appears to be approximated to the station-

ary bias. This indicates that the trajectories simply

go up or down in the time-location coordinate accord-

ing to T. A total comparison in statistic performance

of the simulation errors e

prop

(t) = p

prop

(t) − p

(t),

ref

(t) = p

ref

(t) − p

(t) are shown in Table 3. The

simulation accuracies of the proposed method are

within several centimeters. It is approximately half

of those with respect to the reference method.

The proposed hybrid model mainly focuses on

compensating noise inﬂuence at a stationary state be-

Table 3: The statistic values of the simulation accuracy

prop

(t)| and |e

ref

(t)| (cm).

Subject

prop

(t)| |e

ref

(t)|

ave. s. d. ave. s. d.

#1 3.87 4.05 8.12 5.74

#2 5.15 5.23 8.87 6.63

#3 4.29 3.99 8.01 5.92

cause it is expected that a little perturbation does not

exhibit a signiﬁcant inﬂuence during a transient pe-

riod. However the simulation accuracy at t < T is

still not high. This conﬁrmed that it is also necessary

to compensate for a relatively low amount of distur-

bance at the beginning of pointing. In actual pointing

situations, pointing often starts by holding indicator’s

hand hanged down. In this case, large amount of noise

may be caused even in a transient period. An indica-

tor does not attempt to cancel such type of large noise

and instead conﬁgure a new target value from the cur-

rent pointer location to the original target location.

5 CONCLUSION

This study involved proposing a mathematical model

of a pointing interface system to simulate its behav-

iors with respect to step signal targets and pointed po-

sition estimation errors. The proposed hybrid feed-

back control model switches its characteristics from a

target value follow-up phase to a noise compensation

phase. The simulation accuracy becames fairly higher

than that of the conventional non-hybrid model. Nev-

ertheless a large amount of simulation error at a tran-

sient period continues to constitute a considerable

problem.

In the experiments, a very simple pointing situa-

tion was assumed in which the subjects stand at the

same location, point with their arm being straight,

and start pointing from previous pointing postures.

The travel distance to the new target is also limited

to only 70 centimeters. The performance in more

various conditions must be evaluated. A further es-

sential issue of human behavior diversity requires a

more advanced framework. Additionally in order to

really contribute interface design, it is necessary to

apply and model various visualization methods such

as an area pointer, a blurred pointer, and showing it at

a smoothed location.

REFERENCES

Blanch, R., Guiard, Y., and Beaudouin-Lafon, M. (2004).

Semantic pointing: improving target acquisition with

control-display ratio adaptation. In Proceedings of the

SIGCHI Conference on Human Factors in Computing

Systems, CHI ’04, pages 519–526.

Fitts, P. M. (1954). The information capacity of the hu-

man motor system in controlling the amplitude of

movement. Journal of Experimental Psychology,

47(6):381–391.

Fukumoto, M., Suenaga, Y., and Mase, K. (1994). Finger-

Pointer: Pointing interface by image processing. Com-

puters & Graphics, 18(5):633–642.

Grossman, T. and Balakrishnan, R. (2005). The bubble cur-

sor: enhancing target acquisition by dynamic resiz-

ing of the cursor’s activation area. In In Proc. of the

SIGCHI conference on Human factors in computing

systems, pages 281–290. ACM.

Kondo, K., Mizuno, M., and Nakamura, Y. (2016). Analysis

of human pointing behavior in vision-based pointing

interface system - difference of two typical pointing

styles-. In In Proc. on The 13th IFAC/IFIP/IFORS/IEA

Symposium on Analysis, Design, and Evaluation of

Human-Machine Systems 2016.

Kondo, K., Nakamura, Y., Yasuzawa, K., Yoshimoto, H.,

and Koizumi, T. (2015). Human pointing modeling for

improving visual pointing system design. In In Proc.

of Int. Symp. on Socially and Technically Symbiotic

Systems (STSS) 2015.

Loper, M., Mahmood, N., and Black, M. J. (2014). Mosh:

Motion and shape capture from sparse markers. ACM

Transactions on Graphics, 33(6):220:1–220:13.

McGufﬁn, M. J. and Balakrishnan, R. (2005). Fitts’ law

and expanding targets: Experimental studies and de-

signs for user interfaces. ACM Trans. Comput.-Hum.

Interact., 12(4):388–422.

Nickel, K. and Stiefelhagen, R. (2003). Pointing gesture

recognition based on 3d-tracking of face, hands and

head orientation. In In Proc. of The IEEE Int. Conf.

on Multimodel Interfaces, pages 140–146.

O’Brien, J. F., Bodenheimer, R., Brostow, G., and Hodgins,

J. K. (2000). Automatic joint parameter estimation

from magnetic motion capture data. In Graphics In-

terface, pages 53–60.

R.S.Woodworth (1899). The accuracy of voluntary move-

ment. Phychological Review Monograph Sullplement,

3(13):1–119.

Shotton, J., Fitzgibbon, A., Cook, M., Sharp, T., Finocchio,

M., Moore, R., Kipman, A., and Blake, A. (2011).

Real-time human pose recognition in parts from sin-

gle depth images. In In Proc. of the 2011 IEEE Con-

ference on Computer Vision and Pattern Recognition,

CVPR ’11, pages 1297–1304.

Slyper, R. and Hodgins, J. K. (2008). Action capture with

accelerometers. In In Proc. of the 2008 ACM SIG-

GRAPH/Eurographics Symposium on Computer Ani-

mation, SCA ’08, pages 193–199.

Ueno, S., Naito, S., and Chen, T. (2014). An efﬁcient

method for human pointing estimation for robot in-

teraction. In In Proc. of IEEE Int. Conf. on Image

Processing 2014, pages 1545–1549.

Worden, A., Walker, N., Bharat, K., and Hudson, S. (1997).

Making computers easier for older adults to use: area

cursors and sticky icons. In Proceedings of the ACM

SIGCHI Conference on Human factors in computing

systems, pages 266–271. ACM.

Yoshimoto, M. and Nakamura, Y. (2015). Cooperative ges-

ture recognition: Learning characteristics of classi-

ﬁers and navigating user to ideal situation. In In Proc.

of The 4th IEEE Int. Conf. on Pattern Recognition Ap-

plications and Methods, pages 210–218.