Reinforcement Learning for Modeling Large-Scale Cognitive

Reasoning

Ying Zhao

, Emily Mooren

and Nate Derbinsky

Naval Postgraduate School, Monterey, CA, U.S.A.

Northeastern University, Boston, MA, U.S.A.

Keywords: Reinforcement Learning, Combat Identification, Soar, Cognitive Functions, Decision Making, Machine

Learning.

Abstract: Accurate, relevant, and timely combat identification (CID) enables warfighters to locate and identify critical

airborne targets with high precision. The current CID processes included a wide combination of platforms,

sensors, networks, and decision makers. There are diversified doctrines, rules of engagements, knowledge

databases, and expert systems used in the current process to make the decision making very complex.

Furthermore, the CID decision process is still very manual. Decision makers are constantly overwhelmed

with the cognitive reasoning required. Soar is a cognitive architecture that can be used to model complex

reasoning, cognitive functions, and decision making for warfighting processes like the ones in a kill chain.

In this paper, we present a feasibility study of Soar, and in particular the reinforcement learning (RL)

module, for optimal decision making using existing expert systems and smart data. The system has the

potential to scale up and automate CID decision-making to reduce the cognitive load of human operators.

1 INTRODUCTION

Accurate, relevant, and timely combat identification

(CID) enables warfighters to locate and identify

critical airborne targets with high precision. The

current CID processes include the use multiple

platforms, sensors, networks and decision makers.

There are diversified doctrines, rules of

engagements, knowledge repositories, and expert

systems used in the current process to address the

complexity of decision making challenges.

Figure

1 shows many people (watch stations) that

are involved in a CID decision-making process for a

Combat Information Center (CIC). However, the

process is still very manual. Decision makers such as

Tactical Action Officers (TAOs) and Air Defense

Officers (ADOs) are constantly overwhelmed with

the cognitive reasoning required (Scruggs, 2009).

The core for the research presented in this paper

is to investigate the efficacy of artificial intelligence

(AI) systems that utilize Machine Learning (ML) for

using, fusing, and improving on existing knowledge

models for CID cognitive functions that lead to

timely and automatic decision-making, such as to

reduce cognitive burden in the operational

environment. The contribution of the paper is that

we present and demonstrate a working

implementation: it applies the rule-based Soar

system jointly with the reinforcement learning

algorithm that is suitable for the CID application

domain. While we know Soar can handle large

numbers of rules (Laird, 2012), this a

position/opinion, rather than fact, which we will

require future work to prove, that the methodology

and framework can be potentially scaled up to large

amount of knowledge bases and ontologies related to

CID.

Figure 1: Complex decision making in the CID current

process.

Zhao Y., Mooren E. and Derbinsky N.

Reinforcement Learning for Modeling Large-Scale Cognitive Reasoning.

DOI: 10.5220/0006508702330238

In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KEOD 2017), pages 233-238

ISBN: 978-989-758-272-1

2 METHODS

2.1 Soar and Reinforcement Learning

Soar (Laird, 2012) is a cognitive architecture that

scalably integrates a rule-based system with many

other capabilities, including RL and long-term

memory. The main decision cycle involves rules that

propose new operators, as well as preferences for

selecting amongst them; an architectural operator-

selection process; and application rules that modify

agent state. The reinforcement learning module

(Soar-RL) modifies numeric preferences for

selecting operators based on a reward signal, either

via internal or external source(s). Soar has been

used in modeling large-scale complex cognitive

functions for warfighting processes like the ones in a

kill chain (Jones et al., 1999).

In this paper, we will show how to use Soar and

specifically the reinforcement learning (Soar-RL)

module to learn an effective combination of existing

CID features for decision-making, as identified by

experts and systems, in an operational environment.

2.2 Combat ID

There are many challenges in the CID process,

including 1) an extremely short time for fusion,

decision-making, and targeting; 2) uncertain and/or

missing data outside sensor (e.g., radar, radio)

ranges; 3) manual decision-making; 4)

heterogeneous data sources for decision making; and

5) multiple decision-makers in the loop.

Existing CID methods, sensors, and systems

include basic CID categories and methodologies as

follows:

1. Procedural. Procedural methods involve

analysis of a target’s “behaviors,” to include

such things as flight profile and point of original

2. Non-cooperative. These methods gather ID

information on a target without that target’s

intentional cooperation/participation.

3. Cooperative. Cooperative CID requires active

participation on the part of the target. A

common example would be an identification

friend or foe (IFF) transponder.

4. Intelligence and ID Fusion methods.

Information derived from various networks

comprises the final CID method.

The existing methods involve wide ranges of

participating platforms such as Destroyers, Cruisers,

Carriers, F/A-18s and E-2Ds; Participating Sensors

such as Radar, Forward Looking Infrared (FLIR),

Identification Friend or Foe (IFF), Precision

Participation Location Identifier (PPLI), National

Technical Means (NTM); and Participating

Networks and Systems such as the Aegis combat

system, Cooperative Engagement Capability (CEC)

and Link-16. There are diversified doctrines, rules

of engagements (ROE), knowledge databases and

expert systems, as smart data used in the current

process. Many existing rules, expert systems and

smart data may be obselete, incomplete, or have low

confidence levels. Some models may be conflicted

with each other, even wrong or not adapative to a

local environment. There is a critical need to

research methodologies to better use, fuse and

improve on all these models to advance the art of

CID a higher symbolic level.

This paper evaluates Soar-RL as a tool for this

purpose due to the fact it can train and fuse the

system at a symbolic level. The complex CID

cognitive functions are mapped to the models

including decision-making, sensor fusion, analytic

processes and workflow initially and then Soar-RL

is applied to integrate them together.

CID decision-making requires a fusion of

existing rules. For example, as shown in Figure 2, a

state at time t can be a track profile of a flying object

with observable data containing longitude/latitude

(x/y position), altitude (z), speed, acceleration, IFF,

point of origin, heading, type, class, etc. The goal is

to classify the CID of the object as friendly, foe or

unknown. So an existing model can be “if an

unknown object is at the position x,y, there is a

probability of p

, p

or p

that the object’s point of

origin to be A, B or C respectively. There is

another model saying “if an unknown object’s point

of origin is from A or B there is probability of p

or p

that the object is a foe respectively. So

when an object is observed at (x,y), then the

probability of the object being a foe is the maximum

of the combined p

11*

12*

, p

12*

13*

, and p

13*

23.

Figure 2: Example of CID requires a fusion of existing

rules.

3 SIMULATION

In order to provide a case for feasibility, Table 1

shows simple three rules, with which a Probability

of Hostile (POH) is specified initially as existing

CID rules. We also assume Probability of Non-

Hostile (PONH)=1-POH. These rules are not real-

life CID rules but used as examples in the

simulation.

Table 1: Simple Rules Used in Simulation.

State Existing CID Rules

X,Y

1.If X<10 && Y<10 then

POH=0.0001

Z 2. If Z<6 then POH=0.2

Mode 3. If mode=4 then POH=0.00001

The goal for Soar-RL was to learn and adjust the

preferences of these rules dynamically which are the

same as POH in this case. The actions for the

reinforcement learning are the two decisions (hostile

or non-hostile) for a flying object based on the

observable data (i.e., State s) for the object at time t.

The preference of a decision (i.e., hostile or non-

hostile) is the expected total POH for each decision

(action) at time t, computed using a recursive

formula in Soar-RL. For example, when

x=9,y=9,z=4 and mode=4 at time t

• POH for Rule 1: 0.0001

• POH for Rule 2: 0.2

• POH for Rule 3: 0.00001

So the combined POH or the preference Q(t+1)

for the decision hostile is 0.20011

Similarly,

• PONH for Rule 1: 0.9999

• PONH for Rule 2: 0.8

• PONH for Rule 3: 0.99999

The combined PONH is 2.79998. The

normalized POH and PONH is 0.933 and 0.067

respectively. In the greedy algorithm of Soar-RL, if

POH >PONH, the decision is hostile; else non-

hostile. The Soar-RL decides non-hostile for the

current state. Then the preference of deciding

hostile or non-hostile that has been updated or

learned from the formula below:



(





,



)

=

(





,



)

+(+



max

∈

(



,)−

(





,



)

The default learning-rate α=0.3 and discount-

rate γ=0.9. The learning formula requires a teacher’s

feedback (correct decision is rewarded with r=1 and

incorrect decision r=-1). The POH or preference is

computed as follows;

• Preference Q(s

t+1

) for Rule 1 with the

decision a

t+1

hostile= 0.0001 since this rule is

not activated

• Preference Q(s

t+1

) for Rule 1 with the

decision a

t+1

non-hostile = 0.9999+0.3(1-

2.79989)/3=0.819911 where Q(s

t+1,

a)=0;

Q(s

)=2.79989. Since all three rules

contributed to the Q-value for the decision, the

change of Q-value 0.3(1-2.79989) is divided

among the three rules.

Similarly:

• Preference Q(s

t+1

) for Rule 2 with the

decision a

t+1

hostile= 0.2

• Preference Q(s

t+1

) for Rule 2 with the

decision a

t+1

non-hostile = 0.8+0.3(1-

2.79989)/3=0.620011.

• Preference Q(s

t+1

) for Rule 3 with the

decision a

t+1

hostile = 0.00001

• Preference Q(s

t+1

) for Rule 3 with the

decision a

t+1

non-hostile = 0.99999+0.3(1-

2.79989)/3=0.820001

For the three simple rules, Table 2 shows the

total 8 possible training examples and their ground

truths were used to train a Soar-RL agent.

Table 2: Total 8 training examples and ground truths of

hostility were used in the simulation: for the purposes of

the experiment, the truthful “hostility” is annotated.. “Y”

means hostile and “N” means non-hostile. (Mooren,

2017).

Track

# X-value Y-value Z-value MODE Hostility

1 5 5 5 0 Y

2 12 12 5 0 Y

3 5 5 12 0 Y

4 5 5 5 4 N

5 5 5 12 4 N

6 12 12 12 4 N

7 12 12 5 4 N

8 12 12 12 0 N

Figure 3 shows the screen shots of the examples

when the Soar-RL agent made correct and incorrect

decisions and how they are rewarded from the

environment by the teacher who knows ground truth.

4 RESULTS

Table 3 shows the 8 data points in Table 2 were fed

sequentially to the Soar-RL agent in Figure 3. Soar

made decisions (i.e., the “Soar says” column)

without any learning. This is a baseline run where

the percentage of overall correctness (PAC) is

62.5%. The baseline PAC was used for comparison

to further runs and parameter testing. Table 4

shows

the same 8 data points were used in the first iteration

of the Soar-RL learning. The PAC increased to 75%.

Figure 3: Examples of the Soar-RL training when Soar-RL

agents made correct and incorrect decisions.

Figure 4 shows the 8 data points were ingested

sequentially and iteratively (5 times, a total of 40

data points) to the Soar-RL agent. The first three

iterations were considered as learning phases (LP).

In a LP, the Soar-RL agent’s decision accuracy was

not good, Soar-RL parameter was set ε=0.1 so the

agent can explore, i.e., 10% of the time the agent

made a decision randomly instead of considering the

POHs. In an operational phase, the agent’s decision

accuracy was dramatically improved (due to the

learning in the previous phase) and ready to operate

the parameters set to be greedy with ε=0 (see

Section 4 for the discussion of the parameters). The

agent makes decisions strictly based on the predicted

POHs. The PAC went from 62.5% to 87.5% for the

4 track iterations (total 32 training data points) as

shown in Figure 4. The statistical significance p-

value was 0.04, where the null hypothesis was that

there is no difference of a PAC after a Soar-RL run

compared to the baseline run with any learning.

When 100 iterations (total 800 training data points)

were applied, the PAC increased to 100% (See

Figure 6). Considering the number of rules in the

feasibility study is very small, the possible different

data points for the rules are only 8, the Soar-RL

prototype proved that the system can gradually turn

a learning agent into an operational one using the 8

data points iteratively.

Table 3: Baseline Run - No Learning: The results from a

Soar CID run where no RL was applied.

Track

# Soar Says

Ground

Truth

(Hostile

Y/N)

Correct

(Teacher’s

Feedback)

Overall

Correctness

1 not hostile Y N

62.50%

2 not hostile Y N

3 not hostile Y N

4 not hostile N Y

not hostile

N Y

not hostile

N Y

not hostile

N Y

8 not hostile N Y

Table 4: The results from the 1

iteration Soar CID run of

using the 8 data points. The percentage of overall

correction (PAC) increased to 75%.

Track

# Soar Says

Ground

Truth

(Hostile

Y/N)

Correct

(Teacher’s

Feedback)

Percentage

of Overall

Correctness

(PAC)

1 hostile Y

75%

2 hostile Y

3 not hostile Y

4 hostile N

not hostile

8 not hostile N

Figure 4: Simulation results of using the 8 data points in

Table 2 for learning with 4 iterations of learning phases

(LP) where ε=0.1 The last iteration (5

) was used as an

operational phase (OP) where ε=0. By changing the RL

parameters, the Soar-RL agent is gradually changed from

LPs to an OP.

5 DISCUSSION (MOOREN 2017)

There are two learning-policies available in

Soar/RL: Q-Learning and SARSA. The two

algorithms control how the data will be treated and

how the expected future reward is chosen (Laird,

2012). Both are based on the concept of Temporal

Difference (TD) learning, where specific methods

estimate value functions prior to user input to

modify the final reward (Sutton & Barto, 1998). Q-

learning is an off-policy TD method where the

future reward is maximized and SARSA is a TD

method where the future reward is the value of the

selected operator.

Once the learning policy has been established the

important parameter decides how the actions will be

chosen. As an agent can only improve when

integrated with an environment, the environment

needs to be explored. There are multiple exploration

strategies in Soar. An exploration policy allows for

decision making based on numeric preferences.

There are two main methods: ε-greedy and softmax.

Greedy strategies look to exploit immediate

maximized rewards (Sutton & Barto, 1998). The

integration of ε adds a randomness to the selection.

As ε decreases there is less randomness in selection,

as it increases more. Ε-greedy strategies seek to

maximize reward return, but may sometimes select

an action at random. The utility of randomness has

been proven in certain scenarios and in fact certain

optimality proofs require non-zero probability of

exploring some states.

Figure 5 displays performance improvement

overall with a higher degree of randomness, ε=0.1 in

comparison to the other two depicted selections. The

ε-greedy methods perform better due to their

continued exploration (Sutton & Barto, 1998).

The second exploration strategy is softmax.

Softmax behaves like greedy strategies in selecting

the maximum reward but ranks and weighs the

remaining actions depending on associated value

estimates (Sutton & Barto, 1998). A variation of

softmax is the Boltzmann distribution. Which uses

an additional variable called “temperature” to further

effect the possibility of randomness. Soar sets a

default temperature value of 25.

Deciding which exploration strategy would be

most useful is important because it will determine if

an environment is still being explored or if it is

being exploited. In terms of the two main strategies

discussed earlier there may be benefits of one over

the other based on variable settings. ε-greedy is

primarily an exploitation strategy, but as ε increases,

there is more exploration due to the randomness.

Softmax/Boltzmann is a combination determined by

the temperature setting. Exploration versus

exploitation has long been considered a dilemma

(Tokic, 2010).

The selection of the learning rate is also

important to developing a stable RL system. The

default value for learning rate in Soar is 0.3, with a

range of 0–1. If the learning rate is set approaching

one, the system will learn quickly. If the learning

rate is set approaching zero, the system will learn

more slowly; when set at 0, the system will not

update reward values. To stabilize a RL application

it is feasible to lower the learning rate once the

percentage of correct decisions has maximized.

Figure 5: ε-greedy performance comparison. (Sutton &

Barto, 1998).

0,00%

20,00%

40,00%

60,00%

80,00%

100,00%

0246

Percentage of Overall

Correctness

Track Iterations (Sets of 8)

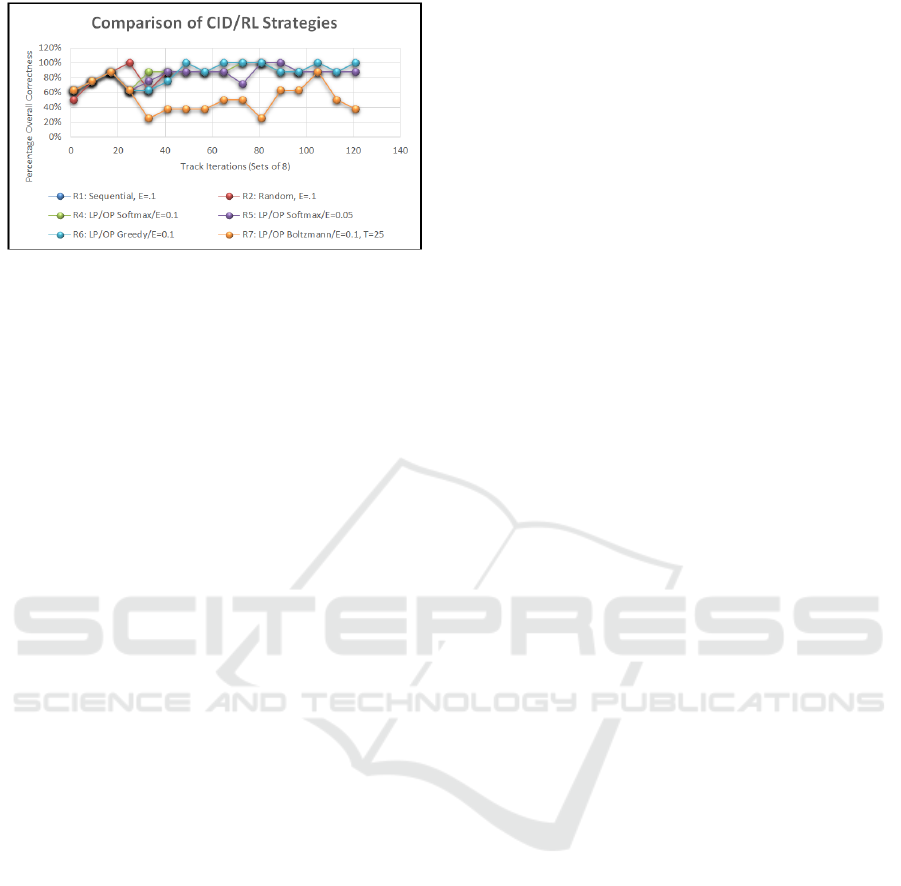
Figure 6: A comparison of ε-greedy action-value methods

for the CID problem (Mooren, 2017).

Figure 6 shows statistical analysis of the PACs

including both the LP and OP. The hypothesis test

was there is no difference of a combined PAC after a

Soar-RL run compared to the baseline run (no

learning). The one-tail p-value for the combined LP

and OP Run 4 is p = 0.0027. Run 6 had the highest

overall LP/OP due to the amount of samples (100

iterations for 800 data points); p = 0.0006. The p-

values in all cases of extended sampling, less Run 7

(p=0.1206) was proven to be statistically significant

and less than the alpha value of 0.05. Therefore, we

reject the null hypothesis and accept the alternative

hypothesis. The integration of RL into a rudimentary

CID problem was successful.

6 CONCLUSIONS

In conclusion, we characterized the CID problem

and apply the Soar-RL method to learn, adapt,

incorporate existing knowledge, models and expert

systems as production rules the CID decision

making application. Specifically, we showed it is

feasible that it is feasible that Soar-RL incorporated

in a combat system can learn from the feedback of

human operators and leverage the existing

knowledge bases. The trained Soar agent can be

used to adapt to the future situations and reduce the

cognitive burdens of human operators. While the

scope of this initial research is limited, the results

are favorable to a dramatic modernization of CID. In

addition to establishing proof of concept, these

findings can aid future research to develop a robust

system that can mimic and/or aid the decision-

making abilities of a human operator. While this

research does focus on a sea-based naval

application, the framework and methodology can

also be expanded and scaled up to DOD-wide

implementations.

ACKNOWLEDGEMENTS

Thanks to the Naval Postgraduate School’s Naval

Research Program for funding this research. Thanks

to Mr. Tom Starai from National Maritime

Intelligence Center who provided insightful

discussion.

REFERENCES

Jones et al., R. M. (1999). Automated Intelligent Pilots for

Combat Flight Simulation. AI Magazine 20.1, 27-41.

Laird, J. E. (2012). The Soar Cognitive Architecture.

Cambridge, MA: The MIT Press.

Mooren, E. (2017). Reinforcement Learning Applications

to Combat Identification. Monterey: Naval

Postgraduate School. Monterey: Naval Postgraduate

School.

Scruggs, V. a. (2009). Combat Identification Training in

the Navy. Center for Naval Analyses Report

D0020254.A3.

Sutton, R. S., & Barto, A. G. (1998). Reinforcement

Learning: An Introduction. Cambridge, MA: The MIT

Press. Retrieved from https://libsearch.nps.edu/

vufind/Record/1124447

Tokic, M. (2010). Adaptive e-greedy exploration in

reinforcement learning based value. Lecture notes in

computer science Vol. 6359. Advances in artificial

intelligence, 203-210.