Entorhinal Grid Cells May Facilitate Pattern Separation

in the Hippocampus

Jochen Kerdels and Gabriele Peters

University of Hagen, Universit

atsstrasse 1, D-58097 Hagen, Germany

Keywords:

Pattern Separation, Grid Cells, Entorhinal Cortex, Dentate Gyrus, Hippocampus.

Abstract:

The dentate gyrus (DG) in the hippocampus of the mammalian brain is known to exhibit strong pattern sepa-

ration. However, how this pattern separation arises in the DG is not well understood. Here we offer a novel

hypothesis regarding this problem by demonstrating that pattern separation can already be performed by en-

torhinal grid cells, which are located just one synapse upstream of the DG. For our simulations we utilize a

recently introduced grid cell model that interprets the behavior of grid cells as just one instance of a general

information processing scheme. The obtained results challenge the established view that pattern separation

occurs primarily in the DG, and they uncover a common misconception regarding the speciﬁcity of ensemble

activity in grid cells.

1 INTRODUCTION

The parahippocampal region (PHR) and the hip-

pocampal formation (HF) in the mammalian brain

are vital for storing and retrieving episodic memories,

i.e., memories of speciﬁc events experienced by the

organism (Tulving and Markowitsch, 1998; Burgess

et al., 2002; Rolls, 2013). A key requirement for this

kind of memory is the ability to distinguish between

similar events that may differ only in minute details.

To accomplish such differentiation it is commonly as-

sumed that parts of the hippocampus carry out some

form of pattern separation that orthogonalizes the in-

put signals before they are stored in an autoassociative

memory (Leutgeb et al., 2007; Yassa and Stark, 2011;

Rolls, 2013). As a result of this pattern separation,

similar input signals cause divergent sets of neurons

to become active and thus reduce confusion of these

inputs in subsequent processing steps. Within the hip-

pocampus such divergent activation of neurons in re-

sponse to similar inputs was primarily observed in

the dentate gyrus (DG) (Leutgeb et al., 2007; Berron

et al., 2016). However, how this observed pattern sep-

aration in the DG arises is not well understood (Rolls,

2013).

In this paper we offer a novel hypothesis regarding

this problem. Based on our recently introduced com-

putational model of entorhinal grid cells (Kerdels and

Peters, 2015; Kerdels, 2016) we will show that the be-

havior of grid cells – if it is interpreted as an instance

of a general information processing scheme – already

results in strong pattern separation within the entorhi-

nal cortex (EC). As the latter provides the main input

to the dentate gyrus (van Strien et al., 2009) we hy-

pothesize that the pattern separation observed in DG

is facilitated by output signals from the EC that are

already well separated and that the DG itself just im-

proves this separation by sparsiﬁcation.

The next two sections provide a brief overview

of the parahippocampal-hippocampal network (PHR-

HF) and our computational model of entorhinal grid

cells. Section 4 outlines the experimental setup and

characterizes the input signal used in the simulations.

In sections 5 and 6 we present and discuss the simu-

lation results.

2 PHR-HF OVERVIEW

The parahippocampal-hippocampal region of the

mammalian brain is part of the limbic system. It

has a long evolutionary history and putative homo-

logues can be found in most vertebrate species (But-

ler and Hodos, 2005). Functionally, the region is nec-

essary for short term and declarative memory, which

includes factual knowledge as well as episodic mem-

ories (Squire et al., 2008).

The parahippocampal region (PHR) consists of

ﬁve main areas designated as perirhinal cortex (PER),

postrhinal cortex (POR), presubiculum (PrS), para-

Kerdels J. and Peters G.

Entorhinal Grid Cells May Facilitate Pattern Separation in the Hippocampus.

DOI: 10.5220/0006514601410148

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 141-148

ISBN: 978-989-758-274-5

Figure 1: The standard view of the parahippocampal-

hippocampal network based on the review by (van Strien

et al., 2009).

subiculum (PaS), and entorhinal cortex (EC). The lat-

ter being further subdivided into a lateral (LEA) and

a medial (MEA) part. The areas of the PHR have six

layers similar to the neocortex with layers II/III and

layers V/VI being the principal cell layers that contain

the majority of neuronal cell bodies. The hippocam-

pal formation (HF) consists of four main areas desig-

nated as dentate gyrus (DG), cornu ammonis 3 (CA3),

cornu ammonis 1 (CA1), and subiculum (Sub). In

contrast to the PHR and the neocortex the areas of the

HF have only three layers, with the central layer con-

taining the majority of cell bodies (Witter et al., 2000;

Squire et al., 2008; van Strien et al., 2009; Somogyi,

2010).

Figure 1 outlines the basic PHR-HF network. It

shows that the PHR acts as a gateway that mediates

both the input from the neocortex to the HF, as well

as the output from the HF to the neocortex. Two ma-

jor, bidirectional projection streams facilitate this ex-

change of signals. The PER connects predominantly

with the LEA, while the POR connects to the MEA.

From the upper layers II/III of the EC the so called

perforant pathway projects then to all areas of the HF.

Signals from the second layer reach the DG and CA1,

whereas signals from the third layer go to CA1 and the

subiculum. The output from the HF projects from ar-

eas CA1 and the subiculum to deep layers V/VI of the

EC (van Strien et al., 2009). As a rough approxima-

tion the hippocampus can be interpreted as a sequence

of processing modules, starting with the DG and end-

ing with the subiculum, that receives inputs from the

upper layers of the EC and feeds its results back to

the lower layers of the EC. As such, the EC can be

interpreted as the main interface to the hippocampus.

A major advance in the understanding of EC func-

tion resulted from the discovery of grid cells and their

subsequent investigation (Fyhn et al., 2004; Hafting

et al., 2005; Rowland et al., 2016). The activity of

grid cells correlates strongly with the animal’s loca-

tion creating a hexagonal pattern of ﬁring ﬁelds that

spans the entire environment of the animal. This

strong spatial correlation provides a rare opportunity

to experimentally observe and interpret the behav-

ior of neurons in this part of the brain. Common

hypothesis regarding the function of grid cells view

these cells as specialized components in a system fa-

cilitating orientation and navigation (Rowland et al.,

2016). However, recent observations of grid like ﬁr-

ing patterns in contexts other than locomotion (Kil-

lian et al., 2012; Constantinescu et al., 2016; Aronov

et al., 2017; Diehl et al., 2017) may indicate that the

behavior of grid cells reﬂects a more general, underly-

ing processing scheme. To investigate this hypothesis

we developed a computational model of grid cells that

implements such a general processing scheme allow-

ing us to apply our model outside of the typical con-

text of navigation and orientation (Kerdels and Peters,

2015; Kerdels, 2016; Kerdels and Peters, 2016). We

brieﬂy outline the model in the next section.

3 GRID CELL MODEL

We developed our grid cell model based on the idea

that the behavior observed in grid cells is just one

instance of a more general information processing

scheme. We hypothesize that grid cells form a simple,

piecewise representation of their entire input space by

learning a limited number of input patterns or proto-

types that reﬂect the input space structure. Simultane-

ously, competition among cells within a local grid cell

group ensures that the simple representations learned

by the individual cells are pairwise distinct and inter-

leave in such a way that a complex representation of

the input space emerges that is distributed over the

entire group of neurons.

On the neurobiological level such a prototype-

based representation could be stored within the den-

dritic tree of a neuron with individual prototypes

being stored in local dendritic subsections. In our

model we utilize the core ideas of the growing neural

gas (GNG) algorithm to describe this learning pro-

cess. The GNG is an unsupervised learning algorithm

that uses biologically plausible competitive Hebbian

learning to approximate the input space structure with

a network of prototypes (Martinetz and Schulten,

1994; Fritzke, 1995). We extended the regular GNG

algorithm into a recursive version (RGNG) that al-

lows us to simultaneously describe both the learning

processes of individual neurons as well as the com-

petition among a group of neurons by the same GNG

dynamics. For a formal description and an in-depth

characterization of the model we refer to (Kerdels and

Peters, 2016; Kerdels, 2016).

Figure 2: Typical samples of the digit 8 in the MNIST

database of handwritten digits (Lecun et al., 1998).

Regarding this work, the most important property of

the RGNG-based grid cell model is its ability to oper-

ate on arbitrary input spaces. Regardless of the par-

ticular input space, e.g., the modality or dimension of

the input signals, the modeled group of neurons will

try to learn the structure of that input space as well

as possible. In addition, as each neuron tries to learn

the structure of the entire input space the learned rep-

resentations of different neurons will be self-similar

and no individual neuron will “specialize” on a par-

ticular region of input space. As a consequence, small

shifts of the input signal are likely to cause a signif-

icant change in the set of active cells in the modeled

neuron group, hence effectively implementing a form

of pattern separation.

4 EXPERIMENTAL SETUP

To investigate the potential pattern separation capa-

bilities of grid cells we simulated multiple groups of

grid cells using the RGNG-based grid cell model and

exposed these groups to a sequence of input samples

from a given input space. For each input sample the

resulting activity of each simulated grid cell was de-

termined and the individual activities within a grid

cell group were then summarized in an activity vec-

tor. This vector can be interpreted as the grid cell

group’s encoding of the respective input sample. To

compare this encoding with the original encoding of

the input signal in terms of orthogonality we decided

to use the cosine similarity measure, as it is a direct

measure of the (non-)orthogonality of two vectors.

As input space we chose the well-known MNIST

database of handwritten digits (Lecun et al., 1998),

which provides a total of 60000 samples of hand-

written digits in the resolution of 28 × 28 = 784 pix-

els. Since the intra-class samples in this database ex-

hibit a high degree of similarity (Fig. 2) it is espe-

cially suited to investigate the pattern separation ca-

pabilities of an encoding scheme. Figure 3 shows the

intra- and inter-class cosine similarity distributions in

the MNIST dataset. Cosine similarity values close to

0 indicate orthogonal vectors, while values close to

1 indicate a high degree of similarity. For any en-

coding that performs pattern separation it is expected

that corresponding distributions of the encoded sig-

Figure 3: Box plot of the intra-class (orange, left columns)

and inter-class (blue, right columns) cosine similarity distri-

butions occurring in the MNIST dataset. Bottom and top of

dashed lines represent minimum and maximum values, bot-

tom and top of each box represent lower and upper quartiles,

thick lines represent medians, and circles represent mean

values of the distributions.

nals will be skewed towards 0.

A total of 15 grid cell groups were simulated. Each

group consisted of 100 neurons and received 2.88 mil-

lion (partial) input samples from the MNIST input

space, i.e., 48 repetitions of 60000 samples. Thus, the

activity vectors derived from each group were 100-

dimensional. The grid cell groups differed by the

number

{

20, 40, 80

}

of prototypes each neuron was

allowed to use for its input space representation, and

by processing either entire input samples or just the

top, bottom, left, or right half of the samples. The

number of prototypes per cell inﬂuences the “reso-

lution” with which the cell can form an input space

representation. A lower number of prototypes results

in a more coarse representation, i.e., grid cells with

a low number of prototypes have larger grid spacing

than grid cells with a high number of prototypes. The

numbers of prototypes used here were chosen from

a range that is biologically plausible (Kerdels, 2016).

The processing of partial input samples was used as

a proxy for simulating multimodal input, i.e., as input

that usually occurs together but that is represented and

encoded by independent groups of neurons. All other

parameters of the RGNG-based grid cell model were

held constant and are provided in the appendix.

5 RESULTS

Figure 4 shows the intra- and inter-class cosine sim-

ilarity distributions occurring in the activity vectors

of grid cell groups that processed 2.88 million in-

put samples from the MNIST input space and used

either 20, 40, or 80 prototypes per cell for their in-

put space representation. The activity vectors were

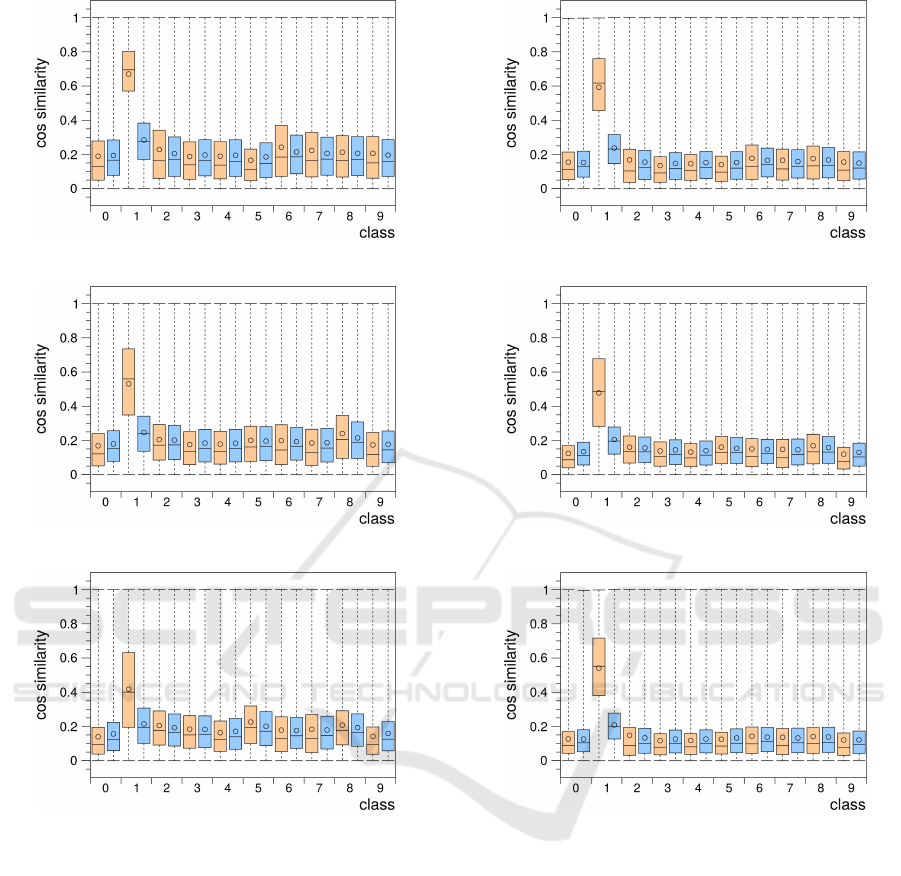
(a) 20 prototypes per cell

(b) 40 prototypes per cell

Figure 4: Box plots as in ﬁgure 3 of the intra- and inter-

class cosine similarity distributions occurring in the activity

vectors of grid cell groups using 20 (a), 40 (b), or 80 (c)

prototypes per cell for their input space representation.

sampled during the 48th input repetition of the 60000

MNIST training samples. For most classes the dis-

tributions show a signiﬁcant decrease in the cosine

similarities when compared with the cosine similar-

ities measured in the MNIST set (Fig. 3). Mean val-

ues for both intra- and inter-class similarities dropped

from about 0.5 and 0.4, respectively, to about 0.2. In

addition, the clear difference of similarity values be-

tween intra- and inter-class distributions visible in the

MNIST set was equalized in the grid cell group activ-

ity vectors. Notably, the intra-class distribution of

(a) combined groups 20 and 40 prot.

(b) combined groups 40 and 80 prot.

Figure 5: Box plots as in ﬁgure 3 of the intra- and inter-class

cosine similarity distributions occurring in combined activ-

ity vectors of grid cell groups. (a) Two grid cell groups us-

ing 20 and 40 prototypes per cell. (b) Two grid cell groups

using 40 and 80 prototypes per cell. (c) Three grid cell

groups using 20, 40, and 80 prototypes per cell.

class 1 deviates from these observations. It is broader

and retains a relatively high median similarity value.

In the case of the grid cell group that only uses 20 pro-

totypes per cell the median value has even increased

rather than decreased when compared to the MNIST

set median value of class 1. These deviations of the

class 1 distributions can be attributed to the fact that

the digit one is typically drawn as just a vertical stroke

with little variation.

It is a common notion within the grid cell literature

that the output signals of entorhinal grid cell groups

that exhibit different grid spacings combine in the hip-

pocampus to uniquely encode speciﬁc places in an

animal’s environment (Solstad et al., 2006). To in-

vestigate the orthogonality of such combined output

signals we concatenated the activity vectors of two

or more simulated grid cell groups that use differ-

ent numbers of prototypes per cell and analysed the

resulting intra- and inter-class cosine similarity dis-

tributions. Figure 5 shows the distributions occur-

ring in the combined activity vectors of groups us-

ing 20 and 40 prototypes (Fig. 5a), 40 and 80 proto-

types (Fig. 5b), as well as 20, 40, and 80 prototypes

(Fig. 5c). In general, the results are qualitatively simi-

lar to that from the non-combined, individual grid cell

groups (Fig. 4), though the widths of the distributions

as well as the mean similarity values have slightly de-

creased.

A different source of combined output signals can

be multimodal input. The entorhinal cortex receives

projections from various areas of the neocortex and

the limbic system. This multimodal input is then

processed and forwarded to the hippocampus. To

simulate input from multiple modalities we split the

MNIST input samples into top, bottom, left, and right

halves and let these partial samples be processed by

four separate grid cell groups. The activity vectors of

these four groups were then concatenated and anal-

ysed. Figure 6 shows the intra- and inter-class cosine

similarity distributions occurring in combined activity

vectors of groups that used 20 (Fig. 6a), 40 (Fig. 6b),

and 80 (Fig. 6c) prototypes per cell. In all three cases

there is a much more pronounced reduction in the

widths of the distributions and the mean similarity

values as compared to the distributions occurring in

the combined activity vectors of grid cell groups with

different grid spacings (Fig. 5). The lowest mean sim-

ilarity values of about 0.05 are achieved by the four

grid cell groups that use 80 prototypes per cell for

their input space representation. Remarkably, even

the mean similarity value of the intra-class distribu-

tion of class 1 decreases in this multimodal setting

down to a value of about 0.25 from about 0.6 mea-

sured in the MNIST set.

6 DISCUSSION

The results presented in the previous section indicate

that – under the given hypothesis – entorhinal grid

cells perform pattern separation on their input signals

and provide already orthogonalized output signals to

the hippocampus. This result provides a novel per-

(a) multi modal / 20 prototypes

(b) multi modal / 40 prototypes

Figure 6: Box plots as in ﬁgure 3 of the intra- and inter-

class cosine similarity distributions occurring in simulated

multimodal activity vectors of grid cell groups encoding

the top, bottom, left, or right halves of the MNIST input

samples using 20 (a), 40 (b), or 80 (c) prototypes per cell.

spective on the possible genesis of the pattern separa-

tion that can be observed in the dentate gyrus (Leut-

geb et al., 2007; Berron et al., 2016). From this per-

spective, the input signals to the DG may already be

well separated and the pattern separation observed in

the DG may just be a result of further sparsiﬁcation,

e.g., due to the neurogenesis occurring in this region.

Furthermore, shifting the “functionality” of pattern

separation from DG to EC would provide orthogonal-

ized inputs not only to the DG but also to all other

parts of the hippocampus (Fig. 1). This shift would

improve the support of hippocampal memory models

that assume that memory retrieval can operate with-

out the involvement of the DG (Tulving and Markow-

itsch, 1998).

Another important aspect is the observation that

pattern separation does not require the collaboration

of multiple grid cell groups (Fig. 4). A typical grid

cell ﬁres if the animal is at one of multiple locations.

In terms of the RGNG-based grid cell model the grid

cell ﬁres if the input to the cell matches one of its

multiple prototypes. Thus, from the activity of a sin-

gle grid cell it is not possible to derive which of the

prototypes caused the cell to ﬁre. The input pattern

could be similar to any of the multiple patterns en-

coded in the prototypes (Fig. 7). Within a grid cell

group the prototypes of grid cells are typically shifted

against each other. In most grid cell models found in

the literature this property is described in an idealized

way such that the relative locations of ﬁring ﬁelds,

i.e., the prototypes of all grid cells in the group are

precisely aligned. In this idealized case the joint ac-

tivity of the grid cell group remains ambiguous with

respect to the actual input pattern. However, in real-

ity the alignment of ﬁring patterns in a grid cell group

is less precise and can exhibit local permutations of

the cell’s ﬁring ﬁelds. As a consequence, these per-

mutations make the joint activity of a grid cell group

much more speciﬁc and less ambiguous than is com-

monly thought. The RGNG-based grid cell model al-

lows for such natural variation in the alignment, and

the resulting speciﬁcity of the grid cell group activity

is reﬂected by the high degree of pattern separation

present in the inter-class distributions shown in ﬁg-

ure 4.

A third important result is the observation that the

joint activity of grid cell groups that process differ-

ent modalities (Fig. 6) shows a much stronger pattern

separation than the joint activity of grid cell groups

that have different grid spacings (Fig. 5). Yet, the grid

cell literature focuses much more on the latter (Rolls

et al., 2006; Solstad et al., 2006; Franzius et al., 2007;

de Almeida et al., 2009; Savelli and Knierim, 2010),

while aspects of multimodality appear to be underrep-

resented (Aronov et al., 2017; Diehl et al., 2017).

7 CONCLUSION

We investigated the degree to which entorhinal grid

cells perform pattern separation and thus may facil-

itate the subsequent pattern separation observed in

areas of the hippocampus. Based on the hypothe-

sis that the behavior of entorhinal grid cells is just

one instance of a more general information process-

(a) cell #1

(b) cell #10

Figure 7: Three examples of 80 prototypes that were

learned by three grid cells {#1,#10,#20} to form an input

space representation. The prototypes typically cover the en-

tire input space in each grid cell and are slightly shifted in

the input space across different cells. The last rows in the

prototype overviews show examples of “unused” prototypes

that the cells haven’t utilized so far.

ing scheme we used our recently introduced RGNG-

based grid cell model (Kerdels and Peters, 2015;

Kerdels, 2016; Kerdels and Peters, 2016) to simulate

several groups of grid cells that processed visual in-

puts derived from the MNIST database of handwritten

digits. The results indicate that entorhinal grid cells

may indeed perform pattern separation on their input

signals and thus may provide already orthogonalized

output signals to the hippocampus.

These results challenge established views on the

parahippocampal-hippocampal region and provide a

novel explanation for the origin of the pattern sepa-

ration that is observed in the dentate gyrus. Further-

more, they uncover a common misconception about

the assumed lack of speciﬁcity in the activity of grid

cell groups. Finally, the results encourage the further

investigation of the inﬂuence of multimodal input on

the processing within the entorhinal cortex.

REFERENCES

Aronov, D., Nevers, R., and Tank, D. W. (2017). Map-

ping of a non-spatial dimension by the hippocampa-

lentorhinal circuit. Nature, 543(7647):719–722.

Berron, D., Sch

utze, H., Maass, A., Cardenas-Blanco, A.,

Kuijf, H. J., Kumaran, D., and D

uzel, E. (2016).

Strong evidence for pattern separation in human den-

tate gyrus. Journal of Neuroscience, 36(29):7569–

7579.

Burgess, N., Maguire, E. A., and O’Keefe, J. (2002). The

human hippocampus and spatial and episodic mem-

ory. Neuron, 35(4):625 – 641.

Butler, A. and Hodos, W. (2005). Comparative Vertebrate

Neuroanatomy: Evolution and Adaptation. Wiley.

Constantinescu, A. O., O’Reilly, J. X., and Behrens, T.

E. J. (2016). Organizing conceptual knowledge in hu-

mans with a grid-like code. Science (New York, N.Y.),

352(6292):1464–1468.

de Almeida, L., Idiart, M., and Lisman, J. E. (2009). The

inputoutput transformation of the hippocampal gran-

ule cells: From grid cells to place ﬁelds. The Journal

of Neuroscience, 29(23):7504–7512.

Diehl, G. W., Hon, O. J., Leutgeb, S., and Leutgeb, J. K.

(2017). Grid and nongrid cells in medial entorhinal

cortex represent spatial location and environmental

features with complementary coding schemes. Neu-

ron, 94(1):83 – 92.e6.

Franzius, M., Vollgraf, R., and Wiskott, L. (2007). From

grids to places. Journal of Computational Neuro-

science, 22(3):297–299.

Fritzke, B. (1995). A growing neural gas network learns

topologies. In Advances in Neural Information Pro-

cessing Systems 7, pages 625–632. MIT Press.

Fyhn, M., Molden, S., Witter, M. P., Moser, E. I., and

Moser, M.-B. (2004). Spatial representation in the en-

torhinal cortex. Science, 305(5688):1258–1264.

Hafting, T., Fyhn, M., Molden, S., Moser, M.-B., and

Moser, E. I. (2005). Microstructure of a spatial map

in the entorhinal cortex. Nature, 436(7052):801–806.

Kerdels, J. (2016). A Computational Model of Grid Cells

based on a Recursive Growing Neural Gas. PhD the-

sis, FernUniversit

at in Hagen, Hagen.

Kerdels, J. and Peters, G. (2015). A new view on grid cells

beyond the cognitive map hypothesis. In 8th Confer-

ence on Artiﬁcial General Intelligence (AGI 2015).

Kerdels, J. and Peters, G. (2016). Modelling the grid-like

encoding of visual space in primates. In Proceedings

of the 8th International Joint Conference on Compu-

tational Intelligence, IJCCI 2016, Volume 3: NCTA,

Porto, Portugal, November 9-11, 2016., pages 42–49.

Killian, N. J., Jutras, M. J., and Buffalo, E. A. (2012). A

map of visual space in the primate entorhinal cortex.

Nature, 491(7426):761–764.

Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Leutgeb, J. K., Leutgeb, S., Moser, M.-B., and Moser, E. I.

(2007). Pattern separation in the dentate gyrus and ca3

of the hippocampus. Science, 315(5814):961–966.

Martinetz, T. M. and Schulten, K. (1994). Topology repre-

senting networks. Neural Networks, 7:507–522.

Rolls, E. (2013). The mechanisms for pattern completion

and pattern separation in the hippocampus. Frontiers

in Systems Neuroscience, 7(74).

Rolls, E. T., Stringer, S. M., and Elliot, T. (2006). Entorhi-

nal cortex grid cells can map to hippocampal place

cells by competitive learning. Network: Computation

in Neural Systems, 17(4):447–465. PMID: 17162463.

Rowland, D. C., Roudi, Y., Moser, M.-B., and Moser, E. I.

(2016). Ten years of grid cells. Annual Review of

Neuroscience, 39(1):19–40. PMID: 27023731.

Savelli, F. and Knierim, J. J. (2010). Hebbian analysis of the

transformation of medial entorhinal grid-cell inputs to

hippocampal place ﬁelds. Journal of Neurophysiol-

ogy, 103(6):3167–3183.

Solstad, T., Moser, E. I., and Einevoll, G. T. (2006). From

grid cells to place cells: A mathematical model. Hip-

pocampus, 16(12):1026–1031.

Somogyi, P. (2010). Hippocampus: Intrinsic organization.

In Shepherd, G. M. and Grillner, S., editors, Hand-

book of Brain Microcircuits, pages 148–164. Oxford

University Press.

Squire, L., Bloom, F., Spitzer, N., Squire, L., Berg, D.,

du Lac, S., and Ghosh, A. (2008). Fundamental Neu-

roscience. Fundamental Neuroscience Series. Elsevier

Science.

Tulving, E. and Markowitsch, H. J. (1998). Episodic and

declarative memory: Role of the hippocampus. Hip-

pocampus, 8(3):198–204.

van Strien, N. M., Cappaert, N. L. M., and Witter, M. P.

(2009). The anatomy of memory: an interactive

overview of the parahippocampal-hippocampal net-

work. Nat Rev Neurosci, 10(4):272–282.

Witter, M. P., Wouterlood, F. G., Naber, P. A., and van

Haeften, T. (2000). Anatomical organization of the

parahippocampal-hippocampal network. Annals of the

New York Academy of Sciences, 911(1):1–24.

Yassa, M. A. and Stark, C. E. L. (2011). Pattern sepa-

ration in the hippocampus. Trends in neurosciences,

34(10):515–525.

APPENDIX

Parameterization

Each layer of an RGNG requires its own set of pa-

rameters. In case of our two-layered grid cell model

we use the sets of parameters θ

and θ

, respec-

tively. Parameter set θ

controls the main top layer

RGNG while parameter set θ

controls all bottom

layer RGNGs. Table 1 summarizes the parameter val-

ues used for the simulation runs presented in this pa-

per. For a detailed characterization of these parame-

ters we refer to Kerdels (Kerdels, 2016).

Table 1: Parameters of the RGNG-based model used

throughout all simulation runs. Parameters θ

control the

top layer RGNG while parameters θ

control all bottom

layer RGNGs of the model.

= 0.004 ε

= 0.001

= 0.004 ε

= 0.00001

= 0.01 ε

= 0.01

λ = 1000 λ = 1000

τ = 300 τ = 300

α = 0.5 α = 0.5

β = 0.0005 β = 0.0005

M = 100 M =

{

20, 40, 80

}