Efﬁcient Approaches for Solving the Large-Scale k-medoids Problem

Alessio Martino, Antonello Rizzi and Fabio Massimo Frattale Mascioli

Department of Information Engineering, Electronics and Telecommunications, University of Rome ”La Sapienza”,

Via Eudossiana 18, 00184 Rome, Italy

Keywords:

Cluster Analysis, Parallel and Distributed Computing, Large-Scale Pattern Recognition, Unsupervised

Learning, Big Data Mining.

Abstract:

In this paper, we propose a novel implementation for solving the large-scale k-medoids clustering prob-

lem. Conversely to the most famous k-means, k-medoids suffers from a computationally intensive phase for

medoids evaluation, whose complexity is quadratic in space and time; thus solving this task for large datasets

and, speciﬁcally, for large clusters might be unfeasible. In order to overcome this problem, we propose two

alternatives for medoids update, one exact method and one approximate method: the former based on solving,

in a distributed fashion, the quadratic medoid update problem; the latter based on a scan and replacement

procedure. We implemented and tested our approach using the Apache Spark framework for parallel and dis-

tributed processing on several datasets of increasing dimensions, both in terms of patterns and dimensionality,

and computational results show that both approaches are efﬁcient and effective, able to converge to the same

solutions provided by state-of-the-art k-medoids implementations and, at the same time, able to scale very

well as the dataset size and/or number of working units increase.

1 INTRODUCTION

The recent explosion of interest for Data Mining and

Knowledge Discovery put cluster analysis on the spot

again. Cluster analysis is the very basic approach in

order to extract regularities from datasets. In plain

terms, clustering a dataset consists in discovering

clusters (groups) of patterns such that similar patterns

will fall within the same cluster whereas dissimilar

patterns will fall in different clusters.

Indeed, not only different algorithms, but different

families of algorithms have been proposed in literat-

ure: partitional clustering (e.g. k-means (MacQueen,

1967; Lloyd, 1982), k-medians (Bradley et al., 1996),

k-medoids (Kaufman and Rousseeuw, 1987)), which

break the dataset into k non-overlapping clusters;

density-based clustering (e.g. DBSCAN (Ester et al.,

1996), OPTICS (Ankerst et al., 1999)) which detect

clusters as the most dense regions of the dataset; hier-

archical clustering (e.g. BIRCH (Zhang et al., 1996),

CURE (Guha et al., 1998)) where clusters are found

by (intrinsically) building a dendrogram in either a

top-down or bottom-up approach.

Moreover, in the Big Data era, the need for

clustering massive datasets emerged. Efﬁcient and

rather easy-to-use large-scale processing frameworks

such as MapReduce (Dean and Ghemawat, 2008) or

Apache Spark (Zaharia et al., 2010) have been pro-

posed, gaining a lot of attention from Computer Sci-

ence and Machine Learning researchers alike. As

a matter of fact, several large-scale Machine Learn-

ing algorithms have been grouped in MLlib (Meng

et al., 2016), the Machine Learning library built-in in

Apache Spark.

In this work, we will focus on the k-medoids al-

gorithm, a (hard) partitional clustering algorithm sim-

ilar to the widely-known k-means. However, con-

versely to k-means, there is still some debate about a

k-medoids parallel and distributed version due to the

fact that the medoid evaluation complexity is quad-

ratic in space and time and might therefore be un-

suitable for large clusters. More into details, we

propose a novel k-medoids implementation based

on Apache Spark with two different procedures for

medoids evaluation: an exact procedure and an ap-

proximate procedure. The former, albeit exact, re-

quires the entire intra-cluster distance matrix evalu-

ation which, as already introduced, might be unsuit-

able for large clusters. The latter overcomes this prob-

lem by adopting a scan-and-replace workﬂow, but re-

turns a (sub)optimal medoid amongst the patterns in

the cluster at hand.

The remainder of the paper is structured as fol-

lows: Section 2 will summarise the k-medoids prob-

Martino A., Rizzi A. and Frattale Mascioli F.

Efﬁcient Approaches for Solving the Large-Scale k-medoids Problem.

DOI: 10.5220/0006515003380347

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 338-347

ISBN: 978-989-758-274-5

lem; in Section 3 the proposed approaches and re-

lated implementations will be described; in Section 4

the efﬁciency and effectiveness of both the proposed

medoid evaluation routines will be evaluated and dis-

cussed; Section 5 will draw some conclusions.

1.1 Contribution and State of the Art

Review

As introduced in the previous section, parallel and

distributed k-means implementations not only have

been proposed in MapReduce (Zhao et al., 2009), but

it is also included in MLlib. As far as k-medoids

is concerned, to the best of our knowledge, there

are very few parallel and distributed implementations

proposed in literature. In (Yue et al., 2016) an im-

plementation based on Hadoop/MapReduce has been

proposed where, similarly to (Zhao et al., 2009),

the Map phase evaluates the point-to-medoid assign-

ment, whereas the Reduce phase re-evaluates the new

medoids. Results show how the proposed implement-

ation scales well with the dataset size, while it lacks

of considerations regarding the effectiveness. In (Ar-

belaez and Quesada, 2013) the k-medoids problem is

decomposed (space partitioning) in many local search

problems which are solved in parallel. In (Jiang and

Zhang, 2014) the k-medoids problem is again solved

using Hadoop/MapReduce with a three-phases work-

ﬂow (Map-Combiner-Reduce). Albeit it is unclear

how the new medoids are evaluated, the Authors show

both efﬁciency and effectiveness. Speciﬁcally, the lat-

ter is measured on a single labelled dataset, thus cast-

ing the clustering problem (unsupervised by deﬁni-

tion) as a post-supervised learning problem. Both

(Yue et al., 2016) and (Jiang and Zhang, 2014) start

from Partitioning Around Medoids (PAM), the most

famous algorithm for solving the k-medoids prob-

lem (Kaufman and Rousseeuw, 2009): a greedy al-

gorithm which scans all patterns in a given cluster

and, for each point, checks whether using that point

as a medoid further minimises the objective function

(§2): if true, that point becomes the new medoid.

In this work, a k-medoids implementation based

on Apache Spark will be discussed which, due to

its caching functionalities, is more efﬁcient than

MapReduce, especially when dealing with iterative

algorithms (§3.1).Moreover, rather than using PAM,

the (large-scale) k-medoids problem will be solved

with the implementation proposed in (Park and Jun,

2009) which has a very k-means-like workﬂow and

therefore it is possible to rely on a very easy-to-

parallelise algorithm ﬂowchart.

However, the medoid(s) re-evaluation/update is a

critical task since it needs to evaluate pairwise dis-

tances amongst patterns in a given cluster in order

to ﬁnd the new medoid, namely the element which

minimises the sum of distances. In order to over-

come this problem, we propose two alternatives: an

exact medoid evaluation based on cartesian product

(suitable for small/medium clusters) and an approx-

imate tracking method (suitable for large clusters as

well), proposed in (Del Vescovo et al., 2014) but never

tested on large-scale scenarios.

2 THE k-MEDOIDS CLUSTERING

PROBLEM

k-medoids is a hard partitional clustering algorithm;

it aims in partitioning the dataset S = {x

,...,x

}

into k non-overlapping groups (clusters), i.e. S =

,...,S

} such that S

∩ S

0 if i 6= j and ∪

i=1

In order to ﬁnd the optimal partition, k-medoids tries

to minimise the following objective function, namely

the Within-Clusters Sum-of-Distances:

WCSoD =

∑

i=1

∑

x∈S

d(x, m(i))

(1)

where d(·, ·) is a suitable (dis)similarity measure, usu-

ally the standard Euclidean distance, and m(i) is the

medoid for cluster i. In this work, a recent implement-

ation based on the Voronoi iteration is adopted and its

main steps can be summarised as follows:

1. select an initial set of k medoids

2. Expectation Step: assign each data point to closest

medoid

3. Maximisation Step: update each clusters’ medoid

4. Loop 2–3 until either medoids stop updating (or

their update is negligible) or a maximum number

of iterations is reached

It is worth stressing that minimising the sum of

squares (1) is an NP-hard problem (Aloise et al.,

2009) and therefore all methods (heuristics) proposed

in literature (both in terms of efﬁciency and effect-

iveness) strictly depend on the initial medoids: this

leaded to the implementation of initialisation heur-

istics such as k-means++ (Arthur and Vassilvitskii,

2007) or DBCRIMES (Bianchi et al., 2016).

It has already been discussed that evaluating the

medoid is more complex than evaluating the mean,

since it requires the complete pairwise distance mat-

rix D between all points in a given cluster S

, form-

ally deﬁned as an |S

|×|S

| real-valued matrix whose

generic entry is given by

)

i, j

= d(x

) (2)

or, as far as the Euclidean distance is concerned, du-

ally deﬁnable in terms of Gram matrix as

)

i, j

)

i, j

− x

i (3)

for any two patterns x

, x

∈ S

Despite its complexity, by minimising the sum of

pairwise distances rather than the squared Euclidean

distance from the average point (i.e. k-means), k-

medoids is more robust with respect to noise and out-

liers. Moreover, k-medoids is particularly suited if the

cluster prototype must be an element of the dataset

(the same is generally not true for k-means) and it is

applicable to ideally any input space, not necessarily

metric, since there is no need to deﬁne an algebraic

structure in order to compute the representative ele-

ment of a cluster.

3 PROPOSED APPROACH

3.1 A Quick Spark Introduction

In this work Apache Spark (hereinafter simply Spark)

has been chosen over Hadoop/MapReduce due to its

efﬁciency, as introduced in §1.1. Indeed, MapRe-

duce forces any algorithm pipeline into a sequence of

Map → Reduce steps, eventually with an intermediate

Combiner phase, which strains the implementation of

more complex operations such as joins or ﬁlters as

they have to be casted as well into Map → Reduce. In

MapReduce, computing nodes do not have memory of

past executions: this does not suit the implementation

of iterative algorithms, as the master process must for-

ward data to workers at each MapReduce job, which

typically corresponds to a single iteration of a given

algorithm.

Spark overcomes these problems as it includes

highly efﬁcient map, reduce, join, ﬁlter (and many

others) operations which are not only natively dis-

tributed, but can be arbitrarily pipelined together. As

far as iterative algorithms are concerned, Spark offers

caching in memory and/or disk, therefore there is no

need to forward data back and forth from/to workers

at each iteration.

Atomic data structures in Spark are the so-

called Resilient Distributed Datasets (RDDs): distrib-

uted (across workers

) collection of data with fault-

tolerance mechanisms, which can be created start-

ing from many sources (distributed ﬁle systems, data-

In Spark, workers are the elementary computational

units, which can be either single cores on a CPU or en-

tire computers, depending on the environment conﬁguration

(i.e. the Spark Context).

bases, text ﬁles and the like) or by applying trans-

formations on other RDDs.

Example of transformations which will turn useful

in the following subsections are:

map(): RDD2 = RDD1.map( f )

creates RDD2 by applying function f to every ele-

ment in RDD1

f ilter(): RDD2 = RDD1. f ilter(pred)

creates RDD2 by ﬁltering elements from RDD1

which satisfy predicate pred (i.e. if pred is True)

reduceByKey(): RDD2 = RDD1.reduceByKey( f )

creates RDD2 by merging according to function f

all values for each key in RDD1: RDD2 will have

the same keys as RDD1 and a new value obtained

by the merging function.

Similarly, examples of actions which can be applied

to RDDs are:

count(): RDD.count()

count the number of elements in RDD

collect(): RDD.collect()

collects in-memory on the master node the entire

RDD content.

3.2 Main Algorithm

The main parallel and distributed k-medoids ﬂowchart

is summarised in the Algorithm 1.

It is possible to ﬁgure datasetRDD to be a key-value

pair RDD

or, in other words, an RDD where each

record has the form hkey ; valuei. Speciﬁcally, the

key is a sequential integer ID and the value is (as a

ﬁrst approach) an n-dimensional real-valued vector.

At the beginning of each iteration, a new key-

value pair RDD will be created (distancesRDD)

where the key is still the pattern ID whereas, the

value (distanceVector) is a k-dimensional real-

valued vector where the i

element contains the dis-

tance with the i

medoid. The following two RDDs

(nearestDistRDD and nearestClusterRDD) map

the pattern ID with the nearest distance value and the

nearest cluster ID (i.e. medoid), respectively. These

evaluations end the Maximisation Step for the Voro-

noi iteration (§2).

nearestClusterRDD is the main RDD for the

medoids update step (i.e. the Expectation Step

for the Voronoi iteration): after gathering the list

In the following subsections and pseudocodes every

variable whose name ends with RDD shall be considered as

an RDD, therefore a data structure whose shards are distrib-

uted across the workers or, similarly, with no guarantee that

a single worker has its entire content in memory.

of pattern IDs (patternsInClusterIDs) belong-

ing to cluster ID clID, an additional RDD contain-

ing the patterns belonging to clID will be created

(patternsInClusterRDD). This RDD, which still is

a key-value pair RDD, is the main input for the

medoids update step which we shall discuss in more

details in the following subsection.

1 Begin main

2 Load datasetRDD from source (e.g. text-

file);

3 Cache datasetRDD on workers;

4 Set maxIterations, k,

approximateTrackingFlag;

5 medoids = initialSeeds();

6 for iter in range(1:maxIterations)

7 previousMedoids = medoids;

8 distancesRDD = datasetRDD.map(d(

pattern,medoids));

9 nearestDistRDD = distancesRDD.map(min(

distanceVector));

10 nearestClusterRDD = distancesRDD.map(

argmin(distanceVector));

11 for clID in range(1:k)

12 patternsInClusterIDs =

nearestClusterRDD.filter(clusterID

== clID);

13 patternsInClusterRDD =

nearestClusterRDD.filter(clusterID

in patternsInClusterIDs);

14 if approximateTrackinFlag is True

15 medoids[clID] =

approximateMedoidTracking();

16 else

17 medoids[clID] =

exactMedoidUpdate();

18 WCSoD = nearestDistRDD.values().sum();

19 if stopping criteria == True

20 break;

21 End main

Algorithm 1: Pseudocode for the main k-medoids skeleton

(namely, Voronoi iterations).

3.3 Updating Medoids

3.3.1 Exact Medoid Update

The Exact Medoid Update consists in evaluating the

pairwise distance matrix amongst all the patterns in a

given cluster and then ﬁnding the element which min-

imises the sum by rows/columns

of such matrix.

We deﬁne a-priori a parameter T , a threshold value

In the following, we suppose that the (dis)similarity

measure d(·,·) is metric, therefore satisﬁes the symmetry

property, i.e. d(a,b) = d(b,a). For metric (dis)similarity

measures the pairwise distance matrix is symmetric by

deﬁnition and the sum by rows or columns leads to the same

result.

which states the maximum allowed cluster cardinal-

ity in order to consider such cluster as ”small”. This

parameter can be tuned considering both the expected

clusters’ sizes and the amount of memory available on

the master node.

1 Begin function exactMedoidUpdate(

patternsInClusterRDD)

2 if patternsInClusterRDD.count() < T

3 patterns = patternsInClusterRDD.

collect().asmatrix();

4 distanceMatrix = pdist(patterns,d);

5 Sum distanceMatrix by rows or columns;

6 medoidID = argmin of rows/columns sum;

7 return patterns[medoidID];

8 else

9 pairsRDD = patternsInClusterRDD.

cartesian(patternsInClusterRDD);

10 distancesRDD = pairsRDD.map(d(pattern1

,pattern2));

11 distancesRDD = distancesRDD.

reduceByKey(add);

12 medoidID = distancesRDD.min(key=dist);

13 return patternsInClusterRDD.filter(ID

== medoidID).collect();

14 End function

Algorithm 2: Pseudocode for the Exact Medoid Update

routine.

Algorithm 2 describes the Exact Medoid Update

routine. Basically, if the cluster is ”small” it is pos-

sible to collect on the master node the entire set of pat-

terns and therefore use one of the many in-memory al-

gorithms (pdist) for evaluating the pairwise distance

matrix according to a given (dis)similarity measure d.

Conversely, if the cluster is ”not-small”, via Spark

it is possible to evaluate the cartesian product of

this cluster’s RDD with itself, leading to a new

RDD (pairsRDD) where each record is a pair of re-

cords from the original RDD, therefore it is pos-

sible to ﬁgure pairsRDD to have the form hID1 ;

pattern1 ; ID2 ; pattern2i. Given these pairs, eval-

uating the (dis)similarity measure is straightforward

and distancesRDD will have the form hID1 ; ID2

; d(pattern1,pattern2)i. Given the analogy with the

pairwise distance matrix, in order to perform the sum

by rows or columns, distancesRDD will be reduced

by using either the ID of the ﬁrst pattern (by rows) or

the ID of the second pattern (by columns) as key and

using the addition operator to values. In other words,

for ID1 (or ID2) we sum all the distances with other

IDs (i.e. other patterns). Given these sums, the ﬁnal

step consists in evaluating the minimum of the result-

ing RDD considering the sum of distances rather than

the ID leading to medoidID, the ID of the new medoid

which will be ﬁltered from patternsInClusterRDD

and returned as the new, updated, medoid.

3.3.2 Approximate Medoid Tracking

Whilst the (large scale) Exact Medoid Update (Al-

gorithm 2, namely the else branch) relies on natively

distributed and highly efﬁcient Spark operations,

the cartesian product might be unfeasible for very

large clusters since it creates an RDD whose size is

squared the size of the cluster (i.e. squared the size of

the input RDD) according to Eqs. (2)-(3).

1 Begin function approximateMedoidTracking(

patternsInClusterRDD,medoids,clusterID)

2 if patternsInClusterRDD.count() < P

3 patterns = patternsInClusterRDD.

collect().asmatrix();

4 distanceMatrix = pdist(patterns,d);

5 Sum distanceMatrix by rows or columns;

6 medoidID = argmin of rows/columns sum;

7 return patterns[medoidID];

8 else

9 pool = patternsInClusterRDD.filter(ID

in range(1:P)).collect().asmatrix();

10 patternsInClusterRDD =

patternsInClusterRDD.filter(ID not in

range(1:P));

11 for pattern in patternsInClusterRDD

12 Extract x1!=x2 from pool;

13 if d(x1,medoids[clusterID])>=d(x2,

medoids[clusterID])

14 Remove x1 from pool;

15 else

16 Remove x2 from pool;

17 pool = pool.append(pattern);

18 distanceMatrix = pdist(pool,d);

19 Sum distanceMatrix by rows or columns;

20 medoidID = argmin of rows/columns sum;

21 return pool[medoidID];

22 End function

Algorithm 3: Pseudocode for the Approximate Medoid

Tracking routine.

To this end, a second, approximate, medoid evalu-

ation based on (Del Vescovo et al., 2014) is proposed.

For the sake of ease, their ﬁndings can be summarised

as follows:

1. set a pool size P and ﬁll the pool with the ﬁrst P

patterns from the cluster at hand

2. for every remaining pattern x, select uniformly at

random two items from the pool (x

and x

) and

check their distances with the current medoid m.

If d(x

,m) ≥ d(x

,m), remove x

from the pool;

otherwise remove x

. Finally, insert x in the pool.

3. evaluate the new medoid with any standard in-

memory routine using the patterns in the pool.

Algorithm 3 describes the Approximate Medoid

Tracking routine. As in Algorithm 2, if the cluster

is ”small” there is not need to trigger any parallel an-

d/or distributed medoid evaluation which can thus be

done locally, in an exact manner. Conversely, if the

cluster is ”not-small” the ﬁrst P items will be cached

and removed from the RDD which contains the pat-

terns in such cluster. Finally, the approximate proced-

ure starts by iterating over the RDD and performing

the steps from (Del Vescovo et al., 2014).

3.4 Selecting Initial Seeds

As discussed in §2, the solution returned by heurist-

ics such as k-medoids is strictly dependent from the

initial medoids (seeds) selection. One of the most

widely-used approaches consists in random selection

and multi-start: a given number (typically 5 or 10)

of sets of k initial medoids are uniformly at random

selected from the dataset and for each set of initial

medoids the k-medoids algorithm will be run. The ﬁ-

nal clustering solution is determined by the run with

minimum WCSoD. Other solutions have been pro-

posed in literature such as k-means++ which we im-

plemented for a more accurate seeds selection. In its

standard form, k-means++ works as follows:

1. select the ﬁrst centroid

uniformly at random from

the dataset S

2. evaluate pairwise distances between patterns and

already-selected centroid, mapping each pattern

with its closest centroid; let us call D(x) the

closest distance between pattern x ∈ S and the

already-selected centroids

3. a pattern from the dataset S is selected as new

centroid with probability

(x)

∑

x∈S

(x)

4. Loop 2–3 until k initial centroids are selected

The Spark k-means++ distributed version is summar-

ised in Algorithm 4.

Many of these RDDs have already been introduced

in §3.2 and, since step #2 in k-means++ actually is

the Maximisation step for the Voronoi iteration (§2),

such RDDs will be created and evaluated in the same

manner as described in Algorithm 1. One might ob-

ject that collecting (i.e. loading into the master node

memory) nearestDistRDD might not be suitable for

large datasets. It is worth noticing that, in order to

save space, only the distance values and not the IDs

will be collected and, moreover, a modern computer

can store several millions of elements within an in-

memory array. Therefore (as a ﬁrst approach) we do

Historically, k-means++ was designed for k-means and

therefore we will refer to the cluster representative as

”centroid”. However, since it returns k data points as ini-

tial seeds, the same procedure holds for ”medoid”.

not consider this operation as prohibitive.

1 Begin function initialSeeds(datasetRDD,k)

2 N = datasetRDD.count();

3 firstMedoidID = random.integer(1,N);

4 medoids = datasetRDD.filter(ID ==

firstMedoidID);

5 for iter in range(1:k-1)

6 distancesRDD = datasetRDD.map(d(

pattern,medoids));

7 nearestDistRDD = distancesRDD.map(min(

distanceVector));

8 distances = nearestDistRDD.values().

collect();

9 distances = distances/sum(distances);

10 newMedoidID = random.choice(range(1:N)

,prob=distances);

11 medoids = medoids.append(datasetRDD.

filter(ID == newMedoidID).collect());

12 End function

Algorithm 4: Pseudocode for k-means++.

4 COMPUTATIONAL RESULTS

4.1 Datasets and Environment

Description

In order to show both the effectiveness and the ef-

ﬁciency of the proposed algorithm, 9 datasets have

been considered. All of them are freely available

from UCI Machine Learning Repository (Lichman,

2013) and their major characteristics are summarised

in Table 1. Classes in labelled datasets (e.g. Wine,

Iris) and eventual pattern IDs (e.g. 3D Road Network)

have been deliberately discarded. All datasets have

been normalised before processing.

Table 1: List of datasets used for analysis.

Dataset Name # patterns # features

US Census 1990 2458285 68

3D Road Network 434874 4

KEGG Metabolic Relation

Network (Directed)

53413 23

Bag of Words (ENRON) 39861 28102

Daily and Sport Activities 9120 5625

Bag of Words (KOS) 3430 6906

Bag of Words (NIPS) 1500 12419

Iris 178 13

Wine 150 4

Experiments shown in §4.2 and 4.3 have been con-

ducted on a Linux Ubuntu 16.04LTS workstation with

two Intel

 Xeon

 CPUs @2.60GHz for a total of 24

physical cores, 32GB RAM and 1TB HDD. Such 24

cores have been grouped in 6 groups of 4 cores each,

in order to simulate 6 PCs working in parallel which

will be the workers for these experiments. The latest

Apache Spark version has been used (v2.2.0) and,

speciﬁcally, its Python API (namely, PySpark) driven

by Python v2.7.13 with NumPy v1.12.1 (van der Walt

et al., 2011) for efﬁcient numerical computations.

4.2 Effectiveness

In order to show the effectiveness of the proposed

distributed implementation, the clustering problem

has not been casted as a semi-supervised or post-

supervised learning problem since, in our opinion,

this is not a good way to address the effectiveness

of a clustering algorithm (which solves unsupervised

problems by deﬁnition) as one might tend to con-

fuse clusters with classes. Rather, the solution (i.e.

the objective function) returned by the distributed k-

medoids implementation will be compared with the

solution returned by a well-established and not dis-

tributed k-medoids implementation, speciﬁcally the

one available in the MATLAB

 R2015a.

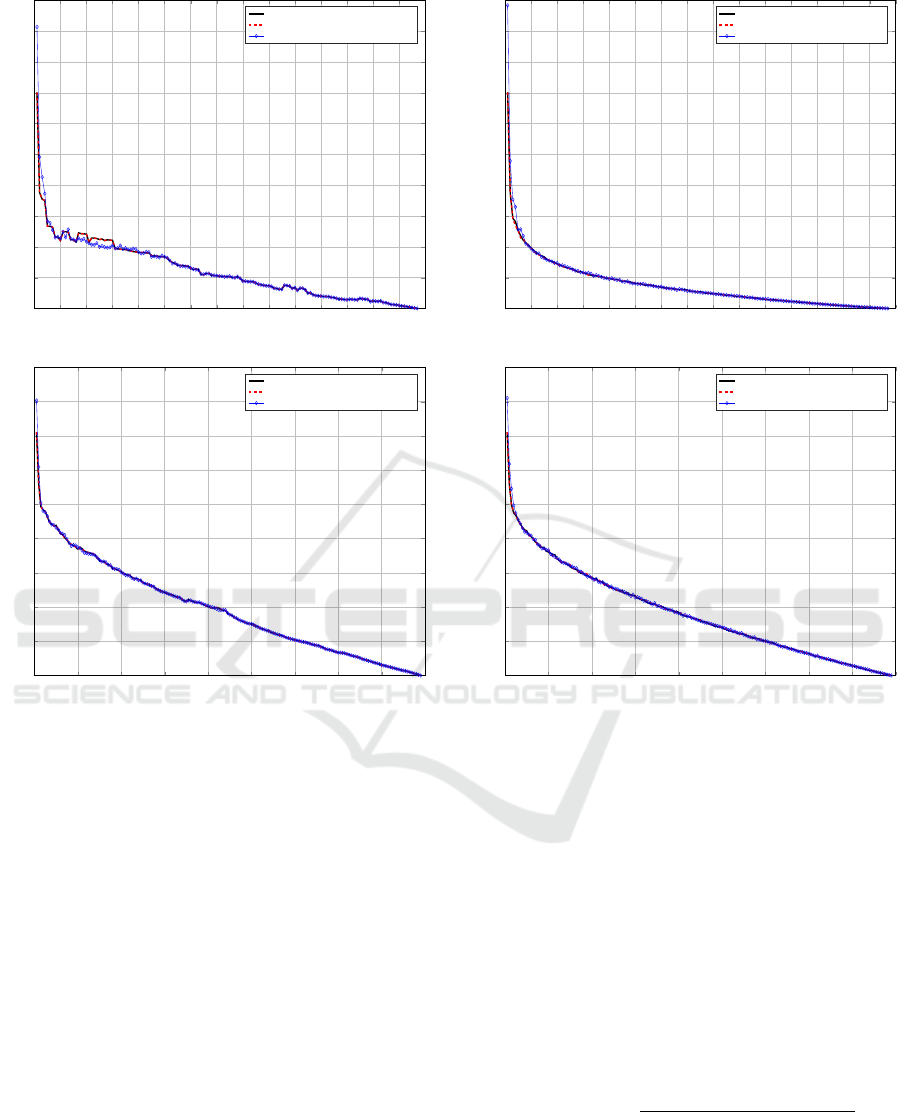
In Figure 1 the objective function returned by

the distributed implementation is shown, considering

both the Approximate Medoid Tracking and the Exact

Medoid Update routines for medoids update, against

the MATLAB k-medoids implementation. We con-

sidered the two smaller datasets (Iris and Wine in Fig-

ures 1(a) and 1(b), respectively) in order to be able

to test every possible value for k; that is, from 1 up

to the singleton (i.e. the total number of patterns).

To ensure a fair comparison, the same (dis)similarity

measure has been used (standard Euclidean distance)

but, more importantly, the three competitors started

from the very same initial seeds

. Since the Approx-

imate Medoid Tracking has some randomness (i.e. its

replacement policy), for every k the average objective

function value across 5 runs is shown.

Clearly, Figure 1 shows that the proposed ap-

proach is effective. Speciﬁcally, when using the Ex-

act Medoid Update, it returns the very same objective

function value

when compared to the state-of-the-art

(albeit local) MATLAB implementation. The Approx-

imate Medoid Tracking has surprising results as well,

especially for Wine (Figure 1(b)).

Similarly, in Figures 2(a) and 2(b) the results

when using k-means++ rather than manual (i.e. de-

terministic) selection for initial medoids is shown. As

in the previous case, the two ﬁgures regard Iris and

Wine datasets, respectively.

Speciﬁcally, for k = i the ﬁrst i patterns have been se-

lected as initial seeds.

Therefore returns the very same medoids and the very

same point-to-medoid assignments.

0 10 20 30 40

50 60

70 80 90 100 110 120 130 140

150

100

WCSoD

Spark w/ Exact Medoid Update

Matlab

Spark w/ Approximate Medoid Tracking

(a) Iris Dataset

0 20 40

80 100 120 140

160

180

100

120

140

160

180

WCSoD

Spark w/ Exact Medoid Update

Matlab

Spark w/ Approximate Medoid Tracking

(b) Wine Dataset

Figure 1: Effectiveness tests with deterministic initial seeds

selection.

Figure 2 does not only conﬁrm that the distrib-

uted k-medoids implementation is effective, but also

that the distributed k-means++ implementation works

very well. Obviously, since k-means++ has random

behaviour, 5 runs have been performed for each com-

petitor and the average objective function is shown.

Finally, it is worth stressing that a threshold of

T = 20 patterns for both datasets has been used.

Certainly the pool size for the Approximate Medoid

Tracking has a major impact on the tracking quality

itself: since the pool must ﬁt in memory (as we ex-

pect from a ”small cluster”), we dually used T ≡ P

to indicate the pool size as well. For the sake of ease

and shorthand we omit any tests regarding how the

medoid tracking quality and the procedure complex-

ity changes as a function of the pool size: such results

have been discussed in (Del Vescovo et al., 2014), to

which we refer the interested reader.

0 10 20 30 40

50 60

70 80 90 100 110 120 130 140

150

100

WCSoD

Spark w/ Exact Medoid Update

Matlab

Spark w/ Approximate Medoid Tracking

(a) Iris Dataset

0 20 40

80 100 120 140

160

180

100

120

140

160

180

WCSoD

Spark w/ Exact Medoid Update

Matlab

Spark w/ Approximate Medoid Tracking

(b) Wine Dataset

Figure 2: Effectiveness tests with k-means++ initial seeds

selection.

4.3 Efﬁciency

In order to address the efﬁciency of the proposed im-

plementation, the aim of this subsection is to show

whether it respects the speedup and sizeup properties,

deﬁned as follows (Xu et al., 1999):

speedup measures the ability of the parallel and dis-

tributed algorithm to reduce the running time as

more workers are considered. More formally, the

dataset size is kept constant and the number of

workers will increase from 1 to m. The speedup

for an m-nodes cluster is deﬁned as:

speedup(m) =

running time on 1 worker

running time on m workers

sizeup measures the ability of the parallel and dis-

tributed algorithm to manage an m times larger

dataset while keeping the number of workers con-

stant. The speedup for an m times larger dataset is

deﬁned as:

sizeup(S,m) =

running time for processing m × S

running time for processing S

Figure 3 shows the sizeup performances for both

1 1.2 1.4

1.6

1.8 2 2.2 2.4

2.6

2.8 3 3.2 3.4

3.6

3.8 4

1.5

2.5

3.5

4.5

5.5

Dataset increasing factor m

Sizeup

Activities

KEGG

Census

3D Road Network

KOS

NIPS

ENRON

(a) Approximate Medoid Tracking

1 1.2 1.4

1.6

1.8 2 2.2 2.4

2.6

2.8 3 3.2 3.4

3.6

3.8 4

Dataset increasing factor m

Sizeup

Activities

KEGG

NIPS

KOS

(b) Exact Medoid Update

Figure 3: Sizeup.

the medoid update routines. Speciﬁcally, the sizeup

parameter m has been set to m = 1,2,3,4. All of

the workers available and all but Wine and Iris data-

sets from Table 1 have been used. Figure 3(a) de-

picts the Approximate Medoid Tracking case which

has a very good sizeup performances, especially for

m ≥ 3 (e.g. a 4-times larger dataset needs from 1.9

to 5.5 times more time). Figure 3(b) depicts the Ex-

act Medoid Update case which has generally lower

performances with respect to the former. However,

as the dataset size increases, the performances tend

to improve (e.g. for KEGG a 4-times larger problem

needs 11-times more time, whereas for Activities it

needs 6-times more time) but, on the other hand, this

approach cannot be adopted for larger datasets under

1.5

2.5

3.5

4.5 5 5.5 6

1.5

2.5

3.5

4.5

# of workers

Speedup

Activities

KEGG

Census

3D Road Network

KOS

NIPS

ENRON

(a) Approximate Medoid Tracking

1.5

2.5

3.5

4.5 5 5.5 6

1.2

1.4

1.6

1.8

2.2

2.4

2.6

2.8

3.2

3.4

3.6

3.8

# of workers

Speedup

Activities

KEGG

NIPS

KOS

(b) Exact Medoid Update

Figure 4: Speedup.

reasonable running times

For the speedup, 1, 2, 4 and 6 workers and the

same datasets as for the sizeup experiment have been

used.

The algorithm has very good speedup perform-

ances when using the Approximate Medoid Update,

Figure 4(a): the bigger the dataset, the better the spee-

dup. For some datasets (typically the smallest ones)

implying more than 4 workers does not improve the

overall performances; indeed, since they are rather

small and due to the Approximate Medoid Track-

ing routine being computationally lighter (§4.4), a

massive parallelisation will unlikely be helpful as

most of the time will be spent in scheduling/commu-

nication tasks rather than pure processing.

Figure 4(b), ﬁnally, shows the Exact Medoid Up-

date case, which has very good speedup performances

Whilst using all of the workers available, updating the

medoid for a 100000-patterns cluster took more than 3

hours.

as well. Indeed, due to the intensive parallel evalu-

ations required for solving the exact evaluation, more

workers are crucial for speeding-up such phase. The

above reasoning regarding smaller datasets still holds.

For the sake of completeness and comparison, in

Table 2 the absolute running times for the Activities

dataset have been reported.

Table 2: Absolute running times in minutes.

# workers Approximate Exact

1 2 30

2 1.3 13

4 0.97 11

6 0.76 8.5

4.4 On Computational Complexity

An additional reason for choosing the implementation

proposed in (Park and Jun, 2009) over other imple-

mentations such as the most famous PAM for solv-

ing the k-medoids problem lies in its complexity. In-

deed, since the chosen implementation is based on the

Voronoi iterations as in k-means, the two algorithms

have the same complexity, that is O(nk) per-iteration,

where n is the number of data points and k is the num-

ber of clusters. For the sake of comparison, PAM has

a per-iteration complexity of O(k(n − k)

) (Ng and

Han, 1994), making it unsuitable for large datasets.

In this work, patterns have been considered as d-

dimensional real-valued vectors and, moreover, such

input space has been equipped with the Euclidean dis-

tance as (dis)similarity measure, whose complexity is

O(d). Therefore, the overall per-iteration complex-

ity can as well be deﬁned as O(nkd). By considering

p computational units, the per-iteration complexity

drops to O(nk/p) (or O(nkd/p) by explicitly taking

into account the Euclidean distance) since the point-

to-medoids distance will be computed in parallel.

As far as the medoid update is concerned, the

Exact Medoid Update procedure has complexity

O(c

/p) where c is the cluster size, whereas the Ap-

proximate Medoid Tracking has complexity O(c −

P) ' O(c) since usually c  P.

5 CONCLUSIONS

In this paper, we proposed a novel implementation for

the large-scale k-medoids algorithm using the Apache

Spark framework as parallel and distributed comput-

ing environment. Speciﬁcally, we proposed two pro-

cedures for the medoid evaluation: an exact (but com-

putationally intensive) procedure and an approximate

(but computationally lighter) procedure which have

been proved to be very effective. As far as efﬁciency

is concerned, we tested our algorithm in a single-

machine multi-threaded environment with satisfact-

ory results.

Starting from this implementation many further

steps can be done. First, this implementation has

been deliberately proposed to be as general as pos-

sible: indeed, by looking at the algorithm description

in §3.2, 3.3 and 3.4, the end-user must just change the

(dis)similarity measure d(·,·) according to the nature

of the input space at hand in order for the whole im-

plementation to work. The same reasoning holds for

k-means++: albeit it is true that there are efﬁcient par-

allel and distributed implementations (e.g. k-means||,

(Bahmani et al., 2012)), they namely work on the Eu-

clidean space only. Moreover, as concerns initialisa-

tion techniques, a future work might focus on devel-

oping a DBCRIMES parallel and distributed imple-

mentation, since it is also suitable for dealing with

non-metric spaces.

Further, we proposed two medoid evaluation pro-

cedures which are ideally robust to any cluster’s size.

This can be seen in Algorithm 1, where a for-loop

scans one cluster at the time. This is robust because

the entire processing power is dedicated to a single

cluster which can therefore be massive as well, but if

one is conﬁdent that clusters cannot be arbitrarily big

it is possible to group the available workers

in such

way that each group processes a given cluster. In this

manner the aforementioned for-loop can be done in

parallel as well.

Albeit the two medoids’ update routines have been

presented separately in order to discuss their respect-

ive strengths and weaknesses, they can be easily used

together by adopting a double-threshold approach.

Speciﬁcally, let T

and T

be two thresholds with

< T

: every cluster whose size is less than T

can be considered as ”small” and processed fully in-

memory; every cluster whose size is in range [T

]

can be considered as ”medium” and processed using

the Exact Medoid Update and, ﬁnally, clusters greater

than T

, to be considered as ”big”, can be processed

using the Approximate Medoid Tracking.

One of the most intriguing works is a direct

extension of the former observation, as discussed

in §2: ideally the k-medoids can work with any

(dis)similarity measure and it does not need to deﬁne

some operations for evaluating the new cluster repres-

entative (e.g. mean or median): whether it is possible

to deﬁne a (dis)similarity measure between two ob-

jects, the k-medoids can be used. This opens a new

horizon on the nature of the input space(s) which can

As we did in order to simulate 4-core PCs.

be clustered, as the so-called non-metric spaces such

as graphs or sequences, for which deﬁning a mean or

median is nonsensical.

REFERENCES

Aloise, D., Deshpande, A., Hansen, P., and Popat, P. (2009).

Np-hardness of euclidean sum-of-squares clustering.

Machine learning, 75(2):245–248.

Ankerst, M., Breunig, M. M., Kriegel, H.-P., and Sander, J.

(1999). Optics: Ordering points to identify the clus-

tering structure. In Proceedings of the 1999 ACM

SIGMOD International Conference on Management

of Data, SIGMOD ’99, pages 49–60, New York, NY,

USA. ACM.

Arbelaez, A. and Quesada, L. (2013). Parallelising the k-

medoids clustering problem using space-partitioning.

In Sixth Annual Symposium on Combinatorial Search.

Arthur, D. and Vassilvitskii, S. (2007). k-means++: The

advantages of careful seeding. In Proceedings of the

eighteenth annual ACM-SIAM symposium on Discrete

algorithms, pages 1027–1035. Society for Industrial

and Applied Mathematics.

Bahmani, B., Moseley, B., Vattani, A., Kumar, R., and

Vassilvitskii, S. (2012). Scalable k-means++. Pro-

ceedings of the VLDB Endowment, 5(7):622–633.

Bianchi, F. M., Livi, L., and Rizzi, A. (2016). Two

density-based k-means initialization algorithms for

non-metric data clustering. Pattern Analysis and Ap-

plications, 3(19):745–763.

Bradley, P. S., Mangasarian, O. L., and Street, W. N. (1996).

Clustering via concave minimization. In Proceedings

of the 9th International Conference on Neural Inform-

ation Processing Systems, NIPS’96, pages 368–374,

Cambridge, MA, USA. MIT Press.

Dean, J. and Ghemawat, S. (2008). Mapreduce: simpliﬁed

data processing on large clusters. Communications of

the ACM, 51(1):107–113.

Del Vescovo, G., Livi, L., Frattale Mascioli, F. M., and

Rizzi, A. (2014). On the problem of modeling struc-

tured data with the minsod representative. Interna-

tional Journal of Computer Theory and Engineering,

6(1):9.

Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In Proceedings of

the Second International Conference on Knowledge

Discovery and Data Mining, volume 96, pages 226–

231.

Guha, S., Rastogi, R., and Shim, K. (1998). Cure: An ef-

ﬁcient clustering algorithm for large databases. SIG-

MOD Rec., 27(2):73–84.

Jiang, Y. and Zhang, J. (2014). Parallel k-medoids cluster-

ing algorithm based on hadoop. In Software Engin-

eering and Service Science (ICSESS), 2014 5th IEEE

International Conference on, pages 649–652. IEEE.

Kaufman, L. and Rousseeuw, P. J. (1987). Clustering by

means of medoids. Statistical Data Analysis Based

on the L1-Norm and Related Methods, pages North–

Holland.

Kaufman, L. and Rousseeuw, P. J. (2009). Finding groups

in data: an introduction to cluster analysis, volume

344. John Wiley & Sons.

Lichman, M. (2013). UCI machine learning repository.

Lloyd, S. (1982). Least squares quantization in pcm. IEEE

transactions on information theory, 28(2):129–137.

MacQueen, J. B. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Cam, L.

M. L. and Neyman, J., editors, Proc. of the ﬁfth Berke-

ley Symposium on Mathematical Statistics and Prob-

ability, volume 1, pages 281–297. University of Cali-

fornia Press.

Meng, X., Bradley, J., Yavuz, B., Sparks, E., Venkatara-

man, S., Liu, D., Freeman, J., Tsai, D., Amde, M.,

Owen, S., et al. (2016). Mllib: Machine learning in

apache spark. Journal of Machine Learning Research,

17(34):1–7.

Ng, R. T. and Han, J. (1994). Efﬁcient and effective cluster-

ing methods for spatial data mining. In Proceedings

of the 20th International Conference on Very Large

Data Bases, VLDB ’94, pages 144–155, San Fran-

cisco, CA, USA. Morgan Kaufmann Publishers Inc.

Park, H.-S. and Jun, C.-H. (2009). A simple and fast al-

gorithm for k-medoids clustering. Expert systems with

applications, 36(2):3336–3341.

van der Walt, S., Colbert, S. C., and Varoquaux, G. (2011).

The numpy array: A structure for efﬁcient numerical

computation. Computing in Science & Engineering,

13(2):22–30.

Xu, X., J

ager, J., and Kriegel, H.-P. (1999). A fast parallel

clustering algorithm for large spatial databases. Data

Mining and Knowledge Discovery, 3(3):263–290.

Yue, X., Man, W., Yue, J., and Liu, G. (2016). Paral-

lel k-medoids++ spatial clustering algorithm based on

mapreduce. arXiv preprint arXiv:1608.06861.

Zaharia, M., Chowdhury, M., Franklin, M. J., Shenker, S.,

and Stoica, I. (2010). Spark: Cluster computing with

working sets. HotCloud, 10(10-10):95.

Zhang, T., Ramakrishnan, R., and Livny, M. (1996). Birch:

An efﬁcient data clustering method for very large

databases. In Proceedings of the 1996 ACM SIGMOD

International Conference on Management of Data,

SIGMOD ’96, pages 103–114, New York, NY, USA.

ACM.

Zhao, W., Ma, H., and He, Q. (2009). Parallel k-means

clustering based on mapreduce. In IEEE Interna-

tional Conference on Cloud Computing, pages 674–

679. Springer.