Deriving Realistic Mathematical Models from Support Vector

Machines for Scientific Applications

Andrea Murari

, Emmanuele Peluso

, Saeed Talebzadeh

, Pasqualino Gaudio

, Michele Lungaroni

Ondrej Mikulin

, Jesus Vega

and Michela Gelfusa

Consorzio RFX (CNR, ENEA, INFN, Università di Padova, Acciaierie Venete SpA),

Corso Stati Uniti 4, 35127 Padova, Italy

Associazione EURATOM-ENEA, University of Rome “Tor Vergata”, Roma, Italy

Institute of Plasma Physics AS CR, ZaSlovankou 3, Prague, Czech Republic

Asociación EURATOM/CIEMAT para Fusión, Avda. Complutense, 22. 28040, Madrid, Spain

Keywords: Machine Learning Tools, Support Vector Machines, Symbolic Regression, Genetic Programming.

Abstract: In many scientific applications, it is necessary to perform classification, which means discrimination

between examples belonging to different classes. Machine Learning Tools have proved to be very

performing in this task and can achieve very high success rates. On the other hand, the “realism” and

interpretability of their results are very low, limiting their applicability. In this paper, a method to derive

manageable equations for the hypersurface between classes is presented. The main objective consists of

formulating the results of machine learning tools in a way representing the actual “physics” behind the

phenomena under investigation. The proposed approach is based on a suitable combination of Support

vector Machines and Symbolic Regression via Genetic Programming; it has been investigated with a series

of systematic numerical tests, for different types of equations and classification problems, and tested with

various experimental databases. The obtained results indicate that the proposed method permits to find a

good trade-off between accuracy of the classification and complexity of the derived mathematical equations.

Moreover, the derived models can be tuned to reflect the actual phenomena, providing a very useful tool to

bridge the gap between data, machine learning tools and scientific theories.

1 THE NEED FOR DATA MINING

TOOLS IN BIG PHYSICS

EXPERIMENTS

In many fields of science, the complexity of the

problems investigated is such that it can become

difficult, if not impossible, to describe the

phenomena to be studied with theoretical models

based on first principles. A typical example in

physics is the case of magnetic confinement

thermonuclear fusion, whose plasmas are so

complex that various levels of modelling (particle,

fluid, kinetic etc) coexist without providing a

satisfactory description of many aspects of the

physics (Wesson, 2004). On the other hand, in the

last decades much more data have become available,

due to the diffusion of cheap sensors and powerful

computers. For example, the Big Physics European

experiments are affected by a data deluge. At

CERN, the ATLAS detector can produce Petabytes

of data per year. The Hubble space telescope

managed to send to earth Gigabytes of data per day

and the data warehouse of the Joint European Torus

exceeds 350 Terabytes. Therefore the inadequacies

of theoretical models and the vast amounts of

information available have motivated the

development of data driven tools, to complement

hypothesis driven theories. In this perspective,

various machine learning methods have been

developed. They range from Neural Networks and

Support Vector Machines to Fuzzy Logic classifiers;

a series of examples from the field of thermonuclear

fusion can be found in (Rattà, 2010; Vega, 2014;

Murari, 2009). Manifold learning tools, such as Self

Organising Maps and Generative Topographic

Maps, and simple classifiers based on the Geodesic

distance on Gaussian manifolds, have provided very

Murari A., Peluso E., Talebzadeh S., Gaudio P., Lungaroni M., Mikulin O., Vega J. and Gelfusa M.

Deriving Realistic Mathematical Models from Support Vector Machines for Scientiﬁc Applications.

DOI: 10.5220/0006517401020113

In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KDIR 2017), pages 102-113

ISBN: 978-989-758-271-4

good results also in terms of describing the space in

which the relevant physics takes place (Cannas,

2013; Murari (A), 2013; Vega, 2009).

Even if these data driven tools are providing

quite impressive performance, their main problem is

the mathematical formulation of their models. They

have shown the potential to learn very efficiently

from the provided examples but their results are

expressed in such a way that does not allow an easy

interpretation of the physics behind the phenomena

under study. This aspect is quite worrying and has

hampered the penetration of many machine learning

tools in scientific disciplines such as physics. Some

of the main problems are: a) poor “physics fidelity”

i.e. excessive difference between the mathematical

form of the models and the physical reality of the

phenomena investigated b) difficulties to interpret

the results in terms of traditional mathematical

formulations c) consequent impossibility to compare

the obtained results with traditional mathematical

models and theories d) lack of extrapolability of the

results.

In order to overcome these limitations, a new

methodology has been developed to profit from the

knowledge acquired by the machine learning tools,

but presenting it in a more traditional format, in

terms of manageable formulas. The techniques,

developed in the framework of the activities

presented in this paper, address the basic goal of

classification. This is a very important task in many

scientific applications, both “per se” and as a

preliminary step to more sophisticated

investigations. The main idea behind this work

consists therefore of combining the learning

capabilities of the machine learning tools with the

“realism” and interpretability of more traditional

mathematical formulations.

The sequence of steps required to implement the

proposed technique is:

1. Training of the SVM with the available data;

Populating the hypersurface on a suitable grid

of points

Identification of the hypersurface equation

with Symbolic Regression via Genetic

Programming

Double checking of the obtained equation

using the SVM

This approach reconciles the prediction and

knowledge discovery capability of machine learning

tools with the need to formulate the results in such a

way that they can be related to scientific theories and

models. It is worth emphasizing that the objective of

the present work is not simply improving

interpretability of machine learning tools, on which

significant work has already been done. The most

important aspect indeed is “physics fidelity” i.e. the

formulation of the results in mathematical terms,

which can be compared with theories and models of

the various scientific disciplines. Therefore, the

proposed method must have the potential to derive

mathematical expressions, which reflect the

underlining dynamics of the phenomena to be

investigated.

In the presented approach, the first knowledge

discovery step is based on Support Vector Machines

(SVM), whose mathematical background is

summarized in Section 2. The choice of SVM is

mainly due to their structural stability, their

capability to maximize the safety margins in the

classification. Indeed in many applications, SVM

can classify with a success rate well in excess of

95%; therefore their hyperplane can be considered a

good approximation of the boundary between the

classes (Murari (A), 2013). As a consequence, the

equation of their hypersurface in the original space

can be considered an excellent approximation of the

boundary. On the other hand, their mathematical

representation of the boundary is extremely non

intuitive (see Section 2). Again referring to a

complex system of the complexity of the Joint

European Torus, in the case of disruptions, the

equation of the hypersurface can comprise hundreds

of support vectors and therefore the equation of the

hypersurface contains an equal number of addends.

More importantly, in addition to presenting serious

problems for human understanding, the SVM

models do not reflect the actual dynamics of the

phenomena under study. It has indeed been shown,

also with many numerical examples (see Section 6),

that the models provided by SVM have absolutely

no relation with the ones generating the data. A

simple methodology has already been proposed and

applied to complex problems, to recover the

equation of the boundary in the case of linear kernels

(Gaudio, 2014). In this paper, a new technique is

developed, which is fully general. Indeed the

proposed method can be applied to SVM with any

type of kernel and therefore it has a much wider

range of applications than the more traditional

techniques. This aspect is very important in many

scientific fields, whose phenomena cannot be simply

modelled by linear tools or logistic regression.

To formulate the outputs of SVM in way suitable

for scientific investigations, extensive used is made

of Symbolic Regression (SR) via Genetic

Programming (GP); these tools are therefore

described in Section 3. Symbolic regression is

basically used to fit points on the hypersurface found

by the SVM, which is the boundary between the

classes.

The actual combination of the various tools, to

provide the equation of the boundary between two

regions of the operational space in a physically

relevant form, is described in detail in Section 4. The

results of a systematic series of numerical tests,

proving the potential of the proposed methodology,

are the subject of Section 5. Some examples of

application to experimental databases, covering

different scientific disciplines, are provided in

Section 6. Discussions and lines of future

developments are the subject of the last Section 7.

2 INTRODUCTION TO SVM FOR

CLASSIFICATION

SVM are mathematical tools which can perform

more general tasks, such as regression, but which are

used as classifiers for the studies described in this

paper. In intuitive terms, given a set of input

examples, which belong to two different classes,

SVM map the inputs into a high-dimensional space

through some suitable non-linear mapping. In this

high dimensional feature space, an optimal

separating hyperplane is constructed in order to

minimize the risk of misclassification. The

minimization of the error risk is obtained by

maximizing the margins between the hyperplane and

the closest points, the support vectors, of each class.

This is achieved by a careful selection of the

constraints of a suitable functional to minimize. In

the case of non-separable problems, the points to

classify are projected into a higher dimensional

space with the help of suitable kernels. The

minimization of the error risk and the maximization

of the margins is then performed in this projected

space. The hyperplane is identified by a subset of

points of the two classes, named Support Vectors

(SV).

In mathematical terms, given a training set of



samples

(





,



)

(





,



)

, where 



∈ℛ



, for a

binary classification problem (i.e. 



∈{+1,−1}),

the SVM estimates the following decision function:



(



)

=







(



,)





(1)

Where (



,) is a kernel function and the

parameters 

,,…,

are the solutions of the

following quadratic optimization with linear

constraints.

Maximization of the functional:



(



)

∑









−





∑











,









(



,)

(2)

subject to the constraints:

∑













/ 0≤



≤





,∀=1,…,

(3)

Where C is a regularization parameter (Vapnik,

2013).

The data points 



associated with nonzero

values of the coefficients α



are called support

vectors, which give the name to the technique. Once

the support vectors have been determined, the SVM

boundary between the two classes can be expressed

in the form



(



)

=







(



,)





(4)



(



)

is the distance (with sign) from the input

to the hyper-plane that separates the two classes and,

hence, the hyper-plane points satisfy

(



)

=0.

The rule to classify a feature vector

as class C

or class C

is given by:

if sgn (D(u)) ≥ 0

u ε C

otherwise

u ε C

where sgn(t) is the sign function.

A comment on the nomenclature is in place at

this point. The SVM operates in the transformed

space and finds a separating hyperplane in that

space. On the other hand, the hyperplane is

expressed in terms of Support Vectors in the original

space, in which the boundary is a hypersurface.

Since typically in scientific applications scientists

are interested in equations in the original space, and

not in the transformed one, the boundary between

the two classes will be indicated with the term

hypersurface and not hyperplane in the following.

3 SYMBOLIC REGRESSION VIA

GENETIC PROGRAMMING

As mentioned in the first Section, this paper

describes a technique to present the results of

machine learning tools in a mathematical form

describing realistically the actual phenomena to be

studied. In the case of classification with SVM, this

task consists of representing the hypersurface

separating the classes in a more meaningful way

than the sum of hundreds of terms as in (4). To this

end, the main tool used is Symbolic regression via

Genetic Programming. The methods developed, on

the one hand, allow identifying the most appropriate

mathematical expression for the hypersurface

without “a priori” hypotheses. In this way therefore

the potential of SVM is fully exploited and no

unnecessary restrictions are imposed on the form of

the solutions. On the other hand, the complexity of

the obtained solutions can be controlled, allowing to

find the best trade-off between complexity, success

rate of classification and realism of the final models,

depending on the objectives of the study.

The method of SR via GP consists of testing

various mathematical expressions to fit a given

database. The main steps to perform such a task are:

1. Identification of the best mathematical form

for the model with SR via GP

Optimization of the models with nonlinear

fitting

Qualification and selection of the best model

with the Pareto Frontier impleemnented with

statistical criteria (e.g BIC, KLD)

First of all, the various candidate formulas are

expressed as trees, composed of functions and

terminal nodes. The function nodes can be standard

arithmetic operations and/or any mathematical

functions, squashing terms as well as user-defined

operators (Schmidt, 2009; Koza, 1992). This

representation of the formulas allows an easy

implementation of the next step, symbolic regression

with Genetic Programming (GP). Genetic Programs

are computational methods able to solve complex

optimization problems (Schmidt, 2009; Koza, 1992).

They have been inspired by the genetic processes of

living organisms. They work with a population of

individuals, e.g mathematical expressions in our

case. Each individual represents a possible solution,

a potential boundary equation in our case. An

appropriate fitness function (FF) is used to measure

how good an individual is with respect to the

database. Genetic operators (Reproduction,

Crossover and Mutation) are applied to individuals

that are probabilistically selected on the basis of the

FF, in order to generate the new population. That is,

better individuals are more likely to have more

children than inferior individuals. When a stable and

acceptable solution, in terms of complexity, is found

or some other stopping condition is met (e.g., a

maximum number of generations or acceptable error

limits are reached), the algorithm provides the

solution with best performance in terms of the FF

(Murari (D), 2015; Murari (C), 2015; Peluso, 2014;

Murari, 2016). It is worth emphasizing that AIC is a

criterion to be minimised; the lower the AIC, the

better the model.

The fitness function is a crucial element of the

genetic programming approach and it can be

implemented in many ways. To derive the results

presented in this paper, the AIC criterion (Akaike

Information Criterion) has been adopted (Hirotugo,

1974) for the FF. The form of the AIC indicator

defined here is:



 = 2 +⋅

(



)



(5)

In equation (5), MSE is the Mean Square Error

between the data and the model predictions, k is the

number of nodes used for the model and "n" the

number of "y

data

" provided, i.e. the number of entries

in the database (DB). The FF parameterized above

allows considering the goodness of the models,

thanks to the MSE, and at the same time their

complexity is penalized by the dependence on the

number of nodes.

To assess the quality of the various equations and

to select the final model, for each level of

complexity the three best models are retained. This

subset of very performing equations is used to build

a Pareto Frontier, a plot of the quality of the

equation versus its complexity (Lotov 2009). To

quantify the quality of the various equations the

well-known criteria of BIC (Bayesian Information

Criterion) and Kullback-Leibler (KLD) divergence

have been implemented. The Pareto Frontier, made

up using the BIC and the complexity of the models,

typically shows a trend resembling a “L”; above a

certain level, improving the complexity does not

increase the accuracy of the models significantly.

Therefore, near the inflection point the models better

describing the trade-off between complexity and

interpretability can be found. Once selected, the

KLD is used to perform the final sifting. The model

with the lowest value of the KLD is in fact the one

finally chosen.

Coming to the indicators used to build the Pareto

Frontier, in practice the BIC criterion (Hirotugo,

1974) is typically defined as:

 =  ⋅

(



)

+⋅

(



)





(6)

where =



−



are the residuals,



(



)



their variance and the others symbols are

defined in analogy with the AIC expression. Again

the better the model, the lower its BIC.

The aim of the KLD is to quantify the difference

between the computed probability distribution

functions, in other words to quantify the information

lost when (







())is used to approximate

(







()) (Murari (D), 2015). The KLD is

defined as:

(||) =





(



)

⋅ln



(



)



(



)



(7)

Where the symbols are defined as above. The

Kullback Leibler Divergence assumes positive

values and is zero only when the two probability

distribution functions (pdfs), p and q, are exactly the

same. In our application p is the pdf of the data,

considered the reference, and q the pdf of the model

estimates. Therefore the smaller the KLD is, the

better the model approximates the data, i.e. the less

information is lost by representing the data with the

model. A detailed overview of SR via GP for

scientific applications is provided in (Kenneth,

2002).

4 SVM AND SYMBOLIC

REGRESSION FOR

BOUNDARY EQUATIONS

This Section describes in detail the combination of

SVM technology with SR via GP to obtain the

equations of the boundary between classes in a form

appropriate for scientific investigations. Subsection

4.1 introduces the proposed way to find points on

the hypersurface identified by the SVM. Subection

4.2 describes the use of symbolic regression for the

derivation of the actual formula of the boundary

between the classes.

4.1 How to Find Points on the SVM

Hypersurface

In order to interpret the results produced by the

SVM, the first step consists of determining a

sufficient number of points on the hypersurface

separating the two classes. These points can be then

given as inputs to the SR to obtain a more

manageable equation for the hypersurface. To obtain

the SVM hypersurface points, a mesh is built first,

with resolution equal or better than the error bars of

the measurements used as inputs to the SVM. In this

step, a suitable mesh throughout the domain defined

by the ranges of variables is generated; therefore, if

the problem presents n dimensions and m grid points

are generated for each dimension, the grid will

consist of m

grid points.

After building the grid, the algorithm starts from

the closest points to the SVs on the positive side of

the hypersurface and moves towards the closest

points of the grid to the SVs on the other side, one

point of the mesh at the time. At each step, the

distance to the hypersurface is computed using the

already trained SVM. If the distance remains

positive, the process is repeated since the new point

remains on the same side of the hypersurface. When

the distance of a new point changes sign, the two

points with different signs are considered points on

the hypersurface. This assumption is more than

reasonable because, by construction of the mesh,

these points, for which the distance changes sign, are

within a distance from the hypersurface equal or

smaller than the error bar of the features (typically

measurements).

Figure 1: Illustrative example of the methodology to find

the SVM hypersurface points. In red or blue the two

classes (points either of the mesh or the class themselves

and classified according to the SVM). In black the points

found for the hypersurface.

Therefore, for all practical purposes, the points

found as previously described are sufficiently close

to the hypersurface to be considered on it. This way

to obtain SVM hypersurface points for synthetic data

is shown pictorially in Figure 1.

It is good practice to repeat the process also

starting from the other side of the hypersurface, in

order to avoid possible bias in the selection of the

points on the hypersurface. An adequate number of

points is typically a multiple of the support vectors.

One order of magnitudes more points than SVs is a

safe choice, in the sense that all the numerical tests

performed have always provided more than

satisfactory results with this number of points or

higher. If a lower number of points on the

hypesurface are considered, the final equation can be

too smooth and might not fully represent the

complexity of the boundary between the classes.

Attention can also be usefully paid to the fact that the

density of the points reflects the density of the SVs in

the feature space. In any case, it is easy to incraese the

number of points up to the number necessary. The

main limitation here is mainly computational time

(see Section 6) not any principle difficulty.

Once obtained the candidate points sufficiently

near to the hypersurface, before proceeding, it is in

any case good practice to perform some checking.

This can be easily achieved using again the already

trained SVM. It is sufficient to input to the SVM the

candidate points, obtained with the previously

described procedure, and verify that the distance to

the hypersurface is smaller than the error bars.

4.2 How to Derive the Equation of the

Hypersurface via SR

Once it has been verified that sufficient points close

to the hypersurface have been found, the equation of

the hypersurface itself can be estimated using SR via

GP. Indeed the points identified with the procedure

described in the previous subsection are on the

boundary between the two classes. Therefore the

equation of that surface is the equation of the

boundary between the two classes.

An efficient way of retrieving the equation of the

hypersurface from the points consists of regressing

them with SR, using the quantity with the largest

dynamic range as the independent variable. The

quality of the obtained equation can be assessed first

with the statistical indicators described in Section 3.

Moreover, an additional and more conclusive test

can be performed, exploiting again the trained SVM.

In this case, it is indeed possible to generate a series

of points from the candidate formula and insert them

in the SVM. If the distance from these points and the

hypersurface is sufficiently close to zero, it can be

confirmed that indeed the equation is a good

representation of the boundary between the two

classes. As a criterion of closeness to the boundary,

typically the value of the error bars of the

measurements can be taken: if the points generated

by the equation are at a distance from the

hypersurface smaller than the error bars, for all

practical purposes the obtained equation can be

considered a sufficient approximation of the

boundary between the two classes.

5 NUMERICAL TESTS AND

RELATED RESULTS

The procedure described in the previous section has

been subjected to a systematic series of numerical

tests. The results have always been positive and the

proposed technique has always allowed recovering

the original equations describing the boundary

between the two classes. In the following, the

detailed procedures for these numerical tests are

described and some results presented. For clarity’s

sake, mainly low dimensional cases are illustrated in

the following, but it has been verified that the

approach is equally valid for high dimensional cases

(up to 8 or 9 independent variables), provided of

course a sufficient number of examples and adequate

computational resources are available.

5.1 Overall Procedure for Producing

Synthetic Data

The main technique to produce synthetic data and to

test the methodology consists of the following 6

steps:

1- Definition of an initial function for the

boundary;

2- Generating samples of the two classes from

the function

3- Training the SVM for classification

4- Building an appropriate mesh on the domain

5- Determining a sufficient number of points on

the hyper-surface identified by the SVM

6- Deploying SR to identify the equation of the

hypersurface from the points previously

obtained

In the following more details about this

procedure are provided. To fix the ideas, the

discussion is particularized for the case of two

independent variables x

and x

In the first step, an initial function as a

combination of arithmetic, trigonometric, and

exponential operators of independent variables x

defined. In general, this function can be written as

follows:

=



(





,



,…,



)





∈(



,



)

(8)

In the second step, for the case of two

independent variables, it is typically sufficient to

generate about 4000 random points in the range of

variables for the x

and to calculate y for them. Then,

a positive offset and some random values are added

to the y for half of the data to produce the first class;

a negative offset and some random values are added

to y for the other half to produce the second class.

The equations for producing the two classes (

,

)

can be summarized as follow:





=+

(

0,

)

+





=+

(

0,

)

−

(9)

Where c stands for the arbitrary offset and

U(0,L) stands for a random uniform distribution

between 0 and the bulk thickness of data L

Table 1: General GP parameters for the calculation of the

boundary equations.

GP Parameters Value(s)

Population size 500

Selection method Ranking and Tournament

Fitness function AIC

Constant range Integers between -10 and 10

Maximum depth of trees 7

Genetic operators

(Probability)

Crossover (45 %)

Mutation (45 %)

Reproduction (10 %)

In the third step, an SVM with "Gaussian Radial

Basis Function kernel" is trained. The method used

to find the separating hyperplane is "Sequential

Minimal Optimization". Depending on the level of

random noise, different success rates can be

obtained. For the numerical tests presented in the

following, the success rate in the classification of the

SVM is always very close to 100%.

In the fourth step, a mesh on the domain has to

be built in order to identify points sufficiently close

to the hypersurface. For this reason, each dimension

of the domain has been subdivided in one hundred

intervals, producing one million mesh points ( 100

The fifth step consists of the identification of the

points sufficiently close to the hypersurface, with the

algorithm described in Section 4.

In the sixth step, the selected hypersurface points

are used as inputs to the symbolic regression code,

to find the appropriate formula for describing the

hypersurface. The settings adopted to run the GP

implementing the SR are reported in Table 1.

In the next sections, some examples are provided

to illustrate the applicability and capability of the

presented methodology for systems of increasing

dimensionality and complexity.

5.2 Examples for Two Independent

Variables

As a first test, a quite complex function comprising

exponential, arithmetic, and power operators has

been assumed for the boundary between the two

classes. The function and ranges of the variables are

reported in equation (10):

=

√





⋅









∈

(

0,1

)

,



∈

(

1,3

)

(10)

After carrying out the six-step procedure

previously described, the expression in equation (11)

has been obtained:

 = 0.974⋅

√





⋅



(11)

SR via GP converges on a final expression that is

in excellent agreement with the initial function

describing the boundary between the two classes,

even without making recourse to the non-linear

fitting step.

As an additional test, a more complex function

comprising trigonometric and arithmetic operators

has been defined and 4% noise was added to the

database. The function and ranges for the variables

are reported in equation (12):

=sin

(





)

+







∈

(

−3,3

)

, 



∈

(

−2,2

)

(12)

After carrying out the six-step procedure

previously described, the expression in equation (13)

has been obtained:

 = 0.985

(

sin

(





)

+



)

(13)

Again SR via GP converges on a final expression

that is in excellent agreement with the initial

function describing the boundary between the two

classes, even without making recourse to the non-

linear fitting step. Figure 2 presents the results of

this example in pictorial form.

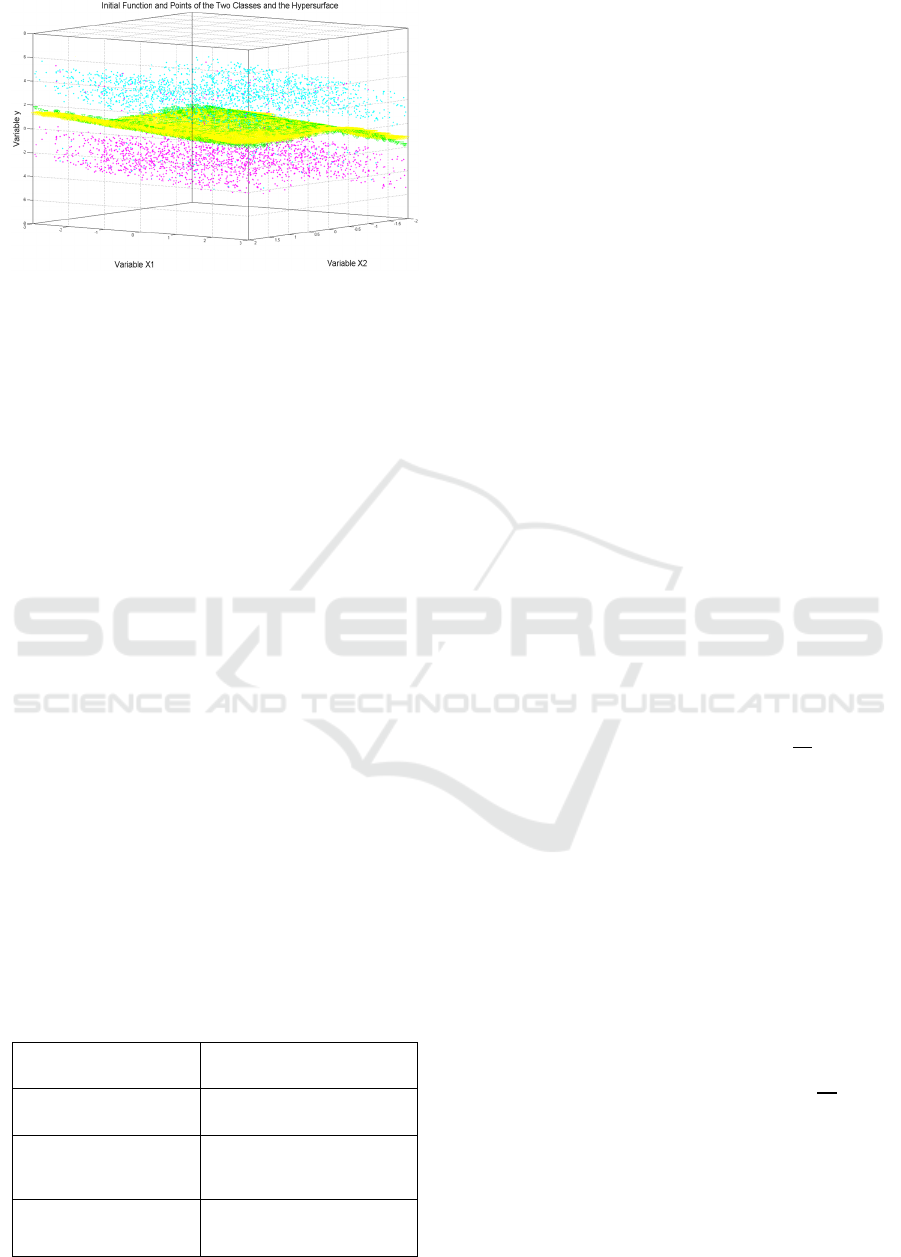
Figure 2: Points and surfaces of the example of equation

(12). Green rectangles are points generated from the initial

function, Cyan points are the points belonging to the first

class, Magenta points are the points belonging to the

second class, and the Yellow surface identifies the hyper-

surface obtained with the SR via GP.

5.3 Effect of Noise and High

Dimensional Data

The numerical examples presented previously

include cases where the success rate of the SVM

classification is close to 100%. This is certainly an

interesting situation from a scientific point of view;

the SVM has learned almost perfectly the boundaries

between the classes and therefore the main issue

remaining consists of formulating the equations of

these boundaries in a mathematical form appropriate

for understanding the phenomena.

On the other hand, it has been checked with

extensive numerical tests that, if the success rate of

classification of the SVM is significantly lower than

100%, the proposed method works well anyway,

since its objective is the reformulation of the

boundary equation found by the SVM. The success

rate required for the SVM and the interpretation of

the results is an issue which depends on the

application and the objectives of the analysis but

does not impact on the validity of the developed

technique.

Table 2: The range of the variables used to generate the

data with function (15).

Steps: Values:

Initial Function Eq.(15)

Ranges of Variables





∈

(

0,2

)

,



∈

(

1.5,3

)





∈

(

−2,4

)

, 



∈

(

0,6

)





∈

(

4,12

)

,



∈

(

1,4

)

Number of Nodes for

Each Class

2000

It is worth also emphasizing that the task of SR

in this context is not to improve the success rate of

the SVM classification. The real goal consists of

representing the equations of the boundary between

the classes in more realistic and interpretable

mathematical forms, so that they can be used by the

scientists for actual understanding (for example for

comparison with theories and first principle models).

To achieve this, a reasonable degradation of

classification success rate is tolerable and typically

not a major issue. In any case, with an appropriate

implementation of the proposed method, typically

the performance of SVM can be preserved by the

final equations obtained with symbolic regression.

As mentioned, there is no conceptual difficulty in

applying the proposed methodology to higher

dimensional problems. Of course, the computational

resources required increase exponentially with the

number of independent variables (the so called curse

of dimensionality). Also the number and quality of

the examples must be adequate. But these are

problems related to the available computational

power and/or the quality of the data; in no way they

affect the applicability of the proposed technique.

Indeed it has been verified with a series of

systematic tests that, with adequate level of

computer time, problems in higher dimensions can

also be solved. A quite demanding example is

reported in the following, for an equation involving

7 variables. The equation used to generate the data

is:

=







+

(





)

+

(





)

−











(14)

It is worth mentioning that in many applications

in physic and chemistry one has to deal with

problem of a dimensionality not higher than 7.

Equation (15) is therefore of realistic complexity for

many applications. A total of 4000 points, 2000 per

class, has been generated starting from equation

(14); more details about the synthetic data are

provided in Table 2. After generating the grid,

training the SVM and finding the hyper-surface

points, SR via GP Genetic has been applied and the

expression for the obtained hyper-surface is reported

in equation (15):

 = 0.9(







)+sin

(





)

+cos

(





)

−









(15)

The equation found by the method is practically

the original one. The slightly different multiplicative

factor in front is not to be ascribed to a weakness of

the method but to the dataset provided as input,

since the accuracies of both the SVM and the

mathematical equation obtained are equal to 100%.

Again, this example proves that, provided the

surface of the boundary between the cases is

sufficiently regular, the dimensionality is not an

insurmountable issue, if enough computational

power is available.

5.4 Computational Requirements

As an indication about the computational resources

required for the application of the proposed

technique, the run time for an example of 5 variables

has been calculated. Using a computer with 8 cores

and 24 gigabyte of RAM (an Intel Xeon E5520, 2.27

GHz, 2 processors), with Windows 64 bit operating

system, finding the hyper-surface points takes 3

hours and the SR calculation 48 hours. The number

of points on the grid is 16

* 51; 16 for the four

independent variables and 51 for the dependent one.

In this respect, the run time to train the SVM is not a

major problem, since it is typically of the order of

minutes and therefore negligible compared to the

other steps of the procedure. Moreover, the

calculation of the grid is also not a major issue since

the step requiring by far most of the computational

resources is the SR. On the other hand, it should be

mentioned that the codes used to obtain these results

had not been parallelized. Therefore, since both the

building of the grid and the Genetic Programs can be

easily parallelized, reduction of the computational

resources of orders of magnitude could be easily

achievable.

6 REAL WORLD EXAMPLES

To show the potential of the proposed methodology

to attack real life problems, in this section its

application to some experimental databases is

reported. The data have been collected in the

framework of various disciplines but the original

measurements have all been obtained via remote

sensing. The term remote sensing indicates the set of

techniques aimed at obtaining information about

objects without being in contact with them. These

techniques can be used to monitor various aspects of

the atmosphere and also the effects of human

activities on the environment.

6.1 Botany: “Wilt” Database

As an example of application to a real-world

problem, first a database related to botany named

“wilt” has been selected. This database was prepared

by Brian Johnson from the Institute of Global

Environmental strategies in Japan in 2013 and

contains the results of a remote sensing study about

detecting diseased trees with Qickbird imagery

(Johnson, 2013). The data set consists of image

parts, generated by segmenting the pansharpened

pictures. The segments contain spectral information

from the Quickbird multispectral image bands and

texture information from the panchromatic (Pan)

image band. In the following, the entries of this

database are listed:

• Class: “w„ (diseased trees) or “n„(all other

land cover)

• GLCM_Pan: GLCM mean texture (Pan

band)

• Mean_G: Mean green value

• Mean_R: Mean red value

• SD_Pan: Standard deviation (Pan band)

This database contains 4339 samples: 74 of them

related to diseased trees and the rest related to all

other land cover. The new proposed methodology

has been applied to this database for finding the

classification hyper-surface between the two

mentioned classes. The entries have been classified

first with the SVM (with the RBF kernel). The

subsequent application of our technique, grid plus

SR, has allowed to find the following equation:





=22.39⋅

(





)

.

(16)

The previous equation provides a Train Accuracy

equals to 99.4% and a Test Accuracy of 99.5 %,

which are practically the same as the SVM, not only

in terms of global statistics but also with regard to

the individual cases properly or improperly

classified. Given the success rate in excess of 99%,

the derived equation (16) indicates that the important

attributes for classifying this database are the Mean

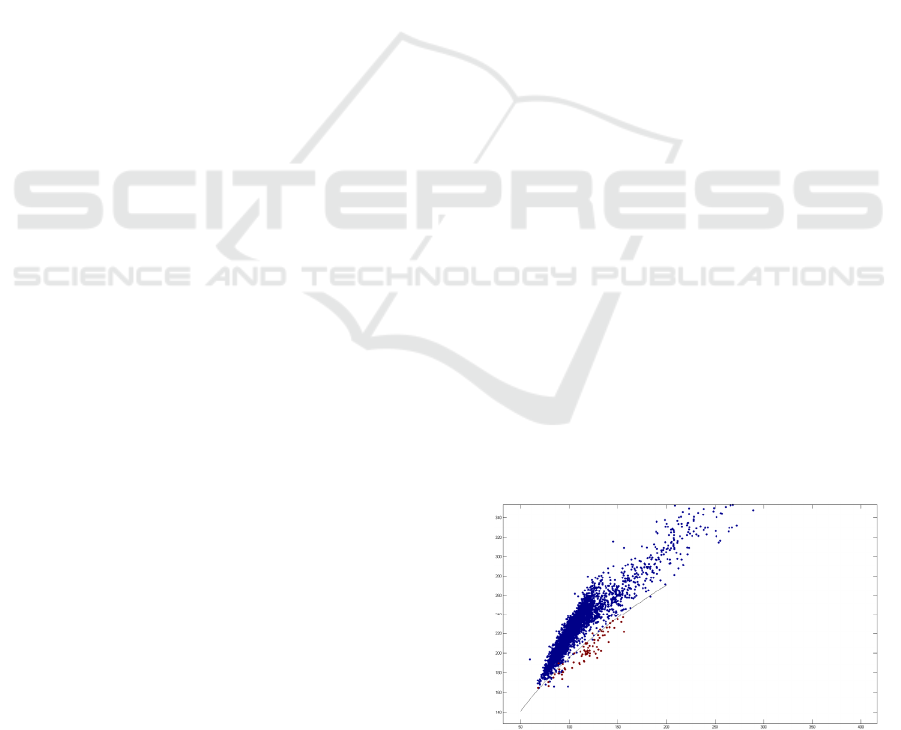
Figure 3: Distribution of data in the “wilt” database. The

red points are diseased trees and the blue points indicate

all other types of land cover. The black line indicates the

equation obtained for the hyper-surface.

Figure 4: Examples of LIDAR back scattered signals: a)

Clear atmosphere (blue line) b) strong smoke plume

(green line) c) widespread smoke (red line).

green values and the Mean red values. Figure 3

reports the entries of the database projected on the

plane of these two variables, together with the

hyper-surface obtained with equation (16).

It is also worth mentioning that, to obtain the

same success rate, the SVM has to utilize 1299

support vectors. Therefore the application of the

proposed methodology results in a simplification of

orders of magnitude in the complexity of the

equation, without any significant loss in terms of

classification accuracy. Moreover, the obtained

formula is susceptible of comparison with models

and theoretical considerations, whereas the SVM

model is practically intractable from this point of

view. It is worth noting that a metric taking into

account the unbalance in the data, such as positive-

predictive ratio, could in principle be considered,

given the fact that examples of diseased trees are

about two orders of magnitude fewer than the

healthy ones. On the other hand, given the accuracy

already achieved, this would not add much to the

present treatment.

6.2 Remote Sensing of the Atmosphere:

Detection of Widespread Smoke

with LIDAR

One of the remote sensing techniques, which is

gaining increasing importance, is LIDAR an

acronym of Light Detection And Ranging. Lidar

originated in the early 1960s, shortly after the

invention of the laser, and combines laser-focused

imaging with radar's ability to calculate distances by

measuring the time for a signal to return. Its first

deployment was in meteorology and now it is

popularly used as a technology to make high-

resolution maps, with applications in geomatics,

archaeology, geography, geology, geomorphology,

seismology, forestry, remote sensing, atmospheric

physics, laser altimetry and contour mapping.

Wild fires have become a very serious problem

in various parts of the world. The LIDAR technique

has been successfully applied to the detection of the

smoke plume emitted by wild fires, allowing the

reliable survey of large areas (Fiocco, 1963;

Andreucci, 1993; Bellecci, 2007; Bellecci, 2010;

Vega, 2010; Gelfusa, 2014; Gelfusa, 2015).

Recently, mobile compact systems have been

successfully deployed in various environments. Up

to now, the attention has been devoted to early

detection of quite concentrated smoke plumes,

characterizing the first stage of fires, as soon as

possible. The main operational approach consists of

continuously monitoring the area to be surveyed

with a suitable laser and, when a significant peak in

the backscattered signal is detected, an alarm is

triggered. In these applications, the backscattered

signal presents strong peaks, which are detected with

various techniques. In other applications, it would be

interesting also to detect the non concentrated,

widespread smoke, which can be the consequence of

strong wind dispersion or non concentrated sources

(Marrelli, 1998). In this case, the signature of the

presence of the smoke is not a strong peak in the

detected power but an overall increase of large

regions of the curve. Typical examples of

backscattered signals for the alternatives of no

smoke, strong smoke plume and widespread smoke

are shown in Figure 4. Starting from the typical

Lidar equation (Andreucci 1993), it has been

decided to fit the backscattered signal intensity with

a mathematical expression of the form:

=









∙

∙



∙

(17)

where K

and K

are constants and R is the

range. The data of Figure 4 have been fitted with this

formula. The result of the non linear fit, for the

widespread smoke is reported in equation (18) and

for clear atmosphere in equation (19):

=

2.648∙10







∙

.∙



∙

(18)

=

1.734∙ 10







∙

.∙



∙

(19)

The results of the fit, equations (18) and equation

(19), indicate quite clearly that the parameter K

are

very similar for both the case of widespread smoke

and clear atmosphere. On the other hand, there is a

clear difference, of the order of 25% in the constants

. This is expected since K

includes the effect of

the coefficient β, which indeed quantifies the

backscattering properties of the atmosphere

(Andreucci, 1993; Bellecci, 2007; Bellecci, 2010;

Vega, 2010).

Table 3: Main characteristics of the database used for the

LIDAR application.

Total number of data: 521

Number of non-smoke data 312

Number of widespread smoke

data

209

Number of train data (~80%) 431

Number of test data (~20%) 90

Since the attempt to identify the presence of

widespread smoke is a quite pioneering application

of the LIDAR technique, it is important not only to

be able to discriminate between the two situations

but also to provide models for the interpretation of

the physics. In particular, the identification of the

boundary in the space of the parameters K

and K

for the two cases is considered an essential piece of

information for comparison with theories. The

proposed methodology has therefore been applied to

a quite substantial database summarized in Table 3.

For the SVM, a radial basis functions kernel has

been used. The best equation found is with SR:





= 0.1083⋅ sin15.61⋅



+

+cos1.59⋅



.



(20)

The above equation provides a Train Accuracy

of 89.33 % and a Test Accuracy of 91.11 %,

practically the same as the SVM success rate. The

equation of the boundary between clear atmosphere

and widespread smoke, in the space of the

parameters K

and K

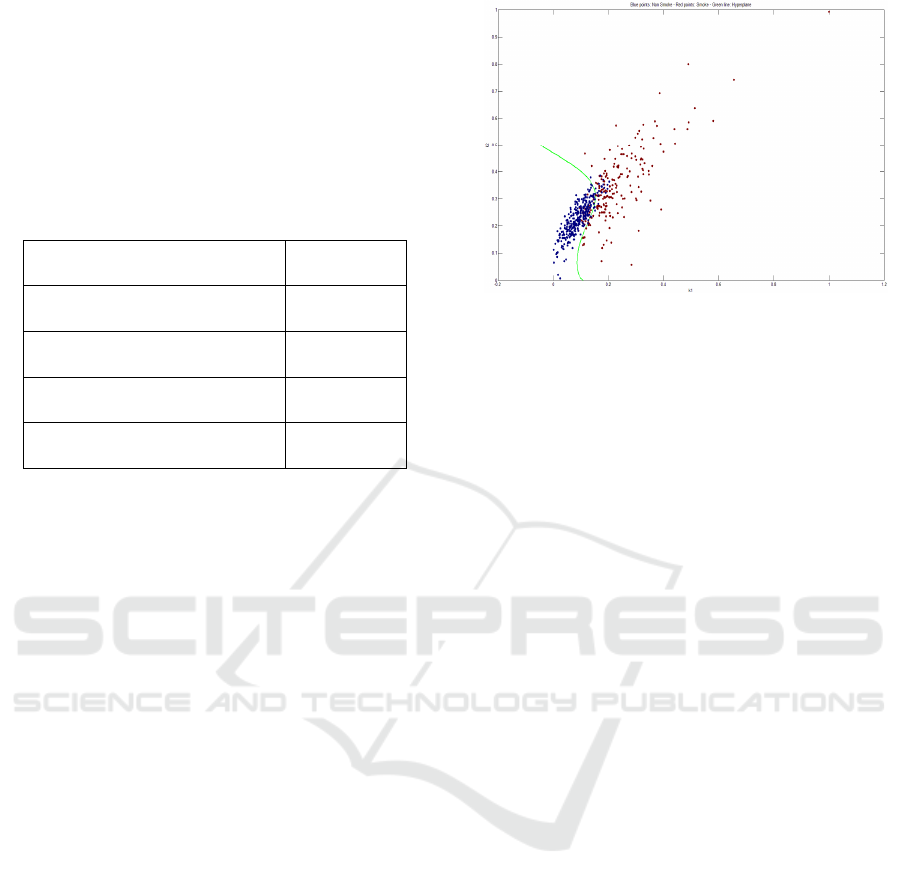
is shown in Figure 5. To

understand the importance of the results obtained, it

should also be considered that the model of the SVM

consists of 154 support vectors. Therefore the level

of simplification obtained with equation (20) is

substantial.

Figure 5: Equation (18), describing the boundary between

the boundary between the cases of clear atmosphere and

widespread smoke, in the space of the parameters K

and

7 CONCLUSIONS

An original methodology has been devised to obtain

the equation of the boundary between two classes,

starting from an SVM classifier. In this way, using

SR via GP, the power of machine learning tools is

combined with the realism, physics fidelity and

interpretability of equations expressed in the usual

formalism of typical scientific theories. In particular,

the choice of SVM ensures that their structural

stability, their capability to maximize the safety

margins in the classification, is fully retained in the

final result. On the other hand, symbolic regression

allows finding the best trade-off between accuracy

of the classification and complexity of the final

equations of the boundary, depending on the

application. Moreover, “a priori” information can

also be exploited in order to steer the solutions

towards mathematical expressions, which reflect the

actual dynamics of the phenomena under study. This

can be achieved for example by selecting properly

the basis functions or by constraining the structure

of the trees. Given the fact that the objectives of the

approach are realism and interpretability, a

reasonable reduction of the classification

performance is not a major issue and can be

tolerated. It is also true that symbolic regression via

genetic programming can reproduce the accuracy of

the classification by the SVM, provided a

sufficiently high number of mesh nodes and the

necessary complexity of the SR are allowed for.

The numerical tests shown have proved the

effectiveness of the proposed technique to identify

the real equation of the boundary between classes

even in relatively high dimensions, provided the

shape of the boundary is a sufficiently regular

surface. Again, this seems to be fully adequate since,

in the majority of the scientific applications, the

boundaries between the various classes are quite

regular functions. This has been confirmed by the

application of the technique to experimental

databases of different scientific disciplines.

On the other hand, the method is susceptible of

various improvements. First of all, the technique

should be extended to other machine learning tools,

such a neural networks. More fundamentally, the

approach is now limited to identifying the

mathematical expressions of boundaries which can

be expressed as functions. It is a topic of future

investigations to apply the method to the

investigation of more complex boundaries (for

example multiply connected hypersurfaces).

Moreover, the task of regression, and not only

classification, should also be tackled (Murari (D),

2015; Murari (C), 2015; Peluso, 2014; Murari,

2016). Also applications to various aspects of

tomography inversion and disruptions are envisaged

(Martin, 1997; Murari (B), 2013).

REFERENCES

Andreucci F and Arbolino M., 1993, Il Nuovo Cimento,

16, 1, 35 (1993).

Bellecci C et al, 2007, Appl. Phys. B, 87, 373.

Bellecci C et al., 2010, Optical Engineering, 49 (12),

124302.

Cannas B. et al, 2013, Nucl. Fusion 53 093023

Fiocco G. and Smullin L. D., 1963, Nature, 199, 1275 .

Gaudio et al., 2014, Plasma Phys. Control. Fusion, 56

114002.

Gelfusa M. et al, 2014, Review Scientific Instr., 85,

063112

Gelfusa M. et al, 2015 “First attempts at measuring

widespread smoke with a mobile lidar system”, IEEE

Xplore, ISBN: 978-1-78561-068-4

Hirotugo A., 1974, IEEE Transactions on Automatic

Control 19 (6): 716–723, 1974

Johnson B.et al, 2013, International Journal of Remote

Sensing, 34 (20), 6969-6982.

Kenneth P. B and Anderson D. R., 2002, “Model Selection

and Multi-Model Inference: A Practical Information-

Theoretic Approach”, Springer (2nd ed)

Koza J.R., 1992, “Genetic Programming: On the

Programming of Computers by Means of Natural

Selection”, MIT Press, Cambridge, MA, USA.

Lotov A. V. et al, 2009 “Interactive Decision Maps:

Approximation and Visualization of Pareto Frontier”,

Springer, ISBN 978-1-4020-7631-2.

Marrelli L. et al, 1998, “Total radiation losses and

emissivity profiles in RFX”, Nucl. Fusion 38 (5), 649

Martin P. et al, 1997, Review of scientific instruments 68

(2), 1256-1260

Murari A., et al, 2009, Nucl. Fusion, 49 055028 (11pp)

Murari A., et al. (A), 2013, Nucl. Fusion 53 033006 (9pp)

Murari A., et al, (B), 2013 Nucl. Fusion, 53 043001

doi:10.1088/0029-5515/53/4/043001

Murari A. et al (C), 2015, Plasma Physics. Control.

Fusion, 57 014008, doi: http://dx.doi.org/10.1088/

0741-3335/57/1/014008

Murari A et al (D), 2015, Nucl. Fusion 55 073009 (14pp)

doi:10.1088/0029-5515/55/7/073009

Murari A. et al., 2016, Nucl. Fusion 56 026005,

doi:http://dx.doi.org/10.1088/0029-5515/56/2/026005

Peluso E. et al, 2014, Plasma Phys. Control. Fusion, 56

114001,doi:http://dx.doi.org/10.1088/0741-

3335/56/11/114001

Rattà G. A. et al., 2010, Nucl. Fusion. 50 025005 (10pp).

Schmidt M. and Lipson H., 2009 April, Science, Vol 324

Vapnik V., 2013 “The Nature of Statistical Learning

Theory”, Springer Science & Business Media, ISBN

1475724403, 9781475724400

Vega et al, 2010, Review of Scientific Instruments, 81 (2),

p. 023505

Vega J et al, 2014, Nucl. Fusion 54 123001

Vega J. et al, 2009, Nucl. Fusion. 49 085023 (11pp)

Wesson J., “Tokamaks”, Clarendon Press, Oxford, 2004.

Third edition.