
Higher Order Neural Units for Efficient Adaptive Control
of Weakly Nonlinear Systems
Ivo Bukovsky
1
, Jan Voracek
1
, Kei Ichiji
2,3
and Homma Noriyasu
2,3
1
College of Polytechnics Jihlava, Czech Republic
2
Dpt. of Radiological Imaging and Informatics, Tohoku University Graduate School of Medicine, Japan
3
Intelligent Biomedical System Engineering Laboratory, Tohoku University, Japan
Keywords: Polynomial Neural Networks, Higher Order Neural Units, Model Reference Adaptive Control, Conjugate
Gradient, Nonlinear Dynamical Systems.
Abstract: The paper reviews the nonlinear polynomial neural architectures (HONUs) and their fundamental
supervised batch learning algorithms for both plant identification and neuronal controller training. As a
novel contribution to adaptive control with HONUs, Conjugate Gradient batch learning for weakly
nonlinear plant identification with HONUs is presented as efficient learning improvement. Further, a
straightforward MRAC strategy with efficient controller learning for linear and weakly nonlinear plants is
proposed with static HONUs that avoids recurrent computations, and its potentials and limitations with
respect to plant nonlinearity are discussed.
Nomenclature
CG … Conjugate gradient batch learning algorithm
CNU … Cubic Neural Unit (HONU r=3)
colx … long column vector of polynomial terms
d … desired value (setpoint)
LNU … Linear Neural Unit (HONU r=1)
QNU … Quadratic Neural Unit (HONU r=2)
k … discrete index of time
L-M … Levenberg-Marquardt batch learning algorithm
n , m … length of vector ,
n
y
, n
u
… length of recent history of y or u [samples]
r , γ … order of polynomial nonlinearity (plant, controller)
… control input gain at plant input
T
… vector transposition
u … control input
w , v … long row vectors of all neural weights (plant, controller)
, … augmented input vector to HONU (plant, controller)
y
… neural output from HONU
y … controlled output variable (measured)
y
ref
… reference model output
e … error between real output and HONU
e
ref
… error between reference model and control loop
µ
… learning rate
1 INTRODUCTION
Computational intelligence tools such as neural
networks or fuzzy systems are booming in the area of
system identification and control of dynamical
systems. We can refer to many novel and powerful
control approaches, and the most important ones are
the Model Predictive Control (MPC), Adaptive
Dynamic Programming (ADP) often with extension
of reinforcement learning, and Model Reference
Adaptive Control (MRAC). MPC control, e.g.
(García et al., 1989; Ławryńczuk, 2009; Morari and
H. Lee, 1999) and references therein, depends on a
model of controlled system, and the unknown is the
actual control input that is being optimized before
every controller actuation to achieve the predefined
sequence of desired outputs. The core distinction of
control via ADP, e.g. (Wang et al., 2009) (WANG et
al., 2007) and references therein, is that the controller
is designed from heuristically obtained observation
of control inputs and corresponding system
responses. Then, using the enforced learning with
penalization of improper controller action, the
controller is directly trained without mathematical
analysis of the controlled plant. In principle, ADP is
thus suitable also for unstable systems, though the
computational costs can be very high. MRAC
control, e.g. (Osburn, 1961; Parks, 1966; Narendra
and Valavani, 1979; Elbuluk et al., 2002) and
references therein, requires model of a system and
the unknowns are the parameters (neural weights) of
a controller that are trained so the control loop adopts
the desired dynamics of a reference model. In this
Bukovsky I., Voracek J., Ichiji K. and Noriyasu H.
Higher Order Neural Units for Efficient Adaptive Control of Weakly Nonlinear Systems.
DOI: 10.5220/0006557301490157
In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 149-157
ISBN: 978-989-758-274-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

paper, we focus on MRAC control scheme that is
more conservative in sense of adaptive feedback
control and generally requires less computing in
contrast to ADP. As regards the computational
intelligence tools for MRAC, we deal with Higher
Order Neural Units (Bukovsky and Homma, 2016;
Madan M. Gupta et al., 2013), that represent
standalone neural architectures within the same
direction of computation that involves polynomial
neural networks , e.g. (Nikolaev and Iba, 2006), or
higher order neural networks (Ivakhnenko, 1971;
Taylor and Coombes, 1993; Kosmatopoulos et al.,
1995; Tripathi, 2015). In (Bukovsky et al., 2015) the
advantages of HONU feedback controllers are
highlighted for real-time application on non-linear
fluid based mechanical systems. Further studies
focussed on practical applications of HONU-MRAC
closed loop control may be recalled in (Benes and
Bukovsky, 2014). Except the famous Levenberg-
Marquardt algorithm, the Conjugate Gradients (CG)
are known to be very fast for linear models and its
nonlinear alternatives are studied (Dai and Yuan,
1999; El-Nabarawy et al., 2013; Zhu et al., 2017).
In this paper, we recall Conjugate Gradient learning
for HONUs as it can practically accelerate plant
identification after first epochs are carried with
Levenberg-Marquardt learning. Then, we newly study
an approach that use merely static HONUs as a plant
models and also as controllers so the recurrent
computations are avoided and convergence of
controller training is naturally accelerated. Then we
newly discuss the drawback of the method that lies in
its suitability for weakly nonlinear dynamical systems.
The most common symbols and abbreviations are
explained in Nomenclature section above, while other
terms are explained at their first appearance.
2 PRELIMINARIES ON HONUS
This section recalls HONUs as nonlinear SISO
models for such linear or nonlinear dynamical
systems, that can be approximated by a HONU with
the user-defined polynomial order r ≤ 3. Thus in this
work, a dynamical system is considered weakly
nonlinear, if it can be approximated with a recurrent
HONU of polynomial order up to r=3, i.e. it is a
dynamical system, resp. the dynamics in data, that can
be reliably captured either by dynamical (recurrent)
LNU or QNU or CNU. In other words, a weak
nonlinear systems is here such a system that can be
approximated via Taylor series expansion of up to 3
rd
order that corresponds to 3
rd
order HONU (i.e. CNU).
Properly learned dynamics of a plant via HONU is
further necessary to train a linear or nonlinear
controller that is realized via another HONU as well.
For example, a sinusoidal nonlinearity is an example
of strong non-linearity that is difficult or even
impossible to fully capture by HONU (r ≤ 3). For
SISO systems, the HONUs of up to third order are
defined in a classical form or in a long vector form as
defined in Table 1, where the augmented input
vector for dynamical system approximation can be
defined in (1)and its total length is
1
yu
nnn=+ + .
Recall, that y as measured one in (1) implies static a
HONU, i.e. static function mapping, because all the
values in x are measured ones.
, (1)
In order to define dynamical (recurrent) HONUs,
real y should be replaced with neural outputs, i.e.
y
y←
resp. in (1), so we would obtain a
recurrent neural architecture that can be more
difficult to train, but it is necessary for tuning a
controller for nonlinear dynamical systems as it is
discussed later in this paper. For batch learning for
plant identification, simple variant of Levenberg-
Marquardt algorithm can be recommended for both
static HONUs as well as for recurrent ones so the
weight updates can be calculated as follows
, (2)
where J is Jacobian matrix, I is identity matrix,
upper index
-1
stands for matrix inversion, and the
error yields . Recall that the Jacobian
matrix for static HONU , i.e. the input vector (1) with
only measured values, is as follows
(3)
where colx is a long column vector of polynomial
terms as indicated in Table 1. Then, equation (3)
shows that J is constant for all training epochs of
static HONUs (i.e. when input vector is defined as in

Table 1: Summary of HONUs for weakly nonlinear systems (of up to 3
rd
polynomial order of nonlinearity).
Order of
HONU
HONU (neural output
()
y
k
)
details
Classical form of HONU = Long vector form of HONU
(LNU)
(QNU)
(CNU)
(1)) and that accelerates real time computations (esp.
when considering the HONUs are nonlinearly
mapping models yet they are linear in parameters).
The Jacobian for recurrent HONUs, i.e. when
y
y←
in (1), with learning formula (2), and
according to per partes derivation rule, generally
yields
,(4)
where the content of a short vector
x
y is apparent
from (1). Recurrent HONUs then perform more
accurate dynamical approximation of weakly
nonlinear dynamical systems from measured data
than a static HONU (as it is shown in the
experimental section); however, the Jacobian of
dynamical HONU varies in time so its rows have to
be recalculated at every time sample resulting in
varying Jacobian for every training epoch.
Further in this paper, it is shown that static HONU
can be sufficient to identify weakly nonlinear
dynamical systems so we can use a very efficient,
well converging and the most straightforward
technique of a feedback controller tuning.
3 CONJUGATE GRADIENT FOR
PLANT IDENTIFICATION
WITH HONUs
The proper plant identification from measured data
is important for further controller tuning. In case of
not well conditioned data in Jacobian, the L-M
formula (2) needs a small learning rate µ for
convergence and then this gradient method can be
slow, i.e. it may need large number of training
epochs. Nevertheless, HONUs are linear in
parameters and the CG learning can be directly
applied to HONUs as it is introduced in this section.
Recall, that CG solves the set of equations as
follows
, (5)
Where b is a column vector of constants, A is
positively semi-definite matrix, and w is a column
vector of unknowns (neural weights). Because
HONUs are linear in parameters, i.e. the Jacobian
(3) is not directly a function of weights, we can
restate the training of HONUs as follows
, (6)
where colX is defined (Bukovsky and Homma,
2016) as follows (assuming all initial conditions are
known)
, (7)
that is in fact the Jacobian of a HONU for all
training data (of total length N). Then, by
mutliplying (6) with from the left, we obtain
, (8)
so we have obtained the positive definite matrix A
and thus we can directly apply the CG learning to
both static or recurrent HONUs as follows. For the
very first epoch of training we initiate CG with
, (9)
and with
. (10)
Then for further epochs of training, i.e. for
, we
calculate parameter
, (11)
and then we can update the weights as
, (12)
where and other CG parameters for
next training epoch are then calculated or updated as
follows
, (13)
and similarly to Fletcher-Reeves nonlinear CG
method
, (14)
and finally
. (15)
This section extended the classical Conjugate
Gradient learning (as known for linear systems) to
HONUs due to their in parameter linearity. This
batch learning algorithm (9)-(15) has no adjustable
parameters except the initial neural weights and the
number of learning epochs; furthermore, the training
of both static or dynamical HONU can be rapidly
accelerated in comparison to L-M algorithm (2). As
demonstrated in experimental section in this paper, it
is suggested to use L-M learning for a few initial
training epochs and then switch for CG to rapidly
accelerate plant identification. Notice that in a
closed loop, the presented CG for HONU is not so
suitable for controller weights
v
training as the
symmetric positive definite matrix is not so
achievable and CG for a controller then becomes
much more complicated task. Thus L-M and CG are
both applicable to plant identification via static or
dynamic HONUs, while only L-M is the most
comprehensible training algorithm for HONUs as
controllers within the MRAC control scheme
(Figure (2))
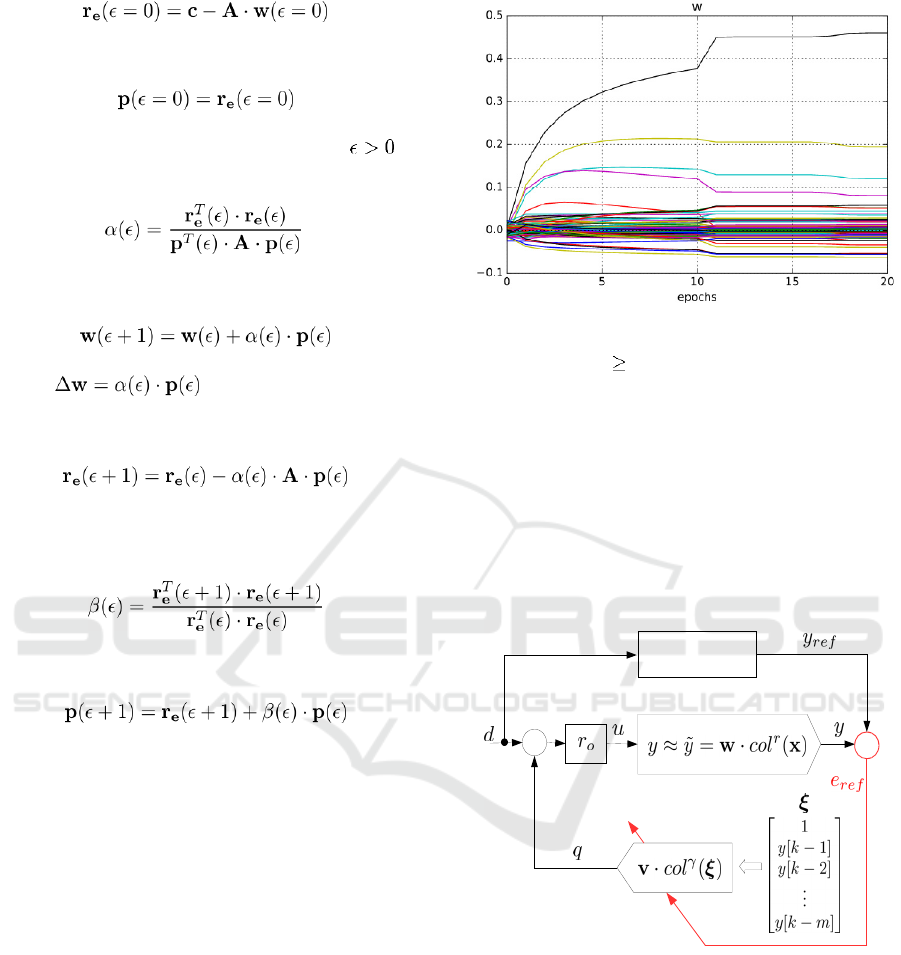
Figure 1: Training of static CNU for system in Figure 3
starting with L-M learning accelerated with CG learning
for training epochs 10.
4 BATCH LEARNING STRATEGY
FOR CONTROL WITH STATIC
HONU AS A PLANT MODEL
The most typical control loop for SISO dynamical
systems with HONUs can be according to Figure2,
where we assume normalized (z-scored) magnitudes
+
plant
controller
+
-
Reference Model
-
-
Figure 2: Discrete time Model Reference Adaptive Control
(MRAC) loop with two HONUs: as plant model and as a
nonlinear state feedback controller.
of input and output variables, i.e. of d, y, and y
ref
and
where the input gain r
o
can be also adaptive and it
compensates for the true static gain of the controlled
plant. In our previous works on HONUs with the
MRAC control scheme in Figure 2, we have usually
identified plants with recurrent HONUs and then we
used a trained HONU as a dynamical plant model
for further controller-tuning computations, i.e.,

including for the control loop simulation with
HONU as a dynamical model of a plant. It means
that for the control law
, (16)
the controller weights are optimized (trained) via L-
M learning rule as follows
, (17)
where the subscript v indicates it is the controller
learning rule, and where the Jacobian matrix J
v
involves recurrent backpropagation computations of
partial derivatives (with properly applied time
indexes as follows
, (18)
so we should calculate the Jacobian (18) recurrently
because
, (19)
where the utmost right matrix has its dimension of
, and n
v
denotes the total number of
neural controller weights (i.e. the lengh of v). For
the above controller training (16)-(19) (with
dynamical HONU as plant model), both the input
vectors x in (1) and
ξ in (Figure 2). Based on our
contemporary knowledge (Benes and Bukovsky,
2014; Benes et al., 2014; Bukovsky et al., 2015,
n.d.), the above control scheme with dynamic plant
HONU works very well if the dynamical HONU can
be trained to identify the plant, i.e. if the plant is not
more nonlinear than as it could be captured by the
dynamical HONU. In other words, we always
suggest to try to identify the plant with a dynamical
HONU for control tuning for MRAC approach.
Nevertheless, in case of weakly nonlinear plants, i.e.
plants that can be well identified by the dynamical
HONUs due to not too high degree of nonlinearity,
we may avoid the recurrent computations and we
can train the controller weights in much more
straightforward and computationally efficient
strategy as follows.
At the beginning of controller training and before
the plant identification, we always need a reasonable
training data, here we define the desired variable d
that we can feed into the plant to measure the
corresponding plant output data y, and we also
simulate the reference model output y
ref
. Recall that
the objective is to modify the control loop so it
adopts the reference model behavior once the
controller is properly trained. In other words, we
desire that the trained controller outputs a proper
value q so in the next corresponding future steps, the
controlled plant y matches the reference model
output y
ref
.
, (20)
Thus, if we feed the reference values directly into
the input vectors of plant (1) and controller
(Figure2) as in (20) i.e. we do not need to simulate
the closed loop output with a recurrent HONU
model of a plant but instead we use directly the
apriori given reference model values, then we can
update the controller weights directly and the k
th
row
of Jacobian (18) can be directly evaluated in (21)
where the weights w were obtained by L-M and/or
CG learning algorithm with static HONU as a plant
model. Thus, we have avoided the recurrent
computations in both plant identification as well as
controller training and the computational efficiency
and convergence of the learning is boosted.
; where (21)
However as mentioned above, the price for this
boosted controller design is that this way trained

controllers are limited to linear or weakly nonlinear
plants, i.e. to such plants for which the static HONU
sufficiently approximates the system from data
(otherwise recurrent HONU has to be used for plant
identification for the control scheme and it can be
more difficult to train dynamical HONU properly or
even impossible depending on nonlinearity of the
approximated system).
5 EXPERIMENTAL ANALYSIS
The plant dynamics was first identified from input-
output data with static HONU and another static
HONU(s) were trained as controllers (Figure 2) with
L-M training, so the recurrent computations and
plant simulation during the plant identification and
controller training were avoided. All the
computations were implemented in Python (2.7)
including the continuous time simulation of plants
and closed control loops (Scipy odeint with default
setups unless noted otherwise).
5.1 Linear Oscillating Dynamical
System
To demonstrate the efficiency of the proposed
control approach with HONU for oscillatory linear
dynamical systems, a SISO plant defined with the
Laplace transfer function is chosen as follows
, (22)
where s is the Laplace operator. The training data
were simulated with sampling
[time unit] and
its dynamics was approximated with a single static
LNU (i.e. HONU r=1, n
y
=5, n
u
=5, µ=0.1, 300
training epochs of L-M training) for the same
constant sampling. To enhance the controller
performance for this dynamical system with
complex conjugate poles and zeros, two parallel
LNUs were used as a controller to enhanced control
performance as introduced recently in (Bukovsky et
al., n.d.). Recall that in such case, the controller
consisted of two summed LNUs so the control law
(16) yielded
, (23)
where q
1
and q
2
are outputs of two parallel LNUs
(while only a single one is shown in Figure 2). Both
controller LNUs were trained with L-M learning
with input vector setups m
1
=5, m
2
=5, and with the
same learning rate
14
v
E
μ
= for the weights and for
r
o
within 30 training epochs. The performance of
the trained controller is shown in Figure 4.
5.2 Weakly Nonlinear System
As an example of a weakly nonlinear system, the
second-order dynamics plant is chosen as defined in
Figure 3,
Figure 3: A weakly nonlinear plant where ()u
ττ
= and
()
uu
SSy= are nonlinear functions (24).
where the time constant τ and the static gain S
u
of
the first subsystem are nonlinear functions as
follows
.(24)
The continuous-time plant (to obtain “measured”
data) and the continuous control loop were simulated
with sampling Δt=0.01 [time unit] with forward
Euler method. The plant was identified from
“measured” data with static CNU (HONU r=3)
with setups n
y
=3, n
u
=3 and with initial 10 epochs of
L-M with µ=0.01 followed with 10 epochs of CG for
accelerated learning (see the accelerated
convergence in Figure 1). Further a single CNU as a
controller (as in Figure 2) with setup m=2 and also
r
o
were trained by L-M (10 epochs, µ
v
=1E6). The
sampling of plant identification and controller
actuation was here Δt
HONU
=0.5 [time unit]. The
performance of the trained control loop compared to
the plant without a controller is shown in Figure 5.
6 DISCUSSION
To discuss the limitations of HONUs of up to 3
rd
polynomial order, i.e. r ≤ 3, as we have investigated
them for nonlinear dynamical systems up to now,
let’s discuss identification and control of an inverted
pendulum model (25) with HONUs in this section.
The model (23) is adopted from (Liu and Wei,
2014); however, it is modified with increased
friction to at least stabilize the system first to obtain
training data for plant identification. It should be
highlighted, that the MRAC control approach
depends on plant model, here learned from training

data, and such data can not be usually obtained from
unstable systems. The modified (stabilized) discrete
time inverted pendulum model is then as follows
(25)
where the measured output is simulated as y=χ
1
,
f
d
=0.6 is the friction and u is control input. A
successful setup for at least imperfect control of this
plant (see Figure 6) was found at doubled sampling
with static CNU for identification (r=3, n
u
=n
u
=4,
trained with 20 epochs of L-M (µ=1) followed with
20 epochs of CG ) and two parallel static HONUs
(LNU and CNU) as a controller, as discussed in
subsection 5.1 (23), both with m=4 and with 30
epochs of L-M training (µ
v
=1). The successful setup
for control of this more strongly nonlinear plant was
not so trivial to find as it was for the previous two
weakly nonlinear plants. The control result for (25)
is shown in Figure 6.
7 CONCLUSIONS
In this paper, we have presented MRAC control
strategy with purely static HONUs that avoids
recurrent computations and thus improves
convergence of controller training. As an aside, the
Conjugate Gradient was presented for HONUs as it
can accelerate plant identification with HONUs.
This adaptive control technique is easy to implement
and it was shown working for weakly nonlinear
dynamical systems, i.e. such systems that can be
well approximated with HONUs of appropriate
polynomial order (here < 3). Investigating this
straight control approach with HONUs for strongly
nonlinear systems is still a challenge.
ACKNOWLEDGEMENT
The work was supported by the College of
Polytechnics, Jihlava, Czech Republic, and by the
Japanese JSPS KAKENHI Grant Number 15J05402.
Special appreciation goes to people that have been
developing Python, LibreOffice and other useful
open-source SW.
REFERENCES
Benes, P., Bukovsky, I., 2014. Neural network approach to
hoist deceleration control, in: 2014 International Joint
Conference on Neural Networks (IJCNN). Presented
at the
2014 International Joint Conference on Neural
Networks (IJCNN), pp. 1864–1869
. doi: 10.1109/
IJCNN.2014.6889831
Bukovsky, I., Benes, P., Slama, M., 2015. Laboratory
Systems Control with Adaptively Tuned Higher Order
Neural Units, in: Silhavy, R., Senkerik, R., Oplatkova,
Z.K., Prokopova, Z., Silhavy, P. (Eds.),
Intelligent
Systems in Cybernetics and Automation Theory,
Advances in Intelligent Systems and Computing.
Springer International Publishing, pp. 275–284
.
Bukovsky, I., Benes, P.M., Vesely, M., Pitel, J., Gupta,
M.M., n.d. Model Reference Multiple-Degree-of-
Freedom Adaptive Control with HONUs, in:
The 2016
International Joint Conference on Neural Networks.
Presented at the IEEE WCCI 2016, IEEE, Vancouver
.
Bukovsky, I., Homma, N., 2016. An Approach to Stable
Gradient-Descent Adaptation of Higher Order Neural
Units.
IEEE Trans. Neural Netw. Learn. Syst. PP, 1–
13.
doi:10.1109/TNNLS.2016.2572310
Dai, Y.H., Yuan, Y., 1999. A Nonlinear Conjugate Gradient
Method with a Strong Global Convergence Property.
SIAM J. Optim. 10, 177–182. doi: 10.1137/
S1052623497318992
Elbuluk, M. E., Tong, L., Husain, I., 2002. Neural-
Network-Based Model Reference Adaptive Systems
for High-Performance Motor Drives and Motion
Controls.
IEEE Trans. Ind. Appl. 38, 879–886.
doi:10.1109/TIA.2002.1003444
El-Nabarawy, I., Abdelbar, A. M., Wunsch, D.C., 2013.
Levenberg-Marquardt and Conjugate Gradient
methods applied to a high-order neural network. IEEE,
pp. 1–7.
doi:10.1109/IJCNN.2013.6707004
García, C. E., Prett, D. M., Morari, M., 1989. Model
predictive control: Theory and practice — A survey.
Automatica 25, 335–348. doi: 10.1016/0005-
1098(89)90002-2
Ivakhnenko, A. G., 1971. Polynomial Theory of Complex
Systems. IEEE Trans. Syst. Man Cybern. SMC-1,
364–378. doi:10.1109/TSMC.1971.4308320
Kosmatopoulos, E. B., Polycarpou, M. M., Christodoulou,
M.A., Ioannou, P.A., 1995. High-order neural network
structures for identification of dynamical systems.
IEEE Trans. Neural Netw. 6, 422–431.
doi:10.1109/72.363477
Ławryńczuk, M., 2009. Neural Networks in Model
Predictive Control, in: Nguyen, N. T., Szczerbicki, E.
(Eds.), Intelligent Systems for Knowledge
Management.
Springer Berlin Heidelberg, Berlin,
Heidelberg, pp. 31–63.
doi: 10.1007/978-3-642-
04170-9_2
Liu, D., Wei, Q., 2014. Policy Iteration Adaptive Dynamic
Programming Algorithm for Discrete-Time Non-linear
Systems.
IEEE Trans. Neural Netw. Learn. Syst. 25,
621–634.
doi:10.1109/TNNLS.2013.2281663

Madan M. Gupta, Ivo Bukovsky, Noriyasu Homma, Ashu
M. G. Solo, Zeng-Guang Hou, 2013.
Fundamentals of
Higher Order Neural Networks for Modeling and
Simulation, in: Ming Zhang (Ed.), Artificial Higher
Order Neural Networks for Modeling and Simulation.
IGI Global, Hershey, PA, USA, pp. 103–133.
Morari, M., H. Lee, J., 1999. Model predictive control:
past, present and future. Comput. Chem. Eng. 23, 667–
682.
doi:10.1016/S0098-1354(98)00301-9
Narendra, K. S., Valavani, L. S., 1979. Direct and indirect
model reference adaptive control. Automatica 15, 653–
664.
doi:10.1016/0005-1098(79)90033-5
Nikolaev, N. Y., Iba, H., 2006. Adaptive learning of
polynomial networks genetic programming,
backpropagation and Bayesian methods.
Springer,
New York.
Osburn, P. V., 1961. New developments in the design of
model reference adaptive control systems.
Institute of
the Aerospace Sciences.
Parks, P. C., 1966. Liapunov redesign of model reference
adaptive control systems
. Autom. Control IEEE Trans.
On 11, 362–367.
Taylor, J. G., Coombes, S., 1993. Learning Higher Order
Correlations.
Neural Netw 6, 423–427. doi: 10.1016/
0893-6080(93)90009-L
Tripathi, B. K., 2015. Higher-Order Computational Model
for Novel Neurons, in: High Dimensional Neurocom-
puting. Springer India, New Delhi, pp. 79–103.
Wang, F.-Y., Zhang, H., Liu, D., 2009. Adaptive Dynamic
Programming: An Introduction. IEEE Comput. Intell.
Mag. 4, 39–47.
doi:10.1109/MCI.2009.932261
Wang, X., Cheng, Y., Sun, W., 2007. A Proposal of
Adaptive PID Controller Based on Reinforcement
Learning. J.
China Univ. Min. Technol. 17, 40–44.
doi:10.1016/S1006-1266(07)60009-1
Zhu, T., Yan, Z., Peng, X., 2017. A Modified Nonlinear
Conjugate Gradient Method for Engineering
Computation. Math. Probl. Eng. 2017, 1–11.
doi:10.1155/2017/1425857
APPENDIX
Figure 4: Results for linear oscillatory plant (22) via static LNU as a plant model (trained via L-M) and two parallel LNUs
as a feedback controllers (trained via L-M); the control loop output follows the desired unit steps reference signal (yref) (the
upper plot), the control input (2
nd
from top), bottom axes shows training by L-M batch learning of static LNU for plant
(bottom left), input gain (middle), and static LNU as controller (bottom right).

Figure 5: Results for control of weakly nonlinear dynamical system (Subsection 5.2) with variable time constant and static
gain (24), static CNU as a plant model (trained via L-M + CG, Figure 1) and static CNU controller (via L-M) (the bottom
axes show the detail of the desired behavior with the trained control loop output).
Figure 6: Control of plant (25); with the increasing desired value (dashed), the accurate control is more difficult to achieve
as the sinusoidal nonlinearity becomes stronger with increasing magnitude of desired value, so it demonstrates current
limits and challenges of the identification and control of strongly nonlinear systems with HONUs.
