Detecting and Assessing Contextual Change in Diachronic Text

Documents using Context Volatility

Christian Kahmann, Andreas Niekler and Gerhard Heyer

Leipzig University, Augustusplatz 10, 04109 Leipzig, Germany

Keywords:

Context Volatility, Semantic Change.

Abstract:

Terms in diachronic text corpora may exhibit a high degree of semantic dynamics that is only partially captured

by the common notion of semantic change. The new measure of context volatility that we propose models the

degree by which terms change context in a text collection over time. The computation of context volatility for

a word relies on the signiﬁcance-values of its co-occurrent terms and the corresponding co-occurrence ranks

in sequential time spans. We deﬁne a baseline and present an efﬁcient computational approach in order to

overcome problems related to computational issues in the data structure. Results are evaluated both, on syn-

thetic documents that are used to simulate contextual changes, and a real example based on British newspaper

texts. The data and software are avaiable at https://git.informatik.uni-leipzig.de/mam10cip/KDIR.git.

1 INTRODUCTION

When dealing with diachronic text corpora, we fre-

quently encounter terms that for a certain span of time

exhibit a change of linguistic context, and thus in

the paradigm of distributional semantics exhibit a

change of meaning. For applications in information

retrieval and machine learning tasks this causes prob-

lems because terms then are not unambiguous, hin-

dering the task of retrieving, or structuring, relevant

documents or information. However, understanding

semantic change can also be a research goal on its

own, such as work in historical semantics (Simpson

et al., 1989), or in the digital humanities where se-

mantic change has been used as a clue to better un-

derstand political, scientiﬁc, and technical changes,

or cultural evolution in general (Michel et al., 2011;

Wijaya and Yeniterzi, 2011). In information retrieval,

ﬁnding terms that signiﬁcantly change their meaning

over some period of time can also be a key to ex-

ploratory search (Heyer et al., 2011).

While there is plenty of work on how to detect

and describe semantic change of particular words,

for example “gay”, “awful”, or “broadcast” in En-

glish between 1850 and 2000 (Hamilton et al., 2016,

cf.) by highlighting the differences in context as de-

rived by co-occurrence analysis (Jurish, 2015, cf.) or

topic models (J

ahnichen et al., 2015, e.g.), it is still

an open question of how to identify those terms in a

diachronic collection of text that undergo by some

degree a change of context, and thus exhibit a se-

mantic change in the paradigm of distributional se-

mantics. In what follows, we present context volatil-

ity as a new and innovative measure that captures a

term’s rate of contextual change during a certain pe-

riod of time. The proposed measure allows to specify

the degree of a term’s contextual changes in a doc-

ument collection over some period of time, irrespec-

tively of the amount of text. This way we are able

to identify terms in a diachronic corpus of text that

are semantically stable, i.e. that undergo little or no

changes in context, as well as terms that are seman-

tically volatile, i.e. that undergo continuous or rapid

changes in their linguistic context. Often, semanti-

cally volatile terms are highly controversial, such as

“Brexit“ in the 2016 British public debate. A term’s

context volatility complements its frequency, a feature

that is of particular interest when we are interested in

detecting weak signals, or early warnings, in the tem-

poral development of a corpus related to low frequent

terms indicating subsequent semantic change. Con-

text volatility is related to the notion of volatility in ﬁ-

nancial mathematics (Taylor, 2007), and we can draw

a rough analogy that just like the rate of change in the

price of a stock is an indication of risk, a high degree

of context volatility of a term is an indication that the

fair meaning of a term is still being negotiated by the

linguistic community.

We begin in section 2 by showing how our ap-

proach differs from other procedures in the spirit of

Kahmann C., Niekler A. and Heyer G.

Detecting and Assessing Contextual Change in Diachronic Text Documents using Context Volatility.

DOI: 10.5220/0006574001350143

In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KDIR 2017), pages 135-143

ISBN: 978-989-758-271-4

distributional semantics. We then explore and eval-

uate different forms of contextual change and iden-

tify computational problems that arise when applying

context volatility to diachronic text corpora. By eval-

uating the basic intuition and strategies to overcome

the difﬁculties we shall then present in section 3 an

approach which robustly calculates context volatility

without any statistical bias, and in section 4 introduce

a novel algorithm which avoids sparsity problems on

diachronic corpora, the MinMax-algorithm. To eval-

uate the measure, we apply the algorithm to a syn-

thetic data set in section 5, based on a distinction be-

tween three cases of how the context of a word may

change, viz. (1) a change in the probability of co-

occurring terms, (2) the appearance of new contexts,

and (3) the disappearance of previous contexts. Fi-

nally we apply our measure to real life data from the

Guardian API and illustrate its usefulness in contrast

to a purely frequency based approach with respect to

the term “Brexit”.

2 RELATED WORK

Several studies address the analysis of variation in

context of terms in order to detect semantic change

and the evolution of terms. Three different areas to

model contextual variations can be distinguished: (1)

methods based on the analysis of patterns and linguis-

tic clues to explain term variations, (2) methods that

explore the latent semantic space of single words, and

(3) methods for the analysis of topic membership. (Ja-

towt and Duh, 2014) use the latent semantics of words

in order to create representations of a term’s evolu-

tion which is a similar information as used in context

volatility. The approach models semantic change over

time by setting a certain time period as reference point

and comparing a latent semantic space to that refer-

ence over time. (Fernndez-Silva et al., 2011; Mitra

et al., 2014) or (Picton, 2011) look for linguistic clues

and different patterns of variation to better understand

the dynamics of terms. The popular word2vec model

has also been utilized for tracking changes in vocab-

ulary contexts (Kim et al., 2014; Kenter et al., 2015).

Both word2vec-based approaches use references in

time or seed words to emphasize the change but do

not quantify it independently to the reference. (Kim

et al., 2014) add the quantity of the changes through-

out growing time windows towards a global context

representation but do not examine the possibility of

detecting different phases in the intensity of change

whereas (Kenter et al., 2015) produce changing lists

of ranked context words w.r.t. the seed words. One

major concern in suing the word2vec approaches is

the fact that those models require large amounts of

text. Both described approaches fulﬁll this require-

ment by a workaround to artiﬁcially boost the amount

of data. This inﬂuences the ability to quantify and de-

scribe contextual changes according to the observable

data. Assuming a Bayesian approach, topic modeling

is another method to analyze the usage of terms and

their embeddedness within topics over time (Blei and

Lafferty, 2006; Zhang et al., 2010; Rohrdantz et al.,

2011; Rohrdantz et al., 2012; J

ahnichen, 2016). How-

ever, topic model based approaches always require an

interpretation of the topics and their context. In ef-

fect, the analysis of a term’s change is relative to the

interpretation of the global topic cluster, and strongly

depends on it. In order to identify contextual varia-

tions, we also need to look at the key terms that drive

the changes at the micro level. Context volatility dif-

fers from previous work in its purpose because it does

not start with a ﬁxed set of terms to study and trace

their evolution, but rather detects terms in a collec-

tion of documents that may be indicative of contex-

tual change for some time. The notion of context

volatility is introduced in (Heyer et al., 2009; Holz

and Teresniak, 2010; Heyer et al., 2016). The respec-

tive works present single case studies to evaluate the

plausibility of the proposed measure. Several nega-

tive effects in the data are not discussed and evalu-

ated. For example, the appearance of new contexts

or the absence of certain word associations in sin-

gle time slices cause gaps in the co-occurrence rank

statistics which were ignored in those works. The

measure determines the quantity of contextual change

by observing the coefﬁcient of variance in the ranks

for all word co-occurrences throughout time. Addi-

tionally, it does not use latent representations but the

co-occurrence information itself without any smooth-

ing. The information of temporarily non-observable

co-occurrences is present and can be used for the de-

termination of contextual change directly. In section 3

we take up on those effects that directly inﬂuence the

procedure and deﬁne alternative approaches to over-

come associated problems. In sum, while related

work on the dynamics of terms usually starts with a

reference (like pre-selected terms, reference points in

time, some pre-deﬁned latent semantics structures, or

given topic structures), context volatility aims at auto-

matically identifying terms that exhibit a high degree

of contextual variation in a diachronic corpus regard-

less of some external reference or starting point. The

measure of context volatility is intended to support

exploratory search for central terms

in diachronic

The notion of centrality of terms is used in (Picton,

2011). It captures the observation that central terms simul-

taneously appear or disappear in a corpus when the key as-

corpora, in particular, if we want to identify peri-

ods of time that are characterized by substantial se-

mantic transformation. However, we do not claim

that the measure quantiﬁes meaning change or seman-

tic change, the measure quantiﬁes the dynamics of a

term’s contextual information within a diachronic cor-

pus.

3 DEFINITION OF CONTEXT

VOLATILITY

The computation of context volatility is based on

term-term matrices for every time slice derived from

a diachronic corpus (Heyer et al., 2016). Those matri-

ces hold the co-occurrence information for each word

w in a time slice t. One can use different signiﬁcance

weights based on the co-occurrence counts such as the

log-likelihood-ratio, the dice measure or the mutual

information to represent the co-occurrences (Bordag,

2008). First, the corpus is divided into sets of docu-

ments belonging to equal years, months, weeks, days

or even hours and minutes to deﬁne the time slices

t. The set of all time slices is T . It is necessary to

determine for every word w of the vocabulary V and

every time slice t the co-occurrences w∗, e.g. a term-

term matrix C

with the co-occurrence counts. The

matrix has dimension V ×V . Based on the counts in

a signiﬁcance-weight can be calculated on all word

pairs which results in a term-term matrix of signif-

icant co-occurrences S

. The signiﬁcance-values for

the co-occurrences of a word w in t are sorted to as-

sign a ranking to the co-occurrences of a word. For

every word which co-occurs with w in t this ranking

may differ in the time slices or the ranking can’t be

applied if this very co-occurrence is not observable.

The ranks are stored in a matrix R

. Based on con-

secutive time stamps the ranks for every word pair in

all R

w,w∗,t

build a sequence. The transition of a word

pairs ranking through the time slices is quantiﬁed by

the coefﬁcient of variance on the ranks. It is possi-

ble to perform this calculation only on a history h of

time slices which gives the variance in the ranking

of a word pair for a shorter time span. The context

volatility for a word w in t is then the mean of all

rank variances from the word pairs w, w*. Note, that

not all combinations in w, w* have a count > 0 in all

time slices simply because not every word co-occurs

with every other word all the time. There are words

which never occur together with w or just in some

time slices. We therefor deﬁne the basic measure of

sumptions, or consensus, amongst the stakeholders of a do-

main change

context volatility of a term as an averaged operation

cv(C

w,i

, h) on all co-occurences of w where C

w,i

is the

co-occurrence of w. In the basic setting the mean

is build over all co-occurrences w* of w which can be

observed in at last 1 time stamp in h. Precisely, we

can deﬁne the ﬁnal calculation of the volatility for h

w,h

∑

cv(C

w,i

, h), (1)

with kC

w,h

k the number of co-occurrences on w which

could be observed in h. For consecutive histories the

context volatility of w forms a time series where each

data point contains the context volatility at a time slice

t for a given history h. This represents the mean con-

text volatility for all contextual information about a

word and we get an average change measure for the

co-occurrences. Informally, context volatility com-

putes a term’s change of context by averaging the

changes in its co-occurrences for a deﬁned number

of time slices. Alternatively, h could be set to all time

slices in T to produce a global context volatility for

the words in a diachronic text source.

3.1 Limitations

So far the main limitation of context volatility has

been an adequate handling of gaps. When applying

context volatility as described in (Holz and Teresniak,

2010) it can be shown that there are many cases for

which a co-occurrence of 2 words at a speciﬁc point of

time not only changes in usage frequency. The effect

could be observed in cases for which new vocabulary

is associated with a given word w in diachronic cor-

pora or some contexts are temporarily not used. This

does not necessarily mean that the absence of a con-

text introduces a lasting change to the semantic mean-

ing of a word. But both cases contain important infor-

mation about the dynamics in the contextual embed-

ding of a word. Thus, the resulting gaps in the rank se-

quence of diachronic co-occurrences for a word must

be handled accordingly to prevent a bias. Different

strategies for the handling of those gaps seem plau-

sible. For example, consider the situation where we

calculate the variance of 10 consecutive ranks, e.g. h

is set to 10 time slices, of a co-occurring word which

is given by R

w,i,h

= 1, X, 2, X, 3, X, 4, X, 5, X. The X

represents a gap, e.g. a co-occurrence count of 0 in

the according time slice. If the volatility of this pro-

gression should be calculated as in (Holz and Teres-

niak, 2010) we would calculate the coefﬁcient of vari-

ation of all ranks which are observable. In the ex-

periments the authors used a very large corpus with a

large h and the inﬂuence of the gaps is presumed to

produce a small bias. However, for smaller corpora

or smaller amounts of documents for a time slice we

can’t ignore the inﬂuence of such decisions. Often, a

co-occurrence can only be observed in a minority of

the time slices if, for example, the corpus is reduced

to a set of documents containing a speciﬁc topic. Fol-

lowing the deﬁnition of (Holz and Teresniak, 2010)

we set

cv(C

w,i

, h) =

σ(R

w,i,h

)

w,i,h

. (2)

Likewise, we can use the signiﬁcance-values for co-

occurring terms directly and set

cv(C

w,i

, h) = σ(S

w,i,h

), (3)

where σ(S

w,i,h

) is the standard deviation of the i

co-

occurrence signiﬁcances of w in the history h. We use

the standard deviation since the signiﬁcance-values

are not linearly distributed and a major amount of co-

occurrences has very little signiﬁcance-values. Using

the coefﬁcient of variance would produce large values

in changes of small signiﬁcances which is an unde-

sired behavior.

To carry out this calculations in a similar man-

ner like (Holz and Teresniak, 2010) only values of

w,i,h

are included which can be observed in the data,

e.g. R

w,i,h

= 1, 2, 3, 4, 5. We do not include the

non-observable co-occurrences with 0 or the maxi-

mum possible rank, e.g. the count of all possible co-

occurrences or the vocabulary, to ﬁll the gaps because

this introduces an undesired bias. A better strategy to

handle the non-observable ranks is to set the missing

co-occurrence in t by other information. We calcu-

late all co-occurrence signiﬁcances on all documents

on all time slices ﬁrst, in order to have a “global“ co-

occurrence statistic S

. If a signiﬁcance value in a

time stamp S

w,i,t

cannot be observed we set this value

to S

w,i

if this signiﬁcance is greater than 0, e.g. the

co-occurrence can be observed in some time stamp in

T but not in all. This deletes the gaps and introduces a

global knowledge about the contexts. Co-occurrences

which are new or emerging or just observable in some

time stamps are somehow of higher signiﬁcance in the

time stamp but of lower signiﬁcance w.r.t. the whole

corpus. This procedure prevents a bias and numerical

problems with missing ranks or signiﬁcances. How-

ever, the dynamics in the co-occurrence statistics are

still determinable. In section 5 we evaluate the base-

line method by using the ranks and measure their co-

efﬁcient of variance by ignoring missing information

(Baseline). Additionally, we test the same setup using

the signiﬁcances directly (Sig). Both setups are eval-

uated once again with beforehand added global co-

occurrence information(GlobalBaseline, GlobalSig).

4 MINMAX-ALGORITHM

In contrast to the notion of context volatility, where

the gaps were either not used at all or replaced by

global information, the MinMax-algorithm does use

the gap information itself. The difference d in the

ranks of a co-occurrence w, w* is measured from time

slice to time slice separately, then summed up and di-

vided by the number of time slices considered. This

results in a mean distance between the ranks of the

time slices w.r.t. w and h. A major distinction is the

introduction of 2 different ranking functions (formula

4 and 5) when setting the ranks for all co-occurences

w, w∗ in a time slice t. We apply both formulas to

all observable co-occurrences resulting in 2 ranks per

co-occurrence. Formula 4 applies the ranks decreas-

ing from the maximum number of co-occurrences w

has in a time slice considered in h. Words w∗ with

signiﬁcance-values of 0, e.g. gaps, share rank 0. In

formula 5 the ranks are assigned decreasing from the

number of co-occurrences w has in time slice t. Sig-

niﬁcances with value 0 again share rank 0. In the fol-

lowing equations R

w,w∗,t

is the list of co-occurrence

ranks for word w w.r.t. time slice t and R

w,i,t

the

rank of the i

co-occurrence for w w.r.t. t. The

quantity max(R

w,w∗,1...h

) is the maximum rank an ob-

servable co-occurrence of w can take in a history h,

e.g. the maximum number of co-occurrences of w

amongst the time slices included in h. Additionally,

this quantity is utilized to normalize the determined

ranks in the interval [0,1]. The normalization re-

moves the strong dependence towards a high number

of co-occurrences because the higher the number of

co-occurrences, the more likely it is to see a higher

absolute change for the ranks. This enables the com-

parison of words with big differences in their frequen-

cies and with that in their number of co-occurrences.

¬0

w,w∗,t

) =

max(R

w,w∗,1...h

) + 1 − R

w,i,t

max(R

w,w∗,1...h

)

(4)

w,w∗,t

) =

max(R

w,w∗,t

) + 1 − R

w,i,t

max(R

w,w∗,1...h

)

(5)

Consequently, besides having an absolute maximum

(rank for highest signiﬁcance) we now conﬁrm having

an absolute minimum (rank 0) over all time slices as

well. The gap-information is used directly because

when new words appear, we are able to measure the

distance between rank 0 and the relative rank a new

appearing word has in t + 1. The ranks of formula 4

are used when neither of the 2 consecutive entries to

calculate d represent a gap (R

¬0

). When either one or

both regarded entries represent a gap we use the ranks

determinded by formula 5 (R

). We can summarize

the procedure of calculating the mean distance of all

w, w* concurrent words to

w,h

k · (h − 1)

w,h

∑

i=1

h−1

∑

t=1

cv(C

w,i,h

) (6)

with cv(C

w,i,h

) =

(

| R

w,t,i

) − R

w,t+1,i

) | if a

| R

¬0

w,t,i

) − R

¬0

w,t+1,i

) | if b

(7)

where condition a : R

w,t,i

∨ R

w,t+1,i

= 0 and b : R

w,t,i

∧

w,t+1,i

= ¬0.

5 EVALUATION USING A

SYNTHETIC DATASET

There is no gold standard to validate the quantity of

contextual change. Such being the case, we are uti-

lizing a synthetic data set in which we can manip-

ulate the change of a word’s context in a controlled

way. We simulate different situations, where the rate

of context change follows clearly deﬁned target func-

tions. We apply the procedures presented in section 3

and 4 to the synthetic data set and compare the results

to the target functions we aimed for.

5.1 Creating a Synthetic Data Set

The creation of the data set follows 2 competing

goals. On one hand we want our data set to be as close

to an authentic data set as possible. Therefore, our

synthetic data set should be Zipf-distributed in word-

frequency which induces noisiness. On the other hand

the context volatility that follows the target functions

has to be measurable. Hence, when manipulating the

context of a word over time, we can’t ensure to not

infringe the regulations for a Zipf-distribution. We

create a data set that is somewhat Zipf-distributed but

still contains the signals we want to measure (ﬁgure

1) as a trade-off between signal and noise. The cre-

ation of the data set requires a number of time stamps

(100), a vocabulary size (1000), the mean-quantity of

documents per time stamp (500) and a mean amount

of words per document (300). To simulate the Zipf-

distribution, we create a factor f

Zip f

1000

, which

assigns to every word w

1,...,1000

a value indicating a

word count. The factors of counts can be normal-

ized to probability distributions when constructing the

documents. We also deﬁne 7 factors f

1,...,7

respon-

sible for simulating a predeﬁned contextual change.

The values for 7 words w

51,...,57

are set to 0 in the

Zipf-factor ( f

51,...,57

Zip f

= 0) because they’ll get boosted

in the respective factors f

1,...,7

and serve as reference

on which we evaluate the contextual change. Addi-

tionally, we designate the ﬁrst 50 words in the artiﬁ-

cial vocabulary, e.g. w

1,...,50

, to act as stopwords. In

each of the 7 factors we set 150 randomly chosen non-

stopwords to simulate an initial context w, w∗ and we

assign some high values according to ∼ N (75, 25).

The values for the reference words w

51,...,57

in their

associated factor is ﬁxed to 200. All other words

in a factor get a value close to 0 (0.1). The 150

other words (w, w∗) in each factor represent the ini-

tial words that are very likely to form co-occurrences

with their respective ﬁxed word at the ﬁrst time stamp.

The simulation of the contextual change now inﬂu-

ences the distribution of the 7 factors f

1,...,7

from time

stamp to time stamp. Thereby, each factor context is

modiﬁed following 1 of the target functions triangle

( f

), sinus ( f

), constant 0 ( f

), slide ( f

), half cir-

cle ( f

), hat ( f

) and canyon ( f

). Illustrations of the

functions are located in the appendix. Having initi-

ated all factors, the words for every document refer-

ring to the ﬁrst time stamp are sampled. We use a

uniform-distribution to choose 1 factor j among f

1,...,7

for every document. Next, we collect a preselected

amount of samples for the document using a multino-

mial distribution

p(w

) =

Zip f

) + f

)

∑

Zip f

) + f

)

(8)

over the whole vocabulary. By adding together the the

Zipf-factor and the sampled factor j we are adding ar-

tiﬁcial noise to the creation of the documents. We

could set the inﬂuence of the Zipf-factor separately.

But a higher proportion leads to more noise inter-

fering the context signals. The result is a bag of

words constituting each document in the ﬁrst time

stamp. To proceed to the next time stamp the fac-

tors f

1,...,7

have to be altered to simulate contextual

change. The target functions control the amount of

change in their corresponding factors in dependence

to the time stamp to inﬂuence the sampling outcome,

and consequently the context of the reference words.

Note, the value for the context word in the respective

factor stays the same and must stay 0 in all other fac-

tors (e.g. f

= 200, f

2,...,7

= 0). Besides the deﬁni-

tions of functions to control the amount of contextual

change we identify 3 different cases how the context

of a word can be inﬂuenced.

i. Exchange the Probability for Co-occurring

Terms: We model this by taking 2 words from the

co-occurrences w, w∗ in a factor and swap their

probabilities. This leads to a change of their like-

lihood to be sampled in the same documents like

their context word.

ii. Appearance of New Contexts: To address this,

we select 1 word in a factor that has a value close

to 0 and replace it with a high value. As a conse-

quence, when sampling the words, we will likely

see a ”new” word w.r.t. the context word of a fac-

tor.

iii. Disappearance of Contexts: We change the

probability value of a co-occurring word (high

value) close to 0. This will likely cause this word

to not appear anymore along with a context word.

In order to create the documents for the following

time stamps, the factors f

1,...,7

are inﬂuenced in de-

pendence to the the factors of the former time stamp

(t − 1) w.r.t a target function.

∼ change

targetF unction

( f

t−1

) (9)

For example if f

is following the triangle function,

for t < 50 the number of exchanged contexts can

be determined by the time stamp index t. For time

stamps t > 50 the number of exchanges is determined

100 −t. With the updated factors the succeeding time

stamps can be sampled until every document in T is

ﬁlled. The ﬁnal data set for the 7 target functions and

all 3 options for contextual change is distributed as

shown in ﬁgure 1. The data set is not exactly Zipf-

distributed because of the forced co-occurrence be-

havior.

2e+03 1e+04 5e+04 2e+05 1e+06

1 5 10 50 100 500 1000

frequency

words

Figure 1: Synthetic dataset with double log scale.

5.2 Results of Evaluation

We created 3 different data sets to test strengths and

weaknesses of the algorithms. In the ﬁrst data set (A)

all 3 described cases of context change are included

(case i., ii., iii.). The second data set (B) is built by

only changing the probability values of already co-

occurring terms (case i.). In the third data set (C) we

deploy the options appearance of new co-occurrences

(case ii.) and disappearance of known co-occurrences

(case iii.). We use cases (ii.) and (iii.) in the same

amount for the data sets A and C, so the quantity of

co-occurrences for the respective context words stays

0.0 0.2 0.4 0.6 0.8 1.0

0 20 40 60 80 100

context volatility

time

targetfunction

minmax

globalsig

Figure 2: Results for MinMax and GlobalSig on ﬁrst data

set.

constant. In data set C we refused to add the Zipf-

factor, because it interferes the forced co-occurrence

gap-effect which we intend to simulate by this conﬁg-

uration. We applied the context volatility measures to

all 3 data sets using a span of h = 2. In the interest of

a quantiﬁable comparison we normalized over all re-

sults (all 3 data sets) for every context volatility mea-

sure. We assess the performance of the measures by

using the mean distance between the calculated con-

text volatility and the intended target functions of the

7 context words. An example how the measures ap-

proximate the target function can be seen in ﬁgure 2.

Table 1: Results using all 3 synthetic data sets; for every

method and every data set we calculated the mean distance

over all 7 target functions.

A B C Mean

Baseline 0.25 0.11 0.29 0.217

GlobalBaseline 0.35 0.18 0.26 0.263

Sig 0.30 0.14 0.10 0.180

GlobalSig 0.22 0.25 0.08 0.183

MinMax 0.24 0.12 0.18 0.180

All calculation methods are able to detect the

function signals for data set A which sends the

strongest signals (table 1). The GlobalSig method

slightly outperforms all other methods in this setting.

The loss of information that occurs when transfer-

ring the signiﬁcances to ranks might be one cause of

the overall worse performance of the baseline meth-

ods, and a opportunity to further improve the MinMax

method. When using data set B the MinMax- and the

Baseline-algorithm perform best. Context changes

where new co-occurrences appear and known disap-

pear (C), again, is best captured by methods based

on signiﬁcances. The third data setting (C without

usage of f

Zip f

) forced the measurements to handle

gap-entries and the inability of the Baseline-method

in this concern is revealed. The produced results in-

clude the fact that the context words w

51,...,57

stay

constant in frequency in all time slices. Under this

condition the algorithms Sig, GlobalSig, and Min-

Max perform best. Additionally, we tested another

case where we set the probability to create a docu-

ment from f

5 times higher than f

. This causes

the number of co-occurrences for w

, w∗ to rise up

as well which is caused by the noise introduced by

Zip f

. The chance of sampling a word from the noise

in combination with w

is also higher when sam-

pling more often from f

according to formula 8. This

introduces more co-occurrences with a low signiﬁ-

cance and the signiﬁcance-based algorithms tend to

diminish the overall volatility (ﬁgure 7). For this ad-

ditional test case we only compared the target func-

tions triangle and sinus. Both respective factors use

the same amount of maximal changes for the time

stamps. In table 2 we show the mean distances be-

tween the volatility values and the expected target

function value. When working with real data (Vo-

cabsize >> 1000) this problem goes to the point,

where the resulting context volatility is inversely pro-

portional to the words frequency. For words with dif-

ferent frequency but similar context changes this re-

sults in different values for the context volatility. The

shape of two context volatility time series might be

similar but differs in the value range. When measur-

ing a global volatility among all T , 2 words of dif-

ferent frequency classes are not comparable in values

even though their contextual change would be com-

parable. Such being the case we cannot compare 2

words, which differ in frequency, considering their

context volatility in a reliant manner when using sig-

niﬁcance based algorithms.

Table 2: Mean distances between the calculated volatility

and the target function at each point of time; the factor re-

ﬂecting the triangle function was used 5 times more than the

one for sinus.

MinMax Sig

Triangle 0.13 0.27

Sinus 0.12 0.15

Comprising the evaluation, the MinMax-

algorithm is the most consistent method against

differences in term frequency and different types

of contextual change. Even though we draw our

conclusion based just on a synthetic dataset, we do

so knowing that the synthetic dataset was specially

designed to make the problems which arise when

working with real data measurable.

6 EXAMPLE ON REAL DATA

In this section we apply the MinMax-algorithm to

process 8156 British newspaper articles from January

1st until November 30th of 2016 which include the

words brexit and referendum.

The used language is

English, but the concept of context volatility is lan-

guage independent. The subject of interest for this

analysis of context volatility are keywords surround-

ing the “Brexit“ referendum in 2016. We split the

documents into sentences, removed stopwords and

used stemming. Furthermore we split the data set into

time slices of weeks. We used the dice coefﬁcient

as signiﬁcance-weight for the co-occurrences in sen-

tences. The MinMax-algorithm was applied using a

span of 3 weeks (h = 3).

0.0 0.1 0.2 0.3

0 10 20 30 40

context volatility

weeks

brexit

farage

cameron

may

referendum

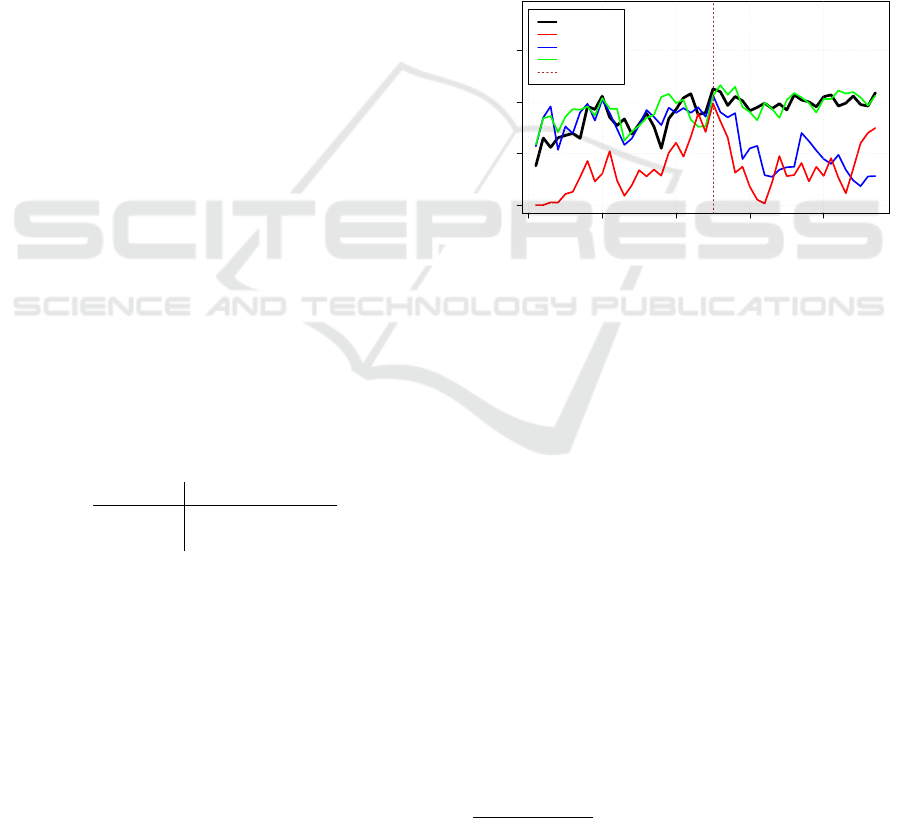
Figure 3: Context volatility for the words brexit, cameron,

may and farage.

In ﬁgure 3 the measured context volatilities for the

words brexit, farage, cameron and may are shown.

The time of the referendum is included as dotted

slash. One can identify different ways of contex-

tual change for the words. For example, the context

for the word cameron reveals some high amount of

change, which suddenly drops right after the refer-

endum. This goes along with the announcement of

Camerons resignation after the referendum. There is

basically no new or altered information resulting in a

decrease of context volatility. In this sense, context

volatility seems also to track the currentness of infor-

mation in consecutive time stamps. In comparison to

that we can see an allover high value for may, which is

even a little bit higher after the referendum. Theresa

May, being the designated prime minister might ex-

plain these results. In ﬁgure 4 the volatility values for

brexit and cameron are shown with their respective

frequencies. Although there is some correlation be-

tween volatility and frequency, it is obvious that there

are lots of phenomena in the volatility values, which

We used the Guardian API (http://open-

platform.theguardian.com/) to acquire the documents.

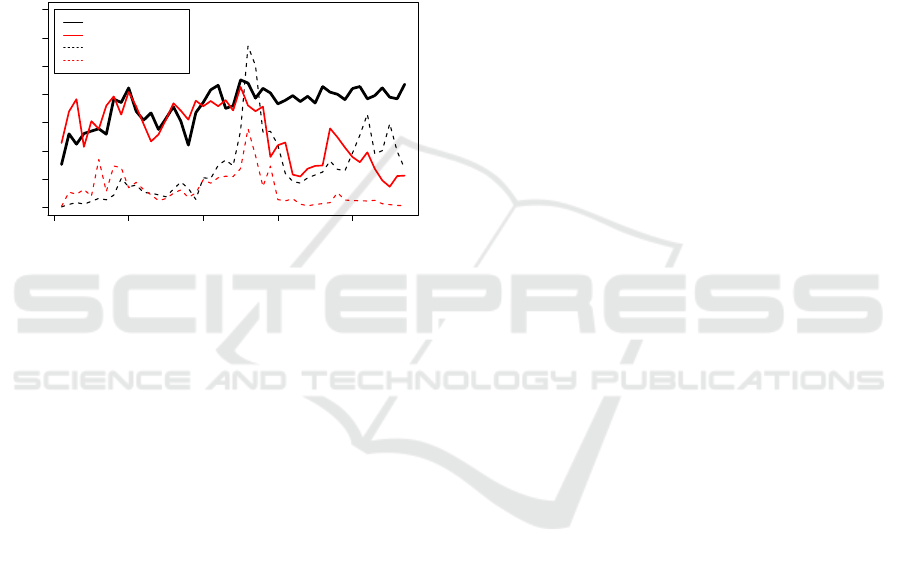
can’t be explained just by frequency. Especially for

the word brexit, we notice continuously a high volatil-

ity value irrespective of its frequency. In the time

immediately around the referendum the frequency of

both words have their highest peaks, which is caused

by the amount of articles released at that time span.

However, we measure almost the same amount of

contextual change for brexit already in February just

after Cameron announced the referendum, indicating

at that stage a high degree of public controversy. Us-

ing the MinMax-algorithm, we can compare a word’s

volatility with its frequency over time as well as 2

words that differ in frequency.

0.00 0.10 0.20 0.30

0 10 20 30 40

context volatility

weeks

brexit−cv

cameron−cv

brexit−frequency

cameron−frequency

Figure 4: Context volatility for the words brexit, cameron

and their frequencies.

7 CONCLUSION

In this work we presented an evaluation and prac-

tical application of the context volatility methodol-

ogy. We’ve shown a solution for evaluating con-

textual change measurements, especially the con-

text volatility measure, by creating a synthetic data

set, which can simulate various cases of contextual

change. Also, we introduced alternative algorithms,

which are superior to the baseline context volatility

algorithm, when facing problems on real diachronic

corpora (co-occurrence gaps). In the evaluation and

application the MinMax-algorithms shows its robust-

ness when competing with other methods by the abil-

ity to use the gap information directly and handle

the dynamics in the number of co-occurrences for a

word. With those improvements in the calculation of

context-volatility, we believe that the measure is able

to produce new results in various applications.

REFERENCES

Blei, D. M. and Lafferty, J. D. (2006). Dynamic topic mod-

els. In Proceedings of the 23rd international confer-

ence on Machine learning, pages 113–120.

Bordag, S. (2008). A comparison of co-occurrence and sim-

ilarity measures as simulations of context. In Com-

putational Linguistics and Intelligent Text Processing,

pages 52–63. Springer.

Fernndez-Silva, S., Freixa, J., and Cabr, M. T. (2011).

Picturing short-period diachronic phenomena in spe-

cialised corpora: A textual terminology description

of the dynamics of knowledge in space technologies.

Terminology, 17(1):134–156.

Hamilton, W. L., Leskovec, J., and Jurafsky, D. (2016). Di-

achronic word embeddings reveal statistical laws of

semantic change. arXiv preprint arXiv:1605.09096.

Heyer, G., Holz, F., and Teresniak, S. (2009). Change

of Topics over Time and Tracking Topics by Their

Change of Meaning. In KDIR ’09: Proc. of Int. Conf.

on Knowledge Discovery and Information Retrieval.

Heyer, G., Kantner, C., Niekler, A., Overbeck, M., and

Wiedemann, G. (2016). Modeling the dynamics of

domain speciﬁc terminology in diachronic corpora.

In TERM BASES AND LINGUISTIC LINKED OPEN

DATA, pages 75 – 90.

Heyer, G., Keim, D., Teresniak, S., and Oelke, D. (2011).

Interaktive explorative Suche in groen Dokumentbest-

nden. Datenbank-Spektrum, 11(3):195–206.

Holz, F. and Teresniak, S. (2010). Towards Automatic De-

tection and Tracking of Topic Change. In Computa-

tional Linguistics and Intelligent Text Processing, vol-

ume 6008, pages 327–339. Springer, Berlin, Heidel-

berg.

ahnichen, P. (2016). Time Dynamic Topic Models.

ahnichen, P., Oesterling, P., Liebmann, T., Heyer, G.,

Kuras, C., and Scheuermann, G. (2015). Exploratory

Search Through Interactive Visualization of Topic

Models. Digital Humanities Quarterly.

Jatowt, A. and Duh, K. (2014). A framework for analyzing

semantic change of words across time. In Proceed-

ings of the 14th ACM/IEEE-CS Joint Conference on

Digital Libraries, pages 229–238.

Jurish, B. (2015). DiaCollo: On the trail of diachronic col-

locations. In De Smedt, K., editor, CLARIN Annual

Conference 2015 (Wro\law, Poland, October 1517

2015), pages 28–31.

Kenter, T., Wevers, M., Huijnen, P., and de Rijke, M.

(2015). Ad hoc monitoring of vocabulary shifts over

time. In Proceedings of the 24th ACM International

on Conference on Information and Knowledge Man-

agement, CIKM ’15, pages 1191–1200.

Kim, Y., Chiu, Y.-I., Hanaki, K., Hegde, D., and Petrov, S.

(2014). Temporal analysis of language through neu-

ral language models. In Proceedings of the ACL 2014

Workshop on Language Technologies and Computa-

tional Social Science, pages 61–65.

Michel, J.-B., Shen, Y. K., Aiden, A. P., Veres, A.,

Gray, M. K., The Google Books Team, Pickett, J. P.,

Hoiberg, D., Clancy, D., Norvig, P., Orwant, J.,

Pinker, S., Nowak, M. A., and Aiden, E. L. (2011).

Quantitative Analysis of Culture Using Millions of

Digitized Books. Science, 331(6014):176–182.

Mitra, S., Mitra, R., Riedl, M., Biemann, C., Mukherjee, A.,

and Goyal, P. (2014). That’s sick dude!: Automatic

identiﬁcation of word sense change across different

timescales. In Proceedings of the 52nd Annual Meet-

ing of the Association for Computational Linguistics

(Volume 1: Long Papers), pages 1020–1029, Balti-

more, Maryland. Association for Computational Lin-

guistics.

Picton, A. (2011). A proposed method for analysing the

dynamics of cognition through term variation. Termi-

nology, 17(1):49–74.

Rohrdantz, C., Hautli, A., Mayer, T., Butt, M., Keim, D. A.,

and Plank, F. (2011). Towards Tracking Semantic

Change by Visual Analytics. In Proceedings of the

49th Annual Meeting of the ACL: Human Language

Technologies: Short Papers - Volume 2, pages 305–

310.

Rohrdantz, C., Niekler, A., Hautli, A., Butt, M., and Keim,

D. A. (2012). Lexical Semantics and Distribution of

Sufﬁxes: A Visual Analysis. In Proceedings of the

EACL 2012 Joint Workshop of LINGVIS & UNCLH,

pages 7–15.

Simpson, J. A., Weiner, E. S. C., and Oxford University

Press, editors (1989). The Oxford English dictionary.

Clarendon Press; Oxford University Press, Oxford:

Oxford; New York, 2nd ed edition.

Taylor, S. J. (2007). Introduction to Asset Price Dynamics,

Volatility, and Prediction. In Asset Price Dynamics,

Volatility, and Prediction. Princeton University Press.

Wijaya, D. T. and Yeniterzi, R. (2011). Understanding Se-

mantic Change of Words over Centuries. In Proceed-

ings of the 2011 International Workshop on DETecting

and Exploiting Cultural diversiTy on the Social Web,

DETECT ’11, pages 35–40, New York, NY, USA.

ACM.

Zhang, J., Song, Y., Zhang, C., and Liu, S. (2010). Evo-

lutionary hierarchical dirichlet processes for multiple

correlated time-varying corpora. In Proceedings of

the 16th ACM SIGKDD international conference on

Knowledge discovery and data mining, pages 1079–

1088.

APPENDIX

0 10 20 30 40 50 60 70

0 20 40 60 80 100

number of changes

time

triangle

hat

halfcircle

Figure 5: Three target functions showing the amount of

changes in the function factors in dependence to the time

0 20 40 60 80

0 20 40 60 80 100

number of changes

time

sinus

no_change

slide

canyon

Figure 6: Other 4 target functions showing the amount of

changes in the function factors in dependence to the time

0.0 0.2 0.4 0.6 0.8 1.0

0 20 40 60 80 100

context volatility

time

target−function

Sig

MinMax

Figure 7: Triangle target function and the calculated volatil-

ities using MinMax and Sig with high frequence for refer-

ence word