
Querying Natural Logic Knowledge Bases
Troels Andreasen
1
, Henrik Bulskov
1
, Per Anker Jensen
2
and Jørgen Fischer Nilsson
3
1
Computer Science, Roskilde University, Denmark
2
Management, Society and Communication, Copenhagen Business School, Denmark
3
Mathematics and Computer Science, Technical University of Denmark, Denmark
Keywords:
From Natural Language to Natural Logic, Formal Ontologies, Deductive Querying of Natural-logic Knowl-
edge Bases, Path finding in Knowledge Bases, Logical Knowledge bases in Bio-informatics and Medicine.
Abstract:
This paper describes the principles of a system applying natural logic as a knowledge base language. Natural
logics are regimented fragments of natural language employing high level inference rules. We advocate the
use of natural logic for knowledge bases dealing with querying of classes in ontologies and class-relationships
such as are common in life-science descriptions. The paper adopts a version of natural logic with recursive
restrictive clauses such as relative clauses and adnominal prepositional phrases. It includes passive as well as
active voice sentences. We outline a prototype for partial translation of natural language into natural logic,
featuring further querying and conceptual path finding in natural logic knowledge bases.
1 INTRODUCTION
We describe principles for a prototype system for nat-
ural logic knowledge bases with focus on the query
answering functionalities and the internal systems
representations for achieving these functionalities.
Natural logics are forms of logic which approach
natural language forms (van Benthem, 1986). Thus,
sentences stated in natural logic can be read and un-
derstood by application domain experts without back-
ground in logic and computer science. This is in
contrast to, say, description logic and logical clauses
as in DATALOG. The applied natural logic dialect,
called NATURALOG, possesses desirable decidabil-
ity and tractability properties, similar to description
logics. However, the deductive query functionalities
differ in that concept terms are themselves considered
first class objects subject to query answering.
The achieved deductive query answering func-
tionalities are realized by devising a joint graph form
for the given natural logic sentences. The system re-
shapes natural logic sentences into atomic sentences
forming the graph in a process termed atomization.
This graph form affords an ontological view by way
of the inclusion relation between concepts (concept
nodes) (Arp et al., 2015). Since the concepts in the
natural logic may be complex as a reflection of recur-
sively composed noun phrases, the ontology is gener-
ative (Andreasen and Nilsson, 2004; Andreasen and
Nilsson, 2014; Andreasen et al., 2015). This means
that ever more specialized concepts can be accommo-
dated in addition to and by means of given primitive
concept terms.
The graph view, in addition to deductive querying
assisted by high level inference rules, supports path
finding as a mechanism to associate two stated query
terms. This is particularly relevant in the considered
bio-domain where causal pathways are in focus, cf.
(Andreasen et al., 2017b). In general, this associa-
tion is computed as a shortest path composed of a se-
quence of relations connecting the terms.
We have previously described the applied natural
logic in (Nilsson, 2015; Andreasen et al., 2015) and
more recently with various linguistic extensions (An-
dreasen et al., 2016; Andreasen et al., 2017a). In our
ongoing stepwise syntactic and semantic extensions
of NATURALOG, here we further extend the natural
logic with passive voice forms and adverbial restric-
tions, which are central in the considered life science
domains and corpora. This logical approach is in con-
trast to established and rather succesful approaches to
text mining based on direct references to phrases in
concrete text sources and advanced information ex-
traction techniques, cf. for example (Li et al., 2014;
Kaewphan et al., 2012; Miwa et al., 2013).
An approach to acquisition of ontology from pro-
cessing natural language is introduced in (de Azevedo
et al., 2014). They present a principle of automated
Andreasen T., Bulskov H., Jensen P. and Fischer Nilsson J.
Querying Natural Logic Knowledge Bases.
DOI: 10.5220/0006574502940301
In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KEOD 2017), pages 294-301
ISBN: 978-989-758-272-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ontology building based on a natural language trans-
lator for expressive ontologies. Our approach differs
from (de Azevedo et al., 2014) in our use of a natural
logic with accompanying graph representation instead
of description logic. A version of natural logic is also
exploited in (MacCartney and Manning, 2009).
Obviously, given the present state of computa-
tional semantics, a natural logic cannot accommodate
the intricate syntactic and semantic forms found in
natural language, not even in the somewhat stereo-
typic scientific language corpora. Our strategy is to
make the system extract as much as possible in a com-
putational text analysis governed by the applied target
natural logic. This part is addressed in section 5.
2 KNOWLEDGE BASE NATURAL
LOGIC
A Natural logic knowledge base consists simply of a
set of natural logic affirmative sentences. The natu-
ral logic sentences consist of two concept terms con-
nected by a relation
Cterm
0
R Cterm
00
Linguistically, this typically corresponds to a subject
term followed by a transitive verb and a linguistic ob-
ject term as in the sample natural logic proposition
betacell produce insulin
where morphologically correct forms in the formal
logical language are neglected in favour of simplify-
ing streamlining. This is an example of an atomic nat-
ural logic sentence. In such atomic sentences the con-
cept terms are plain common nouns. More generally,
the concept terms are noun phrases with a head noun
optionally attributed with restrictions such as prepo-
sitional phrases and relative clauses, cf. the example:
cell that produce insulin reside-in pancreas
where the subject term comprises the restrictive rela-
tive clause that produce insulin. We also consider ad-
verbial prepositional phrases so that the relation (tran-
sitive verb) generalizes to include also relations intro-
duced by prepositions.
Semantically, the natural logic sentences express
relationships between classes of individuals, includ-
ing subclasses formed by the various linguistic re-
strictive expressions.
2.1 Implicit Quantifiers
The considered natural logic sentences are logical
propositions in that there are implicit quantifiers (lin-
guistic determiners) as in
every Cterm
0
R some Cterm
00
strictly giving every betacell produce some insulin for
betacell produce insulin.
As such the sentences are predicate logical sen-
tences in disguise as discussed in (Nilsson, 2015; An-
dreasen et al., 2016). However, the underlying predi-
cate logical construals are not appealed to in the pro-
totype design, which uses inference rules at the natu-
ral logic level as briefly described in section 5.2 and
covered in more detail in (Andreasen et al., 2015).
The natural logic sentence forms
every Cterm
0
R every Cterm
00
and
some Cterm
0
R some Cterm
00
are also supported. The latter form is needed when
considering passive forms of active sentences.
2.2 Copula Sentences
A common and important special case is the copula
sentence form
Cterm
0
isa Cterm
00
as in the atomic sentence insulin isa hormone, which
expresses that the denotation of the subject term
Cterm
0
is included in the denotation of the object term
Cterm
00
.
Notice that every Cterm
0
R some Cterm
00
corre-
sponds to the description logic terminological sen-
tence form Cterm
0
v ∃ R.Cterm
00
and that the copula
form corresponds to Cterm
0
v Cterm
00
, cf. (Baader,
2007). Thus, one may conceive of all description
logic sentences as copula sentences, whereas our nat-
ural logic sentences also use the actually appearing
transitive full verb forms. Obviously, our natural logic
is much closer to natural language description logic
and therefore a natural logic knowledge base can be
understood directly by domain experts. For further
discussion of this issue, we refer to (Nilsson, 2015;
Andreasen et al., 2017a). The natural logic forms
some-some, which is necessary for representing pas-
sive sentences, and every-every are not supported in
common forms of description logic.
3 NATURAL LOGIC GRAPHS
The natural logic knowledge base takes form of a set
of natural logic sentences represented as a joint graph
whose nodes uniquely represent concepts across the
sentences, and whose directed labeled edges are
domain-dependent relations cf. (Smith et al., 2005).
In this view, the copula sentences form an onto-
logical structure partially ordered by the inclusion re-
lation isa. The non-copula natural logic sentences
then contribute with supplementary directed edges be-
tween nodes in the ontology proper. As a main rule,

the sentences in the ontology are definitional, whereas
the given non-copula sentences are observational or
empirical or normative in nature.
As a hallmark of our approach, the natural logic
sentences are computationally reshaped (atomized)
into atomic natural logic sentences. This is accom-
plished by introduction of interior auxiliary concepts
formed by the system from the compound terms. For
instance, the term cell that produce insulin gives rise to
the atomic concept cell-that-produce-insulin, which is
defined by the two systems-generated atomic natural
logic sentences
cell-that-produce-insulin isa cell
cell-that-produce-insulin produce insulin
cell-that-produce-insulin
insulin
produce
cell
Figure 1: Graph representation of the term cell that produce
insulin.
with a contribution to the knowledge graph as illus-
trated in figure 1. Formally and internally the con-
cept cell-that-produce-insulin is primitive, just like cell
and insulin. Both of the two systems-generated sen-
tences are definitional and therefore form part of the
ontology proper. Logically, they are made to ensure
that if something is a cell and is simultaneously some-
thing that produce insulin then it is a cell-that-produce-
insulin.
In the process of computationally building the on-
tology from compound terms in sentences additional
nodes may be necessary. For instance, establishment
of cell-that-produce-insulin calls for introduction and
definition of the concept cell-that-produce-hormone,
given that insulin is a hormone. This may trigger a
cascading effect since hor mone is a substance and so
forth in the inclusion structure.Moreover, a subsump-
tion inference rule ensures that the inclusion cell-
that-produce-insulin isa cell-that-produce-hormone is
recorded, cf. figure 2. See also (Andreasen et al.,
2015).
cell-that-
produce-hormone
cellhormone
produce
cell-that-
produce-insulin
insulin
produce
Figure 2: Concept inferred by subsumption shown with
dashed lines.
Restrictions in concept terms may be nested as in
organ that contain cell that produce hormone under-
stood as organ (that contain cell (that produce hor-
mone)) or aligned as in cell in pancreas [and] that pro-
duce hormone understood as cell (in pancreas) (that
produce hor mone). Evidently, these concepts give
rise to a number of nodes in the generative ontology.
3.1 Passive Sentences
Passive sentences are highly frequent in scientific
texts because the agent, which is the subject of the
corresponding active sentence, is often left unspec-
ified. Our natural logic distinguishes two passive
forms: one in which the agent is absent as in insulin
is released [in body], and one in which the agent is
present as in insulin is-produced-by betacell, where is-
produced-by is understood as the inverse relation of
produce.
At first sight, a passive sentence such as insulin is
produced by betacells may seem to be merely a syn-
tactic variant of the corresponding active voice sen-
tence, in casu betacells produce insulin. However,
from a strictly formal logic point of view from [ev-
ery] betacell produce [some] insulin follows only logi-
cally the weaker [some] insulin is-produced-by [some]
betacell (assuming a non-empty class of betacell by
the principle of existential import) and not [every] in-
sulin is-produced-by [some] betacell, as explained in
(Nilsson, 2015). When arcs representing active tran-
sitive verbs (every-some) are traversed in the oppo-
site direction the corresponding passive interpretation
(some-some) is obtained and vice versa.
3.2 The Structure of the Knowledge
Base
The entire knowledge-base graph may be conceived
of as consisting of two interwoven parts: A genera-
tive skeleton ontology and a propositional knowledge
base. The generative ontology consists of copula sen-
tences with atomic concepts such as
betacell isa cell
insulin isa hormone
hormone isa protein
augmented with all the applied and derived compound
concept terms as explained above in section 3. The
propositional knowledge base is contributed by the
the non-copula natural logic sentences. This part of
the graph is made up of relations between two con-
cept nodes in the generative ontology as in
betacell produce insulin

4 FROM TEXT TO NATURAL
LOGIC
The natural logic graph is built from fragments of
natural language in domain texts by elaborating the
structure in these based on a grammar defining natu-
ral logic. Each domain text is added to the knowledge
base by processing the text sentence by sentence and
extracting relational triples corresponding to natural
logic propositions of the form Cterm R Cterm. These
propositions are then added to the knowledge graph
and thereby extend the knowledge base with the con-
tribution from the text sentence. The transformation
(and the mediating role of NATURALOG) can be il-
lustrated thus:
Sentence from the text
↓
NATURALOG proposition
↓
Edges (triples) in the knowledge graph
The language recognized for extraction of triples
from source texts is defined by the following basic
natural logic grammar:
Prop ::= Cterm R Cterm
Cterm ::= { NOUN | CompNoun} {RelClauseterm |
Prepterm} *
RelClauseterm ::= [that|which|who] R Cterm
R ::= VERB | R
Pas
| R
Adv
R
Pas
::= be VERBppp by
R
Adv
::= be VERBppp R
Prep
R
Prep
::= PREPOSITION
Prepterm ::= R
Prep
Cterm
CompNoun ::= { NOUN }
+
NOUN
By way of example, the sentence cells that produce
insulin are located in the pancreatic gland is recog-
nized by the grammar as cell that produce insulin is-
located-in pancreatic gland, where is-located-in is the
relational form R
Adv
in the grammar. The atomization
(see section 3) introduces the two atomic argument
terms: cell-that-produce-insulin and pancreatic-gland
and extracts an edge corresponding to the main propo-
sition:
cell-that-produce-insulin is-located-in
pancreatic-gland
as well as edges to express the meaning of the argu-
ment terms:
cell-that-produce-insulin isa cell
cell-that-produce-insulin produce insulin
The resulting subgraph, corresponding to the contri-
bution to the knowledge base by the example sen-
tence, is shown in figure 3.
Notice that the copula edges are black and un-
labelled (thus, with isa being implicit) and that edges
corresponding to non-copula relations are drawn in
cell-that-produce-insulin
insulin
produce
cell pancreatic-gland
located_in
gland
Figure 3: Contribution to the graph by the sentence cells
that produce insulin are located in the pancreatic gland.
grey. Furthermore, to distinguish definitional and ob-
servational contributions from the sentence, the defi-
nitional parts are indicated by joined edges – e.g. the
two outgoing edges with joined tails from the node
cell-that-produce-insulin in figure 3 identify the def-
initional part corresponding to the concept cell that
produce insulin.
As it also appears from figure 3, the compound
noun pancreatic gland is atomized into pancreatic-
gland and an inclusion edge indicating that this is a
specialization of the more general concept gland.
Thus, for a given input sentence, first of all, a
proposition of the form Cterm R Cterm is recognized
and extracted as an observational R-arc (located in-
arc in figure 3) to be included in the graph. In addi-
tion, the contributions from each of the subject and
object term arguments (left and right Cterms) are ex-
tracted by atomization (decomposition): an atom cor-
responding to the compound is introduced (e.g. cell-
that-produce-insulin in figure 3) and arcs are added to
define the corresponding concept (e.g. the connec-
tions to cell and insulin in figure 3). Notice that these
additional argument contributions will always be def-
initional and thus be included in the generative part of
the ontology.
The grammar accepts passive sentences, so that
sentences like glucose production is inhibited by con-
centrations of insulin will be recognized as shown in
figure 4. The active paraphrase of this sentence, con-
centrations of insulin inhibits glucose production, will
glucose_production
concentration-of-insulin
be_inhibit_by
production
insulin
of
concentration
Figure 4: Graph representation of glucose production is in-
hibited by concentrations of insulin.

concentration-of-insulin
glucose_production
inhibit
insulin
of
concentration
production
Figure 5: Graph representation of concentrations of insulin
inhibit glucose production.
be recognized as well, and the extracted graph for this
is shown in figure 5. Observe that the extracted edges
are the same for the two sentences, except for the two
propositional relation edges, inhibit and be-inhibit-by.
5 A PROTOTYPE DESIGN
The approach described here involves two main chal-
lenges that relate to the introduced formalism for nat-
ural logic knowledge bases. Firstly, how to build a
knowledge base on top of an initial skeleton genera-
tive ontology by processing source texts and adding
extracted content from these. Secondly, how to pro-
vide a query mechanism that makes it possible to ex-
plore and reason with the content in the base, i.e. with
the knowledge extracted from the source text corpus.
Prototypes for knowledge base building as well as
for querying are under development and these will be
briefly described below.
5.1 Building the Knowledge Base
As exemplified above, the parsing of input sentences
provides contributions to the generative as well as the
propositional part of the ontology. However, to make
it possible to take advantage of valuable ressources
covering the domain of the given text corpus, our
approach introduces the notion of a skeleton ontol-
ogy. A generative skeleton ontology is basically a
collection of copula sentences and thus comprises
a vocabulary of what can be considered as atomic
concepts partially ordered in a taxonomic structure
by the isa relation. In the experiments performed
with the present prototype, we draw on excerpts from
SNOMED (Spackman et al., 1997) to build the skele-
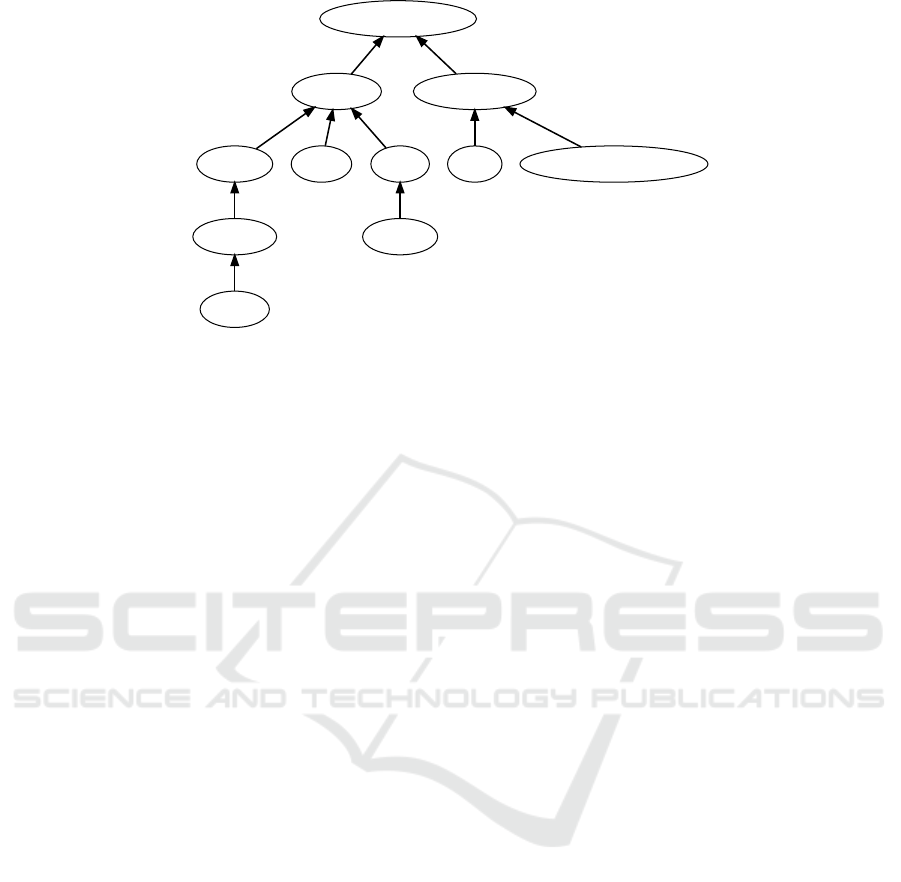
ton ontology. Figure 6 shows an example of an initial
skeleton ontology based on a miniature excerpt from
SNOMED .
The initial skeleton ontology is a graph represent-
ing a natural logic knowledge base, and adding (or
loading) a text into the knowledge base simply means
to extend it with triples extracted from the given text.
Obviously, not in all cases will the extraction reveal
the full meaning of the sentence, but even partial
records of content may be valuable contributions to
the knowledge base.
Furthermore, there may be “knowledge gaps” be-
tween the skeleton ontology and propositions ex-
tracted from texts. To fill these, we will rely on knowl-
edge added by domain experts. Such domain knowl-
edge could be added as taxonomic structures as in the
case of the skeleton ontology or as sentences express-
ing propositions as extracted from texts. As an ex-
ample, figure 7 shows the knowledge base after the
addition of a single piece of domain knowledge
Beta cells produce insulin
and the sentence
Glucose production by the liver is inhibited by
high concentrations of insulin in the blood
Triples are extracted by applying the principles
sketched in section 4 to every sentence in the input
text. More specifically, to extract triples from a sen-
tence, we devise a shallow analysis identifying con-
stituents in a first preprocessing phrase and then link
these into a sentence structure in a subsequent parsing
phase, as described below.
5.1.1 Preprocessing
In the preprocessing phase the words in the sen-
tence are marked up by word-category and lemma-
tized. The sentence is tokenised into a list of lists,
where each word from the sentence is represented
by a list of possible canonical lemma and word cat-
egory (part of speech) combinations. Marked cate-
gories are thus not completely disambiguated. Fur-
thermore, the preprocessing applies a domain specific
vocabulary to identify multiword expressions in the
input sentence and replaces these by unique symbols.
Thus, a preprocessing of the sentence Beta cells pro-
duce insulin returns the following tagged and lem-
matized word list, where the word sequence ’Beta
cells’ is replaced by a symbol: {{beta cell/NOUN},
{produce/NOUN,produce/VERB}, {insulin/NOUN}}.
5.1.2 Parsing
In the second phase, the marked up sentence is parsed
using the natural logic grammar presented in section
4, and triples are extracted. The parsing is devised as
a top down processing where we try to cover as much
as possible of the considered sentence in a (partial)
“best fit” process. As explained in section 4, the sen-
tence is recognized as a proposition centered around
insulin
hormone
enzyme blood
substance
SNOMED-concept
liver
body structure
glucose
sugar endocrine pancreas cell
Figure 6: Initial graph including a skeleton ontology based on a miniature excerpt from SNOMED .
the main verb and subject and object terms are atom-
ized leading to additional triples reflecting the content
in these.
The “best fit” approach is basically a guiding prin-
ciple aiming for the largest possible coverage of the
input text. Thus, if an expression that covers the full
input sentence can be derived, it would be considered
the “best”, and if not, the aim is a partial coverage
where larger means “better”. Hence, the parser should
be able to recognize an input proposition if one such
exists for at least one combination of possible lem-
mata of the input words. Therefore, in addition to pro-
cessing the grammar (given above), the parser must
ensure that all combinations are tried before failing
the recognition of a proposition.
5.2 Query Answering
In order to enable exploration and reasoning with
the content of the graph, and thereby the knowledge
extracted from the source text corpus, we devise a
query mechanism comprising two types of queries:
Affirmation Queries. The simplest form of queries
asks for an affirmation (or rejection) of a sentence by
appealing to one of the monotonicity inference rules.
The monotonicity rules are inheritance and property
generalization (Andreasen et al., 2015) admitting, re-
spectively, specialization of the linguistic subject term
and generalization of the linguistic object term. For
instance
betacell produce hormone
follows by object generalization from the pair of
recorded sentences betacell produce insulin and in-
sulin isa hormone.
Query sentences may further contain variables in
noun phrase positions as in the scheme
X produce insulin
and in
betacell produce Y
The answer to queries using variables will be bind-
ings to the specified variables. So, in the former case
we will get Cterms corresponding to all kinds of cells
known to produce insulin “looking downwards” in the
ontology. Conversely, a query may ask for the prop-
erties of a concept as in
betacell isa Z
“looking upwards” in the ontology in order to retrieve
stated definitional properties of a concept.
In addition to the more traditional deductive
querying principle above, we put forward a new
principle of querying by abstraction over relations.
Connection Abstraction Queries. The so-called
“connection” or chaining abstraction retrieves short-
est relational paths between two stated concepts from
the ontology. The relational paths are computed and
delivered as explanatory answers to the query.
A connection abstraction is requested by letting a
relation term appear as a variable as R in
betacell R insulin
Formally this becomes generalized to graph path find-
ing between stated concept terms by admitting that re-
lation variables R be instantiated to composed relation
terms. These terms represent (heuristically weighted)
shortest paths in the knowledge base graph as in a
hypothetical query liver R glucose, which calls for
traversal of a path to be given as answer to the in-
formal question “what is the connection between the
liver and glucose?”. One answer to this is exemplified
in figure 8.
Chaining abstraction is particularly relevant in the
bio-domain due to the interest in biochemical causa-
tion and conversion paths.

glucose_production-by-liver
high_concentration-of-insulin-in-blood
be_inhibit_by
liver
by
glucose_production
insulin-in-blood
of
high_concentration
blood
in
insulin
substance
hormone
body-structure
production
glucose
produce
sugar
beta_cell
produce
cell
enzyme
SNOMED-concept
Figure 7: Graph after the addition of (1) Beta cell produce insulin, (2) Glucose production by the liver is inhibited by high
concentrations of insulin in the blood and (3) Glucose production produce glucose.
glucose_production glucose
produce
glucose_production-by-liver liver
by
Figure 8: Connection between liver and glucose.
6 SUMMARY AND CONCLUSION
We have described the key principles of a prototype
system intended for deductive querying and pathway
finding in knowledge bases. The knowledge base lan-
guage is a form of natural logic. The prototype un-
der development performs a partial translation of nat-
ural language input texts into the natural logic. This
translation is limited by the semantic coverage of the
natural logic. The natural logic sentences are atom-
ized into an internal graph representation where the
nodes represent complex as well as atomic concepts.
This graph representation facilitates pathfinding be-
tween concepts. Assessment of the viability of this
natural logic approach calls for further development
of and experimentation with the prototype.
REFERENCES
Andreasen, T., Bulskov, H., Jensen, P. A., and Nilsson,
J. F. (2017a). Partiality, Underspecification, and Nat-
ural Language Processing, chapter A Natural Logic
for Natural-Language Knowledge Bases. Cambridge
Scholars.
Andreasen, T., Bulskov, H., Jensen, P. A., and Nilsson,
J. F. (2017b). Pathway Computation in Models De-

rived from Bio-Science Text Sources, pages 424–434.
Springer International Publishing, Cham.
Andreasen, T., Bulskov, H., Nilsson, J. F., and Jensen, P. A.
(2015). A system for conceptual pathway finding and
deductive querying. In Flexible Query Answering Sys-
tems 2015, pages 461–472. Springer.
Andreasen, T., Bulskov, H., Nilsson, J. F., and Jensen,
P. A. (2016). On the relationship between a compu-
tational natural logic and natural language. In van den
Herik; Joaquim Filipe, J., editor, the 8th International
Conference on Agents and Artificial Intelligence, vol-
ume 1.
Andreasen, T. and Nilsson, J. F. (2004). Grammatical spec-
ification of domain ontologies. Data Knowl. Eng.,
48(2):221–230.
Andreasen, T. and Nilsson, J. F. (2014). A case for em-
bedded natural logic for ontological knowledge bases.
In 6th International Conference on Knowledge Engi-
neering and Ontology Development.
Arp, R., Smith, B., and Spear, A. D. (2015). Building On-
tologies with Basic Formal Ontology. The MIT Press.
Baader, F. (2007). The description logic handbook: theory,
implementation, and applications. Cambridge Univer-
sity Press, Cambridge, 2nd ed edition.
de Azevedo, R. R., Freitas, F., Rocha, R., de Menezes, J.
A. A., and Pereira, L. F. A. (2014). Generating de-
scription logic ALC from text in natural language. In
Foundations of Intelligent Systems, pages 305–314.
Springer.
Kaewphan, S., Kreula, S., Van Landeghem, S., Van de Peer,
Y., Jones, P. R., and Ginter, F. (2012). Integrating
large-scale text mining and co-expression networks:
Targeting nadp(h) metabolism in e. coli with event
extraction. In Proceedings of the Third Workshop
on Building and Evaluating Resources for Biomedical
Text Mining (BioTxtM 2012), pages 8–15.
Li, C., Liakata, M., and Rebholz-Schuhmann, D. (2014).
Biological network extraction from scientific litera-
ture: state of the art and challenges. Briefings in Bioin-
formatics, 15(5):856–877.
MacCartney, B. and Manning, C. D. (2009). An extended
model of natural logic. In Proceedings of the eighth
international conference on computational semantics,
pages 140–156. Association for Computational Lin-
guistics.
Miwa, M., Ohta, T., Rak, R., Rowley, A., Kell, D. B.,
Pyysalo, S., and Ananiadou, S. (2013). A method for
integrating and ranking the evidence for biochemical
pathways by mining reactions from text. Bioinformat-
ics, 29(13):44–52.
Nilsson, J. F. (2015). In pursuit of natural logics for
ontology-structured knowledge bases. In The Sev-
enth International Conference on Advanced Cognitive
Technologies and Applications.
Smith, B., Ceusters, W., Klagges, B., K
¨
ohler, J., Kuma, A.,
Lomax, J., Mungall, C., Neuhaus, F., Rector, A., and
Rosse, C. (2005). Relations in biomedical ontologies.
Genome Biology, 6(5):R46.
Spackman, K. A., D, P., Campbell, K. E., D, P., Ct, R. A.,
and (hon, D. S. (1997). Snomed rt: A reference termi-
nology for health care. In J. of the American Medical
Informatics Association, pages 640–644.
van Benthem, J. (1986). Essays in Logical Semantics, Vol-
ume 29 of Studies in Linguistics and Philosophy. D.
Reidel, Dordrecht, Holland.
