Attractor Neural States: A Brain-Inspired Complementary Approach to

Reinforcement Learning

Oussama H. Hamid

and Jochen Braun

Department of Computer Science and Engineering, University of Kurdistan Hewl ˆer, Erbil, Kurdistan Region, Iraq

Department of Cognitive Biology, Otto-von-Guericke University, Magdeburg, Germany

Keywords:

Attractor Neural Networks, Model-Based and Model-Free Reinforcement Learning, Stability-Plasticity

Dilemma, Multiple Brain Systems, Temporal Statistics.

Abstract:

It is widely accepted that reinforcement learning (RL) mechanisms are optimal only if there is a predeﬁned

set of distinct states that are predictive of reward. This poses a cognitive challenge as to which events or

combinations of events could potentially predict reward in a non-stationary environment. In addition, the

computational discrepancy between two families of RL algorithms, model-free and model-based RL, creates

a stability-plasticity dilemma, which in the case of interactive and competitive multiple brain systems poses

a question of how to guide optimal decision-making control when there is competition between two systems

implementing different types of RL methods. We argue that both computational and cognitive challenges can

be met by infusing the RL framework as an algorithmic theory of human behavior with the strengths of the

attractor framework at the level of neural implementation. Our position is supported by the hypothesis that

‘attractor states’ which are stable patterns of self-sustained and reverberating brain activity, are a manifestation

of the collective dynamics of neuronal populations in the brain. Hence, when neuronal activity is described at

an appropriate level of abstraction, simulations of spiking neuronal populations capture the collective dynamics

of the network in response to recurrent interactions between these populations.

1 INTRODUCTION

In machine learning and other artiﬁcial intelligence

(AI) related disciplines, the theory of reinforcement

learning (RL) provides an algorithmic account for

gaining optimal action control in sequential decision-

making processes when only limited feedback is

available (Sutton and Barto, 1998; Daw et al., 2005;

Lewis and Vrabie, 2009; van Otterlo and Wiering,

2012; Krigolson et al., 2014; Marsland, 2015). In

the corresponding ﬁelds of cognitive science and psy-

chology, RL describes the practice by which animals

and humans probe reward contingencies while acting

in a novel environment (Schultz et al., 1997; Doya,

2007; Niv and Montague, 2008; Shteingart et al.,

2013).

Despite indisputable advances in RL research over

the past two decades, two challenges still remain: a

computational and a cognitive one (Gershman and

Daw, 2017). One accumulating evidence from cog-

nitive science and brain research suggests two quite

different conceptual frameworks for thinking about

learning (Gallistel and King, 2009). Though meth-

ods of both frameworks involve experience, they dif-

fer in the way and extent to which they impose com-

putational load so as to achieve a high level perfor-

mance (Dayan and Berridge, 2014). In the ﬁrst frame-

work, termed as model-free RL, learning is the abil-

ity of a plastic brain to modify itself (by experience)

in order to operate more efﬁciently in a novel envi-

ronment. Such a modiﬁcation affects both the struc-

ture and the function of the brain (Davidson and Be-

gley, 2012; Phelps et al., 2014). Synonym terms for

this type of RL approach are habitual learning, ret-

rospective revaluation, and reﬂexive decision-making

(Dolan and Dayan, 2013). The second framework,

called model-based RL, conceptualizes learning as

the process of deducing (also from experience) struc-

tural characteristics of the operating environment in

order to shape subsequent behavior (Hamid, 2015).

Informing behavior takes place in that the derived in-

formation is carried forward in memory (Gallistel and

King, 2009). Synonym terms for this type of RL ap-

proach are goal-directed behavior, prospective plan-

ning, and reﬂective decision-making (Friedel et al.,

2015). In the human brain, mechanisms of model-

H. Hamid O. and Braun J.

Attractor Neural States: A Brain-Inspired Complementary Approach to Reinforcement Learning.

DOI: 10.5220/0006580203850392

In Proceedings of the 9th International Joint Conference on Computational Intelligence (IJCCI 2017), pages 385-392

ISBN: 978-989-758-274-5

free RL were linked to corticostriatal circuits, in-

volving ventral striatum and regions of the amygdala

(Balleine et al., 2007), whereas the prefrontal cortex

was found to be the substrate for model-based RL

mechanisms (Mante et al., 2013). Though each of

the two frameworks was successfully tested in its own

domain, current research points out some of the chal-

lenging issues in rounding out the theory of RL as an

integrative account of human behavior.

Computational considerations, too, are the focus

of extensive comments on RL methods. Speciﬁcally,

comparing the apparently simplistic laboratory con-

ditions with the relatively more complex real-world

decision-making scenarios, as encountered by biolog-

ical agents in their natural environments, a number of

technical factors turn out to be exceptionally decisive

when considering the computational load that should

be imposed by any of the RL learning paradigms on

one side and the biological world on the other side

(Dayan and Berridge, 2014). While laboratory exper-

iments assume mainly low-dimensional, discrete, and

almost fully treatable state spaces, real-world situa-

tions have high-dimensional, continuous and partially

observable state spaces. This implies that the learning

algorithm has to struggle with minimal sets of data

and low frequency of probed situations, as it is almost

impossible for a real-world situation to be encoun-

tered twice with all its circumstantial characteristics

(Gershman and Daw, 2017). Moreover, the discrep-

ancy between the two frameworks of RL in the way

they perform computations creates a dilemma, the

stability-plasticity dilemma, when state-reward con-

tingencies are reversed (Mermillod et al., 2013). It

turns out, although context-speciﬁcity is beneﬁcial for

learning in novel stationary environments, it is detri-

mental for ﬂexibility in non-stationary environments.

These inspections point to a fundamental limitation of

the RL framework.

In the following, we shall be arguing that the

above limitations can, nevertheless, be resolved by in-

tegrating the ‘attractor’ framework as a complemen-

tary approach at the level of neural implementation to

the behavioral success of RL theory at the algorith-

mic level. Our position is supported by the hypothe-

sis that ‘attractor states’, which are stable patterns of

self-sustained and reverberating brain activity, are a

manifestation of the collective dynamics of neuronal

populations in the brain (Amit et al., 1994; Hopﬁeld,

1982). Hence, when neuronal activity is described

at an appropriate level of abstraction, simulations of

spiking neuronal populations capture the collective

dynamics of the network in response to recurrent in-

teractions between these populations (Braun and Mat-

tia, 2010). As an illuminating example for potency,

we shall consider the ﬁeld of associative learning.

The remainder of the paper is organized as fol-

lows. In Section 2 we introduce the theory of re-

inforcement learning including a formal description

of the underlying Markov decision processes and the

two major classes of RL algorithms. Section 3 points

out to current challenges in linking human behavior

to existing RL algorithms. Section 4 discusses how

models in the attractor framework could complement

the RL framework, accounting for the current cogni-

tive challenges. We ﬁnally conclude and portray our

plans for future work in Section 5.

2 RL: THEORY & FORMALISM

Historically, RL has its origin in mathematical psy-

chology and operations research (Dayan and Niv,

2008). Inspired by the psychological literature on

Pavlovian (classical) and instrumental conditioning,

Richard Sutton developed, together with Andrew

Barto, algorithms for agent-based learning that later

on became the core ideas for the theory of RL (Sut-

ton and Barto, 1998). Parallel to their research, yet

in a separate line, Dimitri Bertsekas and John Tsit-

siklis, two electrical engineers working in the ﬁeld of

operations research, developed stochastic approxima-

tions to dynamic programming that allow a system

to learn about its behavior through simulation (ex-

perience) and improve its performance through iter-

ative reinforcement (Bertsekas and Tsitsiklis, 1996).

These lines of research marked the emergence of RL

as an algorithmic theory for optimal decision making

on the basis of behavior and subsequent effects (Niv

and Montague, 2008).

2.1 RL and Markov Decision Processes

In a typical RL setting, a goal-directed agent (this

could be a natural or an artiﬁcial system) interacts

with an environment via embedded sets of sensors and

actuators. The sensors provide the agent with infor-

mation about the state of the environment, whereas

the actuators enable the agent to act upon the environ-

ment, causing its current state to change. As a con-

sequence, the agent receives reinforcement in terms

of a numerical signal that describes how close (or far)

it moved to (or away from) its predeﬁned goal (Sut-

ton and Barto, 1998; van der Ree and Wiering, 2013;

Castro-Gonz

alez et al., 2014). As the agent moves

along the several states of the environment, the cor-

responding sequence of action-reward combinations

moves on, too.

Decisions in RL can be modeled as a Markov deci-

sion process (MDP). When the state of the operating

environment, however, is subject to inherent uncer-

tainty, modeling takes the form of a partially observ-

able Markov decision process (POMDP) (Kaelbling

et al., 1996; Sutton and Barto, 1998). Formally, an

MDP process consists of two functions, R and T, de-

ﬁned over two sets, S and A . The functions represent

the resulting rewards and state transitions, whereas

the two sets describe the available states and effective

actions, respectively.

In an MDP process, the environment evolves

stochastically under simple discrete temporal dynam-

ics. At time t, the environment is in state s

= s. The

agent chooses some action a

∈ A, expecting to reap a

certain reward ˆr (expected outcome). Nevertheless, it

experiences the actual consequence of its choice (ei-

ther immediately or later on) in terms of a numerical

reinforcement r ∈ R (actual outcome). Subsequently,

the state of the environment changes its instance into

t+1

= s

at the next time step t + 1. Moreover, the

agent updates its knowledge about reward contingen-

cies within the operating environment as a reﬂection

on its very experience. To denote the probability

P(s

t+1

= s

= s, a

= a) of moving from state s into

when taking action a, we write T(s, a, s

). Analo-

gously, the notion R(s, a, r) refers to the probability

P(r

= r|s

= s, a

= a) of receiving a reward at state

when taking action a. Note that formalizing the re-

ward and transition functions in terms of the current

state rather than the entire history of the environment,

a characteristic referred to as Markov property, pro-

vides a computational advantage, for it requires the

learning algorithm to remember and work with the

parameters that are related only to the current state.

This is deﬁnitely easier than dealing with all previous

states of the environment (Maia, 2009; Hamid, 2014).

2.2 Model-Free and Model-Based RL

Based on the way they optimize their learning

and decision-making processes, RL methods can be

sorted into two main classes: model-free and model-

based methods (Dayan and Berridge, 2014).

Though both use experience, model-free RL al-

gorithms assume no a priori knowledge of the MDP

but learn a state-action value function, known as the

‘value function’ (Dayan, 2008). One of the success-

ful implementations of model-free RL methods is the

well-known temporal difference (TD) learning algo-

rithm. It utilizes a reward-prediction error, which is

the discrepancy between the actual and expected re-

wards, to ‘cache’ actually observed information about

the long-term rewarding potencies of the probed ac-

tions. This approach represents a computationally

simple way to exploit experience, for the model needs

only to learn one or two simple quantities (state/action

values). However, it is statistically less efﬁcient, be-

cause the cached information is stored as a scalar

quantity without connecting outcomes to their direct

causes in a distinguishable manner (Dayan and Niv,

2008). Consequently, the model’s performance is

most likely to suffer from two shortcomings. First,

the model cannot (later on) extricate insights about

rewards or transitions from the cached value. Sec-

ond, the cached information intermixes previous es-

timates or beliefs about state values regardless their

sometimes erroneous valence. As a result, model-free

RL methods lack an appropriately quick adaptation

to sudden changes in reward contingencies (Hamid,

2015). Because of this characteristic, model-free RL

was proposed as the underlying model for habitual

controllers, in which actions are presumably based

on habits (Daw et al., 2005). This key characteris-

tic links model-free RL to corticostriatal circuits in-

volving, in particular, the ventral striatum and regions

of the amygdala in the human’s brain (Packard and

Knowlton, 2002; Balleine et al., 2007; Dayan and

Balleine, 2002).

Model-based RL is a family of algorithms that

generate goal-directed choices by utilizing an explicit

model of the underlying MDP process. This sums

up representations of the environment, expectations,

and prospective calculations to make cognitive pre-

dictions of future values (Daw et al., 2005; Dayan and

Berridge, 2014). Speciﬁcally, model-based RL algo-

rithms capture the dynamics of the MDP in terms of

state transition probabilities. Such probabilities can

be presented as a tree connecting short-term predic-

tions about immediate outcomes of each action in an

arbitrary sequence of actions. Deciding which ac-

tion is more beneﬁcial can then be done by exploring

branching sets of possible future situations. There are

several ‘tree search’ techniques that can do this (Daw

et al., 2005). It turns out that exploiting experience

in the case of model-based RL is more efﬁcient than

in model-free RL for two reasons. First, it provides

more statistical reliability, especially when storing the

sometimes unrelated morsels of information. Second,

and importantly, it ensures more ﬂexibility in terms

of adaptive planning, which becomes necessary when

changes occur in the learning environment. Hence,

model-based RL accounts best for goal-directed be-

havior that contains more cognitive planning. This

key characteristic links model-based RL to the pre-

frontal cortex in the primate’s brain (Owen, 1997).

3 COGNITIVE CHALLENGES

Besides the above mentioned computational consider-

ations, RL faces cognitive challenges as well. On one

hand, the theory could successfully explain several

characteristics of human and animal learning, e.g.,

blocking (Kamin, 1969), overshadowing (Reynolds,

1961), and inhibitory conditioning (Rescorla and

Lolordo, 1968). It also proved able to predict new

phenomena such as over-expectation (Kremer, 1978)

and managed to account for the relatively touchy ‘sec-

ondary conditioning’: a phenomenon in which a pre-

dictor of a predictor servers as a predictor (Dayan and

Abbott, 2005). However, it still suffers from difﬁcul-

ties in accounting for some human instrumental learn-

ing behaviors. For example, analysis of the stock mar-

ket suggests that a positively surprising obtained pay-

off and a negatively surprising forgone payoffs trigger

a reversal of choice behavior rather than repeating that

behavior according to the recency assumption (Nevo

and Erev, 2012).

Furthermore, consistent with the idea of inter-

active and competitive multiple memory systems in

the brain (Poldrack and Packard, 2003), recent re-

search addressed the question of how to guide opti-

mal decision-making control in the face of a running

competition between two systems, each of which im-

plements a different type of RL methods (Dolan and

Dayan, 2013).

Another challenge concerns the architecture of the

theory itself. Speciﬁcally, it has been argued that

RL mechanisms are optimal only if there is a pre-

deﬁned set of distinct states that are predictive of re-

ward (Doya, 2007). This implies, for an agent be-

having in an RL fashion to achieve successfully opti-

mal action control, it is necessary to deﬁne the states

such that they contain all reward-relevant information,

even if task-irrelevant (Hamid, 2015). But the ques-

tion becomes: how do such states emerge in the brain

or more generally within the decision-making com-

ponent of the agent in the ﬁrst place (Rigotti et al.,

2010)?

In a recent study of conditional associative learn-

ing, the authors accounted for the effect of temporal

order on accelerating the learning of arbitrary asso-

ciations by devising a model-free RL rule that sets

a probabilistic response choice, reﬂecting reward ex-

pectations that have been accumulated in the form of

‘action values’ (Hamid et al., 2010). The reinforce-

ment rule modiﬁes these ‘action values’ in propor-

tion to the reward-prediction error that corresponds

to the chosen response. The key feature of the de-

vised model is that ‘action values’ are expanded in

time: some attach to the object of the current trial and

others attach to objects of preceding trials. This pro-

vides them with a cumulative effect in the sense that

the more ‘action values’ favor a particular response,

the more likely this response is chosen. Accordingly,

when successive objects appear in a consistent order,

more than one ‘action value’ will favor the correct

response, which will therefore be chosen more fre-

quently.

Though the model could account qualitatively and

quantitatively to the behavioral observations, it failed

to account for the same associative task in a rever-

sal learning paradigm (Hamid and Braun, 2010). The

main goal of the reversal paradigm was to test the

model’s key assumption, i.e., the reinforcement of

pairings between past stimuli and present response.

Speciﬁcally, let S

t−2

and S

t−1

be the visual stimuli

presented at trials t − 2 and t − 1 in ﬁgure 1, respec-

tively. S

is the target stimulus at trial t with motor

response R

. A: learned response R

for the target

stimulus is replaced by response R

in the second run

of the object sequence (‘action reversal’). Before re-

versal, the model reinforces, in addition to the paring

→ R

), the pairings (S

t−1

→ R

) and (S

t−2

→ R

After reversal, however, these pairings become in-

valid, as the model has to learn the new response R

Hence, the model’s performance is expected to fall

to chance level. B: target stimulus S

is replaced by

stimulus S

, which has the same response as that of

. Before reversal, the model reinforces the pairings

→ R

), (S

t−1

→ R

), and (S

t−2

→ R

). These pair-

ings remain valid after reversal. Hence, predicted per-

formance remains above chance level.

The cognitive experiment was conducted using

mixed sequences of visual objects as presented in

ﬁgure1 with type A, B, and C objects similar to exper-

iment 2 in (Hamid et al., 2010). Speciﬁcally, Thirty

two fractal objects were used to create sequences of

72 trials. Eight of these objects were recurring. Four

of the recurring objects formed two consistent pairs

(5, 6) and (7, 8), each of which appeared six times

in the sequence. The ‘predecessor’ objects (5 and 7)

were termed type A and the ‘successor’ objects (6 and

8) type B. Four additional recurring objects were used

to form twelve random pairs (1, 2), (1, 3), (1, 4) . . .,

(4, 1), (4, 2), (4, 3), each appearing once per sequence

(type C). Random pairs and consistent pairs were al-

ternated and separated by 24 one-time objects to form

sequences of 72 trials. Human subjects learned by

trial and error to associate each visual object with one

of four possible motor responses: up, down, left, or

right. Each of the 72 trials long temporal sequences

was presented twice without interruption making up

new sequences of 144 trials long. In the ‘action rever-

sal’ condition, target objects were associated with a

time

tt-1t-2 tt-1t-2

time

tt-1t-2 tt-1t-2

Action reversal

Object reversal

Figure 1: Predictions for ‘action’ and ‘object’ reversals as suggested by the devised model in (Hamid et al., 2010) (schematic).

The upper row shows the effect of action reversal, whereas the lower row demonstrates that of object reversal. The left column

represents reinforcement before reversal, whereas the right column illustrates decision-making after reversal.

new motor response in the second half of the tempo-

ral sequence. In the ‘object reversal’ condition, target

objects were replaced by other objects in the second

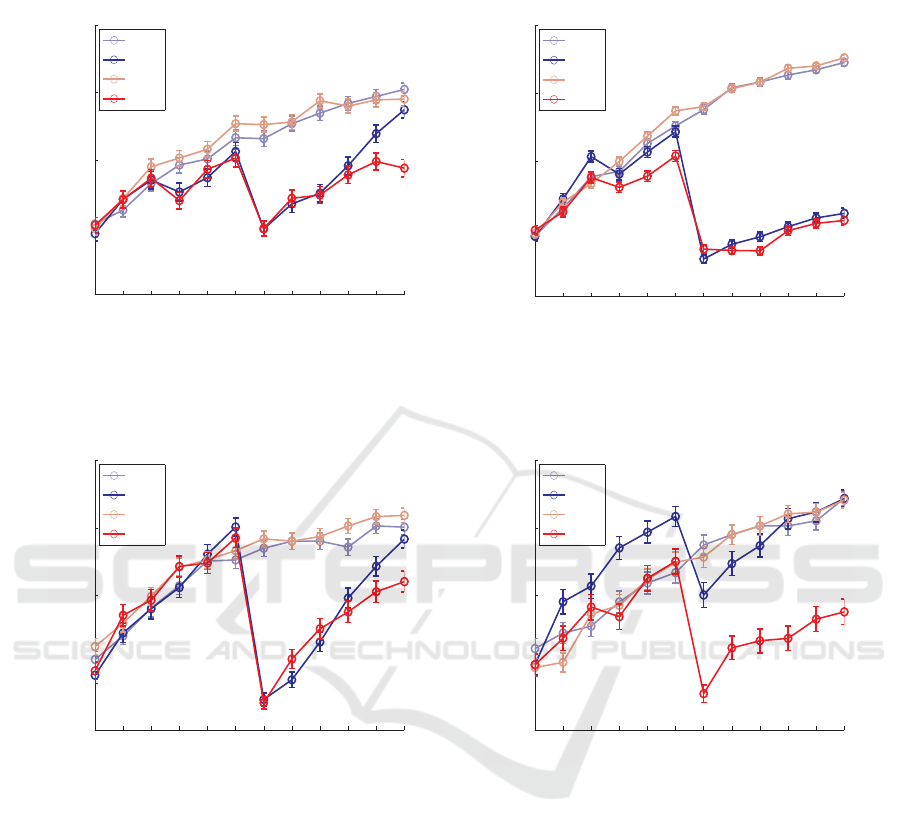
half of the temporal sequence. Figure 2 illustrates be-

havioral and modeling results of the cognitive exper-

iment. We can brieﬂy summarize the results as fol-

lows. First, contrary to the predictions of our rein-

forcement model (Hamid et al., 2010), any type of re-

versal reduced performance to chance level. Second,

the rate of recovery seemed to differ between reversal

types, appearing to be faster for an ‘object reversal’

than for an ‘action reversal’.

4 MODELS IN THE ATTRACTOR

FRAMEWORK

It is widely accepted that reinforcement mechanisms

are optimal only if there is a predeﬁned set of distinct

states that are predictive of reward (Sutton and Barto,

1998; Daw et al., 2005; Doya, 2007; Niv and Mon-

tague, 2008; Dayan and Niv, 2008). Thus, reinforce-

ment models beg the question as to which events or

combinations of events could potentially predict re-

ward in a non-stationary environment. This brings us

to the crucial question of how our brain selects and

creates neural representations for potentially reward-

predicting events. An interesting approach to this

question is the attractor framework, which postulates

that the formation of such representations is based

on temporal statistics of the environment. The key

idea is that mental representations are realized by sta-

ble patterns of reverberating activity, which are stable

steady-states (‘attractors’) in the neural dynamics of

the network (Hopﬁeld, 1982; Amit et al., 1997; Fusi

et al., 2005).

The central tenets of attractor theory are that (i)

the network is plastic, that is, connection strengths de-

velop in an activity-driven, Hebbian manner and that

(ii) associations (e.g., stimulus-response pairings) are

maintained as self-sustained, persistent patterns of ac-

tivity that represent attractors of the neural dynamics.

These tenets predict the formation of associative links

whenever a set of events occurs repeatedly in a con-

sistent temporal order (Griniasty et al., 1993; Amit,

1995; Brunel, 1996).

A recent study of behavioral ﬂexibility in reversal

situations exempliﬁes the attractor framework (Rig-

otti et al., 2010). The authors of this study postulate

1 2 3 4 5 6 7 8 9 10 11 12

0.25

0.5

0.75

Performance correct

B rev

C rev

1 2 3 4 5 6 7 8 9 10 11 12

0.25

0.5

0.75

B rev

C rev

Object reversal (behavioral results)

1 2 3 4 5 6 7 8 9 10 11 12

0.25

0.5

0.75

Appearance number

Performance correct

B rev

C rev

1 2 3 4 5 6 7 8 9 10 11 12

0.25

0.5

0.75

Appearance number

B rev

C rev

Action reversal (behavioral results) Action reversal (modeling results)

Object reversal (modeling results)

Figure 2: Behavioral and modeling results for ‘action’ and ‘object’ reversals.

two neural circuits, one for learning reward-relevant

conditional associations (‘associative network’) and

another for observing temporal contingencies (‘con-

text network’). The interaction between these two

networks leads to the formation of distinct neural

representations for different contexts. More speciﬁ-

cally, the associative network comprises two popula-

tions of excitatory neurons, which represent alterna-

tive stimulus-response associations. One population

represents the stimulus-response associations appro-

priate for one context, whereas the other population

codes the appropriate associations for another con-

text. The two excitatory populations compete through

a third, inhibitory population. As long as the reward

predictions of one population are fulﬁlled, the cur-

rently dominant population will continue to suppress

the other population, and new stimuli will be evalu-

ated in the light of the experience encoded in the dom-

inant population. However, when predicted rewards

fail to materialize, the other population may gain as-

cendancy and behavior may now be governed by the

experience accumulated in another, alternative con-

text.

So how can a representation of context be formed,

which can link all the stimulus-response associa-

tions that are rewarded in a particular context? The

key idea is that different stimulus-response associa-

tions become linked on the basis of temporal statis-

tics. Speciﬁcally, as long as one context holds for

much longer than one trial, stimulus-response asso-

ciations within this context follow each other more

frequently than stimulus-response associations in dif-

ferent contexts. This correlational difference can

be translated by Hebbian mechanisms into selective

meta-associations among the stimulus-response asso-

ciations of a given context. Mechanistically, the for-

mation of these meta-associations relies on the tem-

poral overlap between the representation of a current

stimulus-response association and lingering represen-

tations of stimulus-response associations in the recent

past. Further details can be found in (Rigotti et al.,

2010).

5 CONCLUSIONS

Although most attempts to test the attractor frame-

work experimentally have used single-unit recordings

in behaving, non-human primates, we believe that this

framework makes some predictions even at the behav-

ioral level. For example, the neurophysiological ﬁnd-

ings of (Miyashita, 1988) and (Yakovlev et al., 1998)

imply that reverberative delay activity exists only af-

ter an attractor representation has formed. In the con-

text of (Hamid et al., 2010), this suggests that linger-

ing representations of past events are available only

after these past events have become familiar. On this

basis, we would expect that the presence of consis-

tent predecessor objects becomes inﬂuential only af-

ter these objects have become familiar and are recog-

nized. Accordingly, it would be an interesting exten-

sion of the present study to examine whether the fa-

cilitative effect of temporal context is conditional on

correct performance with regard to predecessor ob-

jects.

ACKNOWLEDGEMENTS

We would like to thank the anonymous reviewers for

their helpful comments.

REFERENCES

Amit, D. J. (1995). The Hebbian paradigm reintegrated:

local reverberations as internal representations. Behav.

Brain Sci., 18:617–626.

Amit, D. J., Brunel, N., and Tsodyks, M. V. (1994). Correla-

tions of cortical hebbian reverberations: theory versus

experiment. J. Neurosci., 14:6435–6445.

Amit, D. J., Fusi, S., and Yakovlev, V. (1997). Paradigmatic

working memory (attractor) cell in it cortex. Neural

Comput., 9:1071–1092.

Balleine, B. W., Delgado, M. R., and Hikosaka, O. (2007).

The role of the dorsal striatum in reward and decision-

making. J. Neurosci., 27(31):8161–8165.

Bertsekas, D. P. and Tsitsiklis, J. N. (1996). Neuro-Dynamic

Programming. Athena Scientiﬁc.

Braun, J. and Mattia, M. (2010). Attractors and noise: Twin

drivers of decisions and multistability. NeuroImage,

52(3):740 – 751. Computational Models of the Brain.

Brunel, N. (1996). Hebbian learning of context in recurrent

neural networks. Neural Comput., 8:1677–1710.

Castro-Gonz

alez,

A., Malfaz, M., Gorostiza, J. F., and

Salichs, M. A. (2014). Learning behaviors by an au-

tonomous social robot with motivations. Cybernetics

and Systems, 45(7):568–598.

Davidson, R. J. and Begley, S. (2012). The emotional life of

your brain: How its unique patterns affect the way you

think, feel, and live–and how you can change them.

Hudson Street Press, Penguin Group.

Daw, N., Niv, Y., and Dayan, P. (2005). Uncertainty-based

competition between prefrontal and dorsolateral stri-

atal systems for behavioral control. Nat Neurosci,

8(12):1704–1711.

Dayan, P. (2008). The role of value systems in decision

making. In Engel, C. and Singer, W., editors, Better

than Conscious? Decision Making, the Human Mind,

and Implications for Institutions, pages 50–71. The

MIT Press, Frankfurt, Germany.

Dayan, P. and Abbott, L. F. (2005). Theoretical Neuro-

science: Computational and Mathematical Modeling

of Neural Systems. The MIT Press.

Dayan, P. and Balleine, B. W. (2002). Reward, motivation,

and reinforcement learning. Neuron, 36(2):285–298.

Dayan, P. and Berridge, K. C. (2014). Model-based and

model-free pavlovian reward learning: revaluation, re-

vision, and revelation. Cognitive, Affective, & Behav-

ioral Neuroscience, 14(2):473–492.

Dayan, P. and Niv, Y. (2008). Reinforcement learning: the

good, the bad and the ugly. Curr. Opin. Neurobiol.,

18:185–196.

Dolan, R. J. and Dayan, P. (2013). Goals and habits in the

brain. Neuron, 80(2):312–325.

Doya, K. (2007). Reinforcement learning: Computational

theory and biological mechanisms. HFSP journal,

1(1):30–40.

Friedel, E., Koch, S. P., Wendt, J., Heinz, A., Deserno, L.,

and Schlagenhauf, F. (2015). Devaluation and sequen-

tial decisions: linking goal-directed and model-based

behavior. Habits: plasticity, learning and freedom.

Fusi, S., Drew, P. J., and Abbott, L. F. (2005). Cascade mod-

els of synaptically stored memories. Neuron, 45:599–

611.

Gallistel, C. R. and King, A. P. (2009). Memory and the

Computational Brain. Wiley-Blackwell, West Sussex,

United Kingdom, ﬁrst edition.

Gershman, S. J. and Daw, N. D. (2017). Reinforcement

learning and episodic memory in humans and animals:

An integrative framework. Annual review of psychol-

ogy, 68:101–128.

Griniasty, M., Tsodyks, M. V., and Amit, D. J. (1993). Con-

version of temporal correlations between stimuli to

spatial correlations between attractors. Neural Com-

put., 5:1–17.

Hamid, O. H. (2014). The role of temporal statistics in

the transfer of experience in context-dependent rein-

forcement learning. In 14th International Conference

on Hybrid Intelligent Systems (HIS), pages 123–128.

IEEE.

Hamid, O. H. (2015). A model-based Markovian context-

dependent reinforcement learning approach for neu-

robiologically plausible transfer of experience. In-

ternational Journal of Hybrid Intelligent Systems,

12(2):119–129.

Hamid, O. H. and Braun, J. (2010). Relative importance of

sensory and motor events in reinforcement learning.

Perception ECVP abstract, 39:48–48.

Hamid, O. H., Wendemuth, A., and Braun, J. (2010).

Temporal context and conditional associative learn-

ing. BMC Neuroscience, 11(45):1–16.

Hopﬁeld, J. J. (1982). Neural networks and physical sys-

tems with emergent collective computational abili-

ties. Proceedings of the national academy of sciences,

79(8):2554–2558.

Kaelbling, L. P., Littman, M. L., and Moore, A. W. (1996).

Reinforcement learning: A survey. Journal of Artiﬁ-

cial Intelligence Research, 4:237–285.

Kamin, L. J. (1969). Predictability, surprise, attention,

and conditioning. In Campbell, B. A. and Church,

R. M., editors, Punishment and Aversive Behavior,

pages 242–259. Appleton-Century-Crofts, New York.

Kremer, E. F. (1978). The Rescorla-Wagner model: losses

in associative strength in compound conditioned stim-

uli. J. Exp. Psychol. Animal Behav. Proc., 4:22–36.

Krigolson, O. E., Hassall, C. D., and Handy, T. C. (2014).

How we learn to make decisions: Rapid propagation

of reinforcement learning prediction errors in humans.

J. Cognitive Neuroscience, 26(3):635–644.

Lewis, F. L. and Vrabie, D. (2009). Reinforcement learning

and adaptive dynamic programming for feedback con-

trol. IEEE Circuits and Systems Magazine, 9(3):32–

50.

Maia, T. V. (2009). Reinforcement learning, conditioning,

and the brain: Successes and challenges. Cogn. Affect.

Behav. Neurosci., 9:343–64.

Mante, V., Sussillo, D., Shenoy, K. V., and Newsome, W. T.

(2013). Context-dependent computation by recurrent

dynamics in prefrontal cortex. Nature, 503(7474):78–

84.

Marsland, S. (2015). Machine learning: an algorithmic

perspective. Chapman & Hall / CRC press.

Mermillod, M., Bugaiska, A., and Bonin, P. (2013). The

stability-plasticity dilemma: Investigating the contin-

uum from catastrophic forgetting to age-limited learn-

ing effects. Frontiers in psychology, 4.

Miyashita, Y. (1988). Neuronal correlate of visual associa-

tive long-term memory in the primate temporal cortex.

Nature, 335:817–820.

Nevo, I. and Erev, I. (2012). On surprise, change, and the

effect of recent outcomes. Frontiers in psychology, 3.

Niv, Y. and Montague, P. R. (2008). Theoretical and empir-

ical studies of learning. In Glimcher, P. W., Camerer,

C., Fehr, E., and Poldrack, R., editors, Neuroeco-

nomics: Decision Making and The Brain, pages 329–

349. NY: Academic Press, New York.

Owen, A. M. (1997). Cognitive planning in humans: neu-

ropsychological, neuroanatomical and neuropharma-

cological perspectives. Prog. Neurobiol., 53(4):431–

450.

Packard, M. G. and Knowlton, B. (2002). Learning and

memory functions of the basal ganglia. Ann. Rev. Neu-

rosci., 25:563–593.

Phelps, E. A., Lempert, K. M., and Sokol-Hessner, P.

(2014). Emotion and decision making: multiple mod-

ulatory neural circuits. Annual Review of Neuro-

science, 37:263–287.

Poldrack, R. A. and Packard, M. G. (2003). Competi-

tion among multiple memory systems: converging ev-

idence from animal and human brain studies. Neu-

ropsychologia, 41(3):245–251.

Rescorla, R. A. and Lolordo, V. M. (1968). Inhibition

of avoidance behavior. J. Comp. Physiol. Psychol.,

59:406–412.

Reynolds, G. S. (1961). Attention in the pigeon. J. Exp.

Anal. Behav., 4:203–208.

Rigotti, M., Rubin, D. B. D., Morrison, S. E., Salzman,

C. D., and Fusi, S. (2010). Attractor concretion as

a mechanism for the formation of context representa-

tions. Neuroimage, 52(3):833–847.

Schultz, W., Dayan, P., and Montague, P. R. (1997). A

neural substrate of prediction and reward. Science,

275(5306):1593–1599.

Shteingart, H., Neiman, T., and Loewenstein, Y. (2013).

The role of ﬁrst impression in operant learn-

ing. Journal of Experimental Psychology: General,

142(2):476.

Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-

ing: An Introduction. The MIT Press, Cambridge,

Massachusetts.

van der Ree, M. and Wiering, M. (2013). Reinforcement

learning in the game of othello: Learning against

a ﬁxed opponent and learning from self-play. In

Adaptive Dynamic Programming And Reinforcement

Learning (ADPRL), 2013 IEEE Symposium on, pages

108–115. IEEE.

van Otterlo, M. and Wiering, M. (2012). Reinforcement

learning and markov decision processes. In Wiering,

M. and van Otterlo, M., editors, Reinforcement Learn-

ing: State of the Art, pages 3–42. Springer, Berlin,

Heidelberg.

Yakovlev, V., Fusi, S., Berman, E., and Zohary, E. (1998).

Inter-trial neuronal activity in inferior temporal cor-

tex: a putative vehicle to generate long-term visual

associations. Nat. Neurosci., 1:310–317.