Measuring the Complexity of User Processes using Shannon Entropy

and Stochastic Petri Nets

Martin Ibl and Žaneta Boruchová

Institute of System Engineering and Informatics, Faculty of Economics and Administration,

University of Pardubice, Pardubice, Czech Republic

Keywords: User-Friendliness, Petri Nets, Entropy, Complexity, Measure, Process.

Abstract: Measuring complexity of processes or systems is currently a very popular topic. There is a wide range of

defined complexity measures that quantify features such as legibility, modifiability, uncertainty,

comprehensibility, easiness of implementation, user-friendliness and many others. The content of this work

is a presentation of a method for quantification of complexity using Shannon entropy and stochastic Petri

nets. Shannon entropy and Petri nets are an appropriate combination because they allow analysing the

complexity of processes not only in terms of their structure but also in terms of their dynamic development

under tension. On a simple example are outlined possible analyses and the correlation analysis examines the

comparability with other selected complexity measures.

1 INTRODUCTION

Growth in the complexity of Information and

Communication Technologies (ICTs) is one of the

greatest challenges today. Today, ICT is not only an

integral part of all major corporations and

institutions but also influences the everyday life of

modern people in many ways.

In the area of IT management, complicated systems

bring on the advantage of being able to support all

process variants, and to meet the demanding

requirements of customers or users while giving the

company a competitive edge on the market. On the

other hand, it is penalised by higher acquisition costs,

higher maintenance expenses, changes and interfaces

with other systems. Therefore, it is important that the

information system is sophisticated (complex) enough

that it can efficiently cover the maximum of

enterprise requirements, but at the same time, it must

not contain complexity beyond these requirements.

Problems associated with quantification of complex

variables (e.g., user-friendliness, comprehensibility,

etc.) are mostly solved through a certain form of a

statistical survey among users. However, this

solution is time and cost consuming, and in many

cases, it is based on a subjective assessment of a

representative sample of the population. This paper

aims to specify a method for quantifying the

complexity of process models, i.e., the processes

themselves. The degree of complexity is, in a

number of cases, defined to assess the quality of user

interactions with the system/process that reflect

features such as clarity, usability, user friendliness,

predictability, uncertainty, modifiability, etc. The

suitability of using complexity measures to assess

user-friendliness confirms methods that allow their

theoretical validation (Weyuker, 1988).

Ergonomics and the structure of the user interface

play a significant role in the efficiency of work. The

system builder usually does not give the user-

friendliness enough weight. For example, if a user

needs 6 mouse clicks instead of two to perform a

certain activity, his productivity will deteriorate

significantly in the long run. In the case of scarcely

used applications, this does not usually play a role,

but if it is an application that for example ten people

in an enterprise work with eight hours a day, it

means tripling their work. Effects on efficiency are

obvious. It is, therefore, necessary to manage the

complexity of information systems, as otherwise

costs and risks increase and the efficiency is

reduced. Complexity in information systems is

difficult to reduce. Therefore, the main objective is

not to allow a process/system to increase its optimal

complexity, both during design and development of

the information system and during its operation and

maintenance. The optimal complexity of the

Ibl M. and BoruchovÃ ˛a Å¡.

Measuring the Complexity of User Processes using Shannon Entropy and Stochastic Petri Nets.

DOI: 10.5220/0006584502120217

In Proceedings of the International Conference on Computer-Human Interaction Research and Applications (CHIRA 2017), pages 212-217

ISBN: 978-989-758-267-7

information system is the lowest possible complexity.

Complexity can be also analysed, for example, within

system integration (Jirava and Toseafa, 2016) or

social network analysis (Panus, 2016).

2 MEASURES OF COMPLEXITY

Analysing complexity at all stages of process

lifecycle development helps to avoid the

disadvantages associated with high complexity.

Currently, organizations have not accepted

complexity metrics as part of their process

management projects. As a result, simple processes

can be designed unnecessarily complex. Using

Complexity analysis helps design and implement

processes and workflows that are more simple,

reliable, and robust. In-depth analysis is needed to

correct defects in high complexity process parts.

Three questions are often asked when measuring the

complexity of a process (Lloyd, 2001):

How difficult is the process to describe?

How difficult is the process to create?

What is the level of organization?

According to (Lloyd, 2001), complexity

measurements can be grouped into the following

categories depending on which question they are

dealing with:

Difficulty of description, typically measured in

bits, including Information and Entropy

(Shannon, 1948), Algorithmic Information

Content (Zurek, 1990), Minimum Description

Length (Rissanen, 1978), Fisher information

(Lehmann and Casella, 2006), Renyi entropy

(Renyi, 1960), Code Length (Huffman, 1952),

Chernoff information (Chernoff, 1972, Nielsen,

2011), Lempel-Ziv complexity (Lempel and

Ziv, 1976), Dimension and Fractal Dimension

(Mandelbrot and Hudson, 2004);

Difficulty of creation, working with time,

currency, or energy, such as Computational

Complexity (Arora and Barak, 2009), Time

Computational Complexity, Spatial

Computational Complexity, Information-based

Complexity (Traub et al., 1988), Logical Depth

(Bennett, 1995), Thermodynamic Depth (Lloyd

and Pagels, 1988), Cost and Crypticity

(Mahoney et al., 2011);

The degree of organization that can be divided

into the difficulty of describing the

organizational structure and the amount of

information divided into the parts of the system.

This category includes, for example, Metric

Entropy (Lorentz, 1966), Stochastic Complexity

(Rissanen, 1996), Sophistication (Mota et al.,

2013), Effective Complexity (GellMann and

Lloyd, 1996), True Complexity, Ideal

Complexity, Hierarchical Complexity

(Commons et al., 1998), Schema length,

Grammar complexity, Mutual Information

(Shannon, 1948).

Measurement has a long tradition and is a basic

discipline in any type of engineering. Engineers

must be experienced in estimating and valuing,

which means understanding the activities and risks

associated with process development, forecasting

and managing activities, risk management, reliable

delivery and proactive management to avoid a crisis.

One of the most sophisticated methodologies to

analyse the complexity of business processes has

been developed by Cardoso (Cardoso, 2008), which

identifies four main views of complexity levels,

namely complexity of activities, control-flow

complexity, data-flow complexity and complexity of

resources.

Another, widely used complexity measure is

McCabe’s Cyclomatic Complexity (MCC)

(McCabe, 1976). Since its development, it has been

one of the most promising software metrics. The

resulting empirical knowledge base has enabled

software developers to calibrate their own software

measurements and gain some understanding of its

complexity. Software metrics are often used to

obtain a quantitative expression of program

complexity. They cannot be confused with the

complexity of algorithms that aim to compare the

performance of the algorithm. It has been found that

software metrics are useful in reducing software

maintenance costs by assigning a numeric value that

reflects the easiness or difficulty of with which the

program module can be understood.

Finally, we can mention the entropy-based measure

of complexity (Jung et al., 2011). However, the

entropy is calculated only from the model structure

and ignores its dynamic component.

3 ENTROPY-BASED MEASURE

OF COMPLEXITY IN

STOCHASTIC PETRI NETS

The Petri nets are a suitable tool for modelling and

analysing discrete event dynamic systems that are

characterised by concurrency, parallel processing,

synchronization, or non-determinism. Their main

advantage is the ability to accurately verify

assumptions imposed on the model. Since the 1960s,

when Petri nets were defined by Carl Adam Petri

(Petri, 1962), their development has evolved in a

number of directions. One way was to extend the

original definition of new elements, the example of

which is the stochastic Petri nets.

Stochastic Petri Nets (SPN) are predominantly

used for performance analyses (Ajmone Marsan,

1990). Problems associated with stochastic

processes in connection with Petri nets include, for

example (Ciardo et al., 1994, Haas, 2002)

A Stochastic Petri net (Molloy, 1981) is a 7-

tuple, =(,,,Λ,,,



)where:

•  ={



,



,

,

,…,



} – a finite set of

places,

•  ={



,



,



,…,



}– a finite set of

transitions,

• ∩ = ∅ – places and transitions form

disjoint sets,

•  ⊆(⨯)∪(⨯) – a set of

edges, defined as a subset of all possible

connections,

• Λ: →



– a parameter of exponential

distribution for transitions,

• : →



– a weighting function that

defines the multiplicity of edges,

• :→



– capacity of places,

• 



:→



– an initial marking.

Entropy of a Stochastic Petri net

Let =(,,,Λ,,,



) is a Stochastic

Petri net, (



) is the set of all reachable markings

and is a vector of steady-state probabilities



(





)

,



∈(



). Entropy of  is defined as:



(



)

=−  



log







|

(





)



4 EXAMPLE OF A SIMPLE

MODEL AND COMPARISON

TO OTHER MEASURES

The presented method for quantification of entropy

in stochastic Petri nets is, in this section, illustrated

with a sample example. In addition, a comparison

will be made with selected alternative measures of

complexity.

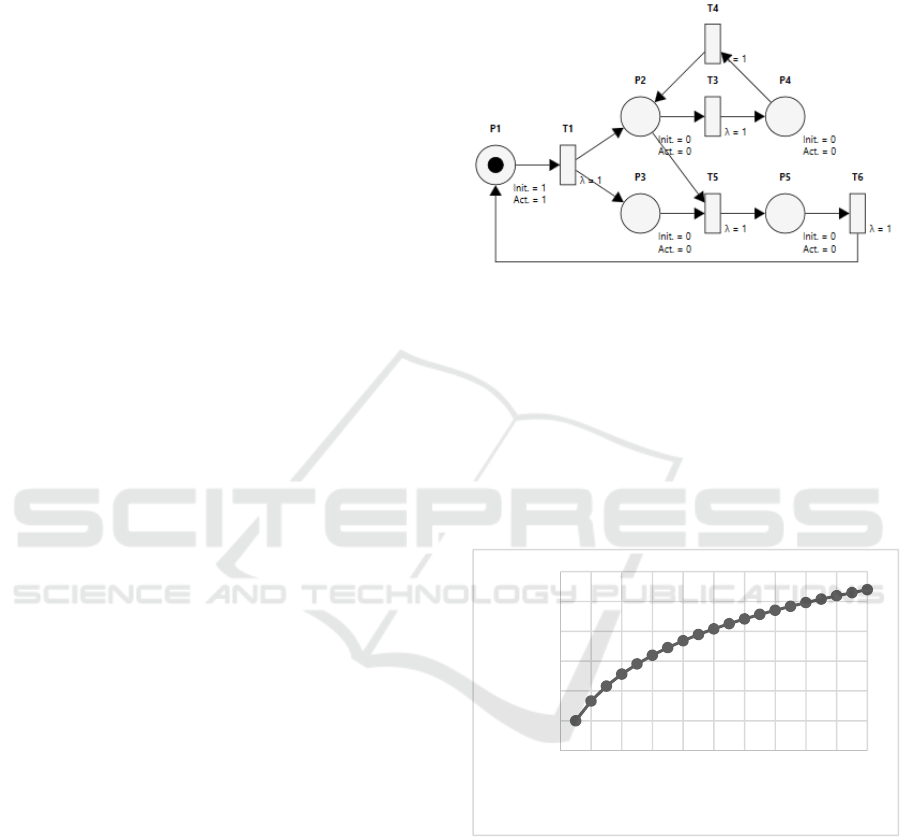
Figure 1 represents a process model consisting of

5 places and 5 transitions. The model can represent

any process, for example, the business process,

workflow, software process, etc.

Figure 1: Petri net example.

The entropy of this example is equal to 1.9219.

For comparison, the MCC is equal to 5 and

Cardoso’s Control-Flow Complexity (CFC) measure

equals 2. The advantage of this measure is the ability

to analyse the complexity change with increasing

tension (number of tokens) of the process under

investigation. Figure 2 illustrates the increasing

entropy with an increasing number of tokens at the

place P1.

Figure 2: Entropy development with different number of

tokens at P1.

Moreover, the calculation of entropy in the Petri

nets allows quantification of the upper limit of

complexity, which is equal to the maximum entropy.

Figure 3 shows the values of entropy divided by the

maximum entropy, which we denote the uncertainty

index. It can be seen from the figure that with the

increasing number of tokens at P1, the index

approaches one, i.e., with the increasing number of

tokens the process approaches its maximum entropy.

0 2 4 6 8 10 12 14 16 18 20

Entropy

Number of tokens at P1

Figure 3: Uncertainty index development with different

number of tokens at P1.

Since other complexities do not allow the

process to be analysed under tension, the

comparison of selected methods is performed

without consideration of tokens. Table 1. illustrates

the results of the correlation analysis of selected

complexity computation methods, namely the

entropy in SPN, MCC, Entropy-Based Uncertainty

(EBU) measure and Cardoso’s CFC measure.

Table 1: Correlations.

Entropy MCC EBU CFC

Entropy

Pearson

Correlation

1 ,844** ,877** ,914**

Sig. (2-tailed) ,008 ,004 ,001

8 8 8 8

MCC

Pearson

Correlation

,844** 1 ,862** ,780*

Sig. (2-tailed) ,008 ,006 ,022

8 8 8 8

EBU

Pearson

Correlation

,877** ,862** 1 ,724*

Sig. (2-tailed) ,004 ,006 ,042

8 8 8 8

CFC

Pearson

Correlation

,914** ,780* ,724* 1

Sig. (2-tailed) ,001 ,022 ,042

8 8 8 8

*. Correlation is significant at the 0.05 level (2-tailed).

**. Correlation is significant at the 0.01 level (2-tailed).

The results show a significant dependency between

all selected.

5 DISCUSSION

Measurement of complexity in dynamic systems is a

growing topic that is rapidly evolving mainly in

economics and informatics. Quantification of

complexity aims to better understand and tailor

(optimize) the development or design of systems or

processes in the sense of user interaction. The use of

information technology is still expanding (e.g., the

Internet of Things) and therefore it is necessary to

take into account the complexity of user interfaces

and processes, i.e. to make the user interface as

simple as possible and to make the important

processes intuitive and transparent (predictable).

In this work was presented the approach of

quantification of the complexity of any process

modelled in Petri nets. Most existing approaches

(Lloyd, 2001, Jung et al., 2011, Cardoso, 2008,

Vanderfeesten et al., 2008) for complexity

measurements only work with the structure of the

process, i.e., it is a simple formula that calculates the

occurrence of certain structures. Petri nets, however,

uses tokens to represent dynamic processes and thus

extend the static structure of the process.

Quantification of entropy in Petri nets allows us to

interpret both the structure and the dynamics of the

behaviour of the process and thus greatly enhances

the predictive ability of complexity as the implicit

property of any system. On the simple example, a

comparison of selected complexity measure with

entropy was made and it is obvious from the

conclusion that they are comparable. The case study

outlined the possible analyses that can be

implemented by entropy in the process. One of the

useful analyses is the exploration of the complexity

of the process with increasing process tension

(increasing number of tokens in the initial marking).

This type of analysis allows, for example, revealing

critical process values (occurrence of phase

transitions) or total scalability of robustness.

Another type of analysis is, for example, sensitivity

analysis, i.e., monitoring the development of

complexity when changing any process parameter.

In stochastic Petri nets, sensitivity analysis is mainly

coupled with testing of various lambda parameters at

transitions. Measurement of complexity is mainly a

tool for decision support, i.e., among functionally

equivalent solutions, the decision maker choose the

one with the lowest entropy.

Advantages of this approach

• Universal approach for measuring the

complexity of processes that can be

modelled using stochastic Petri nets.

0,95

0,96

0,97

0,98

0,99

0 2 4 6 8 101214161820

Uncertainty index

Number of tokens at P1

• The possibility of using the verification

features of Petri nets such as liveness,

boundedness, reachability etc.

• The possibility to set specific

probabilities (exponential distribution)

for branching in the model.

Disadvantages of this approach

• Fundamental shortcomings of Petri nets

in general, i.e., state explosion,

restrictions based on definitions, etc.

6 CONCLUSION AND FUTURE

WORK

In this paper, an approach to quantification of

complexity in Petri nets was defined using the

Shannon entropy. Based on the comparison with the

existing measures, a statistically significant

dependence was found, i.e., the selected measures

are comparable. Quantification of complexity using

entropy in stochastic Petri nets, however, brings a

number of advantages over other measures. The

main advantage of the defined measure is the ability

to investigate the development of complexity while

change process tension (robustness analysis) or

sensitivity analysis (complexity response to

changing, for example, any lambda parameter). In

addition, this approach can be generalized to a whole

range of modelling tools, namely any Petri nets

(timed, generalized stochastic, coloured, etc.), multi-

agent approaches, Markov chains, and more. The

presented approach can be used mainly as a

supporting tool for decision-making.

Future research will focus on expanding the

presented approach to the other above-mentioned

modelling tools as well as deepening, broadening

and generalizing the analyses that can be

implemented by entropy in any process.

ACKNOWLEDGEMENTS

The paper was supported by the University of

Pardubice, Faculty of Economics and

Administration, Project SGS_2017_017.

REFERENCES

Ajmone Marsan, M. 1990. Stochastic Petri nets: an

elementary introduction. In: Grzegorz, R. (ed.)

Advances in Petri nets 1989. Springer-Verlag New

York, Inc.

Arora, S. & Barak, B. 2009. Computational complexity: a

modern approach, Cambridge University Press.

Bennett, C. H. 1995. Logical depth and physical

complexity. The Universal Turing Machine A Half-

Century Survey, 207-235.

Cardoso, J. 2008. Business Process Control-Flow

Complexity: Metric, Evaluation, and Validation.

International Journal of Web Services Research

(IJWSR), 5, 49-76.

Ciardo, G., German, R. & Lindemann, C. 1994. A

characterization of the stochastic process underlying a

stochastic Petri net. IEEE Transactions on Software

Engineering, 20, 506-515.

Commons, M. L., Trudeau, E. J., Stein, S. A., Richards, F.

A. & Krause, S. R. 1998. Hierarchical complexity of

tasks shows the existence of developmental stages.

Developmental Review, 18, 237-278.

GellMann, M. & Lloyd, S. 1996. Information measures,

effective complexity, and total information.

Complexity, 2, 44-52.

Haas, P. J. 2002. Stochastic Petri Nets: modelling,

stability, simulation, New York, Springer.

Huffman, D. A. 1952. A method for the construction of

minimum-redundancy codes. Proceedings of the IRE,

40, 1098-1101.

Chernoff, H. 1972. Sequential analysis and optimal

design, SIAM.

Jirava, P. & Toseafa, E. 2016. Integration of Enterprise

Resource Planning System in the Multinational

Corporation Case Study, Norristown, Int Business

Information Management Assoc-Ibima.

Jung, J.-Y., Chin, C.-H. & Cardoso, J. 2011. An entropy-

based uncertainty measure of process models.

Information Processing Letters, 111, 135-141.

Lehmann, E. L. & Casella, G. 2006. Theory of point

estimation, Springer Science & Business Media.

Lempel, A. & Ziv, J. 1976. On the complexity of finite

sequences. IEEE Transactions on information theory,

22, 75-81.

Lloyd, S. 2001. Measures of complexity: a nonexhaustive

list. IEEE Control Systems, 21, 7-8.

Lloyd, S. & Pagels, H. 1988. Complexity as

thermodynamic depth. Annals of physics, 188, 186-

213.

Lorentz, G. 1966. Metric entropy and approximation.

Bulletin of the American Mathematical Society, 72,

903-937.

Mahoney, J. R., Ellison, C. J., James, R. G. & Crutchfield,

J. P. 2011. How hidden are hidden processes? A

primer on crypticity and entropy convergence. Chaos:

An Interdisciplinary Journal of Nonlinear Science, 21,

037112.

Mandelbrot, B. B. & Hudson, R. L. 2004. The

(mis)behavior of markets: a fractal view of risk, ruin,

and reward, New York, Published by Basic Books.

Mccabe, T. J. 1976. A Complexity Measure. IEEE Trans.

Softw. Eng., 2, 308-320.

Molloy, M. K. 1981. On the integration of delay and

throughput measures in distributed processing models.

Mota, F., Aaronson, S., Antunes, L. & Souto, A.

Sophistication as randomness deficiency.

International Workshop on Descriptional Complexity

of Formal Systems, 2013. Springer, 172-181.

Nielsen, F. 2011. Chernoff information of exponential

families. arXiv preprint arXiv:1102.2684.

Panus, J. 2016. A Discussion of Random Graph Models

Utilization For Global Strategic Management, Zilina,

Univ Zilina, Fac Operation & Economics Transport &

Communication.

Petri, C. A. 1962. Kommunikation mit Automaten. Bonn:

Institut für Instrumentelle Mathematik, Schriften des

IIM Nr. 2.

Renyi, A. On measures of information and entropy.

Proceedings of the 4th Berkeley Symposium on

Mathematics, Statistics and Probability, 1960. 547-

561.

Rissanen, J. 1978. Modeling by shortest data description.

Automatica, 14, 465-471.

Rissanen, J. J. 1996. Fisher information and stochastic

complexity. IEEE Transactions on Information

Theory, 42, 40-47.

Shannon, C. E. 1948. A mathematical theory of

communication. Bell System Technical Journal, 27,

379-423.

Traub, J. F., Wasilkowski, G. W. & Wozniakowski, H.

1988. Information-based complexity, Academic Press

New York.

Vanderfeesten, I., Reijers, H. A., Mendling, J., Van Der

Aalst, W. M. P. & Cardoso, J. 2008. On a Quest for

Good Process Models: The Cross-Connectivity

Metric. In: Bellahsène, Z. & Léonard, M. (eds.)

Advanced Information Systems Engineering: 20th

International Conference, CAiSE 2008 Montpellier,

France, June 16-20, 2008 Proceedings. Berlin,

Heidelberg: Springer Berlin Heidelberg.

Weyuker, E. J. 1988. Evaluating Software Complexity

Measures. IEEE Trans. Softw. Eng., 14, 1357-1365.

Zurek, W. H. 1990. Algorithmic information content,

Church-Turing thesis, physical entropy, and Maxwell's

demon. Los Alamos National Lab., NM (USA).