The Sociomathematical Norms in Linear Algebra Lecture

Rahayu Kariadinata, Hamdan Sugilar, Ehda Farlina, and Opik Taufik Kurahman

Mathematics Education Study Program, UIN Sunan Gunung Djati Bandung , Jl. A.H. Nasution No.105 Bandung, Indonesia

{rahayu.kariadinata, hamdansugilar, ehda.farlina}@uinsgd.ac.id

Keywords: Social interaction, problem solving process, linear algebra problem.

Abstract: Social interaction between students through discussions in solving linear algebra problems is needed. It is

because the linear algebra problem requires various strategies and is open-ended. This is called the

sociomatematic norm. This study aims to analyze sociomatematic norms in Linear Algebra lectures in terms

of two aspects namely sociomatematic norms associated with solving linear algebra problem and

sociomatematic norms associated with participation in joint activities to solve linear algebra problem. The

method used is descriptive-quantitative method. The subject of the research is the students of Mathematics

Education UIN Sunan Gunung Djati Bandung, semester 3 academic year 2016/2017, as many as 120 students.

The result of the research concludes that: sociomatic norms related to problem solving of good category Linear

Algebra (70,52%), this is seen from problem solving strategy used by students in solving open problems;

sociomatematic norms associated with participation in joint activities to solve the problem of linear Algebra

category enough and well, all indicators including sociomatematic norms are implemented.

1 INTRODUCTION

Understanding Linear Algebra requires a number of

thinking skills such as the ability to communicate

mathematically and problem solving.

Communication is the most important part in learning

mathematics. (NCTM, 2000) emphasizes the

importance of communication skills in mathematics

and mathematics education. This must be supported

through a planned and constructed classroom

atmosphere so that students have the opportunity to

interact and collaborate with each other (Tatsis and

Koleza, 2008). In addition, the provision of a number

of challenging issues to be solved through open-

ended strategies will support the interaction between

students (NCTM, 2000).

According to (Tatsis and Koleza, 2008) the

interaction is contained in the teaching of

mathematics more on aspects of analysis, so that

many researchers who study issues related to learning

mathematics. Each class as a group that interacts with

certain interactions and behavior patterns will affect

the quality of student learning (Zembat, I. O. and

Yasa, 2015). In the classroom, norms are regular

patterns of behavior that affect the nature of learning

that occurs in them (Zoest, Stockero and Taylor,

2011).

The formation of social norms in the

mathematics class aims to enable students to

understand their role in the discussion. Students are

not only required to speak out in response to math

problems but are also required to analyze, criticize,

and make solutions together, especially in terms of

their mathematical reasoning (Roy, Tobias and

Dixon, 2014). These activities are known as

sociomatematic norms. Sociomatematics according

to (Wedege, 2003) is a relationship between

individuals, mathematics, and society in which there

is activity numeracy, analysis and etnomatematics.

While sociomatic norms are rules that apply to an

interaction between students in solving problems,

argue math and negotiate in understanding the

concept of mathematics.

Sociomatematic norms evolved in the process of

interaction and mutual participation during the course

of mathematics learning. This is closely related to the

negotiation and collective agreement on the

application of relevant, appropriate, or different

problem-solving procedures in problem solving and

communicating the idea of settlement and way of

thinking (Yacke, E and Cobb, 1996; Kang and Kim,

2016; Lopez, LM and Allal, 2007). This study aims

to analyze the sociomatematic norms in the Linear

Algebra lecture from two aspects, namely

Kariadinata, R., Sugilar, H., Farlina, E. and Kurahman, O.

The Sociomathematical Norms in Linear Algebra Lecture.

In Proceedings of the 2nd International Conference on Sociology Education (ICSE 2017) - Volume 2, pages 75-80

ISBN: 978-989-758-316-2

sociomatematic norms related to solving linear

algebra problem and sociomatematic norms related to

participation in joint activity to solve linear algebra

problem.

2 METHODOLOGY

The subjects in this study are students of semester 3

academic year 2016/2017 who took courses Linear

Algebra about 120 people, mathematics education

program, UIN Sunan Gunung Djati Bandung,

Indonesia. Linear Algebraic topics studied in this

research are Linear Independence and Basis. The

topic has a very wide scope and requires analysis and

construction of a strong mathematical understanding.

2.1 Classroom Organization

Learning strategies are implemented through small

group discussions followed by class discussions to

solve linear algebra problems. Previously the lecturer

introduced the rules to be used. Lecturers are actively

involved during small group activities, including

involvement in encouraging collaborative dialogue

and dialogue and discussion of problem-solving

efforts (Zembat, I. O. and Yasa, 2015). This research

will analyze in depth how problem solving process of

Linear Independence, Basis and student activity in

group discussion.

Students are encouraged to solve problems

through arguments and mathematical reasoning to

obtain solutions with various strategies through the

problem-solving process recommended by (Polya,

1973), namely: understanding the problem, devising

a plan, carrying out the plan, and looking back. After

students solve problems, the lecturers facilitate by

setting the rules of reasoning verbalization and the

mathematical strategies used to establish and

maintain norms (Roy, Tobias and Dixon, 2014).

2.2 Research Instruments

The research instruments consist of observation

sheets, student work results, homework and tests at

the end of the lesson.

2.3 Data Collection Technique

The data collected includes observation and

discussion activities in class. The linear algebra

problem given is a challenging and open issue.

2.4 Data Analysis Technique

Linear Algebra problem-solving process based on

Polya steps was analyzed quantitatively using

percentage, while student discussion activity using

sociomatematic norm indicator was analyzed

descriptively.

3 RESULTS AND DISCUSSION

3.1 The Sociomathematical Norms

Associated with Algebra Problem

Solving

The following will describe the Linear Algebra

problem-solving process through student work

results. Examples of problems with the given Base

topic:

The set of S = {v

, v

} where vectors:

= (2,1,-1), v

= (-1,5,1) and v

= (2,1,3). Investigate

whether S is the basis for R

Description of problem solving process done by

students using problem-solving steps (Polya, 1973) as

below:

3.1.1 Understanding the Problem

Results Analysis: Students can organize the structure

of the problem they are facing through their writing

about: a) what is known, b) what is asked, c) the

problem condition to find what is being asked.

Achievement: 86.45%.

3.1.2 Devising a Plan

Analysis Result:

 Students can write down the definition of Basis,

that is: If V is any vector and S = {v1, v

…., v

is a finite set of vectors in V, then S can be said

to be a basis for V if: (i) S is linearly

independent and (ii) S span V. Achievement:

63,54%.

 Students can create mathematics model

representative, that is:

A vector equation that meets linear

independence, S= {v

, v2, v3} is linearly

independent, then it must meet: k

+ k

= 0 and requirement S span R

there is a

consistent solution. Achievement: 50,78 %.

ICSE 2017 - 2nd International Conference on Sociology Education

3.1.3 Carrying Out the Plan

Analysis Result:

Students solve problems with several strategies:

 Starting proof of S is linearly independent

followed by S span V (1)

 Proof of S is linearly independent S span V

done together through the coefficient matrix

representation of the linear system form

obtained from the linear independence and span

description, as follows:

A =















311

151

212

(2)

Students using the strategy (1) take the following

steps:

 Student prove S is linearly independent and S

span V by row reduction by elementary row

operation of a corresponding equation system.

Achievement: 60.03%

 Students make conclusions based on the

exploration of is linearly independent and S

span V Achievement: 63.45%

Students using strategy (2) take steps:

 Students reorganize the structure of

mathematical problems that compose, organize

and develop it by looking for the determinant

value of the coefficient matrix A.

Based on the results of calculations on the

sociomatematic norms in Linear Algebra lectures

related to linear Algebra problem solving are

presented in the table as follows:

det (A) =

311

151

212



= 44

Achievement: 80,01%

 Students use the theorem to make conclusions

based on the value of determinants that have been

obtained. Achievement: 70,09%

3.1.4 Looking Back

Students perform the examinations that have been

obtained. Achievement:

 Students using strategy (1) : 70,07%

 Students using strategy (2) : 70,01%

Based on the description of sociomatematic

norms related to linear algebra problem solving are

presented in Table 1.

Table 1: Achievement of linear algebra problem solving

process.

Steps of Problem

Solving (Polya, 1973)

Achievement

(Percentage)

Strategy

(1)

Strategy

(2)

Understanding the

problem

86,45%

Devising a plan

57,16%

Carrying out the plan

61,74%

75,05%

Looking back

70,07%

70,01%

Total

275,42 %

288,67 %

Average achievement of

each strategy

68,86 %

72,17%

Average overall

achievement

70,52 %

The results of the analysis in Table 1 obtained the

average of achievement of Linear Algebra problem-

solving process using steps (Polya, 1973) of 70.52%.

This is a good category.

3.2 The Sociomathematical Norms

Associated with Participation in

Joint Activities to Solve Linear

Algebra Problems

Based on observations and interviews, the following

describes the activities of one of the student

discussions in small groups when solving the Linear

Independence topic problem. Examples of problems

as follows:

The set of vectors S = {v

, v

}, where v

= (1,-

1,1), v

= (2, -2, 1), v

= (3, -1, 1) and v

= (2,1,-

2). Investigate whether S is linearly independent!

Student A

Do we need to write down the

definition completely ?

Student B

Yes, we need! so that we can

easily make the path of

completion

Both students start to write down the definition of

Linear Independence, it is:

If S = {v

, v

,…., v

} the set of vectors, then the vector

equation: k

+ .....+k

=0 has only solution,

namely k1

= 0, k

= 0, ..., kr

= 0.

Based on that definition, the student starts

exploring by first writing the vector equation: k

+.....+ k

= 0, then substituting the known

vectors so that the system forms the following linear:

The Sociomathematical Norms in Linear Algebra Lecture

+ 2 k

+ 3 k

+2 k

= 0

-k

- 2 k

- k

+ k

= 0

+ k

- 2 k

= 0

(3)

Student A

Consider the form (3) do you

have an opinion about the form?

Student B

Looking at the form (3) is

somewhat different from what

we have learned, here all the

constants are 0, does the system

have certain characteristics?

Sociosemantics Norm Aspect :

Students ask each other questions that emphasize the

mathematical understanding

Lecturer activities:

 Providing assistance (scaffolding) is the

provision of assistance in the early stages of

guidance, encouragement, and describe the

problem

 Providing direction to all groups to pay attention

to form (3) and to recall material learned

(Algebra Matrix) as a supporter of completion.

 Stimulating students’ social interactions

 Directing the discussion on understanding the

concept of Linear Algebra and its prerequisite

concepts

Student A

I remember when learning Algebra

Matrix, the form (3) is called the

Homogeneous Linear Equation

System but I forgot the practical

way to solve the linear equations

system of that form.

Student B

We have previously learned about

the system of linear equations,

what if we complete the form (3)

with the Gauss-Jordan Elimination

procedure.

Student A

OK! you work with Gauss-Jordan

Elimination, I will study the shape

characteristics (3)

Lecturer activities :

 Giving scaffolding by reminding material about

form (3), whose solution is always consistent

(trivial and non trivial)

 Recalls the theorem of the Homogeneous Linear

Equation System.

Some students describe the theorem, namely:

"The system of homogeneous linear equations with

more unknown numbers (r) than the number of

equations (n) then always has the number of solutions

(non-trivial)"

Student B

I will finih it by using theorem

Sociomatematic Norm Aspects :

Students reach agreement using reasoning and

mathematical proof to solve problems in different

ways.

Student A

I have solved the system of linear

equations (3) with the Gauss-

Jordan Elimination obtained by

the non-trivial settlement i.e. in

addition to k

= 0, k

= 0 dan

= 0 thus the conclusion S is a

linearly dependent

Student B

By using the theorem it appears

that the system of equation (3) has

4 unknown numbers (r = 4) and 3

equations (n = 3), since r is greater

than n, then the form (3) has so

many non- trivial) i.e. in addition

to k

= 0, k

= 0 dan k

= 0thus

the conclusion S is a linearly

dependent

Lecturer activities :

Help students to draw on the conclusion

Sociomatematic Norm Aspects:

 Students explain the solutions they have using

mathematical arguments

 Students compare their strategies to find

mathematically important similarities and

differences

 Students use mistakes as an opportunity to

rethink the concepts of their mathematical ideas

and test contradictions.

Based on the observation about sociomatematic

norms related to participation in joint activity to solve

linear algebra problem, the result obtained with fair

and good category, it can be seen from student

activity in small group discussion. Indicators of

sociomatematic norms are always visible so as to

assist the students in solving the given problems.

Lecturer intervention appears through scaffolding.

The summary is presented in Table 2.

ICSE 2017 - 2nd International Conference on Sociology Education

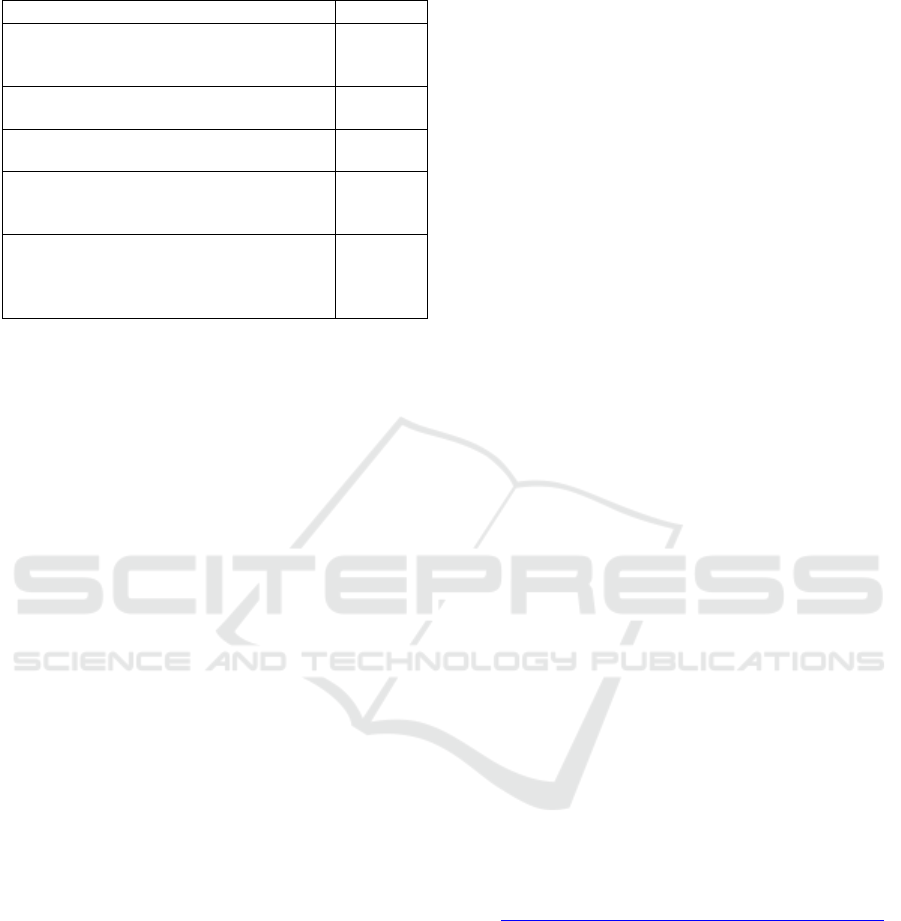
Tabel 2: Sociothematic Norm related to students’

participation in sharing activity.

Sociosemantic Norm Indicator

Category

1) Students ask each other questions that

emphasize reasoning and

mathematical understanding

Good

2) Students explain the solutions they

have using mathematical arguments

Enough

3) Students reach agreement using

reasoning and mathematical proof

Good

4) Students compare their strategies to

find mathematically important

similarities and differences

Good

5) Students use mistakes as an

opportunity to rethink the concepts of

their mathematical ideas and test

contradictions.

Enough

Based on table 2 it can be concluded that the

sociomatematic norms associated with participation

in joint activities to solve the problem of linear

Algebra category is fair and good.

3.3 Discussion

The results showed that the sociomatematic norms

associated with solving linear algebra problems were

good with 70.52% achievement. This can be seen

from the completion steps done by students using

Polya problem solving. Based on the analysis at the

"understanding the problem" stage all students

understand what is known, what is asked. Students

can organize the problem structure.

At the "deceiving a plan" stage students apply

some problem-solving strategies such as creating

patterns, writing an equation, testing special cases or

simpler cases of problems encountered to get a better

picture of problem solving, and identifying parts of

the whole.

At the "carrying out the plan" stage, students have

been able to execute the strategy as planned in the

previous stage, and at the "looking back" stage the

student can check the results on the original problem.

The sociomatematic norms associated with

participation in joint activities to solve linear algebra

problems resulted in quite good results. This is in line

with the results of the research (Hurst et al., 2013)

social interaction provides a means for students to

view topics from different perspectives and improve

their thinking, critical issues and problem-solving

abilities. As according to (Tatsis, 2007) social norms

and sociomatematic norms developed during

interaction among students when working together to

solve a mathematical problem and in presenting a

mathematical solution result.

Open-ended problem solving supports the

creation of sociomatematic norms. As an opinion

(Capraro, M. M., Capraro, R. M and Cifarelli, 2007)

that open-ended problem solving provides a free and

supportive learning environment for students to

develop and express their mathematical

understanding.

4 CONCLUSIONS

Based on the results of the study and discussion it can

be concluded that the sociomatematic norms

associated with Algebra linear problem solving is in

a good category (70.53%), it can be seen from the

problem solving strategy used by students in solving

the problems that are open-ended, students solve

linear algebra problem with various strategies,

including the use of definitions and theorems, so that

students are not fixated on procedural settlement.

Completion is done following the procedure (Polya,

1973); the sociomatematic norms associated with

participation in joint activities to solve the Linear

Algebra category problem are sufficient and good, all

indicators including sociomatematic norms are

implemented in all student discussion groups.

ACKNOWLEDGEMENTS

Acknowledgments researchers convey to the

Research and Publishing Center UIN Sunan Gunung

Djati Bandung who has facilitated this research.

REFERENCES

Capraro, M. M., Capraro, R. M., Cifarelli, V.V. 2007.

What are students thinking as they solve open-ended

mathematics problems? Research Gate.

https://www.researchgate.net/publication/242096594.

Developing the STEM Academic Culture View project

Hurst, B. Wallace, R., Nixon, B.S. 2013. The Impact of

Social Interaction on Student Learning. Reading

Horizons. Volume 52, Issue 4 2013 Article 5,

SEPT/OCT 2013

Kang M.,S., Kim, K.M. 2015. Sociomathematical norms

and the teacher’s mathematical belief : A case study

from a Korean in-service elementary teacher. Eurasia

Journal of Mathematics, Science and Technology

Education, 2016, 12(10), 2733-2751 doi:

10.12973/eurasia.2016.1308a

Lopez, L.M., Allal, L. 2007. Sociomathematical norms and

the regulation of problem solving in classroom

The Sociomathematical Norms in Linear Algebra Lecture

multicultures. International Journals of Educational

Research 46: 252 – 265

NCTM. 2000. Principles and Standards for School

Mathematics. US: National Council of Teachers of

Mathematics, Inc.

Polya. 1973. How to Solve it. An New Aspect of

Mathematical Method. Second Edition. New Jersey:

Princeton University Press

Roy,J.G, Tobias,M.J, Safi,F. Dixon,K.J, 2014.

Investigation in Mathematics Learning @ The

Research Council on Mathematics Learning. Winter

Edition 2014, Volume 7, Number 2. http://files

eric.ed.gov/fulltext/EJ052938.pdf.

Tatsis, K. 2007. Investigating the Influence of Social and

Sociomathematical Norms in Collaborative Problem

Solving. Paper presented at The Fifth Conference of the

European Society for Research in Mathematics

Education.

http://ermeweb.free.fr/CERME5/WG8/8_Tatsis.pdf

Tatsis, K., Koleza, E. 2008. Social and socio-mathematical

norms in collaborative problem-solving. European

Journal of Teacher Education Vol. 31, No. 1, February

2008, 89–100.Routledge. Taylor and Francis Group.

http://

jwilson.coe.edu/EMAT7050/Student/Traxler/sociomat

hematical.norm.pdf.

Van Zoest, S., Taylor, 2011. The durability of professional

and sociomathematical norms intentionally fostered in

an early pedagogy course. J Math Teacher Educ. DOI

10.1007/s10857-011-9183-y. Springer

Science+Business Media B.V. 2011. Publish online: 19

April 2011

Wedege, T., 2003. Sociomathematics: people and

mathematics in society. Adults Learning Maths

Newsletter, No. 20, December 2003. p. 2.

http://www.mmf.ruc.dk/~tiw/eng/papers.htm.

Yackel, E. Cobb,P., Wood,T. 1991. Small-Group

Interactions as a Source of Learning Opportunities in

Second-Grade Mathematics. Journal for Research in

Mathematics Education, Vol. 22, No. 5 (Nov., 1991),

pp. 390-408. Published by: National Council of

Teachers of Mathematics.

http://www.jstor.org/stable/749187

Yacke, E., Cobb, P 1996. Sociomathematical Norms,

Argumentation, and Autonomy in Mathematics.

Journal for Research in Mathematics Education, Vol.

27, No. 4 (July, 1996), pp. 458-477.

http://www.jstor.org/stable/749877

Zembat, I. O., Yasa, S. A. 2015. Using classroom scenarios

to reveal mathematics teachers’ understanding of

sociomathematical norms. International Journal of

Education in Mathematics, Science and Technology,

3(3), 242-261.

ICSE 2017 - 2nd International Conference on Sociology Education