Reading Comprehension
Ability to Understand Text Mathematics to Solve Basic Mathematical Questions
Yeti Mulyati, Vismaia S. Damaianti and Daris Hadianto D.
Departemen Pendidikan Bahasa Indonesia, Fakultas Pendidikan Bahasa dan Sastra, Universitas Pendidikan Indonesia
Keywords: Understanding Mathematical Text, Solving Basic Mathematics Questions.
Abstract: This study aims to determine the relationship between the ability to understand mathematical text and the
ability to solve basic math problems. Mathematical problems can be presented in two forms, namely in the
form of verbal and in the form of numbers. The verbal question is packed through a narrative text stimulus.
Failure to understand the contents of narrative texts causes chaos in understanding the essence of basic
mathematical concepts. Basic mathematical concepts include addition, subtraction, multiplication, and
division. The interpretation of what basic mathematical concepts should be used is determined by the
students' ability to understand the content of the text. In this case, students' reasoning ability plays a very
important role. The ability to reason can be trained through reading learning. The data of this study were
taken from the second graders of elementary school in Bandung. Using correlational method, there is
evidence that both variables have positive correlation. This implies the importance of integrative learning
implementation between reading and learning of mathematics in low grade elementary school.
1 INTRODUCTION
Students reading and reading competencies in
Indonesia are still low. Based on the results of PISA
tests and evaluations in 2015 the performance of
Indonesian students in a row showed average scores
for science, reading, and maths ranked 62, 61, and
63 of 69 countries evaluated. The rating and average
score of Indonesia does not differ greatly from
previous PISA test results and surveys in 2012
which are also in the low material mastery group
(Wuttke, 2007; Grek, 2009; OECD (Organisation for
Economic Co-operation and Development), 2013).
The Progress in International Reading Literacy
Study (PIRLS) study of fourth grade students
showed that the reading and counting achievement
of Indonesian students was very low. Indonesian
students' reading ability in 45th out of the 49
countries studied. The Indonesian score (405) is
above Katar (353), Morocco (323), and South Africa
(302) (Mullis et al., 2012).
Based on these data, reading ability and
numeracy ability of students seem not far adrift.
Counting instruments in PISA and PIRLS research
are essentially presented in the form of narrative
texts. That is, both reading and numeracy tests, both
using verbal text stimulus. To understand the
intended verbal text required reading ability and
high-order thinking skills (Bell, 1995; Aitchison and
Lewis, 2004; Myles, 2010). A person's thinking
ability is influenced by language skills (Waters,
2006; Rezaei, Derakhshan and Bagherkazemi, 2011;
DePoy and Gitlin, 2016). The development of
language competence is an indicator of cognitive
development (Carruthers, 2002; Clark, 2006). A
person's language skills reflect his or her thinking
skills (Piaget, 1964; Albert, Albert and Radsma,
2002). To communicate a concept is necessary
means of language that is understood together
between communicator and communicant. Language
is needed to communicate a concept to others (Bell,
1995)
Mathematical problems can be presented in two
ways, namely by using mathematical symbols and
verbal symbols. Understanding of the two symbols
will facilitate a person in solving mathematical
problems (Lin, et. al., 2013; Björn, Aunola and
Nurmi, 2016). From both ways of presenting the
counting problem, the questions presented through
verbal symbols tend to show worse results than the
results presented through mathematical symbols
(Vilenius-Tuohimaa, Aunola and Nurmi, 2008;
Ozuru, Dempsey and McNamara, 2009). Why does
454
Mulyati, Y., Damaianti, V. and D., D.
Reading Comprehension - Ability to Understand Text Mathematics to Solve Basic Mathematical Questions.
DOI: 10.5220/0007169104540458
In Proceedings of the Tenth Conference on Applied Linguistics and the Second English Language Teaching and Technology Conference in collaboration with the First International Conference
on Language, Literature, Culture, and Education (CONAPLIN and ICOLLITE 2017) - Literacy, Culture, and Technology in Language Pedagogy and Use, pages 454-458
ISBN: 978-989-758-332-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

this happen? Could these two have a positive
correlation?
Several related studies have been done before,
such as "Supporting the Formal Verification of
Mathematical Text" by Claus Zinn in 2005. This
study proves that the organizing of math problems
can be traced and determined by an application.
What operation should be used in solving math
problems can be determined by the truth of the
language in its mathematical text (Zinn, 2006).
Another study of "Covariation between Reading and
Arithmetic Skills from Grade 1 to Grade 7" by Heidi
Korpipa 2017 proves that low grade students rely
heavily on phonological awareness while high-class
students rely on nonverbal reasoning (Korpipää, et.
al., 2017). Anna Teledah's research in 2015 on
"Different modes in teachers' discussions of
students' mathematical texts" proves that students'
understanding of the type of counting operation
depends on the style of the teacher in explaining the
mathematical text (Teledahl, 2015). These three
research results indicate the important role of
language competence in understanding the text, both
verbal and nonverbal texts. The possession of
adequate language competence is the main
ingredient in reading activities (Vilenius-Tuohimaa,
Aunola and Nurmi, 2008; Ozuru, Dempsey and
McNamara, 2009; Lin, et. al., 2013). The difference
of this study with previous studies lies in the focus
of research which is focused on the amount of
correlation between the ability to understand the text
and the ability to count. The results of this study can
be used as a basis for determining and considering
the strategies of learning to read and count / math in
low grade primary schools appropriately.
2 RESEARCH METHODS
This research uses correlational method. The
correlated research variables are the ability to
understand mathematical text with the ability to
solve basic mathematics problems (numeracy). The
data source is the result of the reading ability test of
mathematics text and numeracy ability of the 2nd
graders of elementary school in West Bandung
regency as much as 71 people. The school sample
represents three categories, namely schools with less
accreditation (C), good (B), and excellent (A).
The research instrument consists of two sets of
tests, namely the ability to read mathematical text
and numeracy tests. Both of these test devices use
the same text stimulus, i.e. the mathematical text
presented verbally. The reading test is focused on
questions of understanding and interpretation of
reading content related to basic mathematical
operations (addition, subtraction, multiplication, and
division); while the numeracy skills test is focused
on completion of numeracy problems presented in
the form of numbers.
3 RESULTS AND DISCUSSION
The ability to read comprehension of mathematical
text of low grade students in Bandung, West Java
region is low, with average value of 44.3 from
standard 100. To reach the average value of reading
ability of mathematics text based on school category
with accreditation of C, B, and A, respectively -
shows the average value achievement as follows.
Schools with category C earn an average of 37.5;
schools with category B earn an average of 45.8; and
schools with category A earned an average of 49.6.
The average reading ability of mathematical text
based on the category of school shows a grade
gradation that corresponds to the school category.
Schools that have category A get the average value
of reading ability is relatively better than schools
that are categorized B and C. Similarly, with school
categories B better than schools that categorize C.
Reading activities that not only recognize the print
symbols but meaning and interpretation of the
printed symbols. The interpretation of the code /
symbol refers to the split of the code symbol, while
understanding refers to the meaning of the message
(Cain, Oakhill and Bryant, 2004; Koponen, et. al.,
2013; Liu, Lin and Zhang, 2016).
The essence of reading is the understanding of
the content and the reading message. The failure to
reap the meaning of the print emblem in
understanding mathematical texts leads to a failure
to interpret the operating procedures of basic
mathematical computations. When a basic
mathematical process of operation must be
accomplished through numeracy, such as summed,
subtracted, multiplied, or divided, will be largely
determined by one's understanding of his verbal text.
It is evident that students who are well versed in
reading comprehension (mathematical text) show
good ability in solving their math problems (Kirby,
et. al., 2012; Koponen, et. al., 2016). Reading
activities allow people to gain meaning from the text
(Vellutino, et. al., 2007; Afflerbach, Pearson and
Paris, 2008; Compton-Lilly, 2011).
Achievements that are not too different from the
ability to read mathematical text is also indicated by
the average ability to count. In general, the average
numeracy ability of low grade students in Bandung
area is also low, that is 43.93 from the standard 100.
Reading Comprehension - Ability to Understand Text Mathematics to Solve Basic Mathematical Questions
455

The achievement of the mean value of numeracy
ability based on the category of schools that
accredited C, B and A respectively shows the
average value of numeracy ability 40, 40.5. and
51.3. The gap between the mean value of reading
ability of mathematics text and the mean of
numeracy ability for each school category is as
follows. For categorized schools C is 2.5 (40 - 37.5).
In schools with category C, the mean value of
numeracy skills is better than the ability to read
mathematical text. Gap at school with category B of
5.3. (45.8 - 40.5). In the B categorized schools, the
mean value of reading ability of mathematics text is
better than the mean of numeracy ability. Gap at
school with category A equal to 1.7. (51.3 - 49.6). At
school A category, show the opposite. The mean
value of numeracy ability is better than the mean
value of reading ability of mathematics text.
The data value of both variables in this study
then performed by correlational testing with
correlational statistical techniques. Correlation test
results indicate a positive correlation between the
ability to read mathematical text and the ability to
count for 0676 (high). Significant correlations are
shown by schools categorized C (0.756) and
category B (0.787); whereas schools with category
A show correlation results that are not high (0.473 =
enough). The average value of reading ability of
mathematics text, the mean of numeracy ability, and
correlation, both per school category and overall can
be seen in table 1 below.
Table 1: Average value of reading and counting
competency and its correlation.
Schoo
l’s
catego
ries
Reading
Competencies
Counting
Competence
Correla
tion
Value
Me
an
Mo
de
Med
ian
Me
an
Mo
de
Med
ian
C
37.
5
30 30 40 60 40 0.756
B
45.
8
30 50
40.
5
40 40 0.787
A
49.
6
50 50
51.
3
50 50 0.473
The correlation of mathematics text and
numeracy skills for each school category can be seen
in figures 1, 2, and 3. The graph shows evidence of a
strong relationship between the two variables
studied.
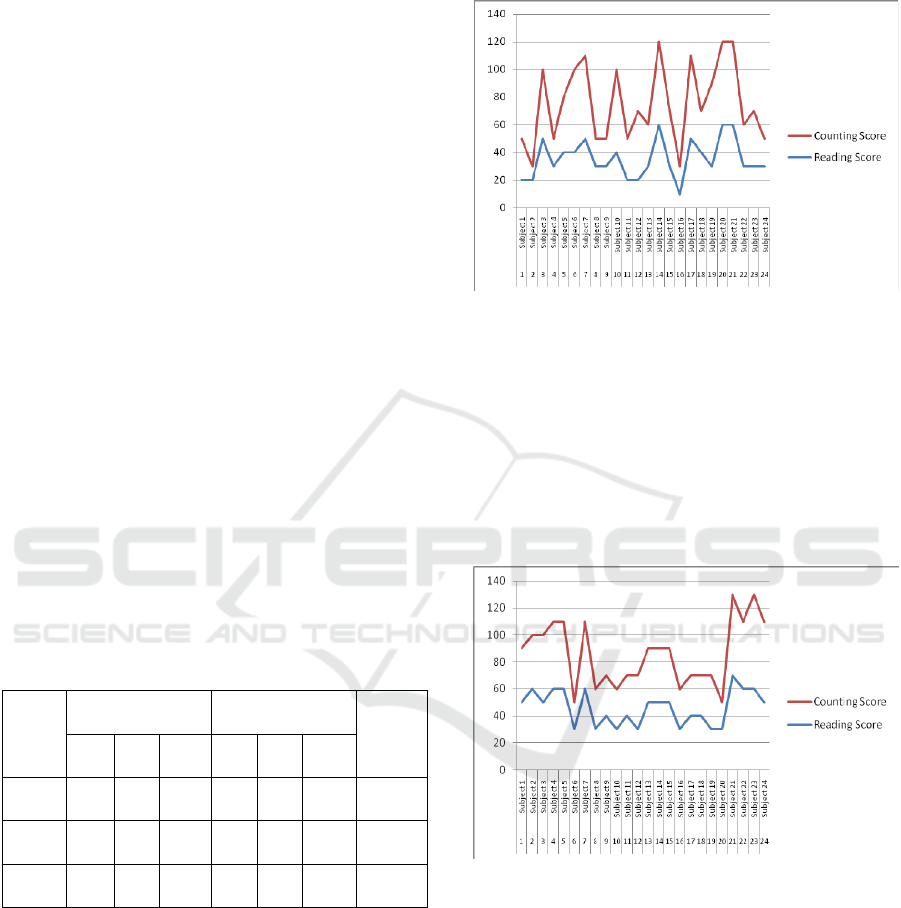
Graphic that proves a strong relationship
between the ability to read mathematical text and
numeracy skills in C school can be seen in Figure 1.
Reading competence is parallel to the scores
obtained by students on numeracy competence. This
is reinforced by the value of r or the correlation
between reading competence and arithmetic at
school categorized C is at 0.756.
Figure 1: Values of reading ability and counting ability of
low grade students in categorized schools C.
Graphic that proves a strong relationship
between reading ability of mathematics text and
numeracy ability at school B can be seen in Figure 2.
Read competence in the same direction as the score
obtained by students on the numeracy competence.
This is reinforced by the value of r or the correlation
between reading competence and numeracy at
school B is at 0.787.
Figure 2: Correlation of ability to read mathematics text
and counting students at school categorized B.
The opposite evidence occurs in schools categorized
A. The mean value of numeracy ability of students
in school categorized A is better than the average
value of reading ability of mathematics text.
Meanwhile, the correlation numbers are not too
strong (0.473). Children who have relatively high
intelligence tend to be more talented in the exact
field, including counting affairs. The numerical
questions presented in the form of numbers will be
more interesting to them, rather than presented in
verbal text form. The reluctance to read verbal texts
CONAPLIN and ICOLLITE 2017 - Tenth Conference on Applied Linguistics and the Second English Language Teaching and Technology
Conference in collaboration with the First International Conference on Language, Literature, Culture, and Education
456

that are influenced by interest will impact on the
inaccurate interpretation of content and text
messages (Piaget, 1920, 1964; Barrouillet, 2015).
Some respondents show a parallel between the
reading test results of mathematical text and
numeracy skills. However, several other respondents
pointed out the opposite. The value of good or bad
numeracy skills is not followed by good or bad text
reading skills. The full picture can be seen in Figure
3 below.
Figure 3: Values of student reading and counting skills at
school a category.
From the three data, the researcher can conclude
that the competence of reading and counting does
have a positive correlation or correlation. The
interpretation of the code refers to the breaking of
code symbols, whereas comprehension refers to the
notion of message (Koponen, et. al., 2013). It should
be realized that the most important in the process of
reading is understanding. However, understanding
will not happen if the reader does not recognize the
symbol (letter) code. It is evident that students who
have a good ability to understand reading or text on
math problems better in solving math problems
compared with students who have less ability to
understand the text. This is proven by students
whose high reading ability has implications for high
numeracy skills (Kirby, et. al., 2012; Koponen, et.
al., 2016).
4 CONCLUSIONS
Competence of reading and computing competence
are two competencies that have a strong relationship.
Students can solve basic mathematics problems
(arithmetic) based on mathematics text stimulus
(verbal and narrative) if the student has good reading
competence. Thus, reading competence will be the
main foundation in educational construction and
teaching in schools. Reading activity is part of the
literacy activity. In micro, literacy activity is only
interpreted as activity of reading and writing. In its
development, literacy activities related to various
abilities related to life skill for the benefit of life and
life. Therefore, literacy education becomes an urgent
thing to be implanted in schools, either through the
learning process or the process of habituation.
Learning to read and study mathematics in lower
classes should be done in an integrative, not
disaggregated. Separation of self-discipline can be
done in high school or next level.
REFERENCES
Afflerbach, P., Pearson, P.D. and Paris, S.G., 2008.
Clarifying differences between reading skills and
reading strategies. The reading teacher, 61(5), pp.364-
373.
Aitchison, J. and Lewis, D.M., 2003. New media language.
Psychology Press.
Albert, R.T., Albert, R.E. and Radsma, J., 2002.
Relationships among bilingualism, critical thinking
ability, and critical thinking disposition. Journal of
Professional Nursing, 18(4), pp.220-229.
Barrouillet, P., 2015. Theories of cognitive development:
From Piaget to today. Developmental Review, 38, pp.
1–12.
Bell, A., 1995. Language and the media. Annual Review of
Applied Linguistics, 15, pp.23-41.
Björn, P.M., Aunola, K. and Nurmi, J.E., 2016. Primary
school text comprehension predicts mathematical
word problem-solving skills in secondary
school. Educational Psychology, 36(2), pp.362-377.
Cain, K., Oakhill, J. and Bryant, P., 2004. Children's
reading comprehension ability: Concurrent prediction
by working memory, verbal ability, and component
skills. Journal of educational psychology, 96(1),
pp.31-42.
Carruthers, P., 2002. The cognitive functions of
language. Behavioral and Brain Sciences, 25(6), pp.
657-674.
Clark, A., 2006. Language, embodiment, and the cognitive
niche. Trends in cognitive sciences, 10(8), pp. 370-374.
Compton-Lilly, C., 2011. Counting the uncounted: African
American students in reading recovery. Journal of
Early Childhood Literacy, 11(1), pp.3-24.
DePoy, E. and Gitlin, L. N., 2016. Language and Thinking
Processes. In Introduction to Research, pp. 112–132.
Grek, S., 2009. Governing by numbers: The PISA “effect”
in Europe. Journal of Education Policy, 24(1), pp. 23–
37.
Kirby, J.R., Deacon, S.H., Bowers, P.N., Izenberg, L.,
Wade-Woolley, L. and Parrila, R., 2012. Children’s
Reading Comprehension - Ability to Understand Text Mathematics to Solve Basic Mathematical Questions
457

morphological awareness and reading ability. Reading
and Writing, 25(2), pp.389-410.
Koponen, T., Salmi, P., Eklund, K. and Aro, T., 2013.
Counting and RAN: Predictors of arithmetic
calculation and reading fluency. Journal of
Educational Psychology, 105(1), pp.162–175.
Koponen, T., Salmi, P., Torppa, M., Eklund, K., Aro, T.,
Aro, M., Poikkeus, A.M., Lerkkanen, M.K. and Nurmi,
J.E., 2016. Counting and rapid naming predict the
fluency of arithmetic and reading skills. Contemporary
Educational Psychology, 44, pp.83-94.
Korpipää, H., Koponen, T., Aro, M., Tolvanen, A., Aunola,
K., Poikkeus, A.M., Lerkkanen, M.K. and Nurmi, J.E.,
2017. Covariation between reading and arithmetic
skills from Grade 1 to Grade 7. Contemporary
Educational Psychology, 51, pp.131-140.
Lin, X., Gao, L., Tang, Z., Baker, J., Alkalai, M. and
Sorge, V., 2013. A text line detection method for
mathematical formula recognition. In Document
Analysis and Recognition (ICDAR), 2013 12th
International Conference on (pp. 339-343). IEEE.
Liu, Y., Lin, D. and Zhang, X., 2016. Morphological
awareness longitudinally predicts counting ability in
Chinese kindergarteners. Learning and Individual
Differences, 47, pp. 215–221.
Mullis, I.V., Martin, M.O., Foy, P. and Drucker, K.T.,
2012. PIRLS 2011 International Results in Reading.
International Association for the Evaluation of
Educational Achievement.
Myles, J.F., 2010. Bourdieu-Language-Media.
In Bourdieu, Language and the Media, pp. 9-22.
OECD (Organisation for Economic Co-operation and
Development), 2013. PISA 2012 Assessment and
Analytical Framework: Mathematics, reading, science,
problem solving and financial literacy, OECD Report.
Ozuru, Y., Dempsey, K. and McNamara, D. S., 2009.
Prior knowledge, reading skill, and text cohesion in
the comprehension of science texts. Learning and
Instruction, 19(3), pp. 228–242.
Piaget, J., 1920. Psychoanalysis in its relations with child
psychology. In Gruber, H. and Voneche, J.J., 1977.
The Essential Piaget. London: Routledge & Kegan
Paul.
Piaget, J., 1964. Part I: Cognitive development in children:
Piaget development and learning. Journal of Research
in Science Teaching, 2(3), pp. 176–186.
Rezaei, S., Derakhshan, A. and Bagherkazemi, M., 2011.
Critical Thinking in Language Education. Journal of
Language Teaching and Research, 2(4).
Teledahl, A., 2015. Different modes in teachers’
discussions of students’ mathematical texts. Teaching
and Teacher Education, 51, pp. 68–76.
Vellutino, F.R., Tunmer, W.E., Jaccard, J.J. and Chen, R.,
2007. Components of reading ability: Multivariate
evidence for a convergent skills model of reading
development. Scientific studies of reading, 11(1),
pp.3-32.
Vilenius-Tuohimaa, P. M., Aunola, K. and Nurmi, J. E.,
2008. The association between mathematical word
problems and reading comprehension. Educational
Psychology, 28(4), pp. 409–426.
Waters, A., 2006. Thinking and language learning. ELT
Journal, 60(4), pp. 319–327.
Wuttke, J., 2007. Uncertainty and bias in PISA. Hopmann,
Brinek, Retz ( eds.), pp.241-263.
Zinn, C., 2006. Supporting the formal verification of
mathematical texts. Journal of Applied Logic, 4(4), pp.
592–621.
CONAPLIN and ICOLLITE 2017 - Tenth Conference on Applied Linguistics and the Second English Language Teaching and Technology
Conference in collaboration with the First International Conference on Language, Literature, Culture, and Education
458