Learning and Extracting Priori-driven Representations

of Face Images to Understand the Human Visual

Recognition System

Carlos E. Thomaz

, Gilson A. Giraldi

, Duncan F. Gillies

, and Daniel Rueckert

FEI University Center, Sao Paulo, Brazil

National Laboratory of Scientiﬁc Computing, Rio de Janeiro, Brazil

Imperial College London, U.K.

Abstract. Faces are familiar objects that can be easily perceived and recognized

by humans. However, the computational modeling of such apparently natural and

heritable human ability remains challenging. This chapter shows theoretical and

empirical results about the processes underlying face perception using frontal

and well-framed images as stimuli. Exploring eye movements of a number of

participants on distinct classiﬁcation tasks, we have implemented a multivari-

ate statistical method that combines variance information with focused human

visual attention. Our experimental results carried out on publicly available face

databases have indicated that we might emulate the face perception processing as

a pattern-based coding scheme rather than a feature-based one to properly explain

the proﬁciency of the human visual system in recognizing face information.

1 Introduction

Similarities between facial images can be described as a high dimensional and sparse

statistical pattern recognition problem well addressed by humans but with non-trivial

scientiﬁc issues related to feature extraction and automatic coding of relevant infor-

mation, classiﬁcation and prediction of patterns, modeling and visual reconstruction of

discriminant subspaces. These issues are multidisciplinary and inherent to several ap-

plications in Computer Science, Psychology and Neuroscience, among others, with the

aim to explain and emulate how humans accomplish so successfully this discriminant

process of coding and decoding high dimensional visual patterns that may be metrically

very close to each other.

Although faces are expected to have a global and common spatial layout with all

their parts such as eyes, nose and mouth arranged consistently in a multidimensional

representation, speciﬁc variations in local parts are fundamental to explain our percep-

tion of each individual singularity, or groups of individuals when distinguishing, for

example, between gender or facial expression [9–15]. To understand and emulate how

humans accomplish this process of coding faces, it seems necessary to investigate and

develop computational extraction methods that explore the combination and relative in-

teraction of the global and local types of information, considering as well the embedded

visual knowledge that might be behind the human face perception task under investi-

gation. For instance, recent research on human face processing using eye movements

Thomaz, C., Giraldi, G., Gillies, D. and Rueckert, D.

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System.

DOI: 10.5220/0008861900420055

In OPPORTUNITIES AND CHALLENGES for European Projects (EPS Portugal 2017/2018 2017), pages 42-55

ISBN: 978-989-758-361-2

has consistently demonstrated the existence of preferred facial regions or pivotal areas

involved in successful identity, gender and facial expression human recognition [2–5].

In fact, these works have provided evidence that humans analyze faces focusing their

visual attention on a few inner facial regions, mainly on the eyes, nose and mouth, and

such sparse spatial ﬁxations are not equally distributed and depend on the face percep-

tion task under investigation.

In this context, this chapter describes a uniﬁed computational method that com-

bines global and local variance information with eye-tracking ﬁxations to represent

task-driven dimensions in a multidimensional physiognomic face-space. Our uniﬁed

computational method allows the exploration of two distinct embedded knowledge ex-

tractions, named here feature- and pattern-based information processing, to disclose

some evidence of how humans perceive faces visually. The eye-tracking ﬁxations are

based on measuring eye movements of a number of participants and trials to frontal and

well-framed face images during separate gender and facial expression classiﬁcation

tasks. In all the automatic classiﬁcation experiments carried out to evaluate the uniﬁed

computational method proposed, we have considered: different numbers of face-space

dimensions; gender and facial expression sparse spatial ﬁxations; and randomly gener-

ated versions of the distribution of the human eye ﬁxations spread across faces. These

randomly generated spatial attention maps pose the alternative analysis where there

are no preferred viewing positions for human face processing, contrasting the literature

ﬁndings.

The remaining of this chapter is organized as follows. In section 2, we describe the

eye-tracking apparatus, participants, and frontal face stimuli used to generate different

ﬁxation images depending on the classiﬁcation task. Then, section 3 translates in a uni-

ﬁed method the combination of face-space dimensions and eye movements sources of

information for feature- and pattern-based multivariate computational analysis. Section

4 describes the eye-tracking experiments carried out and the training and test face sam-

ples used from distinct image datasets to evaluate the automatic classiﬁcation accuracy

of the method. All the results have been analyzed in section 5. Finally, in section 6, we

conclude the paper, summarizing its main ﬁndings.

2 Materials

In this section, we describe mainly the eye-tracking apparatus, participants and frontal

face stimuli used to generate different ﬁxation images with distinct classiﬁcation tasks.

2.1 Apparatus

Eye movements were recorded with an on-screen Tobii TX300 equipment that com-

prises an eye tracker unit integrated to the lower part of a 23in TFT monitor. The eye

tracker performs binocular tracking at a data sampling rate of 300Hz, and has minimum

ﬁxation duration of 60ms and maximum dispersion threshold of 0.5 degrees. These are

the eye tracker defaults for cognitive research. A standard keyboard was used to collect

participants responses. Calibration, monitoring and data collection were performed as

implemented in the Tobii Studio software running on an attached notebook (Core i7,

16Gb RAM and Windows 7).

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

2.2 Participants

A total number of 44 adults (26 males and 18 females) aged from 18 to 50 years par-

ticipated in this study on a voluntary basis. All participants were undergraduate and

graduate students or staff at the university and had normal or corrected to normal vi-

sion. Written informed consent was obtained from all participants.

2.3 Training Face Database

Frontal images of the FEI face database [16] have been used to carry out the eye-

movements stimuli. This database contains 400 frontal 2D face images of 200 subjects

(100 men and 100 women). Each subject has two frontal images, one with a neutral or

non-smiling expression and the other with a smiling facial expression. We have used

a rigidly registered version of this database where all these frontal face images were

previously aligned using the positions of the eyes as a measure of reference. The regis-

tered and cropped images are 128 pixels wide and 128 pixels high and are encoded in

gray-scale using 8-bits per pixel. Figure 1 illustrates some of these well-framed images.

Fig. 1. A sample of the face stimuli used in this work.

2.4 Stimuli

Stimuli consisted of 120 frontal face images taken from the training face database. All

the stimuli were presented centralized on a black background using the 23in TFT mon-

itor with a screen resolution of 1280x1024 pixels. To improve the stimuli visualization

on the TFT monitor all the face images were resized to 512x512 pixels. Presentation of

the stimuli was controlled by the Tobii Studio software.

2.5 Spatial Attention Maps

Eye-movements were processed directly from the eye tracker using the Tobii Studio

software. Fixation was deﬁned by the standard Tobii ﬁxation ﬁlter as two or more con-

secutive samples falling within a 50-pixel radius. We considered only data from partici-

pants for whom on average 25% or more of their gaze samples were collected by the eye

tracker. One participant (1 female) did not meet this criterion and was excluded from

the analysis. The standard absolute duration heat maps available at the Tobii Studio

software were used to describe the accumulated ﬁxation duration on different locations

in the face images at the resolution of 512x512 pixels. These absolute duration heat

maps were averaged from all participants and from all face stimuli, generating different

ﬁxation images, called here spatial attention maps, depending on the classiﬁcation task.

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

3 Method

The computational method combines face images variance with the spatial attention

maps modeled as feature- and pattern-based information sources in a multidimensional

representation of the face-space physiognomic dimensions [17, 18]. It builds on our

previous works [16, 19, 4] of incorporating task-driven information for a uniﬁed multi-

variate computational analysis of face images using human visual processing.

3.1 Face-space Dimensions

We have used principal components to specify the face-space physiognomic dimensions

[17, 18] because of their psychological plausibility for understanding the human face

image multidimensional representation [20–23, 18], where the whole face is perceived

as a single entity [24].

A single entity face image, with c pixels wide and r pixels high, can be described

mathematically as a single point in an n-dimensional space by concatenating the rows

(or columns) of its image matrix [20], where n = c × r. The coordinates of this point

describe the values of each pixel of the image and form a n-dimensional 1D vector

x = [x

, x

, . . . , x

]

Let an N × n data matrix X be composed of N face images with n pixels, that is,

X = (x

, x

, . . . , x

)

. This means that each column of matrix X represents the val-

ues of a particular pixel all over the N images. Let this data matrix X have covariance

matrix

S =

(N − 1)

i=1

− ¯x)(x

− ¯x)

, (1)

where ¯x is the grand mean vector of X given by

¯x =

i=1

= [¯x

, ¯x

, . . . , ¯x

]

. (2)

Let this covariance matrix S have respectively P and Λ eigenvector and eigenvalue

matrices, that is,

SP = Λ. (3)

It is a proven result that the set of m (m ≤ n) eigenvectors of S, which corresponds

to the m largest eigenvalues, minimizes the mean square reconstruction error over

all choices of m orthonormal basis vectors [25]. Such a set of eigenvectors P =

, p

, . . . , p

] that deﬁnes a new uncorrelated coordinate system for the data ma-

trix X is known as the (standard) principal components.

The calculation of the standard principal components is based entirely on the data

matrix X and does not express any domain speciﬁc information about the face percep-

tion task under investigation. We describe next modiﬁcations on this calculation that

handle global and local facial differences using feature- and pattern-based combina-

tions of variance and the spatial attention maps.

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

3.2 Feature-based Combination of Variance and Spatial Attention Map (wPCA)

We can rewrite the sample covariance matrix S described in equation (1) in order to

indicate the spatial association between the n pixels in the N samples as separated n

features. When n pixels are observed on each face image, the sample variation can be

described by the following sample variance-covariance equation [26]:

S = {s

} =

(

(N − 1)

i=1

− ¯x

)(x

− ¯x

)

, (4)

for j = 1, 2, . . . , n and k = 1, 2, . . . , n. The covariance s

between the j

and k

pixels reduces to the sample variance when j = k, s

= s

for all j and k, and the

covariance matrix S contains n variances and

n(n − 1) potentially different covari-

ances [26]. It is clear from equation (4) that each pixel deviation from its mean has the

same importance in the standard sample covariance matrix S formulation.

To combine these pixel-by-pixel deviations with the visual information captured by

the eye movements, we ﬁrst represent, analogously to the face images, the correspond-

ing spatial attention map as a n-dimensional 1D w vector, that is,

w = [w

, w

, . . . , w

]

, (5)

where w

≥ 0 and

j=1

= 1. Each w

describes the visual attention power of

the j

pixel separately. Thus, when n pixels are observed on N samples, the sample

covariance matrix S

∗

can be described by [19, 4]

∗



∗



(

(N − 1)

i=1

√

− ¯x

)

√

− ¯x

)

. (6)

It is important to note that s

∗

= s

∗

for all j and k and consequently the matrix S

∗

is a

nxn symmetric matrix. Let S

∗

have respectively P

∗

and Λ

∗

eigenvector and eigenvalue

matrices, as follows:

∗T

∗

= Λ

∗

. (7)

The set of m

∗

≤ n) eigenvectors of S

∗

, that is, P

∗

= [p

∗

, p

∗

, . . . , p

∗

], which

corresponds to the m

∗

largest eigenvalues, deﬁnes the orthonormal coordinate sys-

tem for the data matrix X called here feature-based principal components or, simply,

wPCA.

The step-by-step algorithm for calculating these feature-based principal compo-

nents can be summarized as follows:

1. Calculate the spatial attention map w = [w

, w

, . . . , w

]

by averaging the ﬁxa-

tion locations and durations from face onset from all participants and from all face

stimuli for the classiﬁcation task considered;

2. Normalize w, such that w

≥ 0 and

j=1

= 1, by replacing w

with

j=1

;

3. Standardize all the n variables of the data matrix X such that the new variables

have ¯x

= 0, for j = 1, 2, . . . , n. In other words, calculate the grand mean vector

as described in Equation (2) and replace x

with z

, where z

= x

− ¯x

for

i = 1, 2, . . . , N and j = 1, 2, . . . , n;

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

4. Spatially weigh up all the standardized z

variables using the vector w calculated

in step 2, that is, z

∗

= z

√

;

5. The feature-based principal components P

∗

are then the eigenvectors correspond-

ing to the m

∗

largest eigenvalues of Z

∗

)

, where Z

∗

= {z

∗

, z

∗

, . . . , z

∗

}

and

∗

≤ n.

3.3 Pattern-based Combination of Variance and Spatial Attention Map (dPCA)

We can handle the problem of combining face samples variance with the perceptual

processing captured by the eye movements assuming a pattern-based approach rather

than a feature-based one as previously described. Here, we would like to investigate the

spatial association between the features with their perceptual interaction preserved, not

treated separately.

The set of n-dimensional eigenvectors P = [p

, p

, . . . , p

] is deﬁned in equation

(3) as the standard principal components, and the n-dimensional w spatial attention

representation, where w = [w

, w

, . . . , w

]

, is described in equation (5).

To determine the perceptual contribution of each standard principal component we

can calculate how well these face-space directions align with the corresponding spatial

attention map, that is, how well p

, p

, . . . , p

align with w, as follows:

= w

· p

, (8)

= w

· p

...

= w

· p

Coefﬁcients k

, where i = 1, 2, . . . , m, that are estimated to be 0 or approximately 0

have negligible contribution, indicating that the corresponding principal component di-

rections are not relevant. In contrast, largest coefﬁcients (in absolute values) indicate

that the corresponding variance directions contribute more and consequently are impor-

tant to characterize the human perceptual processing.

We select then as the ﬁrst principal components [16] the ones with the highest visual

attention coefﬁcients, that is,

= [p

, p

, ..., p

] = arg max



, (9)

where {p

|i = 1, 2, . . . m

}is the set of eigenvectors of S corresponding to the largest

coefﬁcients |k

| ≥ |k

| ≥ . . . ≥ |k

| calculated in Equation (8), where (m

< m ≤

n).

The set of m

eigenvectors of S, that is, P

= [p

, p

, . . . , p

], deﬁnes the or-

thonormal coordinate system for the data matrix X called here pattern-based principal

components or, simply, dPCA.

The step-by-step algorithm for calculating these pattern-based principal compo-

nents can be summarized as follows:

1. Calculate the spatial attention map w = [w

, w

, . . . , w

]

by averaging the ﬁxa-

tion locations and durations from face onset from all participants and from all face

stimuli for the classiﬁcation task considered;

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

2. Normalize w, such that w

≥ 0 and

j=1

= 1, by replacing w

with

j=1

;

3. Calculate the covariance matrix S of the data matrix X and then its respectively P

and Λ eigenvector and eigenvalue matrices. Retain all the m non-zero eigenvectors

P = [p

, p

, . . . , p

] of S, where λ(j) > 0 for j = 1, 2, . . . , m and m ≤ n;

4. Calculate the spatial attention coefﬁcient of each non-zero eigenvector using the

vector w described in step 2, as follows: k

= w

· p

, for j = 1, 2, . . . , m;

5. The pattern-based principal components P

= [p

, p

, . . . , p

], where m

m, are then the eigenvectors of S corresponding to the largest coefﬁcients |k

| ≥

| ≥ . . . ≥ |k

3.4 Geometric Idea

We show in Figure 2 the main geometric idea of the feature- and pattern-based principal

components. The hypothetical illustration presents samples depicted by triangles along

with the spatial attention vector w represented in red.

It is well known that the standard principal components [p

, p

] are obtained by

rotating the original coordinate axes until they coincide with the axes of the constant

density ellipse described by all the samples.

On the one hand, the feature-based approach uses the information provided by w

for each original variable isolated to ﬁnding a new orthonormal basis that is not neces-

sarily composed of the same principal components. In other words, in this hypothetical

example the inﬂuence of the variable deviations on the x

axis will be relatively mag-

niﬁed in comparison with x

because w is better aligned to the original x

axis than x

one, that is, |w

| > |w

|. This is geometrically represented in the ﬁgure by large gray

arrows, which indicate visually that the constant density ellipse will be expanded in the

axis and shrunk in the x

axis, changing the original spread of the samples illus-

trated in black to possibly the constant density ellipse represented in blue. Therefore,

the feature-based principal components [p

∗

, p

∗

] would be different from the standard

principal components [p

, p

], because p

∗

is expected to be much closer to the x

di-

rection than x

, providing a new interpretation of the original data space based on the

power of each variable considered separately.

On the other hand, the pattern-based approach uses the information provided by w

as a full two-dimensional pattern, ranking the standard principal components by how

well they align with the entire pattern captured by w across the two-dimensional space

samples. Since w as a whole is better aligned to the second standard principal compo-

nent p

direction than the ﬁrst one p

, i.e. |w

· p

| > |w

· p

|, then p

= p

and

= p

. Therefore, the pattern-based approach selects as its ﬁrst principal component

the standard variance direction that is most efﬁcient for describing the whole spatial

attention map, which comprises here the entire pattern of the eye movements across the

whole faces, rather than representing all the pixels visual attention power as unit apart

features.

4 Experiments

The experiments consisted of two separate and distinct classiﬁcation tasks: (1) gender

(male versus female) and (2) facial expression (smiling versus neutral). During the gen-

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

Fig. 2. An hypothetical example that shows samples (depicted by two-dimensional points rep-

resented by triangles) and the geometric idea of the feature- and pattern-based approaches. The

former magniﬁes or shrinks the deviation of each variable separately depending on the direction

of w, where |w

| > |w

|, and [p

, p

] and [p

∗

, p

∗

] are respectively the standard and feature-

based principal components. The latter re-ranks the standard principal components [p

, p

] by

how well such directions align with w as a whole, where |w

· p

| > |w

· p

| and [p

, p

]

are consequently the pattern-based principal components.

der experiments, 60 faces equally distributed among gender were shown on the Tobii

eye tracker, all with neutral facial expression (30 males and 30 females). For the facial

expression experiments, all the 60 faces shown were equally distributed among gen-

der and facial expression (15 males smiling, 15 females smiling, 15 males with neutral

expression and 15 females with neutral expression).

Participants were seated in front of the eye tracker at a distance of 60cm and initially

ﬁlled out an on-screen questionnaire about their gender, ethnicity, age and motor pre-

dominance. They were then instructed to classify the faces using their index ﬁngers to

press the corresponding two keys on the keyboard. Participants were asked to respond

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

as accurately as possible and informed that there was no time limit for their responses.

Each task began with a calibration procedure as implemented in the Tobii Studio soft-

ware. On each trial, a central ﬁxation cross was presented for 1 second followed by a

face randomly selected for the corresponding gender or facial expression experimental

samples. The face stimulus was presented for 3 seconds in both tasks and was followed

by a question on a new screen that required a response in relation to the experiment,

that is, ”Is it a face of a (m)ale or (f)emale subject?” or ”Is it a face of a (s)miling or

(n)eutral facial expression subject?”. Each response was subsequently followed by the

central ﬁxation cross, which preceded the next face stimulus until all the 60 faces were

presented for each classiﬁcation task. Each participant completed 60 trials for the gen-

der classiﬁcation task and 60 trials for the facial expression one with a short break in

between the tasks.

We adopted a 10-fold cross validation method drawn at random from the gender

and smiling corresponding sample groups to evaluate the automatic classiﬁcation accu-

racy of the feature- and pattern-based dimensions. Additionally to the FEI face samples

described previously and used for training only, we have used frontal face images of

the well-known FERET database [27], registered analogously to the FEI samples, for

testing. In the FERET database, we have also considered 200 subjects (107 men and

93 women) and each subject has two frontal images (one with a neutral or non-smiling

expression and the other with a smiling facial expression), providing a total of two dis-

tinct training and test sets of 400 images to perform the gender and expression automatic

classiﬁcation experiments. We have assumed that the prior probabilities and misclassi-

ﬁcation costs are equal for both groups. On the principal components subspace, the

standard sample group mean of each class has been calculated from the corresponding

training images and the minimum Mahalanobis distance from each class mean [25] has

been used to assign a test observation to either the smiling and non-smiling classes in

the facial expression experiment, or to either the male or female classes in the gender

experiment.

In all the automatic classiﬁcation experiments, we have considered different num-

bers of principal components, both gender and facial expression task-driven spatial at-

tention maps accordingly, and their corresponding randomly generated versions with

the distribution of the human eye ﬁxations uniformly spread across faces to pose the

alternative analysis where there are no preferred viewing positions for human face pro-

cessing.

5 Results

The classiﬁcation results of the 43 participants on the gender and facial expression

tasks were all above the chance level (50%). Their performance on the male versus fe-

male (gender) and smiling versus non-smiling (facial expression) tasks were on average

97.2%(±2.3%) and 92.8%(±4.3%), respectively.

Figure 3 illustrates the spatial attention maps (left side) along with their correspond-

ing randomly generated versions (right side) used to calculate the feature- and pattern-

based principal components. The spatial attention maps (left) are summary statistics

that describe the central tendency of the ﬁxation locations and durations from face onset

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

Fig. 3. An illustration of the spatial attention maps (left) and their corresponding randomly gen-

erated versions (right). The upper and lower panels describe the facial expression and gender

classiﬁcation tasks, respectively, superimposed on the grand mean face of the training database

used.

from all participants and from all face stimuli after 3 seconds for the facial expression

(top panel) and gender (bottom) classiﬁcation tasks. We have disregarded the ﬁrst two

ﬁxations of all participants to avoid the central cross bias. There are location similarities

in the manner all the faces were perceived, highlighting relevant proportion of ﬁxations

directed at mainly the pivotal areas of both eyes, nose and mouth. These results show

that participants made slightly different ﬁxations in the two classiﬁcation tasks on these

areas known as optimal for human processing of the entire faces [1, 2, 5]. In contrast,

as expected, the randomly generated versions (right) of the spatial attention maps are

uniformly distributed, showing essentially a sub-sampling of the entire face without any

preferred features or viewing positions.

Figure 4 shows the recognition rates of the facial expression (top panel) and gen-

der experiments (bottom panel) for the feature- and pattern-based principal components

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

using the spatial attention maps and their corresponding random versions. The number

of principal components considered varied from 20 to 240 because all the recognition

rates leveled off or decreased with additional components. We can see that both feature-

and pattern-based automatic mappings of the high-dimensional face images into lower-

dimensional spaces are accurately equivalent, with no signiﬁcant statistical difference

on their recognition rates, when using the facial expression and gender spatial attention

maps to highlight accordingly the preferred inner face regions for automatic classiﬁca-

tion. In other words, both processings have shown to be computationally effective to

automatically classify the facial expression and gender samples used.

However, the feature-based behavior is noteworthy when using the random versions

of the aforementioned maps. In Figure 4, there is no statistical difference between the

feature-based and its random version of results on the facial expression experiments

and, in fact, there is some statistical signiﬁcant improvement (p < 0.05) on its auto-

matic recognition performance when using the randomly generated version of the spa-

tial attention maps in the gender experiments. On the condition of analyzing frontal and

well-framed face images, the results indicate that the feature-based approach shows no

speciﬁc exploitation of the manner in which all the participants have viewed the entire

faces when classifying the samples. These results suggest indeed that there is no crit-

ical region or pivotal areas involved in successful gender and facial expression human

recognition, despite the clear evidence of focused visual attention on the eyes, nose and

mouth described in the previous Figure 3.

Interestingly, though, the ﬁndings of the pattern-based dimensions are exactly the

opposite. We can see clearly in Figure 4 statistical differences between the pattern-based

and its random version results (p < 0.001) on both facial expression and gender exper-

iments, where the preferred participants ﬁxation positions augment considerably the

automatic recognition of their face-space dimensions when using the spatial attention

maps rather than their randomly generated versions. These results provide multivariate

statistical evidence that faces seem to be analysed visually using a pattern-based strat-

egy, instead of decomposing such information processing into separate and discrete

local features.

6 Conclusion

Exploring eye movements of a number of participants on gender and facial expression

distinct classiﬁcation tasks, we have been able to implement an automatic multivariate

statistical extraction method that combines variance information with sparse visual pro-

cessing about the task-driven experiment. The two methods for incorporation of the eye

tracking information described here are radically different: (1) weighting the individual

pixels can be considered a feature-based approach, because we are trying to improve

the face-space using the new knowledge; (2) ranking the features can be considered a

pattern-based approach, because we are seeking the best face-space directions to use.

It is well-known that the procedure of weighting the individual pixels works well

when the corresponding weights have signiﬁcant discriminant information. However,

our experimental results carried out on publicly available face databases have shown

that such procedure does not work using the spatial attention maps obtained from eye

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

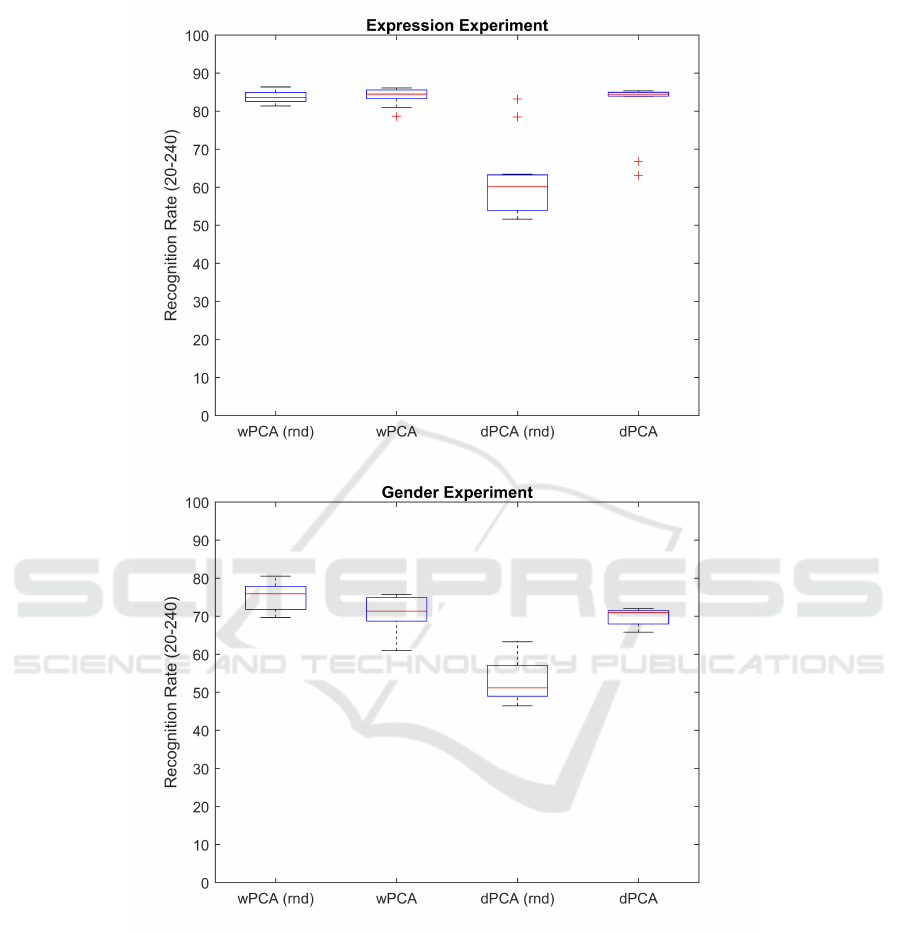
Fig. 4. Facial expression (top) and gender (bottom) boxplots of the recognition rates of feature-

based (wPCA) and pattern-based (dPCA) dimensions given the corresponding spatial attention

maps and their randomly generated versions (rnd). The number of principal components consid-

ered for automatic classiﬁcation varied from 20 to 240.

tracking. In fact, random weights can even outperform the attention maps when trying to

improve the face-space using this knowledge on a feature-by-feature method. Overall,

we must conclude that the ﬁxation points in human vision are not speciﬁc feature points

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System

chosen for their discriminant information, suggesting that the human visual recognition

system is pattern-based by nature.

Acknowledgements The authors would like to thank the ﬁnancial support provided by

FAPESP (2012/22377-6) and CNPq (309532/2014-0). This work is part of the New-

ton Advanced Fellowship (NA140147) appointed by the Royal Society to Carlos E.

Thomaz.

References

1. Hsiao, J.H.W., Cottrell, G.: Two ﬁxations sufﬁce in face recognition. Psychological Science

19 (2008) 998–1006

2. Peterson, M.F., Eckstein, M.P.: Looking just below the eyes is optimal across face recogni-

tion tasks. Proceedings of the National Academy of Sciences 109 (2012) E3314–E3323

3. Moreno, E.P., Ferreiro, V.R., Gutierrez, A.G.: Where to look when looking at faces: Visual

scanning is determined by gender, expression and task demands. Psicologica 37 (2016) 127–

150

4. Thomaz, C.E., Amaral, V., Gillies, D.F., Rueckert, D.: Priori-driven dimensions of face-

space: Experiments incorporating eye-tracking information. In: Proceedings of the Ninth

Biennial ACM Symposium on Eye Tracking Research & Applications. ETRA ’16 (2016)

279–282

5. Bobak, A.K., Parris, B.A., Gregory, N.J., Bennetts, R.J., Bate, S.: Eye-movement strategies

in developmental prosopagnosia and ”super” face recognition. The Quarterly Journal of

Experimental Psychology 70 (2017) 201–217

6. Crookes, K., McKone, E.: Early mature of face recognition: no childhood development of

holistic processing, novel face encoding, or face-space. Cognition 111 (2009) 219–247

7. Wilmer, J.B., Germine, L., Chabris, C.F., Chatterjee, G., Williams, M., Loken, E., Nakayama,

K., Duchaine, B.: Human face recognition ability is speciﬁc and highly heritable. Pro-

ceedings of the National Academy of Sciences of the United States of America 107 (2010)

5238–5241

8. McKone, E., Palermo, R.: A strong role for nature in face recognition. Proceedings of the

National Academy of Sciences of the United States of America 107 (2010) 4795–4796

9. Cabeza, R., Kato, T.: Features are also important: Contributions of featural and conﬁgural

processing to face recognition. Psychological Science 11(5) (2000) 429–433

10. Joseph, R.M., Tanaka, J.: Holistic and part-based face recognition in children with autism.

Journal of Child Psychology and Psychiatry 44(4) (2003) 529–542

11. Wallraven, C., Schwaninger, A., Bulthoff, H.H.: Learning from humans: Computational

modeling of face recognition. Network: Computation in Neural Systems 16(4) (2005) 401–

418

12. Maurer, D., OCraven, K.M., Grand, R., Mondloch, C.J., Springer, M.V., Lewis, T.L., Grady,

C.L.: Neural correlates of processing facial identity based on features versus their spacing.

Neuropsychologia 45(7) (2007) 1438–1451

13. Shin, N.Y., Jang, J.H., Kwon, J.S.: Face recognition in human: the roles of featural and

conﬁgurational processing. Face Analysis, Modelling and Recognition Systems 9 (2011)

133–148

14. Miellet, S., Caldara, R., Schyns, P.G.: Local jekyll and global hyde: The dual identity of face

recognition. Psychological Science 22(12) (2011) 1518–1526

EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects

15. Seo, J., Park, H.: Robust recognition of face with partial variations using local features and

statistical learning. Neurocomputing 129 (2014) 41–48

16. Thomaz, C.E., Giraldi, G.A.: A new ranking method for principal components analysis and

its application to face image analysis. Image and Vision Computing 28 (2010) 902–913

17. Valentine, T.: A uniﬁed account of the effects of distinctiveness, inversion, and race in

face recognition. The Quarterly Journal of Experimental Psychology Secion A: Human

Experimental Psychology 43 (1991) 161–204

18. Valentine, T., Lewis, M.B., Hills, P.J.: Face-space: A unifying concept in face recognition

research. The Quarterly Journal of Experimental Psychology (2015) 1–24

19. Thomaz, C.E., Giraldi, G.A., Costa, J.P., Gillies, D.F.: A priori-driven PCA. In: ACCV 2012

Workshops (LNCS 7729), Springer (2013) 236–247

20. Sirovich, L., Kirby, M.: Low-dimensional procedure for the characterization of human faces.

Journal of Optical Society of America 4 (1987) 519–524

21. Hancock, P.J.B., Burton, M.A., Bruce, V.: Face processing: Human perception and principal

component analysis. Memory and Cognition 24(1) (1996) 26–40

22. Todorov, A., Oosterhof, N.N.: Modeling social perception of faces. IEEE Signal Processing

Magazine March (2011) 117–122

23. Frowd, C.D.: Facial composite systems. Forensic facial identiﬁcation: Theory and practice

of identiﬁcation from eyewitnesses, composites and CCTV (2015) 43–70

24. Rakover, S.S.: Featural vs. conﬁgurational information in faces: A conceptual and empirical

analysis. British Journal of Psychology 93 (2002) 1–30

25. Fukunaga, K.: Introduction to Statistical Pattern Recognition. Academic Press, New York

(1990)

26. Johnson, R., Wichern, D.: Applied Multivariate Statistical Analysis. New Jersey: Prentice

Hall (1998)

27. Philips, P.J., Wechsler, H., Huang, J., Rauss, P.: The feret database and evaluation procedure

for face recognition algorithms. Image and Vision Computing 16(5) (1998) 295–306

Learning and Extracting Priori-driven Representations of Face Images to Understand the Human Visual Recognition System