Epoch Analysis and Accuracy 3 ANN Algorithm using Consumer

Price Index Data in Indonesia

Anjar Wanto

M. Fauzan

, Dedi Suhendro

, Iin Parlina

, Bahrudi Efendi Damanik

, Pani Akhiruddin

Siregar

, Nani Hidayati

Tunas Bangsa College of Computer Science, Sudirman street Blok A Number 1, 2, 3 Pematangsiantar,

North Sumatra - Indonesia

Academy of Informatics and Computer Management, Sudirman street Blok A Number 1, 2, 3 Pematangsiantar,

North Sumatra – Indonesia

Islamic College of Religion. Panca Budi Perdagangan, North Sumatra – Indonesia

iin@amiktunasbangsa.ac.id, bahrudiefendi@gmail.com, siregarpaniakhiruddin@yahoo.co.id,

nanihidayati@stikomtunasbangsa.ac.id

Keywords: Epoch, Akurasi, Backpropagation, CGFR, Resilient

Abstract: This research uses Backpropagation Algorithm, Conjugate Gradient Fletcher-Reeves (CGFR) and Resilient.

The purpose of this research is to see how much iteration and accuracy using this method compared with the

level of iteration and accuracy in previous research using only backpropagation algorithm with Conjugate

Gradient Fletcher-Reeves (CGFR) only in measuring consumer price index level. The data used as an example

in this study is the Consumer Price Index (CPI) data based on foodstuffs sourced from the Central Statistics

Agency Pematangsiantar Indonesia. There are 5 similar network architectures used in previous research and

in this study for more objective results, including 12-6-1, 12-15-1, 12-24-1, 12-33-1 and 12- 34-1. In the

previous study, the best architecture was 12-15-1, with epoch level when using backpropagation algorithm of

821 iterations with 75% accuracy and Gradient fletcher reeves of 2 iterations with 67% accuracy. While the

results of this study using the same architecture will be obtained epoch of 19 iterations with an accuracy of

50%. So it can be concluded that the use of backpropagation algorithm and gradient fletcher reeves to produce

iteration and accuracy level better when compared with Resilient Algorithm.

1 INTRODUCTION

The theory of ANN is inspired by the animal brain

neuron structure and its ability to deal with huge

information. This network achieves the purpose of

processing information by adjusting the relationship

between a large number of nodes connected to each

other, and it has the ability of self-learning and is

adaptive (Wang et al. 2017). Artificial Neural

Network is one of the artificial representations of the

human brain that always tries to simulate the learning

process in the human brain (Wanto, Windarto, et al.

2017). ANN approach can imitate any complex and

non-linear relationship through non-linear units

(neurons) and has been widely used in the forecasting

area (Wang et al. 2016) (Huang and Wu 2017)

(Wanto, Zarlis, et al. 2017).

Prediction (forecasting) is basically a presumption

about the occurrence of an event or event in the

future. Prediction (forecasting) is very helpful in

planning and decisionmaking activities of a policy.

There are several Artificial Neural Network

Algorithms that are often used for forecasting, among

others: Backpropagation Algorithm, Conjugate

Gradient Fletcher-Reeves (CGFR) And Resilient. It's

just between these 3 algorithms need to be tested

again the level of accuracy and speed in terms of

forecasting. Therefore the author will analyze the

epoch and accuracy of the 3 algorithms to obtain the

best results.

The data used to test the 3 algorithms is taken

from the Consumer Price Index data sourced from the

Central Statistics Agency Pematangsiantar-

Indonesia. Consumer Price Index (CPI) is one of the

important economic indicators that can provide

information about the price development of

goods/services paid by consumers in a region. The

calculation of the CPI is aimed at knowing the price

Wanto, A., Fauzan, M., Suhendro, D., Parlina, I., Damanik, B., Siregar, P. and Hidayati, N.

Epoch Analysis and Accuracy 3 ANN Algorithm using Consumer Price Index Data in Indonesia.

DOI: 10.5220/0010037400350041

In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 35-41

ISBN: 978-989-758-496-1

changes of a fixed group of goods/services commonly

consumed by the local community. The Consumer

Price Index (CPI) measures the average change in the

price paid by consumers for consumer goods and

services (Yaziz, Mohd, and Mohamed 2017).

Inflation is defined as a situation where generally the

price of goods has increased continuously. In order to

measure inflation, Statistics of Indonesia (BPS) use

the Consumer Price Index (CPI) (Bonar, Ruchjana,

and Darmawan 2017). Therefore predict the

Consumer Price Index is very important to do. This

research is expected to be widely used, both for local

government and for academics as study

material/research especially related to the economic

field and public policy.

In previous research, (Wanto, Zarlis, et al. 2017)

Conducting research to predict the Consumer Price

Index (CPI) of foodstuffs group using artificial neural

network backpropagation and Conjugate Gradient

Fletcher-Reeves. The research resulted in an accuracy

of 75% when using backpropagation method, the best

architecture used 12-15-1. While using the method

Fletcher-Reeves produce the level of 67% drain

which also use architectural model 12-15-1. The

drawback of this research is the result of less accurate

accuracy as it decreases, which is probably caused by

the inappropriate selection of network architecture.

2 RUDIMENTARY

2.1 Algoritma Backpropagation

Artificial Neural Network (ANN) is a computational

model, which is based on Biological Neural Network.

Artificial Neural Network is often called as Neural

Network (NN) (Sumijan et al. 2016).

Backpropagation (BP) algorithm was used to develop

the ANN model (Antwi et al. 2017). The typical

topology of BPANN (Backpropagation Artificial

Neural Network) involves three layers: input

layer,where the data are introduced to the network;

hidden layer, where the data are processed; and output

layer,where the results of the given input are

produced (Putra Siregar and Wanto 2017).

Backpropagation training method involves

feedforward of the input training pattern, calculation

and backpropagation of error, and adjustment of the

weights in synapses (Tarigan et al. 2017).

2.2 Algoritma Fletcher Reeves

The conjugate gradient method (CGM) is particularly

effcient and simple approaches with low storage,

good numerical performances and global convergent

properties for solving unconstrained optimization

problems (Keshtegar 2016). Conjugate gradient

method, as an efficient method, is used to solve

unconstrained optimization problems (Li, Zhang, and

Dong 2016). The conjugate gradient (CG) method

can be considered as an instance of the heavy ball

method with adaptive step size (Yao and Ning 2017).

In the above types, the weights update, for each

iteration, is made by the step size in the negative

gradient direction by learning rate. In the conjugate

gradient algorithms, this step size is modified by a

search function at every iteration such that the goal is

reached as early as possible within a few iterations

Fletcher-Reeves update (cgf) is much faster than

variable learning rate algorithms & resilient

backpropagation but requires a little more storage as

computations are more but suffers from the fact that

the results may vary from one problem to another

(Madhavan 2017).

2.3 Algoritma Resilient

The concept of resilient propagation was floated by

Riedmiller in 1993 (Riedmiller and Braun 1993),

which had been exploited in single (Igel and Husken

2003) and two dimension (Tripathi and Kalra 2011)

(Kantsila, Lehtokangas, and Saarinen 2004)

problems, where it proved its momentousness. This

paper proposes a quaternionic domain resilient

propagation algorithm (RPROP) for multilayered

feed-forward networks in quaternionic domain and

presents its exhaustive analysis through a wide

spectrum of benchmark problems containing three or

four dimension information and motion interpretation

in space.

The propagation of this procedure is based on the

sign of partial derivatives of error function instead of

its value as in back-propagation algorithm. The basic

idea of the proposed algorithm is to modify the

components of quaternionic weights by an amount Δ

(update value) with a view to decrease the overall

error and the sign of gradient of error function

indicates the direction of weight update. Without

increasing the complexity of algorithm, the proposed

RPROP algorithm is boosted by error-ependent

weight backtracking step, which accelerates the

training speed appreciably and provides better

approximation accuracy. The neural network

(ARENA et al. 1996) (Minemoto et al. 2016) and

backpropagation algorithm in quaternionic domain

(BP) (Cui, Takahashi, and Hashimoto 2013) has been

widely applied in problems dealing with three and

four dimensional information; recently its

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

comparison with quaternionic scaled conjugate

gradient (SCG) learning scheme is presented in (Popa

2016). This paper proposes an RPROP algorithm and

compare with BP and SCG algorithms through

application in 3D imaging and chaotic time series

predictions. Though, BP and SCG learning

algorithms can solve the typical class of 3D and 4D

dimensional problems, but the proposed ℍ-RPROP

algorithm has demonstrated its superiority over BP

and SCG in all respects, which is reported by different

statistical parameters (Kumar and Tripathi 2018).

3 RESEARCH METHODS

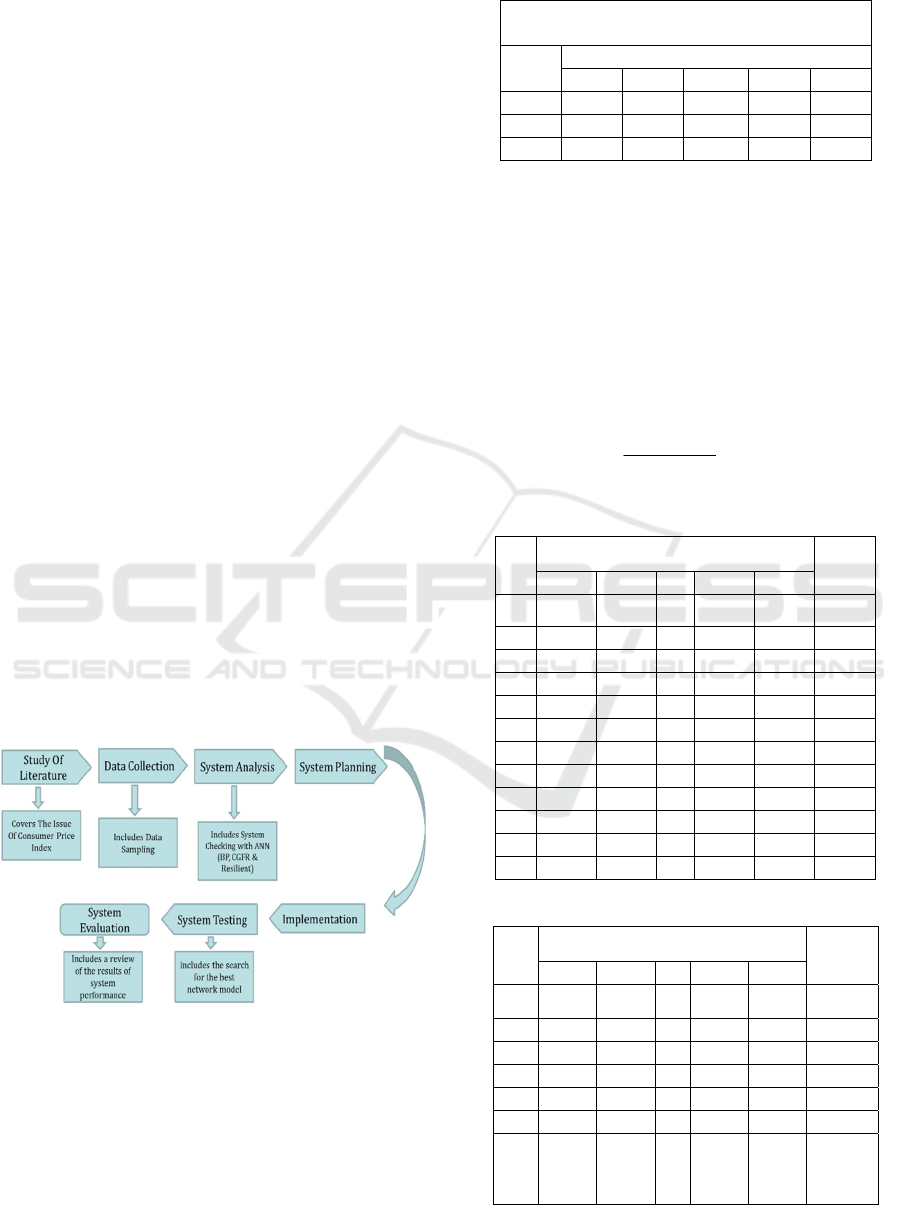
3.1 Research Framework

The research methodology can be seen in Figure 1.

The literature study used to collect data or sources

related to the topic raised was obtained from various

sources, journals, documentation books, and internet.

Then the sampling of data from the Central Bureau of

Statistics (BPS) -Indonesia, which will be processed

by using ANN (Backpropagation, Conjugate

Gradient Fletcher-Reeves and Resilient).

System design means designing inputs, file

structures, programs, procedures necessary to support

information systems. Implementation is an action or

implementation plan that has been prepared based on

system design. System testing is the evaluation phase

of the system architecture that has been built. System

Evaluation includes a review of the performance

results of the system.

Figure 1: Research Framework

3.2 Data Used

The data used in this paper is the Consumer Price

Index (CPI) data based on the Foodstuffs of

Pematangsiantar-Indonesia from 2014 to 2016

January to December.

Table 1: Data Used

Consumer Price Index 2014-2016

Sector: Foodstuff

Year

Month

Jan Feb ... Nov Dec

2014 116,22 116,03 ... 126,17 127,07

2015 125,95 119,60 ... 123,72 128,40

2016 130,65 128,53 ... 141.85 144,06

Based on table 1. It can be explained that, the

Consumer Price Index (CPI) dataset based on

Foodstuff Sector on 2014-2015 is used as training

with target 2015, while dataset on 2015-2016 is used

as testing with target 2016.

3.3 Normalization Data

The data will be normalized using the following

formula

(1)

Table 2: Normalization of training data

Data

Input

Target

Jan Feb ... Nov Dec

1 0,2285 0,2180

...

0,7771 0,8267 0,7649

2 0,2180 0,3012 ... 0,8267 0,7649 0,4148

3 0,3012 0,1000 ... 0,7649 0,4148 0,3470

4 0,1000 0,4435 ... 0,4148 0,3470 0,3216

5 0,4435 0,4253 ... 0,3470 0,3216 0,5560

6 0,4253 0,4396 ... 0,3216 0,5560 0,8250

7 0,4396 0,3939 ... 0,5560 0,8250 0,7418

8 0,3939 0,4358 ... 0,8250 0,7418 0,6657

9 0,4358 0,6315 ... 0,7418 0,6657 0,5565

10 0,6315 0,7771 ... 0,6657 0,5565 0,5940

11 0,7771 0,8267 ... 0,5565 0,5940 0,6420

12 0,8267 0,7649 ... 0,5940 0,6420 0,9000

Table 3: Normalization of testing data

Data

Input

Target

Jan Feb ... Nov Dec

1 0,3460 0,1517

...

0,2777 0,4209 0,4898

2 0,1517 0,1141 ... 0,4209 0,4898 0,4249

3 0,1141 0,1000 ... 0,4898 0,4249 0,4913

4 0,1000 0,2300 ... 0,4249 0,4913 0,4179

5 0,2300 0,3793 ... 0,4913 0,4179 0,4953

6 0,3793 0,3331 ... 0,4179 0,4953 0,5207

7 0,3331 0,2909

...

0,4953 0,5207

0,5280

0.8( )

'0.1







Epoch Analysis and Accuracy 3 ANN Algorithm using Consumer Price Index Data in Indonesia

Data

Input

Target

Jan Feb ... Nov Dec

8 0,2909 0,2303 ... 0,5207 0,5280 0,5925

9 0,2303 0,2511 ... 0,5280 0,5925 0,6433

10 0,2511 0,2777 ... 0,5925 0,6433 0,7146

11 0,2777 0,4209 ... 0,6433 0,7146 0,8324

12 0,4209 0,4898 ... 0,7146 0,8324 0,9000

3.4 Analysis and Results

3.4.1 Analysis

This study uses 5 architectural models, among others:

12-6-1, 12-15-1, 12-24-1, 12-33-1 and 12-34-1. This

training and testing parameter uses Target Minimum

Error = 0.001 - 0.01, Maximum Epoch = 10000 and

Learning Rate = 0, 01 when using backpropagation

algorithm. Whereas in conjugate gradient fletcher

reeves and resilient do not use learning rate. For more

details about the parameters used for the 3 algorithms

can be seen in the following description:

a. Backpropagation

net=newff(minmax(P),[Hidden,Target],{'tansig','logsi

g’},'traingd');

>> net.IW{1,1};

>> net.b{1};

>> net.LW{2,1};

>> net.b{2};

>> net.trainparam.epochs=10000;

>> net.trainparam.Lr=0.01;

>> net.trainParam.goal = 0.001;

>> net.trainParam.show = 1000;

>> net=train(net,P,T);

b. Conjugate Gradient Fletcher Reeves

net=newff(minmax(P),[Hidden,Target],{'tansig','logsi

g'},'traincgf');

>> net.IW{1,1}

>> net.b{1}

>> net.LW{2,1}

>> net.b{2}

>> net.trainParam.epochs=10000;

>> net.trainParam.goal = 0.001;

>> net=train(net,P,T)

c. Resilient

net=newff(minmax(P),[15,1],{‘tansig’,’logsig‘},’train

rp');

>> net.IW{1,1};

>> net.b{1};

>> net.LW{2,1};

>> net.b{2};

>> net.trainParam.epochs=10000;

>>net.trainParam.goal = 0.001;

>>net=train(net,P,T)

3.4.2 Results

Overall, the best results of 5 models of network

architecture using Backpropagation Algorithm,

Conjugate Gradient Fletcher-Reeves and Resilient

are 12-15-1, with 75% accuracy when

backpropagation, 67% using conjugate gradient

Fletcher-Reeves and 50% when using resilient. While

the epoch on the backpropagation method of 821

iterations, conjugate gradient fletcher reeves of 2

iterations and 19 iterations resilient

For more details can be seen in the following

picture:

Figure 2: Training with Algorithm Backpropagation

Figure 3: Training with Algorithm CGFR

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

Figure 4: Training with Algorithm Resilient

As for the comparison of Epoch and accuracy of

the 3 algorithms can be seen in the following table:

Table 4: Epoch Comparison

Architecture

Epoch (Iterations)

Backpropagation CGFR Resilient

12-6-1 5308 6 48

12-15-1 821 2 19

12-24-1 4999 15 29

12-33-1 961 16 16

12-34-1 1491 149 34

Table 5: Comparison of Accuracy

Architecture

Accurate

Backpropagation CGFR Resilient

12-6-1 50% 58% 42%

12-15-1 75% 67% 50%

12-24-1 58% 50% 50%

12-33-1 25% 42% 42%

12-34-1 25% 33% 50%

From table 4 and 5 it can be explained that the best

architectural model of 5 architectural models used is

12-15-1. The testing results of the 3 algorithms with

architectural model 12-15-1 can be seen in the

following table

Table 6: Results of Testing Backpropagation Algorithm

Pattern Target Output Error SSE

Results

Pattern 1 0,4898 0,4070 0,0828 0,0068477998 True

Pattern 2 0,4249 0,4827 -0,0578 0,0033414368 True

Pattern 3 0,4913 0,4482 0,0431 0,0018559787 True

Pattern 4 0,4179 0,1914 0,2265 0,0512834561 False

Pattern 5 0,4953 0,5469 -0,0516 0,0026668831 True

Pattern 6 0,5207 0,4776 0,0431 0,0018533107 True

Pattern 7 0,5280 0,5700 -0,0420 0,0017646425 True

Pattern 8 0,5925 0,4542 0,1383 0,0191387915 False

Pattern 9 0,6433 0,3757 0,2676 0,0716241896 False

attern 1

0,7146 0,6659 0,0487 0,0023724722 True

Pattern

0,8324 0,7609 0,0715 0,0051108283 True

Pattern

0,9000 0,8408 0,0592 0,0035046400 True

0,1713644294

75%

MSE 0,0142803691

Table 7: Results of CGFR Testing Algorithm

Pattern Target Output Error SSE

Results

Pattern 1 0,4898 0,4246 0,0652 0,0042447094 True

Pattern 2 0,4249 0,5277 -0,1028 0,0105689014 False

Pattern 3 0,4913 0,4969 -0,0056 0,0000315724 True

Pattern 4 0,4179 0,2228 0,1951 0,0380478218 False

Pattern 5 0,4953 0,5439 -0,0486 0,0023660319 True

Pattern 6 0,5207 0,4983 0,0224 0,0004995268 True

Pattern 7 0,5280 0,5951 -0,0671 0,0045034364 True

Pattern 8 0,5925 0,4892 0,1033 0,0106797800 False

Pattern 9 0,6433 0,4546 0,1887 0,0356178654 False

Pattern 10 0,7146 0,7284 -0,0138 0,0001902184 True

Pattern 11 0,8324 0,8018 0,0306 0,0009357516 True

Pattern 12 0,9000 0,8787 0,0213 0,0004536900 True

0,1081393054

67%

MSE 0,0090116088

Epoch Analysis and Accuracy 3 ANN Algorithm using Consumer Price Index Data in Indonesia

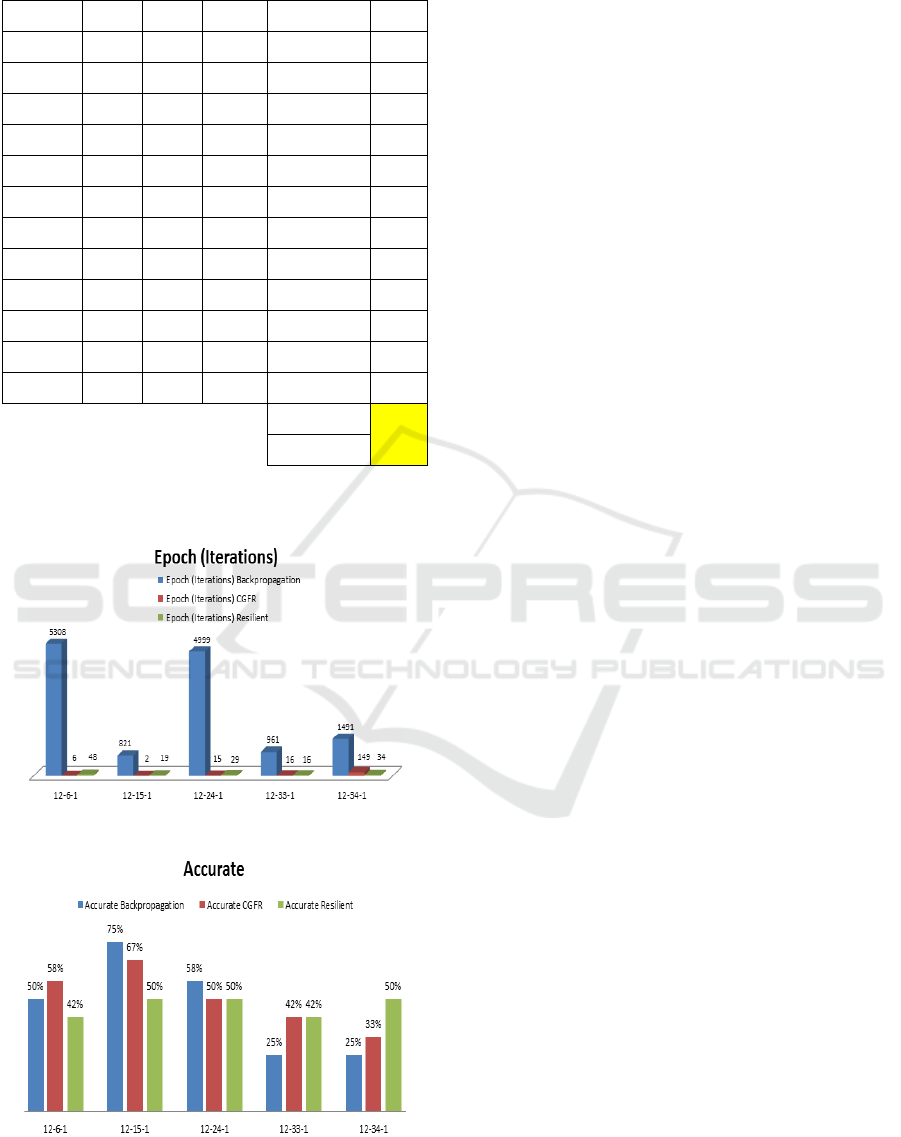
Table 8: Results Testing Algoritma Resilient

Pattern Target Output Error SSE

Results

Pattern 1

0,4898 0,5622 -0,0724 0,0052487947

True

Pattern 2

0,4249 0,6476 -0,2227 0,0495975894

False

Pattern 3

0,4913 0,5967 -0,1054 0,0111131506

False

Pattern 4

0,4179 0,3279 0,0900 0,0080925333

True

Pattern 5

0,4953 0,6973 -0,2020 0,0408209188

False

Pattern 6

0,5207 0,7009 -0,1802 0,0324900280

False

Pattern 7

0,5280 0,7581 -0,2301 0,0529495298

False

Pattern 8

0,5925 0,6464 -0,0539 0,0029005742

True

Pattern 9

0,6433 0,5372 0,1061 0,0112629316

False

Pattern 10

0,7146 0,7823 -0,0677 0,0045822027

True

Pattern 11

0,8324 0,8127 0,0197 0,0003876984

True

Pattern 12

0,9000 0,8738 0,0262 0,0006864400

True

0,2201323915

50%

MSE

,0183443660

The Epoch comparison graph and the accuracy of

the 3 algorithms can be seen in the following figure:

Figure 5: Graphic Level Epoch 3 Algorithm

Figure 6: Graphic Level Accuracy 3 Algorithm

4 CONCLUSIONS

The conclusions that can be drawn from this research

are as follows:

1. The accuracy of the Backpropagation

Algorithm is the best compared to CGFR and

Resilient. However, his training time is

relatively long. While CGFR algorithm can

accelerate the training, but the accuracy level

is still lower than backpropagation.

2. Network Architecture model used greatly

affect the level of training and testing.

3. By viewing Results test, it can be concluded

that the speed and Results accuracy varied on

5 experiments in each test performed.

REFERENCES

Antwi, Philip et al. 2017. “Estimation of Biogas and

Methane Yields in an UASB Treating Potato Starch

Processing Wastewater with Backpropagation

Artificial Neural Network.” Bioresource Technology

228:106–15. Retrieved

(http://dx.doi.org/10.1016/j.biortech.2016.12.045).

ARENA, Paolo, Riccardo CAPONETTO, Luigi

FORTUNA, Giovanni MUSCATO, and Maria

Gabriella XIBILIA. 1996. “Quaternionic Multilayer

Perceptrons for Chaotic Time Series Prediction.”

IEICE TRANSACTIONS on Fundamentals of

Electronics, Communications and Computer

79(10):1682–88.

Bonar, Hot, Budi Nurani Ruchjana, and Gumgum

Darmawan. 2017. “Development of Generalized Space

Time Autoregressive Integrated with ARCH Error

(GSTARI – ARCH) Model Based on Consumer Price

Index Phenomenon at Several Cities in North Sumatera

Province.” Statistics and Its Applications 1827:1–8.

Retrieved

(http://aip.scitation.org/doi/abs/10.1063/1.4979425).

Cui, Yunduan, Kazuhiko Takahashi, and Masafumi

Hashimoto. 2013. “Design of Control Systems Using

Quaternion Neural Network and Its Application to

Inverse Kinematics of Robot Manipulator.”

Proceedings of the 2013 IEEE/SICE International

Symposium on System Integration 527–32. Retrieved

(http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?

arnumber=6776617).

Huang, Daizheng and Zhihui Wu. 2017. “Forecasting

Outpatient Visits Using Empirical Mode

Decomposition Coupled with Backpropagation

Artificial Neural Networks Optimized by Particle

Swarm Optimization.” PLoS ONE 12(2):1–17.

Igel, Christian and Michael Husken. 2003. “Empirical

Evaluation of the Improved Rprop Learning

Algorithms.” Neurocomputing 50:105–23.

Kantsila, Arto, M. Lehtokangas, and J. Saarinen. 2004.

“Complex RPROP-Algorithm for Neural Network

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

Equalization of GSM Data Bursts.” Neurocomputing

61(1–4):339–60.

Keshtegar, B. 2016. “Limited Conjugate Gradient Method

for Structural Reliability Analysis.” Engineering with

Computers 33(3):1–9.

Kumar, Sushil and Bipin Kumar Tripathi. 2018. “High-

Dimensional Information Processing through Resilient

Propagation in Quaternionic Domain.” Journal of

Industrial Information Integration 1–9. Retrieved

(http://linkinghub.elsevier.com/retrieve/pii/S2452414

X17300870).

Li, Xiangli, Wen Zhang, and Xiaoliang Dong. 2016. “A

Class of Modified FR Conjugate Gradient Method and

Applications to Non-Negative Matrix Factorization.”

Computers and Mathematics with Applications

73(2):270–76. Retrieved

(http://dx.doi.org/10.1016/j.camwa.2016.11.017).

Madhavan, K. S. 2017. “Knowledge Based Prediction

through Artificial Neural Networks and Evolutionary

Strategy for Power Plant Applications.” Journal of

Scientific and Engineering Research 4(9):371–76.

Minemoto, Toshifumi, Teijiro Isokawa, Haruhiko

Nishimura, and Nobuyuki Matsui. 2016. “Feed

Forward Neural Network with Random Quaternionic

Neurons.” Signal Processing 1–10. Retrieved

(http://dx.doi.org/10.1016/j.sigpro.2016.11.008).

Popa, Calin-Adrian. 2016. “Scaled Conjugate Gradient

Learning for Quaternion - Valued Neural Networks.”

International Conference on Neural Information

Processing 243–52.

Putra Siregar, Sandy and Anjar Wanto. 2017. “Analysis

Accuracy of Artificial Neural Network Using

Backpropagation Algorithm In Predicting Process

(Forecasting).” International Journal Of Information

System & Technology 1(1):34–42.

Riedmiller, Martin and Heinrich Braun. 1993. “A Direct

Adaptive Method for Faster Backpropagation

Learning: The RPROP Algorithm.” IEEE International

Conference on Neural Networks - Conference

Proceedings 586–91.

Sumijan, Sumijan, AgusPerdana Windarto, Abulwafa

Muhammad, and Budiharjo Budiharjo. 2016.

“Implementation of Neural Networks in Predicting the

Understanding Level of Students Subject.”

International Journal of Software Engineering and Its

Applications 10(10):189–204. Retrieved

(http://dx.doi.org/10.14257/ijseia.2016.10.10.18).

Tarigan, Joseph, Nadia, Ryanda Diedan, and Yaya Suryana.

2017. “Plate Recognition Using Backpropagation

Neural Network and Genetic Algorithm.” Procedia

Computer Science 116:365–72. Retrieved

(https://doi.org/10.1016/j.procs.2017.10.068).

Tripathi, Bipin Kumar and Prem Kumar Kalra. 2011. “On

Efficient Learning Machine with Root-Power Mean

Neuron in Complex Domain.” IEEE Transactions on

Neural Networks 22(5):727–38.

Wang, Shouxiang, Na Zhang, Lei Wu, and Yamin Wang.

2016. “Wind Speed Forecasting Based on the Hybrid

Ensemble Empirical Mode Decomposition and GA-BP

Neural Network Method.” Renewable Energy 94:629–

36. Retrieved

(http://dx.doi.org/10.1016/j.renene.2016.03.103).

Wang, Zhen-Hua, Dian-Yao Gong, Xu Li, Guang-Tao Li,

and Dian-Hua Zhang. 2017. “Prediction of Bending

Force in the Hot Strip Rolling Process Using Artificial

Neural Network and Genetic Algorithm (ANN-GA).”

The International Journal of Advanced Manufacturing

Technology 1–14. Retrieved

(http://link.springer.com/10.1007/s00170-017-0711-

5).

Wanto, Anjar, Agus Perdana Windarto, Dedy Hartama, and

Iin Parlina. 2017. “Use of Binary Sigmoid Function

And Linear Identity In Artificial Neural Networks For

Forecasting Population Density.” International Journal

Of Information System & Technology 1(1):43–54.

Wanto, Anjar, Muhammad Zarlis, Sawaluddin, and Dedy

Hartama. 2017. “Analysis of Artificial Neural Network

Backpropagation Using Conjugate Gradient Fletcher

Reeves in the Predicting Process.” Journal of Physics:

Conference Series 930(1):1–7.

Yao, Shengwei and Liangshuo Ning. 2017. “An Adaptive

Three-Term Conjugate Gradient Method Based on Self-

Scaling Memoryless BFGS Matrix.” Journal of

Computational and Applied Mathematics 1–27.

Retrieved (https://doi.org/10.1016/j.cam.2017.10.013).

Yaziz, Mohd, Bin Mohd, and Zulkifflee Bin Mohamed.

2017. “Unit Roots and Co-Integration Tests : The

Effects of Consumer Price Index ( CPI ) on Non-

Performing Loans ( NPL ) in the Banking Sector in

Malaysia.” Journal of Advanced Statistics 2(1):16–25.

Epoch Analysis and Accuracy 3 ANN Algorithm using Consumer Price Index Data in Indonesia