Analysis of Combination RSA Algorithm using EM2B Keys Genertor

Algorithm in Data Encription

Elwin Yunith Purba

, Syahril Efendi

, Pahala Sirait

, Rahmad W. Sembiring

Department of Informatics Engineering, “Universitas Sumatera Utara”

Jl. Universitas Kampus USU, Medan, 20155, Sumatera Utara

Politeknik Negeri Medan, Medan-Indonesia

Keywords: Cryptography, Encryption, Decryption, RSA Algorithm, EM2B Key Generator.

Abstract: In this increasingly sophisticated era almost all circles of government, industry, business to individual

companies do computer work. In addition to the advantages that can be obtained from the use of computers,

the most important thing to note is part of the security, if information / data stored on the computer

damaged due to interference from hackers it can lead to huge losses as well. There are many cryptographic

algorithms such as One Time Pad, RC4, RSA, and so on that are considered really capable of maintaining

the security and confidentiality of the data. Therefore cryptographers are trying to create complex

algorithms to better ensure their safety. Of the many public key cryptography algorithms ever made, the

most popular algorithm is the RSA algorithm. RSA algorithm is a modern cryptographic algorithm that is

often used for data security, until now still no one can solve it. RSA algorithm security lies in the difficulty

of factoring large numbers into prime factors. The factoring is done to obtain private key. During the

factoring of large numbers into prime factors has not found the right algorithm, so long as it is also RSA

algorithm security is guaranteed. The combination of RSA algorithm with EM2B Key Generator can secure

data more difficult to solve, and able to overcome the problem of execution time of encryption and

decryption.

1 INTRODUCTION

Information Technology has caused a change and a

way of looking at human life as well as an

organization. Such rapid development brought the

world into a new era faster than ever imagined. Such

a computer that not only serves as a data processing

tool, but has become a major weapon in competing.

This is because with the computer can simplify and

accelerate a job in accessing information (Pahrizal,

David Pratama, 2016). Of the many advantages

derived from the use of technology, not least the

opportunity losses contained in it either a small loss

or a big loss can even lead to someone lose

everything. Some examples of hacking cases in 2016

include Ransomware emerges as a top cyber threat

to business, UK second only to US in DDoS attacks,

412 million user accounts exposed in FriendFinder

Networks hack, Financial Conduct Authority

concerned about cyber security of banks and other

cases caused by the weakness of the security system.

For that required a computer security system.

Security of data in a computer is very important to

protect the data from other parties that do not have

the authority to determine the content of the data

(Zaeniah, Bambang Eka Purnama, 2015). Security

concerns relate to risk areas such as external data

storage, dependency on the public internet, lack of

control, multi-tenancy and integration with internal

security (K Hashizume et al, 2013).

2 LITERATURE REVIEW

Cryptography from Greek , "hidden, secret"

respectively is the practice and study of techniques

for secure communication in the presence of third

parties (called adversaries). More generally, it is

about constructing and analyzing protocols that

overcome the influence of adversaries and which are

related to various aspects in information security

such as data confidentiality, data integrity,

authentication, and non-repudiation. Modern

cryptography intersects the disciplines of

122

Purba, E., Efendi, S., Sirait, P. and Sembir ing, R.

Analysis of Combination RSA Algorithm using EM2B Keys Genertor Algorithm in Data Encription.

DOI: 10.5220/0010039401220128

In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 122-128

ISBN: 978-989-758-496-1

mathematics, computer science, and electrical

engineering. Applications of cryptography include

ATM cards, computer passwords, and electronic

commerce (M. Preetha, M. Nihiya, 2013).

Cryptography is one field of science that studies

about information security / data to avoid the adverse

effects of misuse of information by irresponsible

parties. Cryptography has an important role in

maintaining the confidentiality of information both in

the computer and at the time of transaction data.

Cryptography also uses techniques applied for

encryption and decryption (William Stallings, 2011).

In the field of cryptography there are several

techniques available for encryption / decryption.

This technique can generally be grouped into two

major groups, namely conventional and public key

cryptography (Sundram Prabhadevi, Rahul De,

Pratik Shah, 2013). To determine the Cryptographic

algorithm that will be used in data security system in

addition to consideration of strength against

Cryptanalis and Bruteforce attacks is no less

important is the consideration of speed. At present

there are various algorithms of cryptography as well

as symmetry and asymmetry. If a cryptographic

algorithm is believed to be robust, but it is known to

be slow in its encoding process it will not be user

choice. This consideration of speed will be more

important, if the use of Cryptographic algorithms

concerning computer networks, especially on clien-

server architecture (K Hashizume et al, 2013).

RSA is one of the modern cryptographic

algorithms that until now is still widely developed

by researchers. The RSA algorithm was made by

three researchers from MIT (Massachusetts Institute

of Technology) in 1976. The name RSA is an

abbreviation of the name of the three inventors,

namely Rivest, Shamir, and Adleman. RSA

algorithms do factoring of very large numbers into

prime factors. Factoring is done to obtain private key

(Muhammad Arief, Fitriyani, Nurul Ikhsan, 2015).

2.1 Rivest-Shamir-Adleman (RSA)

The RSA is an algorithm used by modern computers

to encrypt and decrypt. It is a type of an asymmetric

cryptographic algorithm. RSA algorithm includes

two keys a public key and a private key. The public

key is distributed to all so will be known to

everyone, it is used to encrypt datas. Datas

encrypted with public key only decrypted with

private key (S. Kamara, and K. Lauter, 2010). RSA

can be used for digital signatures, key exchange, or

encryption of small block data. The size of the key

that is used by RSA algorithm is variable not fixed

and also the size of the encryption block. RSA has

been widely used for establishing a secure

communications channel and for authentication and

the identity of the service provider over insecure

communication medium (K., Dr Ch., and S. Yogesh,

2013). In proposed scheme RSA algorithm is used to

find out the key pair for both mobile user and third

party auditor. These keys are used to encrypt and

decrypt the file (W. , C. , et al. 2010). The figure

below illustrates the work of the RSA Algorithm:

Figure 2.1: Working of RSA

RSA algorithm has the following scale:

1. p and q are primes  Secret

2. n = p q  Not a secret

3. (n) = (p – 1)(q – 1)  Secret

4. e (Encryption key)  Not a secret

Stipulation: PBB (e, (n)) = 1

5. d (Decryption key)  Secret

d Calculated from d ≡ e - 1

mod ( (n) )

6. m (Plaintext)  Secret

7. c (Ciphertext)  Not a secret

The following procedures describe the encryption

and decryption of RSA (D.Welsh, 1998):

1. Choose two prime numbers, a and b  Secret

2. Calculate the product n = a b.

Magnitudes of n no need to be kept secret.

3. Calculate (n) = (a – 1)(b – 1).

4. Select an integer for the public key, say its name

e, which is relatively prime against (n).

5. Calculate the decryption key, d, through

ed ≡ 1 (mod m) or d ≡ e - 1

mod (φ (n))

Results from the above algorithm:

1. The public key is a couple of (e, n)

2. Private key is couple of (d, n)

2.2 EM2B Key Generator Algorithm

EM2B key algorithm is an algorithm that functions to

change the primary key into a new key that is

Analysis of Combination RSA Algorithm using EM2B Keys Genertor Algorithm in Data Encription

123

converted into ASCII characters. The EM2B

algorithm also has an increment key algorithm that

works if the key length is less than the length of the

plaintext. Increment key is a method to add key cha-

racter length by summing two previous key characters

and is modulated with 256 ASCII-based letters. The

EM2B algorithm has the following equation:

i [new]

= [ K

+ (K

mod 26) ] mod 256 (2.1)

Explanation:

a. K

= The Main Key,

b. K

= The Main Key do mod with 26 (K

mod 26),

c. K

i [new]

= New Key Generated.

Figure 2.2: The Process of EM2B Key Generator

Algorithm

As for icreament key algorithm:

IncK

= K

i [max]

+ K

i[max] - 1

mod 256 (2.2)

Explanation:

a. K

i[max]

= The last Key index in ASCII,

b. IncK

= Icreament Key,

P1 P2 P3 P4

P5 P6

K1 K2 K3 K4 K5

Figure 2.3: The Process of Increament Key

To help convert decimal numbers to ASCII code or

vice versa, ASCII table is required as shown below:

Figure 2.4: ASCII Code Table (Source: www.alhakim.

wordpress.com )

Another supporting algorithm is Vigenere

Cipher. This type of encryption algorithm is well

known for being easy to understand and implement.

i[New]

mod 26

+ K

) mod 256

80

2

STX

(K5 + K4)

(K4 + K3)

P Q R

E M 2

New

ASCII

E M 2 B t ¶

69 77 50

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

124

Techniques to produce ciphertext can be done using

the substitution of numbers and square vigènere

(Ahmad Rosyadi, 2015). Character letters used in

vigenere cipher are A, B, C, ..., Z and equated with

the numbers 0, 1, 2, ..., 25. The encryption process is

done by writing the key repeatedly. Repeated key

writing is performed until each character in the Data

has a pair of characters from the key. The characters

in the Data are then encrypted using the caesar

cipher method with the key value that has been

paired with the number (Katz, J. and Y. Lindell,

2015). The encryption process can be calculated by

the following equation (Stallings, W, 2011).

= (P

+ K

) mod 26 (2.3)

where 𝐸

𝑖

, 𝑃

𝑖

and 𝐾

𝑖

are encrypted characters, Data

characters and key characters. While the decryption

process can use the following equation:

= (C

– K

) mod 26 (2.4)

with 𝐷

𝑖

is a decrypted character, 𝐶

𝑖

is a ciphertext or

password character, 𝐾

𝑖

is a key character.

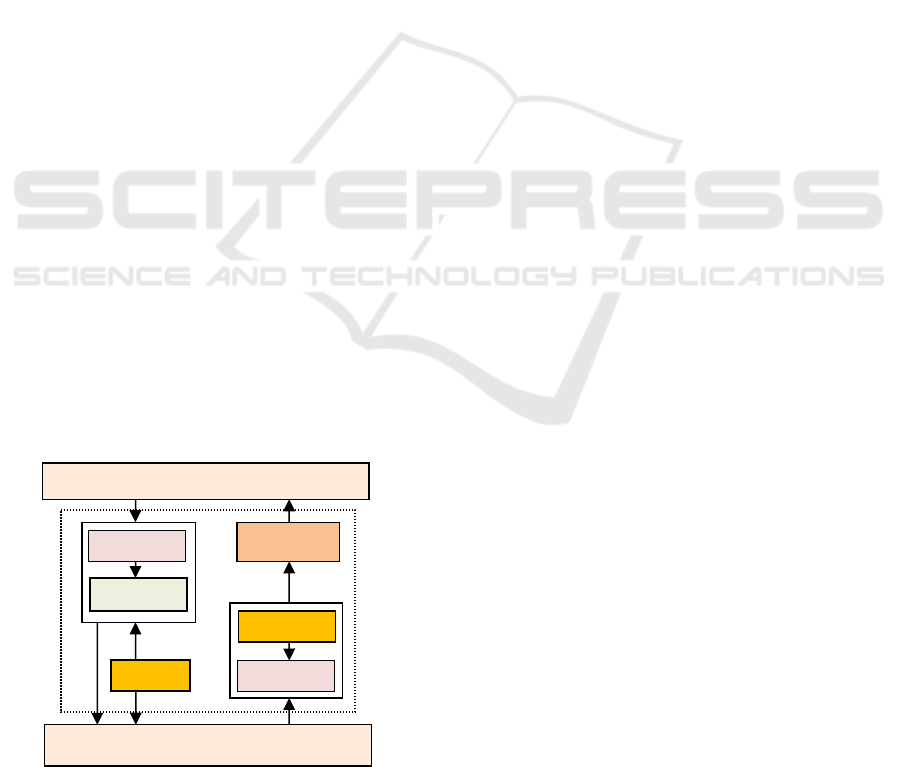
3 MATERIALS AND METHODS

In designing a cryptographic algorithm, a maximum

accuracy is required. The level of security is the key

to the success of the cryptographic algorithm itself.

Time efficiency also needs to be considered because

if the encryption and decryption process takes a long

time, it will be bad for encrypting Datas on a large

scale. Broadly speaking the process of encryption

and decryption on RSA algorithm implementation

and EM2B Keys Generator Algorithm in encrypting

data can be observed through the following diagram

blog.

Figure 3.1: Encryption and Decryption Process

In this research used RSA Cryptography

Algorithm and EM2B Key Generator to improve the

security of encrypted data. It is expected that EM2B

Key Generator can be a key algorithm for encrypting

plaintext as well as RSA algorithm capability in

encrypting keys will make the data very difficult to

solve. Therefore it is necessary to analyze each

algorithm both RSA and EM2B key generator used

in encrypting the data. RSA Algorithm Analysis can

be seen as follows:

A. Take randomly two large and different p and q

primes, but the size of both or the number of

digits in the base of numbers used should be the

same.

B. Calculate the n modulus and Euler's Totient

function φ (n) by the formula: n = p q

φ (n) = (p – 1) [q - 1]

with :

n = modulus (public key)

p and q = Two primes generated randomly.

C. Select an integer e such that I < e < φ (n) and

gcd(e, φ(n)) = 1 where:

I = Integer number,

E = Public Key (Encryption Key),

gcd = Greatest common divisor.

D. Calculate the integer value d where I < d < φ

(n)

such that:

d = e – 1 mod φ (n) or I(mod φ (n)),

where:

d = Private Key (Decryption Key).

E. Create a table to present each character.

F. The plaintext (encrypted text) is encrypted with

numbers corresponding to the table formed by

process E and an M will be obtained which is a

collection of numbers from the plaintext, then the

set of numbers is blocked every 4 numbers into

, m

, ..., m

. The encryption process is done

per block and each block of the encryption

formula is:

= m

(mod n), c

= m

(mod n), ... etc, so

resulting in a value of C where C is a collection

of numbers from c

, c

, ..., c

G. The decryption process is done by using logic

like step F by performing an inverse calculation,

ie: m

= c

(mod n)

, m

= c

(mod n), ...,etc, so resulting in the

value of M where M = m

, m

the final value

of M is re-presented with the constructed table as

in process E above.

Plaintext

Chipertex

Decryption

EM2B

Encr

tion

EM2B

Analysis of Combination RSA Algorithm using EM2B Keys Genertor Algorithm in Data Encription

125

To improve the security of RSA algorithm, then

specified security key in the form of private key

password, public key and modulo generated from

two prime numbers. This key will continue to be

used by the sender and recipient of the data in

encrypting and decrypting the data. If the security

key password by the system owner is deemed to be

insecure, then both parties immediately inform it to

be changed altogether. This security key view

consists of:

Analysis of EM2B algorithm as follows:

A. Specify some words used as the primary key for

encrypting datas. Key is given a symbol with K

where K

= K

, K

, ..., K

B. The key is converted into decimal ASCII

numbers.

C. Determine the modulus value of 26 of each key

character that has been converted into decimal

places.

= K

Mod 26.

D. Add K

with K

+ K

) then modulated with

256 and generate a new key (K

i[new]

) which is

converted in decimal ASCII characters.

In the EM2B algorithm, the key we choose does

not have to have the same character length as

plaintext. Plaintext may consist of several sentences

and even paragraphs. The key will adjust the length

of its character with plaintext by using the

increament key algorithm already stored in it. The

performance analysis of the increment key algorithm

can be noted below.

A. The maximum character index is summed with

the previous character index (K

i[max]–Ki[max‐1]),

and generate a new key character index (K

i[new]).

B. New key index (K

i[new]) becomes the maximum

key index, then added again to the previous key

index.

C. This looping step will stop if the maximum index

of the key is equal to the plaintext maximum

index. K

i[max]

= P

i[max].



The implementation process of RSA and EM2B

algorithms in encrypting the data can be explained

by the following steps.

A. A data or plaintext is encrypted using a key.

B. First the key is converted into EM2B and then

generates a new ASCII character.

i [new]

= [ K

+ (K

mod 26) ] mod 256

C. If the key length is still smaller than the length of

the plaintext, then the key in the process with

increament key IncK

= K

i [max]

+ K

i[max] - 1

mod

256.

D. Next do the encryption where, every plaintext is

added with the key and modulated with 256 to

generate a ciphertext. C

i = Pi + Ki  mod 256.

Ciphertext in the process is a data that will be

sent to the recipient.

E. Then the primary key value is put together into

one block and then split into several blocks. The

value of each block is not greater than the value

of n on the RSA generator.

F. After the block process is done then it is

decrypted using RSA. E

k = Me mod n. Ek is the

encrypted result of Ki.

G. The information sent to the recipient is ciphertext

), and key encryption results (E

Furthermore the following process to decrypt the

data.

A. The first stage by decrypting the key using the

formula K

= D

= M

mod n.

B. The decryption results are separated into each

two-digit number, which will generate the main

key character.

C. The primary key is reprocessed into the EM2B

algorithm to generate a new key in the decimal

ASCII number.

D. Re-used the increament key algorithm to obtain

the same key length as plaintext.

After that the ciphertext is decrypted by

using the new key, using the equation

P = C -

K mod 256.

4 RESULTS AND DISCUSSION

The results offered in this study are methods to

improve data security from irresponsible parties.

This study provides an example of a process of

encryption and decryption. Plaintext used are

“HERLINAWATI” with the main key "PURBA" as

in the following figure:

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

126



Figure 4.1: EM2B Key Generator Encryption Process

Plaintext is converted into decimal. Then the key

is processed with EM2B into characters (R, \, V, P,

N), and the key length increases by using increament

key. The key generated is ASCII characters. The

Generate new keys consist of: (R\VPNžìŠvNULv).

The next step is to encrypt the plaintext with a new

key that has been generated previously. Cipherteks

generated include: (š¡¨œ—ì-áꞏT¿).

Next the RSA key creation process by following the

steps below:

* Find the value of p and q: p & q primes,

* Find p x q to generate the value of n,

* Determine the value of φ(n) = (p-1)*(q-1),

* Determine the value of e as the encryption key,

e relative prime 1 < e < φ(n),

* Calculate the value of d as the decryption key.

          

p q n

φ(n)

e d

7  17  119  96  13  37

          

Figure 4.2: Key Making In the determination of the key

Figure 4.3: Calculation of Value (e)

Figure 3.5: Calculation of Value (d)

From this process we find the key value for

encrypting data on RSA is e = 13 and the decryption

key is d = 37.

Figure 4.4: EM2B Generator Key Encryption With RSA

Cipherteks above is an information or data

obtained from a combination of several algorithms

and their implementation in the information. To

decrypt the data obtained test results as follows.

Figure 4.5: Key Decryption Process using RSA algorithm

Figure 4.6: Decryption of EM2B Key Generator

Algorithm

Analysis of Combination RSA Algorithm using EM2B Keys Genertor Algorithm in Data Encription

127

Figure 4.7: Ciphertext Decryption with EM2B Key

Generator Algorithm

5 CONCLUSION

Based on the results of the above discussion, it can

be concluded that: The application of data security

using RSA algorithm has two readings technique

that is encryption technique (convert original file

into unreadable file) and decryption technique

(convert unreadable file into original file). Security

applications have passphare / password passphrases

that must be remembered and are sensitive, ie capital

and small letters are distinguished, so that passphare

is difficult to guess by anyone.

REFERENCES

Pahrizal, David Pratama, “Implementation Of RSA

Algorithm For Data Security Text”, Jurnal

Pseudocode, Vol. 3, No. 1, 2016, ISSN 2355-5920.

Zaeniah, Bambang Eka Purnama, “An Analysis of

Encryption and Decryption Application by using One

Time Pad Algorithm”, (IJACSA) International Journal

of Advanced Computer Science and Applications,

6(9), 2015.

K Hashizume et al., “An analysis of security issues for

cloud computing”, Journal of Internet Services and

Applications, a Springer open journal, pp 1-13, 2013.

M. Preetha, M. Nihiya, “A Study And Performance

Analysis Of RSA Algoritm, (IJCSMC) International

Journal Of Computer Science and Mobile Computing,

Vol. 2, 2013, ISSN 2320-088X.

William Stallings, “Cryptography and Network Security:

Principles & Practices”, Fifth edition, Prentice Hall,

ISBN-13: 978-0136097044, 2011.

Sundram Prabhadevi, Rahul De, Pratik Shah, “Cost

Effective Poly Vernam Cipher With Cache

Optimization”, Journal of Theoretical and Applied

Information Technology, ISSN: 1992-8645, 2013.

Muhammad Arief, Fitriyani, Nurul Ikhsan, “Kriptografi

Rsa Pada Aplikasi File Transfer Client- Server

Based”, Jurnal Ilmiah Teknolog informasi Terapan

Volume I, No 3, 10 Agustus 2015, ISSN : 2407 – 3911

S. Kamara, and K. Lauter, ―Cryptographic cloud

storage‖, Financial Cryptography and Data Security,

Springer Berlin Heidelberg, pp. 136-149, 2010.

K., Dr Ch., and S. Yogesh. "Enhanced Security

Architecture for Cloud Data Security." International

Journal of Advanced Research in Computer Science

and Software Engineering, Vol. 3.5, pp. 571-575 ,

2013.

Ahmad Rosyadi, Electrical engineering major, University

Of Diponegoro Semarang, “Implementation of AES

Cryptography Algorithm for Email Encryption and

Decryption”, Transient, vol. 1, no. 3, September 2012,

ISSN: 2302- 9927,64

W. , C. , et al. ―Privacy-preserving public auditing for

data storage security in cloud computing.‖ INFOCOM,

2010 Proceedings IEEE. Ieee, 2010.

D.Welsh, "Codes and Cryptography, Oxfors Science

Publication." (1988).

Stallings, W. 2011. Cryptography and Network Security:

Principles and Practice. 5th ed. Pearson Education

Inc. New York.

T. Gunasundari and K. Elangovan, "A ComparativeSurvey

on Symmetric Key Encryption

Algorithms,"International Journal of Computer

Science and Mobile Applications, ISSN, pp. 2321-

8363, 2014.

Digital Economy Promotion Agency, under the

Administrative Supervision of the Minister of Digital

Economy and Society, 2016.

M. Agrawal and P. Mishra, "A comparative survey on

symmetric key encryption techniques," International

Journal on Computer Science and Engineering

(IJCSE), vol. 4, pp. 877-882, 2012.

V. Beal. (2009, Encryption. Available:

http://www.webopedia.com/TERM/E/encryption.html

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

128