Manipulation Vigenere Cipher Algorithm with Vernam Cipher

through Matrix Table Rotation

Elwinus Mendrofa

, Elwin Yunith Purba

, Boy Yako Siahaan

, Rahmad W. Sembiring

Department of Informatics Engineering, University of Sumatera Utara

Jl. UniversitasKampus USU, Medan 20155

Keywords: Vernam Cipher, One Time Pad, plaintext, ciphertext, random keys

Abstract: Delivery of data is done by online are particularly vulnerable to be hacked by the owner of interests. The

combination of Vernam Cipher and One Time Pad and its manipulation expected to be able to prevent hacking

of data. Vernam cipher method works with plaintext is combined with streamkey (randompseudo) of the same

length to produce a temporary ciphertext, One Time Pad method works by giving special conditions on the

key used which is made of characters or letters are random (random keys or pad), and its randomization is not

using a specific formula. One Time Pad encryption method is obtained by adding or subtracting the original

text of the key. The combination and manipulation of these two algorithms were able to secure the data and

returns back to its original form (plaintext), so it does not cause the integrity of the data is missing.

1 INTRODUCTION

We often use computer networks to interact or send a

message in writing where there are a lot of

confidential information that the data transmission

process brings huge impact, that is security issues of

data sent. Therefore, no good data transmission over

a computer network in plain, but should be done

security process for data to be sent, one way to do

encryption on the data. Data security method used is

cryptography, cryptography is one of security data

that can be used to maintain the confidentiality of the

data, as well as the authenticity of the sender.

Currently very much the cryptographic algorithm that

has been developed based on algorithms previously,

one of them is the Vernam cipher algorithm in which

use method of the one-time pad (OTP). One time pad

method is very popular today due to the difficulty to

guess the contents of the original message that was

sent by the sender to the recipient. The Key length be

the main factor that makes this algorithm is difficult

to solve. The length of the key used is equal to the

length of the plaintext which is randomly generated

key of plaintext bits. However, the key length

becomes a problem for a very long message in which

the message sender must use the network completely

safe in distributing the keys of course this also entails

substantial costs as well as ensure the safety key.

In this paper we will be reviewed how the

encryption process data by applying a one-time pad

to encrypt the key and add a rotation algorithm to

generate a new ciphertext by manipulating the

Vernam Cipher algorithm. It aims to improve the

security of data, so that the transmitted data is

encrypted prior with a method that has been

manipulated before being transmitted over the

Internet network so that the data sent unknowable,

modified or utilized by others who want to hack the

data sent.

2 LITERATURE REVIEW

2.1 Cryptography

Any text or material outside the aforementioned

margins will not be printed.

The word Cryptography is derived from the

Greek,namely from word Cryptos meaning of the

word hidden and graphein means writing.

Cryptography can be interpreted as an art or a science

which researched how the data is converted into a

certain shape that is difficult to understand.

Cryptography aims to maintain the confidentiality of

information or data that can not be known by

unauthorized parties (unauthorized person).

Mendrofal, E., Purba, E., Siahaan, B. and Sembiring, R.

Manipulation Vigenere Cipher Algorithm with Vernam Cipher through Matrix Table Rotation.

DOI: 10.5220/0010040201790186

In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 179-186

ISBN: 978-989-758-496-1

179

2.1.1 Cryptography Components

Basically, the cryptographic component consists of

several components, such as:

1. Encryption: is very important in cryptography, is

a way of securing the transmitted data that are

kept confidential. The original message is called

plaintext, which is converted into code that is not

understood. Encryption can be interpreted with a

cypher or code. Similarly, do not understand a

word then we will see it in a dictionary or

glossary. Unlike the case with encryption, to

convert plain text into text-code we use

algorithms to encode the data that we want.

2. Decryption: is the opposite of encryption. The

encrypted message is returned to the original form

(original text), called the message encryption

algorithm used for encryption is different from the

algorithm used for encryption.

3. Keywords: that means here is the key used for

encryption and description.

Security of cryptographic algorithms depending

on how the algorithm works, therefore this kind of

algorithm is called finite algorithm. Limited

algorithm is an algorithm used a group of people to

keep the messages they send.

2.2 Vigenere Chiper

The Vigenère cipher is a method of encrypting

alphabetic text by using a series of different Caesar

ciphers based on the letters of a keyword. It is a

simple form of polyalphabetic substitution. The

characters used in the Cipher Vigenere that is A, B,

C, ..., Z and united with the numbers 0, 1, 2, ..., 25.

The encryption process is done by writing the key

repeatedly. Writing the key repeatedly performed

until each character in messages have a couple of key

characters. Furthermore, the characters in the

message is encrypted using the Caesar Cipher key

values that have been paired with numbers. The

Confederacy's messages were far from secret and the

Union regularly cracked their messages. Throughout

the war, the Confederate leadership primarily relied

upon three key phrases, "Manchester Bluff",

"Complete Victory" and, as the war came to a close,

"Come Retribution". The table below show the

example of encription using Vigenere Chiper consist

of Plaintext, Key and Chipertext.

Figure 1 Examples Using Encryption Vigenere Cipher

(Bruen, 2005)

Examples of encryption in Figure 1, the message

character "E" is encrypted with a key "M" and

generate cipher text "R". The results obtained from

the code encrypting the message "E" is worth 5 and a

key character "M" which is worth 13. Each character

value added 5 + 13 = 18. Because 18 is less than the

26 which is the number of characters used, then 18

divided by 26. The rest of the division is 18 which is

a character "R". The encryption process can be

calculated by the following equation (Stalling, 2011):

𝐸𝑖=(𝑃𝑖+𝐾𝑖) 𝑚𝑜𝑑 26 (2.0)

Where 𝐸𝑖, 𝑃𝑖 and 𝐾𝑖 an encrypted character, the

character of the message and the character key. While

the decryption process can use the following

equation:

𝐷𝑖=(𝐶𝑖−𝐾𝑖) 𝑚𝑜𝑑 26 (2.1)

With 𝐷𝑖 is the result of the decryption code, 𝐶𝑖 is

character cipher text or cipher, 𝐾𝑖 is a key character.

While other methods to perform the encryption

process with Vigenere Cipher method that uses tabula

recta (also called Vigenere square).

Figure 2: Tabula recta Vigenere algorithm

The leftmost column of squares states key letters,

while the top line states plaintext letters. Each line

in the rectangle states the letters ciphertext obtained

by Caesar Cipher, in which the number of shifts letter

plaintext specified numerical values of letters that key

(ie, a = 0, b = 1, c = 2, ..., z = 25) ,Vigenère square is

used to obtain the ciphertext by using a key that has

been determined. If the key length is shorter than the

length of the plaintext, then the keyare repeatedit’s

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

180

use (the periodic system). When the key length is m,

then the period is said to be m.

2.3 Vernam Chiper

Cryptography for most people is something that is

very difficult and we as beginners tend to be lazy to

learn it. However there is a cryptographic method that

is rather easy to learn and the experts have stated that

this method is a cryptographic method that is safe

enough to use. The method is commonly known by

the name of One Time Pad (OTP) or better known as

the Vernam Cipher. Vernam Cipher invented by

Major J.Maugborne and G. Vernam in 1917.

Algorithms One Time Pad (OTP) is a diversified

symetric key algorithm, which means that the key

used to encrypt and decrypt the same key. In the

process of encryption, algorithm it uses the stream

cipher derived from the XOR between bits of

plaintext and key bits. In this method, the plain text is

converted into ASCII code and then subjected to an

XOR operation on the key that has been converted

into ASCII code.

2.4 On Time Pad

One-time pad (OTP) is a stream cipher to encrypt and

decrypt one character each time. This algorithm was

found in 1917 by Major Joseph Mauborgne as

improvement of Vernam Cipher to produce a perfect

security. Mauborgne proposes the use of One-Time

Padcontaining a row of characters randomly

generated key. One pad is used only once (one-time)

only to encrypt a message, after the pad has been used

demolished so as not be reused for other encrypting

messages. Encryption can be expressed as the sum

modulo 26 of the plaintext character with one key

character one-time pad. This is the equation of one-

time pad encryption 26 characters shown in Equation

2.2 below:

Ci= (Pi+Ki) mod 26 (2.2)

If the character that is used is a member of the set

of 256 characters (such as characters with ASCII

encoding), then the encryption equation shown in

equation 2.3 below.

Pi= (Ci–Ki) mod 26 (2.3)

After the sender encrypts the message with the

key, he destroyed the key. Recipient of the message

using the same pad to decrypt the ciphertext

characters into characters plaintext with equation 2.4

below.

Pi= (Ci–Ki) mod 26 (2.4)

for the 26-letter alphabet, or for the 256-character

alphabet with equation 2.5 below.

Pi= (Ci–Ki) mod 256 (2.5)

The ways of working one time pad method:

C = P XOR K (2.6)

P = C XOR K (2.7)

Note that the key length should be equal to the

length of the plaintext, so there is no need to repeat

the use of the key during the encryption process (as in

vernam cipher).

2.5 Rotation Matrix

Rotation matrix is shifting ciphertext character that

has been incorporated into the matrix column

clockwise, along the defined distance of the key. How

to determine the length of shifts and the number of

shifts can be seen in the following table below:

Table 1. Calculation of Long Shifts in Matrix

Ki M A N O R S A

A =

Dec(Ki) 77 65 78 79 82 83 65

(2.8)

B = A+C

76 90 91 79 83 87 70

(2.9)

C = A

mod 26 25 13 0 1 4 5 13

(2.10)

D = B+C

mod 26

23 25 13 2 9 14 5

(2.11)

Char W Y M B I N E

G =

Dec(Char)

87 89 77 66 73 78 69

(2.12)

Rg = G

mod 26

9 11 25 14 21 0 17

(2.13)

Explanation:

Ki : Key

A : Decimal ASCII value of the key

characters

B : Results Summation with a decimal

value key with the previousresult (C).

C : The decimal value of a key character

mod 26

D : Number of B + C mod 26

Manipulation Vigenere Cipher Algorithm with Vernam Cipher through Matrix Table Rotation

181

Char : The result of the shift in the index table

alphabetic characters as much as the value of D

G : Decimal ASCII value of the key

characters

Rg : Long shifts in the character matrix

table

Whereas for the amount of shift is determined by

the character key

3 METHOD

Forms of research conducted by the authors in this

paper is a review of literature. The literature review is

a framework, concepts, or orientation to perform the

analysis and classification of facts collected in a

study. Referral sources from books and journals,

which are referred to in this paper are directly related

to the object under researched, that is the plaintext

encryption. The method of research that used in this

paper is a flowchart. This method includes

determining a model of encryption, the completion of

the encryption algorithm, encryption simulation

manufacture and analysis of simulation results

encryption. Flowchart design simulations on

complete this researchcan be seen in Figure 3

Figure 3. Flowchart Modification Research Vigenere Ciphe

4 RESULT

4.1 Encription

Vigenere Cipher

Encryption on the principle of the algorithm is to

combine each character in the plaintext with the

characters on the keys. Therefore, the key length must

be at least equal to the length of the plaintext. In the

first stage plaintext change them into first

ciphertextby using a key.If the plaintext length

exceeds the length of the key, then the key will be

written repeatedly. Vigenere Cipher encryption

algorithm process can be seen in the following figure:

Plaintext : ELWIN PURBA MANORSA

Key : MANORSAMANORSAMANOR

Cipherteks : RMKXFSQHSPPRFBAPFHS

Figure 4:Table Testing of Encryption Vigenere Cipher

Rotation Key Algorithm

Rotation key generation algorithm aims to improve

the security of the plaintext by changing the keys into

a new character. Furthermore, the new character is

converted to decimal and then look for the value of

the modulation to determine the length of a shift

towards the characters in the matrix table.Consider

the following figure.

Figure 5: Process Key Algorithm determining Long Shifts

on Matrix rotation

Rotation algorithm

In this process, all the characters ciphertext that has

been generated on Vigenere Cipher algorithm written

into the matrix table where condition matrix which

must consist of a matrix of squares, where the number

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

182

of rows equals the number of columns. To run this

algorithm, first consider the following steps.

1. Write down all of the ciphertext into the matrix

2. The matrix will be formed must consist of the

same number of rows and columns.

3. To define a matrix of rows and columns calculate

the amount of n ciphertext;n = length of

ciphertext.

4. If 0<n <= 9, it will form a 3 x 3 matrix.

If 9<n<= 16, it will form a matrix of 4 x 4

If 16<n<= 25, it will form a matrix of 5 x 5,

etc.

5. If the matrix column empty, fill it with the

alphabet from A until the empty column full of

character.

6. Copy the first column then make a new ending

column

7. After that copy the first line and then make a new

ending line.

8. Make the first shift in which the shift length is

determined by the rotation of key algorithms.

Rotation matrix will end after reaching n MAX

of keys.

Figure 6: Process of Rotation Matrix

4.1.1 Retrieved End Cipertext:

BRFXKMPDCFRRPEFBQBSFHSHP

RAAPSPFXKMRS

Vernam Cipher

Encryption can be expressed as the result of the

Exclusive OR (XOR) of the plaintext character with

an OTP key characters.This algorithm acts to encrypt

the plaintext where the key is generated randomly.

This key is valid only disposable where if you want

to decrypt the same message then the generated key

will be changed.

One Time Pad

In this method, there are two things that need to be

encrypted is the key and the ciphertext obtained from

vigenere chipper.This method works in advance

ischange the main key with One Time Pad methodeto

produce the Ciphertext of the key then this key will

be the second key or a new key.

Ei : Pi XOR Ki

The main key : MANORSA

Random key :

Key Ciphertext : "€ +« "n%

Plaintext Binary

Bit

Random

Bit

XOR Key

M 01001101 11100101 10101000 “

A 01000001 11000001 10000000 €

N 01001110 01100101 00101011 +

O 01001111 11100100 10101011 «

R 01010010 11111010 10101000 “

S 01010011 00111101 01101110 n

A 01000001 01100100 00100101 %

Figure 7: Encryption Results of Main Key

The next new key that has been generated is used

to encrypt the ciphertext that has been obtained from

vigenere cipher.

From the results of the main key encryption in the

previous process we obtain a new key and then the

key is repeated until the key length equal to the length

of the plaintext.The result of the encryption of the

plaintext and the key will be the end of the process to

produce a strong ciphertext.

Plaintext :

BRFXKMPDCFRRPEFBQBSFHSHPRAAPSPFX

KMRS

Key :

“€+«“n%“€+«“n%“€+«“n%“€+«“n%“€+«“n%“

Matrix5X5 RT = 9

R MK X F R 1 X KMR B P

SQHSP SFDCFR P

PRF B A P R EHFQS

PFHSAP B F SBH R

BCDE FB P AAP SM

RMK X F R PSRFXK

RT = 14 RT = 21

4 R SPPBR5 R SPPBR

F AFEDF F A FEDF

X A HFC X X A HFCX

K P S B F K KPSBFK

M SHQ R M MS HQRM

RSP P BR RSPPBR

RT = 11 RT = 25

2 K XFRSP 3P S R MK X

MS PAAP PQHS P F

R H B S FB BR B S A R

SQF HERRF FHA S

PRFCDF M CDEFP

PBRMKX KXFRBP

RT = 0 RT = 17

4 R SPPBR 5BRFXKM

FAFEDF PDC F RR

X AHF CX P E FBQ B

KPSBFK SF HSH P

MS HQRM RAAPSP

RSPPBR F XKMRS

Manipulation Vigenere Cipher Algorithm with Vernam Cipher through Matrix Table Rotation

183

Ciphertext :

ÛÊm¾Ò#uý├m¨·>`¯┬zÚ¹(m¹╚{¨Ú/u¹ðm¾Ò#w¹

The encryption process is represented in binary form:

Pi : 01000010 01010010 01000110

01011000 01001011 01001101

Ki : 10101000 10000000 00101011

10101011 10101000 01101110

Ci : 11101010 11010010 01101101

11110011 11100011 00100011

Pi : 01010000 01000100 01000011

01000110 01010010 01010010

Ki : 00100101 10101000 10000000

00101011 10101011 10101000

Ci : 01110101 11101100 11000011

01101101 11111001 11111010

Pi : 01010000 01000101 01000110

01000010 01010001 01000010

Ki : 01101110 00100101 10101000

10000000 00101011 10101011

Ci : 00111110 01100000 11101110

11000010 01111010 11101001

Pi : 01010011 01000110 01001000

01010011 01001000 01010000

Ki : 10101000 01101110 00100101

10101000 10000000 00101011

Ci : 11111011 00101000 01101101

11111011 11001000 01111011

Pi : 01010010 01000001 01000001

01010000 01010011 01010000

Ki : 10101011 10101000 01101110

00100101 10101000 10000000

Ci : 11111001 11101001 00101111

01110101 11111011 11010000

Pi : 01000110 01011000 01001011

01001101 01010010 01010011

Ki : 00101011 10101011 10101000

01101110 00100101 10101000

Ci : 01101101 11110011 11100011

00100011 01110111 11111011

The encryption process with the one-time pad method

The results of encryption on this method obtain

ciphertext to be sent to the recipient where there are

two keys that are sent, among others, the key to

decrypt the plaintext and the key to decrypt the key.

4.2 Description

One Time Pad

To know the plaintext from the ciphertext received by

the rightful recipient of the message, that is by first

using the one-time pad method.The message

recipients require a new key as a reference to recover

the plaintext.

Ciphertext :

ÛÊm¾Ò#uý├m¨·>`¯┬zÚ¹(m¹╚{¨Ú/u¹ðm¾Ò#w¹

New Key : “€+«“n%

Ciphertext and the key then is XORed using the

formula:

Di : Ci XOR Ki

The process of the message recipient to get a new

message that is still in the form of Ciphertextare:

BRFXKMPDCFRRPEFBQBSFHSHPRAAPSPFX

KMRS.

After successful decryption of the message recipient

to decrypt back to find out the main key is still the

one-time pad method.

Ciperteks key : “€+«“n%

Key : åÁeäú=d

Main Key = Ci XOR Ki

“ : 10101000 XOR å :

11100101 = 01001101 : M

€ : 10000000 XOR Á :

11000001 =01000001 : A

+ : 00101011 XOR e :

01100101 =01001110 : N

« : 10101011 XOR ä :

11100100 =01001111 : O

“ : 10101000 XOR ú :

11111010 =01010010 : R

N : 01101110 XOR = :

00111101 =01010011 : S

% : 00100101 XOR d :

01100100 =01000001 : A

Main Key : MANORSA

Rotation algorithm

The next decryption algorithm is an algorithm in

which the rotation that has been encrypted ciphertext

of the previous methods to be put into a matrix table.

See the figure below.

Ciphertext :

BRFXKMPDCFRRPEFBQBSFHSHPRAAPSPFX

KMRS

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

184

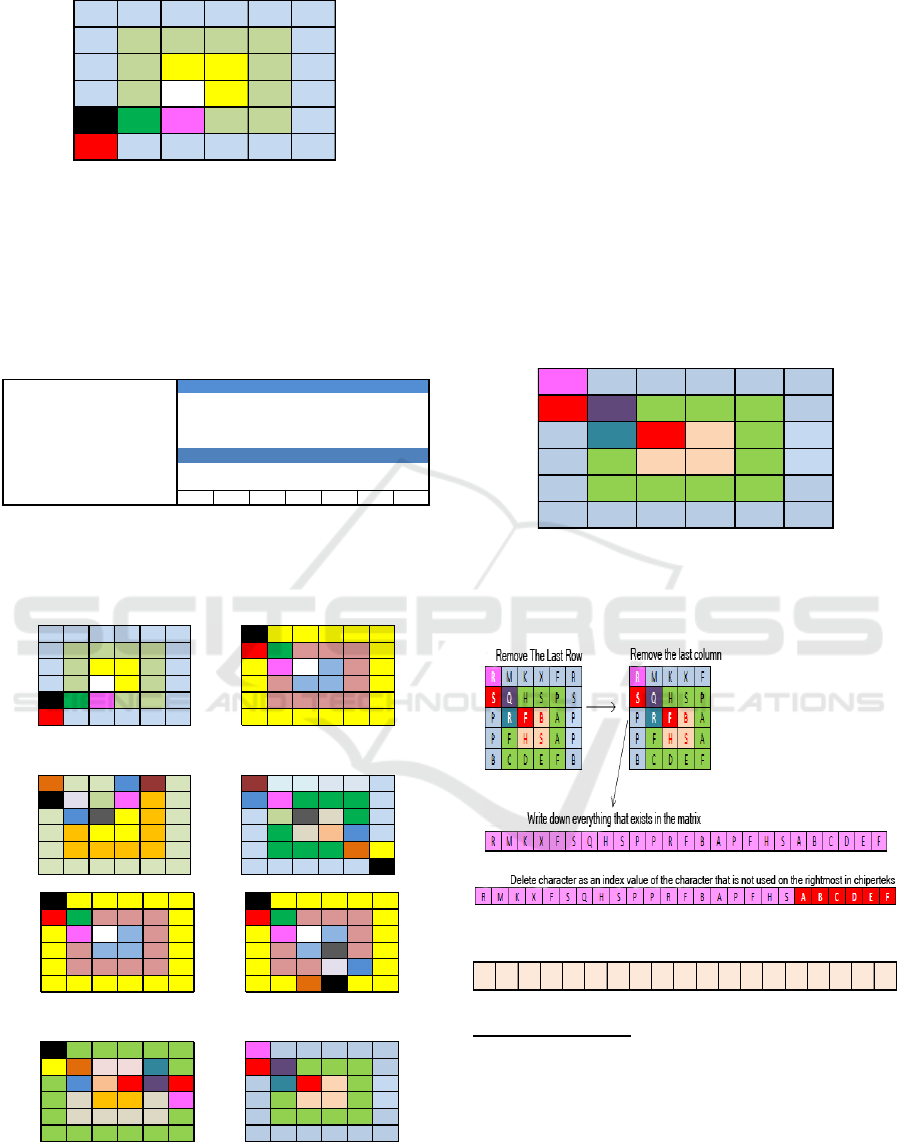
Figure 8: Matrix Ciphertext

In the previous encryption process, ciphertext

character that is in the column of the matrix are

moved forward along key value, but on the decryption

algorithmciphertext character that is in the matrix

table is sliding backwards or revers along key value

and repeated as much as the key length. The key value

is obtained from the following process :

Figure 9: The process of determining the value of the key

After a successful key value is determined next

process is to do a rotation matrix algorithm.

Figure 10: Process Description ciphertext with Matrix

Ciphertext Algorithm

The results of the first rotation indicated at

number one in the previous figure 10 wherein R is on

the line five-column one. If we look at previous

matrix characters that are in row one column one is

B, then calculated spin clockwise as key values

obtained from the previous process. The key value is

taken values that are at the end of the index is 17,the

next process is the value at the previous indexup until

the beginning of the index, this is certainly the

opposite of encryption algorithms. Having calculated

the characters are on the order of 17 is Rthen R is

placed on row one column one on the following

matrix and is followed by the next character, then

repeated continuously until the last process.In the

process of this algorithm obtained the final matrix

below:

Figure 11: The Results of Algorithm Rotation Matrix

The next stage remove the last row and the last

column of the matrix

The Ciphertext become :

AlgoritmaVigenere

Last decryption algorithm using the algorithm

vigenere cipher by using the key with formula:

Di = (Ci – Ki) mod 26

So the result we can see below:

Ciphertext : RMKXFSQHSPPRFBAPFHS

Key : MANORSAMANORSAMANOR

BRFXKM

PDCFRR

PEFBQB

SFH SHP

RAAPSP

F XKMRS

Key MANO R S A

A=A SCIICode 77 65 78 79 82 83 65

B=A+C(n‐1) 76 90 91 79 83 87 70

C=Mod(ASCIICode) 2513014513

D=Mod(B+C) 23 25 13 2 9 14 5

Chiper_Key WYMB I N E

X=ASCIICode 87 89 77 66 73 78 69

Y=Mod(X) 9 11251421 0 17

RT9 RT11 RT25 RT14 RT21 RT0 RT17

RV = 17

BRFXKM 1R SPPBR

PDCFRR FAFEDF

PEFBQB XA H F CX

SFH SHP KPSBFK

RAAPSP MSH QRM

F XKMRS RSPPBR

RV = 14 RV = 25

4 P S R MK X A 5 K X F RSP

P Q H S PF MS PAAP

B RB S AR RH B S F B

RFFHAS SQ FHE R

MC D E F P P RFCD F

KXFRBP PBRMKX

RV = 0 RV = 21

2 R SPPBR 3R SPPBR

FAFEDF FAFEDF

X A H F CX XA H F CX

KPSBFK KPS B FK

MS H QRM MSHQR M

RSPPBR RSPPBR

RV = 11 RV = 9

6 X KMRB P 7R MK X F R

F D CFR P SQHSP S

R E H FQS P RFB AP

BFSBHR PFHSAP

PAAPSM BCDEFB

PSRFXK RMKXFR

R MK X F R

SQHSP S

P RFB AP

PFHSAP

BCDEFB

RMK X F R

RMKXFSQHSPPRFBAPFHS

Manipulation Vigenere Cipher Algorithm with Vernam Cipher through Matrix Table Rotation

185

Plaintext : ELWIN PURBA MANORSA

5 CONCLUSION

Arch is still modest or simple, but is expected to be

useful as a first step to enter into the world of

cryptography,particularly in the implementation of

message security algorithms using other

combinations. To the future, this research is expected

to be developed,used and applied in the areas of life

that is more complex.

REFERENCES

Moore, R., Lopes, J., 1999. Paper templates. In

TEMPLATE’06, 1st International Conference on

Template Production. SCITEPRESS.

Smith, J., 1998. The book, The publishing company.

London, 2

edition.

Bruce Schneier (1996). "Applied Cryptography 2nd edition

Source Code in C".John Wiley & Sons.

Bruen, Aiden A. &Forcinito, Mario A. (2011).

Cryptography, Information Theory, andError-

Correction: A Handbook for the 21st Century

(http://books.google.com/books?id=fd2LtVgFzoMC&

pg=PA21). John Wiley & Sons.p. 21.ISBN 978-1-118-

03138-4.

David, Kahn (1999). "Crises of the Union". The

Codebreakers: The Story of Secret Writing. Simon &

Schuster. pp. 217–221. ISBN 0-684-83130-9.

Vernam, Gilbert S. (1926), "Cipher Printing Telegraph

Systems For Secret Wire and Radio Telegraphic

Communications", Journal of the IEEE, 55: 109–115

SharadPatil , Ajay Kumar:Effective Secure Encryption

Scheme(One Time Pad) using Complement Approach-

International Journal of Computer Science &

Communication, Vol.1,No.1,January-June

2010,pp.229-233.

Jonathan Katz , Yehuda Lindell : Introduction to Modern

Cryptography,Chapman&Hall/CRC Taylor & Francis

Group

RMKXFSQHSPPRFBAPFHS

18 13 11 24 6 19 17 8 19 16 16 18 6 2 1 16 6 8 19

MANO R S AMA N OR S AMANO R

13 1 14151819 1 13 1 14151819 1 13 1 141518

5 1223 9 14 0 162118 2 1 0 13 1 14151819 1

ELWIN PU

BA MANO

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

186