Feature Selection with Harmony Search for Classification: A Review

Norfadzlan Yusup

, Azlan Mohd Zain

, Nur Fatin Liyana Mohd Rosely

, Suhaila Mohamad Yusuf

Faculty of Computer Science and Information Technology, University Malaysia Sarawak, Kota Samarahan, Sarawak,

Malaysia

Applied Industrial Analytics Research Group, Faculty of Computing, Universiti Teknologi Malaysia, Skudai, Johor Darul

Takzim, Malaysia

Keywords: Data Mining, Feature Selection, Nature Inspired Metaheuristic Algorithm, Harmony Search, Classification.

Abstract: In the area of data mining, feature selection is an important task for classification and dimensionality

reduction. Feature selection is the process of choosing the most relevant features in a datasets. If the datasets

contains irrelevant features, it will not only affect the training of the classification process but also the

accuracy of the model. A good classification accuracy can be achieved when the model correctly predicted

the class labels. This paper gives a general review of feature selection with Harmony Search (HS) algorithm

for classification in various application. From the review, feature selection with HS algorithm shows a good

performance as compared to other metaheuristics algorithm such as Genetic Algorithm (GA) and Particle

Swarm Optimization (PSO).

1 INTRODUCTION

Data mining is a process of discovering patterns and

extracting knowledge from a large set of data. There

are various tasks of data mining such as association

analysis, anomaly detection, regression, clustering

and classification. These data mining tasks can be

solved by using a number of different approaches or

algorithm (Kotu and Deshpande, 2015).

Classification is a data analysis method that extracts

models describing important data classes. Such

models, called classifiers, predict categorical class

labels (Han et al., 2012). Recently, classification

using nature inspired metaheuristics algorithms have

caught the attention of many researchers.

In the literature, there has been intensifying

demand in growth of computational models or methods

that motivated by nature inspired or how animals

interact and communicate among each other to find

food sources. Many optimisation algorithms have been

designed and developed by adopting a form of

biological-based swarm intelligence. Harmony search

(HS) algorithm for example is an optimization

algorithm inspired by harmony improvisation process

by the musician. There is also a swarm-based

algorithm such as Artificial Bee Colony (ABC) that

mimics the foraging behaviour of swarm honey bee.

Similar to the concept of Ant Colony Optimization

(ACO) and Particle Swarm Optimization (PSO), these

type of exploration algorithms is capable of tracing

good quality of solutions. Based on Fister et al (2013),

all of these algorithms can be named swarm-

intelligence based, bio-inspired, physics and chemistry

based depending on the sources of inspiration. ACO

and PSO are among the most popular swarm-

intelligence based algorithms for data mining problems

(Martens et al, 2011).

Feature selection methods generally can be

categorized into three types which are filter, wrapper

and embedded. In addition to these methods, there is

a new development of feature selection method such

as hybrid method and ensemble method (Ang et al.,

2016). The feature selection process is described

more details in next section.

For learning and prediction of the models, there

are various types of classifiers that have been used

with feature selection such as Naïve Bayesian, K-

Nearest Neighbour (KNN), Support Vector Machine

(SVM), Decision Tree and Artificial Neural Network

(ANN).

2 FEATURE SELECTION

Feature selection is a pre-processing techniques that

was used to identify relevant features. It is an

294

Yusup, N., Zain, A., Mohd Rosely, N. and Yusuf, S.

Feature Selection with Harmony Search for Classiﬁcation: A Review.

DOI: 10.5220/0010042002940302

In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 294-302

ISBN: 978-989-758-496-1

important part of pattern recognition and machine

learning where it can reduce computation cost and

increased classification performance (Polat and

Gurnet, 2009). By using different approaches,

features will be reduced where only significant

features are selected which can leads to

dimensionality reduction. A reduced feature set will

improve the classification accuracy compared to the

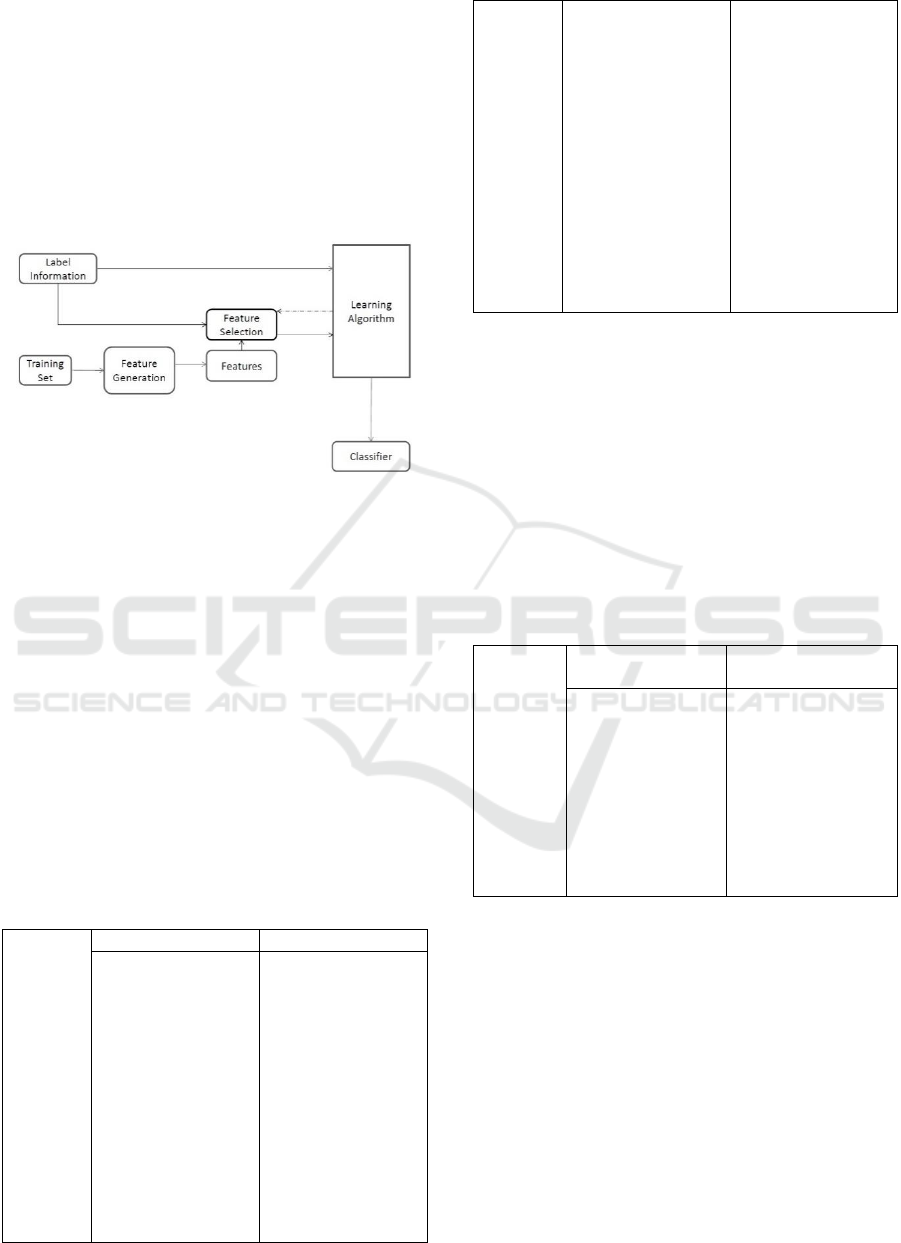
original datasets. A general framework of feature

selection process is shown in Figure 1.

Figure 1: Feature Selection General Framework (Tang et al,

2013).

As been mentioned in the previous section, feature

selection methods generally can be categorized into

three types which are filter, wrapper and embedded.

In filter methods, the feature selection process is

independent from the learning process. Filter methods

have a tendency to select redundant features because

it did not consider the interactions between features.

Once the best features are selected, it will be ranked

and evaluated by using either univariate or

multivariate techniques. Filter method did not

necessarily used with classifiers, therefore it is

usually used as a pre-processing steps. Filter method

is computationally less complex and faster than

wrapper method.

Table 1: Filter feature selection techniques.

Filter

feature

selection

Univariate

Multivariate

 Information

Gain (IG)

 Gain ratio

 Term variance

(TV)

 Gini index (GI)

 Laplacian Score

(L-Score)

 Fisher Score (F-

Score)

 Minimal

redundancy-

maximal-

relevance

(mRMR)

 Random

subspace

method

(RSM)

 Relevance-

redundancy

feature

selection

(RRFS)

 Unsupervised

Feature

Selection Ant

Colony

(UFSACO)

 Relevancy-

Redundancy

Feature

Selection Ant

Colony

(RRFSACO)

 Graph

Clustering

Ant Colony

(GCACO)

In wrapper method, the feature selection and

learning process will be wrapped together in order to

select the best feature subset. A specific classifier will

be used to evaluate the performance of features subset

that have been selected. This process will be repeated

until the prediction error rate is minimized or a

desirable quality is reached. The advantages of

wrapper method is the performance accuracy is

higher than filter but it is most likely to have over

fitting problems since it use an iterative process to

evaluate the best feature subset.

Table 2: Wrapper feature selection techniques.

Wrapper

feature

selection

Sequential/Greedy

Global/Random

 Sequential

backward

selection

 Sequential

forward

 ACO

 PSO

 ABC

 GA

 Random

mutation

hill-climbing

 Simulated

annealing

(SA)

Table 1 and 2 shows the different types of filter

and wrapper feature selection techniques as

mentioned by (Moradi and Gholampour, 2016).

In embedded method, the feature selection

process is integrated as part of the learning process.

Embedded method is more efficient than wrapping

method because it will avoid the iterative process in

finding the best feature subset. While the model is

being created, the learning process will identify the

best feature that contribute to the accuracy. The

computational process in embedded method is more

complex than wrapper method however it is hard to

modify the classification model to get higher

performance accuracy (Hancer et al., 2017).

Feature Selection with Harmony Search for Classiﬁcation: A Review

295

There are two new techniques in feature selection

which are hybrid and ensemble method. The filter and

wrapper methods are usually combined together to be

a hybrid method in order to select the best features. In

this method, filter will be used to select the best

features and wrapper will use learning algorithm to

evaluate the feature subset. The advantages of these

two methods are exploited in order to achieve the best

performance in terms of higher accuracy and better

computational complexity. The filter-wrapper hybrid

methods are also combined with various

mathematical algorithm such as mutual information,

fuzzy-rough set, and local-learning (Ryu and Kim,

2014).

For ensemble method, a different features subset

will be selected from the original datasets. For each

of these feature subsets it will create a group of best

subset. To build an ensemble classifiers, there are two

techniques which are heterogeneous such as decision

tree and instance-based learning. The other technique

is homogenous representation such as bagging and

boosting.

According to Diao and Shen (2015), different

nature inspired metaheuristics algorithm can identify

feature subsets with unique characteristics. The

authors suggested that it is worth to investigate

whether these unique characteristics can build a

collection of higher quality feature selection. Based

on the previous research, the results of each natured

inspired metaheuristics have its own advantages and

disadvantages when dealing with different datasets,

but the performance most of it is enhanced with the

use of feature selection method. The authors also

suggested that it may be beneficial to develop a meta-

framework in which suitable algorithms may be

dynamically identified, and employed either

concurrently or consecutively, in order to form a more

intelligent, hybrid approach for feature selection.

Swarm-intelligence based optimization algorithm

such as PSO and ABC for example also has been used

to train with ANN. According to Moradi and

Gholampour (2016), among the many existing

metaheuristic methods, GA, PSO and ACO are

widely used for the feature selection problem. GA is

mostly preferable due to its simplicity while PSO and

ACO have higher accuracy in similar tasks.

3 HARMONY SEARCH (HS)

ALGORITHM

Harmony Search (HS) is a global optimization

algorithm which inspired by harmony improvisation

process of musicians, proposed by Geem et al (2001).

A harmony which is every solutions in this algorithm

will be stored in an area of promising solutions called

Harmony Memory (HM). At every iteration of

Harmony Search, new harmonies are generated

considering harmonies stored in the HM, with the

probability of HMCR (harmony memory

consideration rate), or using randomized elements,

with the probability of 1-HMCR. Then, the pitch

adjustment is performed. In this step, every

component of solution (harmony) is deviated within a

range called Fret Width (FW), just like the techniques

used by musicians when playing guitar or violin.

There are five parameters in HS, three are main

parameters and another two are optional parameters.

The main parameters are size of harmony memory

(HMS), the harmony memory considering rate

(HMCR), and the maximum number of iterations, K.

The other two optional parameters are the pitch

adjustment rate (PAR) and the adjusting bandwidth or

fret width (FW). The number of variables in

optimization function is represented by N, the number

of musician defined by the problems.

As mentioned by Geem et al. (2005), the HS

algorithm works based on the following five steps, (1)

initialize the parameters for problem and algorithm,

(2) initialize the harmony memory (HM), (3)

improvise a new harmony, (4) update the HM, and (5)

check the stopping criterion. The details of each of

these five steps are explained in the following section.

3.1 Initialize the Parameters for

Problem and Algorithm

In this step, the optimization problem is specified as

follows:

Minimize f (x)

(1)

Subject to x

∈ X

i =1, 2, ... , N .

(2)

where f (x) is an objective function; x is the set of each

decision variable x

; X

is the set of possible range of

values for each decision variable, that is, Xi = {xi (1),

xi (2),..., xi (K)} for discrete decision variables (xi (1)

< xi (2) < ... < xi (K)) ; N is the number of decision

variables (number of music instruments); and K is the

number of possible values for the discrete variables

(pitch range of each instrument).

The HS algorithm parameters are also specified in

this step: Harmony Memory Size (HMS) = number of

solution vectors), Harmony Memory Considering

Rate (HMCR), Pitch Adjusting Rate (PAR), and

Stopping Criteria = number of improvisation). Here,

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

296

HMCR and PAR are the parameters of HS algorithm

explained in Step 3.3

3.2 Initialize the Harmony Memory

(HM)

In this step, the Harmony Memory (HM) matrix, as

shown in Equation 3, is filled with as many randomly

generated solution vectors as the size of the HM

(HMS).

(3)

3.3 Improvise a New Harmony

A generated new Harmony vector,

𝑥

′

= 𝑥

′

𝑥

2,…….

′

𝑥

𝑁

′

by following three rules: HM

consideration; Pitch adjustment; or totally random

generation. For instance, the value of the first

decision variable (𝑥

′

) for the new vector can be

chosen from values stored in HM

(𝑥

1 ~

𝑥

𝐻𝑀𝑆

). Value of other variables (𝑥

𝑖

′

) can be

chosen in the same style. There is also a possibility

that totally random value can be chosen. HMCR

parameter, which varies between 0 and 1, sets the rate

whether a value stored in HM is chosen or a random

value is chosen, as follows:

(4)

The HMCR is the rate of choosing one value

from historical values stored in HM while (1-HMCR)

is the rate of randomly choosing one value from the

possible value range.

After choosing the new harmony vector 𝑥

′

𝑥

′

𝑥

2,…….

′

𝑥

𝑁

′

, pitch-adjusting decision is examined for

each component of the new vector. This procedure

uses the PAR parameter to set the rate of pitch

adjustment as follows:

(5)

In the pitch adjusting process, a value moves to its

neighbouring value with probability of PAR, or just

stays in its original value with probability (1-PAR). If

the pitch adjustment for 𝑥

𝑖

′

is determined, its position

in the value range X

is identified in the form of 𝑥

𝑖

′

(𝑘)

(the k

element in X

), and the pitch-adjusted value for

𝑥

𝑖

′

(𝑘) becomes

𝑥

𝑖 ←

′

𝑥

𝑖

(𝑘 + 𝑚)

(6)

where 𝑚 ∈{..., −2, −1,1, 2, ...} is a neighbouring

index used for discrete-type decision variables. The

HMCR and PAR parameters in Harmony Search help

the algorithm find globally and locally improved

solution, respectively.

3.4 Update the Harmony Memory

If the new harmony vector, 𝑥

′

= 𝑥

′

𝑥

2,…….

′

𝑥

𝑁

′

is better

than the worst harmony in the HM, judged in terms of

the objective function value, the new harmony is

included in the HM and the existing worst harmony is

excluded from the HM.

3.5 Check the Stopping Criterion

If the stopping criterion (maximum number of

improvisations) is satisfied, computation is

terminated. Otherwise, Steps 3.3 and 4 are repeated.

The overall flowchart of HS algorithm is depicted in

Figure 2.

Feature Selection with Harmony Search for Classiﬁcation: A Review

297

Figure 2: Flowchart of HS algorithm.

4 HS FOR FEATURE SELECTION

Diao and Shen (2012) provide a key concept mapping

with illustrative example to describe how feature

selection problems can be translated into optimization

problems and further solved by HS algorithm. The

number of variables in optimization problems are

predetermined by the optimized function. However in

feature selection, the number of variables or features

is not fixed in a subset. The size of evolving

developed subset should be reduced similar to the

optimization of the subset evaluation score.

In HS algorithm, each musician may vote for one

feature to be included in the feature subset when such

an emerging subset is being improvised. The

harmony is then the combined vote from all

musicians, indicating which features are being

nominated. The entire pool of the original features

forms the range of notes available to each of the

musicians. Multiple musicians are allowed to choose

the same attribute, and they may opt to choose no

attribute at all. The fitness function used will become

a feature subset evaluation method, which analyses

and merits each of the new subsets found during the

search process. Table 3 shows the mapping concept

from HS algorithm to feature selection. Feature

selector is equivalent to a musician where available

features of feature selector translate the notes to the

musician.

Table 3: Harmony Search to Feature Selection Concept

Mapping.

Harmony

Optimization

Feature

selection

Musician

Variable

Feature selector

Note

Variable Value

Feature

Harmony

Solution Vector

Subset

Harmony

Memory

Solution

Storage

Subset Storage

Harmony

evaluation

Fitness

Function

Subset

Evaluation

Optimal

harmony

Optimal

Solution

Optimal Subset

In Figure 3, there are three types of harmony

produced where M1 to M6 represents six different

types of musicians. In the first harmony {B, A, C, D,

G, J} represents a feature subset of size 6, all six

musicians decided to choose distinctive notes. For the

second harmony {B, B, B, C, P, −} there is a

duplication of choices from the first three musicians

(M1,M2,M3) and a discarded note (represented by -)

from the last musician (M6), which reduced subset to

Step 1: Specification of each decision variable, a

possible value range in each decision variable,

harmony memory size (HMS), harmony memory

considering rate (HMCR), pitch adjusting rate (PAR),

termination criterion (maximun number of search)

Step 2: Generation of initial

Harmony [solution vector] (as

many as HMS)

Step 3: Based on three rules:

Memory Considering, Pitch

Adjusting, Random Choosing

A new

harmony

is better than a

stored

harmony in

Step5:

Termination

Criterion

satisfied?

Step 4: Updating of HM

Start

Uniform Random

HCM,

Sorted value of obj f(x)

Stop

Yes

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

298

{B,C,P} of size 3. The last harmony {B, −, B, C → F,

P, D} will translate into feature subset {B, F, P, D},

original vote of musician four, C → F was forced to

change into F by HMCR activation.

Figure 3: Harmony Encoded Feature subset.

In conventional optimization problems, generally

each musician will have a range of possible note

choices which were different from the other

musicians. For feature selection, all musicians share

one single value range, which is the set of all features.

5 HS WITH FEATURE

SELECTION APPLICATION

From the literature, HS algorithm has been applied in

many areas as a feature selection method. This

include in image and speech recognition, computer

network, electrical power, image steganalysis, gene

selection and etc.

Diao and Shen (2011) proposed a novel approach

to classifier ensemble selection based on fuzzy-rough

as feature selection with HS for 9 UCI datasets. HS

was used to select minimal subset that maximizes the

fuzzy-rough dependency measure. The experiments

give a promising results and the author suggested that

the proposed technique can be apply with other

feature selection technique and heuristic search

strategies. In Diao and Shen (2012), HS was able to

find good-quality feature subsets for most 10 UCI

datasets. The authors used HS parameter control and

iterative refinement technique to further improve the

HS performance which make it a strong search

mechanism for datasets with large number of

features. The performance of HS was better compared

with other algorithm such as GA and PSO.

Zheng et al (2013) proposed three improvements

for HS algorithm to enhance its feature selection

performance for 8 UCI datasets. The three

improvements are restricted feature domain, self-

configuration of subset size and convergence

detection. The experiment results shows that the

proposed techniques is capable of automatically

adjusting the internal components of the HS

algorithm and make the performance more efficient.

Krishnaveni and Arumugam (2013) proposed HS

algorithm as feature selection with 1-Nearest

Neighbour classifier for 4 UCI datasets. The proposed

technique give more better performance in terms of

classification accuracy and convergence rate

compared to other algorithm such as PSO and GA. A

new technique was proposed by (Nekkaa and

Boughaci, 2016) where they hybrid search method

HS and stochastic local search (SLS). HS was used to

explore the search space and to detect potential region

with optimum solutions. SLS was then used to find

effective refinement by HS. The performance of this

method was compared for 16 UCI datasets and

different support vector machine (SVM) classifiers

were tested in this research. The experiments shows

the proposed method gives good performance in

terms of classification accuracy.

César et al. (2012) reviewed three types of

evolutionary techniques for feature selection such as

PSO, HS and Gravitational Search Algorithm (GSA).

These feature selection techniques were used to select

the most relevant features to identify possible frauds

in power distribution system. There are two labelled

data sets that were used from Brazilian electric power

company and a number of classifier were employed

such as Optimum Path Forest (OPF), SVM-with

Radial Basis Function, SVM-noKernel, ANN with

Multi Layer Percepton (MLP), Kohonen Self

Organizing Map (SOM) and k-NN. From the

experiments HS-OPF considered give the best

performance in terms of accuracy and computational

complexity.

Chen et al. (2012) proposed HS feature selection

with SVM classifier to increase testing and

classification results of image steganalysis. From the

experiment, the proposed method successfully

decreased the training complexity and increased the

correct classification rate. Shreem et al. (2014)

proposed symmetrical uncertainty (SU) filter and HS

algorithm wrapper (SU-HSA) for gene selection

problems in microarray datasets. Experimental results

shows that the SU-HSA is better than HSA for all

microarray datasets in terms of the classification

accuracy.

Hamid et al. (2015) presented a method of HS-

SVM to improve computer network intrusion

detection. From the experiment, HS-SVM improved

the accuracy of intrusion detection and reduced the

test time of previously studied intrusion detection

models. HS as feature selection was proposed Tao et

al. (2015) to select relevant features from speech data

for accurate classification of speech emotion. The

datasets used in the experiment were from Berlin

Feature Selection with Harmony Search for Classiﬁcation: A Review

299

German emotion database (EMODB) and Chinese

Elderly emotion database (EESDB). LIBSVM was

used as classifier. From the experimental results, HS

was effective as feature selector although there is no

sharp degeneration on accuracy and the accuracy

almost maintains the original ones. Abualigah et al.

(2016) used HS to enhance the text clustering (TC)

technique by obtaining a new subset of informative or

useful features. Experiments were applied by using

four benchmark text datasets. The results shows that

the proposed technique improved the performance of

the k-mean clustering algorithm measured by F-

measure and Accuracy.

Das et al. (2016) proposed HS algorithm feature

selection method for feature dimensionality reduction

in handwritten Bangla word recognition problem. The

proposed feature selection method produced a high

accuracy rate. The algorithm also showed high

classification accuracies compared to GA and PSO

and statistical feature dimensionality reduction

technique like Principal Component Analysis (PCA).

Rajamohana et al (2017) proposed a hybrid Cuckoo

Search (CS) with HS for feature selection to select the

optimized feature subset from the dataset. Naive

Bayes was used as a classifier. Experimental results

shows that the proposed hybrid technique is capable

of identifying good quality feature subsets. The

proposed approach give better classification accuracy

results than binary CS with an optimized feature

subset.

Table 3 shows the summary of feature selection

using HS in the literature from 2011 - 2017.

Table 3: Summary of feature selection using HS.

Authors

Application

Method

Classifier

Diao and

Shen (2011)

UCI

benchmark

datasets

Ensemble

Mixed

classifier

Diao and

Shen (2012)

UCI

benchmark

datasets

Wrapper

C4.5,

(VQNN),

(NB),

(SVM)

César et al

(2012)

Nontechnical

loses (electrical

power)

characterization

Wrapper

OPF,

SVM

Chen et al

(2012)

Image

Steganalysis

Wrapper

LIBLINEAR

SVM-Opf,

SVM –

Nokernel,

ANN-MLP,

SOM,

k-NN

Zheng et al

(2013)

UCI

benchmark

datasets

Wrapper

C4.5

Krishnaveni

and

Arumugam

(2013)

UCI

benchmark

datasets

Wrapper

1-NN

Shreem et al

(2016)

Gene selection

Filter-

Wrapper

Naïve-

Bayes,

Instance

Based (IB1)

Hamid et al

(2015)

Intrusion

Detection

Wrapper

SVM

Tao et al

(2015)

Speech

Emotion

Recognition

Wrapper

LIBSVM

Abualigah

et al (2016)

Text Clustering

Wrapper

k-mean

Nekkaa and

Boughaci

(2016)

UCI

benchmark

datasets

Wrapper

C4.5,

Naïve-Bayes,

PART,

Zero-R,

JRIP,

Attribute

Selection,

SVM

Das et al

(2016)

Handwritten

Word

Recognition

Wrapper

Naïve-Bayes,

Bagging,

BayesNet,

SVM, MLP,

Logistic,

Random

Forest

Rajamohana

et al (2017)

Review Spam

Detection

Wrapper

Naïve-Bayes,

k-NN

6 CONCLUSIONS

From the literature, it can be concluded that feature

selection with HS gives a good performance in many

research areas as compared to other nature inspired

metaheuristics algorithm. HS algorithm is good at

identifying the high performance areas of a solution

space within a reasonable time. HS has some

advantages such as less tuneable parameters, imposes

less mathematical requirements and find the solution

easily. However, there are some drawbacks of HS

such as not efficient in performing a local search in

numerical optimization, premature and slow

convergence, poor adaptability and limited search

range. There are many strategies that have been

proposed by the researchers to further improve the

performance of HS as discussed in section 5. Some of

these strategies for example are controlled parameters

and iterative refinement of HS (Diao and Shen, 2012),

restricted feature domain, self-configuration of subset

size and convergence detection (Zheng et al 2013). A

number of researchers proposed HS with hybrid

techniques like stochastic local search (Nekkaa and

Boughaci, 2016) and CS (Rajamohana et al (2017) to

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

300

further improve the performance of feature selection

with HS.

ACKNOWLEDGEMENT

The authors would like to thank the editors and

reviewers for their valuable comments. We also

would like to thank Universiti Teknologi Malaysia

(UTM) for providing Research University Grant

(GUP) – Tier 1, Grant no: Q1.J130000.2528.18H53.

Thank you to Ministry of Higher Education (MOHE)

Malaysia and UTM for providing SLAB and Zamalah

scholarship.

REFERENCES

Abualigah, L. M., Khader, A. T., & Al-Betar, M. A. (2016).

Unsupervised feature selection technique based on

harmony search algorithm for improving the text

clustering. 2016 7th International Conference on

Computer Science and Information Technology (CSIT),

1–6. https://doi.org/10.1109/CSIT.2016.7549456

César, C., Ramos, O., Souza, A. N. De, Falcão, A. X., &

Papa, J. P. (2012). New Insights on Nontechnical

Losses Characterization Through Evolutionary-Based

Feature Selection, 27(1), 140–146.

Chen, G., Zhang, D., Zhu, W., Tao, Q., Zhang, C., & Ruan,

J. (2012). On Optimal Feature Selection Using

Harmony Search for Image Steganalysis. 2012 8th

International Conference on Natural Computation,

(Icnc), 1074–1078.

https://doi.org/10.1109/ICNC.2012.6234730

Das, S., Singh, P. K., Bhowmik, S., Sarkar, R., & Nasipuri,

M. (2016). A Harmony Search Based Wrapper Feature

Selection Method for Holistic Bangla Word

Recognition. Procedia Computer Science, 89, 395–403.

https://doi.org/10.1016/j.procs.2016.06.087

Diao, R., & Shen, Q. (2011). Fuzzy-rough classifier

ensemble selection. IEEE International Conference on

Fuzzy Systems, 1516–1522.

https://doi.org/10.1109/FUZZY.2011.6007400

Diao, R., & Shen, Q. (2012). Feature selection with

harmony search. IEEE Transactions on Systems, Man,

and Cybernetics. Part B, Cybernetics : A Publication of

the IEEE Systems, Man, and Cybernetics Society, 42(6),

1509–23.

https://doi.org/10.1109/TSMCB.2012.2193613

Diao, R., & Shen, Q. (2015). Nature inspired feature

selection meta-heuristics. Artificial Intelligence

Review, 44(3), 311–340.

https://doi.org/10.1007/s10462-015-9428-8

Fister, I. Jr., Yang, X-S., Fister, I., Brest, J., Fister, D.,

(2013) A Brief Review of Nature Inspired Algorithms

for Optimization. Elektrotehniski Vestnik 80(3):1–7,

2013 (English Ed.).

Geem, Z.W., Kim, J. H., Loganathan, G. V.: A new

heuristic optimization algorithm: Harmony search.

Simulation, 76, 60-68 (2001).

Geem, Z.W., Tseng, C., Park, Y.: Harmony search for

generalized orienteering problem: best touring in

China. LNCS, vol. 3412, pp. 741–750. Springer,

Heidelberg (2005)

Han, J., Kamber, M., & Pei, J. (2012). Data Mining:

Concepts and Techniques. San Francisco, CA, itd:

Morgan Kaufmann. https://doi.org/10.1016/B978-0-

12-381479-1.00001-0

Hancer E, Xue B, Zhang M, Karaboga D, Akay B (2017)

Pareto front feature selection based on artificial bee

colony optimization. Inf Sci 422:462–479

Hamid Ghaffari Gotorlar, J. B. Mohammad, Pourmahmood

Aghababa, Masoumeh Samadi Osalu, "Improving

Intrusion Detection Using a Novel Normalization

Method along with the Use of Harmony Search

Algorithm for Feature Selection", 7th International

Conference.

J. Tang, S. Alelyani, H. Liu, “Feature Selection for

Classification: A Review,” Data Classification:

Algorithms and Applications, CRC Press, 2013.

J. C. Ang, A. Mirzal, H. Haron and H. N. A. Hamed,

"Supervised, Unsupervised, and Semi-Supervised

Feature Selection: A Review on Gene Selection,"

in IEEE/ACM Transactions on Computational Biology

and Bioinformatics, vol. 13, no. 5, pp. 971-989,

September 1 2016.

doi: 10.1109/TCBB.2015.2478454

Krishnaveni, V., & Arumugam, G. (2013). Harmony search

based wrapper feature selection method for 1-nearest

neighbour classifier. Proceedings of the 2013

International Conference on Pattern Recognition,

Informatics and Mobile Engineering, PRIME 2013, 24–

29. https://doi.org/10.1109/ICPRIME.2013.6496442

Martens, D., Baesens, B. & Fawcett, T. Mach Learn

(2011) 82: 1. https://doi.org/10.1007/s10994-010-

5216-5

Moradi, P. & Gholampour, M. A hybrid particle swarm

optimization for feature subset selection by

integrating a novel local search strategy. Applied Soft

Computing 43, 117–130 (2016).

Nekkaa, M., & Boughaci, D. (2016). Hybrid Harmony

Search Combined with Stochastic Local Search for

Feature Selection. Neural Processing Letters, 44(1),

199–220. https://doi.org/10.1007/s11063-015-9450-5

Rajamohana, S. P., Umamaheswari, K., & Keerthana, S. V.

(2017). An effective hybrid Cuckoo Search with

Harmony search for review spam detection.

Proceedings of the 3rd IEEE International Conference

on Advances in Electrical and Electronics, Information,

Communication and Bio-Informatics, AEEICB 2017,

524–527.

https://doi.org/10.1109/AEEICB.2017.7972369

Ryu SJ., Kim JH. (2014) An Evolutionary Feature

Selection Algorithm for Classification of Human

Activities. In: Kim JH., Matson E., Myung H., Xu P.,

Karray F. (eds) Robot Intelligence Technology and

Feature Selection with Harmony Search for Classiﬁcation: A Review

301

Applications 2. Advances in Intelligent Systems and

Computing, vol 274. Springer, Cham

Shreem, S. S., Abdullah, S., & Nazri, M. Z. A. (2016).

Hybrid feature selection algorithm using symmetrical

uncertainty and a harmony search algorithm.

International Journal of Systems Science, 47(6), 1312–

1329. https://doi.org/10.1080/00207721.2014.924600

Tang, J., Alelyani, S., & Liu, H. (2014). Feature Selection

for Classification: A Review. Data Classification:

Algorithms and Applications, 37–64.

https://doi.org/10.1.1.409.5195

Tao, Y., Wang, K., Yang, J., An, N., & Li, L. (2015).

Harmony search for feature selection in speech emotion

recognition. 2015 International Conference on

Affective Computing and Intelligent Interaction (ACII),

362–367. https://doi.org/10.1109/ACII.2015.7344596

Vijay Kotu and Bala Deshpande, Predictive Analytics and

Data Mining, Morgan Kaufmann, Boston, 2015, Pages

1-16, ISBN 9780128014608,

https://doi.org/10.1016/B978-0-12-801460-8.00001-X.

Zheng, L., Diao, R., & Shen, Q. (2013). Efficient Feature

Selection using a Self-Adjusting Harmony Search

Algorithm. IEEE Computational Intellegence (UKCI),

167–174.

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

302