Substantial Differences between Fuzzy Set and Soft Set Theories
Muhammad Sadiq Khan*, Tutut Herawan
Department of Information Systems University of Malaya, Kuala Lumpur, Malaysia
Key words: Fuzzy data; Crisp data; Fuzzy set; Soft set.
Abstract: Set theories like fuzzy set, rough set, and soft set for dealing with vague or uncertain data have their own
scopes. Fuzzy set theory was considered as most suitable tool for vague data before the concept of soft set
theory, but after its presentation, soft set is considered as most appropriate among all. Beside hundreds of
applications, the main superiority and reason of most appropriateness of soft set theory over fuzzy set theory
is still lying as hidden and unclear as the vagueness of uncertain data itself. In this paper, we reveal the main
differences between soft set and fuzzy set theory which discloses the appropriateness of soft set theory.
1 INTRODUCTION
In today’s scientific era, data is one of the most
crucial-key-instruments being dealt in more than tetra
bytes every hour. There exists both crisp as well as
vague data for everyday data dealing in computer
science, engineering, medical, social science and
every field of life. Crisp or clear data is processed
using traditional simple or complicated mathematical
tools and techniques but vague data can’t be
processed for obtaining meaningful knowledge,
information and decisions using those common tools
and techniques of crisp data. Special tools and
hundreds of applications are used for vague data
based on elementary theories like the theory of
probability, interval mathematics, fuzzy set, rough set
and soft set [1-8]. Most recent and appositely
considered theory of soft set claims that fuzzy set
theory is most appropriate between all previous
theories. But fuzzy set theory has its own limitations
which are covered by soft set theory. But no one has
shown the clear difference between fuzzy set and soft
set theories and it is becoming difficult for every new
researcher to conclude it from thousands of articles
e.g. [9-24] in the field of vague data and soft
computing. Every scholar including Molodtsov in his
pioneer work of soft set has used the word “possibly”
for adequate parametrization being used by soft set
and lacked by previous theories, especially fuzzy set
theory.
In this paper, we present the main difference and
similarity of fuzzy set and soft set theories. We use a
common vague data example for describing both
theories in a short systematic manner. We also
introduce a method for deriving fuzzy set
membership functions from soft set.
Remaining of our work is organized as follow.
Section 2 contains the basic definitions and examples
of vague data, basic review of fuzzy and soft set
theories, furthermore an initial application of soft set.
In section 3, we present main difference and
similarity of fuzzy set and soft set theories. Finally,
we conclude our work in section 4.
2 RUDIMENTARY
Data having no ambiguity or uncertainty is called
crisp or clear data. For example, a university data base
containing student’s record is crisp data and after
certain processing through specific tools and
techniques it also yields the output in crisp form as
student GPA, requirements fulfilled and due fees. In
contrast to crisp data, the fuzzy, uncertain, vague and
unclear data contains uncertainty and ambiguity. We
can’t process such data with ordinary tools of crisp
data and if still processed will result in unexpected,
very small, too big or misleading result. For example
the word birds (penguin, bat?) tall man, beautiful
women, creditworthy customer, responsible person
and trusty friend. We need special tools for
processing of such datum or its combination.
384
Khan, M. and Herawan, T.
Substantial Differences between Fuzzy Set and Soft Set Theories.
DOI: 10.5220/0010043403840387
In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 384-387
ISBN: 978-989-758-496-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2.1. Fuzzy Set Theory
Let
X
be a Universal set (objects/space of points)
with its members
x
, i.e.
}{xX 
. A fuzzy set
A
in
X
is represented by characteristic function
)( xf
.
Such that
)( xf
associates with each point of
X
through interval
]1,0[
,
X
takes a real value in this
interval for each of its membership association level
e.g.
1)(xf
if
Ax
and
0)(xf
if
Ax

,
closer the value of
x
to 1 means higher grade of
membership and closer the values of
x
to
0
means
lower grade of membership, e.g. we can have
membership functions
)( xf
of
A
like
0301 .)(

f
,
2102 .)( f
,
1703 .)( f
,
730101 .)(

f
,
840996 .)( f
and
11000 )(f
. In contrast to
fuzzy set, the ordinary set (simply set), crisp set or
“set” takes only two values i.e. either 1 or 0 for
completely belonging or completely not-belonging to
X
.
2.2. Definition of Soft Set Theory
Let
U
be a Universal set and let E be a set of
parameters then a fair
),( EF
is called to be soft set
over
U
if and only if F is a mapping of
E
into the
set of all subsets of
U
i.e. the soft set is a
parameterized family of the subsets of the set U.
Every fuzzy set can be considered a special case of
soft set.
2.3. Initial Application of Soft Set
Theory in Fuzzy Data
[25] implemented soft set in tabular form and
indicated that how it can be used in decision making.
Let
},,,,,{
654321
hhhhhh
U 
be a set of houses
and
E =
{
expensive, beautiful, wooden, cheap, in
the green surroundings, modern, in good repair, in
bad repair
}
be a set of parameters. Consider the soft
set
),( EF
which describes the attractiveness of the
houses, given by
),( EF
=
{
Expensive houses

)(
0
e
, beautiful
houses
},,,,,{)(
6543211
hhhhhhe

, wooden
houses
},,{)(
6212
hhhe

, cheap houses
},,,,,{)(
6543213
hhhhhhe

, in the green
surroundings houses
},,,,{)(
643214
hhhhhe

, in
good repair houses
},,{)(
6315
hhhe

, modern
houses
},,{)(
6216
hhhe

in bad repair houses
},,{)(
5427
hhhe

}
.
The
),( EF
is represented in tabular form as shown
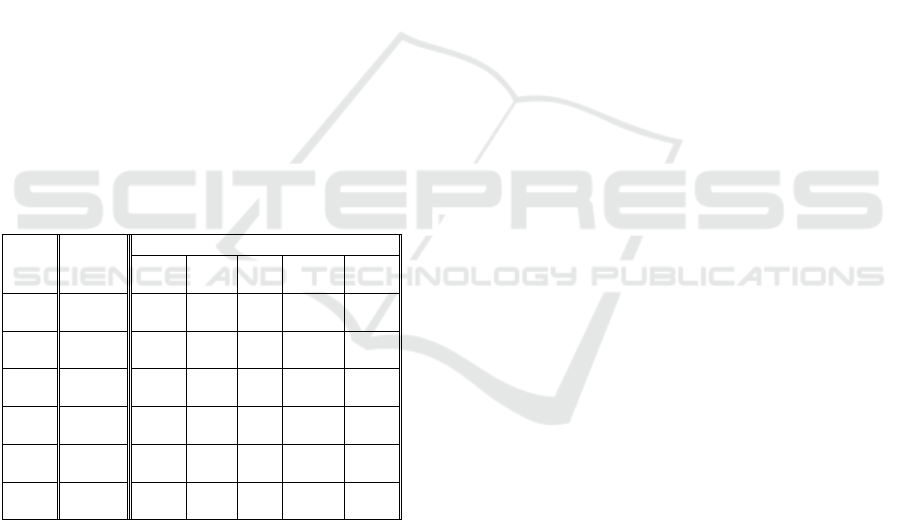
in Table 1. All objects are shown by rows and
parameters by columns, for an object having certain
parameter present is shown by putting its value equal
to 1, otherwise zero.
Table 1: Representation of soft set

EF,
in Tabular form
U
e
0
e
1
e
2
e
3
e
4
e
5
e
6
e
7
h
1
0 1 1 1 1 1 1 0
h
2
0 1 1 1 1 0 1 1
h
3
0 1 0 1 1 1 0 0
h
4
0 1 0 1 1 0 0 1
h
5
0 1 0 1 0 0 0 1
h
6
0 1 1 1 1 1 1 0
Suppose Mr. X is interested in buying house on the
bases of parameter having subset
P
=
{
beautiful,
wooden, cheap, in green surrounding, in good repair
}
=
},,,,{
54321
eeeee
. Then the tabular representation
for this choice should be as given in Table 2. Choice
of Mr. X is calculated by simply adding all parameters
value in last column as shown by
d
i
for each object
(house).
Table 2: Decision value or choice value calculation from
soft set
U
e
1
e
2
e
3
e
4
e
5
d
i
h
1
1 1 1 1 1 5
h
2
1 1 1 1 0 4
h
3
1 0 1 1 1 4
h
4
1 0 1 1 0 3
h
5
1 0 1 0 0 2
h
6
1 1 1 1 1 5
Substantial Differences between Fuzzy Set and Soft Set Theories
385

It can be observed from Table 2 that
h
1
and
h
6
have
highest
d
i
value, therefore either of them is best
choice or optimal choice for Mr. X, while
h
2
and
h
3
having second highest value are the sub-optimal
choices and
h
5
is the worst choice having lowest
value among all.
3 COMPARISON OF FUZZY SET
AND SOFT SET THEORIES
Consider above example of Mr. X house choice.
Choice values of all houses for soft set are re-entered
from Table 2 into new Table 3, plus fuzzy set
membership function values are calculated by
dividing the sum of belonging parameters by number
of total parameters. Total parameters are 5 in this
example, therefore every object’s belonging
parameters are divided by 5 in this case. For example
h
5
has only two parameters belonging among total
five, therefore
4.05/2)(
5


h
f
.
Table 3: Fuzzy set and soft set values description for same
vague data
U Fuzzy
set
Soft Se
t
e
1
e
2
e
3
e
4
e
5
h
1
1 1 1 1 1 1
h
2
0.8 1 1 1 1 0
h
3
0.8 1 0 1 1 1
h
4
0.6 1 0 1 1 0
h
5
0.4 1 0 1 0 0
h
6
1 1 1 1 1 1
It is obvious from Table 3 that description of
fuzziness for all houses in fuzzy set is narrow and
restricted to one value only, while same is described
comprehensively in soft set. For further illustration,
h
2
and
h
3
are treated same having same
accumulated value equal to 0.8 in fuzzy set, but in soft
set it is different and described with detail of
parameters i.e.
h
3
is not wooden but in good repair
condition, while
h
2
is wooden but in bad repair
status. This difference of fuzzy set and soft set is
further revealed if a parameter is deleted from or
inserted into this comparison Table 3, [26-28]. Based
on this example, we state below differences between
fuzzy set and soft set theory.
a. Soft set describes fuzzy data in term of each
parameter presence or absence while fuzzy set
describe it in term of all parameter’s
accumulative weight only.
b. Each parameter is described in crisp from i.e. one
or zero in soft set while fuzzy set has no
description for parameter’s description at all.
c. Fuzzy set membership function values are in
]1,0[
range while in soft set, membership is
calculated for each object by adding parameters
weights.
In addition to above differences between soft set and
fuzzy set, there is a big similarity between both
theories.
“Decision making or calculating
maximal choice has same results
for both soft set and fuzzy set
theories”
Like soft set maximal choice in Table 2,
h
1
and
h
6
are maximal choices of Mr. X in fuzzy set as well in
Table 3. It is because both have maximum values
equal to 1 among all other houses. Similarly,
h
2
and
h
3
are sub optimal choices having value equal to 0.8
and
h
5
is the worst choice.
4 CONCLUSION
In this paper, we revealed the main difference
between two famous theories of uncertain data named
fuzzy set and soft set. We used existing application
for representation of soft set and derived its
equivalent membership function for fuzzy set. In
comparison of both theories through same example,
their significant differences and similarity are
exposed with a reasonable brief clarification.
ACKNOWLEDGMENT
This work is supported by University of Malaya High
Impact Research Grant no vote
ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and
Technology
386

UM.C/625/HIR/MOHE/SC/13/2 from Ministry of
Education Malaysia
REFERENCES
Molodtsov, D., Soft set theory—first results. Computers &
Mathematics with Applications, 1999. 37(4): p. 19-31.
Pawlak, Z.,
Rough sets. International Journal of Computer
& Information Sciences, 1982. 11(5): p. 341-356.
Pawlak, Z.,
Rough set theory and its applications to data
analysis.
Cybernetics & Systems, 1998. 29(7): p. 661-
688.
Pawlak, Z.,
Rough Sets: Theoretical Aspects of Reasoning
about Data
. 2012: Springer Netherlands.
Pawlak, Z., L. Polkowski, and A. Skowron,
Rough set
theory.
Wiley Encyclopedia of Computer Science and
Engineering, 2008.
Zadeh, L.A.,
Fuzzy sets. Information and control, 1965.
8(3): p. 338-353.
Zimmermann, H.-J.,
Fuzzy set theory—and its applications.
2001: Springer Science & Business Media.
Zimmermann, H.-J.,
Fuzzy Set Theory-and Its Applications.
2014.
Ahmad, B. and A. Kharal,
On fuzzy soft sets. Advances in
Fuzzy Systems, 2009. 2009.
Akdag, M. and A. Ozkan,
On Soft β-Open Sets and Soft β-
Continuous Functions.
The Scientific World Journal,
2014. 2014.
Alhazaymeh, K. and N. Hassan,
Interval-valued vague soft
sets and its application.
Advances in Fuzzy Systems,
2012. 2012: p. 15.
Alkhazaleh, S. and A.R. Salleh,
Soft expert sets. Advances
in Decision Sciences, 2012. 2011.
Çağman, N. and S. Enginoğlu,
Soft matrix theory and its
decision making.
Computers & Mathematics with
Applications, 2010. 59(10): p. 3308-3314.
Herawan, T. and M.M. Deris,
A soft set approach for
association rules mining.
Knowledge-Based Systems,
2011. 24(1): p. 186-195.
Jun, Y.B., K.J. Lee, and C.H. Park,
Soft set theory applied
to ideals in d-algebras.
Computers & Mathematics with
Applications, 2009. 57(3): p. 367-378.
Jun, Y.B. and C.H. Park,
Applications of soft sets in ideal
theory of BCK/BCI-algebras.
Information Sciences,
2008. 178(11): p. 2466-2475.
Kalaichelvi, A. and P.H. Malini, Application of fuzzy soft
sets to investment decision making problem. Int. J. of
Mathematical Sciences and Applications, 2011. 1(3).
Kalayathankal, S.J. and G. Suresh Singh,
A fuzzy soft flood
alarm model.
Mathematics and Computers in
Simulation, 2010. 80(5): p. 887-893.
Sulaiman, N.H. and D. Mohamad,
Multiaspect soft sets.
Advances in Fuzzy Systems, 2013. 2013: p. 1.
Tanay, B. and M.B. Kandemir,
Topological structure of
fuzzy soft sets.
Computers & Mathematics with
Applications, 2011. 61(10): p. 2952-2957.
Xiao, Z., K. Gong, and Y. Zou,
A combined forecasting
approach based on fuzzy soft sets.
Journal of
Computational and Applied Mathematics, 2009.
228(1): p. 326-333.
Xin, X. and W. Li,
Soft congruence relations over rings.
The Scientific World Journal, 2014. 2014.
Yuksel, S., et al.,
Application of soft sets to diagnose the
prostate cancer risk.
Journal of Inequalities and
Applications, 2013. 2013(1): p. 1-11.
Yüksel, Ş., Z. Güzel Ergül, and N. Tozlu,
Soft Covering
Based Rough Sets and Their Application.
The Scientific
World Journal, 2014. 2014.
Maji, P., A.R. Roy, and R. Biswas,
An application of soft
sets in a decision making problem.
Computers &
Mathematics with Applications, 2002. 44(8): p. 1077-
1083.
Kong, Z., et al.,
The normal parameter reduction of soft sets
and its algorithm.
Computers & Mathematics with
Applications, 2008. 56(12): p. 3029-3037.
Kong, Z., et al.,
An efficient decision making approach in
incomplete soft set.
Applied Mathematical Modelling,
2014. 38(7): p. 2141-2150.
Ma, X., et al.,
A new efficient normal parameter reduction
algorithm of soft sets.
Computers & Mathematics with
Applications, 2011. 62(2): p. 588-598
Substantial Differences between Fuzzy Set and Soft Set Theories
387