Concept and Design of an Intelligent Strategy to Mitigate Traffic

Congestion at Intersection

Zulkifli Lubis and Abdullah Zawawi Talib

School of Computer Sciences, Universiti Sains Malaysia, Malaysia

Keywords: Traffic congestion; Signalized and Unsignalized Intersections, Fixed-time Traffic Light Control System,

Discrete Event Simulation, DITC System

Abstract: Traffic congestion on public roads is one of the leading causes of lost productivity and decrease in the standard

of living in urban setting. The continuous increase in the congestion level, especially at rush hour, is a critical

problem and is becoming a major concern to transportation specialists and decision makers. Traffic congestion

causes excessive delays, reduced safety and increase in environmental pollution. An intersection is the area

where one street or road crosses another. Almost all modes of travel i.e. pedestrian, bicycle, motor vehicle,

and transit involve dealing with the intersection area for a given time period, which in turn makes it as a focus

of activity, conflicting movements area and a traffic control centre, and as a consequence reducing its capacity.

Traffic control at the intersection is an old and ever growing problem in cities all over the world. In many

cities, intersections represent bottlenecks in the traffic flow. Evaluating and managing intersections are

complex, difficult, costly, and time consuming. The existing methods for traffic management, surveillance

and control, are not adequately efficient in terms of performance, cost, maintenance, and support. In this

paper, we propose a framework of an intelligent approach for the Dynamic Intersection Traffic Control

(DITC) system. We also present some intersection designs that would benefit from the proposed DITC. The

proposed strategy reduces conflicts through geometric design and an intelligent traffic control systems. The

proposed DITC system has no waiting time and has a specific configuration.

1 INTRODUCTION

The goal of Intelligent Transport System (ITS) is

applying information technology, communications,

sensor technology and the internet to transportation

systems to improve travel safety, reliability,

passenger convenience, mobility, and mitigate traffic

congestion as well as reduce fuel consumption. The

Intelligent Traffic Control System is an important part

of the ITS (Shandiz, Khosravi, & Doace, 2009).

Traffic congestion appears when a large number

of vehicles attempt to use common transportation

infrastructure which has limited capacity. It leads to

queuing phenomena and corresponding delay (in the

best case), and a degraded use of the available space

and thus, reduce throughput (in the worst case).

Traffic congestion is a severe problem in many cities

around the world (Liu, 2008). Wen (2008), Yang and

Wen (2008), and Liu (2008) found that traffic

congestion results in excessive delays, reduced

safety, and increased environmental pollution. To a

commuter or traveller, it means lost time, missed

opportunities, and frustration while to an employer

congestion means lost worker productivity and trade

opportunities, delivery delays, and increase costs.

In this paper, we describe a framework for an

intelligent approach for the Dynamic Intersection

Traffic Control (DITC) system. We also present some

intersection designs that would benefit from the

proposed DITC.

2 RELATE WORK

We need some programming languages or software to

build a model/simulation model such as Java and

Matlab/Simulink, and software such as, Excel,

VISSIM, Arena, StellaTM, and Quadstone Paramics

and Azalient Commuter.

Groenewoud and Rinkel (2012) depicted the

classification of different kinds of simulation models

as illustrated in Figure 1.

518

Lubis, Z. and Talib, A.

Concept and Design of an Intelligent Strategy to Mitigate Trafﬁc Congestion at Intersection.

DOI: 10.5220/0010045805180522

In Proceedings of the 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and Technology (ICEST 2018), pages 518-522

ISBN: 978-989-758-496-1

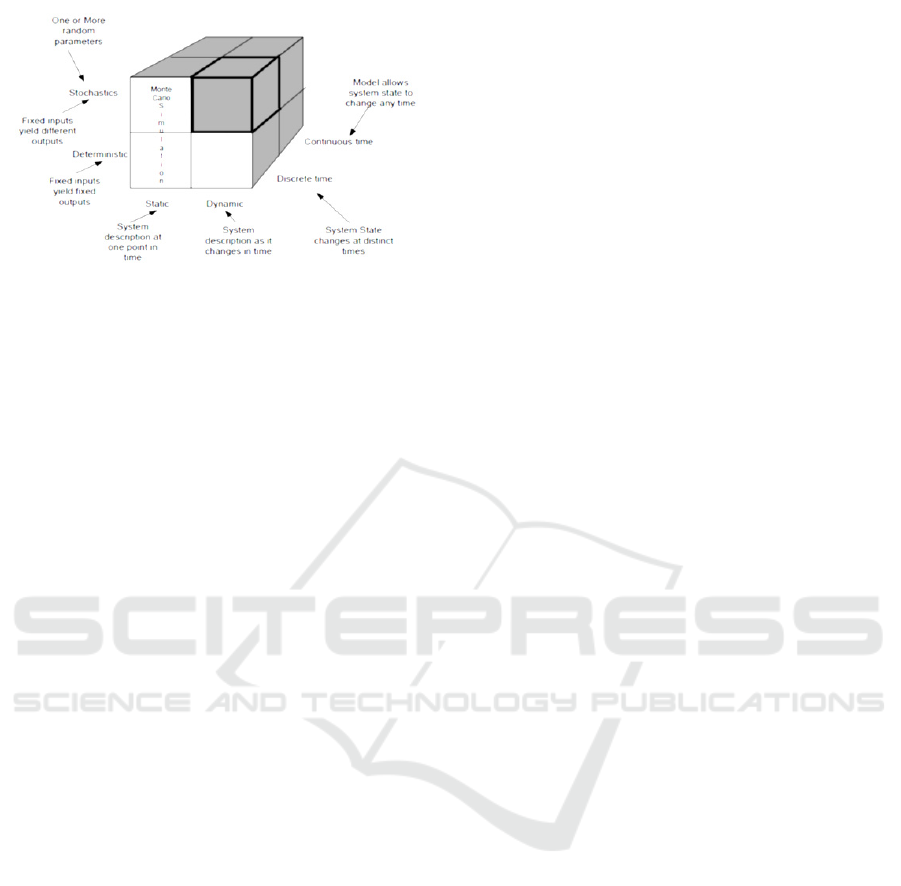
Figure 1: Classification of different types of simulation

models

There are three model of approaches in simulation

models, i.e. 1) continuous simulation; 2) static,

stochastic simulation (Monte-carlo simulation); and

3) discrete, dynamic, stochastic simulation also called

Discrete Event Simulation (Groenewoud & Rinkel,

2012). In a continuous model, state variables change

continuously as a function of time. In general

analytical method such as inductive mathematical

reasoning is used to define and solve a system.

According to Groenewoud and Rinkel (2012), the

Monte Carlo methods varies, but tends to follow a

particular pattern:

1. Define a domain of possible inputs.

2. Generate inputs randomly from a probability

distribution over the domain.

3. Perform a deterministic computation on the

inputs.

4. Aggregate the results.

Discrete event models represents only those time

steps at which change occurs, and consequently it is

called event base or event driven, where the system

jumps from one event to another, leaving out the

irrelevant behaviour for the model, in between the

events.

Ross (2005) defined the simulation approach

based on a framework which generates the stochastic

mechanisms of the model and then observes the

resultant flow of the model over time as the discrete

event simulation approach. Depending on the reasons

for the simulation, there will be certain quantities of

interest that someone wants to determine.

Furthermore, the key elements in a discrete event

simulation are variables and events. In general, there

are three types of variables that are often utilized, i.e.

the time variable t, refers to the amount of (simulated)

time that has elapsed; counter variables, which keep

a count of the number of times that certain events

have occurred by time t; and the system state variable,

that describes the “state of the system” at the time t.

Whenever an “event” occurs, the values of the above

variables are changed or updated, and any relevant

data of interest are collected as output.

There are a lot of ways to classify simulation

models. Kelton, Sadowski, and Swets (2010), and

also Groenewoud and Rinkel (2012) claimed that one

of the useful ways is along these three dimensions:

1. Static or Dynamic

2. Continuous or Discrete

3. Deterministic or Stochastic

In the static model, time does not play a natural

role but does in dynamics model. The Buffon needle

problem is an example of static model. Most

operational models are dynamic. In a continuous

model, the state of the system can change

continuously over time while in a discrete model,

change can occur only at certain times. An example

of continuous model would be the level of reservoir

as water flows in and is let out, and as precipitation

and evaporation occur. A manufacturing system with

parts arriving and leaving at specific times, machines

going down and coming back up at specific times is

an example of a discrete model. Models that have no

random input are deterministic, a strict appointment

with a booked operation with fixed service time is an

example. On the other hand, stochastic models

operate with at least some inputs being random. An

example is a bank with randomly arriving customers

requiring varying service times.

From traffic simulation models point of view,

there are two common approaches for traffic

modelling i.e., macroscopic and microscopic models.

Macroscopic traffic models are based on gas-kinetic

models and use equations relating to traffic density

and velocity while microscopic traffic models offer a

way of simulating various driver behaviours and it

consists of an infrastructure that is occupied by a set

of vehicles. Each vehicle interacts with its

environment according to its own rules, so different

kinds of behaviour emerge when groups of vehicles

interact (Wiering et al., 2004). Meanwhile

TransModeler (2013) and Salimifard and Ansari

(2013) divided traffic simulation models into three

kinds of models i.e., microscopic, macroscopic and

mesoscopic models. Microscopic models predict the

mood of single and individual vehicles both

continuous and discrete types such as individual

vehicle speed and locations, macroscopic models

make ready an extensive depiction of the traffic flow

simulation, end mesoscopic include the mixed aspects

of both microscopic and macroscopic models.

Concept and Design of an Intelligent Strategy to Mitigate Trafﬁc Congestion at Intersection

519

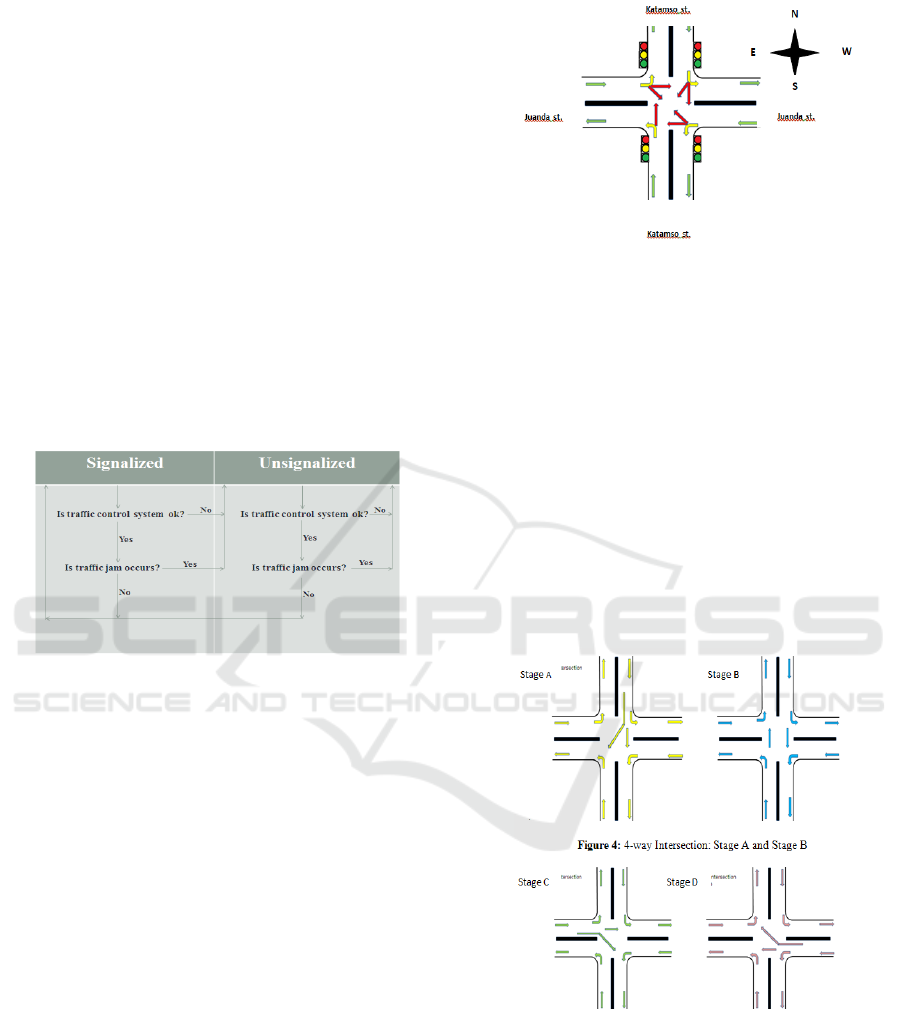
3 THE PROPOSED DITC

ALGORITHM

By applying lane closure strategy, continuous flow

treatment in intersection zone provides an amazing

idea to create a reliable intersection traffic control. A

signalized intersection is treated as if it is an

unsignalized intersection for certain condition. Figure

2 shows how this combined technique performs its

function. The intersection normally functions as a

signalized intersection, but in certain situation when

the traffic control system is out of order (control

system failure or due to electrical power supply

failure) or traffic jam occurs at the intersection then it

will function as an unsignalized intersection with

special treatments. If the situation returns to normal

again, i.e. the traffic control systems is working as

usual or the jam or congestion has reduced, the

intersection reverts to a signalized intersection.

Figure 2: Main algorithm of proposed DITC Model

4 THE 4-WAY INTERSECTION

TIME-BASED SYSTEM

Medan is the largest city outside of Java, and the 3

largest city in Indonesia, after Jakarta and Surabaya.

This study concentrate on one of the main 4-way

intersections and one of the main 3-way intersections

of the urban traffic system in Medan, the capital city

of the province of North Sumatera, Indonesia. The

observed intersections are an isolated (single) 4-way

signalized intersection located at Juanda street and

Katamso street as depicted in Figure 3.

Figure 3: Traffic Flow of 4-way Intersection

There are some patterns in traffic light control

system, and they depend on traffic condition,

government policies and others. At Juanda street and

Katamso street, the intersection has the patterns and

stages as given in Figure 4 and Figure 5. In the 4-way

intersection there are four stage sequences, i.e. stage

A, stage B, stage C and stage D, with special patterns,

and they are all controlled by three signals: red,

yellow, and green lights of the signals. Stage B has a

sligtly different pattern from stage A, stage C and

stage D where in the former vehicles may not turn to

the right permanently and in the latter, they may turn

to the right. These patterns are designed to reduce the

complexity of system.

Figure 5: 4-way Intersection Stage C and Stage D

Almost all traffic light control system in Medan

are fixed-time control where all signal timing

parameters are pre-computed and kept constant i.e.

fixed-time which is also called time-based system. In

this study, the simulation will be based on this system.

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

520

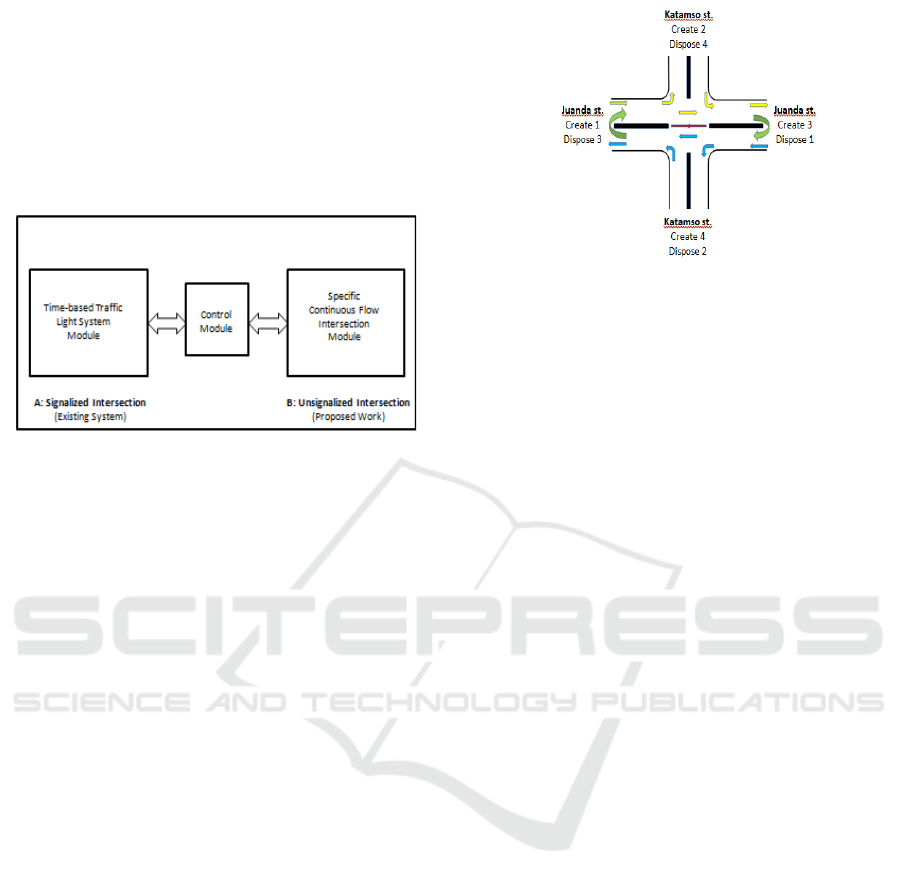
5 OVERVIEW OF THE

PROPOSED FRAMEWORK OF

THE DITC SYSTEM

The proposed DITC System framework consists of

three blocks i.e. block A (Signalised intersection),

block B (Unsignalised Intersection), and the control

module block as shown in Figure 6.

Figure 6: Proposed Framework of the DITC system

This DITC System divided into several modules

in its implementation. All modules in this study will

be implemented, tested and the result will be obtained

using Arena version 14.50.00002 (Student version).

6 THE PROPOSED DITC

MODELING FOR 4-WAY

INTERSECTION

In reducing or mitigating traffic jam or to overcome

power failure at intersection zone, this study will use

the optimal configuration of lane closure strategy by

completely closing four lanes in the middle of an

intersection zone of one road or street (with four

lanes, divided road or street), diverting all vehicles to

the left side of that direction and then detouring some

of them by means of U-turn rotation, following the

rest of the road and then at the intersection zone,

turning to the left to continue their movement in the

previous direction. This proposed strategy is shown

in Figure 7 and an illustration of Intersection’s lane

closure is given in Figure 8.

Figure 8: Illustration of intersection’s lane closure

7 CONCLUSION

The strategy used in this study is by reducing conflicts

through geometric design improvement, operating

speeds on approaches, choosing appropriate traffic

control, and improving management access by using

lane closure (in the middle of the intersection), U-

turn, and continuos flow intersection treatment. The

proposed DITC system has no waiting time, no phase

movement to follow and has specific configuration

when acting as unsignalized intersection. In this study

only two lanes are considered, it could be expanded

into multi-lane in a future work.

REFERENCES

Groenewoud, P., & Rinkel, A. (2012, July). The analysis

and simulation of a supply chain with Arena. (Thesis).

Retrieved from https://eprints.hsr.ch/140/1/

TechnicalReport.pdf

Kelton, W.D., Sadowski, R.P., & Swets, N.B. (2010).

Simulation with Arena. (5

Ed.). Singapore: McGraw-

Hill International.

Liu, T.I. (2008). Automatic Traffic Light Control System.

California State University, Sacramento, ME233 Final

Project Report.

Ross, S.M. (2005). Simulation, (3

Ed.). New Delhi:

Elsevier Publisher.

Salimifard, K. & Ansari, M. (2013, April). Modeling and

Simulation of Urban Traffic Signals. International

Journal of Modeling and Optimization, 3(2), 172-175.

Shandiz, H.T., Khosravi, M., & Doace, M. (2009).

Intelligent Transport System Based on Genetic

Algorithm. World Applied Sciences Journal 6(7), 908-

913.

TransModeller (2013). Traffic Simulation Models.

Retrieved from http://www. caliper.com/transmodeler/

Wen, W. (2008), A dynamic and automatic traffic light

control expert system for solving the road congestion

Concept and Design of an Intelligent Strategy to Mitigate Trafﬁc Congestion at Intersection

521

problem, in Expert Systems with Applications no 34, pp.

2370-2381, 2008.

Wiering, M., Veenen, J., Vreeken, J., & Koopman, A.

(2004, July). Intelligent Traffic Light Control. IICS,

Utrecht University, Netherlands, Tech. Rep. UU-CS-

2004-029.

Yang, C.L., & Wen, W. (2008). Solving the Traffic

Problem by Using A Simulation Model. International

Conference on Information Resource Proceedings

(CONF-IRM 2008).

ICEST 2018 - 3rd International Conference of Computer, Environment, Agriculture, Social Science, Health Science, Engineering and

Technology

522