Application of Buoyancy Weighing-bar Method to Measure the

Droplet Size Distribution of Kerosene in Water

R. Tambun

, P. Sibagariang

, B. Alphantaria

, A. A. Silaen

, A. M. Rambe

and F. Batubara

Chemical Engineering Department, Universitas Sumatera Utara, Padang Bulan, Medan 20155, Indonesia

Keywords: Buoyancy Weighing Bar, Droplet Size Distribution, Kerosene, Water, Separation Time.

Abstract: Buoyancy Weighing-Bar Method has been proven to be capable of measuring the particle size distribution of

the settling particles and floating particles. Besides a simple operations and low-cost equipment, the Buoyancy

Weighing-Bar Method could produce high accuracy results in measurement of particle size distribution. In

this study, the Buoyancy Weighing-Bar Method is developed to measure droplet size distribution in the liquid-

liquid systems. The samples used in this study are the mixture of kerosene of 1% in water of 99%, the mixture

of kerosene of 2% in water of 98%, the mixture of kerosene of 3% in water of 97%, the mixture of kerosene

of 4% in water of 96%and the mixture of kerosene of 5% in water of 95%. This study also decides the

separation time of kerosene – water mixtures. The weighing-bar’s diameter is 15 mm, and the vessel’s

diameter is 65 mm. The result by the Buoyancy Weighing-Bar Method are checked by using the gas

chromatography to verify the purity of sample, and the droplet size distribution of kerosene in water is

calculated by Stokes formula and compared to that measured by Coulter LS100. Based on the results obtained,

the Buoyancy Weighing-Bar Method can decide the separation time of kerosene and water mixtures, and the

droplet size distribution that calculated by Stoke formula is proportional to the Coulter L100.

1 INTRODUCTION

Application of buoyancy weighing-bar method had

been done for measurement particle size distribution

either floating particles or settling particles (Obata, et

al., 2009; Motoi, et al., 2010). In this

Buoyancy

Weighing-Bar Method, the density change of solution

due to droplet migration is determined by weighing

buoyancy against a weighing bar hung in the

suspension. Theoretically, the Buoyancy Weighing-

Bar Method also could be applicable to measure

droplet size distribution either in Stoke region or

Allen region (Obata, et al., 2009; Motoi, et al., 2010;

Tambun, et al., 2011; Tambun, et al., 2012a; Tambun,

et al., 2012b; Tambun, et al., 2018). In this study, the

Buoyancy Weighing-Bar Method will determine the

measure droplet size distribution for liquid-liquid

systems with the different density. The measure

droplet size distribution had been investigated by

using light scattering method (Mao, et al., 1998),

microscope (Boxall,et al., 2010), nuclear magnetic

resonance (Fridjonsson, et al., 2014), and laser

diffraction with a Coulter LS-230 (Jurado, et al.,

2007). In a short time, all methods can give highly

precise results but require extremely expensive

equipment. Hence, the

Buoyancy Weighing-Bar Method

will be a low cost method in droplet size distribution

determination.

The principle of Buoyancy Weighing-Bar Method

that measurement the density change in a suspension

due to liquid migration is determinated by weighing

buoyancy against a weighing bar hung in the

suspension. The tools of Buoyancy Weighing-Bar

Method consists of an analytical balance with a hook

for under-floor weighing and a weighing bar, which

is used to determine the density change of suspension

(Obata, et al., 2009; Motoi, et al., 2010). Besides, the

Buoyancy Weighing-Bar Method has been proven to

be able to estimate the fine particles by using the

Rosin-Rammler equation (Tambun, et al., 2016).

In this study, Buoyancy Weighing-Bar Method

will be applied in liquid-liquid systems of different

densities, where in this experiment the sample used is

kerosene and water (O/W) mixture. The Buoyancy

Weighing-Bar Method used to investigate the

measure droplet size distribution of kerosene in water

(O/W) and the separation time of kerosene – water

mixture. The principle of this study is similar to

distributions system of the settling particles and

floating particles, where the initial buoyant mass of

Tambun, R., Sibagariang, P., Alphantaria, B., Sialaen, A., Rambe, A. and Batubara, F.

Application of Buoyancy Weighing-bar Method to Measure the Droplet Size Distribution of Kerosene in Water.

DOI: 10.5220/0010087402910296

In Proceedings of the International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches (ICOSTEERR 2018) - Research in Industry 4.0, pages

291-296

ISBN: 978-989-758-449-7

291

the weighing bar according to the mixtures of liquid

between the bottom and top of the weighing bar in a

suspension (Tambun, et al., 2018a; Tambun, et al.,

2018b).

2 METHODS

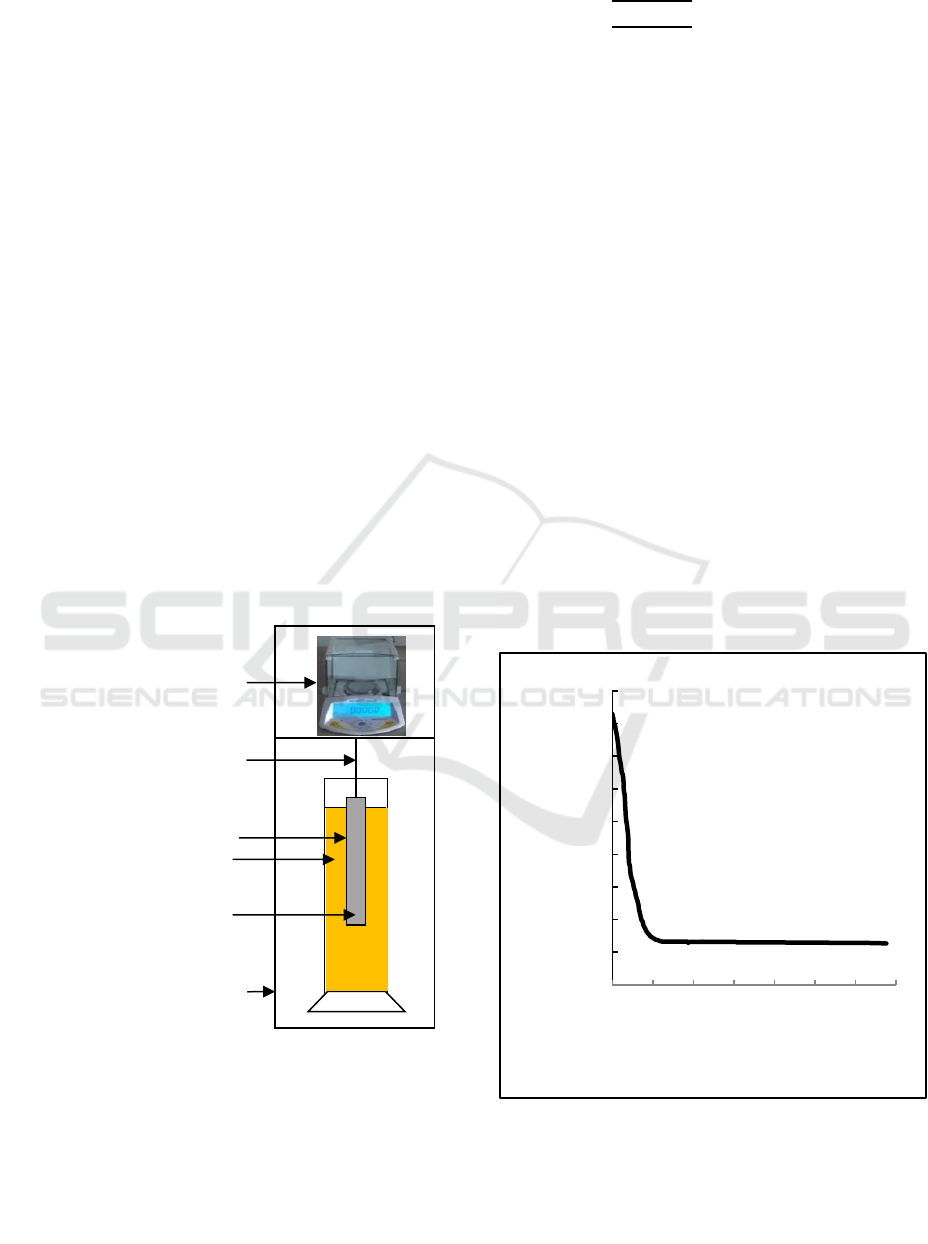
The illustration of the experimental apparatus is

shown at Figure 1. The weighing bar is made of

aluminum rod with the diameter of 15 mm, the length

of 210 mm, and the density of 2700 kg/m

. The

sample materials are water (ρ= 0.99708 g/cm

) and

kerosene (ρ= 0.810 g/cm

). The material samples is

put into glass cylinder with volume 1000 ml

(diameter: 65 mm) with the mixture of kerosene of

1% in water of 99%, the mixture of kerosene of 2%

in water of 98%, the mixture of kerosene of 3% in

water of 97%, the mixture of kerosene of 4% in water

of 96%and the mixture of kerosene of 5% in water of

95%. All experiments are operated at room

temperature (approximately 298 K). The measuring

time is 1 h and the measure droplet size distribution

is calculated by Stokes formula and the result is

compared to that measured by Coulter LS100.

Figure 1: Schematic diagram of experiment to measure

droplet size distribution of O/W by using Buoyancy

Weighing-Bar Method.

The Stokes formula can be seen in equation 1 below:

𝑥























(1)

where g is the gravitational acceleration and

is the

viscosity of the solution. The stokes equation applies

only to laminar flow types with Reynold Numbers,

Rep < 0,2 (Allen T, 1990). After the separations time

of samples are obtained from this research, the purity

of samples are then analyzed by using gas

chromatography.

3 RESULTS AND DISCUSSION

3.1 Effect of Time on Apparent Mass of

the Weighing-Bar When

Comparison of O/W Water is 1 % :

99%

Figure 2 shows the correlation between apparent mass

of the weighing-bar and time when comparison 1% :

99% of O/W is used. In the figure 2, the apparent

mass of the weighing-bar decreased until all the

kerosene floated above the weighing-bar, and then the

apparent mass of the weighing-bar become constant.

Figure 2: The correlation between apparent mass of the

weighing-bar with the time separation when comparison of

O/W is 1 % : 99%.

The mass of weighing bar is decreased rapidly

from beginning (at 0 second) until at 100 seconds and

68,56

68,57

68,58

68,59

68,60

68,61

68,62

68,63

68,64

68,65

0 100 200 300 400 500 600 700

Apparent Mass (10⁻⁶ kg)

Time (second)

Analytical balance

Hanging wire

Weighing bar

Insulation vessel

Graduated cylinder

Liquids (O/W)

ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches

292

then the mass of weighing-bar tends to be constant. In

this experiment, the weighing bar detect that all of the

larger droplets have floated after 100 seconds. This is

because the largest droplets will float first, then the

medium droplets and the smaller droplet, so the

weighing-bar mass decrease gradually and then

constant after all the droplets is floating above the

weighing bar. The results obtained by the Buoyancy

Weighing-Bar Method are compared with those

measured by gas chromatography. At 100 seconds of

experiment, the purity of water is 94.9496% and at

680 seconds the purity of water is 97.1326%. At this

experiment, at 680 seconds the mass of weighing-bar

had not changed again and the water and kerosene are

already separate but not complete. Hence, the

separation time of O/W had been detected by using

the Buoyancy Weighing-Bar Method.

3.2 Effect of Time on Apparent Mass of

the Weighing-Bar When

Comparison of O/W is 2 % : 98%

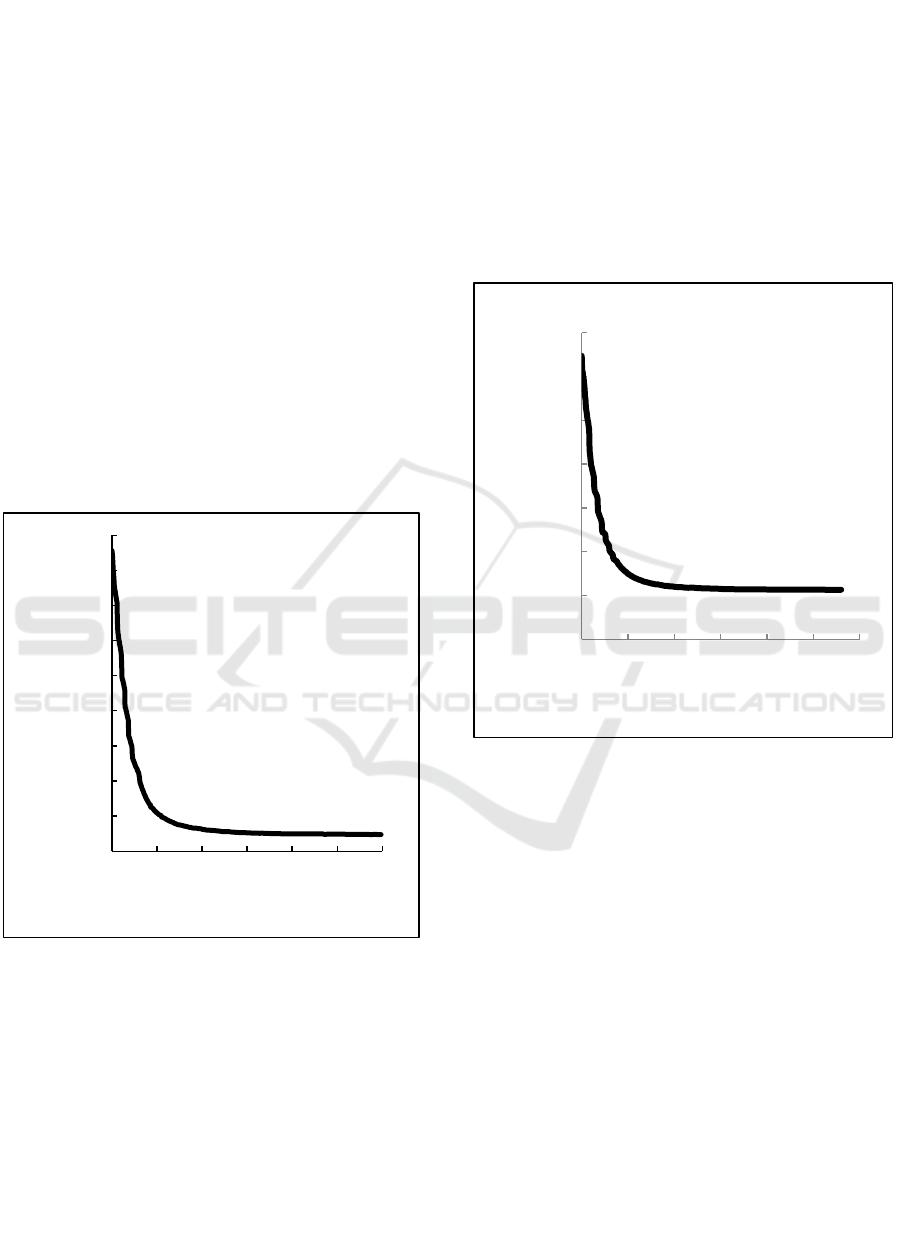
Figure 3: The correlation between apparent mass of the

weighing-bar with the time separation when comparison of

O/W is 2 % : 98%.

Figure 3 shows the correlation between apparent

mass of the weighing-bar with the time separation

when comparison of O/W is 2 % : 98%. Similar with

the figure 3, the mass of weighing bar is decreased

rapidly from beginning until at 146 seconds and then

the mass of weighing-bar tends to be constant. In this

experiment, the weighing bar detect that all of the

larger droplets have floated after 146 seconds. This is

because the largest droplets will float first, then the

medium droplets and the smaller droplet, so the

weighing-bar mass decrease gradually and then

constant after all the droplets is floating above the

weighing bar. At this experiment, at 597 seconds the

mass of weighing-bar has been constant and the water

and kerosene are already separate but not complete.

3.3 Effect of Time on Apparent Mass of

the Weighing-Bar When

Comparison of O/W is 3 % : 97%

Figure 4: The correlation between apparent mass of the

weighing-bar with the time separation when comparison of

O/W is 3 % : 97%.

Figure 4 shows the correlation between apparent

mass of the weighing-bar with the time separation

when comparison of O/W is 3 % : 97%. At this

comparison, the mass of weighing bar is decreased

rapidly from beginning until at 157 seconds and then

the mass of weighing-bar tends to be constant. In this

experiment, the weighing bar detect that all of the

larger droplets have floated after 157 seconds. This is

because the largest droplets will float first, then the

medium droplets and the smaller droplet, so the

weighing-bar mass decrease gradually and then

constant after all the droplets is floating above the

weighing bar. At this experiment, at 560 seconds the

mass of weighing-bar has been constant and the water

and kerosene are already separate but not complete.

68,78

68,8

68,82

68,84

68,86

68,88

68,9

68,92

68,94

68,96

0 100 200 300 400 500 600

Apparent Mass (10⁻⁶ kg)

Time (second)

67,80

67,85

67,90

67,95

68,00

68,05

68,10

68,15

0 100 200 300 400 500 600

Apparent Mass (10⁻⁶ kg)

Time (second)

Application of Buoyancy Weighing-bar Method to Measure the Droplet Size Distribution of Kerosene in Water

293

3.4 Effect of Time on Apparent Mass of

the Weighing-Bar When

Comparison of O/W is 4 % : 96%

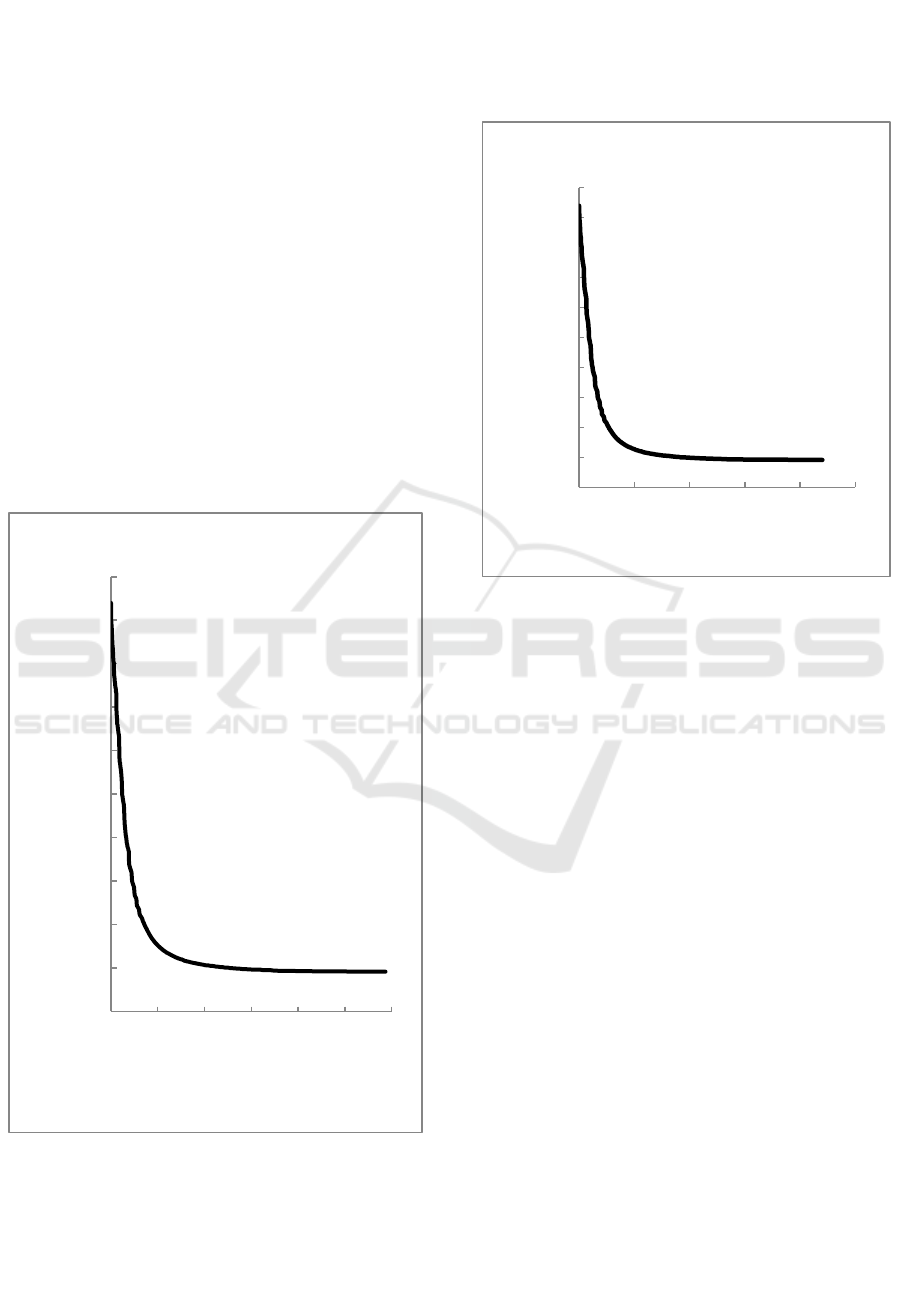
Figure 5 shows the correlation between apparent mass

of the weighing-bar with the time separation when

comparison of O/W is 4 % : 96%. At this comparison,

the mass of weighing bar is decreased rapidly from

beginning until at 164 seconds and then the mass of

weighing-bar tends to be constant. In this experiment,

the weighing bar detect that all of the larger droplets

have floated after 146 seconds. This is because the

largest droplets will float first, then the medium

droplets and the smaller droplet, so the weighing-bar

mass decrease gradually and then constant after all

the droplets is floating above the weighing bar. At this

experiment, at 870 seconds the mass of weighing-bar

has been constant and the water and kerosene are

already separate but not complete.

Figure 5: The correlation between apparent mass of the

weighing-bar with the time separation when comparison of

O/W is 4 % : 96%.

3.5 Effect of Time on Apparent Mass of

the Weighing-Bar When

Comparison of O/W is 5 % : 95%

Figure 6: The correlation between apparent mass of the

weighing-bar with the time separation when comparison of

O/W is 5 % : 95%.

Figure 6 shows the influence of time separation on

apparent mass of the weighing-bar when comparison

of O/W is 5 % : 95%. At the figure 6, we could see

that mass of weighing bar is decreased rapidly from 0

second until at 245 seconds and then the mass of

weighing-bar tends to be constant. In this experiment,

the weighing bar detect that all of the larger droplets

have floated after 245 seconds. This is because the

largest droplets will float first, then the medium

droplets and the smaller droplet, so the weighing-bar

mass decrease gradually and then constant after all

the droplets is floating above the weighing bar. At this

experiment, at 880 seconds, the mass of weighing-bar

has not changed again and the water and kerosene are

already separate but not complete.

3.6 Determination Measure Droplet

Size Distribution by using

Buoyancy Weighing-Bar Method

Figure 7 shows the measure droplet size distribution

measured by using Buoyancy Weighing-Bar Method

when the concentration 99% water : 1% kerosene.

The measure droplet size distribution is calculated by

68,55

68,60

68,65

68,70

68,75

68,80

68,85

68,90

68,95

69,00

69,05

0 150 300 450 600 750 900

Apparent Mass (10⁻⁶ kg)

Time (second)

68,55

68,60

68,65

68,70

68,75

68,80

68,85

68,90

68,95

69,00

69,05

0 200 400 600 800 1000

Apparent Mass (10⁻⁶ kg)

Time (second) Time (second)

ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches

294

Stokes formula, and the results obtained are

compared with Coulter LS 100. The result obtained

by measuring the BWM is comparable to that

measured by Coulter LS100. In figure 5 can be seen

that the results obtained by Buoyancy Weighing-Bar

Method and Coulter are close. According to these

results, Buoyancy Weighing-Bar Method could identify

the measure droplet size distribution of O/W when

comparison of O/W is 1% : 99%.

Figure 7: The measurement comparison of droplet size

distribution of O/W between BWM and Coulter LS 100

when comparison of O/W is 1 % : 99%.

4 CONCLUSION

The Buoyancy Weighing-Bar Method has been

applied to experimentally investigate the droplet size

distribution of O/W and to detect the separation time

of O/W mixtures. The conclusions of this study are:

1. The Buoyancy Weighing-Bar Method could

identify the droplet size distribution of O/W when

comparison of O/W is 1% : 99% by using Stoke

equation, and the precision of result is near to that

measured by a Coulter LS100.

2. The

Buoyancy Weighing-Bar Method could decide

the separation time of O/W mixtures when

comparison of O/W are 1% : 99%, 2% : 98%, 3% :

97%, 4% : 96% and 5% : 95%.

3. The separation time for each comparison of O/W

is different.

ACKNOWLEDGEMENT

This research is supported by Directorate of Research

and Community Service (DRPM) of the Ministry of

Research, Technology, and Higher Education of

Republic Indonesia for Research Grant, under

Fundamental Research scheme, 2018.

REFERENCES

Allen, T, Particle Size Measurement, Fourth Edition,

London : Chapman and Hall, 1990.

Boxall, J. A., Koh, C. A., Sloan, E. D., Sum, A. K., and Wu,

D. T. (2010). Measurement and calibration of droplet

size distribution in water in oil emulsion by particle

video microscope and focused beam reflectance

method. Ind. Eng. Chem. Res. 49(3) pp 1412-1418.

Fridjonsson, E. O., Graham, B. F., Akhfash, M., May, E. F.,

and Johns, M. L. (2014). Optimized droplet sizing of

water in crude oil emulsion using nuclear magnetic

resonance. Energy & Fuels. 28(3) pp 1756-1764.

Jurado, E., Bravo, V., Camacho, F., Vicaria, J. M., and

Arteaga, A. F. (2007). Estimation of the distribution of

droplet size, interfacial area and volume in emulsions.

Colloids and Surfaces A: Physicochem. Eng. Aspects.

295 pp 91-98.

Mao, Y., Yong, L., Tao, H., Shimin, W., and Yiqian, X.

(1998). In situ measurement of droplet size distribution

by light scattering method. Wuhan University Journal

of Natural Sciences. 3(4) pp 418-422.

Motoi, T., Ohira, Y., and Obata, E. (2010). Measurement of

the floating particle size distribution by buoyancy

weighing–bar method. Powder Technology. 201 pp

283–288.

Obata, E., Ohira, Y., and Ohta, M. (2009). New

measurement of particle size distribution by buoyancy

weighing–bar method. Powder Technology. 196 pp

163–168.

Tambun, R., Furukawa, K., Hirayama, M., Shimadzu, M.,

Yamanaka, S., and Ohira, Y. (2016). Measurement and

estimation of the particle size distribution by the

buoyancy weighing-bar method and the Rosin-

Rammler equation. Journal of Chemical Engineering of

Japan. 49 (2) pp 229-233.

Tambun, R., Motoi, T., Shimadzu, M., Ohira, Y., and

Obata, E. (2011). Size distribution measurement of

floating particles in the allen region by a buoyancy

weighing–bar method. Advanced Powder Technology.

22 pp 548–552.

Tambun, R., Nakano, K., Shimadzu, M., Ohira, Y., and

Obata, E. (2012). Sizes influences of weighing bar and

vessel in the buoyancy weighing-bar method on

floating particle size distribution measurements.

Advanced Powder Technology. 23 pp 855-860.

Tambun, R., Shimadzu, M., Ohira, Y., and Obata, E.

(2012). Definition of the new mean particle size based

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0 25 50 75 100 125 150

Cumulative mass undersize (%)

Droplet size (μm)

Coulter LS

100

Application of Buoyancy Weighing-bar Method to Measure the Droplet Size Distribution of Kerosene in Water

295

on the settling velocity in liquid. Journal of Chemical

Engineering of Japan. 45 (4) pp 279-284.

Tambun, R., Sibagariang, P., Alphantaria, B., and Rambe,

A. M. (2018). Droplet size distribution measurement of

water in kerosene by the buoyancy weighing-bar

method. MATEC Web of Conferences. 154.

Tambun, R., Sibagariang, Y., J Manurung, J.2018.

Influence of the Weighing Bar Size to Determine

Optimal Time of Biodiesel-Glycerol Separation by

Using the Buoyancy Weighing-Bar Method.

TALENTA-CEST 2017. IOP Conf. Series: Materials

Science and Engineering. 309.

Tambun, R., Sihombing, R. O., Simanjuntak, A., F Hanum,

F. 2018. Influence of the weighing bar position in

vessel on measurement of cement’s particle size

distribution by using the buoyancy weighing-bar

method. TALENTA-CEST 2017 IOP Conf. Series:

Materials Science and Engineering. 309.

ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches

296