A Logical Approach to Extreme Opinion Diffusion

Enzo Battistella and Laurence Cholvy

ONERA, 2 avenue Edouard Belin, 31055 Toulouse, France

Keywords:

Opinion Diffusion, Logic, Modelisation, Simulation.

Abstract:

This paper focuses on diffusion of extreme opinions among agents which inﬂuence each other. In this work,

opinions are modeled as formulas of the propositional logic or equivalently, as sets of propositional interpreta-

tions. Moreover, we assume that any agent changes its opinion by merging the opinions of its inﬂuencers, from

most to least inﬂuential. We propose a ﬁrst deﬁnition of extreme opinions and extremism. We then consider

degrees of extremism. Formal studies of these deﬁnitions are made as well as simulations.

1 INTRODUCTION

Understanding the dynamics of the diffusion of opin-

ions and especially of extremism is a tremendous

question in Multi-Agent System and Artiﬁcial Intel-

ligence communities. See for instance (Crawford

et al., 2013; Christoff and Hansen, 2015; Cholvy,

2016; Grandi et al., 2015; Haﬁzoglu and Sen, 2012;

Jager and Amblard, 2004; Tsang and Larson, 2014;

Christoff and Grossi, 2017) for the study of opinion

diffusion and (Chau et al., 2014; Deffuant et al., 2002;

Sureda et al., 2017) for the study of extremism diffu-

sion.

Opinions are usually represented by a single real

value between 0 (or -1) and 1 corresponding to the

adequacy to a given afﬁrmation: the closer to 1 an

agent’s opinion is, the more this agent agrees with the

afﬁrmation. However some works, mainly in Artiﬁ-

cial Intelligence community, represent an opinion by

a single binary vector ((Grandi et al., 2015; Christoff

and Grossi, 2017)) corresponding to adequacies to

several afﬁrmations. For instance, if the two afﬁrma-

tions are “Canada will host Winter Olympics in 2026”

and “there will be acroski trials”, then the vector (1, 0)

represents the opinion of an agent which thinks that

Canada will host Winter Olympics in 2026 but that

there will not be acroski trials.

In the present paper, we consider the model of

Inﬂuence-Based Opinion Diffusion Structure (IODS)

deﬁned in (Cholvy, 2016) in which opinions are rep-

resented by propositional logic formulas or, equiv-

alently, sets of binary vectors. There, the set

{(1, 1), (0, 1), (0, 0)} represents the opinion of an

agent which thinks that, if the hosting country is

Canada then there will be acroski trials.

As for extremism, when opinions are represented

by a single real value, it is obviously deﬁned by hav-

ing an opinion which is close to 0 (or -1) or to 1.

Moreover, in such models, agents can easily be clas-

siﬁed from most to least extremist. But for IODS, this

is not so obvious and deﬁnitions of extreme opinions

and extremists have to be proposed. This is the aim of

the present paper.

A difﬁculty we will face is to deﬁne structures of

inﬂuence that are relevant in some real cases. This dif-

ﬁcult task, aiming at characterizing social networks,

has been paid a huge attention to. One of the initiators

of this domain was Milgram (Milgram, 1967) who

proposed the theory of six degrees of separation or

“small world” phenomenon. In response to this the-

ory, several authors in graph theory deﬁned models

to describe this kind of networks (Easley and Klein-

berg, 2010; Prettejohn et al., 2002; Watts and Stro-

gatz, 1998; Watts, 1999). The difﬁculty dwells on

adapting these models to IODS.

This paper is organized as follows.

Section 2 recalls the deﬁnition of IODS. In section

3, we list some properties of extremism diffusion in-

spired from sociology. In section 4, we deﬁne extrem-

ism so that extremists are people with rather strong

opinions. Then, we study some properties about this

deﬁnition. In section 5, we introduce degrees of ex-

tremism and we study some properties of this deﬁ-

nition. In section 6, we present and comment several

simulations. Finally, section 7 presents some perspec-

tives of this work.

Battistella, E. and Cholvy, L.

A Logical Approach to Extreme Opinion Diffusion.

DOI: 10.5220/0006530900170028

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 17-28

ISBN: 978-989-758-275-2

2 THE UNDERLYING DIFFUSION

MODEL

We consider a ﬁnite propositional language L. The set

of its interpretations is denoted 2

. If ϕ is a formula

of L, Mod(ϕ) denotes the set of models of ϕ i.e., the

set of interpretations in which ϕ is true. A multi-set

of formulas {ϕ

, ..., ϕ

} equipped with a total order

≺ s.t. ϕ

≺ ϕ

i+1

(i = 1...n − 1) is called an ordered

multi-set of formulas and denoted ϕ

≺ ... ≺ ϕ

Deﬁnition 1 (Importance-Based Merging Operator).

An Importance-Based Merging Operator is a function

∆ which associates a formula µ and a non-empty or-

dered multi-set of consistent formulas ϕ

≺ ... ≺ ϕ

with a formula denoted ∆

(ϕ

≺ ... ≺ ϕ

) so that:

Mod(∆

(ϕ

≺ ... ≺ ϕ

)) = Min

≤

d,ϕ

≺...≺ϕ

Mod(µ)

with:

• w ≤

d,ϕ

≺...≺ϕ

iff [D(w, ϕ

), ..., D(w, ϕ

)] ≤

lex

[D(w

, ϕ

), ..., D(w

, ϕ

)]

• [D(w, ϕ

), ..., D(w, ϕ

)] is a vector which k

ele-

ment is D(w, ϕ

)

• D(w, ϕ) = min

∈Mod(ϕ)

d(w, w

), w and w

being

two interpretations and d is a pseudo-distance

between interpretations (ie., ∀w∀w

d(w, w

) =

d(w

, w) and d(w, w

) = 0 =⇒ w = w

• ≤

lex

is a lexicographic comparison of vectors

of reals deﬁned by: [v

, ..., v

] ≤

lex

, ..., v

]

iff (i) ∀k v

= v

or (ii) ∃k v

< v

and ∀ j <

k v

= v

Some simple distances d which can be used for

instantiating the previous deﬁnition are: d

, the dras-

tic distance, (d

(w, w

) = 0 iff w = w

, 1 otherwise);

, the Hamming distance (d

(w, w

) = m iff w and

differ on m propositional letters).

Deﬁnition 2 (Inﬂuence-Based Opinion Diffusion

Structure ). An Inﬂuence-Based Opinion Diffusion

Structure (IODS) is a quadruplet S = (A,µ, B, In f )

where:

• A = {1, ..., n} is a ﬁnite set of agents.

• µ is a consistent formula of L.

• B is a function which associates any agent i of A

with a consistent formula of L denoted for short

such that B

|= µ.

• In f is a function which associates any agent i

of A with a non-empty set of agents {i

, ..., i

}

equipped with a total order ≺

s.t. i

≺

k+1

for

k = 1...(n

−1). The agents of In f (i) will be called

inﬂuencers of i. The inﬂuencer i

will be called

the ﬁrst inﬂuencer or the main inﬂuencer of i. For

short, we denote In f (i) = {i

≺

... ≺

A is the ﬁnite set of agents. The formula µ rep-

resents the information which is true in the world. It

is called integrity constraint. For any agent i, the for-

mula B

represents its initial opinion. We assume that

agents are rational and thus that B

is consistent and

satisﬁes the integrity constraint µ. In f (i) is the non-

empty set of agents which inﬂuence agent i. These

inﬂuencers are ranked so that j ≺

k means that, ac-

cording to i, its own opinion is more inﬂuenced by j’s

opinion than by k’s opinion.

Deﬁnition 3 (Inﬂuence-Based Opinion Sequence).

Let S = (A, µ, B, In f ) be an IODS and i ∈ A with

In f (i) = {i

≺

... ≺

}. The Inﬂuence-Based Opin-

ion Sequence of i, denoted (B

)

s∈N

, is deﬁned by:

(i) B

= B

(ii) ∀s > 0, B

= ∆

s−1

≺ ... ≺ B

s−1

)

The Inﬂuence-Based Opinion Sequence (or Opin-

ion Sequence for short) of agent i, (B

)

s∈N

, represents

the history of i’s opinion evolution. This evolution is

done according to operator ∆

: i’s opinion at step s is

the result of ∆

applied to the ordered multi-set of its

inﬂuencers’ opinions: B

s−1

≺ ... ≺ B

s−1

Example 1. Consider a language with propositional

letters a and b. Let S = (A, µ, B, In f ) be an IODS

with: A = {1, 2, 3}, µ is a tautology, B

= ¬a, B

a ∨ b, B

= ¬b, In f

= {1}, In f

= {2 ≺

1}, In f

{3 ≺

2}. Table 1 shows the evolution of the agents

opinions.

Table 1: Opinion evolution in example 1.

s = 0 s = 1 s ≥ 2

i = 1 ¬a ¬a ¬a

i = 2 a ∨ b ¬a ∧ b ¬a ∧ b

i = 3 ¬b a ∧ ¬b a ∧ ¬b

Finally, let us recall three deﬁnitions which will

be useful in the rest of the paper.

Deﬁnition 4 (Self-conﬁdent agent). Let

S = (A, µ, B, In f ) and i

∈ A. i

is self-conﬁdent

iff In f (i

) = {i

≺

... ≺

} with n

≥ 1.

Deﬁnition 5 (Dogmatic agent). Let S = (A, µ, B, In f )

and i ∈ A. i dogmatic iff In f (i) = {i}.

Deﬁnition 6 (Sphere of Inﬂuence of an Agent). Let

S = (A, µ, B, In f ) and i ∈ A. The sphere of inﬂuence

of i is deﬁned by: Sphere(i) =

k≥1

Sphere

(i) with

• Sphere

(i) = { j

: In f ( j

) = {i ≺ ...}}

• Sphere

(i) = { j

: In f ( j

) = { j

k−1

≺

...} and j

k−1

∈ Sphere

k−1

(i)}

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

3 PROPERTIES OF EXTREMISM

DIFFUSION

In this section, we recall some observations made

in the sociology litterature (Bronner, 2009), (Atran,

2015) about extremism diffusion and we translate

them in our setting as properties. Notice that these

observations are not supposed to be general rules but

only tendancies. In the two following sections, we

will check if these properties are satisﬁed or not by

the deﬁnitions we will introduce.

The ﬁrst observation about extremism is that in

general extremist people are close-minded, sure of

their opinions and listen exclusively people with sim-

ilar beliefs. But, on an other hand, extremism can and

often arise in groups of friends with moderate opin-

ions. Atran highlighted the fact that extremist people

have often been introduced to extremism by a social

connection.

We have retained the following ﬁve properties for

our study. The ﬁrst property states that if all the in-

ﬂuencers of an agent are extremist, then after updat-

ing its opinion, the agent is extremist. The second

states that if all the inﬂuencers of an agent are moder-

ate (i.e. not extremist), then after updating its opinion

the agent is moderate. The third one states that ex-

tremist agents are more certain of their opinions than

moderate ones. The fourth states that extremist agents

are more inﬂuential in the sense that an agent inﬂu-

enced by extremist agents should be ”more prone” to

become extremist than moderate. The ﬁfth property,

called persistence of discredited beliefs, states that an

opinion will persist even if the evidence that made the

opinion emerge is removed.

S being the IODS (A, µ, B, In f ), these properties

are formalized as follows:

Deﬁnition 7.

• (P1) S satisﬁes (P1) iff ∀i ∈ A, ∀t ∈ N, if ∀ j ∈

In f (i), j is extremist at step t, then i is extremist at

step t + 1.

• (P2) S satisﬁes (P2) iff ∀i ∈ A, ∀t ∈ N, if ∀ j ∈

In f (i), j is moderate at step t, then i is moderate

at step t + 1.

• (P3) S satisﬁes (P3) iff ∀i ∈ A, ∀ j ∈ A, ∀t ∈ N,

if i is extremist at t and j is moderate at t then

| Mod(B

) |<| Mod(B

) |.

• (P4) S satisﬁes (P4) iff ∀t ∈ N, there are more

agents i which are extremist at step t + 1 and

which main inﬂuencers were extremist at step t

than agents i which are moderate at step t + 1 and

which main inﬂuencers were extremist at step t.

• (P5) S satisﬁes (P5) iff ∀t ∈ N, ∀i ∈ A, if i is ex-

tremist at step t + 1, its main inﬂuencer was ex-

tremist at step t and moderate at step t + 1, then i

remains extremist at step t + 2.

The previous deﬁnitions are applicable only if we

have a binary deﬁnition of extremism stating whether

a given agent is extremist or not. In case we have a

deﬁnition stating only if an agent i is more extremist

than an other agent j at some step t, denoted d

extr

(i) ≥

extr

( j), we adapt the properties as follows:

The ﬁrst property states that if all the inﬂuencers

of an agent are very extremist at some step, then after

the opinion updating the agent should be very extrem-

ist. The second one says symmetrically that if all the

inﬂuencers of an agent are very moderate, then after

the opinion updating the agent should be very moder-

ate. The third expresses the fact that an agent should

be more certain than less extremist ones in the sense

of an agent’s opinion should have less models than

the ones of less extremist agents. The fourth states

that the extremist agents should be more inﬂuential in

the sense that any agent inﬂuenced by more extremist

agents should become more extremist. The ﬁfth prop-

erty, called Persistence of discredited beliefs, states

that an opinion will persist even if the evidence that

made the opinion emerge is removed. At these prop-

erties we can add two reality constraints stating that

an agent cannot have its degree of extremism increase

”too much” above (respectively decrease ”too much”

below) the maximal degree of extremism of its inﬂu-

encers.

S being the IODS (A, µ, B, In f ) and N

∗

being the

set of integers strictly greater than 0, these properties

are formalized as follows:

Deﬁnition 8.

• (Q1) Given L

extr

∈ N

∗

. S satisﬁes (Q1) iff ∀i ∈

A, ∀t ∈ N, if ∀ j ∈ In f (i), d

extr

( j) ≥ L

extr

, then

t+1

extr

(i) ≥ L

extr

• (Q2) Given L

mod

∈ N

∗

. S satisﬁes (Q2) iff ∀i ∈

A, ∀t ∈ N, if ∀ j ∈ In f (i), d

extr

( j) ≤ L

mod

, then

t+1

extr

(i) ≤ L

mod

• (Q3) S satisﬁes (Q3) iff ∀i, j ∈ A, ∀t ∈ N, if

extr

(i) ≤ d

extr

( j) then | Mod(B

) |≥| Mod(B

) |.

• (Q4) S satisﬁes (Q4) iff ∀i ∈ A, ∀t ∈ N, if ∀ j ∈

In f (i), d

extr

(i) ≤ d

extr

( j) then d

extr

(i) ≤ d

t+1

extr

(i).

• (Q5) Given L

extr

∈ N

∗

. S satisﬁes (Q5) iff ∀i ∈ A

such that its ﬁrst inﬂuencer j satisﬁes d

extr

( j) ≥

extr

, d

t+1

extr

( j) ≤ L

extr

and d

t+1

extr

(i) ≥ L

extr

then

t+2

extr

(i) ≥ L

extr

• (Q6) Given Lim ∈ N. S satisﬁes (Q5) iff ∀i ∈ A,

∀t ∈ N, d

t+1

extr

(i) − max

j∈In f (i)

extr

( j) ≤ Lim .

• (Q7) Given Lim ∈ N. S satisﬁes (Q5) iff ∀i ∈ A,

∀t ∈ N, min

j∈In f (i)

t+1

extr

( j) − d

extr

(i) ≤ Lim .

A Logical Approach to Extreme Opinion Diffusion

4 EXTREME OPINIONS AND

EXTREMIST AGENTS

In this section, we consider that extreme opinions are

strong opinions i.e. formulas which have “few” mod-

els. Moreover, we adopt a binary deﬁnition of extrem-

ism by considering that people are divided into two

distinct groups: the extremist ones and the moderate

ones.

4.1 Deﬁnitions

Deﬁnition 9 (Extreme Opinions). Let R be a given

integer closer to 1 than to 2

|L|

. An opinion o is extreme

iff 1 ≤| Mod(o) |≤ R.

The choice of the threshold R will depend on the

application. But R has to be much smaller than the

number of interpretations in the language. Moreover,

inconsistent opinions are not considered as extreme.

For instance, consider that the two letters of the lan-

guage are a, b. If R = 1 then a ∧ b, a ∧ ¬b, ¬a ∧ b,

¬a ∧ ¬b are the extreme opinions.

As for extremist agents, we deﬁne them as agents

which opinions are extreme. Moreover, an agent is

moderate when it is not extremist. This leads to the

following deﬁnition:

Deﬁnition 10 (Extremist, Moderate). At step s, agent

i is extremist iff B

is an extreme opinion. Otherwise

it is moderate.

Example 2. Consider two propositional letters a, b

and assume that at a given step t agents opinions are:

= a ∨ b, B

= a, B

= a ∧ b. If R = 1 then only k is

extremist. If R = 2 then j and k are extremist.

4.2 Formal Analysis

In the following, we prove some results on extrem-

ism diffusion and in particular we focus on properties

described in section 3.

The following proposition gives a description of

extremist agents from a syntactical point of view.

Proposition 1. Assume that the propositional letters

are a

, ..., a

. Consider an IODS S = (A, µ, B, In f ).

Agent i is extremist at step t iff B

≡

k=1

1,k

∧... ∧l

n,k

with ∀k ∈ [1, N], ∀p ∈ [1, n], l

p,k

a literal correspond-

ing to a

p,k

= a

or l

p,k

= ¬a

) and N ≤ R.

Thus, the opinion of an extremist agent is equiva-

lent to a disjunction of less than R conjunctions of all

the literals.

The following proposition states that an agent

which main inﬂuencer is extremist at some step will

be extremist at the next step.

Proposition 2. In an IODS S = (A, µ, B, In f ), for i ∈

A with In f (i) = { j ≺

...}, for t ∈ N, if j is extremist

at step t, then i is extremist at step t + 1.

As a consequence, a self-conﬁdent agent (see def-

inition 4) which is extremist at some step will remain

extremist ever after:

Proposition 3. In an IODS S = (A, µ, B, In f ), for i ∈

A with In f (i) = {i ≺

...}, if ∃t ∈ N, i is extremist at t,

then ∀s ≥ t, i is extremist at s.

The following proposition states that an agent

which k-th inﬂuencer has an opinion consistent with

the merging of the ones of the previous inﬂuencers at

step t and which k-th inﬂuencer is extremist at step t

will be extremist at step t + 1.

Proposition 4. In an IODS S = (A, µ, B, In f ), for i ∈

A with In f (i) = { j

≺

... ≺

≺

... ≺

}, for t ∈ N,

if ∆

≺

... ≺

k−1

) ∧ B

is consistent and j

extremist at step t, then i is extremist at step t + 1.

More generally, an agent will be extremist at step

t + 1 iff for some k, the merging of the k ﬁrst inﬂu-

encers’ opinions at step t has less than R models.

Proposition 5. In an IODS S = (A, µ, B, In f ), for i ∈

A with In f (i) = { j

≺

... ≺

≺

...}. Let t ∈ N.

If ∃k ∈ N, such that | Mod(∆

≺ ... ≺ B

)) |≤ R

then, i is extremist at t + 1. Otherwise, it is moderate

at step t + 1.

The following proposition states that a self-

conﬁdent extremist agent spreads extremism in its

sphere of inﬂuence.

Proposition 6. Let S = (A, µ, B, In f ) an IODS and i ∈

A extremist at step t with In f (i) = {i ≺

...}. ∃t

≥ t,

∀s ≥ t

, ∀ j ∈ Sphere(i) j is extremist at step s.

The last proposition shows which are the proper-

ties formalized in section 3 that are satisﬁed.

Proposition 7. Any IODS satisﬁes (P1), (P3) and

(P4). (P2) and (P5) are not always satisﬁed.

5 EXTENSION TO DEGREES OF

EXTREMISM

In this section, we extend the notion of extreme opin-

ions according to a more relative point of view.

5.1 Deﬁnitions

Deﬁnition 11 (Degree of Extremism of Opinions).

An opinion ϕ is extreme at degree

−|Mod(ϕ)|

−1

and

moderate at degree 1 −

−|Mod(ϕ)|

−1

with N the num-

ber of propositional letters.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Example 3. For instance, if we consider the letters a

and b then a ∧ b is extreme at degree 1 and a ∨ ¬b is

extreme at degree 1/3.

Deﬁnition 12 (Degree of Extremism of Agents). At

step s, the degree of extremism of agent i is the degree

at which B

is extreme. It is denoted d

ext

(i). Similarly,

at step s, the degree of moderation of agent i is the

degree at which B

is moderate. It is denoted d

mod

(i).

Deﬁnition 13. At step s, agent i is more extremist than

agent j iff d

ext

(i) ≥ d

ext

( j). At step s, agent i is more

moderate than agent j iff d

mod

(i) ≥ d

mod

( j).

Example 4. An agent which current opinion is a ∧ b

is more extremist (i.e. less moderate) than an agent

which current opinion is a ∨ b.

5.2 Formal Analysis

This ﬁrst proposition states that an agent is more ex-

tremist at step t (t > 0) than its ﬁrst inﬂuencer at step

t − 1.

Proposition 8. Consider an IODS S = (A, µ, B, In f ),

and an agent i ∈ A with In f (i) = { j ≺

...}. Then

∀t > 0, d

ext

(i) ≥ d

t−1

ext

( j).

In particular, the degree of extremism of a self-

conﬁdent agent can only increase.

The following proposition is a generalization of

the previous one. It states that an agent is more ex-

tremist at some step t than its k-th inﬂuencer at the

previous step if the opinions of this inﬂuencer is con-

sistent with the merging of the opinions of the previ-

ous ones.

Proposition 9. Consider an IODS S = (A, µ, B, In f )

and an agent i with In f (i) = { j

≺

... ≺

}. Then,

∀t > 0, ∀k ∈ [1, n], if ∆

≺ ... ≺ B

) ∧ B

consistent and j

is an extremist agent at step t then

t+1

ext

(i) ≥ d

ext

( j

)

The following proposition states that an agent will

be extremist at degree at least d at step t + 1 if one

of its inﬂuencers j has an opinion at step t such that

during the opinion updating process, the merging of

the previous inﬂuencers’ opinions has less than 2

−

−1)d models at minimal distance from B

with N

the number of letters in the language.

Proposition 10. In an IODS S = (A, µ, B, In f ) with

A = {a

, ..., a

}, for i ∈ A, t ∈ N, with In f (i) = { j

≺

... ≺

}, i is of degree of extremist at least d at step

t + 1 iff ∃k ∈ [1, n], | Mod(∆

≺ ... ≺ B

)) |≤

− (2

− 1)d.

The following proposition states that a self-

conﬁdent extremist agent spreads extremism in its

sphere of inﬂuence.

Proposition 11. Let S = (A, µ, B, In f ) an IODS and

i ∈ A with In f (i) = {i ≺

...}. ∀t ∈ N, ∃t

≥ t, ∀s ≥ t

∀ j ∈ Sphere(i) d

ext

( j) ≥ d

ext

(i).

The last proposition shows which are the proposi-

tions formalized in section 3 that are satisﬁed.

Proposition 12. Any IODS satisﬁes (Q1), (Q3), (Q4)

and (Q7). (Q2), (Q5) and (Q6) are not always satis-

ﬁed.

6 EXPERIMENTS

In this section, we focus on simulations realized with

Netlogo. First, we address the question of generating

IODS corresponding to real social networks. For that,

we review some propositions made in graph theory

during the last decades. Then, we adapt them to our

context by using a notion of distances between opin-

ions.

6.1 Graph Theory Bases

One of the most used models of graph is the one of

Erd

os-R

enyi. It is a model of random graph (see

(Easley and Kleinberg, 2010)).

Deﬁnition 14 (Erd

os-R

enyi Graph). Given a number

of nodes n and an integer m. An Erd

os-R

enyi Graph

is any graph obtained by selecting randomly m edges

among the 2

possible ones.

Another model of graph that is widely used is the

model of Watts-Strogatz. This model has been made

to describe the phenomenon of Small-World or ”six

degrees of separation” highlighted by Milgram (Mil-

gram, 1967). This psychologist established through

an experiment the theory that a message can be trans-

mitted from one person to one another by passing by

an average of six friends. The Small-World theory is

commonly formalized (Easley and Kleinberg, 2010;

Prettejohn et al., 2002; Watts and Strogatz, 1998) as

follows:

Deﬁnition 15 (Small-World). A graph G is said

Small-World if it satisﬁes:

(i) G is connected.

(ii) G is sparse: the average degree of the nodes k is

low compared to the number of nodes n, k  n.

(iii) G is decentralized: the maximal degree of the

nodes k

max

is low compared to the number of

nodes n, k

max

 n.

(iv) The characteristic path L (the average number

of nodes traversed by a short path between two

nodes) is close to the one of a random graph with

A Logical Approach to Extreme Opinion Diffusion

the same number of nodes n and the same average

degree k, L ≈ L

random

∼

ln(n)

ln(k)

(v) The clustering coefﬁcient C (the probability that

two nodes i and j are connected given that they

share a common neighbor) is high compared to

the one of a random graph with the same number

of nodes n and the same average degree k, C 

random

∼

One can notice that Erd

os-R

enyi graphs as ran-

dom graphs have low characteristic paths by deﬁni-

tion.

The following model, from (Easley and Klein-

berg, 2010) and adapted from a model generally at-

tributed to Watts and Strogatz, deﬁne Small-World

graphs:

Deﬁnition 16 (Rank-Based Friendship Graph).

Given a number of nodes n, a threshold r, an expo-

nent q and a dimension d, the nodes are randomly

distributed in a space of dimension d. Rank-Based

Friendship Graph is obtained by going as follows:

For each node i, we rank the other nodes accord-

ing to their distances to i and we break ties with a

chosen method. There will be an edge from a node

j to the node i with probability

Z.rank

( j)

, rank

( j)

being the rank of j in i’s neighbors and Z a coefﬁcient

of normalization, Z =

∑

i=1

rank

( j)

∑

i=1

6.2 Distances between Opinions

Considering a pseudo-distance d between two inter-

pretations, there are many ways to characterize how

close two opinions are. (Eiter and Mannila, 1997)

highlights several pseudo-distances between sets of

points, we adapt some to opinions as follows:

Deﬁnition 17 (Pseudo-Distances on opinions). Let o

and o

be two propositional formulas.

• Sum of minimum distances: d

summin

, o

) =

(

∑

w∈Mod(o

)

D(w, o

) +

∑

w∈Mod(o

)

D(w, o

))

• Hausdorff distance: d

Hau

, o

) =

max(max

w∈Mod(o

)

D(w, o

), max

w∈Mod(o

)

D(w, o

))

• Surjection distance d

, o

) =

min

η∈F

)

∑

)∈η

d(w

, w

) with F

)

the set of surjections from the larger set between

Mod(o

) and Mod(o

) on the other.

• Link distance: d

, o

) =

min

R∈L

)

∑

)∈R

d(w

, w

) with L

)

the

set of linkings. A linking R ⊆ Mod(o

)×Mod(o

)

satisﬁes ∀w

∈ Mod(o

), ∃w

∈ Mod(o

, w

) ∈ R and ∀w

∈ Mod(o

∃w

∈ Mod(o

), (w

, w

) ∈ R.

But, as we consider relations of inﬂuence that

are not symmetric, dropping the property of symme-

try and considering weaker functions than pseudo-

distances will also give interesting IODS to study. We

thus deﬁne Difference functions as follows:

Deﬁnition 18 (Difference of Opinions).

• d

max

, o

) = max

∈Mod(o

),w

∈Mod(o

)

d(w

, w

)

• d

min

, o

) = min

∈Mod(o

),w

∈Mod(o

)

d(w

, w

)

• d

maxmin

, o

) =

max

∈Mod(o

)

min

∈Mod(o

)

d(w

, w

)

• d

sum

, o

) =

∑

∈Mod(o

),w

∈Mod(o

)

d(w

, w

)

In the following we will indifferently refer to the

previously deﬁned functions as distances by lack of a

better term.

6.3 Models

Here we adapt the previous models of graphs to IODS

and explain how we construct them for our simula-

tions. In the following we take an integrity constraint

being a tautology.

The ﬁrst model we adapt is the one of the random

graph deﬁned by Erd

os and R

enyi. The following

deﬁnition shows how we construct Erd

os and R

enyi

IODS. Notice that we add a parameter, the number of

self-conﬁdent agents,which is an interesting variable

to study.

Deﬁnition 19 (Erd

os-R

enyi-Based IODS). Given the

parameters num-letters, num-nodes, num-links and

num-self-conﬁdent, the IODS is constructed as fol-

lows:

We begin by creating num-nodes agents, each of

them has a random opinion in a language of num-

letters letters. Then, we create num-links relations

of inﬂuence by choosing randomly an inﬂuencer and

an inﬂuenced agent (potentially the same). The inﬂu-

encers are ordered according to the order of creation

of the relation of inﬂuence, the sooner a relation of

inﬂuence would have been created the more inﬂuenc-

ing it is. Finally, each agent with no inﬂuencers will

become dogmatic and, if necessary, we add relations

of self-inﬂuence until we have num-self-conﬁdent self-

conﬁdent agents (dogmatic agents included). We pick

randomly an agent and if it does not already inﬂu-

ence himself we make it self-conﬁdent by putting it as

its main inﬂuencer (the order of the other inﬂuencers

remains unchanged).

This second model adapts the model of Rank-

Based Friendship by considering a distance between

opinions instead of a physical distance as for the

graph model.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Deﬁnition 20 (Rank-Based Inﬂuenceship IODS).

Given the parameters num-letters, num-nodes,

opinions-distance, q and num-self-conﬁdent, the

IODS is constructed as follows:

We begin by creating num-nodes agents, each of

them has a random opinion in a language of num-

letters letters. Then, we ﬁll a matrix with the distances

between every couple of agents according to the dis-

tance between their opinions and computed with the

distance opinions-distance. For each agent i we have

a list l

of all the agents (i included) sorted accord-

ing to their distances to i. If two agents j

and j

are at the same distance of i, then the tie will be ran-

domly solved. Each agent j will be an inﬂuencer of i

with probability

Z.rank

( j)

, rank

( j) being the rank

of j in l

and Z being a coefﬁcient of normalization,

Z =

∑

num−nodes

i=1

rank

( j)

∑

num−nodes

i=1

. The in-

ﬂuencers of i are ordered as in l

. Finally, if neces-

sary, we add relations of self-inﬂuence such as we

have num-self-conﬁdent self-conﬁdent agents (dog-

matic agents included). We pick randomly an agent

and if it is not already self-conﬁdent we make it so by

putting it as its main inﬂuencer (the order of the other

inﬂuencers remains unchanged).

The third model is a variant of the previous one,

here an agent will be inﬂuenced by the m agents that

have the closest opinions from its own one for a given

integer m.

Deﬁnition 21 (Deterministic Rank-Based Inﬂuence-

ship IODS). Given the parameters num-letters, num-

nodes, opinions-distance, m and num-self-conﬁdent,

the IODS is constructed as follows:

We begin by creating num-nodes agents, each of

them has a random opinion in a language of num-

letters letters. Then, we ﬁll a matrix with the distances

between every couple of agents according to the dis-

tance between their opinions and computed with the

distance opinions-distance. For each agent i, we con-

serve the m closest agents to i to be its inﬂuencers.

If two agents j

and j

are at the same distance of

i, then the tie will be randomly solved. The inﬂu-

encers of i are ordered according to their distances

to i. Finally, we add relations of self-inﬂuence such

as we have num-self-conﬁdent self-conﬁdent agents

(dogmatic agents included). We pick randomly an

agent and if it is not already self-conﬁdent we make

it so by putting it as its main inﬂuencer (the order of

the other inﬂuencers remains unchanged).

The fourth model is a generalization of the Rank-

Based Inﬂuenceship in which we have in addition

to the distance between opinions a physical distance

along a circle. The inﬂuencers of an agent i are or-

dered according to the distance between their opin-

ions and the one of i.

Deﬁnition 22 (Opinions and Physical Rank-Based

Inﬂuenceship IODS). Given the parameters num-

letters, num-nodes, opinions-distance, r, q and num-

self-conﬁdent, the IODS is constructed as follows:

We begin by creating num-nodes agents, each of

them has a random opinion in a language of num-

letters letters. We ﬁll a matrix with the distances be-

tween every couple of agents according to the dis-

tance between their opinions and computed with the

distance opinions-distance. For each agent i we have

a list l

of all the agents (i included) sorted accord-

ing to their distances to i. If two agents j

and j

are at the same distance of i, then the tie will be ran-

domly solved. Each agent j will be an inﬂuencer of i

with probability

Z.rank

( j)

, rank

( j) being the rank

of j in l

and Z a coefﬁcient of normalization Z =

∑

num−nodes

i=1

rank

( j)

∑

num−nodes

i=1

. At the previ-

ous inﬂuencers we add inﬂuencers that are physically

close. Indeed, all the agents will be placed on a cir-

cle. The agents that are separated on the circle from

an agent i by less than r agents will inﬂuence i. The

inﬂuencers of i are ordered as in l

(according to the

distance between opinions). Finally, if necessary, we

add relations of self-inﬂuence such as we have num-

self-conﬁdent self-conﬁdent agents (dogmatic agents

included). We pick randomly an agent and if it is not

already self-conﬁdent we make it so by putting it as

its main inﬂuencer (the order of the other inﬂuencers

remains unchanged).

To study and compare the results between the dif-

ferent models and distances, we carried out several

simulations with the same settings. Furthermore, in

order to do comparable and reproducible experiments

we chose some values of seeds for the random oper-

ations in Netlogo. Seeds allow to have the same re-

sults in the same order for random operations when

we repeat the simulations. The values we study are

the number of extremist agents for R = 1, the average

number of models per agents which is proportional to

the average degree of moderation and the number of

dogmatic agents.

In the simulations we present here, we have

taken the following values: seed {0, 100, 200}, num-

letters {3, 4, 5, 6}, num-nodes {10, 60, 110, 160, 210},

num-self-conﬁdent {0, 50, 100, 150, 200, 210}. For

the three models using ranks we tested d

summin

, d

Hau

max

, d

min

, d

maxmin

, d

sum

. with the drastic pseudo-

distance between interpretations. For the Erd

os-

enyi-Based model we took num-links varying from

10 to 2000 with an increment of 50. For the Rank-

A Logical Approach to Extreme Opinion Diffusion

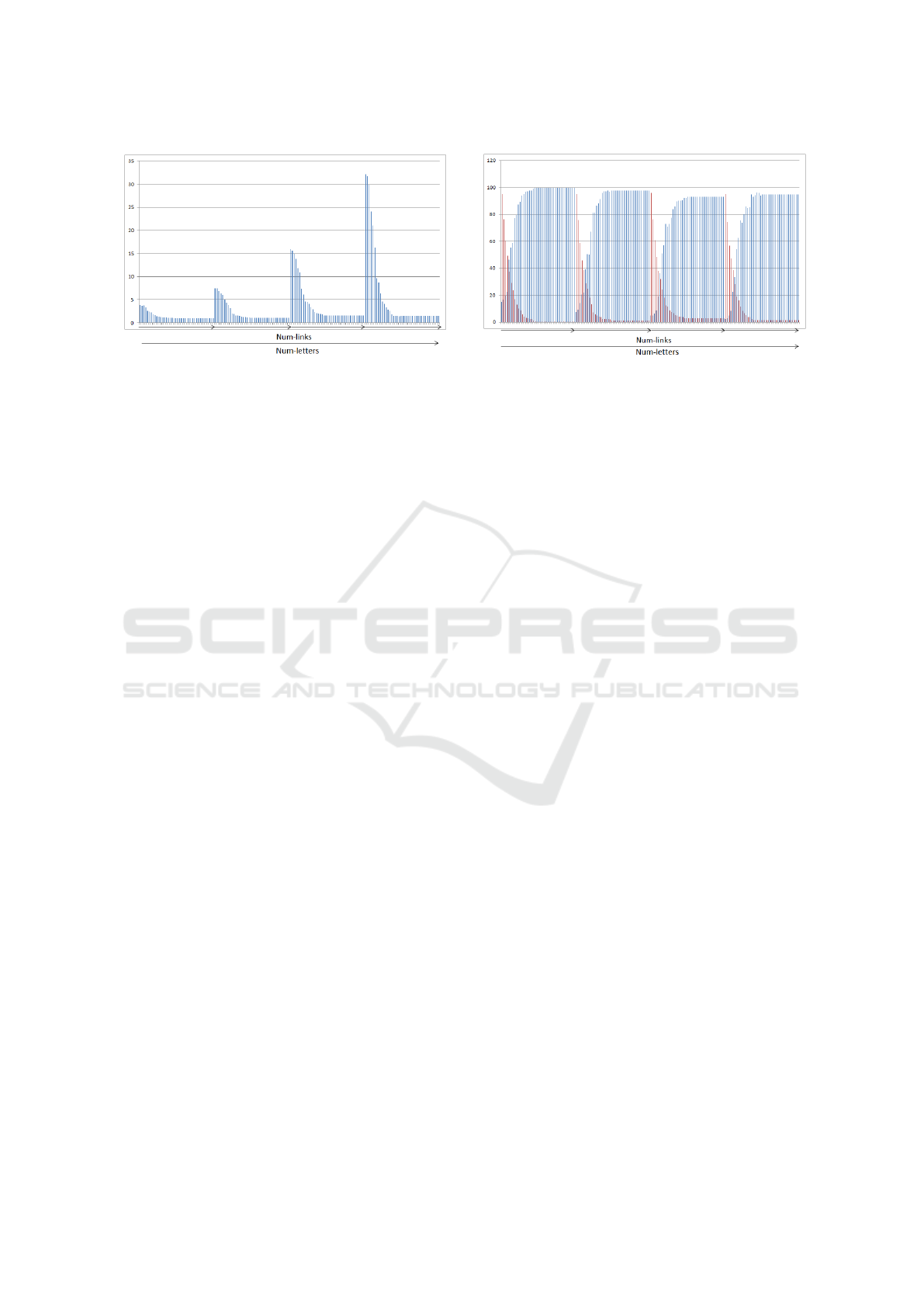
Average Number of Models per Agents Proportion of extremist agents (blue) and dogmatic agents (red)

Figure 1: Example: Erd

os-R

enyi-Based model seed=0, num-nodes =210, num-self-conﬁdent=0.

Based Inﬂuenceship and the Opinions and Physical

Rank-Based Inﬂuenceship models we took the values

{1, 2, 3, 4, 5} for q, for the Deterministic Rank-Based

Inﬂuenceship model we took m in {1, 2, 3, 4} and

for the Opinions and Physical Rank-Based Inﬂuence-

ship model we took r in {1, 2, 3, 4, 5}. The pseudo-

distance used to compute the Importance-based Merg-

ing operator is the drastic one.

First of all, with the drastic pseudo-distance, we

can notice that the different distances we used have

particular behaviors. d

summin

, o

) ∈ [0, 2

num−letters

]

and d

summin

, o

) = 0 iff o

≡ o

. d

summin

favors

relations of inﬂuence between agents which opin-

ions have models very close according to D, in av-

erage. d

Hau

, o

) is 0 or 1 and d

Hau

, o

) = 0

iff o

≡ o

. d

Hau

favors relations of inﬂuence be-

tween agents which opinions have no models very

far from one another. So, in the case of the dras-

tic pseudo-distance, it favors relations between agents

that have the same opinion. So, for the number of

letters and agents we will consider, as such a case

is unlikely the relations of inﬂuence will be mostly

random. d

max

, o

) is 0 or 1 and d

max

, o

) = 0

iff ∃w, Mod(o

) = Mod(o

) = {w}. So, as hav-

ing two agents with only one model and the same

model is very unlikely for the number of letters and

agents we consider, d

max

favors random relations of

inﬂuence and it will be interesting to compare the re-

sults obtained with this distance and the ones obtained

with the other distances. d

min

, o

) is 0 or 1 and

min

, o

) = 0 iff ∃w ∈ Mod(o

) ∩ Mod(o

). Then,

for a given agent i, d

min

favors relations of inﬂuence

that are from agents that share a model with i’s opin-

ion but that are otherwise random. d

maxmin

, o

) is

0 or 1 and d

maxmin

, o

) = 0 iff o

|= o

. So, d

maxmin

favors relations of inﬂuence from an agent i to an

agent j such that all the models of B

are models of

. d

sum

, o

) ∈ [0, 2

num−letters

] and d

sum

, o

) = 0

iff Mod(o

) = Mod(o

) = {w}. d

sum

favors relations

of inﬂuence from agents which opinions have the less

models.

For the Erd

os-R

enyi-Based model (see ﬁgure 1),

we have several peaks of the average number of mod-

els and of the number of dogmatic agents, corre-

sponding to having low num-links. Indeed, in these

cases, there are potentially more agents that are not

inﬂuenced by other agents and that keep their initial

opinions. Furthermore, we can see that the dogmatic

agents are almost the only agents that are not extrem-

ist and thus contribute the more to the average number

of models. So, the diffusion of extremism depends

a lot on the ratio between num-links and num-nodes,

the more there are relations of inﬂuence the more the

agents will become extremist. We can only notice that

the peaks of average number of models are higher and

higher according to the increasing of the number of

letters. Another experiment in which we took 200

agents and much more relations of inﬂuence (up to

7000) showed that for more than 2000 there are very

few simulations with non-extremist agents.

For the Rank-Based Inﬂuenceship model (see ﬁg-

ure 2), we have several plateaus higher and higher

according to the increasing of the number of letters.

Furthermore, there are cases with very low numbers

of extremist agents and without very much dogmatic

agents. Then, we can notice that there are big dif-

ferences according to the distance we use. Indeed, a

thorougher analysis highlights that the biggest peaks

are with d

summin

and then with d

Haus

and d

maxmin

. d

max

and d

min

cause some lesser peaks when q gets bigger

(more than 3) and d

sum

causes very small peaks for

q = 5. For q = 1 almost all the agents are extremist

whatever the distance we use. It can be explained by

the fact that the lesser q is the more likely relations

of inﬂuence are to be created, furthermore for q high

enough the distance used matter less then even d

sum

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

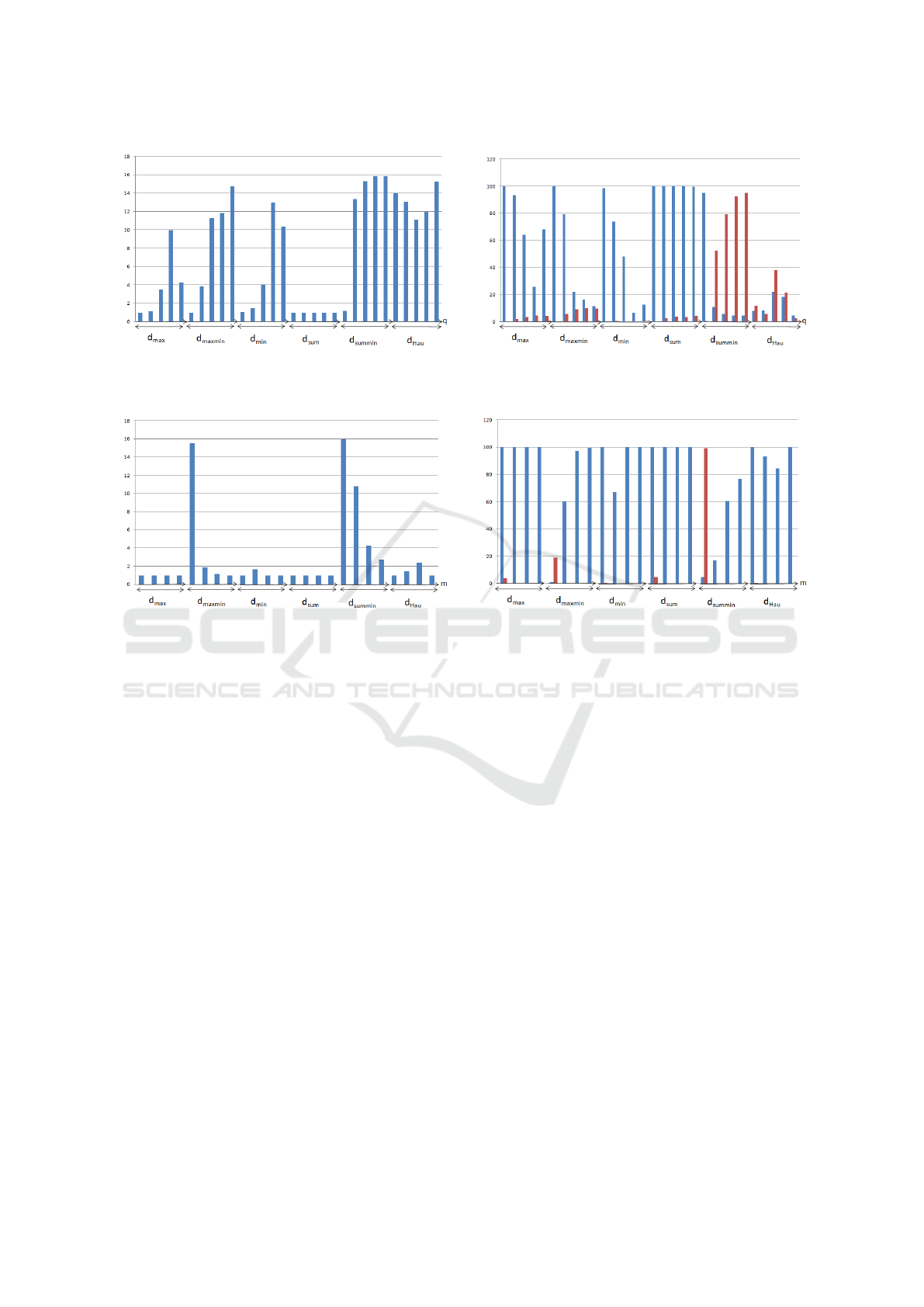
Average Number of Models per Agents Proportion of extremist agents (blue) and dogmatic agents (red)

Figure 2: Example: Rank-Based Inﬂuenceship model seed=0, num-letters=5,num-nodes=210, num-self-conﬁdent=0.

Average Number of Models per Agents Proportion of extremist agents (blue) and dogmatic agents (red)

Figure 3: Example: Deterministic Rank-Based Inﬂuenceship model seed=0, num-nodes=210, num-self-conﬁdent=0.

that in the other cases spread extremism may be used

to create an IODS where they may remain some mod-

erate agents. But, according to (Easley and Klein-

berg, 2010) in the case of graphs, the Rank-Based

Friendship generates graphs the closest of reality for

q = 1. Furthermore, when the number of agents in-

creases, the average number of models decreases be-

cause more relations of inﬂuence may be created. One

can notice that with this model d

summin

and d

Haus

par-

ticularly favor moderation. So, having inﬂuencers

with opinions for which each model is close of one

of us model or for which each model is not far of any

of our model favor moderation. But, we can notice

that with d

Haus

agents are much less dogmatic than

with d

summin

For the Deterministic Rank-Based Inﬂuenceship

model (see ﬁgure 3), extremism spreads more and

more when m gets bigger. Moreover, this time there

is much more differences according to the distance

we used because the ranking is more important in

the choice of the inﬂuencers than before. Then, only

summin

keeps many non-extremist agents when m is

at its highest. Indeed, this distance characterizes the

best the similarity between opinions, the ﬁrst agents in

the ranking of an agent i actually have opinions that

share many models with the one of i and it often is i

itself. Thus, when m = 1, we have almost only dog-

matic agents with d

summin

. When m gets higher than 3

only models with d

summin

keep moderate agents.

For the Opinions and Physical Rank-Based Inﬂu-

enceship model (see ﬁgure 4), we have very few non-

extremist agents even with d

summin

and even less when

r increases. It is due to the fact that here there can-

not be any dogmatic agent (contrary to the case of

the Rank-Based Inﬂuenceship) and that an agent may

have inﬂuencers with very different opinions (con-

trary to the case of the Deterministic Rank-Based In-

ﬂuenceship).

In all the simulations, the number of letters does

not affect the proportion of extremist agents. The

number of nodes affects the proportion of extrem-

ist agents for the Erd

os-R

enyi-Based model because

of our deﬁnition of the model, in fact it is the ra-

tio between the number of agents and the number of

relations of inﬂuence that truly matters. It also has

an inﬂuence for Rank-Based Inﬂuenceship model and

the Opinions and Physical Rank-Based Inﬂuenceship

model because it increases the average number of in-

A Logical Approach to Extreme Opinion Diffusion

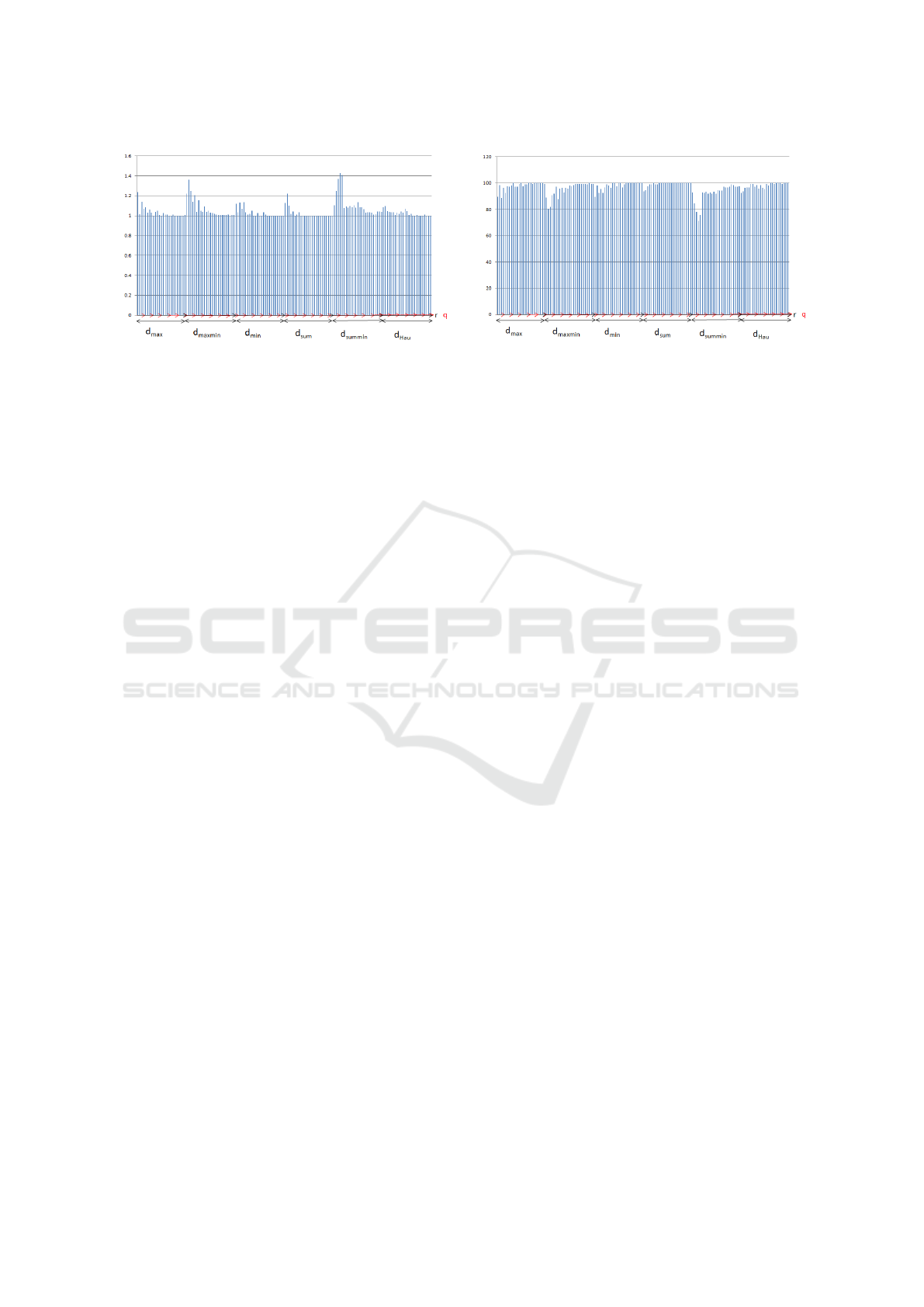
Average Number of Models per Agents Proportion of extremist agents

Figure 4: Example: Opinions and Physical Rank-Based Inﬂuenceship model seed=0, num-letters=5, num-nodes=210, num-

self-conﬁdent=0.

ﬂuencers.

For summarizing, we have that for the models of

generation of IODS, the ones which spread extrem-

ism the less are the Rank-Based Inﬂuenceship when

q is very high and the Erd

os-R

enyi-Based when num-

links is much lower than num-nodes. But, those mod-

els have many dogmatic agents, on the other hand,

the Deterministic Rank-Based Inﬂuenceship spreads

extremism very little with d

summin

and a small m and

without many dogmatic agents. For the distances, it

is d

summin

that spreads extremism the less because it

favors relations of inﬂuence from agents with opin-

ions sharing many models and it spreads extremism

less than d

max

(the random one). At the opposite, d

sum

spreads extremism very well by creating hubs, agents

with very few models that inﬂuence a lot of agents.

min

spreads extremism a little less because it is less

random, there is a constraint on one model. So, with

the Importance-Based Merging Operator, the extrem-

ism spreads very well when the most extremist agents

are very inﬂuential and much less when agents are in-

ﬂuenced by agents with opinions similar to its own in

the sense of they share many models. So, what makes

that an agent remains moderate is the fact that he is in-

ﬂuenced by agents which opinions share many mod-

els between them and that he does not have too many

inﬂuencers. Having many self-conﬁdent agents fa-

vor extremism spreading with the Erd

os-R

enyi-Based

model as it increases the average number of inﬂu-

encers but in the other models it favors moderation.

Indeed, in this case the agents keep opinions close to

their initial ones and so agents’ inﬂuencers keep close

opinions.

We can notice that, in every simulation, we

reached the convergence very quickly in general in

less than 5 updates.

It would have been interesting to test the mod-

els for much larger numbers of agents to increase the

probabilities we have deemed negligible in our study

of the distances for instance. Indeed, the Small-World

phenomenon is considered interesting for very large

number of nodes i.e. billions of nodes (see (Watts,

1999)) but the computation time that would be needed

only for models of thousands of agents is very impor-

tant.

Furthermore, other simulations with Hamming

pseudo distance both for the computation of the dis-

tances between opinions and the update of the opin-

ions gave similar results. Notwithstanding, extremism

spreads slightly much, in average 0.8 less models per

agents and 9% less extremist agents. This can mainly

be explain by the fact that Min

≤

,ϕ

≺ϕ

Mod(µ) con-

tains generally less models than Min

≤

,ϕ

≺ϕ

Mod(µ)

as the second one keeps all the models of ϕ

if ϕ

and ϕ

are inconsistent. The only type of IODS that

spreads less extremism in this case is the Rank-Based

Inﬂuenceship model, in average there are 2 more

models per agents and 10% less extremist agents.

But, it can be explained by the fact that there are

twice more (15% more) dogmatic agents, the ham-

ming pseudo-distance allows a more accurate rank-

ing of the agents and thus, it is less likely that agents

with very different opinions inﬂuence an agent. It ap-

pears that this accuracy is all the more signiﬁcant that

the number of letters is important. However, the ﬁrst

agents in the rankings do not change a lot, so the De-

terministic Rank-Based Inﬂuenceship model spreads

more extremism. Another noticeable difference are

for d

Hau

and d

summin

which spread extremism much

less in the three Rank-Based Inﬂuenceship models.

What we can notice is that the more relations of in-

ﬂuence there are, the more extremism spreads. And,

the more inﬂuencers of agents have close opinions,

the less extremism spreads. This result can be in-

terpreted as follows: When someone makes its own

mind by taking into account the opinions of many

people it considers as reliable or experts on the matter

and with different opinions then, it will be very sure

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

of its new opinion as it is a compromised between the

opinions of many experts. And so, this person will

become extremist according to our deﬁnition.

7 CONCLUDING REMARKS

This paper focused on modelling extreme opinion dif-

fusion when opinions are modelled as propositional

formulas. It can be extended according to several di-

rections.

First, we could add a dynamic aspect in the dif-

ferent types of IODS, by changing the relations of in-

ﬂuence through time as it is often done in the usual

models (Crawford et al., 2013; Christoff and Hansen,

2015; Chau et al., 2014; Deffuant et al., 2002). It will

be especially interesting with the rank-based models

where the ranking of the inﬂuencers is based on the

distances between opinions. Since opinions change

through time these distances also change and comput-

ing new rankings could be done.

Another aspect that may be complexiﬁed is the

deﬁnition of extreme opinions. In the deﬁnitions we

considered here, the main parameter is the number

of the models of an opinion. They do not take into

account what opinions are about. For instance, ac-

cording to this model, the opinion using pesticides is

safe is as extreme as growing tomatoes is easy. Tak-

ing the domain into account would allow us to dis-

tinguish some sensitive letters and to use them for a

more reﬁned deﬁnition of extremism. In the agricul-

ture domain, having a strong position towards pesti-

cides (pro or cons) is obviously more noticeable than

having a strong position towards tomatoes.

Similarly, we could consider a more complex def-

inition of extremism which would deﬁne extremist

agents as agents which opinions are close to some ref-

erential extreme opinions. In the agriculture example,

an agent which thinks that with caution, using pesti-

cides is safe is more extremist than an agent which

thinks with water, growing tomatoes is easy because

its opinion is not far from the sensitive opinion using

pesticides is safe.

ACKNOWLEDGEMENTS

We thank the anonymous reviewers whose comments

helped us to improve the paper.

REFERENCES

Atran, S. (2015). On youth, violent extremism and promot-

ing peace. https://www.unisa.edu.au/Global/EASS/

MnM/Publications/Address UN Security Council

Scott Atran.pdf.

Bronner, G. (2009). La pens

ee extr

eme. Comment les

hommes ordinaires deviennent des fanatiques. Edi-

tions Deno

el, Paris.

Chau, H., Wong, C., Chow, F., and Fung, C. (2014). Social

judgment theory based model on opinion formation,

polarization and evolution. Physica A, 415:133–140.

Cholvy, L. (2016). Diffusion of opinion and inﬂuence.

In Scalable Uncertainty Management - 10th Interna-

tional Conference, SUM 2016, Nice, France, Septem-

ber 21-23, 2016, Proceedings, pages 112–125.

Christoff, Z. and Grossi, D. (2017). Stability in binary opin-

ion diffusion. In Logic, Rationality, and Interaction

- 6th International Workshop, LORI 2017, Sapporo,

Japan, September 11-14, Proceedings, 2017, pages

166–180.

Christoff, Z. and Hansen, J. U. (2015). A logic for diffusion

in social networks. J. Applied Logic, 13(1):48–77.

Crawford, C., Brooks, L., and Sen, S. (2013). Opposites

repel: the effect of incorporating repulsion on opin-

ion dynamics in the bounded conﬁdence model. In

International conference on Autonomous Agents and

Multi-Agent Systems, AAMAS ’13, Saint Paul, MN,

USA, May 6-10, 2013, pages 1225–1226.

Deffuant, G., Amblard, F., Weisbuch, G., and Faure, T.

(2002). How can extremism prevail? A study based on

the relative agreement interaction model. J. Artiﬁcial

Societies and Social Simulation, 5(4).

Easley, D. A. and Kleinberg, J. M. (2010). Networks,

Crowds, and Markets - Reasoning About a Highly

Connected World. Cambridge University Press.

Eiter, T. and Mannila, H. (1997). Distance measures for

point sets and their computation. Acta Inf., 34(2):109–

133.

Grandi, U., Lorini, E., and Perrussel, L. (2015). Proposi-

tional opinion diffusion. In Proceedings of the 2015

International Conference on Autonomous Agents and

Multiagent Systems, AAMAS 2015, Istanbul, Turkey,

May 4-8, 2015, pages 989–997.

Haﬁzoglu, F. M. and Sen, S. (2012). Analysis of opinion

spread through migration and adoption in agent com-

munities. In PRIMA 2012: Principles and Practice of

Multi-Agent Systems - 15th International Conference,

Kuching, Sarawak, Malaysia, September 3-7, 2012.

Proceedings, pages 153–167.

Jager, W. and Amblard, F. (2004). A dynamical perspec-

tive on attitude change. In Proceedings of NAACSOS

(North American Association for Computational So-

cial and Organizational Science) Conference, Pitts-

burgh, USA, June 22-25.

Milgram, S. (1967). The small world problem. Psychology

Today, 2:60–67.

Prettejohn, B. J., Berryman, M. J., and McDonnell, M. D.

(2002). Methods for generating complex networks

with selected structural properties for simulations: A

A Logical Approach to Extreme Opinion Diffusion

review and tutorial for neuroscientists. Frontiers in

Computational Neuroscience, 5(11).

Sureda, C., Gaudou, B., and Amblard, F. (2017). An

agent-based simulation of extremist network forma-

tion through radical behavior diffusion. In Proceed-

ings of the 9th International Conference on Agents

and Artiﬁcial Intelligence - Volume 1: ICAART,, pages

236–243. INSTICC, ScitePress.

Tsang, A. and Larson, K. (2014). Opinion dynamics of

skeptical agents. In International conference on Au-

tonomous Agents and Multi-Agent Systems, AAMAS

’14, Paris, France, May 5-9, 2014, pages 277–284.

Watts, D. J. (1999). Networks, dynamics, and the small-

world phenomenon. American Journal of Sociology,

105(2).

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of small-world networks. Nature, (393):440–442.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence