
A Heuristic for a Rich and Real Two-dimensional
Woodboard Cutting Problem
Claudio Arbib
1
, Fabrizio Marinelli
2
, Andrea Pizzuti
2
and Roberto Rosetti
2
1
Dipartimento di Scienze/Ingegneria dell’Informazione e Matematica, Universit
`
a degli Studi dell’Aquila,
Via Vetoio, Coppito, I-67010 L’Aquila, Italia
2
D.I.I., Universit
`
a Politecnica delle Marche, Via Brecce Bianche, I-60131 Ancona, Italia
Keywords:
Cutting Problem, Heuristics, Manufacturing.
Abstract:
Cutting operations in manufacturing are characterized by practical requirements and utility criteria that usually
increase the complexity of formulations or, even worse, are difficult to be modeled in terms of mathematical
programming. However, disregarding or just simplifying those requirements often leads to solutions consid-
ered not attractive or even useless by the manufacturer. In this paper we consider a rich two-dimensional
cutting stock problem that covers the whole specification of a family of wood cutting machines produced by
a worldwide leader in industrial machinery manufacturing. A sequential value correction heuristic is imple-
mented to minimize the employed stock area while reducing additional objective functions.
1 INTRODUCTION
The CUTTING STOCK PROBLEM (CSP) is a well-
known model of real-world optimization problems
arising in manufacturing. This difficult problem has
a very simple statement: find an efficient way of cut-
ting small objects from large ones.
A wide literature investigates the basic CSP and
its variants, see (W
¨
ascher et al., 2007) for a com-
prehensive survey. Indeed, variants exist to fill the
gap between theory and practice, and a variant is re-
garded of interest for the academia as far as it requires
a non-standard model and/or a novel methodological
approach.
Unfortunately, it is often hard to encapsulate re-
ality into a single elegant mathematical formulation.
Moreover, it is generally recognized that the success
of an optimization method depends on the concur-
rency of transversal skills: one is indeed mathematical
modeling, but it is not the only one. A fundamental
role is for instance played by the bi-directional inter-
face that must be developed to feed the model with
data and to present the solutions to decision-makers:
a development that normally requires more IT than
math skills.
On the other hand, the more a model is close to op-
erational decision, the more attention is to be devoted
to process details. Disregarding such details (which is
often done in research papers in order to capture the
mathematical essence of the problem) would simply
cause the software product not to work, and the man-
agement not to buy it. For example, edge trimming
is generally neglected in CSP models; but a cutting
pattern that does not take it into account, may not be
realizable in practice.
While a specification on edge trimming can eas-
ily be dealt with after prototype development, this
is not the case of other apparently irrelevant issues.
For example, blade thickness expressed in fractions
of millimeters can increase the precision required of
the packing algorithm, with important effects on its
efficiency if, as usual, it has pseudo-polynomial time
complexity.
A twofold challenge has therefore to be addressed:
• On software design. Technical issues — be they
expressed as constraints or utility criteria — have
both a local impact on the feasibility of cutting
patterns (number of stages, item rotation etc.) and
a global one on the cutting plan as a whole (num-
ber of patterns, cut sequence etc.). Pattern gener-
ation algorithms can differ a lot from each other
in order to take care of the former issues, and the
latter can affect the whole software architecture.
• On decision making. A hierarchical problem de-
composition based on the various utility criteria
(e.g. first minimize trim-loss, then setups, then
open stacks) can output low-quality or even infea-
Arbib, C., Marinelli, F., Pizzuti, A. and Rosetti, R.
A Heuristic for a Rich and Real Two-dimensional Woodboard Cutting Problem.
DOI: 10.5220/0006534500310037
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 31-37
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
31

sible solutions. On the other hand, combining dif-
ferent objectives into a single goal may produce
solutions not appreciated by all the involved deci-
sion makers.
We here propose to address this challenge by a
single architectural choice in which patterns are gen-
erated via Sequential Value Correction heuristics and
then used to provide a collection of non-dominated
solutions.
Problems with a level of detail that covers indus-
trial specification as a whole and puts the solution
method in a condition to operate in the plant, are
called rich. In this paper we consider a rich Multiple-
stock-size two-Dimensional CSP (M2D-CSP) com-
pliant with the specification of a family of wood cut-
ting machines produced by SCM Group (SCM, 2017).
The M2D-CSP is a variant of the CSP that can
be presented as follows. Let I be a set of n distinct
rectangles (part types). Each i ∈ I has length l
i
and
height h
i
, and must be cut in d
i
copies from a stock
set J of m different (and larger) rectangles. Each j ∈ J
has length L
j
and height H
j
, and is available in b
j
copies. The cut should be done so as to minimize
used stock area; other objectives — such as reduction
of employed stocks, setup minimization etc. — can
however be selectively or entirely considered.
Our problem has these main features:
• Cuts proceed parallel to stock item from edge to
edge (guillotine cut).
• Items (either produced or in stock) can be orthog-
onally rotated.
• 2 and (simplified) 3-stage cuts are possible: in a
first stage, a configuration c = hstock type, first
cut orientation (horizontal or vertical)i is selected,
and multiple cuts are done orthogonally to orien-
tation; then the stock item is rotated by 90
◦
and
the stage is repeated.
• Precut is possibly allowed as a pre-processing
step.
Part types admit overproduction if explicitly indi-
cated, but demand is in general to be fulfilled exactly.
Indeed, relaxing demand constraints by overproduc-
tion can yield solutions with very small trim-loss; but
a substantial number of excess items are cut, increas-
ing too much the necessary amount of stock items and
consequently production costs.
2 LITERATURE REVIEW
Real cutting processes often deal with heterogeneous
stock types. The relevant M-CSP is handled in var-
ious ways. In (Belov and Scheithauer, 2002) an
exact cutting plane approach is proposed for one-
dimensional CSP with multiple stock lengths. The
same problem is solved heuristically in (Poldi and
Arenales, 2009). In (Yanasse et al., 1991), the two-
dimensional CSP in the wood industry is addressed
and a heuristic algorithm is proposed for the multiple
stock sizes case.
Trim-loss minimization is not the only criterion
considered in an industrial cutting process: indeed,
setup costs and the number of stacks maintained open
throughout the process can affect process quality as
well. Examples of CSP seeking both setup minimiza-
tion and open stack limitation can be found in (Belov
and Scheithauer, 2007), where a sequential heuris-
tic for the one-dimensional case is proposed, and in
(Non
˚
as and Thorstenson, 2000), where the problem
is formulated as a non-linear concave minimization
problem and solved through global or local proce-
dures. Metaheuristics and an exact approach that sep-
arately address the CSP with setup minimization are
reported respectively in (Umetani et al., 2003) and
(Aloisio et al., 2011); moreover CSP with open stack
limitation is considered in (Arbib et al., 2016) and
(Yanasse and Lamosa, 2007).
Although industrial applications require consider-
ation of several practical issues, these are taken into
account by very few papers; and in those cases, very
few additional issues are regarded simultaneously.
Here is a list of exceptions (to the best of our knowl-
edge):
• (Malaguti et al., 2014) describes a truncated
Branch-and-Price algorithm to solve an M2D
guillotine CSP in woodboard cutting industry,
where orthogonal rotation of items and boards is
allowed, and stacked boards can be cut concur-
rently. The objective is to minimize a weighted
combination of stock usage, number of cutting cy-
cles and of 3-stage cuts.
• (Varela et al., 2008) presents a 1D-CSP arising in
a plastic manufacturing facility, with five objec-
tive functions hierarchically ranked, some tech-
nical parameters related to the employed cutting
machines and order priorities. A GRASP algo-
rithm with a call to a sequential heuristic proce-
dure is implemented.
• (Chu and Antonio, 1999) proposes a mathemat-
ical formulation for a rich 1D-CSP in the metal
industry. The various technical constraints taken
into account significantly affect the total cost
and involve trim-loss, material reusability and cut
time. Approximation algorithms based on dy-
namic programming are devised.
In conclusion, it is worth quoting sequential heuris-
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
32

tics. Instead of a rigorous (but slow) solution of the
pricing problem with exact dual prices, algorithms
of this type use pseudo-prices to sequentially (and
quickly) compose each single patterns, and in this
way can achieve good solutions. Various implementa-
tions have been proposed for 1D bin packing and CSP
(Belov and Scheithauer, 2007), (Varela et al., 2008),
and 2D bin-packing and CSP (Cui et al., 2015), (Chen
et al., 2016).
3 A SEQUENTIAL VALUE
CORRECTION HEURISTIC
The basic idea behind the sequential value correc-
tion scheme consists in assigning a value (the pseudo-
price) to each part type and generate cutting pattern
sequentially, each one with the parts not yet allocated
that maximize the total value of the pattern. After a
solution has been computed, pseudo-prices are con-
veniently updated and the process reiterated in order
to fill a pool of non dominated solutions. Dominance
relationship are based on the following minimization
criteria: total used stock area, total trim-loss, number
of used stocks, number of distinct setups, and total
number of precuts (Notice that used area, trim-loss
and number of used stocks measure distinct perfor-
mance due the overproduction features and the pres-
ence of stocks of different sizes).
The whole procedure is composed by three main
steps, each one optimizing a distinct performance in-
dicator by resorting to Algorithm 1, which is a se-
quential value correction heuristic (SVC).
The algorithm can be summarized as following:
• Step 1: SVC solves the M2D-CSP with non-
batched demand, seeking used area minimization.
• Step 2: The second step tries to reduce the number
of setups by demand rounding. In particular, the
demand of each part type is aggregated by increas-
ing batch dimension (parameter size) and SVC is
called to find solutions with reduced number of
setups. Starting from size = 2, the procedure is
iterated for increasing values of size, chosen as
the largest integer in [size + 1,max
i∈I
d
i
] that mini-
mizes the area associated to the residual demand
r
0
. Step 2 terminates when SVC does not find any
new non-dominated solution.
• Step 3: in this phase SVC searches for solutions
with reduced number of precuts. A suitable op-
portunity threshold δ is used to trigger decreasing
chances of employing a precut. The procedure it-
erates by updating δ until new generated solutions
have no precut.
Algorithm 1: Sequential value correction heuristic.
1: procedure SVC(d,size,δ)
2: λ
i
← S
i
3: cuts ← 0
4: for i ← 1. .. N do
5: g ← random(1,ρ)
6: r ← d
7: s = Ø
8: repeat
9: d
0
←
r
size
10: r
0
← r mod size
11: while d
0
> 0 do
12: P = Ø
13: for c ∈ C do
14: p[c] ← getPattern(c, λ,δ, d
0
)
15: P = P ∪ {p[c]}
16: end for
17: (a,cuts) ← getBestPattern(P)
18: f illingPattern(a,cuts)
19: s ← a
20: h ← random(1/g,g)
21: λ ← updatePrices(a,λ,h)
22: end while
23: r ← r
0
24: size = 1
25: until r > 0
26: patternSeq(s,cuts)
27: if notDominated(s) then
28: Sol = Sol ∪ {s}
29: end if
30: end for
31: end procedure
3.1 SVC Heuristic
The SVC heuristic is the core of the algorithm and is
implemented to build the CSP solutions.
Let I
0
be the set formed by the items of I and
their rotated counterparts. In its general framework,
SVC starts by defining a price λ
i
for each part type
i ∈ I
0
. Each price is initialized at the item area S
i
.
Part type demand is batched by size, that is, stock
items are stacked and each pattern is activated at mul-
tiples of size. A partial CSP solution is obtained
by sequentially building patterns through subroutine
getPattern: the subroutine attempts to solve sub-
problems where the sum of prices is maximized un-
der bounded knapsack and compatibility constraints.
For each configuration c = hstock type, first cut
orientationi in the set C of all possible configurations,
a cutting pattern is generated and added to a set P.
The most profitable pattern a ∈ P is then selected us-
ing getBestPattern, which also set the corresponding
A Heuristic for a Rich and Real Two-dimensional Woodboard Cutting Problem
33

activation level cuts. The f illingPattern function is
implemented to insert unplaced items in empty sec-
tions, given the residual demand and the value of cuts
of the chosen pattern. Subsequently, prices λ
i
are up-
dated by promoting items with high current demand
d
0
i
and small multiplicity in a. A complete CSP so-
lution s is finally obtained by combining the partial
solution computed for demand d
0
with the one found
for the residual demand r
0
.
In general, open stacks are not an objective to be
minimized, but are limited by the number of unload-
ing stations that equip the cutting machine. Although
the pattern generation procedure already respects the
limited availability of unloading stations, an attempt
at reducing the stacks opened by the current solution
s is made by the patternSeq procedure. The function
patternSeq implements a simple pattern sequencing
heuristic that compares each pattern with all the sub-
sequent ones, and swaps pattern pairs that allow the
largest decrease of open stacks.
The current solution is added to a pool (Sol) if it
fulfills all the constraints and is not dominated by any
other. The process is iterated a prescribed number N
of times unless certain halting conditions hold (e.g.,
user stop or minimum used area reached). Finally, the
pool Sol is filtered and reduced to a frontier of non-
dominated solutions.
It may happen that Sol consists of partial solu-
tions only, due to insufficient stock availability. In that
case, non dominated solutions are limited to those that
fulfills the largest demand.
For the sake of conciseness, in the following we
shall assume c = h j,Hi, i.e., the cut of the first stage is
always parallel to the height H
j
of the stock item: the
arguments presented maintain validity when replac-
ing ”horizontal” with ”vertical” and ”H
j
” with ”L
j
”.
3.2 Patterns Generation and Selection
For a given configuration c = h j,Hi ∈ C, function get-
Pattern creates a pattern that depends on the current
prices λ and demands d
0
. First, for each part type i ∈ I
0
a vertical section of width l
i
is defined, and a bounded
integer knapsack problem is solved. The knapsack ca-
pacity is set equal to the stock height H
j
and element
sizes correspond to the heights h
i
of the part types
selected. Clearly, only part types k ∈ I
0
with l
k
≤ l
i
,
demand d
0
k
> 0 and prices λ
k
> 0 are considered. Ac-
tually, each knapsack element describes a horizontal
strip containing a single item k (2-stage patterns), or
multiple copies of the same part-type (3-stage pat-
terns) wide at most l
i
. In the latter case, the maxi-
mum multiplicity m
k
is given by
b
l
i
/l
k
c
, and prices
are computed accordingly.
Let Q
c
be the set of sections generated so far, each
one provided with a certain activation level defined
with respect to the current part type demand d
0
. The
pattern is obtained by solving a further bounded knap-
sack problem that optimally selects sections in Q
c
. In
particular, the knapsack capacity is equal to L
j
and
knapsack elements correspond to sections, where the
size and value of element q are respectively equal to
the width and price of section q (the price of a sec-
tion is the sum of the prices of items it contains).
The resulting solution provides a subset of sections
¯
Q
c
that may present overproduction. In order to preserve
the structure of the knapsack problem, only activation
levels of the elements (sections) are explicitly con-
sidered, whereas part type multiplicities in sections
are neglected; moreover, the simultaneous presence
of part types and rotated part types is not accounted
for. It follows that part types overproduction is not
prevented and a post-processing may be required to
exactly fulfill part type demands. Sections q ∈
¯
Q
c
are
sorted by non-increasing order of the ratio
V
q
S
q
, where
V
q
and S
q
are respectively the price and the area of
section q.
Sections are possibly added to the pattern p fol-
lowing the prescribed order, and demand d
0
is accord-
ingly updated. In particular, a section is discarded
if it causes demand overproduction, or overflow of
the allowed limit on open stacks. In that case, the
resulting pattern p may present a residual stock area
of length R
j
that can be further filled. Therefore the
whole procedure, i.e., sections generation and selec-
tion, is repeated in order to generate a sub-pattern for
the configuration c = h
¯
j, Hi ∈ C, where stock item
¯
j
has length R
j
and height H
j
. The sub-pattern is placed
next to p and merged with it, and the process reiter-
ated until the residual stock area cannot be filled any
longer. Pattern p is then added to the set P.
Once patterns are generated for each c ∈ C, the
procedure getBestPattern selects the most profitable
pattern a ∈ P, that is, a pattern that maximizes the
total price of the sections it contains. Pattern a is fi-
nally added to the partial CSP solution s with acti-
vation level cuts, computed according to the current
demand d
0
and stock items availability. The pattern
generation process is iterated until the whole demand
is fulfilled.
Since the presence of real-valued prices, all the
above bounded integer knapsack are solved by en-
coding the integer variables as binary variables and
then by using an own implementation of the algorithm
for the 0-1 knapsack described in (Martello and Toth,
1990).
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
34
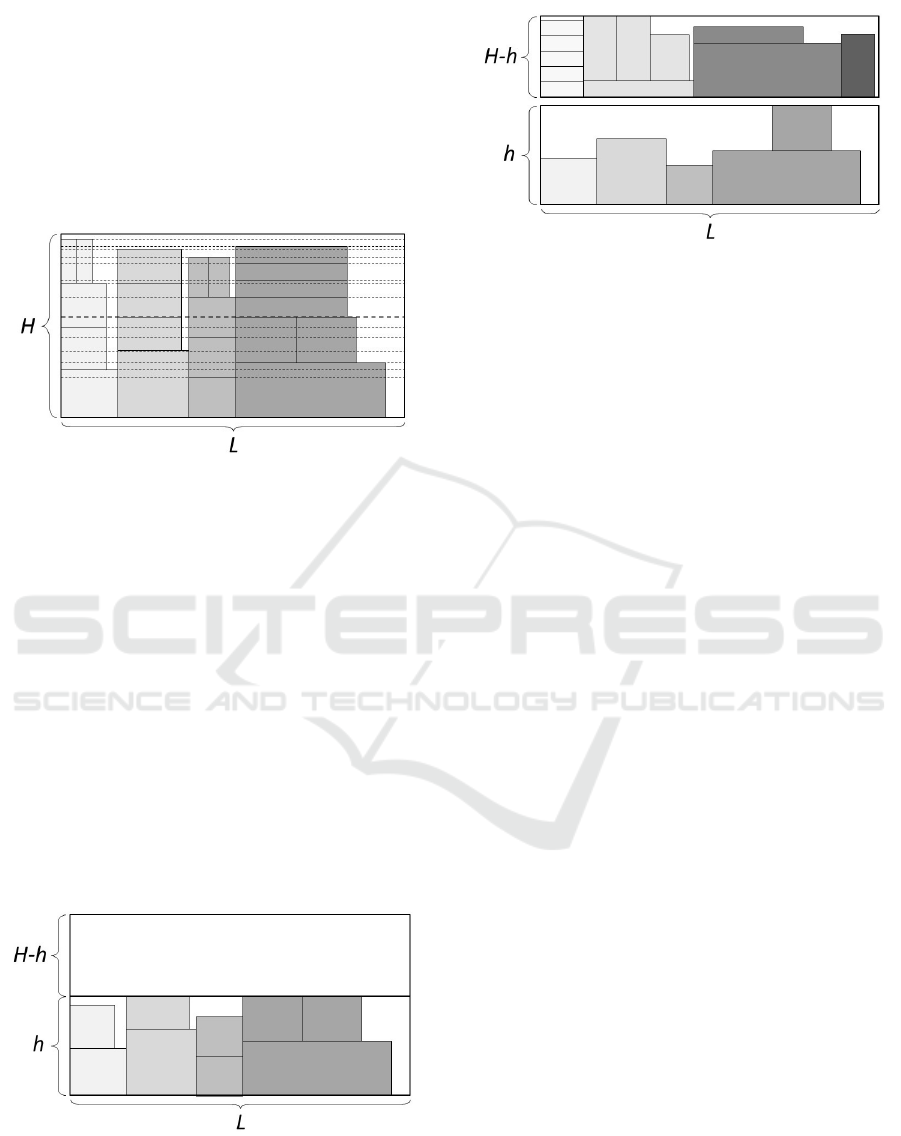
3.2.1 Precut Policy
For each pattern p, function getPattern generates also
a pattern p
0
that contains a precut, and then evaluates
the opportunity of replacing p with p
0
. For a given
pattern p, the algorithm scans all the cuts of the sec-
ond stage (those required to separate strips), choosing
one whose quota h is closest to the middle of H
j
, see
Figure 1.
Figure 1: Dotted lines indicate the potential cuts of the sec-
ond stage. The bold line refers to the cut closest to the mid-
dle of the stock height H
j
.
Stock item j (and pattern p) is split into new stock
items j
l
and j
u
(sub-patterns p
l
and p
u
) of sizes h×L
j
and (H
j
− h) × L
j
, respectively; the items that cross
quota h are removed and the sub-pattern p
u
deleted,
see Figure 2. Stock item j
u
is used to build a new
pattern p
0
u
(by the same procedure described above),
and a pattern with precut p
0
is obtained by merging
p
0
u
and p
l
, see Figure 3. If the difference between
the reduced costs of p and p
0
is larger than a given
threshold δ, then the pattern with precut is selected;
otherwise getPattern selects p.
The value of δ is set to zero in Steps 1 and 2 of
the heuristic, and is progressively increased in Step 3,
where the algorithm aims at producing solutions with
a decreasing number of precuts.
Figure 2: Sub-pattern p
l
.
Figure 3: Sub-patterns p
l
and p
0
u
.
4 COMPUTATIONAL RESULTS
The SVC was implemented in C++ and experiments
were performed on a Intel
r
Core2 Duo E8500 3.16
GHz with 8Gb RAM. The SVC heuristic has been
tested on ten real instances provided by SCM Group,
with n ∈ [58,972] and ρ = 1.15. The results have
been compared to those provided by the software pre-
viously adopted by the company and developed by a
national software house devoted to the design of cut-
ting optimization software. In order to be consistent,
the non-dominated solution using the minimum total
stock area has been promoted to the best solution and
compared to the single solution provided by the com-
pany own software.
Table 1 and 2 show the results for the case with
disabled and allowed precut, respectively. For each
instance, the SVC performance is evaluated in terms
of total used stock area (Area), number of used stocks
(#stocks), total number of patterns (#patterns) and
CPU time. The last three columns show the percent-
age gaps with the results obtained by the company
software (positive values mean an improvement ob-
tained by SVC; the symbol ‘-’ means that the CPU
time limit of three hours has been reached by the com-
pany software).
On average, the SVC heuristic reduces the total
used stock area by 2.34% without precuts (1.42%
with precuts), while the percentage trim-loss is re-
duced by a factor between 1.5 and 4. The number
of used stocks is also reduced by 7.62% (1.19 %) on
the mean. When precut is disabled, an average re-
duction of 3.61% in the number of distinct patterns
is achieved, although a meaningful mean increase of
11.02% arises when precut is allowed. However, such
worsening is mainly due to the greater material usage
efficiency attained by the SVC best solution: in most
of the cases, SVC computes non-dominated solutions
requiring comparable used material and less number
of patterns. The CPU time required to solve real in-
A Heuristic for a Rich and Real Two-dimensional Woodboard Cutting Problem
35
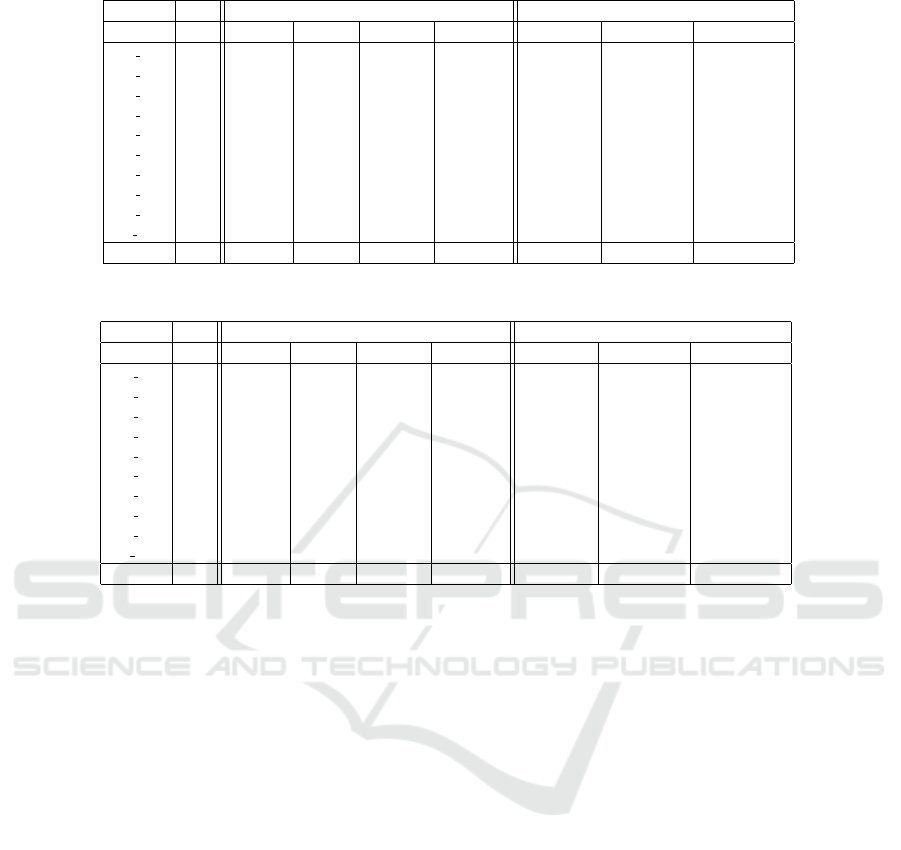
Table 1: Results without precut on ten real instances.
SVC heuristic Company software
Name n Area #stocks #patterns CPU time ∆Area (%) ∆stocks (%) ∆patterns (%)
I 1 58 2403.12 304 69 26.69 1.31 1.32 2.90
I 2 83 1454.8 251 102 6.67 1.19 1.20 -6.86
I 3 141 1512.21 508 165 121.14 1.58 1.57 0.61
I 4 500 221.32 29 29 103.52 2.40 34.48 34.48
I 5 500 273.84 36 36 - - - -
I 6 747 3158.81 620 546 634.72 2.13 1.94 -14.65
I 7 759 495.92 96 96 760.08 5.45 5.21 5.21
I 8 869 2923.78 563 269 972.06 - - -
I 9 951 354.72 67 67 34.63 - - -
I 10 972 903.11 179 178 494.59 - - -
Average - 1370.16 265.30 155.70 350.46 2.34 7.62 3.61
Table 2: Results with precut on ten real instances.
SVC heuristic Company software
Name n Area #stocks #patterns CPU time ∆Area (%) ∆stocks (%) ∆patterns (%)
I 1 58 2403.12 304 80 5.92 1.64 1.64 -18.75
I 2 83 1454.8 251 105 34.55 0.79 0.80 -6.67
I 3 141 1509.24 507 152 332.28 1.18 1.18 -8.55
I 4 500 220.78 29 29 139.09 - - -
I 5 500 273.3 36 36 471.14 - - -
I 6 747 3158.27 620 524 632.56 2.08 1.13 -10.11
I 7 759 494.83 96 96 104.28 - - -
I 8 869 2908.4 566 264 549.39 - - -
I 9 951 354.72 67 67 84.11 - - -
I 10 972 903.33 179 177 1332.55 - - -
Average - 1368.08 265.50 153 368.587 1.42 1.19 -11.02
stances is about 6 minutes on the mean, with just few
instances that exceed 10 minutes.
The heuristic was also tested on 52 benchmark
instances with n ∈ [10,250]. With the precut option
disabled (enabled) the algorithm reduces trim-loss in
17.3% (15.4%) of the cases. By using the continuous
lower bound of the total requested area, the optimal-
ity of the best solution with respect to the material
usage has been certified in the 80.8% (82.7%) of the
cases. Independently of the precut policy, in 17.3%
of the cases a solution with one pattern less is found,
and only 1.9% of the instances require an additional
pattern.
5 CONCLUSIONS AND FUTURE
WORK
Mathematical programming is a powerful tool that
can be used to model many relevant industrial prob-
lems. However, those mathematical formulations are
often challenging and, in some cases, real process
constraints are hard to be modeled. This is also true
for many CSP variants that try to simplify resolution
by encoding just a restricted number of real-world
constraints. Software applications based on those
CSP formulations may then happen to be inappropri-
ate, and companies are continuously looking for tools
able to deal with the whole process features and spec-
ification.
This paper addressed such an issue and presented
an SVC heuristic to solve a rich M2D-CSP that ful-
fills the specification of a family of wood cutting ma-
chines produced by SCM Group. The objectives of
used stock area minimization and of additional crite-
ria, as well as the fulfillment of open stack constraints,
were considered. Computational tests demonstrated
the improvement achieved on the previous software
solution, in terms of both solution quality and CPU
time requirements.
Further research is needed to include additional
optimization criteria, e.g., the minimization of cut-
ting times and the management of left-overs, and
to provide an exact formulation of the pricing prob-
lem when the whole set of specification is consid-
ered. Also, cutting processes are strongly affected
by operations scheduling: the formulation of a bi-
objective rich M2D-CSP that simultaneously mini-
mizes a scheduling function (such as the maximum
lateness or the weighted sum of tardiness) should then
deserve investigation.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
36

ACKNOWLEDGEMENTS
We gratefully acknowledge dr. eng. Federico Ratti,
Stefano Oliva and Simone Cera of SCM Group for
the fruitful discussions and constructive remarks that
helped us design and refine the algorithm described in
this paper.
REFERENCES
Aloisio, A., Arbib, C., and Marinelli, F. (2011). On lp re-
laxations for the pattern minimization problem. Net-
works, 57(3):247–253.
Arbib, C., Marinelli, F., and Ventura, P. (2016). One-
dimensional cutting stock with a limited number of
open stacks: bounds and solutions from a new inte-
ger linear programming model. International Trans-
actions in Operational Research, 23(1-2):47–63.
Belov, G. and Scheithauer, G. (2002). A cutting plane algo-
rithm for the one-dimensional cutting stock problem
with multiple stock lengths. European Journal of Op-
erational Research, 141(2):274 – 294.
Belov, G. and Scheithauer, G. (2007). Setup and open-
stacks minimization in one-dimensional stock cutting.
INFORMS J. on Computing, 19(1):27–35.
Chen, Q., Cui, Y., and Chen, Y. (2016). Sequential value
correction heuristic for the two-dimensional cutting
stock problem with three-staged homogenous pat-
terns. Optimization Methods and Software, 31(1):68–
87.
Chu, C. and Antonio, J. (1999). Approximation algorithms
to solve real-life multicriteria cutting stock problems.
Operations Research, 47(4):495–508.
Cui, Y.-P., Cui, Y., and Tang, T. (2015). Sequential heuris-
tic for the two-dimensional bin-packing problem. Eu-
ropean Journal of Operational Research, 240(1):43 –
53.
Malaguti, E., Durn, R. M., and Toth, P. (2014). Ap-
proaches to real world two-dimensional cutting prob-
lems. Omega, 47:99 – 115.
Martello, S. and Toth, P. (1990). Knapsack Problems: Al-
gorithms and Computer Implementations. John Wiley
& Sons, Inc., New York, NY, USA.
Non
˚
as, S. L. and Thorstenson, A. (2000). A combined
cutting-stock and lot-sizing problem. European Jour-
nal of Operational Research, 120(2):327 – 342.
Poldi, K. and Arenales, M. (2009). Heuristics for the one-
dimensional cutting stock problem with limited mul-
tiple stock lengths. Computers and Operations Re-
search, 36(6):2074–2081.
SCM (2017). SCM group. https://www.scmgroup.com. Ac-
cessed: 2017-06-30.
Umetani, S., Yagiura, M., and Ibaraki, T. (2003). One-
dimensional cutting stock problem to minimize the
number of different patterns. European Journal of Op-
erational Research, 146(2):388 – 402.
Varela, R., Vela, C. R., Puente, J., Sierra, M., and Gonz
´
alez-
Rodr
´
ıguez, I. (2008). An effective solution for a real
cutting stock problem in manufacturing plastic rolls.
Annals of Operations Research, 166(1):125.
W
¨
ascher, G., Haußner, H., and Schumann, H. (2007).
An improved typology of cutting and packing prob-
lems. European Journal of Operational Research,
183(3):1109 – 1130.
Yanasse, H. H. and Lamosa, M. J. P. (2007). An inte-
grated cutting stock and sequencing problem. Euro-
pean Journal of Operational Research, 183(3):1353 –
1370.
Yanasse, H. H., Zinober, A. S. I., and Harris, R. G. (1991).
Two-dimensional cutting stock with multiple stock
sizes. Journal of the Operational Research Society,
42(8):673–683.
A Heuristic for a Rich and Real Two-dimensional Woodboard Cutting Problem
37
