
Learning to Evaluate Chess Positions with Deep Neural Networks and
Limited Lookahead
Matthia Sabatelli
1,2
, Francesco Bidoia
2
, Valeriu Codreanu
3
and Marco Wiering
2
1
Montefiore Institute, Department of Electrical Engineering and Computer Science, Université de Liège, Belgium
2
Institute of Artificial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands
3
Surfsara BV, Science Park 140, Amsterdam, The Netherlands
Keywords:
Artificial Neural Networks, Classification, Regression, Chess Patterns, Deep Learning.
Abstract:
In this paper we propose a novel supervised learning approach for training Artificial Neural Networks (ANNs)
to evaluate chess positions. The method that we present aims to train different ANN architectures to understand
chess positions similarly to how highly rated human players do. We investigate the capabilities that ANNs
have when it comes to pattern recognition, an ability that distinguishes chess grandmasters from more amateur
players. We collect around 3,000,000 different chess positions played by highly skilled chess players and label
them with the evaluation function of Stockfish, one of the strongest existing chess engines. We create 4 different
datasets from scratch that are used for different classification and regression experiments. The results show
how relatively simple Multilayer Perceptrons (MLPs) outperform Convolutional Neural Networks (CNNs) in
all the experiments that we have performed. We also investigate two different board representations, the first
one representing if a piece is present on the board or not, and the second one in which we assign a numerical
value to the piece according to its strength. Our results show how the latter input representation influences the
performances of the ANNs negatively in almost all experiments.
1 INTRODUCTION
Despite what most people think, highly rated chess
players do not differ from the lower rated ones in
their ability to calculate a lot of moves ahead. On the
contrary, what makes chess grandmasters so strong is
their ability to understand which kind of board situa-
tion they are facing very quickly. According to these
evaluations, they decide which chess lines to calculate
and how many positions ahead they need to check, be-
fore committing to an actual move.
In this paper we show how to train Artificial Neu-
ral Networks (ANNs) to evaluate different board posi-
tions similarly to grandmasters. This approach is lar-
gely inspired by (van den Herik et al., 2005), where
the authors show how important it is in the field of
Computational Intelligence and Games, to not only
take into account the rules of the considered game,
but also the way the players approach it. To do so, we
model this particular way of training as a classifica-
tion task and as a regression one. In both cases dif-
ferent ANN architectures need to be able to evaluate
board positions that have been played by highly rated
players and scored by Stockfish, one of the most po-
werful and well known chess engines (Romstad et al.,
2011). To the best of our knowledge, this is a comple-
tely new way to train ANNs to play chess that aims to
find a precise evaluation of a chess position without
having to deeply investigate a big set of future board
states.
ANNs have recently accomplished remarkable
achievements by continuously obtaining state of the
art results. Multilayer Perceptrons (MLPs) are well
known both as universal approximators of any mathe-
matical function (Sifaoui et al., 2008), and as power-
ful classifiers, while Convolutional Neural Networks
(CNNs) are currently the most efficient image clas-
sification algorithm as shown by (Krizhevsky et al.,
2012). However, whether the pattern recognition abi-
lities of the latter ANN architecture would be as ef-
fective in chess, rather than more simple MLPs, is still
an open question.
The main goal of this work is twofold: on the one
hand we aim to answer the question whether MLPs
or CNNs would be a powerful tool to train programs
to play chess, while on the other hand we propose a
novel training framework that is based on the previ-
ously mentioned grandmasters’ games. The outline
276
Sabatelli, M., Bidoia, F., Codreanu, V. and Wiering, M.
Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead.
DOI: 10.5220/0006535502760283
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 276-283
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of the paper is as follows. Section 2 investigates the
link between machine learning and board games by
focusing on the biggest breakthroughs that have made
use of ANNs in this domain. In section 3 we present
the methods that have been used for the experiments,
the datasets and the ANN structures that have perfor-
med best. In section 4 we present the results that are
later discussed in section 5. The paper ends with our
conclusions in section 6 where we summarize the re-
levance and novelty of our research. Moreover, we
provide further insights about our results and relate
them to some potential future work.
2 MACHINE LEARNING AND
BOARD GAMES
Literature related to the applications of machine lear-
ning techniques to board games is very extensive. The
task of teaching computer programs to play games
such as Othello, Backgammon, Checkers and more
recently Go has been tackled numerous times from a
machine learning perspective. Regardless of what the
considered game is, the main thread that links all the
research that has been done in this domain is very sim-
ple: teaching computers to play as highly ranked hu-
man players without providing them with expert han-
dcrafted knowledge. In (Chellapilla and Fogel, 1999)
the authors show how, by making use of a combi-
nation of genetic algorithms together with an ANN,
the program managed to get a rating > 99.61% of
all players registered on a reputable checkers server.
This has been achieved without providing the system
with any particular expert and domain knowledge fea-
tures. A very similar approach, is presented in (Fogel
and Chellapilla, 2002) where the program managed to
play Checkers competitively as a ≈ 2050 rated player.
An alternative approach to teach programs to play
board games that does not make use of evolutio-
nary computing is based on the combination between
ANNs and Reinforcement Learning. This approach is
based on the famous TD(λ) learning algorithm pro-
posed by (Sutton, 1988) and made famous by (Te-
sauro, 1994). Tesauro’s program, called TD-Gammon
managed to teach itself how to play the game of back-
gammon by only learning from the final outcome of
the games. Also in this case, no pre-built know-
ledge besides the general rules of the game itself was
programmed into the system before starting the trai-
ning. Thanks to the detailed analysis described in
(Sutton and Barto, 1998), the TD(λ ) algorithm has
been successfully applied to Othello (van den Dries
and Wiering, 2012), Draughts (Patist and Wiering,
2004) and Chess firstly by (Thrun, 1995), and later by
(Baxter et al., 2000) and (Lai, 2015). It is worth men-
tioning that all the research presented so far has only
made use of MLPs as ANN architecture. In (Schaul
and Schmidhuber, 2009) a scalable neural network ar-
chitecture suitable for training different programs on
different games with different board sizes is presen-
ted. Numerous elements of this work already sugge-
sted the potential of the use of CNNs that have been so
successfully applied in the game of Go (Silver et al.,
2016) and the End-to-End ANN architecture used by
(David et al., 2016) in chess.
The idea of teaching a program to obtain particu-
lar knowledge about a board game, while at the same
time not making any use of handcrafted features, has
guided the research proposed in this paper as well.
Nevertheless, neither the Reinforcement Learning nor
Evolutionary Computing techniques will be used. In
fact, as already introduced, the coming sections will
present the performances of ANNs in a Supervised
Learning task that aims to find a very good chess eva-
luation function.
3 METHODS
This section explains how we have created the data-
sets on which we have performed all our experiments.
Furthermore, we describe the board representations
that have been used as input for the ANNs and the
architectures that have provided the best results.
3.1 Dataset and Board Representations
The first step of our research is creating a labeled da-
taset on which to train and test the different ANN ar-
chitectures. We have downloaded a large set of ga-
mes played by highly ranked players between 1996
and 2016 from the Fics Games Database
1
and par-
sed them to create two different board representations
suitable for the ANNs. The first technique represents
all 64 squares on the board in a linear sequence of bits
and the second one as 8 × 8 images. For both techni-
ques we have two categories of input: Bitmap Input
and Algebraic Input.
The Bitmap Input represents all the 64 squares of
the board through the use of 12 binary features. Each
of these features represents one particular chess piece
and which side is moving it. A piece is marked with
0 when it is not present on that square, with 1 when it
belongs to the player who should move and with −1
when it belongs to the opponent. The representation
is a binary sequence of bits of length 768 that is able
1
http://www.ficsgames.org/download.html
Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead
277

to represent the full chess position. There are in fact
12 different piece types and 64 total squares which
results in 768 inputs.
In the Algebraic Input we not only differentiate
between the presence or absence of a piece, but also
its value. Pawns are represented as 1, Bishops and
Knights as 3, Rooks as 5, Queens as 9 and the Kings
as 10. These values are negated for the opponent.
Both representations have been used as inputs for the
CNNs as well, with the difference that the board sta-
tes have been represented as 8 × 8 images rather than
stacked vectors. The images have 12 channels in total,
that again correspond to each piece type on the board.
Every single square on the board is represented by
an individual pixel. These pixels can either have va-
lues of −1, 0 and 1, in the case of the Bitmap Input
as used by (Oshri and Khandwala, 2016), or between
[−10, 10] for the Algebraic Input.
Once these board representations have been cre-
ated we made Stockfish label around 3,000,000 po-
sitions derived from the previously mentioned Fics
Games Database through the use of its evaluation
function and lookahead algorithm. Stockfish mainly
evaluates chess positions based on a combination of 5
different features and the Alpha-Beta pruning looka-
head algorithm.
The output of the evaluation process is a value
called the centipawn (cp). Centipawns correspond to
1/100th of a pawn and are the most commonly used
method when it comes to board evaluations. As alre-
ady introduced previously, it is possible to represent
chess pieces with different integers according to their
different values. When Stockfish’s evaluation output
is a value of +1 for the moving side, it means that the
moving side has an advantage equivalent to one pawn.
Through the use of this cp value we have created
4 different datasets. The first 3 have been used for
the classification experiments, while the fourth one is
used for the regression experiment.
• Dataset 1: This dataset is created for a very ba-
sic classification task that aims to classify only 3
different labels. Every board position has been la-
beled as Winning, Losing or Draw according to
the cp Stockfish assigns to it. A label of Winning
has been assigned if cp > 1.5, Losing if it was
< −1.5 and Draw if the cp evaluation was bet-
ween these 2 values. We have decided to set this
Winning/Losing threshold value to 1.5 based on
chess theory. In fact, a cp evaluation > 1.5 is alre-
ady enough to win a game (with particular excep-
tions), and is an advantage that most grandmasters
are able to convert into a win.
• Dataset 2 and Dataset 3: These datasets consist
of many more labels when compared to the previ-
ous one. Dataset 2 consists of 15 different labels
that have been created as follows: each time the
cp evaluation increases with 1 starting from 1.5, a
new winning label has been assigned. The same
has been done if the cp decreases with 1 when
starting from −1.5. In total we obtain 7 different
labels corresponding to Winning positions, 7 la-
bels for Losing ones and a final Draw label as al-
ready present in the previous dataset. Considering
Dataset 3, we have expanded the amount of labels
relative to the Draw class. In this case each time
the cp evaluation increases with 0.5 starting from
−1.5 a new Draw label is created. We keep the
Winning and Losing labels the same as in Dataset
2 for a total of 20 labels.
• Dataset 4: For this dataset no categorical labels
are used. In fact to every board position the tar-
get value is the cp value given by Stockfish. Ho-
wever we have normalized all these values to be
in [0, 1]. Since ANNs, and in particular MLPs,
are well known as universal approximators of any
mathematical function we have used this dataset
to train both an MLP and a CNN in such a way
that they are able to reproduce Stockfish’s evalua-
tions as accurately as possible.
For all the experiments we have split the data-
set into 3 different parts: we use 80% of it as Trai-
ning Set while 10% is used as Testing Set and 10%
as Validation Set. All experiments have been run on
Cartesius, the Dutch national supercomputer. We
use Tensorflow and Python 2.7 for all program-
ming purposes in combination with cuda 8.0.44
and cuDNN 5.1 in order to allow efficient GPU sup-
port for speeding up the computations.
3.2 Neural Network Architectures
This subsection presents in detail the ANN architectu-
res that have achieved the results presented in Section
4. Considering the first 3 Datasets, related to the dif-
ferent classification experiments, all ANNs are trai-
ned with the Categorical cross entropy loss function.
On the other hand, the ANNs that are used for the re-
gression experiment on Dataset 4 use the Mean Squa-
red Error loss function. No matter which kind of in-
put is used (Bitmap or Algebraic), in order to keep the
comparisons fair we did not change the architectures
of the ANNs.
It is also important to highlight that we have per-
formed a lot of preliminary experiments in order to
fine tune the set of hyperparameters of the different
ANNs. The best performing parameters will now be
described.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
278

3.2.1 Dataset 1
We have used a three hidden layer deep MLP with
1048, 500 and 50 hidden units for layers 1, 2, and 3
respectively. In order to prevent overfitting a Dropout
regularization value of 20% on every layer has been
used. Each hidden layer is connected with a non-
linear activation function: the 3 main hidden layers
make use of the Rectified Linear Unit (ReLU) activa-
tion function, while the final output layer consists of
a Softmax output. The Adam algorithm has been used
for the stochastic optimization problem and has been
initialized with the following parameters: η = 0.001;
β
1
= 0.90; β
2
= 0.99 and ε = 1e − 0.8. The network
has been trained with Minibatches of 128 samples.
The CNN consists of two 2D convolution layers
followed by a final fully connected layer of 500 units.
During the first convolution layer 20 5 × 5 filters are
applied to the image, while the second convolution
layer enhances the image even more by applying 50
3 × 3 filters. Increasing the amount of filters and the
overall depth of the network did not provide any signi-
ficant improvements to the performances of the CNN.
The Exponential Linear Unit (Elu) activation function
has been used on all the convolution layers, while the
final output consists of a Softmax layer. The CNN
has been trained with the SGD optimizer initialized
with η = 0.01 and ε = 1e − 0.8. We do not use Nes-
terov momentum, nor particular time based learning
schedules, however, a Dropout value of 30% was used
on all layers together with Batch Normalization in or-
der to prevent the network from overfitting. Also this
ANN has been trained with Minibatches of 128 sam-
ples.
It is important to mention that the CNNs have been
specifically designed to preserve as much geometrical
information as possible related to the inputs. When
considering a particular chess position, the location of
every single piece matters, as a consequence no pool-
ing techniques of any type have been used. In addition
to that also the “border modes” related to the outputs
of the convolutions has been set to “same”. Hence,
we are sure to preserve all the necessary geometrical
properties of the input without influencing it with any
kind of dimensionality reduction.
3.2.2 Dataset 2 and Dataset 3
On these datasets we have only changed the structure
of the MLP while the CNN architecture remained the
same. The MLP that has been used consists of 3 hid-
den layers of 2048 hidden units for the first 2 layers,
and of 1050 hidden units for the third one. The Adam
optimizer and the amount of Minibatches have not
been changed. However, in this case all the hidden
layers of the network were connected through the Elu
activation function.
3.2.3 Dataset 4
A three hidden layer deep perceptron with 2048 hid-
den units per layer has been used. Each layer is
activated by the Elu activation function and the SGD
training parameters have been initialized as follows:
η = 0.001; ε = 1e − 0.8 in combination with a Neste-
rov Momentum of 0.7. In addition to that Batch Nor-
malization between all the hidden layers and Minibat-
ches of 256 samples have been used. Also in this case,
except for the final single output unit, the CNN archi-
tecture has not been changed when compared to the
one used in the classification experiments. We tried to
increment the amount of filters and the overall depth
of the network, however, this only drastically incre-
mented the amount of training time without any per-
formance improvement.
4 RESULTS
This section presents the results that have been obtai-
ned on the previously described 4 datasets. We show
comparisons between the performances of MLPs and
CNNs and investigate the role of the two different in-
put representations: the Bitmap one, that only pro-
vides the ANNs with information whether a piece is
present on the board or not, and the Algebraic one that
includes a numerical value according to the strength
of the piece. Training has been stopped as soon as
the validation loss did not improve when compared to
the current minimum loss for more than 5 epochs in a
row, meaning that the ANNs started to overfit.
4.1 Dataset 1
Starting from the experiments that have been perfor-
med on Dataset 1, presented in Figure 1, it is possi-
ble to see that the MLP that has been trained with the
Bitmap Input outperforms all other 3 ANN architec-
tures. This better performance can be seen both on an
accuracy level and in terms of convergence time. Ho-
wever, the performance of the CNN trained with the
same input is quite good as well. In fact the MLP only
outperforms the CNN with less than 1% on the final
Testing Set
2
.
We noticed that adding the information about the
value of the pieces does not provide any advantage to
the ANNs. On the contrary both for the MLP and the
2
All the experiments have been performed on exactly the
same dataset.
Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead
279
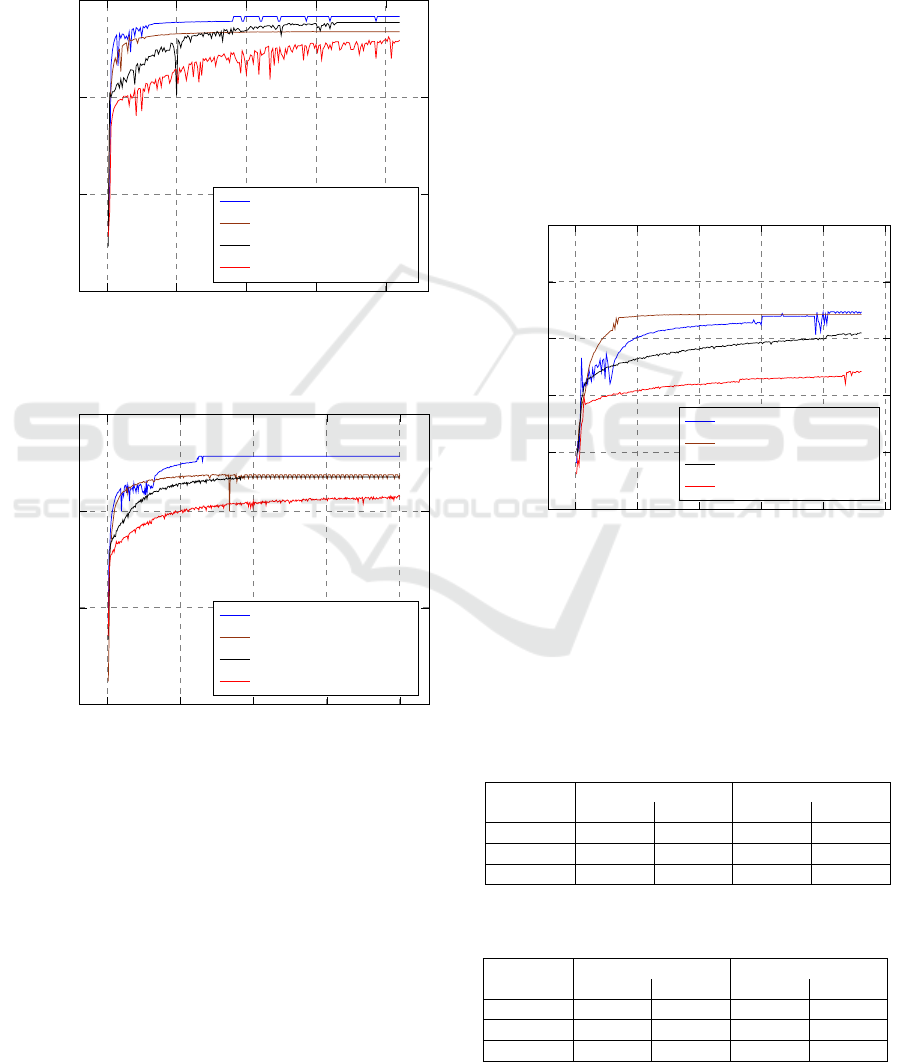
CNN this penalizes their overall performances. Ho-
wever, while on the experiments that have been per-
formed on Dataset 1 this gap in performance is not
that significant, with the MLP and the CNN that still
obtain > 90% of accuracy, the same cannot be said for
the ones that have been run on Dataset 2 and Dataset
3.
0
50
100
150
200
0.4
0.6
0.8
1
Epochs
Accuracy
MLP Bitmap Input
MLP Algebraic Input
CNN Bitmap Input
CNN Algebraic Input
Figure 1: The Testing Set accuracies on Dataset 1.
0 100 200 300 400
0.4
0.6
0.8
1
Epochs
Accuracy
MLP Bitmap Input
MLP Algebraic Input
CNN Bitmap Input
CNN Algebraic Input
Figure 2: The Testing Set accuracies on Dataset 2.
4.2 Dataset 2
On Dataset 2, a classification task consisting of 15
classes, we observe in Figure 2 lower accuracies by
all the ANNs. But once more, the MLP trained with
the Bitmap Input is the ANN achieving the highest
accuracies. Besides this, we also observe that for the
CNNs, and in particular the one trained with the Alge-
braic Input, the increment in the amount of classes to
classify starts leading to worse results, which shows
the superiority of the MLPs. A superiority that beco-
mes evident on the experiments performed on Dataset
3.
4.3 Dataset 3
This dataset corresponds to the hardest classification
task on which we have tested the ANNs. As already
introduced, we have extended the Draw class with 6
different subclasses. As Figure 3 shows, the accura-
cies of all ANNs decrease due to the complexity of
the classification task itself, but we see again that the
best performances have been obtained by the MLPs,
and in particular by the one trained with the Bitmap
Input. In this case, however, we observe that the lear-
ning curve is far more unstable when compared to the
one of the Algebraic Input. This may be solved with
more fine tuning of the hyperparameters.
0
50
100
150
200
250
0
0.2
0.4
0.6
0.8
1
Epochs
Accuracy
MLP Bitmap Input
MLP Algebraic Input
CNN Bitmap Input
CNN Algebraic Input
Figure 3: The Testing Set accuracies on Dataset 3.
We summarize the performances of the ANNs on
the first 3 datasets in the following tables. Table 1 re-
ports the accuracies obtained by the MLPs while Ta-
ble 2 shows the accuracies of the CNNs.
Table 1: The accuracies of the MLPs on the classification
datasets.
Dataset
Bitmap Input Algebraic Input
ValSet TestSet ValSet TestSet
Dataset1 98.67% 96.07% 96.95% 93.58%
Dataset2 93.73% 93.41% 87.45% 87.28%
Dataset3 69.44% 68.33% 69.88% 66.21%
Table 2: The accuracies of the CNNs on the classification
datasets.
Dataset
Bitmap Input Algebraic Input
ValSet TestSet ValSet TestSet
Dataset1 95.40% 95.15% 91.70% 90.33%
Dataset2 87.24% 87.10% 83.88% 83.72%
Dataset3 62.06% 61.97% 48.48% 46.86%
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
280

With the regression experiment that aims to
train the ANNs to reproduce Stockfish’s evaluation
function, we have obtained the most promising results
from all architectures. Table 3 reports the Mean Squa-
red Error (MSE) that has been obtained on the Valida-
tion and Testing Sets.
Table 3: The MSE of the ANNs on the regression experi-
ment.
ANN
Bitmap Input Algebraic Input
ValSet TestSet ValSet TestSet
MLP 0.0011 0.0016 0.0019 0.0021
CNN 0.0020 0.0022 0.0021 0.0022
We managed to train all the ANNs to have a Mean
Squared Error lower than 0.0025. By taking their
square root, it is possible to infer that the evaluations
given by the ANNs are on average less than 0.05 cp
off when compared to the original evaluation function
provided by the chess engine. Once again, the best
performance has been obtained by the MLP trained
on the Bitmap Input. The MSE obtained corresponds
to 0.0016, meaning that Stockfish evaluates chess po-
sitions only ≈ 0.04 cp differently when compared to
our best ANN that does not use any lookahead. It is
also important to highlight the performances of the
CNNs. While during the classification experiments
the superiority of the MLPs was evident, the gap bet-
ween CNNs and MLPs is not that large, even though
the best results have been obtained by the latter ar-
chitecture. Our results show in fact how both types
of ANNs can be powerful function approximators in
chess.
4.4 The Kaufman Test
In order to evaluate the final performance of the
ANNs we have tested our best architecture with the
Kaufman Test
3
, a special dataset of 25 extremely com-
plicated positions, created by the back then Internatio-
nal Master Larry Kaufman (Kaufman, 1992). The test
has been specifically designed to evaluate the strength
of chess playing programs and has as main goal the
prediction of what, given a particular board state, is
considered as the best possible move. This optimal
move is chosen according to the evaluation that is gi-
ven by the strongest existing chess engines.
We have performed this experiment with the MLP
trained on the Bitmap Input on Dataset 4. The ANN
only evaluates the board states corresponding to a
lookahead depth of 1 node. This means that, given
3
The test can be downloaded in the PGN format from
http://utzingerk.com/test_kaufman
one particular position as input, it scores the possible
future board states corresponding to the set of candi-
date moves of depth 1, without exploring any further.
The final move is the one corresponding to the highest
evaluation given by the ANN.
Besides checking if the move played by the ANN
corresponds to the one prescribed by the test we also
introduce the ∆cp measurement, which is able to esta-
blish the goodness or badness of the moves performed
by the ANN. We compute ∆cp as follows: we firstly
evaluate the board state that is obtained by playing
the move suggested by the test with Stockfish. The
position is evaluated very deeply for more than one
minute, as a result we assign Stockfish’s cp evalua-
tion to it. We name this evaluation δ
Test
. We then do
the same on the position obtained by the move of the
ANN in order to obtain δ
NN
. ∆cp simply consists of
the difference between δ
Test
and δ
NN
. The closer this
value is to 0, the closer the move played by the ANN
is to the one prescribed by the test.
Table 4 reports the results that have been obtained
on the Kaufman Test. For each position in the dataset
we show which is the best move that should be played
according to the test, and the move that has been cho-
sen by our ANN.
We observe that the MLP only plays Kaufman’s
optimal move twice, in Position 3 and in Position 6.
Even though at first glance these results can seem di-
sappointing, a deeper analysis of the quality of the
moves played by the ANN lead to more promising re-
sults. Reconsidering the logic that has been used for
labeling positions as Draws in the classification ex-
periments performed on Datasets 2 and 3, 17 moves
played by the ANN do not exceed a cp evaluation of
1.5. This means that, even though the move that is
chosen is not the optimal one, the position on the bo-
ard remains balanced. Furthermore, while the ANN
does not play the same move as the test dictates in
Position 1, this move was still evaluated equally well
by the engine. Hence a cp difference of 0.
There are, however, moves chosen by the ANN
that lead to a Losing position, in particular the ones
played in Positions 12, 14, 15, 19, 22 and 23. These
positions are very complex: they rely on deep look-
ahead calculations necessary to see tactical combina-
tions that are very hard to see, even for expert hu-
man players. Even though the ANN is still far from
the strongest human players it still reached an Elo ra-
ting of ≈ 2000 on a reputable chess server
4
. The
ANN played in total 30 games according to the follo-
wing time control: 15 starting minutes are given per
player at the start of the game, while an increment of
10 seconds is given to the player each time it makes a
4
https://chess24.com/en
Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead
281

Table 4: Comparison between the best move of the Kauf-
man Test and the one played by the ANN. The value of 10
in position 22 is symbolic, since the ANN chose a move
leading to a forced mate.
Position Best Move ANN Move ∆cp
1 Qb3 Nf3 0
2 e6 Bd7 0.8
3 Nh6 Nh6 0
4 b4 Qc2 0.8
5 e5 e6 0.3
6 Bxc3 Bxc3 0
7 Re8 Bc4 0.1
8 d5 Qd2 0.9
9 Nd4 Ne7 0.3
10 a4 a3 0.1
11 d5 h5 1.2
12 Bxf7 Nf3 4.2
13 c5 Nxe4 1.7
14 Df6 f5 5.9
15 exf6 Bd4 4.6
16 d5 Rb8 0.6
17 d3 c4 0.8
18 d4 Qe1 1.4
19 Bxf6 h3 4.2
20 Bxe6 Bd2 1.7
21 Ndb5 Rb1 1.4
22 dxe6 Kxe6 10
23 Bxh7+ Nh4 5.7
24 Bb5+ b4 1.2
25 Nxc6 bxc6 0.6
move.
The ANN played against opponents with an Elo
rating between 1741 and 2140 and obtained a final
game playing performance corresponding to a strong
Candidate Master titled player. The games show how
the ANN developed its own opening lines both when
playing as White and as Black and performed best du-
ring the endgame stages of the game, when the chan-
ces of facing heavy tactical positions on the board are
very small. The chess knowledge that it learned, al-
lowed it to easily win all the games that were played
against opponents with an Elo rating lower than 2000,
which correspond to ≈ 70% of the total games. Ho-
wever, this knowledge turned out to be not enough
to competitively play against Master titled players,
where only two Draws were obtained. An analysis
of the games shows how the chess Masters managed
to win most of the games already during the middle
game.
5 DISCUSSION
The results that have been obtained make it possible
to state three major claims. The first one is related
to the superiority of MLPs over CNNs as best ANN
architecture in chess, while the second one shows the
importance of not providing the value of the pieces as
inputs to the ANNs.
We think that the superiority of MLPs over CNNs,
that is highlighted in our classification experiments,
is related to the size of the board states. The large
success of CNNs is mainly due to their capabili-
ties to reduce the dimensionality of pictures while at
the same time enhancing their most relevant featu-
res. Chess, however, is only played on a 8 × 8 board,
which seems to be too small to fully make use of the
potential of this ANN architecture in a classification
task. Generalization is made even harder due to the
position of the pieces. Most of the time they cover the
whole board and move according to different rules.
On the other hand, this small dimensionality is ideal
for MLPs since the size of the input is small enough to
fully connect all the features between each other and
train the ANN to identify important chess patterns.
Considering the importance of not providing the
ANNs with the material information of the pieces,
we have identified a bizarre behavior. Manual checks
show how the extra information provided by the Al-
gebraic Input is able to trick the ANNs especially in
endgame positions.
Last, but not least, considering the results obtai-
ned on the Kaufman Test and on the chess server, we
show that it is possible to create a chess program that
mostly does not have to rely on lookahead algorithms
in order to play chess at a high level. It is important to
mention however, that to make this possible, the ANN
needs to be able to learn as much domain knowledge
as possible. Taking inspiration from (Berliner, 1977),
we state that deep lookahead can be discarded as long
as it is properly compensated with relevant chess kno-
wledge.
Nevertheless, we are also aware that the perfor-
mance of the ANN still needs to be improved when it
faces heavy tactical positions. Hence, we believe that
the most promising approach for future work will be
to combine the evaluations given by the current ANN
together with quiescence search algorithms. By doing
so the ANN will be able to avoid the horizon effect
(Berliner, 1973) and also perform well on tactical po-
sitions.
6 CONCLUSION
We believe that this paper provides strong insights
about the use of ANNs in chess. Its main contributi-
ons can be summarized as follows: Firstly we propose
a novel training framework that aims to train ANNs to
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
282

evaluate chess positions similar to how highly skilled
players do. Current State of the Art methods have al-
ways relied a lot on deep lookahead algorithms that
help chess programs to get as close as possible to an
optimal policy. Our method focuses a lot more on the
discovery of the pattern recognition knowledge that is
intrinsic in the chess positions without having to rely
on expensive explorations of future board states.
Secondly we show that MLPs are the most suit-
able ANN architecture when it comes to learning
chess. This is both true for the classification expe-
riments as for the regression one. Furthermore, we
also show how providing the ANNs with information
representing the value of the pieces present on the bo-
ard is counter-productive.
To the best of our knowledge this is one of the few
papers besides (Oshri and Khandwala, 2016) that ex-
plores the potential of CNNs in chess. Even though
the best results have been achieved by the MLPs we
believe that the performance of both ANNs can be im-
proved. As future work we want to feed both ANN ar-
chitectures with more informative images about chess
positions and see if the gap between MLPs and CNNs
can be reduced. We believe that this strategy, appro-
priately combined with a quiescence or selective se-
arch algorithm, will allow the ANN to outperform the
strongest human players, without having to rely on
deep lookahead algorithms.
REFERENCES
Baxter, J., Tridgell, A., and Weaver, L. (2000). Learning to
play chess using temporal differences. Machine Lear-
ning, 40(3):243–263.
Berliner, H. J. (1973). Some necessary conditions for a mas-
ter chess program. In IJCAI, pages 77–85.
Berliner, H. J. (1977). Experiences in evaluation with BKG-
A program that plays Backgammon. In IJCAI, pages
428–433.
Chellapilla, K. and Fogel, D. B. (1999). Evolving neural
networks to play checkers without relying on expert
knowledge. IEEE Transactions on Neural Networks,
10(6):1382–1391.
David, O. E., Netanyahu, N. S., and Wolf, L. (2016). Deep-
chess: End-to-end deep neural network for automatic
learning in chess. In International Conference on Ar-
tificial Neural Networks, pages 88–96. Springer.
Fogel, D. B. and Chellapilla, K. (2002). Verifying Ana-
conda’s expert rating by competing against Chinook:
experiments in co-evolving a neural checkers player.
Neurocomputing, 42(1):69–86.
Kaufman, L. (1992). Rate your own computer. Computer
Chess Reports, 3(1):17–19.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).
Imagenet classification with deep convolutional neu-
ral networks. In Advances in neural information pro-
cessing systems, pages 1097–1105.
Lai, M. (2015). Giraffe: Using deep reinforcement learning
to play chess. arXiv preprint arXiv:1509.01549.
Oshri, B. and Khandwala, N. (2016). Predicting moves in
chess using convolutional neural networks. Stanford
University Course Project Reports-CS231n.
Patist, J. P. and Wiering, M. (2004). Learning to play draug-
hts using temporal difference learning with neural net-
works and databases. In Benelearn’04: Proceedings
of the Thirteenth Belgian-Dutch Conference on Ma-
chine Learning, pages 87–94.
Romstad, T., Costalba, M., Kiiski, J., Yang, D., Spitaleri,
S., and Ablett, J. (2011). Stockfish, open source chess
engine.
Schaul, T. and Schmidhuber, J. (2009). Scalable neural net-
works for board games. Artificial Neural Networks–
ICANN 2009, pages 1005–1014.
Sifaoui, A., Abdelkrim, A., and Benrejeb, M. (2008). On
the use of neural network as a universal approximator.
International Journal of Sciences and Techniques of
Automatic control & computer engineering, 2(1):336–
399.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre,
L., Van Den Driessche, G., Schrittwieser, J., Antonog-
lou, I., Panneershelvam, V., Lanctot, M., et al. (2016).
Mastering the game of Go with deep neural networks
and tree search. Nature, 529(7587):484–489.
Sutton, R. S. (1988). Learning to predict by the methods of
temporal differences. Machine learning, 3(1):9–44.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement le-
arning: An introduction, volume 1. MIT press Cam-
bridge.
Tesauro, G. (1994). TD-gammon, a self-teaching back-
gammon program, achieves master-level play. Neural
computation, 6(2):215–219.
Thrun, S. (1995). Learning to play the game of chess. In
Advances in neural information processing systems,
pages 1069–1076.
van den Dries, S. and Wiering, M. A. (2012). Neural-
fitted td-leaf learning for playing othello with struc-
tured neural networks. IEEE Transactions on Neural
Networks and Learning Systems, 23(11):1701–1713.
van den Herik, H. J., Donkers, H., and Spronck, P. H.
(2005). Opponent modelling and commercial games.
In Proceedings of the IEEE 2005 Symposium on Com-
putational Intelligence and Games (CIG’05), pages
15–25.
Learning to Evaluate Chess Positions with Deep Neural Networks and Limited Lookahead
283
