Mathematical Programs and Computations for a Class of

Anti-aircraft Mission Planning Problems

Trang T. Nguyen, Trung Q. Bui, Bang Q. Nguyen and Su T. Le

C4I Department, Viettel Research and Development Institute, Vietnam

Keywords:

Military, Theater Defense Distribution, Mixed Integer Programming.

Abstract:

The theater defense distribution is an important problem in the military that determines strategies against a

sequence of offensive attacks in order to protect his targets. This study focuses on developing mathematical

models for three important defense problems that generate anti-aircraft mission plans for a group of missile

battalions. The simple Anti-aircraft Launching Assignment problem speciﬁes number of missiles should be

launched from each battalion to each ﬂeet of attacking aircraft to maximize the defensive effectiveness, pro-

vided that the locations of missile battalions are given. On the other hand, the Anti-aircraft Mission Planning

problem maximizes the defender’s effectiveness using all his available battalions, while the Inverse Anti-

aircraft Mission Planning problem computes necessary weapon resources (battalions and their missiles) to

obtain a given defensive effectiveness value. The proposed formulations are Integer Programs and proved as

NP-hard. A comprehensive set of experiments is then evaluated to show that these proposed programs can be

applied to solve fast real-life instances to optimality.

1 INTRODUCTION

The Theater Distribution Model (TDM) is speciﬁ-

cally designed to support the combatant commander

to ensure his effective plans within area of operations

(Shalikashvili, 1996). Most of researches in the litera-

ture focus on the military theater distribution problem

associated with determining positions of defender’s

missile battalions within a potentially geographical

region (Shalikashvili, 1993). In most cases, the de-

fender faces with so many risks from terrorist attacks

of all kinds. The work we research here is directly

motivated by such one risk assessment: surface-to-

air missile battalions defense against many ﬂeets of

penetrating aircraft. Beside the role of specializing

anti-aircraft, missile battalions in an air defense sy-

stem also protect a target such as capital, political

area, economy or military center. The Department

of Air Defense and Air Force has conducted some

risk assessment exercises and estimated risks of many

attack possibilities. One area that is still undeve-

loped is an algorithm for determining an intelligent

package of missile battalion’s actions to aircraft at-

tack. A missile battalion package consisting of only

one missile type might be ineffective but when se-

veral types of missiles are combined properly, they

conﬁdently destroy the attacking aircraft and protect

their target. More precisely, we develop mathemati-

cal formulations for anti-aircraft mission planning ef-

fectively for a group of missile battalions. A missile

battalion is considered as a fundamental tactical buil-

ding block which recruits or conscripts in one geo-

graphical area assigned by a feudal lord. Given some

threat, the defender must decide where to locate de-

fensive missile battalions among potential locations

and how they should engage ﬂeets of attacking air-

craft. We express the defender’s courses of action as

following mathematical optimization problems. The

ﬁrst and simple problem is the Anti-aircraft Laun-

ching Assignment (ALA) that computes number of

missiles should be launched from each battalion to

each ﬂeet of attacking aircraft to maximize the de-

fensive effectiveness, provided that the locations of

missile battalions is given. On the other hand, the

Anti-aircraft Mission Planning problem (AMP) cal-

culates not only the launching assignment for the bat-

talions but also locations of the battalions while In-

verse Anti-aircraft Mission Planning problem (IAMP)

computes necessary weapon resources, battalions’ lo-

cations, and a launching assignment to obtain a gi-

ven effectiveness threshold. The most valuable con-

tribution of this paper comes from the statements and

practical mathematical formulations for these three

crucial problems in the TDM class. The ALA arises

Nguyen, T., Bui, T., Nguyen, B. and Le, S.

Mathematical Programs and Computations for a Class of Anti-aircraft Mission Planning Problems.

DOI: 10.5220/0006539801550163

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 155-163

ISBN: 978-989-758-285-1

155

in the crowded cities where there are not many choi-

ces for locating missile battalions while the AMP is

necessarily tackled in sparsely populated area. On the

contrary, the IAMP is necessarily considered when

the protected target should not be fallen in any ca-

ses. Although these problems are proven as NP-hard,

the computational results show the efﬁcient of our for-

mulations since they can be applied directly to solve

fast real-life instances to optimality. The message

is that, with the validation of experienced soldiers,

we have gained conﬁdence that the formulations have

signiﬁcant implementation in any defender’s combat

ﬁeld. The rest of paper is organized as follows. In

Section 2, we state the problems, formulate them as

mixed integer programs as well as prove their hard-

ness. The experimental results are reported and ana-

lyzed in Section 3. Finally, we conclude the paper and

draw some future directions in Section 4.

The TDM has been motivated and validated for

both defensive side and offensive side in general

((Robert, 2006), (Crino and Moore, 2004), (Jackson,

1989), (Studies and Agency, 1992), (Brian, 1994),

(Seichter, 2005), (Moore, 2002), (Brown et al., 2008)

). Some of these studies have been developed into

mathematical models which are related to the AMP

can be classiﬁed as the Weapon-Target Assignment

(WTA)and the Defender- Attacker Model (DAM).

The WTA is the assignment of weapon to the hos-

tile target in order to protect assets, which can be

formulated as a nonlinear integer programming pro-

blem and is known to be NP-hard complete. Although

several heuristic methods have been propose for sol-

ving the WTA, such as genetic algorithm, tabu search,

simulated annealing, and variable neighborhood se-

arch ((Murphey, ), (Tokgoz and Bulkan, 2013)), an

integer programming and network ﬂow-based lower

bounding method has been introduced in (Ahuja Ra-

vindra and James, 2007). An instance of DAM in a

fast theater model is introduced in (Seichter, 2005),

which is built upon the existing air model. The air

strike attacker’s main objective is maximizing target

value destroyed by killing as many targets with high

values as possible, while the ground combat wants

to minimize its own losses. The resulting model is

a Mixed Integer Program (MIP) ﬁnding an optimal,

actively defensive actions by the ground force that

can signiﬁcantly reduce the air attacker’s effective-

ness. The defender-attacker problem is continued stu-

dying in (Moore, 2002), in which a new methodo-

logy for strategy optimization under uncertainty has

been proposed. The authors describe the implemen-

tation of a genetic programming algorithm to deter-

mine an optimized evasion strategy for the extended

two-dimensional pursuer-evader problem under con-

ditions of uncertainty about the type of pursuer. The

DAM model is also applied to defender’s risk asses-

sment and mitigation,(Brown et al., 2008).

2 PROBLEM FORMULATIONS

We now state and formulate the anti-aircraft mission

planning problems. The complexity of these pro-

blems is also discussed at the end of this section.

2.1 Problem Descriptions

Direction

Height (km)

3π

5π

3π

7π

2π

Oppressive ﬂeet: F15, F16, F14

Bomb ﬂeet: F15, F16

Diversionary ﬂeet

Escort ﬁghter ﬂeet

Bomb ﬂeet: B52, B1, B2

Radar-jamming ﬂeet: EF111A, EC130H, EA6B

Reconnaissance ﬂeet: TR1, U2, SR71

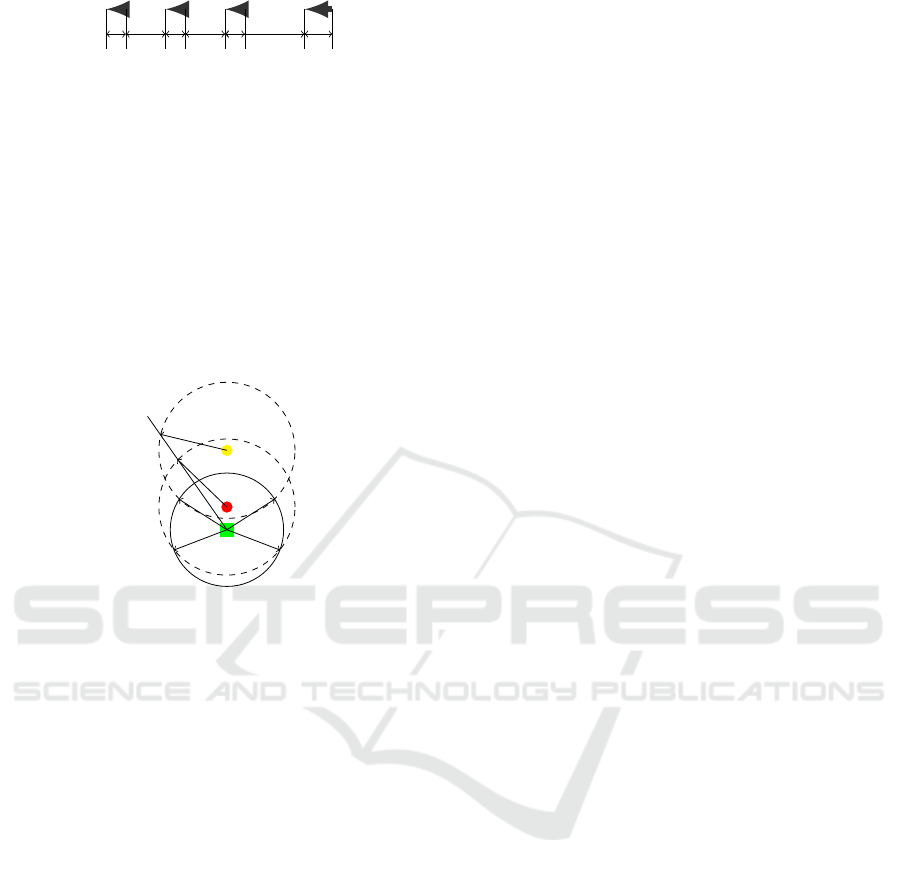
Figure 1: An example of an attacking plan.

Suppose that the attacker’s plan can be observed

by an intelligence system of the defender and is des-

cribed as follows. In the offensive side, the attacker

strikes the target by a group of ﬂeets of attacking ai-

rcraft. For a sake simplicity, from now on, the term

“ﬂeet” is used stead of “ﬂeet of attacking aircraft”.

Each ﬂeet is organized by a group of aircraft which

have same missions such as carrying bombs or ma-

king radar noise; enter the theater at same height, di-

rection; and ﬂy with same velocity. Each ﬂeet is asso-

ciated with a weight of importance depending mainly

on its mission. Figure 1 illustrates an attacking plan,

in which the horizontal axis represents the directions

of the ﬂeets, considered as angles between attacking

directions and a predeﬁned axis; while the vertical

axis represents the height of the ﬂeets. There are se-

ven ﬂeets at different heights, directions and veloci-

ties, drawn by seven arrows. The color of the arrows

reﬂects the ﬂeets’ weights. For instance, the darkest

arrow describes the ﬂeet with the highest weight, car-

rying bombs such as B52, B1, B2. Further, ﬂying po-

sitions of aircraft in a ﬂeet must be captured in detail,

for example, a ﬂying position of a four-aircraft ﬂeet is

illustrated in Figure 2.

In the defensive side, the defender’s responsibility

is engaging ﬂeets to protect its point target. In or-

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

156

2.5km 5km 2.5km 5km 2.5km 10km 3km

Figure 2: An example of an attacking ﬂeet.

der to formulate a class of anti-aircraft mission plan-

ning problems, we take into account following fac-

tors. The ﬁrst one is critical radius corresponding to

each ﬂeet that deﬁnes a critical circle centered at the

target. The defender has to make a defensive plan

such that no attacking aircraft in that ﬂeet is able to

get inside that circle. This critical radius is compu-

ted depending on the height, velocity of that ﬂeet and

type of bombs carried by that ﬂeet. For instance, in

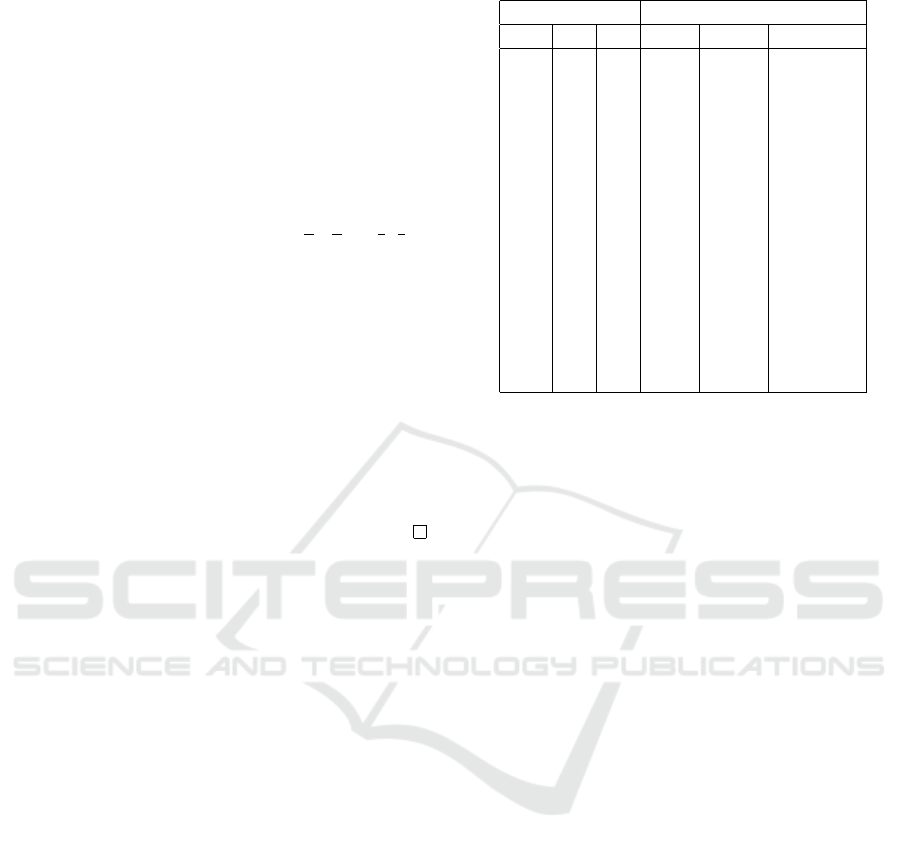
Figure 3, the point target is described by the green

rectangle with critical radius OX corresponding to a

ﬂeet coming from the AO direction. The second fac-

X Y

V W

Figure 3: An example of inﬂuence of battalion’s locations

on their ﬁrepower capabilities.

tor is action range of a battalion corresponding to a

ﬂeet that can be understood as a ﬂeet’s ﬂying path

where the ﬂeet will be intercepted by that battalion.

In Figure 3, the action range of battalion B

is CD

segment, where D is the intersection of the attacking

direction AO and the critical circle, and C is the inter-

section of the direction AO and the circle centered at

of radius B

C which is deﬁned as the long range

of missiles belonging to that battalion. Similarly, the

action range of battalion B

is BD segment. The third

factor maximum launches representing ﬁrepower ca-

pabilities of a battalion can be seen as maximum num-

ber of missiles that can be launched from the battalion

to the ﬂeet in its action range. This number is calcula-

ted basing on the type of missile, number of missiles

in that battalion, as well as the shortest time between

two successive launches. The fourth factor is the ex-

pected number of killed aircraft of a ﬂeet caused by a

battalion in a number of launches. This value can be

estimated by number of missiles, probability of kill,

defensive mode related to each ﬂeet, and set of coefﬁ-

cients corresponding to each missile battalion such as

technical coefﬁcient, control coefﬁcient, and complex

coefﬁcient of combat. Lastly, a minimum distance be-

tween each pair of battalions is required to avoid ra-

dar jamming between missiles in the battalions. Note

that if two battalions locate at a same position, this

constraint can be ignored. As a defender, we would

like to measure the result of our defense. An effective

criterion is then introduced as defensive effectiveness,

calculated by fraction between value of killed aircraft

and value of all aircraft in attacking ﬂeets. The effecti-

veness is strongly inﬂuenced by battalions’ locations,

that motivates us to study an adaptable, efﬁcient, and

cost-effective process to analyse missile battalion de-

fense against aircraft threats. Three problems propo-

sed in this paper, the ALA, AMP and IAMP, belong

to the defensive side, where the defender preserves a

point target. The attacker’s plan including all infor-

mation about the offensive side stated above is sup-

posed to be observed clearly by the intelligence sy-

stem of the defender. While in the AMP, the defender

not only ﬁnds optimal locations for missile battalions

but also indicates numbers of missiles launched from

battalions to ﬂeets; in the ALA, the defenders is not

required to ﬁnd locations for battalions. We consi-

der now somewhat inverse version of the AMP, the

IAMP. Assume, in particular, that the defender has

a set of battalions, in stead of using all battalions to

maximize his defensive effectiveness, one generates

a defensive mission plan such that the corresponding

effectiveness is greater than or equal to a given value.

The detailed mathematical programs of these models

are proposed in Section 2.2.

2.2 Mathematical Programs

For a simplicity of presentation, we ﬁrst introduce

some indices and notations.

Inputs

• B: set of missile battalions;

• F: set of ﬂeets of attacking aircraft;

• L: set of potential locations for battalions;

• For a battalion b ∈ B, denote m(b) and c(b) by

number of missiles distributed to b and cost of a

missile of b, respectively;

• For a ﬂeet f ∈ F, denote n( f ) and w( f ) by num-

ber of aircraft in ﬂeet f and weight of that ﬂeet,

respectively;

• For a pair (b, f ) (b ∈ B, f ∈ F), denote t(b, f ) by

the maximum number of missiles that battalion b

is able to launch to ﬂeet f in its action range;

• Last, for a triple (b, f ,t) (b ∈ B, f ∈ F and t ∈ Z

denote e(b, f ,t) by the expected number of killed

aircraft in ﬂeet f caused by t missiles launched

from battalion b to ﬂeet f .

Mathematical Programs and Computations for a Class of Anti-aircraft Mission Planning Problems

157

2.2.1 ALA Mathematical Program

Given the locations of battalions, the objective of the

ALA is to compute number of missiles should be

launched from each battalion toward each ﬂeet such

that the defensive effectiveness is maximized. This

program arises naturally in real-life instance when the

target and battalions are ﬁrmly positioned in a given

area. To formulate the ALA program, we introduces

binary variables x

b, f ,t

where b ∈ B, f ∈ F and t ∈ Z

indicating that whether t missiles are launched from

battalion b to ﬂeet f or not. The mathematical pro-

gram of the ALA problem can be stated as a mixed

integer program as follows.

Max

∑

f ∈F

w( f )

∑

b∈B

t(b, f )

∑

t=1

e(b, f ,t)x

b, f ,t

n( f )

(1a)

s.t.

∑

f ∈F

t(b, f )

∑

t=1

b, f ,t

≤ m(b), ∀b ∈ B

(1b)

∑

b∈B

t(b, f )

∑

t=1

e(b, f ,t)x

b, f ,t

≤ n( f ), ∀ f ∈ F

(1c)

b, f ,t

∈ {0,1}, ∀b ∈ B, f ∈ F,t ∈ {1,.. .,t(b, f )}.

(1d)

In this program, the objective function (1a) is the

defensive effectiveness which can be calculated as the

fraction between the value of killed aircraft and the

value of aircraft in these ﬂeets. Constraints (1b) sim-

ply stipulate that the number of launched missiles of

each battalion should not be greater than its given

load-out. Constraints (1c) ensure the number of ai-

rcraft destroyed in a ﬂeet do not exceed the number

of aircraft in that ﬂeet; while the launching times con-

straints are hidden in (1b) and (1c) since t takes values

in [1,t(b, f )]. The variables are restricted to be binary

in constraints (1d).

2.2.2 AMP Mathematical Program

We consider now a situation that the defender need to

decide where to locate missile battalions among a set

of limited number of available locations and missiles

to distribute a defensive mission plan that maximizes

his defensive effectiveness. The AMP can be viewed

as an extension of the ALA model. The AMP formu-

lation introduces more variables representing locati-

ons of battalions and missile-distance constraints de-

ﬁning lower bounds for geographic distances between

battalions at different locations. In addition to notati-

ons, variables and constraints introduced in the ALA

formulation, the AMP considers more categories of

factors as follows.

Inputs:

• For a pair of locations (l

) (l

∈ L), denote

d(l

) by the geometric distance between l

and

;

• For a pair of battalions (b

) (b

∈ B), denote

d(b

) by the minimum distance between b

and

if they are located at two different positions;

• For each triple (b,l, f ) (b ∈ B,l ∈ L, f ∈ F), de-

note t(b,l, f ) by the maximum number of missi-

les that battalion b located at l is able to launch to

ﬂeet f in its action range;

• For a quadruple (b,l, f ,t) (b ∈ B, l ∈ L, f ∈ F and

t ∈ Z

), e(b,l, f ,t) indicates the expected number

of killed aircraft in ﬂeet f caused by t missiles

launched from battalion b located at l to ﬂeet f .

Further, we introduce binary variables y

b,l

where

b ∈ B,l ∈ L, indicating whether battalion b locates

at location l or not. Second, binary variables z

b,l, f ,t

where b ∈ B,l ∈ L, f ∈ F and t ∈ Z

, state that if t

missiles are launched from battalion b located at lo-

cation l to ﬂeet f . In addition to constraints given

in the ALA formulation, the AMP requires minimum

distance between any two battalions such that if batta-

lions b

and b

locate at location l

and l

respectively,

then

d(l

) ≥ d(b

), ∀b

6= b

6= l

(2)

The MIP model for the AMP problem can be repre-

sented as:

Max

∑

f ∈F

w( f )

∑

l∈L

∑

b∈B

t(b,l, f )

∑

t=1

e(b,l, f ,t)z

b,l, f ,t

n( f )

(3a)

s.t.

∑

l∈L

b,l

= 1, ∀b ∈ B

(3b)

∑

l∈L

∑

f ∈F

t(b,l, f )

∑

t=1

b,l, f ,t

≤ m(b),∀b ∈ B

(3c)

(2 − y

− y

)∞ + y

d(l

) ≥ d(b

)

∀b

∈ B,b

6= b

,∀l

∈ L,l

6= l

(3d)

∑

l∈L

∑

b∈B

t(b,l, f )

∑

t=1

e(b,l, f ,t)z

b,l, f ,t

≤ n( f ),∀ f ∈ F

(3e)

∑

f ∈F

t(b,l, f )

∑

t=1

b,l, f ,t

≤ y

b,l

,∀b ∈ B, l ∈ L

(3f)

b,l

b,l, f ,t

∈ {0,1}, ∀b ∈ B,l ∈ L, f ∈ F,

t ∈ {1,. . .,t(b,l, f )}.

(3g)

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

158

In the AMP formulation, the defender’s objective

is maximizing its effectiveness (3a) which is the sum

of fractions of expected number of killed aircraft and

number of aircraft n( f ) for all ﬂeets while considering

additionally the importance weights of these ﬂeets.

Constraints (3b) simply limit each missile battalion

to one location. Constraints (3c) stipulate that the

number of launches from each battalion should not

be greater than its given number of missiles. Con-

straints (3d) describes the missile-distance constraints

(2), showing that if two missile battalions b

and b

are at locations l

and l

where l

6= l

, respectively,

the distance between these battalions must be grea-

ter than a required minimum distance

d(b

). Con-

straints (3e) deﬁne upper bounds for number of air-

craft in these ﬂeets. Constraints (3f) tell us that there

are some missiles launched from a location to a ﬂeet

if and only if there exists at least one missile batta-

lion located at that location. Lastly, constraints (3g)

indicate that x

b,l

b,l, f ,t

where b ∈ B,l ∈ L, f ∈ F,t ∈

{1,... ,t(b,l, f )} are binary variables.

2.2.3 IAMP Mathematical Program

An other signiﬁcant situation that usually appears in

the real combat ﬁeld is the inverse AMP problem, the

IAMP. Assume, in particular, that the defender has

a set of battalions, in stead of using all battalions to

maximize his defensive effectiveness, one generates

a defensive mission plan such that the corresponding

effectiveness is greater than or equal to a given value

with the lowest cost. Intuitively, one would like to lo-

cate defensive battalions as well as compute number

of missiles with the lowest cost such that its effective-

ness is at least γ (such as γ = 0.5, 0.6,...). In addition

to the inputs introduced in the ALP and the AMP, the

IAMP program need some more notations.

Inputs:

• For a battalion b ∈ B, denote c(b) by the cost of a

missile of b;

• For each pair (b, l) of a battalion b ∈ B and a lo-

cation l ∈ L, c(b,l) refers to the cost of allocating

battalion b at location l;

Further, the IAMP mathematical formulation in-

troduces more integer variables u

∈ Z

, indicating

number of missiles launched from battalion b ∈ B.

The mathematical program for the IAMP is given as:

The objective of this formulation is to minimize

the total cost (4a) that is calculated by sum of esta-

blishing battalion cost and launched missile cost on

these battalions. Constraints (4b) are different from

(3b) since not every missile battalion is required to

locate at some location. Constraint (4d) requires the

obtained effectiveness be at least a given value, γ. The

number of missiles on each battalion is set at con-

straints (4e) while its upper bound has been given

in constraints (4f). The other constraints are similar

to ones in the AMP formulation given in constraints

(4c), except that number of launched missiles are in-

teger variables as in constraints (4g).

Min

∑

b∈B

∑

l∈L

c(b,l)y

b,l

∑

b∈B

c(b)u

(4a)

s.t.

∑

l∈L

b,l

≤ 1, ∀b ∈ B

(4b)

Constraints(3c),(3d),(3e),(3 f ), (3g)

(4c)

∑

f ∈F

w( f )

∑

l∈L

∑

b∈B

t(b,l, f )

∑

t=1

e(b,l, f ,t)z

b,l, f ,t

n( f )

≥ γ,

(4d)

−

∑

l∈L

∑

f ∈F

t(b,l, f )

∑

t=1

b,l, f ,t

= 0, ∀b ∈ B

(4e)

≤ m(b)

∑

l∈L

b,l

, ∀b ∈ B

(4f)

∈ Z

, ∀b ∈ B

(4g)

where γ ∈ [0, 1] is a given effectiveness value.

Note here that, the ALA and the AMP always re-

sult in an optimal solution with the effectiveness be-

longing to [0, 1], while the IAMP sometimes returns to

no solution in case the weapon resources are not suf-

ﬁciently available to reach the expected effectiveness.

Further, one of the difﬁculties to deal with these pro-

grams is to deﬁne the values of parameters that suppo-

sed to be known. This study clariﬁes how to compute

the expected number of killed aircraft, the maximum

number of launches and the minimum distance bet-

ween two missiles for special situation of a defensive

missile battalion plan against aircraft attack, that can

be found in the Appendix.

2.3 NP-Hardness

The NP-completeness is indicated as the complexity

of these mathematical programs in this section.

Theorem 1. The ALA is NP-complete.

Proof. To prove this, we reduce the 3-Partition Pro-

blem (3PP) to the decision problem of ALA since the

3PP is known as NP-complete (Garey and Johnson,

1990).

Recall that in the 3PP, we are given a multi-set S

of 3b positive integers i

,... , i

, where the value

of every element in the set belongs to interval (

for a positive integer C; and we are asked to decide if

Mathematical Programs and Computations for a Class of Anti-aircraft Mission Planning Problems

159

there are b disjoint subsets of S such that sum of all

elements in each subset equals to C.

For any instance of the 3PP, an instance of the de-

cision problem of ALA is simultaneously created as

follows: The set of battalion B is initialized by b mis-

sile battalions; each battalion is allocated 3 missiles;

the set of ﬂeets includes 3b ﬂeets, f

, f

,... , f

(each

positive integer in the 3PP instance corresponds to a

ﬂeet in the instance of the decision problem of ALA);

each ﬂeet is formed by just one aircraft; each batta-

lion can launch at most one missile to each ﬂeet; the

expected number of killed aircraft is

(

∈ (

) )

when one missile is launched from any battalion to a

ﬂeet f

; for all k ∈ [1, 2, ...,3b], and the lower bound

on the defensive effectiveness is set to 1.

As a result, the 3PP instance has a partition into

b disjoint subsets, sum of elements in each subset

is equal to C, if and only if all battalions located at

the unique location, each battalion launches exactly 3

missiles to 3 ﬂeets and the defender’s effectiveness re-

aches to its ideal value of 1 or all ﬂeets are destroyed

completely. Thus 3PP reduces to the question whet-

her the decision problem of the ALA has a solution

or not. Thus, a pseudo polynomial reduction has been

given, showing that the ALA is NP-complete.

The NP-completeness of the AMP and the IAMP

are proved in the same way as above.

3 EXPERIMENTS

This section dedicates to report and analyze experi-

mental results on variety of instances for the ALA,

AMP and IAMP. For each problem, we generated

randomly 15 instances with the help of experienced

soldiers to make them real and reliable. The coef-

ﬁcients used to generate instances were carefully ex-

tracted from the historical data and technical guides of

missiles S-75 and S-125. The mathematical formula-

tions for the ALA, AMP and IAMP were implemen-

ted in C++ programming language, using IBM Ilog

Cplex Concert Technology, version 12.5. The stan-

dard cuts of Cplex were automatically added. Since

the number of constraints (3d) in the AMP and IAMP

programs is large and they belong to Miller-Tucker-

Zemlin class (Miller et al., 1960), these constraints

are treated as lazy constraints to reduce the computa-

tion time as follows. At the beginning of resolution,

these constraints are all relaxed. Each time, an inte-

ger feasible solution is counted at a node in the search

tree, this solution is checked for the satisﬁability of all

these constraints, all violated constraints are injected

more in the model. This cut-addition strategy always

Table 1: Experimental results for the ALA.

Instances Branch-and-Cut

No. b f Gap Eff. Time

1 5 5 0 0.246 0.004

2 7 8 0 0.462 0.005

3 6 5 0 0.742 0.012

4 6 8 0 0.546 0.025

5 7 5 0 0.673 0.004

6 10 10 0.02 0.767 7202.291

7 10 10 0 0.706 21.608

8 10 10 0 0.648 0.083

9 10 10 0.04 0.815 7201.130

10 10 10 0 0.787 2.292

11 10 10 0 0.780 142.796

12 10 10 0.02 0.699 7200.970

13 10 10 0 0.521 1.129

14 10 10 0 0.776 0.252

15 10 10 0 0.999 0.024

ensures the returning solution is correct since all con-

straints (3d) are strictly respected. All computations

were performed in multi-thread mode on a compu-

ter with an Intel Core i7-479 CPU, 3.6 GHz, and 4

GB RAM running Ubuntu version 16.4, 64 bits. A

time limit of 2 hours of CPU time was set for each

instance resolution. All computational results for the

ALA, AMP and IAMP are respectively indicated in

Table 1, 2 and Table 3. The columns in the tables

have the following meanings: No.: Instance number,

b: Number of battalions, m: Number of missiles in

each battalion, l: Number of potential locations, f :

Number of attacking aircraft ﬂeets, Gap: Gap (%) be-

tween the optimal solution of the integral relaxation

of an integer program and integer feasible solution of

that program found so far, Eff.: Defensive effective-

ness value, and Time: Overall CPU time in seconds.

Considering the ﬁrst ﬁve instances in Table 1

where the number of battalions and the number of

ﬂeets are small as the size of a regiment, the Cplex

solver gives optimal solutions very fast. In the instan-

ces (6,9,12), it takes the Cplex solver about 2 hours to

get its best solution, but not the optimal solution. On

the other aspect, it can be seen from instance 8 that the

optimal solution is easily achieved by the Cplex sol-

ver in lest than 1 second. It may be concluded from

the numerical results that the Cplex solver runs fast

and achieves optimal solutions in small size instances

but sometimes it takes several hours to obtain its best

solution.

In reality, the practical AMP usually allocates a

missile regiment of 4 to 6 missile battalions to pro-

tect an important target which is attacked by 5 to 8

attacking aircraft ﬂeets. Instances of those sizes can

be solved so fast by our formulation as report in the

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

160

Table 2: Experimental results for the AMP.

Instances Branch-and-Cut

No. b l f Gap Eff. Time

1 7 38 8 0 0.717 0.63

2 6 8 5 0 0.922 508.87

3 5 58 8 0 0.619 1.52

4 7 50 5 0 1.000 0.50

5 5 83 8 0 0.488 0.65

6 10 100 10 0 1.000 7.67

7 10 100 10 0 0.701 212.89

8 10 100 10 0 0.7919 5.11

9 10 100 10 0 0.7819 172.56

10 10 100 10 0 0.8143 9.66

11 10 100 10 0 0.633 49.81

12 10 100 10 0.02 0.913 7201.38

13 10 100 10 0.05 0.936 7211.39

14 10 100 10 0.07 0.91089 7217.53

15 10 100 10 0.01 0.7099 7201.81

ﬁrst ﬁve rows of Table 2, specially instances (1, 4,5)

of these sizes were solved in less than one second.

This result motivates us to increase the size of test in-

stances up to 10 battalions, 100 locations and 10 ﬂeets

to evaluate the tackling ability of the formulation. In

the time limit of 2 hours, the 11 easy instances (obtai-

ned optimal solutions by Cplex solver) among 15 in-

stances were completely solved to optimality, most of

them take less than 1 minutes; while the 4 hard instan-

ces (not obtained optimal solutions by Cplex solver)

were solved nearly to optimality since the gaps are

so small (0.01% − −0.07%). Although 10 last test

instances have same sizes in term of the number of

battalions, the number of ﬂeets and the number of lo-

cations, the computational difﬁculty is different. This

diversiﬁcation comes from the geographic of the po-

tential locations. In comparison to defensive effecti-

veness of easy instances, the hard ones have greater

effectiveness. Sets of available missile battalions in

IAMP instances were generated around 20 battalions

that are larger than the ones used in Table 2. Among

15 instances in Table 3, there are 9 easy instances

solved to optimality in less than 30 seconds, while

5 hard instances were not completely solved in the

time limit, and one instance (No. 15) returned to “Out

of memory” error during the resolution. Similar to

hard AMP instances, the hard IAMP instances gene-

rate very large search trees that may cause no feasi-

ble solution. It is essentially seen that the easy IAMP

instances correspond to reasonable effectiveness va-

lues, while the hard IAMP instances usually are as-

sociated with high effectiveness values. These expe-

rimental results were validated and recommended by

the experienced soldiers that this formulation should

be packaged for the purpose of training and integrated

into a C4I system.

Table 3: Experimental results for IAMP.

Instances Branch-and-Cut

No. b m l f Eff. Gap Time

1 21 12 56 11 0.72 0 18.6

2 21 12 41 11 0.81 0 5.6

3 22 12 42 12 0.97 0.83 7209.9

4 20 12 45 10 0.52 0 11.7

5 21 12 51 11 0.57 0 20.5

6 24 12 54 14 0.98 0.05 7213.7

6 23 12 48 13 0.46 0 9.8

8 23 12 58 13 0.91 0.12 7210.6

9 22 12 47 12 0.71 0 22.1

10 21 12 41 11 0.56 0 29.8

11 23 12 48 13 0.94 0.12 7225.7

12 20 12 55 10 0.84 0.09 7217.6

13 22 12 47 12 0.44 0 8.6

14 22 12 47 12 0.65 0 15.2

15 22 12 57 12 0.60 Out of memory

4 CONCLUSION

In this paper, we formulated three problems in the

class of defensive missile battalions mission planning

against aircraft attack model, that support defensive

decision makers not only decide where to locate their

missile battalions, but also point out that how many

missiles should be launched from each battalion to

each attacking aircraft ﬂeet. The mathematical for-

mulations are IPs, proved as NP-hard. These mathe-

matical programs were implemented and experimen-

ted on test instances generated basing on the help of

experienced veterans, in which parameters on proba-

bility of kill, maximum number of launches, as well

as minimum distance between two battalions, were

pre-processed for a particular set of defensive battali-

ons and aircraft attack. The numerical results provide

the incidence that the proposed formulations should

be widely applied in real-life combat ﬁeld. As future

works, we intend to formulate and tackle other vari-

ance of the defensive distribution models.

REFERENCES

Ahuja Ravindra, Kumar Arvind, J. K. and James, O. (2007).

Exact and heuristic algorithms for the weapon-target

assignment problem. Operations Research, 55(6).

Brian, J. (1994). An air mission planning algorithm for a

theater level combat model. Master thesis, Air force

Institute of Technology.

Brown, G., Carlyle, M., and Wood, K. (2008). Applying

defender-attacker optimization to terror risk asses-

sment and mitigation. Calhoun, the NPS Institutional

Archive.

Mathematical Programs and Computations for a Class of Anti-aircraft Mission Planning Problems

161

Crino, J. and Moore, J. (2004). Solving the theater distri-

bution vehicle rounting and scheduling problem using

group theoretic tabu search. Mathematical and Com-

puter Modelling, 39(6):599–616.

Garey, M. R. and Johnson, D. S. (1990). Computers

and Intractability; A Guide to the Theory of NP-

Completeness. W. H. Freeman & Co., New York, NY,

USA.

Jackson, J. (1989). A taxonomy of advanced linear pro-

gramming techniques and the theater attack model.

Master thesis, Air Force Institute of Technology.

Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). In-

teger programming formulation of traveling salesman

problems. J. ACM, 7(4):326–329.

Moore, F. W. (2002). A methodology for missile counter-

measures optimization under uncertainty. Evolutio-

nary Computation, 10(2):129–149.

Murphey, R. A. Target-Based Weapon Target Assignment

Problems, Nonlinear Assignment Problems: Algo-

rithms and Applications.

Robert, E. (2006). An adaptive tabu search heuristic for the

location rounting pickup and delivery problem with

time windows, a theater distribution application. Doc-

toral Thesis, Air force Institute of Technology.

Seichter, S. (2005). The fast theater model optimization

of air-to ground engagements as a defender-attacker

model. Master thesis, Naval Postgraduate School.

Shalikashvili, G. (1993). Joint tactics, techniques, and pro-

cedures for movement control. Chairman of the Joint

Chiefs of Staff,Joint Publication, Washington, 4-01.2.

Shalikashvili, G. (1996). Joint tactics, techniques, and pro-

cedures for movement control. Chairman of the Joint

Chiefs of Staff, Joint Publication, Washington, 4-01.3.

Studies, A. F. and Agency, A. (1992). Tac thunder analysis

manual. Arlington VA: CACI Products Company.

Tokgoz, A. and Bulkan, S. (2013). Weapon target assign-

ment with combinatorial optimization techniques. In-

ternational Journal of Advanced Research in Artiﬁcial

Intelligence, 2(7).

APPENDIX

4.1 Compute e(b, f ,t)

Suppose that a battalion b ∈ B plan to launch t mis-

siles to ﬂeet f ∈ F that has n( f ) aircrafts. We are

given coefﬁcient corresponding to each missile batta-

lion b ∈ B, c

= c

, where c

is technical coefﬁ-

cient, c

is control coefﬁcient and c

is combat com-

plex coefﬁcient. The probability of kill of each mis-

sile launched from battalion b to ﬂeet f is known as

p (p ∈ [0,1]). Based on defensive mode, we consider

following situations:

1. Disperse mode: Suppose that each time a batta-

lion decides to launch 2 missiles to an aircraft of

a ﬂeet. Since the probability of kill is p(b, f ) = p

for all b ∈ B, f ∈ F, expected number of killed ai-

rcraft is e(b, f ,t) = t(1 − (1 − p)

2. Focus mode: Suppose that battalion b launches t

times focusing on ﬂeet f , where t = n( f )t

+ t

then probability of kill on each aircraft in t

laun-

ches is 1 − (1 − p)

. Battalion b has t

< n( f ))

launches left, inferring probability of kill on one

aircraft in each launch is p(1 − p)

n( f )−1

. Then,

expected number of killed aircraft can be esti-

mated by eb, f ,t = n( f )(1 − (1 − p)

) + t

p(1 −

n( f )−1

3. Random mode: Let X

where i = 1,2,...,n( f ), be

random variables deﬁned as 1 if aircraft i is kil-

led and 0 otherwise. While probability of kill

on aircraft i in ﬂeet f is 1 − (1 −

n( f )

)

, expected

number of killed aircraft can be approximated as

e(b, f ,t) = E(

∑

n( f )

i=1

) = n( f )E(X

) = n( f )(1 −

(1 −

n( f )

)

4.2 Compute t(b,l, f )

Value t(b,l, f ) is maximum number of launches that

a battalion b located at location l can launch to ﬂeet

f . This number depends on following quantities. For

a ﬂeet f , we let v( f ), h( f ) and l( f ) be its velo-

city, height and length, respectively. In an attack,

ﬂeet brings different type of bomb that can be veri-

ﬁed as tb( f ) = 1 if ﬂeet f brings nuclear bomb and

tb( f ) = 0 if ﬂeet f brings regular bomb. For a batta-

lion b, we denote d

max

and r

by long range of missile

on battalion b and distance between that battalion and

the target, respectively. We suppose that the shortest

time between two consecutive launches, t

, as well as

obscured coefﬁcient, δ, are known. Furthermore, an-

gle of battalion location, α

, and angle of in-coming

ﬂeet, α

, are parameters. Function t(b,l, f ) can be

computed as follows:

1. Compute critical radius r

= 5000tb( f ) +

v( f )

2h( f )

− ∆ where 5000m is active radius of

nuclear bomb, g ≈ 9.8m/s

is gravity accelera-

tion, ∆ = 0.25h( f ) if v( f ) ≤ 300m/s, ∆ = 0.4h( f )

if v( f ) > 300m/s.

2. Compute shape time of ﬂeet t

f s

: t

f s

l( f )

v( f )

3. Compute launching time of battalion t

(a) Angle between battalion’s location and ﬂeet ϕ:

ϕ = |α

− α

(b) If (r

+ r

> d

max

and r

+ d

max

> r

and r

max

> r

) then

i. If ϕ > ϕ

∗

then t(b,l, f ) = 0 where ϕ∗ =

arccos(

−d

max

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

162

ii. If ϕ ≤ ϕ

∗

then t

x−r

v( f )

where x is root of

equation x

+ r

− d

max

= 2xr

cosϕ.

max

≥ r

)then t

y−r

where y is root

of equation y

+ r

− d

max

= 2yr

cosϕ.

(d) If (r

≥ d

max

+ r

) then t(b, l, f ) = 0.

(e) If (r

≥ d

max

+ r

) then

i. If ϕ > ϕ

∗

then t(b,l, f ) = 0 where ϕ∗ =

arcsin(

max

ii. If ϕ ≤ ϕ

∗

then t

max

−r

sin

4. Compute t(b,l, f ) = 1 +

δt

f s

Mathematical Programs and Computations for a Class of Anti-aircraft Mission Planning Problems

163