
Speeding up the Search of a Global Dynamic Equilibrium
from a Local Cooperative Decision
S
´
ebastien Maignan, Carole Bernon and Pierre Glize
IRIT, Universit
´
e de Toulouse, Toulouse, France
Keywords:
Multi-Agent System, Adaptation, Cooperation, Dynamic Equilibrium.
Abstract:
Systems composed of many interdependent active entities working on shared resources can be challenging to
regulate and multi-agent simulation is an efficient means for finding the suitable entities’ behaviors. On the
other hand, the search space for a stable solution of the system is usually forbidding and hinders any effort
to solve the problem using a top-down approach. Furthermore, the complexity of possible global functions
to optimize increases rapidly with the size of the system and can prove difficult to define and/or evaluate at
each system simulation step. The difficulty when designing bottom-up systems is to be able to identify all
their emergent properties and the parameters to modulate them. Here we propose a local cooperative decision
making process that helps to stabilize such systems. These local processes prove to be very efficient to quickly
find dynamic equilibrium solutions where the system continues to function and fulfills its global function.
Regulation emerges from simple local interactions.
1 INTRODUCTION
As opposed to a stable equilibrium, a dynamic equi-
librium is a balanced state which requires negative or
positive feedbacks to stay in its steady state.
In order to remain functional or to operate in an
efficient manner, complex dynamical or open sys-
tems often need to reach such a dynamic equilibrium.
Economy (Aruoba et al., 2006), finance (Shimomura,
1998), ecology (Tuljapurkar and Semura, 1977) or bi-
ology (Bernado and Blackledge, 2010) are a few ex-
amples of areas in which such systems may exist.
As such, this study focuses on how a dynamic
equilibrium may take place in cellular complex sys-
tems by modelling early stages of cell communi-
ties where interdependent cell species live together,
but without having developed a communication sys-
tem. Theoretically, a dynamic equilibrium should be
reached for every cell to continue to exist and share
resources. In principle, achieving such a state is pos-
sible if actions performed by the system’s cells are
specifically suited to give the feedbacks required.
A complex system is subject to unexpected behav-
iors due to bifurcations, non linearities, openness; and
consequently cannot be designed in a top-down ap-
proach. A bottom-up design, where the global func-
tion of the system emerges from the interactions of
its more basic components, becomes unavoidable and
makes knowledge of the suited actions impossible.
Finding a way to constrain the actions locally made
by the basic components for speeding up the conver-
gence of the global system toward a dynamic equilib-
rium becomes therefore necessary.
The aim of this paper is thus to study how reach-
ing this dynamic equilibrium can be sped up if local
cooperation is used by the basic components.
Numerous works on cooperation found their ori-
gin on the computer tournament in the 1980s, based
on Robert Axelrod’s “The Evolution of Cooperation”
(Axelrod, 1984). Usually the payoffs in game theory
are fixed, which cannot be the case in the general sit-
uations such as the ones presented in this paper. The
kind of cooperation we consider is seen as helping the
most critical component in the system (Georg
´
e et al.,
2011), it is not simple cooperation towards a common
goal (Hogg and Huberman, 1992) nor pure altruism;
it is rather seen as benevolence.
For this study, multi-agent based simulation is
used as it is known to be an efficient approach to
simulate complex systems and study their properties
(Moss, 2000). We consider a system where inter-
dependent cells of different types are indirectly ex-
changing resources via a common environment. Ex-
changes are made using basic actions: a cell is able
to gather resources from the environment, to inter-
nally transform some resources into others, and to
Maignan, S., Bernon, C. and Glize, P.
Speeding up the Search of a Global Dynamic Equilibrium from a Local Cooperative Decision.
DOI: 10.5220/0006540101430150
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 1, pages 143-150
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
143

release resources in the environment. The studied
system is simulated as a Multi-Agent System (MAS)
(Wooldridge, 2009) where cells are agents situated on
nodes of a grid that form their environment. These
cells are not aware of their neighbors’ actions, are
not able to directly communicate with them, and are
only able to act for gathering, producing or transform-
ing resources units. A cell-agent may live a certain
amount of time depending on the current resources it
possesses and should it die, its node is in charge of
finding a replacement. Once released by a cell-agent
at a particular node of the environment, a resource
may circulate and be gathered by another cell-agent
on its own node. The environment also produces re-
sources and regenerates the cells when they disap-
pear; and, in this sense, nodes are also considered as
agents because they take decisions for processing this
regeneration.
The aim is therefore to endow agents with purely
local behaviors based on cooperation in order to
study how the simulated system behaves globally and
whether these cooperative behaviors enable finding a
dynamic equilibrium in an efficient manner. In other
terms, we want to verify whether cooperation, as de-
fined here, is an effective behavior to build an agent-
based simulation in a bottom-up way considering that
agents, as in real life, have a very limited knowledge
of their surrounding and no knowledge at all of the
global state to reach.
The paper is structured as follows. The features of
the studied system as well as the cooperation used for
replacing component-agents and selecting their ac-
tions are presented in section 2. Section 3 presents
some results when cooperation is used in systems
with populations of 2 or 10 component species. Be-
fore concluding in section 5, section 4 studies the sta-
bility and robustness of the cooperative heuristics.
2 SIMULATED SYSTEM
As mentioned earlier, the studied system simulates
early stages of cell communities where interdepen-
dences exist between cell types but no communication
system exists yet to coordinate their actions. While
being a very simplified version of actual cell commu-
nities, this system is already complex enough to ob-
serve emergence of some interesting behaviors.
Cells are the interdependent components of the
system, they release into or gather, from the environ-
ment, molecules representing resources which they,
as a whole, require to survive. Reaching a dynamic
equilibrium in such a cellular system means that all
the cells find a way to survive by exchanging the right
resources in the right way without having any prior
knowledge about this. The system template is loosely
based on cell communities sustaining each other by
producing specific resources required by other cell
types and receiving vital resources from other mem-
bers of the community. The working model of each
cell is a very simplified version of actual cells and
only gathering, release and production functions have
been kept.
This section presents the general features of the
simulated system and describes the cooperative be-
haviors used by its agents in order to reach a dynamic
equilibrium in a faster way. The parameters actually
used for the simulation are given in section 3.
2.1 System
The simulated system has therefore two parts: cell
agents (later on, simply “cells”) and their environ-
ment. This environment is a two-dimensional tore
seen as a grid of node agents (later on, simply
“nodes”) on which cells are regularly placed.
A given number of resources (nR) are available in
the system. Each node of the environment contains
external resources eR
i
where i is the resource index.
Each cell contains internal resources iR
i
and a set of
actions. Three different types of actions enable a cell
to act on resources:
• Gathering: Transfers a given amount from the
node resource eR
i
to the cell resource iR
i
.
• Production: Transforms a given amount of lin-
ear combination of iR
i
s into another kind iR
j
i.e.
∑
i
a
i
.iR
i
→ iR
j
where
∑
a
i
= 1.
• Release: Transfers a given amount of cell resource
iR
i
to the node resource eR
i
.
Only one action can be performed by a cell dur-
ing each simulation cycle. Performing this action will
cost the cell a certain amount of one particular re-
source that can be viewed as its energy source. How-
ever, as in real life, a cell does not have any knowl-
edge that a particular resource is actually its energy
source and is therefore unable to optimize its behav-
ior towards energy maximization.
The longer a real cell exists the more errors it
will accumulate. These errors are simulated by giving
each cell a probability to disappear which increases
with its age. When a cell fails, it is immediately re-
placed on the node it occupied (see section 2.4).
Internal or external resources are divided into two
subsets: SetA = {R
i
, i ≤
nR
2
}, which contains abun-
dant resources supplied by the nodes, and SetB =
{R
i
, i >
nR
2
}, which contains resources only produced
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
144

by cells. Resources from SetA are replenished ev-
ery cycle either at each node and are always available
to cells. On the contrary, a constant amount of re-
sources from SetB is removed every cycle from ev-
ery node to simulate their transport away from the
system. Resources diffuse from high content nodes
to low content neighboring nodes
1
. To summarize,
there are three mechanisms to modify resource con-
tent at each nodes: passive diffusion, active gath-
ering/release from cells and outside world influence
(positive for SetA and negative for SetB).
The overall goal of the system is to reach a dy-
namic equilibrium and to provide a steady output
of resources from SetB. Robustness to resources
changes and/or component distribution is also an im-
portant criterion to consider.
As introduced before, cooperation is used to reg-
ulate the actions performed by the cell/node agents in
the system, and it is supposed that every agent knows
that its neighbors expect reciprocal cooperation. A
cooperative behavior is a balance between selfishness
and altruism and is implemented in two parts: (1) dur-
ing the action selection for each cell (see section 2.3),
and (2) during the creation of a new cell (see section
2.4).
2.2 Resources Criticality
The notion of criticality is used by a cooperative agent
to decide which agent is considered as having the
highest degree of dissatisfaction in its neighborhood
(No
¨
el and Zambonelli, 2015) in order to help it if pos-
sible.
Here, cells do not know how other cells perform
so their degree of dissatisfaction can only be related
to resources variations. Thus internal and external re-
sources criticalities reflect this information. In the
same way, nodes also require access to external re-
source criticality to operate the cooperative agent re-
placement process (see section 2.4).
Resource criticality is a measure of the current
available quantity of a resource combined with its
forecast availability. The current available quantity
of a resource could translate as “is it rare or plenti-
ful?”. Its forecast availability could translate as “is it
disappearing from the environment or not, and how
fast?”. So, an abundant resource replenished every
cycle will have a very low criticality whereas a very
rare resource consumed by all neighbor cells will have
a very high criticality. Whatever the actual numerical
1
The fact that cells are immobile does not reduce the
problem scope since resources may move and each agents
neighborhood changes over time.
implementation of the criticality evaluation, its fun-
damental characteristic is that it can be compared and
ranked.
Criticality is a local measure available only to a
single cell and its containing node.
2.3 Cooperative Action Selection
Process
Every cycle, each cell selects an action and performs
it.
The default algorithm, for comparison purposes,
consists in randomly choosing this action. The ac-
tion selection process proposed is based on coopera-
tion between cells to improve the status of resources
in critical situations.
Firstly, resources criticalities for all resources, in-
ternal and external, are calculated and ranked.
All actions that could be performed by the cell are
then put in a working set. For example, a gathering
action will only be added if the external resource this
action involves is available in the environment.
Starting from the most critical resource, actions
from the working set are sorted according to their pos-
itive impact on this resource i.e. the amount of re-
source it would add either internally or externally. If
several actions have the same impact, the one with the
least impact on other resources is selected. If no ac-
tion can improve the status of this critical resource,
the next most critical resource is evaluated. If no ac-
tion can improve the status of any critical resource, a
random action is selected.
The final action selected after this process is then
performed by the cell.
This process will select all the necessary actions to
gather, produce and release all the resources ensuring
the cell’s survival and that of its neighbourhood.
Several experiments (data are not shown here)
proved that a random selection of actions always
quickly leads to a global system failure. In conse-
quence, all the results presented thereafter use the co-
operative process for action selection.
2.4 Cooperative Agent Replacement
Process
Any given cell can fail for two reasons: it has become
too old or its energy resource has fallen to zero. A
failed cell disappears and needs to be replaced so that
each node of the system is occupied at all time. The
new cell has to be the daughter of an existing cell from
its neighbourhood.
All cells in a specific radius (small compared to
the system size) around the failed cell position are
Speeding up the Search of a Global Dynamic Equilibrium from a Local Cooperative Decision
145

candidates to replace it, but only those with enough
energy resource to last a predefined number of cycles
are considered as potential candidates.
The default algorithm, applied by a node to re-
place the cell which failed at its location, consists of
randomly selecting one of the potential candidates.
The agent replacement process proposed uses coop-
eration to make the node select the candidate that will
help the most critical external resource in its direct
neighborhood.
Only external resources are used during this pro-
cess since the nodes and cells do not have any knowl-
edge of the resource content in the neighboring cells.
A node has access to resource criticalities (as defined
in section 2.2) in the neighboring nodes. This is the
way to make cooperation possible.
First, for each resource eR
i
, its criticalities on each
neighboring nodes are calculated and compared, and
the worst one becomes the criticality for eR
i
.
Then, starting from the most critical eR
i
, candi-
date cells are ranked according to the amount of iR
i
they released in the recent past. If more than one can-
didate released iR
i
, they are ranked by the amount
released and the top half remain candidates for the
next comparison round using the next most critical
resource. This is repeated until only one candidate
remains or all critical resources have been tested. The
right candidate is then duplicated (i.e. with its current
sets of resources and actions) to the failed cell posi-
tion.
If there are no candidates, the node stays empty
and the process starts over during the next cycle. This
can potentially lead to full system halt if mass cell
failure occurs.
3 SIMULATION RESULTS
In order to evaluate the efficiency of local cooperation
– as described in the previous section – to regulate a
running system, several simulations were performed
and are described in this section. After describing
how the simulation is initialized, results are given for
simulations where 2 or 10 interdependent cell types
are considered.
3.1 System Initialization
“Abundant” resources from SetA are distributed ran-
domly on the nodes of the system and within the
cells. “Rare” resources from SetB are distributed ran-
domly within the cells to provide them with enough
energy resources to survive for at least a given num-
ber (nMinS) of cycles.
Initially, nCa cell types are distributed on the sys-
tem nodes; these types are classes of cells that differ
by their energy resources and their production action.
For each cell type j ∈ {1, ..., nCa}, one resource
from SetB is chosen as the energy source for this type
(which is not known by the cells). Furthermore, this
cell type is given a set of actions: shared common
actions to gather or release any type of resource, along
with one specific production action allowing this cell
type to produce one unit of its energy resource using
a
j1
units of one resource from SetA and a
j2
units of
one resource from SetB:
a
j1
.iR
j
+ a
j2
.iR
( j+1+
nR
2
) mod nCa
→ iR
( j+
nR
2
)
with
a
j1
+ a
j2
= 1
At the start of the simulation, each cell instance of
a given type j has a unique random set of (a
j1
, a
j2
).
To illustrate this a 2-cell type and 4-resource sys-
tem would give the following cyclic interdependence:
cell type 1: a
11
.iR
1
+ a
12
.iR
4
→ iR
3
cell type 2: a
21
.iR
2
+ a
22
.iR
3
→ iR
4
In other words, each cell is able to produce its en-
ergy resource but needs resources only produced by
another cell type to do so. Without any knowledge
about its energy resource, and although it is vital to
its survival, a cell must somehow manage to release
some of it so that other cell types can survive.
The proportion and location of cells using a spe-
cific energy resource can be set randomly or following
a predefined pattern. In all the following examples,
cells of a given type are spatially grouped together at
the beginning of the simulation and the proportions
for each cell type are the same.
For the results given hereinafter, the features of
the simulated system are as follows: nCa is set to 2 or
10, nR is set to 20 i.e. SetA = {R
0
...R
9
} and SetB =
{R
10
...R
19
} and nMinS is arbitrarily set to 80.
The size of the simulated system is 60 × 60 with
3600
nCa
of the cells for each type. The speed at which
resources can move from one node to its neighbors
(diffusion factor) is set to 0.01 unit/cycle. The radius
for candidate selection is set to 4 nodes in the coop-
erative agent replacement process: this is larger than
the direct neighborhood of a node using a radius of 1
(involving 8 nodes) but lower enough for not consid-
ering the whole grid as its neighborhood.
A rough estimation of the parameter space for the
system is as follows: every cycle, each of the 3600
cells may perform 1 out of 40 actions that are common
to all cell types, and 1 action, specific to its type. Con-
sidering that cell type populations are roughly equiv-
alent, there are (40 + nCa)
3600
possible choices every
cycle. As observed in several simulations, the system
can be balanced within 1000 cycles.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
146
The parameter space for this period is therefore at
least (40+nCa)
3600
1000
. Random walk in such a huge
space is very unlikely to succeed. Actually, starting
from an identical initial state, in all the experiments
performed none of the system configurations of the
random simulation ever matched one of the coopera-
tive simulation.
We are fully aware that comparing the results ob-
tained by the system, when cooperation is used to
constrain the actions performed locally by the agents,
with other works in the same vein is compelling.
However, to the best of our knowledge, we did not
find simulations of similar systems to perform such a
comparison. Furthermore, since a global cost func-
tion cannot be considered to use machine learning ap-
proaches such as neural networks (Colak, 2006) or
genetic algorithms (Gen and Cheng, 2000), we chose
to randomly explore the search space to show the dif-
ficulty to find solutions and their sparsity.
3.2 Two Interdependent Cell Types
For this scenario, there are nCa = 2 cell types.
The cooperative system quickly reaches a dy-
namic equilibrium (figure 1) whereas random selec-
tion of new cells cannot maintain a dynamic equilib-
rium after the stabilization period (figure 2).
In figure 1, resources R
12
to R
19
quickly disappear
from the system since none of the two cell types can
produce or use them. These resources are then always
the most critical ones but no action can improve their
state. This is not a problem for the system as a whole
as these resources do not impact the viability of the
cells.
It is noteworthy to mention that the spatial distri-
bution of type 1 and type 2 cells is not regular and
does not display any kind of (visually) distinctive pat-
tern (result not shown here).
Interestingly after a few thousand cycles, only one
instance of type 1 and one instance of type 2 cells are
left from the initial random sets and occupy all the
simulation space. It can be noted that the surviving
instances selected by the cooperation process always
have a
j1
above 0.8 and a
j2
below 0.2. This can be
explained by the fact that cells using more scarce re-
sources from SetB will have a shorter lifespan and be
replaced more often. This indicates that the system
maximizes the use of abundant resources (R
1
to R
9
)
and minimizes the consumption of rare resources (R
10
and R
11
).
3.3 Ten Interdependent Cell Types
For this scenario, there are nCa = 10 cell types.
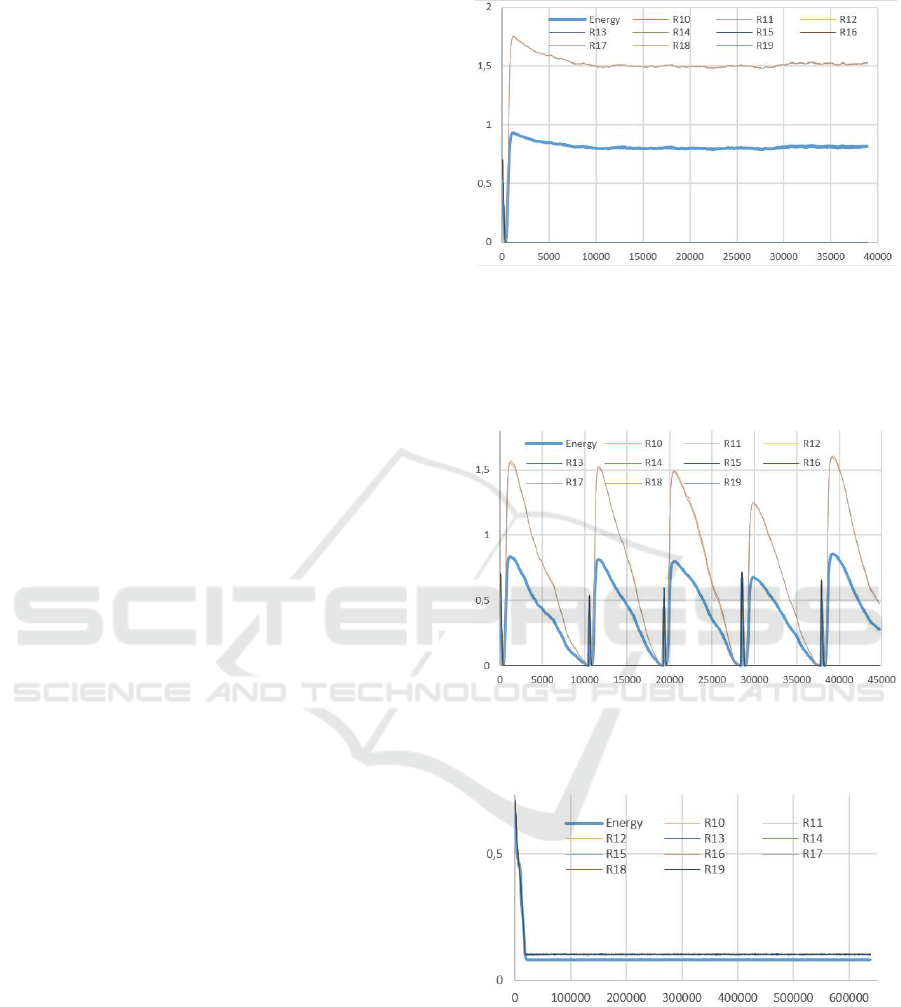
Figure 1: Result of dynamic equilibrium between 2 interde-
pendent cell types using cooperation. The x axis represents
the number of simulation cycles. The mean quantity of each
resource from SetB(R
10
−R
19
) in the nodes (top curve) and
the mean energy of the cells (bottom thicker curve) are rep-
resented on the y axis. R
10
and R
11
are nearly superimposed
and R
12
−R
19
are equal to zero very early in the simulation.
Figure 2: Same setup as Fig. 1 but using random selection
for failed cells. Each spike denotes a system restart when
at least one component type disappeared compromising the
future of the whole system.
Figure 3: Result of dynamic equilibrium between 10 in-
terdependent cell types using cooperation. Resources are
nearly surimposed and show very small fluctuations (bot-
tom curve).
As shown in figure 3, after around twenty thou-
sand cycles the system reaches a dynamic equilibrium
using the cooperation selection process (contrary to
figure 4 where the random one is used). All resources
from SetB are used by one cell type or another. This
explains why none of the resource quantities falls to
Speeding up the Search of a Global Dynamic Equilibrium from a Local Cooperative Decision
147

Figure 4: Same setup as figure 3 but using random selection
for failed cells. The number of cycles before failure may
vary but the system is always unstable and never reaches
a dynamic equilibrium state (noted also in all the different
random simulations launched).
Figure 5: Same setup as figure 3 but using a slower resource
diffusion factor (10×). This impacts the resource values and
the cell type distribution. The fluctuations are cyclic instead
of random.
zero.
Again, when the system becomes stable, it is filled
with instances for which a
j1
is above 0.8 and a
j2
is
below 0.2.
Using the same system setup but with a much
slower diffusion factor (10 times slower) the sys-
tem behaves slightly differently (see figures 5 and 6).
Fluctuations of a resource R
j
become cyclic and cor-
related with those of R
j−1
and R
j+1
. This correlation
is the result of resource coupling in the production ac-
tions of the interdependent cell types. The diffusion
factor impact can be explained by the fact that cells
will deplete the medium of resources they need be-
fore they can be replenished by the passive diffusion
mechanism. Cells will start to die but resource quan-
tities will allow a small population to subsist. Even-
tually diffusion will replenish the depleted resources
and cells will thrive again.
In parallel, cell type populations also present
cyclic and correlated behaviors (these data are not
shown). Although in most simulations the system is
dynamically stable, it happened on some occasions
that the fluctuation amplitudes increased with time
and led to system failure.
Figure 6: Same setup as figure 5 showing the resource oscil-
lations and interdependence. Cell type population displays
a similar oscillating behavior.
Figure 7: When a stabilized system is switched to random
selection of new cells, it oscillates for a while before even-
tually failing after around 15000 cycles (when one cell type
vanishes from the system). For clarity, cycles 0-50000 were
removed.
4 COOPERATION AND
DYNAMIC EQUILIBRIUM
Through three experiments derived from the simula-
tion used in section 3.3, this section studies how ro-
bust is cooperation when a certain percentage of cells
are replaced using the basic random algorithm.
4.1 Solution Stability without
Cooperative Selection
Using the scenario and solution found in section 3.3
with 10 cell types, the system is switched from a co-
operative selection of new cells to a random one.
At the time of the switch, {(a
j1
, a
j2
)} for the pro-
duction actions of all cells has been optimized by the
cooperation for the best possible performance. The
consequence is that the system is able to survive for
much longer than a new system using the much wider
selection of {(a
j1
, a
j2
)} available at the simulation
start. Nevertheless, as illustrated in figure 7, after
several thousand cycles the equilibrium between cell
types is not maintained and the system fails.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
148

4.2 Robustness to Noise
This scenario studies the robustness to noise of the
cooperative algorithm described in section 3.3. Each
time a cell needs to be replaced there is a given prob-
ability to use the random selection or the cooperative
process.
An insight of the effect of cooperation is given in
figure 8. The cooperative process is efficient in sta-
bilizing the system even when new cells are selected
randomly 99% of the time. Nevertheless, at high ran-
dom percentage the system is more sensitive to ini-
tial conditions and cell distribution. Statistical stud-
ies need to be performed in order to evaluate the ex-
act percentage of cooperative replacement process re-
quired to hold the system steady.
4.3 Saving a Failing System
In this experiment, a system, as described in section
3.3, is simulated using random selection of cells until
failure. Every thousand cycles the system is saved.
Failure occurs after around 23 thousand cycles. Then
every saved instance of the system is continued using
cooperative selection of cells and the system survival
time is measured. This procedure is not equivalent
to restarting the system with different random seeds
since during system restart each cell receives enough
energy resource to survive a given number of cycles.
As shown in figure 9 and 10, the system can be
saved if cell selection is switched to cooperation early
enough (around 15K cycles). After this time, it is not
possible to rebalance the system. One reason is that
some cell type populations are so low that they can-
not be increased before random failure from old age
Figure 8: These graphs represent the mean cells energy
during the simulation when replacement cells are selected
increasingly randomly. Up to 99% of random selection
the system is still stable. Nevertheless, some of the ran-
dom starting system configurations cannot be balanced as
demonstrated by the restart pikes observed in most of the
graphs.
or low energy remove them from the system. Another
reason is that the number of instances with interest-
ing {(a
j1
, a
j2
)} for the system balancing might not be
present anymore.
4.4 Scalability
The largest system tested so far consists of a 300×300
grid with 30 cellular types and 60 different resources.
After 5K cycles, the system reaches a dynamic equi-
librium and is still stable after over 62K cycles. Nev-
ertheless due to its size this experiment has not been
repeated extensively and is only mentioned here as an
indicator of the scalability for this approach.
5 DISCUSSION
This article aimed at showing that a specific kind of
cooperation enables a global dynamic equilibrium to
be found in a faster way than randomly and has used
a multi-agent system to simulate a complex system of
interdependent components where the dynamic equi-
librium means survival of the components.
Figure 9: The system was simulated for 15K cycles us-
ing random selection then switched to cooperative selection.
The system is stabilized and reaches dynamic equilibrium.
Figure 10: Close up on the transition phase from figure 9
The system oscillates for around 20K cycles before cell type
populations and resources are balanced.
Speeding up the Search of a Global Dynamic Equilibrium from a Local Cooperative Decision
149

Optimizing localized production and consump-
tion of various resources globally can prove to be a
very challenging endeavor. The formal global func-
tion to minimize is not straightforward to derive from
the system description nor to evaluate at each cycle.
Therefore it becomes necessary to endow components
with a local attitude which enables emergence of the
right global behavior. The local actions considered
here always tend to help the most critical entity in the
local environment of the component, as such they are
said to be cooperative.
A cellular system in which resources are produced
or consumed by cells was chosen to perform experi-
ments with a growing number of cell types, and re-
lated results were presented.
As expected from its huge size, a random explo-
ration of the search space is unsuccessful even when
repeatedly tried with different starting systems (these
data are not shown). On the other hand, local cooper-
ation allows components/cells to regulate efficiently
the resource management although the global goal of
the system is locally unknown and the cell knowledge
about its neighborhood is quite restricted.
Furthermore, the processing is totally distributed
within the nodes and cells. Their interactions depend
only on a very limited neighborhood: the ones to se-
lect a new cell to duplicate. This makes the simula-
tion very simple to parallelize and reduces computa-
tion time. Also the code of the nodes and cells which
facilitates the progression in the search space is ex-
tremely simple. This stems from the fact that the local
decision based on cooperation replaces the complex-
ity of the global problem.
The result of the resolution process is totally emer-
gent in the sense that no part of the code is guided by
an evaluation of the overall quality of the solution in
progress (which is almost impossible to estimate).
The more resources to regulate the more challeng-
ing the regulation is. In this paper we have demon-
strated that local cooperative processes to select cell
actions to perform and to replace failed components
are able to regulate a system with 10 interdependent
cell types working on 20 resources.
Two interesting observations have been made dur-
ing these simulations. First, the factors in the pro-
duction actions {(a
j1
, a
j2
)} always tend to be large
for abundant resources from SetA and small for scarce
resources from SetB. This is intuitively a good thing
to do when you optimize such a system. Neverthe-
less, this is not coded in the cooperative processes but
emerges from them.
Secondly, the mean value of the resources quan-
tities in the system tends toward a value that is not a
parameter in the system simulation: around 0.8 for 2
cell types, and 0.1 for 10 cell types. These values also
emerge from the cooperative processes and no single
parameter in the simulation seemed to be able to alter
them significantly (these data are not shown).
As demonstrated in section 4.1, stabilization of
the system with the cooperative processes must be
continuous since it eventually fails sooner or later if
switched to random selection. Nevertheless, as shown
in section 4.2, only a very small amount of coopera-
tive selection is necessary to continue to stabilize the
system.
REFERENCES
Aruoba, S. B., Fernandez-Villaverde, J., and Rubio-
Ramirez, J. F. (2006). Comparing solution methods
for dynamic equilibrium economies. Journal of Eco-
nomic dynamics and Control, 30(12):2477–2508.
Axelrod, R. (1984). The Evolution of Cooperation. Basic
books.
Bernado, P. and Blackledge, M. (2010). Proteins in dynamic
equilibrium. Nature, 468(7327):1046–1047.
Colak, S. (2006). Neural Networks Based Metaheuris-
tics for Solving Optimization Problems. University of
Florida.
Gen, M. and Cheng, R. (2000). Genetic algorithms and
engineering optimization, volume 7. John Wiley &
Sons.
Georg
´
e, J.-P., Gleizes, M.-P., and Camps, V. (2011). Co-
operation. In Di Marzo Serugendo, G., Gleizes, M.-
P., and Karageorgos, A., editors, Self-organising Soft-
ware: From Natural to Artificial Adaptation, pages
193–226. Springer.
Hogg, T. and Huberman, B. A. (1992). Better than the best:
The power of cooperation. SFI, pages 163–184.
Moss, S. (2000). Editorial introduction: Messy systems-
the target for multi agent based simulation. In Multi-
Agent-Based Simulation, pages 1–14. Springer.
No
¨
el, V. and Zambonelli, F. (2015). Methodological guide-
lines for engineering self-organization and emergence.
In Software Engineering for Collective Autonomic
Systems, pages 355–378. Springer.
Shimomura, K. (1998). A dynamic equilibrium model of
durable goods monopoly. Journal of Economic Be-
havior & Organization, 33(3-4):507–520.
Tuljapurkar, S. and Semura, J. (1977). Dynamic equilib-
rium under periodic perturbations in simple ecosystem
models. Journal of Theoretical Biology, 66(2):327–
343.
Wooldridge, M. (2009). An Introduction to Multiagent Sys-
tems. John Wiley & Sons.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
150
