
A Deep Convolutional Neural Network for Location Recognition and
Geometry based Information
Francesco Bidoia
1
, Matthia Sabatelli
1,2
Amirhossein Shantia
1
, Marco A. Wiering
1
and Lambert Schomaker
1
1
Institute of Artificial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands
2
Montefiore Institute, Department of Electrical Engineering and Computer Science, Universit
´
e de Li
`
ege, Belgium
Keywords:
Deep Convolutional Neural Network, Image Recognition, Geometry Invariance, Autonomous Navigation
Systems.
Abstract:
In this paper we propose a new approach to Deep Neural Networks (DNNs) based on the particular needs of
navigation tasks. To investigate these needs we created a labeled image dataset of a test environment and we
compare classical computer vision approaches with the state of the art in image classification. Based on these
results we have developed a new DNN architecture that outperforms previous architectures in recognizing
locations, relying on the geometrical features of the images. In particular we show the negative effects of
scale, rotation, and position invariance properties of the current state of the art DNNs on the task. We finally
show the results of our proposed architecture that preserves the geometrical properties. Our experiments show
that our method outperforms the state of the art image classification networks in recognizing locations.
1 INTRODUCTION
Autonomous Navigation Systems (ANS) are becom-
ing more and more relevant nowadays. For a long
time these systems have been used in the production
industries, but now they are expanding to new fields.
Just by considering the imminent release of the self
driving cars, it is clear that these systems will be at
the center of the next technological revolution.
Other than these applications, ANS are find-
ing applications in home robotics, and even in the
health care department: autonomous vacuum clean-
ers, robotic nurses, autonomous delivery robots etc.
(Floreano and Wood, 2015; Everett and Gage, 1999;
Levinson et al., 2011). In order to expand the use
of ANS for domestic purposes it is crucial to find a
cheap and yet reliable system. Classic ANS rely on
a multitude of sensor technologies, based on differ-
ent physical principles: from lasers to sonars (Guiv-
ant et al., 2000; Elfes, 1987), to compasses and GPS
(Sukkarieh et al., 1999). In this paper we consider an
indoor and low cost sensor-based system. The best
choice is a visual-based navigation system, because
it can perform its task by only relying on camera and
odometry information of the robot, making the system
cheap to build. In particular the localization is man-
aged by a subsystem that relies on visual information
of the surroundings, while navigation and mapping
are achieved with a combination of odometry and vi-
sual information.
At the core of navigation itself, geometrical prop-
erties of the environment are fundamental: to navigate
can be considered as the ability to understand and per-
ceive the environment, and be able to maneuver an au-
tonomous vehicle or robot in a safe and efficient man-
ner. For this task, the effective use of images obtained
with cameras is very challenging (Bonin-Font et al.,
2008). Even if at the moment there are already many
well performing artificial neural networks (ANNs) for
image classification, they all lack the ability to use
and preserve the geometrical properties of the pro-
cessed information. Most of the tasks nowadays focus
on the identification or classification of objects in pic-
tures or videos, or understanding if the environment
belongs to a city landscape or to a countryside (LeCun
et al., 2015). For such tasks, the geometrical informa-
tion is irrelevant. As an example, if the task consists
of distinguishing between a city landscape or a coun-
tryside one, current ANNs focus more on finding the
presence of a skyscraper or a mountain, without mak-
ing any use of the position of it in the picture. The
same principle applies to the process of identifying if
the picture contains a dog or a table.
This completely changes in navigation tasks. In
Bidoia, F., Sabatelli, M., Shantia, A., Wiering, M. and Schomaker, L.
A Deep Convolutional Neural Network for Location Recognition and Geometry based Information.
DOI: 10.5220/0006542200270036
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 27-36
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
27

this field, the position in the picture of a specific ob-
ject is as important as finding the object itself. If a
system needs to localize itself based on visual infor-
mation, the presence of a mountain on the left side
of a picture has a different meaning than finding the
same mountain on the right side. The same applies
when looking at the back of a building or at the front.
Or, in case of autonomous driving cars, if another car
is in the front or on the side. Given these considera-
tions, the importance of geometrical information for
navigation tasks is highly relevant.
Contributions. In this paper we propose a novel
Deep Neural Network (DNN) architecture that relies
on the geometrical properties of the input. This per-
fectly copes with the needs of navigation tasks, that
heavily rely on geometrical features. Furthermore we
created two novel datasets, one for recognizing scenes
and one for recognizing locations. Finally, we com-
pared different computer vision methods to the new
architecture on these datasets.
Structure. This paper is structured as follows: in
Section 2 we describe the different image recognition
fields, addressing the two main ones we will focus
on. In Section 3 we present and describe the differ-
ent image recognition algorithms and introduce our
novel deep convolutional neural network architecture.
In Section 4 we present the results obtained, and fi-
nally in Section 5 we discuss the results obtained and
conclude with several directions for future work.
2 IMAGE RECOGNITION
PROBLEMS
Computer vision is the field that aims to extrapolate
information or knowledge from raw pixel images. We
can divide this field in different sub-fields by distin-
guishing them by their goals or application tasks: im-
age classification, object tracking, scene recognition
etc.
In this paper we focus on two very similar sub-
fields, namely: scene recognition and location recog-
nition. While they are very similar in the data they
use, they differ for their tasks. Scene recognition fo-
cuses on distinguishing and classifying different en-
vironments such as kitchens, bedrooms, parks etc. To
distinguish and classify these scenes the approach re-
lies on finding different and unique features per class.
Once the unique features of the class are found, it is
possible to distinguish the different scenes or images.
The location recognition field has a different aim.
Instead of dividing the different scenes in classes,
specific points of view inside the scenes are distin-
guished. As an example, for scene recognition we
have a class kitchen, while in location recognition we
have multiple classes, all part of the kitchen, repre-
senting different points of view, or locations. Relying
on only finding unique features is not enough to dis-
tinguish these classes. In fact, it is possible that two
classes share the same unique features, but in differ-
ent positions. As an example we can consider an en-
trance of a building. One class can be the left side
of it, having the door on the right side of the point of
view, while another class is on the other side, having
the door on the left side. Assuming that the build-
ing is symmetrical, it is not possible to distinguish
these classes just by looking at the features them-
selves. Something else is needed: geometrical fea-
tures. For this task, the position of the features is as
important as the features themselves.
In navigation, especially for the localization task,
we need to use the location recognition approach; as
geometrical information is at the core of navigation.
In order to investigate the effectiveness of different
methods in this task, we created two datasets, each of
them focusing on the main characteristic of the scene
and location recognition tasks.
2.1 Dataset for Scene Recognition
The dataset is created with the main goal of evaluat-
ing different scene recognition algorithms that can be
used as part of a navigation system. The approach that
we use is based on lazy supervised learning. We di-
vide the generation of labels for the test environment,
and the actual training of the proposed methods into
two subtasks. In order to generate the labels for the
dataset, we use Visual Markers (VMs), that can be la-
beled automatically. Figure 1 shows an example of a
VM used. These are printed and applied in particular
areas of the test environment. Later videos of the en-
vironment are recorded, with the VMs in it. We then
analyze every single frame of the video and classify
each frame based on the VM present in it. The whole
procedure has been done in a semi-autonomous way,
thanks to a specific algorithm that detects the VMs
and their Id number, very similar to a QR code detec-
tor. After the majority of the frames and pictures have
been classified correctly, we manually remove any
possible false positives derived from the VM identi-
fier algorithm. The final result is a dataset contain-
ing all the frames of the video with a VM in it, di-
vided by the different Ids of these. The dataset results
in 8144 pictures that are divided in 10 classes where
each class represents a different VM.
In this way we are able to create a labeled dataset
from virtually any environment in a fast and efficient
way.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
28

Figure 1: Visual Marker.
Figure 2: Dataset Scene Recognition Picture Example.
The final step consists in using data augmentation
techniques, such as HSV light enchanting, as used by
(Dosovitskiy et al., 2014), to further increase the size
of the dataset up to 32,564 samples. For all the exper-
iments we use 80% of the dataset as training set, with
10% each as validation and testing sets. An example
image of this dataset can be seen in Figure 2.
2.2 Dataset for Location Recognition
After the considerations presented in Section 1, we
decided to create this dataset with explicit geometri-
cal variance properties. The dataset adds a new class
with all the images of our scene dataset that have been
flipped. We use half of them as training, and the other
half as testing. We randomize the order of the pic-
tures to prevent the presence of only particular flipped
classes in the training set while the other are in the
testing set. In this case we only use the non enhanced
images. This has been done to avoid too many similar
frames.
More precisely, the training set has all the original
images, divided in their respective classes, and a new
class is made, with a copy of the flipped images. We
note that the test set has no original images, but only
flipped ones. Half of these are in the training set, and
the other half form the whole test set. With this ex-
treme we can be sure to investigate how the different
methods can use necessary geometrical information.
This new dataset, with 11 classes, takes inspira-
tion from the one-vs-all approach similar to what has
been proposed in (Rifkin and Klautau, 2004). In fact,
this new class should be seen by the ANN as a noisy,
unique class. In order to do so, the network must find
a way to distinguish this class from all the others: this
is only possible if the specific geometrical features are
considered.
An example of how we flipped the pictures can be
seen by comparing Figure 2 and Figure 3.
Figure 3: Flipped Image Example.
3 METHODS
In this section we describe the different algorithms
that have been used for the experiments. Furthermore
we present a novel Deep Neural Network (DNN) ar-
chitecture that has been specifically designed for loca-
tion recognition in navigation tasks. We also present
the main considerations for developing our new archi-
tecture.
It is important to mention that all the experiments,
datasets and ANN architectures that are proposed are
contextualized with the creation of an optimal naviga-
tion system, based on visual information.
3.1 Histogram of SIFT Features
The first approach that we evaluate is the Bag Of vi-
sual Words (BOW) based on the Scale Invariant Fea-
ture Transform. The Scale Invariant Feature Trans-
form, or SIFT (Lowe, 2004), has been used exten-
sively in the computer vision field. The combination
of the SIFT key points descriptor algorithm, together
with the Bag Of visual Word (BOW) (Yang et al.,
2007), has performed very well in different scene
recognition tasks. This was the state of the art method
before the advent of Convolution Neural Networks.
The SIFT algorithm provides the detection of key
points and their relative descriptors. However, since
A Deep Convolutional Neural Network for Location Recognition and Geometry based Information
29

our dataset is generated from actual real world scenes,
it contains pictures with very little information. Ex-
amples of this information lack are white walls that
are not very informative in general, since they have
very few unique features.
As a consequence of this lack of information we
noticed that the SIFT detector only identifies strong
key points on the VMs that are actually present in
the picture or frame. This results in a poor proper
generalization from the BOW representation of the
scenes and we therefore decided to not use the SIFT
detection algorithm. Instead, we use a dense grid of
key points over the pictures, and only rely on the key
points descriptor algorithm. We take a key point ev-
ery 8 pixels, in both dimensions, and generate a total
amount of 5440 key points (160 × 34). For each key
point we consider a 16 × 16 pixel cell around it, and
divide it into four 4×4 cells. We then compute orien-
tations and magnitudes and order them in a histogram,
using 8 oriented bins. This generates, for every key
point, a 128 (4 · 4 · 8) features long vector. Figure 4
shows this approach.
Figure 4: SIFT Key Point Descriptors. Image taken from
(Lowe, 2004).
Since the neighbor cell shape is 16 × 16, and we
take a key point every 8 pixels, we have an overlap
for each descriptor. This overlap consists of 50% of
the size of a key point. This pipeline was also used in
(Marszałek et al., 2007).
Once we obtain 5440 × 128 features per picture,
we use the BOW clustering algorithm to reduce the
total number of features and create a visual codebook.
We train the BOW algorithm with a fixed number of
cluster points, and use them to generate a histogram
of visual word occurrences. The length of this vector
is equal to the number of cluster points. The final step
consists in using this vector as input for a neural net-
work (NN) used for the final classification task. We
show the full pipeline of the BOW approach in Figure
5.
The NN architecture that we use is the following:
• Number of inputs: as many as the BOW cluster
points.
• Number of layers: input layer, one or two fully
connected hidden layers, output layer.
Figure 5: BOW pipeline.
• Activation function: the hidden layers use the
Leaky Rectified Linear Unit (LReLU). The output
layer uses the Softmax activation function.
• Number of outputs: as many as the VMs.
3.2 Convolutional Neural Networks
Convolutional Neural Networks (CNNs) are one of
the latest and most successful neural network archi-
tectures. This type of architecture started to become
extremely popular in 2012 (Krizhevsky et al., 2012),
and started to outperform all the other image recog-
nition methods, giving them a strong focus from the
scientific community. In particular CNNs perform re-
ally well with large datasets containing high resolu-
tion images. For these reasons they find a vast utiliza-
tion in the computer vision field.
Nowadays there exist many different types of
CNN architectures, that usually share the combina-
tion of Convolution Layer - Pooling Layer; making
this last type of layers vastly used. Pooling layers
were designed to reduce the size of the input, while
maintaining the key features in it. By applying a
pooling operation on the input, it can reduce the in-
put by a factor of 2, 3 or more while maintaining the
most prominent information. This is done by apply-
ing computational inexpensive operations like com-
puting the average or max. With these functions the
CNN can well represent the input information, and
drastically reduce its dimensionality. However, the
disadvantage is that precise geometrical information
is lost in this process. Performing a max operation
over a 3 × 3 grid, will hold on the most relevant fea-
tures in it, at the expense of the position of the fea-
tures. The deeper in the architecture this operation is
performed, the more geometrical precision is lost.
3.3 Inception Neural Network
The Inception Neural Network (INN) (Szegedy et al.,
2015) is a very promising novel CNN architecture.
The current state of the art in image classification is
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
30

achieved with the Inception V3 (Szegedy et al., 2016),
which is a tuned version of the original INN.
Figure 6: Inception Module. Image taken from (Szegedy
et al., 2015)
3.3.1 Inception Module
In the Inception Module, four different operations are
performed: a convolution with 5 × 5, 3 × 3 and 1 × 1
filters; and an average pooling operation. Also both
convolution operations are preceded by a 1 ×1 convo-
lution operation, in order to increase the depth of the
Inception Module. This architecture is represented in
Figure 6.
3.3.2 Inception V3
The Inception V3 (INN V3) architecture is a modi-
fied version of the INN architecture. The main goal
of this architecture is to optimize as much as possible
deep neural network architectures. In fact the authors
achieved to create a deeper and wider structure, com-
pared to the original Inception module, without dras-
tically increasing the total number of weights. This
work takes inspiration from the Hebbian theory (Se-
jnowski and Tesauro, 1989), and follows the method
of (Arora et al., 2014). The key is to consider how
an optimal local sparse structure of a convolutional
neural network can be approximated and covered by
readily available dense components.
Figures 6 and 7 represent the original Inception
Module, and the adapted Inception V3 Module. It
can be seen that instead of the 5 × 5 convolution, two
consecutive 3 × 3 convolutions are used. This imme-
diately reduces the computational cost of the opera-
tions, given the smaller amount of weights to calcu-
late. In fact, a 5 × 5 convolution operation is com-
putationally more expensive than a 3 × 3 convolution
filter by a factor of 25/9 = 2.78. And while the 5 × 5
convolution filter can detect dependencies of signals
in further away units, if the same number of inputs is
Figure 7: Inception V3 Module. Image taken from
(Szegedy et al., 2016).
used for the first 3 × 3 convolution, the second 3 × 3
convolution will reduce to 1 output maintaining intact
the 5 × 5 input/output ratio as shown in Figure 8.
This replacement reduces the computational cost,
while losing even more geometrical information.
When it is used for image classification we can rely
on the translation invariance property: in order to de-
termine to which class an image belongs, it is only
needed to find determinate features without consider-
ing where these are in the picture. As an example,
the system can determine if an image contains a dog,
regardless if it is on the left or right side of the picture.
Figure 8: Use of two 3 × 3 convolutions instead of 5 × 5.
Following the same idea, it is possible to exploit it
further, by considering to replace a 3 × 3 convolution
with a 3 × 1 and a 1 × 3 convolution in succession.
Again this will reduce the computational time, while
not losing meaningful information for object recog-
nition tasks thanks to the translation invariance prop-
erty.
Thanks to these adjustments the Inception V3 is
a 33 layers deep neural network, with a more than
acceptable number of weights of ≈ 1.3 millions. This
architecture is the current state of the art for image
classification.
To test the performance of the Inception V3 archi-
A Deep Convolutional Neural Network for Location Recognition and Geometry based Information
31

tecture we use the pretrained network that is publicly
available on GitHub
1
. On the top of the architecture
we have added a fully connected layer of 250 hidden
units that is connected to the output layer consisting
of ten output units. The weights for these final two
layers are the only parts of the network that we train
on the dataset.
3.4 New DNN Architecture
Considering the importance of geometrical informa-
tion in the navigation domain that we have presented
in section 1, we decided to build an ANN that would
never rely on geometrical invariance properties. As
already discussed, State of the Art methods vastly
use them. Furthermore, we also want to rely on
the effectiveness and efficiency of CNNs that are
very successful in the computer vision field. In fact
since (Krizhevsky et al., 2012) they outperform all
other methods such as BOW for many different im-
age recognition problems.
The INN V3 heavily relies on geometrical in-
variance properties. This is because the architecture
makes extended use of e.g. pooling layers which
completely ignore the local geometry in their kernels
given their max or mean operations. If these layers are
applied in the deepest layers of the architecture, most
of the geometrical features get lost and are ignored
by the network. Besides pooling layers, other tech-
niques, such as the consecutive use of small convolu-
tion layers, extensively used in the INN V3, lose geo-
metrical properties. The use of two consecutive 3 × 3
convolution filters, instead of a 5 × 5 one; or even
more the use of 3 × 1 convolution followed by 1 × 3
convolution, heavily relies on the translation invari-
ance property. An extensive use of these techniques,
especially in the deeper levels of the architecture, has
a strong negative impact on the whole geometry of the
input.
Here we present the architecture of our novel Nav-
DNN. The full structure can be seen in Figure 9. The
architecture consists of an input layer, followed by 4
convolution layers, an adapted Inception Module, a
hidden layer, and a final output layer. The input pic-
tures have a 300 × 300 × 3 size, with the 3 final chan-
nels corresponding to the RGB ones.
Hereafter we present into detail the parameters of
all the layers:
• Input: 300 × 300 × 3.
• Conv1: k=7; c=48; s=3; d=0.1; Ts=98x98x48.
• Conv2: k=9; c=32; s=2; d=0.1; Ts=45x45x32.
1
https://github.com/tensorflow/models/tree/master/inception
Figure 9: Nav-DNN architecture.
• Conv3: k=11; c=24; s=1; d=0.1; Ts=35x35x24.
• Conv4: k=22; c=16; s=1; d=0.1; Ts=14x14x16.
• Inception Layer: described in Figure 10
• Hidden: hidden units = 200.
• Output = 10.
Where k is the kernel size; c the number of chan-
nels; s the number of strides; d the dropout rate; and
T s the size of the output tensor size at each layer. The
Rectified Linear Unit (ReLU) activation function is
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
32

used in all the convolution and hidden layers. A fi-
nal softmax activation function is used for the output.
Figure 9 shows the just explained architecture.
As we can see from Figure 9 we use a modified
version of the Inception Module. We take inspiration
from the original one, with the difference that the one
that we create is able to maintain the geometrical in-
formation of the input. This difference is highlighted
in Figure 10.
Figure 10: Modified Inception Module.
We use in parallel 2 deep convolutions: on the left
a 1×1 kernel followed by a 3×3 one is used, while on
the right a 1×1 kernel followed by a 5 ×5 one is used.
We remove the pooling layer and all the weight opti-
mization techniques discussed in section 3.3.2. But
we still use the 1 × 1 convolution: in fact this allows
us to generate a deeper network while being at the
same time extremely cheap in terms of computational
resources.
Overall we maintained the benefits of the origi-
nal inception layer: by placing this layer deep in our
architecture, we can have the benefits of precise ge-
ometry relations, with the use of 3 × 3 convolutions
and more sparse geometry relations given by the 5×5
convolutions. Noticing that at this layer level the input
tensor has a shape of 14 ×14 × 16, so a 5×5 kernel is
able to find relations in a geometrical space of more
than 1/3 of the original input, ≈ 100 × 100 pixels.
3.5 Training
The training procedures of the three methods pro-
posed slightly differ from each other given the diver-
sity of the algorithms.
The BOW algorithm, described in Section 3.1, has
been trained only on the original 8,141 HD pictures.
The training procedure took 72 hours. This is the rea-
son we decided to not use the enhanced dataset for
this algorithm, in order to not increase even more the
training time. We note that the clustering procedure
took 71.5 hours, while the training of the NN on top
of it took the remaining 30 minutes. Also for this
training the data set was split in 80% training, 10%
validation and test set. We trained the BOW only on
the Scene Recognition task.
The INN V3 algorithm, described in Section 3.3.2,
has been trained on a 32,564 pictures dataset for the
Scene Recognition task. This dataset is described in
Section 2.1, and we used 80% for training and 10%
for validating and testing. Since we used the pre-
trained INN V3, we only trained the last layer of the
network. In order to do this we computed the bottle-
neck tensor of every picture, then we used these for
the actual training of the last layer. Generating the
bottleneck tensors took 2.2 hours, while the training
of the last layer took less than 10 minutes. For the Lo-
cation Recognition Task, the total number of pictures
increased to 65,128. From these, 48,846 were used
for training and 16,282 were used for testing, as we
described in Section 2.2.
The Nav-DNN algorithm, described in Section
3.4, has been trained on 32,564 pictures for the Scene
Recognition task. This dataset is described in Section
2.1, and we used 80% for training and 10% for vali-
dating and testing. This algorithm took 1.5 hours to
train. For the Location Recognition Task, we used the
dataset described in Section 2.2.
4 RESULTS
In this section we present the results obtained on the
datasets. We will compare the performance of the
INN V3 with our novel Nav-DNN on the location
dataset described in section 2.2. We will also show
how geometrical information is intrinsic and used by
our DNN.
4.1 Results on Scenes Dataset
Here we report the results obtained on the dataset dis-
cussed in section 2.1. All the results can be seen in
Table 1. Here τ represents the computation time in
hours. The BOW approach obtained 88.5% accuracy
on the test set. These results were obtained with 1000
BOW cluster points, two hidden layers with 1000 and
500 hidden units, and a ReLU (Rectified Linear Unit)
activation function.
On the same dataset, the INN V3 outperforms the
BOW. The INN V3 obtained an accuracy of 100%.
A Deep Convolutional Neural Network for Location Recognition and Geometry based Information
33
Comparing the training time, the BOW trained for al-
most 3 days, while the INN V3 was trained for only 2
hours and 30 minutes. It is notable that the clustering
part of the BOW took the majority of the training time
since it was single threaded on the CPU, while the
INN V3 is pretrained except for the last hidden layer.
Most of the computation time was invested in creat-
ing the bottleneck output of the pretrained layers of
the INN V3. Nevertheless this last one, significantly
outperforms the BOW.
Table 1: Scene Recognition Results.
Methods Val set Test set τ
BOW 89.7% 88.5% 72
INN V3 100% 100% 2.3
Nav-DNN 100% 98.7% 1.5
When we compare INN V3 with our architecture:
we can see that our network obtains an accuracy of
98.7% on the test set. While this is slightly worse
than the INN V3, it is important to verify how this
last architecture actually generalizes the pictures. In
particular to see if both DNN architecture generalize
the data in a meaningful way for a navigation system.
4.2 Results on Location Dataset
To verify this, we trained and tested both DNNs on the
location dataset described in section 2.2. The results
can be seen in Table 2.
Table 2: Location Recognition Results
NN architecture Correct Tricked Missed
INN V3 0% 97.43% 2.57%
Nav-DNN 99.7% 0% 0.3%
Here: Correct means the NN labeled the image
correctly; Tricked means the NN labeled the flipped
image as the original one; and Missed means the NN
labeled the image as neither flipped, neither as the
original image, but just as another class at random.
It is important to highlight that it is not possible
to distinguish a flipped image from its original one by
only relying on the features. In fact, the two images
have exactly the same features, due to the way they
were constructed. The only successful approach to
distinguish the two pictures is to consider the geom-
etry of the image and the geometrical distribution of
the features.
These results perfectly show that it is possible to
create Deep Neural Networks, using convolution lay-
ers, that are able to maintain the geometrical property
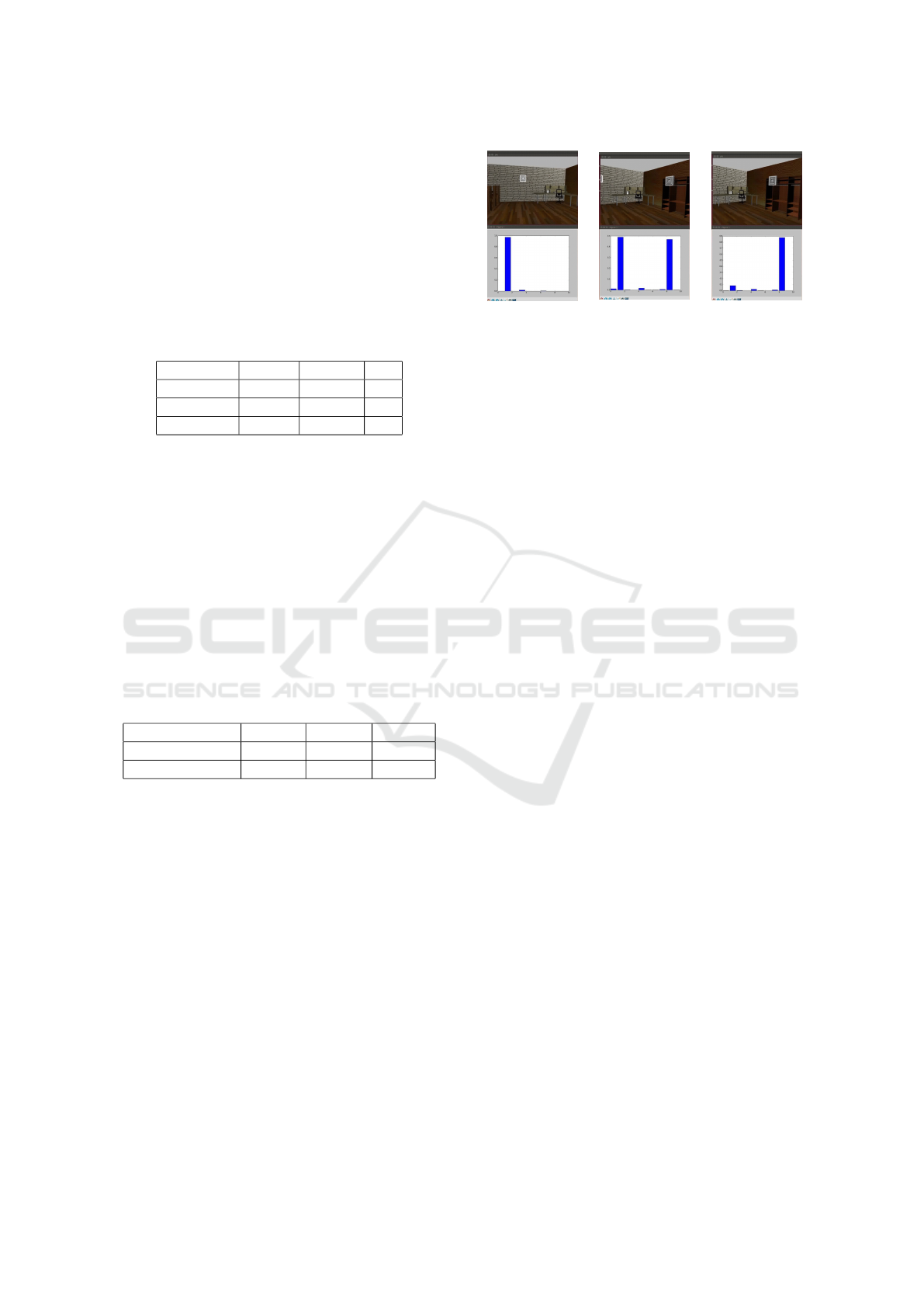
of the input. As can be seen from Figure 11, this is
essential for navigation tasks: identifying a specific
Figure 11: DNN output over camera rotation.
feature in the input is not enough, the position of this
feature is also essential.
Although we used real-word images for our ex-
periments, Figure 11 is constructed by using a sim-
ulator, Gazebo (Koenig and Howard, 2004), and the
new DNN we proposed. The top part of the pictures
show the point of view of the simulated robot, and the
bottom part shows the real output of the DNN as a
histogram of probabilities of the detected scene. This
process is in real time, with a live stream of frames
from the simulated camera, and real time classifica-
tion of the DNN. In Figure 11 we show the most rel-
evant frame of the transition. From left to right, the
simulated robot turns right: we can see this move-
ment from the turning of the environment in the pic-
tures. This rotation changes the view from a scene to
the next one. Looking at the output of the DNN we
can see how we have a transition on scene probabili-
ties: this correlation between the physical rotation and
the transition of the probability from one scene to the
other is the clear sign of intrinsic geometrical infor-
mation derived from the DNN. This was completely
absent in the INN V3.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we proposed a novel Deep Convolutional
Neural Network architecture that does not rely on the
geometrical invariance property. While using layers
like Pooling and weight optimization like the one used
in INN V3 greatly increase the performance of DNN
for scene recognition tasks, it is not the optimal choice
in every field. Here we focused on navigation, where
geometry is essential for any navigation system. We
showed that it is possible to create high performing
DNNs that can also maintain the geometrical proper-
ties of the input, giving an intrinsic knowledge of the
geometry of the environment to the network itself.
Since the proposed DNN can be a key component
of a visual based navigation system, we focused on
experimenting on datasets which represent real world
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
34

scenarios. The whole pipeline consists of an almost
autonomous way of generating labels, to create in a
fast way a dataset of the environment. This is used
to train the proposed DNN, which can generalize the
training data in a meaningful way: a direct correlation
between geometrical movement and the DNN output
probability. This is only possible when the DNN re-
lies on geometrical properties. It is also important to
notice that we experimented with removing the VMs
from the environment, and the DNN performances re-
main the same; but no extensive experiments were
performed with this focus.
To conclude, we show that it is possible to use
convolution layers to create deep architectures, while
maintaining all the geometrical properties of the data.
This can be applied in all the fields where the posi-
tion, or geometrical properties of the features are as
important as the features themselves.
Future Work. The new approach proposed in this
paper showed that is possible to use DNNs for ge-
ometrically based data. Moreover it can be applied
as the core localization subsystem for a visual based
navigation system. This would rely on the geometri-
cal properties of the real world environment to possi-
bly create a human like approach to navigation. If we
consider that humans are able to perfectly navigate in
any environment with solely visual information, then
the proposed approach would fit the need of a human
like navigation system. To accomplish this, more con-
siderations and research needs to be done, focusing on
the system itself: the use of 3D cameras, stereoscopic
cameras and more.
On a more general level this approach shows po-
tential in applications where geometrical structure
matters. As an example we could consider FMRI
scans: these visual data are directly correlated to the
brain areas. Another example could be visual games:
from chess to Atari games. Given the ability of the
proposed DNN to rely on the positions of the fea-
tures and to generalize the geometrical properties of
the data, the possible benefits are clear.
REFERENCES
Arora, S., Bhaskara, A., Ge, R., and Ma, T. (2014). Provable
bounds for learning some deep representations. In In-
ternational Conference on Machine Learning, pages
584–592.
Bonin-Font, F., Ortiz, A., and Oliver, G. (2008). Visual
navigation for mobile robots: A survey. Journal of
intelligent and robotic systems, 53(3):263.
Dosovitskiy, A., Springenberg, J. T., Riedmiller, M., and
Brox, T. (2014). Discriminative unsupervised fea-
ture learning with convolutional neural networks. In
Advances in Neural Information Processing Systems,
pages 766–774.
Elfes, A. (1987). Sonar-based real-world mapping and nav-
igation. IEEE Journal on Robotics and Automation,
3(3):249–265.
Everett, H. R. and Gage, D. W. (1999). From labo-
ratory to warehouse: Security robots meet the real
world. The International Journal of Robotics Re-
search, 18(7):760–768.
Floreano, D. and Wood, R. J. (2015). Science, technology
and the future of small autonomous drones. Nature,
521(7553):460.
Guivant, J., Nebot, E., and Baiker, S. (2000). Autonomous
navigation and map building using laser range sensors
in outdoor applications. Journal of robotic systems,
17(10):565–583.
Koenig, N. and Howard, A. (2004). Design and use
paradigms for gazebo, an open-source multi-robot
simulator. In Intelligent Robots and Systems. Pro-
ceedings. 2004 IEEE/RSJ International Conference
on, volume 3, pages 2149–2154.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-
ing. Nature, 521(7553):436–444.
Levinson, J., Askeland, J., Becker, J., Dolson, J., Held, D.,
Kammel, S., Kolter, J. Z., Langer, D., Pink, O., Pratt,
V., et al. (2011). Towards fully autonomous driving:
Systems and algorithms. In Intelligent Vehicles Sym-
posium (IV), 2011 IEEE, pages 163–168. IEEE.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2):91–110.
Marszałek, M., Schmid, C., Harzallah, H., and Van De Wei-
jer, J. (2007). Learning object representations for vi-
sual object class recognition. In Visual Recognition
Challenge workshop, in conjunction with ICCV.
Rifkin, R. and Klautau, A. (2004). In defense of one-vs-all
classification. Journal of machine learning research,
5(Jan):101–141.
Sejnowski, T. J. and Tesauro, G. (1989). The Hebb rule for
synaptic plasticity: algorithms and implementations.
Neural models of plasticity: Experimental and theo-
retical approaches, pages 94–103.
Sukkarieh, S., Nebot, E. M., and Durrant-Whyte, H. F.
(1999). A high integrity imu/gps navigation loop for
autonomous land vehicle applications. IEEE Transac-
tions on Robotics and Automation, 15(3):572–578.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,
Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-
novich, A. (2015). Going deeper with convolutions.
In Proceedings of the IEEE conference on computer
vision and pattern recognition, pages 1–9.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wo-
jna, Z. (2016). Rethinking the inception architecture
for computer vision. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 2818–2826.
A Deep Convolutional Neural Network for Location Recognition and Geometry based Information
35

Yang, J., Jiang, Y.-G., Hauptmann, A. G., and Ngo, C.-W.
(2007). Evaluating bag-of-visual-words representa-
tions in scene classification. In Proceedings of the
international workshop on multimedia information re-
trieval, pages 197–206. ACM.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
36
