
ICM: An Intuitive Model Independent and Accurate Certainty Measure
for Machine Learning
Jasper van der Waa, Jurriaan van Diggelen, Mark Neerincx and Stephan Raaijmakers
TNO, Soesterberg, The Netherlands
Keywords:
Machine learning, Trust, Certainty, Uncertainty, Explainable Artificial Intelligence.
Abstract:
End-users of machine learning-based systems benefit from measures that quantify the trustworthiness of the
underlying models. Measures like accuracy provide for a general sense of model performance, but offer no
detailed information on specific model outputs. Probabilistic outputs, on the other hand, express such details,
but they are not available for all types of machine learning, and can be heavily influenced by bias and lack of
representative training data. Further, they are often difficult to understand for non-experts. This study proposes
an intuitive certainty measure (ICM) that produces an accurate estimate of how certain a machine learning
model is for a specific output, based on errors it made in the past. It is designed to be easily explainable to
non-experts and to act in a predictable, reproducible way. ICM was tested on four synthetic tasks solved by
support vector machines, and a real-world task solved by a deep neural network. Our results show that ICM is
both more accurate and intuitive than related approaches. Moreover, ICM is neutral with respect to the chosen
machine learning model, making it widely applicable.
1 INTRODUCTION
Machine learning (ML) methods are becoming in-
creasingly popular and effective, from beating hu-
mans at complex games such as Go (Silver et al.,
2016) to supporting professionals in the medical do-
main (Belard et al., 2017). Regardless of the particu-
lar type of machine learning model (e.g. neural nets,
Bayesian networks, reinforcement learning or deci-
sion trees), there will be a human user that relies on
the outcomes and so trust will play a vital role (Cohen
et al., 1998; Schaefer et al., 2017; Dzindolet et al.,
2003). An important prerequisite for the calibration
of user trust in the model, is letting the user know the
certainty or confidence for any decision or classifica-
tion given by the model(Cohen et al., 1998).
This paper considers a use case where an operator
monitors a Dynamic Positioning (DP) system to keep
an ocean vessel in stationary position (Saelid et al.,
1983). Recent work proposed a supportive agent that
uses predictive analytics to predict if operator involve-
ment is required in the near future, or if the system
can continue to operate fully autonomous (van Digge-
len et al., 2017). Based on this prediction, the agent
advises the operator if he can leave his workstation to
perform other tasks or if he should pay attention to the
system. This prediction can be wrong as it cannot be
guaranteed that the ML model is flawless (Harrington,
2012). If the operator leaves his station while the ship
is about to drift, this can cause financial and property
damage, it may even cost human lives depending on
the operation (van Diggelen et al., 2017). If the agent
can provide the operator with a certainty measure that
is intuitive and accurate, then the user has more in-
formation available to make his own decision and is
more likely to trust the measure.
The design of such a certainty measure is not triv-
ial. Machine learning performance measures such as
accuracy, precision, sensitivity, and specificity, lack
the generalization capability to single data points as
they are not meant to form predictions but as a means
to assess overall performance on known data. If we
take the previous example of a supportive decision-
making agent based on a machine learning model, its
performance on a known set of situations may be high
but it will not necessarily tell you how likely a single
output will be correct (Foody, 2005; Nguyen et al.,
2015). Other approaches utilize a distribution of prob-
abilities over possible model outputs and learn to gen-
eralize such distributions to new data points using a
second model stacked on top of the original model
(Park et al., 2016). Hence, such models are not neces-
sarily more intuitive than the original model and those
models themselves can be uncertain (Ribeiro et al.,
314
Waa, J., Diggelen, J., Neerincx, M. and Raaijmakers, S.
ICM: An Intuitive Model Independent and Accurate Certainty Measure for Machine Learning.
DOI: 10.5220/0006542603140321
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 314-321
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2016b). Finally, such stacked certainty measures vary
in their assumptions made about the machine learning
model; from a distribution over model outputs (Park
et al., 2016) to detailed knowledge about the machine
learning method (Castillo et al., 2012) or even trained
parameters (Blundell et al., 2015). This limits such
approaches to just a few methods.
This study answers the following research ques-
tion: How can we design a certainty and uncertainty
measure that is 1) intuitive, 2) model independent and
3) accurate even for a new single data point? We de-
fine an intuitive measure as a measure that is easily
understood by a non-expert in ML and behaves in a
predictable way. Model independence is defined as
making as little assumptions as possible about the ML
model, treating it as a black box. A certainty mea-
sure is accurate only if it respects the performance of
the ML model. In this study we design a measure
with these properties: the Intuitive Certainty Measure
(ICM).
The design of ICM aims to be intuitive by bas-
ing its underlying mechanics on two easily explained
principles: 1) Previous experiences with the ML
model’s performance directly influence the certainty
of a new output, and 2) this influence is based on
how similar those past data points are to the new data
point. In other words, ICM keeps track of previous
data points and how the ML model perform on those
points to interpolate that performance to new data
points. This makes ICM a meta-model that tries to
learn to predict another model’s performance on sin-
gle data points. For learning, ICM uses a lazy learning
approach since it stores past data and only computes
a certainty value when needed. We limit the number
of stored data points for computational efficiency by
sampling only the most informative ones from all pre-
vious data (Wettschereck et al., 1997). This mitigates
the known disadvantage and active research topic of
lazy learning that computing an output is time con-
suming (due to it searching through all data) while
retaining the advantage that no learning occurs be-
fore an output is required (Bottou and Vapnik, 1992).
Finally, this sampling method is designed to handle
sequential data, making it applicable to models that
learn both online as well as offline.
ICM is implemented to be model independent by
treating the model as a black box with access only
to the inputs, outputs and, at some point in time, the
model’s performance on a data point. This perfor-
mance is what ICM will interpolate to other points
and limits the application of ICM to supervised and
semi-supervised learning. We test the model indepen-
dence of ICM by applying it to two different and of-
ten used ML models; a support vector machine and a
neural network.
ICM was compared to a baseline from Park et al.
(2016) that uses a second ML model that outputs the
probability that the actual ML model will be correct
or not. Four test cases were used for this compar-
ison. The first four sets were synthetic classification
problems, each with a trained support vector machine.
These were used to visualize the workings of ICM and
assess its predictability in feature space compared to
the baseline method. The fifth test set was the data
from the Dynamic Positioning (DP) use case men-
tioned earlier with a trained neural network. This data
set was used to assess ICM’s performance on a realis-
tic and high-dimensional data set.
2 RELATED WORK
Studies from agents based on belief, desires and in-
tentions (BDI) mechanisms (Broekens et al., 2010),
rule-based and fuzzy expert systems (Giarratano and
Riley, 1998) indicate that a user of an intelligent sys-
tem requires an explanation from the system that val-
idates the appropriateness of the given advice or per-
formed action. This information focuses mostly on
explaining the reasoning chain (Core et al., 2006) and
also, in the case of fuzzy and Bayesian systems, the
likelihood (Norton, 2013). Machine learning is a dif-
ferent approach for creating an intelligent system then
that of using BDI agents. Machine learning (ML)
fits model parameters to maximize or minimize some
function based on available data. The trained model
in a machine learning system can be sub-optimal in
some situations (Harrington, 2012). Some causes are:
insufficient or biased data, sub-optimal learning al-
gorithms and over- or under-fitting (Dietterich and
Kong, 1995). To adequately use machine learning
systems as a support tool, the user requires an indi-
cation whether the given advice or action is appropri-
ate in the current situation especially when the conse-
quences are unclear to the user (Swartout et al., 1991).
This requirement and the increased successes of ma-
chine learning, gave rise to the research field that stud-
ies self-explaining machine learning systems (Lang-
ley et al., 2017).
Currently, research in self-explaining ML systems
mainly focuses on how the system came to its output
or on how accurate the system believes that output
will be. Examples of the former are ALime (Ribeiro
et al., 2016a), MFI (Vidovic et al., 2016) and QII
(Datta et al., 2016). All of which are relatively model-
free as they do not assume a specific machine learning
method. Other approaches are more model-specific
that use the model’s known structure and learning al-
ICM: An Intuitive Model Independent and Accurate Certainty Measure for Machine Learning
315

gorithm (Antol et al., 2015; Selvaraju et al., 2016).
For example, by analyzing the latent space of deep
learning models to relate input data to supportive, rel-
evant training data (Raaijmakers et al., 2017). All of
these studies explore different methods to visualize or
explain how the system came to the given output.
A second topic of self-explaining machine learn-
ing models is its certainty or confidence of being cor-
rect. Park et al. (2016) base their certainty measure on
a second machine learning model stacked on the ML
model. They propose a novel indicator of certainty;
the difference between the highest and second high-
est class or action probability outputted by the orig-
inal model. The difference becomes the dependent
variable for a logistic regression model trained to use
this difference to predict whether the underlying ML
model will be correct or not. The result is a logistic
regression model stacked on the original model that
outputs the probability of the original model being
correct. This approach was validated on a real-world
data set and showed that it can be used to create an
expected accuracy map of the feature space. We will
use this approach from Park et al. (2016) as a baseline
to compare our method with.
The proposed measure, ICM, is closely related to
the research field of locally weighted learning, a form
of lazy or memory based learning (Bottou and Vapnik,
1992). Similar to ICM, those models use a distance
function to determine the relevance of all stored data
points to a different data point. These distances are
used as weights to interpolate the class or variable of
interest of all stored data points to the new data point.
In the case of ICM, we weigh the error of the machine
learning model on data points to interpolate this error
to new data points.
The selection of the distance function in a locally
weighted model is a difficult but important process
(Bottou and Vapnik, 1992). If an inappropriate func-
tion is selected, it will not match the geometry in the
data. For ICM this would mean that it will not be able
to reflect the underlying ML model’s performance.
However, since we want ICM to also act predictable
according to a human user and easy to explain, we
want the distance function to be consistent with how
the user thinks of distance and similarity.
3 ICM: INTUITIVE
UNCERTAINTY MEASURE
For the uncertainty measure to be useful for a non-
expert user we stated that it should be intuitive and ac-
curate. In this study we define an intuitive measure as
a measure that can be understood by a non-expert user
and acts in a predictable way. The underlying and, ex-
pected, intuitive principle of ICM is that of using the
similarity between data points to interpolate model er-
ror to new points with unknown performance.
We base the certainty and uncertainty of a data
point on the simple notion of its proximity to other
data points of which we know the ground truth (at
some point in time). If a model’s output for a new
data point is the same as the ground truth of similar
data points, then we become more certain the closer
these points are. If, on the other hand, the model’s
output is different than the ground truth of similar data
points then these add to uncertainty (and decrease cer-
tainty). This is a relative simple idea that, we argue,
is easily explained to a non-expert user as long as the
used distance or similarity function is comprehensible
in some way.
Note that the performance of ICM is closely tied
to the chosen distance function. ICM will not be able
to interpolate well if this function does not correspond
with the intrinsic geometry of the data. Therefore a
trade-off may exist between the performance of ICM
and how well the distance function can be understood
by a non-expert. For example, points that are close to
a decision boundary will receive less certainty when
the point density on each side of the boundary is equal
and correct. Although points that are missclassified
(on the wrong side of the boundary) will receive an
even lower certainty. With this, ICM reflects the pos-
sible variance in the learned decision boundary.
Distance computation for all available data points
is usually a demanding task and we cannot always
store an entire data set in memory. Therefore, we
sample the most informative data points based on: 1)
The time since we last added a new data point to the
sample, 2) how unique the current data point is given
the points in the current sample set and 3) how many
ground truth labels we have.
The next two sections describe the uncertainty
measure and sampling method respectively in more
detail. This is followed by a simple application of the
measurement to four synthetic data set to illustrate the
principle
1
.
3.1 The Measurement
Given the i’th feature vector x
i
∈ R
n
from an arbitrary
data set D, the model A outputs A(x
i
) ∈ {y
1
, ...y
c
} for
x
i
with c as the number of different outputs. Also for
each x
i
we assume a ground truth; T (x
i
) ∈ {y
1
, ...y
c
}.
With this we can describe the data points from data
set D as a set of triplets:
1
The code is available on request by e-mail.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
316

D =
{
(x
1
, A(x
1
), T(x
1
)),. . . , (x
N
, A(x
N
), T (x
N
))
}
where N is the number of data points in D.
ICM is based on a distance function d and inter-
polates the performance of A to new data points based
on radial basis functions with a Gaussian function and
the new point as its mean (Rippa, 1999; Sch
¨
olkopf
et al., 1997). This approach makes ICM a locally
weighted model as it uses all available data points but
assigns different weights to each. The Gaussian func-
tion introduces an additional parameter σ
C
∈ [0; ∞)
that is its standard deviation. σ
C
can be used to deter-
mine how large the significant neighborhood, defined
by d, should be around a data point. As such we can
define our certainty measure ICM for a feature vector
x given D and σ
C
as:
C(x|σ
C
, D) =
1
Z(x|σ
C
, D)
P(x|σ
C
, D) (1)
where P is the positive contribution to certainty
denoted as:
P(x|σ
C
, D) =
∑
x
i
∈D(T =A(x))
exp
−
d(x|x
i
)
2
2σ
2
C
(2)
and Z is the normalization constant:
Z(x|σ
C
, D) =
∑
x
i
∈D
exp
−
d(x|x
i
)
2
2σ
2
C
(3)
The uncertainty U is computed similarly as the
certainty C:
U (x|σ
C
, D) = 1 −C (x|σ
C
, D)
=
1
Z(x|σ
C
, D)
N(x|σ
C
, D) (4)
where N is the negative contribution to certainty
denoted as:
N(x|σ
C
, D) =
∑
x
i
∈D(T 6=A(x))
exp
−
d(x|x
i
)
2
2σ
2
C
(5)
3.2 Sampling Data
To apply the above method to real-world cases with
large data sets or on models that learn online, we se-
quentially sample data points from the data set D and
only use this sampled set to compute ICM. We de-
note this sampled set at time t as M
t
. We add a data
point x
t
presented at time t with the ground truth T (x
t
)
based on three aspects; 1) time, 2) distance between
the data point and current points in M and 3) number
of ground truth present in M similar to T (x
t
).
Time: A normal distribution with mean t
add
+
µ
time
where µ
time
is some parameter and t
add
is the
time we last added a data point to M
t
. The selection
of µ
time
and the standard deviation σ
time
of the nor-
mal distribution regulate how often we add a new data
point independent of any other properties (if points
are time dependent). This ensures that we follow any
global data trends with some delay while being ro-
bust to more local trends. More formally, we define
this probability P
t
for data point x
t
at time t, as:
P
t
(x
t
|t
add
, σ
time
) = η(t|t
add
+ µ
time
, σ
time
) (6)
Where η(t|µ, σ) is the normal distribution with
mean µ and standard deviation σ.
Distance: We use a Gaussian function with as
its mean the distance between the new data point x
t
and its closest neighbor y ∈ M
t
mean and σ
C
as its
standard deviation. This results in an exponential ver-
sion of d that can be used to sample data points that
are, on average, σ
C
apart. More formally:
P
d
(x
t
|σ
C,
M
t
) = 1 − min
x
0
∈M
t
exp
−
d(x
t
, x
0
)
2
2σ
2
C
(7)
Ground Truth: A linearly decreasing probabil-
ity depending on the number of ground truths similar
to T (x
t
). More formally:
P
tr
(x
t
|M
t
(T = A(x
t
))) = 1 −
|O| · |M
t
(T = A(x
t
))|
|M
t
|
(8)
where M
t
(T = A(x
t
)) is the set of all data points
with the model’s output for x
t
as their ground truth
and O is the set of all possible outputs.
Given these three probabilities, the probability of
adding x
t
to M
t
is:
P
sample
(x
t
) ∝
1
3
[P
t
(x
t
) + P
d
(x
t
) + P
tr
(x
t
)] (9)
where we omitted parameters for brevity.
The maximum size of M is limited to k to limit
computational demands. Any data points that should
be added when M is fully randomly replaces a point
in M that has the same ground truth as the new point,
if available. Otherwise, a completely random point
from M is replaced. If M replaces D in equation
refeq:measure, we can control the computational de-
mands of ICM by settings the size parameter k.
4 PROOF OF PRINCIPLE
To illustrate the workings of ICM and its predictable
behavior in feature space, multiple binary classifica-
tion problems were generated using the SciKit Learn
ICM: An Intuitive Model Independent and Accurate Certainty Measure for Machine Learning
317

package
2
in Python due to convenience. A total of
four datasets were made, each with four clusters (two
clusters per class) in a two-dimensional space. The
classes were separable in Euclidean space and, to con-
trol complexity, we varied the cluster overlap and the
amount of mixed class labels in each cluster. See fig-
ure 1 for an overview of the datasets. Each dataset
consisted out of 5000 training points and 1000 test
points.
A Support Vector Machine (SVM) (Sch
¨
olkopf
et al., 1997) was trained on each training set. One
unique SVM model was optimized for each of the
four classification problems using a validation set of
20% of the training data. Figure 1 shows the accu-
racy of each SVM model on the test set. These ac-
curacies show that the SVM is capable of approxi-
mating the cluster separation but not able to learn the
ground truth on a local scale inside the noisy clusters.
Combined with the variation in overlapping classes
and mixed class labels, this allowed us to measure the
effect of ambiguous class clusters on ICM.
ICM was compared to a baseline based on the ap-
proach of Park et al. (2016) as explained in section 2.
Platt scaling was used to retrieve the class probabili-
ties from our SVM models that are required for this
approach (Platt et al., 1999). This baseline method
used the same sampled set M as ICM. The compar-
ison between ICM and the baseline was based on
their accuracy and their respective predictability was
tested visually by plotting certainties over the feature
space. The parameters for ICM and the baseline were
optimized by hand using 5-fold cross-validation for
each data set. We chose to use Euclidean distance
for ICM because the classes can be separated in Eu-
clidean space and it is a measure a human user can
easily understand. The accuracy measure Acc was de-
fined as follows, with M being the sampled data set
from section 3.2:
Acc =
1
|M|
M
∑
i=0
δ(C(x
i
),U(x
i
), T (x
i
), A(x
i
))
δ(C,U, T, A) =
1 i f T = A ∧C > U
1 i f T 6= A ∧C < U
0 else
Figure 1 shows the visualization of ICM and
the baseline certainty plotted over the feature space.
These visualizations show that both ICM and the
baseline method learn an approximation of the de-
cision function between the two classes. However,
the baseline method based on a stacked SVM model
shows erratic behavior in the feature space outside the
2
http://scikit-learn.org
original dataset, which make the certainty value un-
predictable for new data as opposed to ICM. Also,
ICM reflects more ambiguous classes by decreasing
and increasing its average certainty and uncertainty
respectively towards 0.5 as seen in figures 1(b), 1(c)
and 1(d). These results show that ICM behaves more
predictable than a similar method.
The accuracies of ICM and the baseline on each
data set are shown in figure 2, and demonstrate that
ICM outperforms the baseline on the accuracy as de-
fined by equation 4. The results on data set 2 and 4
show that ICM is susceptible to ambiguous classes,
though less than the baseline which is also affected
by overlapping classes.
5 EVALUATION
We evaluated ICM on the real-world application of
predictive analytics in a dynamic positioning use case.
A dynamic positioning (DP) system attempts to keep
an ocean ship stationary or sail in a straight line using
only its thrusters to correct for environmental forces
(Saelid et al., 1983). In this study we took the station-
ary DP use case where the system is nearly perfect
in maintaining its position based on several sensors
and thrusters combined with a supportive agent for
DP. This agent uses a predictive model to predict how
much the ships will drift and advises the human oper-
ator to remain or leave his workstation (van Diggelen
et al., 2017). The confidence level of the agent is im-
portant to the operator, who carries a responsibility
for the operation.
5.1 Data Set and Model
To test ICM we created a dynamic positioning data
set on which we trained a predictive model. We
used a simulator of a small vessel and a DP system
with two azimuth and two bow thrusters
3
and several
sensors (GPS, wind speed and angle, current, depth,
wave height and period, yaw, pitch and roll). The
environmental variables were set using a real-world
weather data set from a single buoy in the North Sea.
This weather data set had a period of three hours and
we used common weather models to interpolate data
points to a frequency of one data point per 500 mil-
liseconds. Finally, we added small Gaussian noise to
the sensor values. This resulted in a stationary DP
simulator we could feed plausible environmental data
and retrieve realistic sensor information.
3
Azimuth thrusters are thrusters that can rotate beneath
the ship, while bow thrusters are thrusters that are located at
a ship’s bow and can either exert force to the ‘left’ or ‘right’.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
318

(a) Data set 1, SVM accuracy of 99% and ICM settings of
k = 350, σ
C
= 0.75, µ
time
= 5 and σ
time
= 1.25
(b) Data set 2, SVM accuracy of 75% and ICM settings of
k = 350, σ
C
= 0.25, µ
time
= 5 and σ
time
= 1.25
(c) Data set 3, SVM accuracy of 94.2% and ICM settings of
k = 350, σ
C
= 0.5, µ
time
= 8 and σ
time
= 1.25
(d) Data set 4, SVM accuracy of 72.5% and ICM settings of
k = 350, σ
C
= 0.5, µ
time
= 8 and σ
time
= 1.25
Figure 1: Each figure visualizes the certainty values for ICM and of the baseline based on the method from Park et al. (2016).
The point clouds represent the data points from the test set, the yellow points the sampled data points part of M and the
backgrounds represent the certainty values of each of the two approaches.
Figure 2: The accuracy according to equation 4 for both
ICM and the baseline on the four synthetic data sets.
Two years’ worth of data were simulated of which
80% was used to train a neural network and the other
20% was used as a test set
4
. A neural net with three
4
The data set is available on request by e-mailing one
hidden layers (1536, 256 and 64 neurons respectively)
was used with ReLu activation functions (Nair and
Hinton, 2010), trained using the ADAM optimizer
(Kingma and Ba, 2015). No attempt was made to
fully optimize the model when it reached an accuracy
of 96.59% with hand tuned hyper-parameters on pre-
dicting three classes 15 minutes in the future; a drift
of < 5m, 5 − 10m or > 10m.
5.2 Results
Figure 3 shows the accuracy of both ICM and the
baseline, calculated according to equation 4. Each
point shows the mean accuracy of twenty different
data sets from the DP test data with varying sample
set sizes. This plot shows that ICM outperforms the
baseline on a high-dimensional data set with a non-
linear machine learning model. The lower accuracies
of the authors. It can be used for other applications and as a
benchmark.
ICM: An Intuitive Model Independent and Accurate Certainty Measure for Machine Learning
319
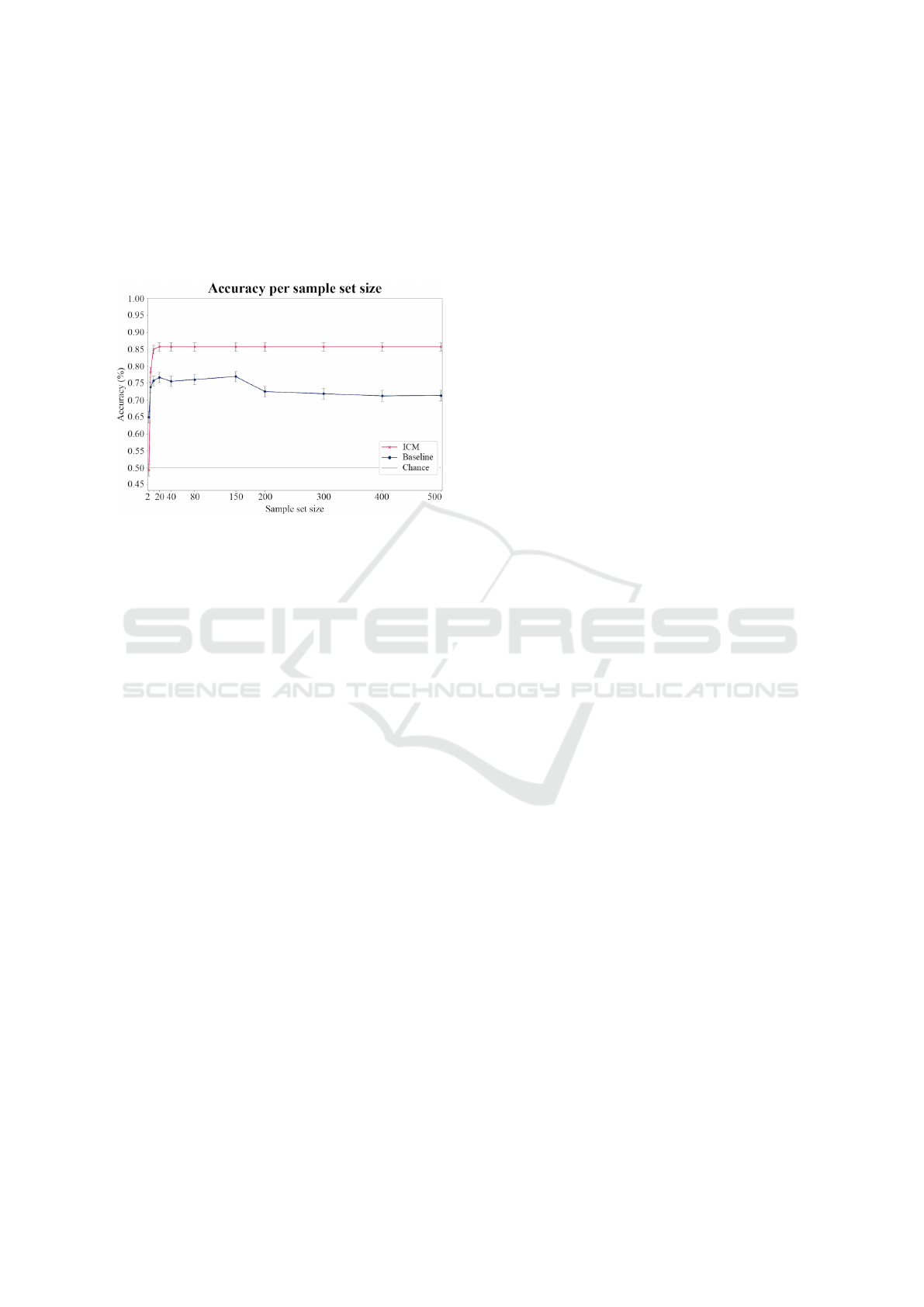
near chance level, of the baseline and ICM method
on smaller memory sizes is due to both methods not
having enough data with which to learn how to gen-
eralize well. However, ICM is robust to the memory
size as long as this size is above some threshold. For
this specific problem with high dimensional data and
three classes that size is a mere 20 data points.
Figure 3: The accuracy of the proposed uncertainty measure
compared to the baseline based on the approach by Park et
al. (2016) for various sample set sizes. Accuracy is deter-
mined according to equation 4. The error bars represent the
standard error.
6 CONCLUSION
The goal of this study was to design an intuitive cer-
tainty measure that is widely applicable and accurate.
In this study we defined an intuitive measure as being
based on easily explained and understood principles
that non-experts in machine learning (ML) can under-
stand and that behaves predictable in feature space.
We developed such a measure, the Intuitive Certainty
Measure (ICM), by treating the ML model as a black
box to make it generic and validated its accuracy on
two different ML models of varying complexity.
We designed ICM to be intuitive by basing it on
the notion of distance and previous experiences; if the
output for the current data point is the same as simi-
lar data points experienced in the past, certainty will
be high. This underlying principle is easily explained
such that non-experts can understand the values of
ICM and where they come from. We showed that
ICM acts in a more predictable manner on various two
dimensional synthetic classification problems, com-
pared to the baseline.
ICM proved to be accurate; it outputs a high cer-
tainty for the ML model’s true positives and negatives,
while it outputs a low certainty for its false positives
and negatives. It outperformed the baseline method
both on the synthetic classification tasks with varying
class separation as well as on a more real-world use-
case with high dimensional data.
Finally, ICM was applied to both support vector
machines and a deep neural network without modi-
fication. This illustrates that ICM is applicable to a
wide array of machine learning approaches, both lin-
ear as non-linear models. The only requirement is that
it learned a (semi-)supervised problem.
In the future we will validate ICM’s intuitive prop-
erties in a usability study to assess whether ICM in-
deed helps to maintain an appropriate level of trust
in a machine learning based agent. Additional explo-
ration of different sampling methods and the effect of
various distance measures on both accuracy and intu-
itiveness for ICM may result in a broader understand-
ing of the measure. Our future research will result
in a further improved version of ICM that will hope-
fully be both accurate and intuitive for non-experts in
Machine Learning to help manage their trust in their
models.
ACKNOWLEDGMENTS
This study was funded as part of the early re-
search program Human Enhancement within TNO.
The work benefited greatly from the domain knowl-
edge of Ehab el Amam from RH Marine.
REFERENCES
Antol, S., Agrawal, A., Lu, J., Mitchell, M., Batra, D.,
Lawrence Zitnick, C., and Parikh, D. (2015). Vqa:
Visual question answering. In Proc. of the IEEE Int.
Conf. on Computer Vision, pages 2425–2433.
Belard, A., Buchman, T., Forsberg, J., Potter, B. K., Dente,
C. J., Kirk, A., and Elster, E. (2017). Precision diag-
nosis: a view of the clinical decision support systems
(cdss) landscape through the lens of critical care. J.
Clin. Monit. Comput., 31(2):261–271.
Blundell, C., Cornebise, J., Kavukcuoglu, K., and Wierstra,
D. (2015). Weight uncertainty in neural networks.
In Proc. of the 32nd Int. Conf. on Machine Learning
(ICML 2015).
Bottou, L. and Vapnik, V. (1992). Local learning algo-
rithms. Neural computation, 4(6):888–900.
Broekens, J., Harbers, M., Hindriks, K., Van Den Bosch,
K., Jonker, C., and Meyer, J.-J. (2010). Do you get it?
User-evaluated explainable BDI agents. In German
Conf. on Multiagent System Technologies, pages 28–
39. Springer.
Castillo, E., Gutierrez, J. M., and Hadi, A. S. (2012). Expert
systems and probabilistic network models. Springer
Science & Business Media.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
320

Cohen, M. S., Parasuraman, R., and Freeman, J. T. (1998).
Trust in decision aids: A model and its training impli-
cations. In Proc. Command and Control Research and
Technology Symp. Citeseer.
Core, M. G., Lane, H. C., Van Lent, M., Gomboc, D.,
Solomon, S., and Rosenberg, M. (2006). Building
explainable artificial intelligence systems. In AAAI,
pages 1766–1773.
Datta, A., Sen, S., and Zick, Y. (2016). Algorithmic trans-
parency via quantitative input influence: Theory and
experiments with learning systems. In IEEE Symp.
Security and Privacy,, pages 598–617. IEEE.
Dietterich, T. G. and Kong, E. B. (1995). Machine learning
bias, statistical bias, and statistical variance of deci-
sion tree algorithms. Technical report, Dep. of CS.,
Oregon State University.
Dzindolet, M. T., Peterson, S. A., Pomranky, R. A., Pierce,
L. G., and Beck, H. P. (2003). The role of trust
in automation reliance. Int. J. Hum. Comput. Stud.,
58(6):697–718.
Foody, G. M. (2005). Local characterization of thematic
classification accuracy through spatially constrained
confusion matrices. Int. J. Remote Sens., 26(6):1217–
1228.
Giarratano, J. C. and Riley, G. (1998). Expert systems. PWS
Publishing Co.
Harrington, P. (2012). Machine learning in action, vol-
ume 5. Manning Greenwich, CT.
Kingma, D. and Ba, J. (2015). Adam: A method for
stochastic optimization. 3rd Int. Conf. for Learning
Representations.
Langley, P., Meadows, B., Sridharan, M., and Choi, D.
(2017). Explainable Agency for Intelligent Au-
tonomous Systems. In AAAI, pages 4762–4764.
Nair, V. and Hinton, G. E. (2010). Rectified linear units
improve restricted boltzmann machines. In Proc. of
the 27th Int. Conf. on Machine Learning (ICML-10),
pages 807–814.
Nguyen, A., Yosinski, J., and Clune, J. (2015). Deep neural
networks are easily fooled: High confidence predic-
tions for unrecognizable images. In Proc. of the IEEE
Conf. on Computer Vision and Pattern Recognition,
pages 427–436.
Norton, S. W. (2013). An explanation mechanism for
bayesian inferencing systems. In Proc. of the 2nd
Conf. on Uncertainty in Artificial Intelligence.
Park, N.-W., Kyriakidis, P. C., and Hong, S.-Y. (2016). Spa-
tial estimation of classification accuracy using indi-
cator kriging with an image-derived ambiguity index.
Remote Sensing, 8(4):320.
Platt, J. et al. (1999). Probabilistic outputs for support
vector machines and comparisons to regularized like-
lihood methods. Adv. in large margin classifiers,
10(3):61–74.
Raaijmakers, S., Sappelli, M., and Kraaij, W. (2017). Inves-
tigating the interpretability of hidden layers in deep
text mining. In Proc. of SEMANTiCS.
Ribeiro, M. T., Singh, S., and Guestrin, C. (2016a). Nothing
Else Matters: Model-Agnostic Explanations By Iden-
tifying Prediction Invariance.
Ribeiro, M. T., Singh, S., and Guestrin, C. (2016b). Why
should i trust you?: Explaining the predictions of
any classifier. In Proc. of the 22nd ACM SIGKDD
Int. Conf. on Knowledge Discovery and Data Mining,
pages 1135–1144. ACM. arXiv: 1602.04938.
Rippa, S. (1999). An algorithm for selecting a good value
for the parameter c in radial basis function interpola-
tion. Adv. Comput. Math., 11(2):193–210.
Saelid, S., Jenssen, N., and Balchen, J. (1983). Design
and analysis of a dynamic positioning system based
on kalman filtering and optimal control. IEEE Trans.
Autom. Control, 28(3):331–339.
Schaefer, K. E., Straub, E. R., Chen, J. Y., Putney, J., and
Evans, A. W. (2017). Communicating Intent to De-
velop Shared Situation Awareness and Engender Trust
in Human-Agent Teams. Cognit. Syst. Res.
Sch
¨
olkopf, B., Sung, K.-K., Burges, C. J., Girosi, F.,
Niyogi, P., Poggio, T., and Vapnik, V. (1997). Com-
paring support vector machines with gaussian kernels
to radial basis function classifiers. IEEE Trans. Signal
Process., 45(11):2758–2765.
Selvaraju, R. R., Das, A., Vedantam, R., Cogswell, M.,
Parikh, D., and Batra, D. (2016). Grad-cam: Why
did you say that? visual explanations from deep net-
works via gradient-based localization. arXiv preprint
arXiv:1610.02391.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L.,
Van Den Driessche, G., Schrittwieser, J., Antonoglou,
I., Panneershelvam, V., Lanctot, M., et al. (2016).
Mastering the game of go with deep neural networks
and tree search. Nature, 529(7587):484–489.
Swartout, W., Paris, C., and Moore, J. (1991). Explanations
in knowledge systems: Design for explainable expert
systems. IEEE Expert., 6(3):58–64.
van Diggelen, J., van den Broek, H., Schraagen, J. M., and
van der Waa, J. (2017). An intelligent operator support
system for dynamic positioning. In Int. Conf. on Ap-
plied Human Factors and Ergonomics, pages 48–59.
Springer.
Vidovic, M. M.-C., Grnitz, N., Mller, K.-R., and Kloft, M.
(2016). Feature Importance Measure for Non-linear
Learning Algorithms. arXiv:1611.07567 [cs, stat].
arXiv: 1611.07567.
Wettschereck, D., Aha, D. W., and Mohri, T. (1997). A
review and empirical evaluation of feature weighting
methods for a class of lazy learning algorithms. In
Lazy learning, pages 273–314. Springer.
ICM: An Intuitive Model Independent and Accurate Certainty Measure for Machine Learning
321
