On the Probability Density Function of Inter-core Crosstalk Power in

Birefringent Homogeneous Multi-core Fibers

Ricardo O. J. Soeiro

, Tiago M. F. Alves

and Adolfo V. T. Cartaxo

1,2

Instituto de Telecomunicac¸

oes, Lisboa 1049-001, Portugal

ISCTE - Instituto Universit

ario de Lisboa, Lisboa 1649-026, Portugal

Keywords:

Coupled Local Mode Theory, Discrete Changes Model, Dual-polarization, Homogeneous Multi-core Fibers,

Inter-core Crosstalk.

Abstract:

In this paper, the inter-core crosstalk (ICXT) of the polarization directions and the probability density func-

tions (PDFs) of the ICXT power of the polarization directions in weakly coupled birefringent homogeneous

multi-core ﬁbers (MCFs) are studied through numerical simulation. The numerical simulator is based on the

coupled local mode theory (CLMT), which is a rigorous model that has the downside of requiring long com-

putational times to compute the ICXT ﬁeld and PDFs of the ICXT power. Conversely, a dual-polarization

discrete changes model (DP-DCM) that allows for much faster estimates of the ICXT ﬁeld is presented. It is

shown that, for perfectly homogeneous MCFs, the mean ICXT power distribution between the polarization di-

rections is similar, despite the power distribution at the MCF input, for a mean linear birefringence parameter

ranging from 10

−7

(low birefringence) to 10

−4

(high birefringence), and for different MCF bending radii. It

is also shown that the mean ICXT power estimates obtained with the CLMT and DP-DCM are very similar.

Furthermore, using the CLMT, the PDFs of the ICXT power of the polarization directions are shown to be

chi-squared distributions with two degrees of freedom, and the PDF of the sum of the ICXT power of the

polarizations is shown to follow a chi-squared distribution with four degrees of freedom.

1 INTRODUCTION

Multi-core ﬁbers (MCFs) have been proposed to in-

crease capacity in long haul transmission (Qian et al.,

2012), access networks and data centers (Lee et al.,

2014). The similar properties of the cores comprising

homogeneous MCFs has been reported as an attrac-

tive feature for signal transmission (Lu

ıs et al., 2016),

(Sakaguchi et al., 2013). In particular, with cores with

similar properties, similar propagation times of the

signals transmitted in each core are obtained, which

promotes the use of multi-dimensional spatial mod-

ulation formats (Puttnam et al., 2014), shared re-

ceiver resources (Feuer et al., 2012) and space-coding

techniques (Eriksson et al., 2015). However, the

similar properties of the cores also promotes signif-

icant crosstalk between them, i.e. inter-core crosstalk

(ICXT) (Lu

ıs et al., 2016). Signiﬁcant reduction of

the ICXT power can be achieved by designing the

MCF appropriately, e.g., by increasing the distance

between cores, which has the downside of reducing

the core count, or by enveloping the MCF cores in

trenches, the so-called trench assisted MCFs (Sak-

aguchi et al., 2013).

The previously mentioned constraints and com-

promises led to the proposal of several ICXT estima-

tion models that take into account the parameters of

the MCF, e.g. the core radii, distance between cores,

ﬁber bending and twisting, and ﬁber length (Hayashi

et al., 2011), (Macho et al., 2016). The discrete

changes model (DCM) proposed in (Hayashi et al.,

2011) allows to estimate the ICXT while studying its

dependence on the ﬁber bending, twist and length in

a very fast way. In (Hayashi et al., 2011), the ICXT

is reported to result mostly from the points along the

longitudinal direction of propagation in which the dif-

ference between the effective refractive index of the

interfering and interfered cores is zero. These points

are referred to as phase matching points (PMPs).

Meanwhile, other studies were carried to upgrade the

DCM, e.g. in (Lu

ıs et al., 2016) the dependence of

the ICXT on the modulation frequency is included

in the DCM, and in (Cartaxo et al., 2016) the ICXT

dependence on the difference between the dispersion

parameters of the cores is included. In (Soeiro et al.,

2017), the DCM is generalized to a dual-polarization

Soeiro, R., Alves, T. and Cartaxo, A.

On the Probability Density Function of Inter-core Crosstalk Power in Birefringent Homogeneous Multi-core Fibers.

DOI: 10.5220/0006542700360042

In Proceedings of the 6th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2018), pages 36-42

ISBN: 978-989-758-286-8

(DP) scheme. The reason why the DCM has been

upgraded to included other effects can be attributed

to the fast ICXT estimates it provides in compari-

son with other models. In particular, models that rely

on solving the coupled-mode equations numerically

are much more computationally demanding, since the

number of steps required to solve the coupled-mode

equations numerically is much larger than the num-

ber of PMPs required to estimate the ICXT with the

DCM (Cartaxo and Alves, 2017). In (Macho et al.,

2016), the ICXT is estimated with a rigorous coupled

local mode theory (CLMT) model while including the

effects of core birefringence, bending and twisting.

However, the estimates obtained with such model are

much more computationally demanding when com-

pared to the DCM, owing to the necessity of solving

the CLMT equations numerically with a step-size that

can be of the order of the wavelength (≈ 10

−6

m).

In (Hayashi et al., 2012), it is shown experimen-

tally that the probability density function (PDF) of the

total ICXT power, i.e. the PDF of the sum of the

ICXT power of the two polarizations, ﬁts quite well

a chi-squared distribution with four degrees of free-

dom. The following assumptions were proposed to

explain this distribution: i) the four ICXT ﬁeld com-

ponents (the in-phase and quadrature components of

the two polarization directions) are uncorrelated and

ii) the ICXT power is equally distributed between the

polarization directions, and the variances of the in-

phase and quadrature components of the ICXT ﬁeld

in the two polarizations are similar.

In this paper, the distribution of the mean ICXT

power between the polarization directions at the MCF

output is analyzed through numerical simulation with

the CLMT model in weakly-coupled birefringent ho-

mogeneous MCFs, for different power distributions at

the MCF input and for different birefringence param-

eters. Additionally, the PDFs of the ICXT power of

the polarization directions and total ICXT power ob-

tained from the CLMT are studied when the power

distribution between the polarization directions at the

MCF input is imposed, in order to assess whether the

PDFs reported in (Hayashi et al., 2012) are observed

under different power distributions between the polar-

ization directions at the MCF input.

2 DISCRETE CHANGES MODEL

WITH DUAL-POLARIZATION

SCHEME

In this section, the DP-DCM proposed in (Soeiro

et al., 2017) is presented. It is considered that, at

the input of a two-core MCF, the slowly varying ﬁeld

amplitude of the signal to be transmitted in the in-

terfering core m, A

(z = 0), where z denotes the

longitudinal direction of propagation, is distributed

between two perpendicular polarization directions, x

and y. The power distribution between the direc-

tions of polarization x and y is controlled by a vari-

able ζ which takes on a real value between 0 and 1.

At the MCF input, the ﬁeld of each direction of po-

larization is given by A

m,x

(z=0) = A

(z=0)·

ζ and

m,y

(z=0) = A

(z=0)·

1 −ζ. For ICXT analysis,

it is assumed that all the power is injected in core m,

i.e. A

(z = 0) = 0. At the MCF output (z=L, where L

is the MCF length), the ﬁeld amplitudes of the polar-

ization directions of the interfered core n, A

n,x

(z = L)

and A

n,y

(z = L) are given by (Soeiro et al., 2017):

n,x

(z = L) =A

(0)·[

ζ·F

x,x

1 −ζ·F

y,x

] (1)

n,y

(z = L) =A

(0)·[

1 −ζ·F

y,y

ζ·F

x,y

] (2)

where the functions F

x,x

, F

x,y

, F

y,x

and F

y,y

model the

ICXT from the input of the interfering core m to the

output of the interfered core n. In particular, F

x,x

and

x,y

model the ICXT from the polarization x of core

m to the polarizations x and y of core n, respectively.

The functions F

y,x

and F

y,y

model the ICXT from the

polarization y of core m to the polarizations x and y

of core n, respectively. These functions include the

impact of the MCF parameters, e.g. ﬁber bending

and twisting. In general, the functions F are given

by (Soeiro et al., 2017):

a,b

−j

√

·e

−jβ

·K

∑

k=1

−j(β

−β

)·z

−jφ

(a,b)

nm,k

(3)

where a and b ∈ {x, y}, N is the number of PMPs,

is the discrete coupling coefﬁcient obtained from

Eq. (28) of (Cartaxo and Alves, 2017) while substi-

tuting the inter-core coupling coefﬁcient, κ

, by the

average inter-core coupling coefﬁcient of the polar-

ization directions, κ

= (κ

(x)

+ κ

(y)

)/2. β

and β

are the average of the propagation constants of the

polarization directions in cores m and n, respectively,

i.e., β

= (β

(x)

+ β

(y)

)/2 and β

= (β

(x)

+ β

(y)

)/2

(Agrawal, 2001). φ

(a,b)

nm,k

is a random variable, uni-

formly distributed between 0 and 2π, that models ran-

dom variations of the MCF parameters (Hayashi et al.,

2011).

The mean ICXT power of the po-

larization directions x and y are given

by hXT



n,x

(L)|

/|A

(0)|



and

hXT



n,y

(L)|

/|A

(0)|



, respectively, where

h·i is the expected value operator.

On the Probability Density Function of Inter-core Crosstalk Power in Birefringent Homogeneous Multi-core Fibers

The DP-DCM was derived under the conditions

that (Soeiro et al., 2017): (i) equal power distribu-

tion between the polarization directions is observed

at the MCF output, i.e. hXT

i=hXT

i, despite the

value of ζ; (ii) the total mean ICXT power is the

same at the MCF output, despite the value of ζ; (iii)

the in-phase and quadrature components of A

n,x

and

n,y

are uncorrelated, and one way to ensure this is

by imposing that the functions F are uncorrelated

between themselves, i.e. hF

x,x

·F

∗

y,y

i = hF

y,x

·F

∗

x,y

i =

x,x

·F

∗

x,y

i = hF

y,x

·F

∗

y,y

i=0 (Soeiro et al., 2017), where

∗

is the complex conjugate. If conditions (i), (ii)

and (iii) are valid, the total mean ICXT power (the

sum of the ICXT power of the polarization directions)

can be estimated from: hXT i = 2hXT

i = 2hXT

i =

2h|F

a,b

i = N|K

(Soeiro et al., 2017). More de-

tails regarding the DP-DCM and its derivation can be

found in (Soeiro et al., 2017).

3 NUMERICAL RESULTS AND

DISCUSSION

In this section, the numerical simulator based on the

CLMT is described and the main parameters of the

MCF are presented. The CLMT model is used in sub-

sections 3.1 and 3.2 to analyze the mean ICXT power

distribution between the polarization directions and

the PDFs of the ICXT power of the polarization di-

rections, respectively.

The numerical CLMT considers weakly coupled

linear propagation, modeled by Eq. (17) in (Macho

et al., 2016) with the non-linear terms made zero, and

a two-core MCF. Each core of the MCF is divided into

0 20 40 80 100 140 180 220

−22

−20

−18

−16

−14

−12

−10

Number of segments

Mean ICXT power [dB]

Figure 1: Mean ICXT power as a function of the number of

segments for a two-core perfectly homogeneous MCF with

mean linear birefringence of 2 ×10

−7

, ζ = 1, R

= 0.2 m

and f

= 0.1 turns/m.

segments, where in each segment a random birefrin-

gence sample, obtained from a Gaussian distribution

(Macho et al., 2016) is generated. The mean value of

the Gaussian distribution, i.e. the mean linear bire-

fringence, ranges between 10

−7

, corresponding to a

case of low-birefringence, and 10

−4

, corresponding

to a case of high-birefringence (Macho et al., 2016).

The standard deviation is 10

−7

. The refractive index

of the cores is 1.4453, and the refractive index of the

cladding is 1.4381. The radii of the cores is 4 µm

and the distance between cores is 30 µm. The MCF

length considered in the numerical results is 200 m

and the wavelength is 1550 nm. At the MCF input

and at the end of each segment the rotation matrix

shown in Eq. (2) of (Wai et al., 1991) is applied to

the ﬁelds of each core and polarization. The rotation

matrix is used in order to ensure random polariza-

tion coupling and equal power distribution between

the polarization directions. In each segment, the ﬁber

twisting and bending effects are modeled by Eq. 19 of

(Macho et al., 2016). In Fig. 1, the total mean ICXT

power (sum of the mean ICXT power of the polariza-

tion directions) is shown as a function of the number

of segments of the cores. The results of Fig. 1 were

obtained for a two-core perfectly homogeneous MCF

with mean linear birefringence of 2×10

−7

, a bending

radius, R

= 0.2 m, and a ﬁber twist, f

= 0.1 turns/m.

The number of ICXT samples used to compute the

mean ICXT power was 500 since it was concluded

that this number leads to a large enough sample size

to observe convergence of the mean ICXT power es-

timates, i.e. if more samples were used, similar mean

ICXT power estimates would be observed. The num-

ber of segments required to observe convergence of

the estimated mean ICXT power can be identiﬁed

from Fig. 1. In particular, it can be concluded that

40 segments are enough for the mean ICXT power

estimates to stabilize, i.e., if more segments are con-

sidered, the mean ICXT power estimates are similar.

Hence, all the results presented from now on will con-

sider 40 segments per core. Table 1 summarizes the

parameters used in our study.

3.1 Analysis of Mean ICXT Power

Distribution between Polarization

Directions

In this subsection, the power distribution between the

polarization directions is analyzed with the CLMT,

for different power distributions between the polariza-

tion directions at the MCF input and MCF parameters.

The total mean ICXT power, i.e. the sum of the mean

ICXT power of the polarizations at the MCF output

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

Table 1: Main parameters of the 2-core MCF.

Parameter Value

Refractive index of cladding 1.4381

Refractive index of core n (n

) 1.4453

Refractive index of core m (n

) 1.4453

Mean linear birefringence variable

Distance between cores n and m 30 µm

Core radii 4 µm

Bending radius (R

) variable

Fiber twist frequency ( f

) 0.1 turns/m

Fiber length (L) 200 m

Wavelength 1550 nm

−7 −6.5 −6 −5.5 −5 −4.5 −4

−5

−4

−3

−2

−1

log

(Mean linear birefringence)

<XT

> / <XT

> [dB]

−7 −6.5 −6 −5.5 −5 −4.5 −4

−3

−2

−1

<XT

> / <XT

> [dB]

ζ=0

ζ=0.5

ζ=1

= 0.2 m

= 1 m

Figure 2: Difference between the mean ICXT power of the

polarizations in the interfered core n as a function of the

mean linear birefringence for different ζ, R

= 0.2 and 1 m,

and f

= 0.1 turns/m.

is also analyzed, and compared to the estimates of the

DP-DCM.

In Fig. 2, the difference between the mean ICXT

power of the polarizations is shown, in decibel, as a

function of the base-10 logarithm of the mean linear

birefringence, for different ζ and bending radii. In

particular, the results corresponding to the left verti-

cal axis were obtained for R

= 0.2 m and the ones

corresponding to the right vertical axis were obtained

for R

= 1 m. The remaining parameters employed to

obtain the results of Fig. 2 are similar to the ones of

Fig. 1. From the results of Fig. 2, it is possible to con-

clude that similar power distribution between the po-

larization directions is observed in the interfered core

for different ζ and bending radii, as the maximum dif-

ference of mean ICXT power between the polariza-

tion directions is around 0.5 dB. It should be noted

that the difference of mean ICXT power of the po-

larization directions does not follow a pattern, i.e. in

some cases the polarization x has more power than po-

larization y (hX T

i/hXT

i > 0 dB), and in other cases

the opposite occurs (hXT

i/hXT

i < 0 dB). This ob-

servation is important to conclude that the different

ζ, mean linear birefringences and bending radii used

−7 −6.5 −6 −5.5 −5 −4.5 −4

−24

−22

−20

−18

−16

−14

−12

−10

−8

Mean ICXT power [dB]

log

(Mean linear birefringence)

ζ=0

ζ=0.5

ζ=1

= 1 m

= 0.2 m

Figure 3: Total mean ICXT power (sum of the mean ICXT

power of the x and y polarization directions) as a function of

the mean linear birefringence for different ζ, R

= 0.2 and

1 m and f

= 0.1 turns/m.

to obtain the results shown in Fig. 2 do not inﬂuence

the power distribution between the polarization direc-

tions at the MCF output. The ﬂuctuations observed in

Fig. 2 are attributed to the randomness of the samples.

Fig. 3 shows the total mean ICXT power (the sum

of the mean ICXT power of the polarizations) as a

function of the base-10 logarithm of the mean linear

birefringence, for different ζ and bending radii. The

parameters employed to obtain the results of Fig. 3 are

similar to the ones of Fig. 2. From Fig. 3 it is possi-

ble to conclude that, for each bending radius, the total

mean ICXT power is always around the same value

despite ζ and the mean linear birefringence. Further-

more, the total mean ICXT powers shown in Fig. 3

for each bending radius are very similar to the one

obtained though the DP-DCM introduced in Section

2, approximately -20.4 dB and -13.0 dB for bending

radii of 0.2 m and 1 m, respectively, which shows

the accuracy of the DP-DCM. Furthermore, the re-

sults obtained with the DP-DCM are much less com-

putationally demanding than the ones obtained with

the CLMT. This is attributed to the smaller number

of PMPs required to estimate the mean ICXT power

when compared to the number of steps required to

solve the CLMT equations numerically. In particu-

lar, the mean ICXT estimates obtained with the DP-

DCM considered 40 PMPs, whereas the step required

to solve the CLMT equations numerically was 10

−4

m. Since a MCF of 200 m is considered, the number

of steps used in the CLMT was 200/10

−4

=2 ×10

which is more than four orders of magnitude above

the number of PMPs considered in the DP-DCM. As

a consequence, the results obtained with the CLMT

can take several days to obtain, whereas the ones ob-

tained with the DP-DCM only take a few seconds.

On the Probability Density Function of Inter-core Crosstalk Power in Birefringent Homogeneous Multi-core Fibers

0 0.01 0.02 0.03 0.04

−1

PDF

ICXT power of

polarization x

Theoretical

Simulated

Figure 4: PDF of the ICXT power of polarization x, in

logarithmic scale, considering a mean linear birefringence

of 2 × 10

−7

, ζ = 1, R

= 0.2 m and f

= 0.1 turns/m.

The curves obtained through numerical simulation with the

CLMT and the corresponding theoretical one are shown.

3.2 Analysis of the PDFs of ICXT

Power of the Polarization Directions

In this subsection, the PDFs of ICXT power of the po-

larization directions are analyzed. The PDF of the to-

tal ICXT power, i.e. the PDF of the sum of the ICXT

power of the polarization directions is also analyzed.

In Figs. 4 and 5, the PDFs of the ICXT power of

polarizations x and y are shown, respectively, obtained

for ζ = 1, a mean linear birefringence of 2 ×10

−7

= 0.2 m, f

= 0.1 turns/m and using 125000 sam-

ples of ICXT power. The y-axis of Figs. 4 and 5 is in

logarithmic scale, and the PDFs obtained through nu-

merical simulation with the CLMT are compared with

theoretical ones. In Figs. 4 and 5, the theoretical PDFs

of the ICXT power in x and y polarizations are chi-

squared distributions with two degrees of freedom.

The variances of each one of the ﬁeld components (in-

phase and quadrature) of the ICXT ﬁeld in the x and

y polarizations are hXT

i/2 and hXT

i/2,respectively,

where hXT

i and hXT

i are computed from the sim-

ulation results. Since hXT

i ≈ hXT

i, it follows that

the variances of each one of the ﬁeld components are

also similar. The agreement between the simulation

and theoretical PDFs shown in Figs. 4 and 5 con-

ﬁrms Hayashi’s statement that the PDFs of the po-

larization directions should be chi-squared distribu-

tions with two degrees of freedom and similar mean

power (Hayashi et al., 2011), even if all the power is

injected in the x polarization at the MCF input (ζ = 1).

It should be noted that the discrepancy between the

theoretical and simulation curves shown in Figs. 4

and 5 is larger for the tail of the PDF. This is a conse-

0 0.01 0.02 0.03 0.04

−1

PDF

ICXT power of

polarization y

Theoretical

Simulated

Figure 5: PDF of the ICXT power of polarization y, in

logarithmic scale, considering a mean linear birefringence

of 2 × 10

−7

, ζ = 1, R

= 0.2 m and f

= 0.1 turns/m.

The curves obtained through numerical simulation with the

CLMT and the corresponding theoretical one are shown.

quence of the limited amount of ICXT power samples

obtained through numerical simulation. In particular,

the lower the probability density, the less likely we

are to obtain the corresponding ICXT power through

numerical simulation. Thus, the lower the probabil-

ity density, the larger the total number of samples we

need to consider.

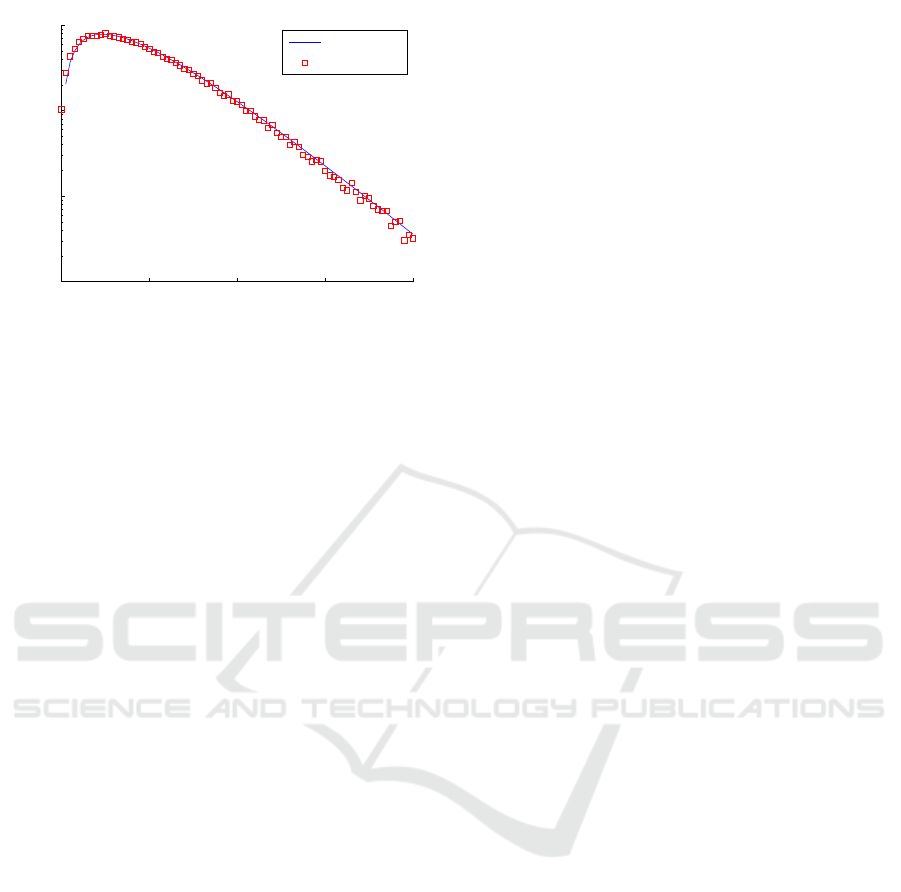
In Fig. 6, the PDF of the sum of the ICXT power

of the polarization directions is shown while consid-

ering the same parameters of Figs. 4 and 5. The y-

axis of Fig. 6 is also in a logarithmic scale, and the

comparison between the PDF obtained through nu-

merical simulation with the theoretical one is also

shown. In Fig. 6, the theoretical PDF curve of the to-

tal ICXT power is obtained from the expression of the

chi-squared distribution with four degrees of freedom.

The variance of each one of the ﬁeld components (in-

phase and quadrature) of the ICXT ﬁeld in the x and y

polarizations is (hXT

i+ hXT

i)/4, where hX T

i and

hXT

i are obtained from the numerical results. The

PDFs shown in Fig. 6 conﬁrm also Hayashi’s results

(Hayashi et al., 2012), even if all the power is injected

in the x polarization at the MCF input (ζ = 1). Similar

conclusions were drawn for other power distributions

between the polarization directions at the MCF input

and bending radii.

4 CONCLUSIONS

The mean ICXT power distribution between the po-

larization directions and PDFs of the ICXT power of

the polarization directions were analyzed in weakly

coupled birefringent homogeneous MCFs through nu-

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology

0 0.01 0.02 0.03 0.04

−1

PDF

ICXT power of

polarizations x+y

Theoretical

Simulated

Figure 6: PDF of the total ICXT power of the polarization

directions, in logarithmic scale, considering a mean linear

birefringence of 2 ×10

−7

, ζ = 1, R

= 0.2 m, f

= 0.1

turns/m. The curves obtained through numerical simulation

with the CLMT and the corresponding theoretical one are

shown.

merical simulation. The numerical simulator based on

the CLMT model allowed to conclude that, for per-

fectly homogeneous MCFs, the mean ICXT power

distribution between the polarization directions is

similar, despite the power distribution at the MCF in-

put, for a mean linear birefringence parameter ranging

from 10

−7

(low birefringence) to 10

−4

(high birefrin-

gence), and for different MCF bending radii. It was

also concluded that the total mean ICXT power es-

timates obtained with the CLMT and DP-DCM are

very similar. Additionally, the PDFs of the ICXT

power of the polarization directions obtained with the

CLMT were shown to be chi-squared distributions

with two degrees of freedom, and the PDF of the sum

of the ICXT power of the polarizations was shown

to be a chi-squared distribution with four degrees

of freedom, showing that Hayashi’s results (Hayashi

et al., 2012) are valid for different power distributions

between the polarization directions at the MCF input.

ACKNOWLEDGEMENTS

This work was supported by Fundac¸

ao para a

encia e Tecnologia (FCT), Portugal, under the

project AMEN-UID/EEA/50008/2013 of Instituto de

Telecomunicac¸

oes, and the FCT researcher contract

IF/01225/2015/CP1310/CT0001.

REFERENCES

Agrawal, G. (2001). Nonlinear Fiber Optics. Academic

Press, 3rd edition.

Cartaxo, A. V. T. and Alves, T. M. F. (2017). Discrete

changes model of inter-core crosstalk of real homoge-

neous multi-core ﬁbers. Journal of Lightwave Tech-

nology, 35(12):2398–2408.

Cartaxo, A. V. T., Lu

ıs, R. S., Puttnam, B. J., Hayashi, T.,

Awaji, Y., and Wada, N. (2016). Dispersion impact

on the crosstalk amplitude response of homogeneous

multi-core ﬁbers. IEEE Photonics Technology Letters,

28(17):1858–1861.

Eriksson, T. A., Lu

ıs, R. S., Puttnam, B. J., Mendinueta,

J. M. D., Andrekson, P. A., Karlsson, M., Awaji, Y.,

Wada, N., and Agrell, E. (2015). Single parity check-

coded 16qam over spatial superchannels in multicore

ﬁber transmission. Optics Express, 23(11):14569–

14582.

Feuer, M. D., Nelson, L. E., Zhou, X., Woodward, S. L.,

Isaac, R., Zhu, B., Taunay, T. F., Fishteyn, M., Fini,

J. M., and Yan, M. F. (2012). Joint digital signal

processing receivers for spatial superchannels. IEEE

Photonics Technology Letters, 24(21):1957–1960.

Hayashi, T., Taru, T., Shimakawa, O., Sasaki, T., and

Sasaoka, E. (2011). Design and fabrication of ultra-

low crosstalk and low-loss multi-core ﬁber. Optics

Express, 19(17):16576–16592.

Hayashi, T., Taru, T., Shimakawa, O., Sasaki, T., and

Sasaoka, E. (2012). Characterization of crosstalk in

ultra-low-crosstalk multi-core ﬁber. Journal of Light-

wave Technology, 30(4):583–589.

Lee, Y., Tanaka, K., Nomoto, E., Arimoto, H., and Sug-

awara, T. (2014). Multi-core ﬁber technology for

optical-access and short-range links. In 2014 12th

International Conference on Optical Internet 2014

(COIN), pages 1–2.

ıs, R. S., Puttnam, B. J., Cartaxo, A. V. T., Klaus, W.,

Mendinueta, J. M. D., Awaji, Y., Wada, N., Nakan-

ishi, T., Hayashi, T., and Sasaki, T. (2016). Time and

modulation frequency dependence of crosstalk in ho-

mogeneous multi-core ﬁbers. Journal of Lightwave

Technology, 34(2):441–447.

Macho, A., Garc

ıa-Meca, C., Fraile-Pel

aez, F. J., Morant,

M., and Llorente, R. (2016). Birefringence effects in

multi-core ﬁber: coupled local-mode theory. Optics

Express, 24(19):21415–21434.

Puttnam, B. J., Eriksson, T. A., Mendinueta, J.-M. D., Lu

ıs,

R. S., Awaji, Y., Wada, N., Karlsson, M., and Agrell,

E. (2014). Modulation formats for multi-core ﬁber

transmission. Optics Express, 22(26):32457–32469.

Qian, D., Ip, E., Huang, M.-F., jun Li, M., Dogariu, A.,

Zhang, S., Shao, Y., Huang, Y.-K., Zhang, Y., Cheng,

X., Tian, Y., Ji, P., Collier, A., Geng, Y., Linares, J.,

Montero, C., Moreno, V., Prieto, X., and Wang, T.

(2012). 1.05pb/s transmission with 109b/s/hz spectral

efﬁciency using hybrid single- and few-mode cores. In

Frontiers in Optics 2012/Laser Science XXVIII, page

FW6C.3. OSA.

On the Probability Density Function of Inter-core Crosstalk Power in Birefringent Homogeneous Multi-core Fibers

Sakaguchi, J., Puttnam, B. J., Klaus, W., Awaji, Y., Wada,

N., Kanno, A., Kawanishi, T., Imamura, K., Inaba, H.,

Mukasa, K., Sugizaki, R., Kobayashi, T., and Watan-

abe, M. (2013). 305 tb/s space division multiplexed

transmission using homogeneous 19-core ﬁber. Jour-

nal of Lightwave Technology, 31(4):554–562.

Soeiro, R. O. J., Alves, T. M. F., and Cartaxo, A. V. T.

(2017). Dual polarization discrete changes model of

inter-core crosstalk in multi-core ﬁbers. IEEE Pho-

tonics Technology Letters, 29(16):1395–1398.

Wai, P. K. A., Menyuk, C. R., and Chen, H. H. (1991).

Stability of solitons in randomly varying birefringent

ﬁbers. Optics Letters, 16(16):1231–1233.

PHOTOPTICS 2018 - 6th International Conference on Photonics, Optics and Laser Technology