Unfolding Ensemble Training Sets for Improved Support Vector

Decoders in Energy Management

Joerg Bremer and Sebastian Lehnhoff

Department of Computing Science, University of Oldenburg, Uhlhornsweg, Oldenburg, Germany

R&D Division Energy, OFFIS – Institute for Information Technology, Escherweg, Oldenburg, Germany

Keywords:

Flexibility Modeling, Folded Distributions, Simulated Annealing, Predictive Scheduling.

Abstract:

Smart grid control demands delegation of liabilities to distributed, rather small energy resources in contrast to

todays large control power units. Distributed energy scheduling constitutes a complex task for optimization

algorithms regarding the underlying high-dimensional, multimodal and nonlinear problem structure. Addi-

tionally, the necessity for abstraction from individual capabilities is given while integrating energy units into

a general optimization model. For predictive scheduling with high penetration of renewable energy resources,

agent-based approaches using classiﬁer-based decoders for modeling individual ﬂexibilities have shown good

performance. On the other hand, such decoder-based methods are currently designed for single entities and

not able to cope with ensembles of energy resources. Combining training sets randomly sampled from individ-

ually modeled energy units, results in folded distributions with unfavorable properties for training a decoder.

Nevertheless, this happens to be a quite frequent use case, e. g. when a hotel, a small business, a school or

similar with an ensemble of co-generation, heat pump, solar power, and controllable consumers wants to take

part in decentralized predictive scheduling. We use a Simulated Annealing approach to correct the unsuitable

distribution of instances in the aggregated ensemble training set prior to deriving a ﬂexibility model. Feasibil-

ity is ensured by integrating individual ﬂexibility models of the respective energy units as boundary penalty

while the mutation drives instances from the training set through the feasible region of the energy ensemble.

Applicability is demonstrated by several simulations using established models for energy unit simulation.

1 INTRODUCTION

Across Europe, especially in Germany where a ﬁ-

nancial security of guaranteed feed-in prices is given

since 1991, the share of distributed energy resources

(DER) is rapidly growing. Following the goal de-

ﬁned by the European Commission (European Par-

liament & Council, 2009), a concept for integration

into electricity markets is needed (Abarrategui et al.,

2009; Nieße et al., 2012) leading in turn to a need for

grouping small energy resources due to their rather

low potential and ﬂexibility and for predictive plan-

ning. A well-known concept for aggregating DER

to a jointly controllable entity is known as virtual

power plant (VPP). Apart from controlling distributed

electricity generation, e. g. combined heat and power

(CHP), photovoltaic or wind power, controllable con-

sumption like shiftable loads, heat pumps or air con-

ditioning might also be included for planning active

power schedules. Battery storages are discussed to

complement such groups of DER.

The general optimization problem to be solved for

scheduling in a VPP is known as predictive schedul-

ing (day-ahead based on predicted conditions) as

approach for the unit commitment problem (Padhy,

2004). Under given constraints, energy unit’s opera-

tion modes have to be chosen for each unit such that

the joint operation meets some desired load proﬁle for

a given planning horizon.

In order to choose an appropriate schedule of op-

eration modes for each participating DER, the algo-

rithm must know for each DER, which schedules are

actually operable and which are not. Depending on

the type of DER, different constraints restrict possible

operations. The information about individual local

feasibility of schedules has to be modeled appropri-

ately in (distributed) optimization scenarios, in order

to allow unit independent algorithm development. For

this purpose, meta-models of constrained spaces of

operable schedules have been shown indispensable as

a means for independently modeling constraints and

feasible regions of ﬂexibility. Each energy unit has its

322

Bremer, J. and Lehnhoff, S.

Unfolding Ensemble Training Sets for Improved Support Vector Decoders in Energy Management.

DOI: 10.5220/0006543503220329

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 322-329

ISBN: 978-989-758-275-2

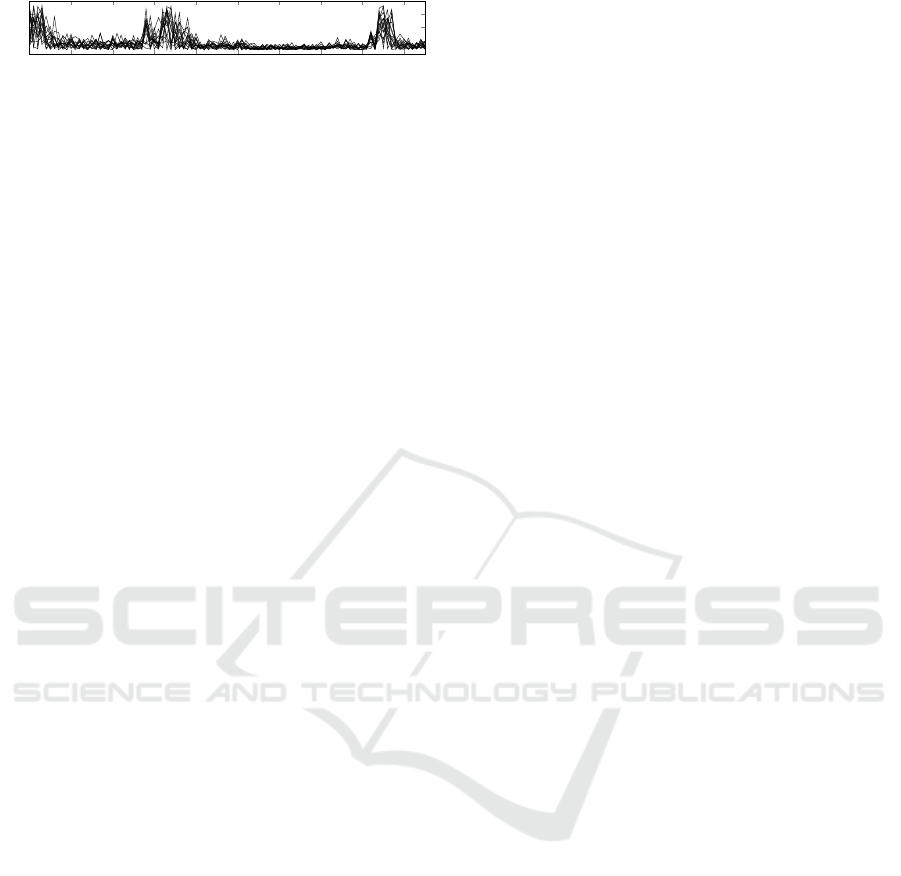
0 10 20 30 40

50 60

70 80 90

time of day / no. of 15 minute intervall

power / kW

Figure 1: Example for a training set of schedules for a co-

generation plant. A state-of-charge of 50% at night and an

increased thermal demand for showering in the morning and

dish washing in the evening result in higher ﬂexibilities dur-

ing these periods.

own individual ﬂexibility – i. e. the set of schedules

that might be operated without violating any tech-

nical operational constraint – based on the capabili-

ties of the unit, operation conditions (weather, etc.),

cost restrictions and so forth. Modeling ﬂexibility

independently from speciﬁc energy units demands a

means for meta-modeling that allows model indepen-

dent access to feasibility information. (Bremer et al.,

2011) introduced a support vector based model that

captures individual feasible regions from training sets

of operable example schedules. Figure 1 shows an

example training set for a co-generation plant. An ex-

tend use case for systematic solution repair with these

models has been introduced in (Bremer and Sonnen-

schein, 2013a). Agent-based approaches can derive a

so called support vector decoder automatically from

the surrogate model and use it as a means for sys-

tematically generating feasible solutions without do-

main knowledge on the (possible, situational) opera-

tions of the controlled energy resource. In general,

the idea works in two successive stages – a decoder

training phase and the actual planning phase. First a

training set of feasible schedules is generated for each

energy unit using a situationally parametrized simu-

lation model of the energy unit. Then, the ﬂexibility

model is derived from the training set. During the suc-

ceeding load planning phase, these decoders may be

used by an optimization algorithm that determines the

optimal partition of a given active power target sched-

ule into schedules for each single unit. The decoder

automatically generates feasible solutions. With this

approach as abstraction layer, the solver does not need

any domain knowledge about the energy units, their

individual constraints, or possible operation.

An example for a recently developed agent ap-

proach for fully decentralized predictive scheduling

is given by the combinatorial heuristics for distributed

agents (COHDA). In COHDA (Hinrichs, 2014) each

agent locally decides on feasible schedules for the

represented unit with a decoder, but, as soon as an

agent has to represent a local ensemble of energy

units instead of a single device, a problem arises be-

cause usually only ﬂexibility models of single units

are available and a concept for statistically sound ag-

gregating a set of ﬂexibility models is missing so far

(Bremer and Lehnhoff, 2017). Generating a single

decoder for handling all constraints and feasible op-

erations of the whole ensemble is hardly possible due

to statistical problems when combining training sets

from individually sampled ﬂexibility models. Due to

the folded densities only a very small portion from

the interior of the feasible region (the dense region)

is captured by the machine learning process. But, a

combined training set is needed. The same holds true

for any other centralized or agent-based orchestration.

In this paper, an approach is presented that intro-

duces an intermediate density optimization step into

the training process. Schedules from individual train-

ing sets modeling individual ﬂexibilities are aggre-

gated to a joint training set. The skewed, aggregated

training set is then unfolded by Simulated Annealing.

The feasibility of the joint training set is maintained

by using the individual feasibility models.

2 PREDICTIVE SCHEDULING

AND FLEXIBILITY MODELING

Virtual power plants are a means for aggregating

and controlling DER (Awerbuch and Preston, 1997).

In scenarios with independently operated units, self-

organizing algorithms are required also for coordina-

tion. In general, distributed control schemes based

on multi-agent systems are considered advantageous

for large-scale problems as expected in future smart

grids due to the large number of distributed energy

resources that take over control tasks from large-scale

central power plants (Nieße et al., 2012). Some recent

implementations are (Hinrichs et al., 2013; Ramchurn

et al., 2011; Kamphuis et al., 2007).

One of the crucial challenges in operating a VPP

arises from the complexity of the scheduling task due

to the large amount of (small) energy units in the dis-

tribution grid (McArthur et al., 2007). In the fol-

lowing, we consider predictive scheduling, where the

goal is to select exactly one schedule x

for each con-

trolled energy unit U

from a search space F

of feasi-

ble schedules speciﬁc to the possible operations and

technical constraints of unit U

and with respect to

a future planning horizon, such that a global objec-

tive function (e. g. resembling a target power proﬁle)

is optimized by the sum of individual contributions. A

basic formulation of the scheduling problem is given

i“1

, ζ

Ñ min; s. t. x

P F

P U. (1)

In equation (1) δ denotes an (in general) arbi-

trary distance measure for evaluating the difference

Unfolding Ensemble Training Sets for Improved Support Vector Decoders in Energy Management

323

Φ : X Ñ H

´1

pSq

(a)

pkq

(b)

Figure 2: General support vector decoder scheme for solu-

tion repair and constraint handling (Bremer and Lehnhoff,

2017).

between the aggregated schedule of the group and the

desired target schedule ζ

ζ. W. l. o. g. we assume that

the Euclidean distance is used.

To each energy unit U

exactly one schedule x

has to be assigned. The desired target schedule is

given by ζ

ζ. Solving this problem without unit inde-

pendent constraint handling leads to speciﬁc imple-

mentations that are not suitable for handling changes

in VPP composition or unit setup and thus leads to

enlarged integration cost for new units.

Flexibility modeling can be understood as the

task of modeling constraints for energy units. Apart

from global VPP constraints, constraints often appear

within single energy components; affecting the local

decision making. Popular methods treat constraints

or aggregations of constraints as separate objectives

or penalties, leading to a transformation into a (un-

constrained) many-objective problem (Kramer, 2010;

Smith and Coit, 1997).

For optimization approaches in smart grid scenar-

ios, black-box models capable of abstracting from the

intrinsic model have proved useful (Pinto et al., 2017;

Gieseke and Kramer, 2013; Schiendorfer et al., 2014;

Bremer and Sonnenschein, 2013a). The units do not

need to be known at compile time. A powerful, yet

ﬂexible way of constraint-handling is the use of a de-

coder that gives a search algorithm hints on where to

look for schedules satisfying local hard constraints

(Bremer and Sonnenschein, 2013b; Coello Coello,

2002).

Thus, a decoder allows for a targeted search by.

It imposing a relationship between a decoder solution

and a feasible solution (Coello Coello, 2002).

A schedule of an energy unit can be seen as a real

valued vector x

x “ px

, . . . , x

q P F

Ă R

with each el-

ement x

denoting mean electrical power during the

jth time interval. F

denotes the speciﬁc feasible sub-

set of schedules that may be operated by energy unit

without violating any technical constraints.

Fig. 2 shows the idea of a support vector decoder

starting with a set of feasible example schedules de-

rived from a simulation model of the respective en-

ergy unit and using it as a stencil for the region that

contains just feasible schedules.

A training set X containing only valid schedules,

can e. g. be derived after a sampling approach from

(Bremer and Sonnenschein, 2013c). From such a

training set, a support vector data description (SVDD)

can derive a geometrical description of the sub-space

that contains the given data (Tax and Duin, 2004); in

our case: the set of feasible schedules. As a prere-

quisite, the samples from the training set have to be

distributed appropriately across the feasible region.

Given a set of data samples, the enclosing envelope

(a model of the feasible region and thus of the ﬂexi-

bility) can be derived as follows: After mapping the

data to a high dimensional feature space, the small-

est enclosing ball in this feature space is determined.

When mapping back the ball to data space, it forms a

set of contours enclosing the given data sample.

This task is achieved by determining a mapping

Φ : X Ă F Ă R

Ñ H ; x ÞÑ Φpxq such that all data

from a training set X is mapped to a minimal hyper-

sphere in H . The minimal sphere with radius R and

center a in H that encloses tΦpx

can be derived

from minimizing }Φpx

q ´ a}

ď R

` ξ

with slack

variables ξ

ě 0 for a smoother ball.

After some relaxations one gets two main out-

comes: the center a “

Φpx

q (with β

β weight-

ing the impact of different schedules) of the minimal

sphere in terms of an expansion into H and a function

that allows to determine the distance of the image of

an arbitrary point from a P H , calculated in R

is de-

rived: R

xq “ 1´2

kpx

, x

xq`

i, j

kpx

, x

with a kernel k that substitutes dot products in Hilbert

space. Because all support vectors are mapped onto

the surface of the sphere, the sphere radius R

can be

easily determined by the distance of an arbitrary sup-

port vector to the center. Thus the feasible region can

now be modeled by a ﬂexibility model M

“ tx

x P R

|Rpx

xq ď R

u « X . (2)

The model can be used as a black-box that abstracts

from any explicitly given form of constraints and al-

lows for a decision on whether a given solution is fea-

sible or not. At the same time, decoders serve as an

abstraction layer. Learned from a training set of fea-

sible example schedules, a decoder hides all unit spe-

ciﬁc details. In this way, no domain speciﬁc knowl-

edge on possible operation, constraints or cost of in-

corporated energy units have to be implemented or

integrated into the algorithm.

For our experiments, we used a decoder as de-

scribed in (Bremer and Sonnenschein, 2013a). Here,

a decoder γ is given as mapping function for sched-

ules x

x γ : R

Ñ R

; γpx

xq ÞÑ x

. With x

having the

following properties (Sonnenschein et al., 2014):

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

324

• x

is operable by the respective energy unit with-

out violating any constraint,

• the distance }x

x ´ x

} is small and small depends

on the problem at hand and often denotes the

smallest distance of x

x to the feasible region.

The right hand side of Figure 2(b) shows how such a

decoder can be derived from model (2). If a schedule

is feasible it is inside the feasible region (grey area

on the left in Fig. 2(b)). Thus, the schedule is in-

side the pre-image (modeling the feasible region) of

the ball and thus its high-dimensional image lies in-

side the ball. An infeasible schedule (e. g. x

x in Fig.

2(b)) lies outside the feasible region and thus its im-

age

lies outside the ball. But, some relations are

known: the center, the distance of the image from the

center and the radius of the ball. Hence, the image

of an infeasible schedule can be moved along the dif-

ference vector towards the center until it touches the

ball. Then, the pre-image of the moved image

rep-

resents a repaired schedule x

at the boundary of the

feasible region. No mathematical description of the

original feasible region or of the constraints is needed

to do this. More sophisticated variants of transfor-

mation are e. g. given in (Bremer and Sonnenschein,

2013a).

With such decoder concept for constraint handling

one can now reformulate the optimization problem as

i“1

q, ζ

Ñ min, (3)

where γ

is the decoder function of unit i that pro-

duces feasible, schedules from x

x P r0, p

max

(with

rated power p

max

) resulting in schedules that are oper-

able by that unit. Please note, that with this constraint

free formulation, many standard algorithms for opti-

mization can be easily adapted and no domain speciﬁc

implementation (regarding the energy units and their

operation schedules) has to be integrated. Equation

(3) is used as a surrogate objective to ﬁnd the solution

to the constrained optimization problem equation (1).

So far, this approach has been proven to work ﬁne

if each entity in a virtual power plant is modeled as

a single controlled entity. On the other hand, many

scenarios exist where also ensembles of energy units

should be integrated. In (Bremer and Lehnhoff, 2017)

the problem has been circumvented by integrating a

second level optimization for orchestrating an ensem-

ble internally and representing it by a single coordi-

nating agent. This approach entails additional opti-

mization effort into the overall coordinating process.

Thus, a single ﬂexibility model would be desirable as

an abstraction layer for ensembles of energy units.

3 SAMPLING FROM

ENSEMBLES OF ENERGY

UNITS

Sometimes the technical equipment of a single unit

in a VPP consists of more than just a single genera-

tor (or prosumer or controllable load). Nevertheless,

the owner as operator is still represented by a sin-

gle controlling agent when embedded into a decen-

tralized agent-based control scheme inside a virtual

power plant. In this case that agent has to handle the

ensemble of energy units as a single unit (in a sense

as a single sub VPP) and negotiate to the other agents

with the aggregated ﬂexibility. Nevertheless, there is

usually no joint model of the whole ensemble, and

thus the agent has to use an individual model of each

unit and thus a set of individual decoders for deciding

on an aggregated schedule for the ensemble.

If an agent covers a set of energy units instead of

a single unit, a decoder for the joint feasible region

of the group of units has to be used. A model of the

operation of the ensemble of units is often not avail-

able. Using the training sets of individual energy units

and randomly combining them (adding up exactly one

from each training set) to joint schedules in order to

gain a training set for the joint behavior is not tar-

geted. The problem is that all source trainings sets

are independent random samples and thus the result-

ing training set exhibits a density (of operable power

levels) that results from folding the source distribu-

tions. Figure 3 shows an example. Uniformly dis-

tributed values for levels of power as in the case of

an co-generation plant with sufﬁcient buffer capac-

ity fold up – in case of ensembles with more than

one CHP – to an multi-modal Irvin-Hall-distribution

(Hall, 1927). This distribution has some similarities

to a sharp normal distribution and the more samples

(energy units in the ensemble) are folded the more

leptokurtic the pdf gets. This leads to a sample with a

very high density in the middle of the feasible region.

At the outskirts the sample is extremely sparse. Thus,

instances from the outer parts are neglected as out-

liers from the support vector approach that generates

the surrogate model and the decoder.

For this reason, a decoder trained from such a

training sample reproduces only a very small, inner

portion of the feasible region. In this way, most of the

ﬂexibility that an ensemble could bring in into a vir-

tual power plant control is neglected. This can also be

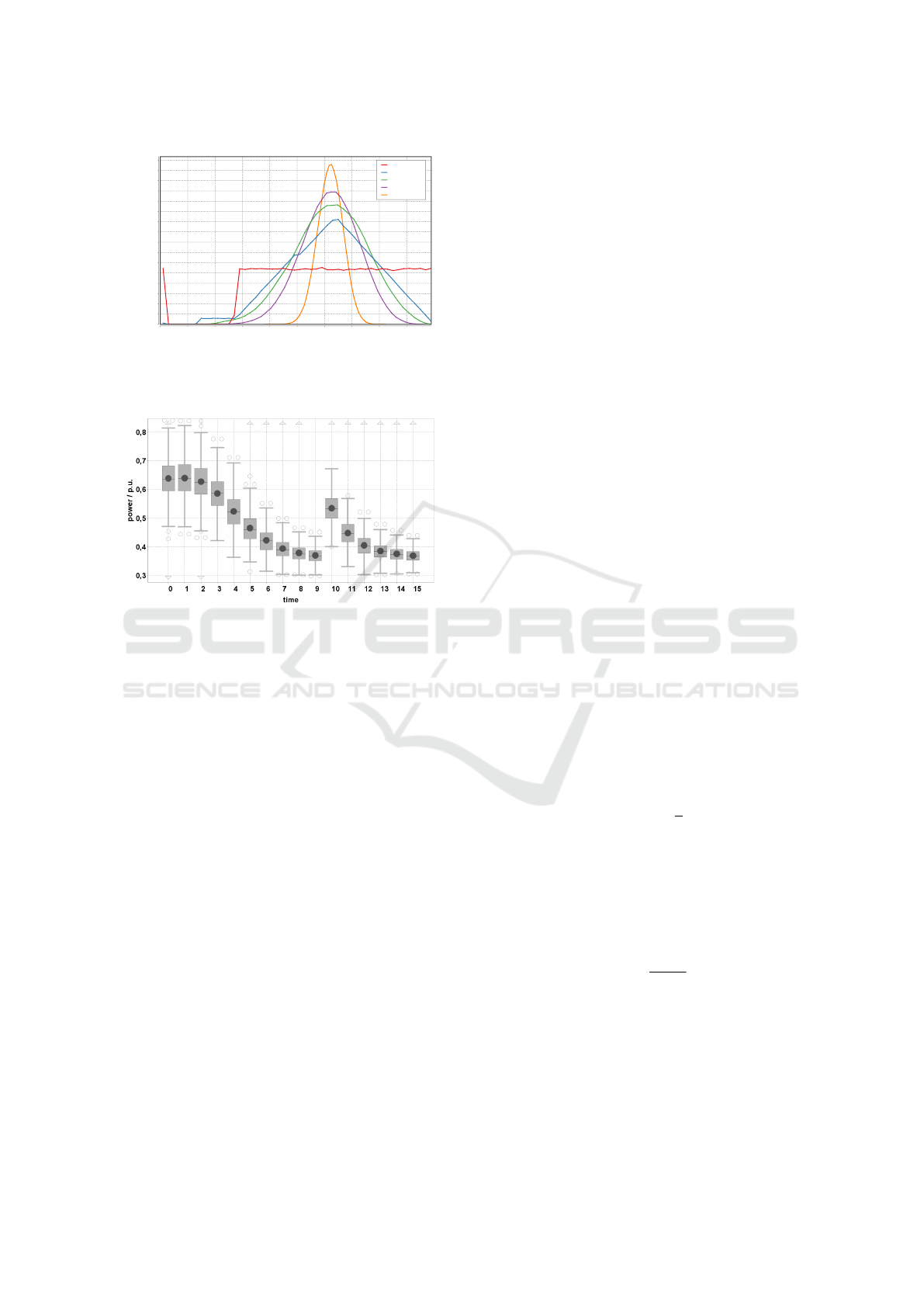
seen in Figure 4. The rather small grey boxes repre-

sent the data (power levels for different time intervals)

that actually should spread over the area denoted by

the outer whiskers. Only the small inner part is going

to be learned by a model.

Unfolding Ensemble Training Sets for Improved Support Vector Decoders in Energy Management

325

0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9

power level / p.u.

0,000

0,005

0,010

0,015

0,020

0,025

0,030

0,035

0,040

0,045

0,050

0,055

0,060

0,065

0,070

0,075

0,080

rel. frequency

1 energy unit

2 energy units

3 energy units

5 energy units

25 energy units

Figure 3: Probability density of different numbers of folded

distributions of operable power levels for co-generation

plants.

Figure 4: Probability distribution of power levels at differ-

ent time intervals of an ensemble of 10 micro CHP units.

The training set exhibits a concentration in the inner part of

the whole ﬂexibility (grey boxes denoting 3{4 of the sam-

ples) making it highly imbalanced.

4 OPTIMIZING THE SAMPLE

DISTRIBUTION

To overcome the problem of folded distributions in

ensemble training sets, we introduce a post process-

ing step that improves a training set of feasible sched-

ules by trying to equally distribute the schedules from

a randomly generated training set across the whole

feasible region that reﬂects the joint ﬂexibility of the

ensemble of energy units.

To achieve this task, we use a Simulated Anneal-

ing approach (Kirkpatrick et al., 1983).

For optimization we consider the following

model. For each energy unit U

a training set X

“

Ď F

Ă R

of feasible schedules is given. Now,

we can deﬁne a set of matrices X

“ tX

, . . . , X

with

“

P X

Ď F

P X

Ď F

‹

‚

, (4)

with uniformly distributed random indices

, . . . , r

„ Up1, mq. Then, row j in matrix X

repre-

sents a randomly chosen sample of a feasible schedule

from energy unit U

. The joint training set that re-

ﬂects the ﬂexibility of the whole group of energy units

can now be deﬁned as X

“ tSpX

q, . . . , SpX

qu,

with SpX

q “

i“1

P X

: ith row of matrix

). In X

each element represents the sum of

randomly chosen elements (schedules); one from

each energy unit in the group. In this way, X

represents the aggregated ﬂexibility of the group. For

deriving a machine learning model, this training set

is hardly suitable because of the folded densities due

to summing up over different random series. In the

next step, we want to improve this training set by

correcting the unfavorable densities. To do this, we

ﬁrst deﬁne

q “

d´1

i“1

txu

i, j

txu

pi`1q, j

. (5)

Function h

q denotes a concave hull (Duckham

et al., 2008) around the training set and as the calcula-

tion of high-dimensional concave hulls quickly grows

intractable, we approximate by summing up over a set

of 2-dimensional concave hulls around neighboring

cross-sections through the d-dimensional schedules

in the training set. Maximizing the area of the con-

cave hull Aph

q ensures that the ﬂexibility is captured

also at the outskirts of the feasible region. In order

to spread samples equally across this maximized area,

the second indicator comes into play. Let x

j,1

ď x

j,2

¨¨¨ ď x

j,m

be the sorted values of the jth elements of

and let x

“ x

i,2

´ x

i,1

, x

i,3

´ x

i,2

, . . . , x

i,n

´ x

i,m´1

be the series of successive differences. Now we deﬁne

the variance

“

m´1

i“1

n´1

jě1

‚

(6)

to measure the spread of differences of the vectors

in the training set. Minimizing this spread ensures

equalizing the spread across the feasible region.

With these two indicators we can now deﬁne our

objective: minimize E:

EpX

qw ¨ σ

1 ´ w

Aph

Ñ min (7)

as a weighted mixture of both criteria, which is to be

optimized with respect to the following constraint.Let

“ SpX

q P X

be an instance from the ensemble

training set. We deﬁne feasibility over SpX

q: x

feasible (cf. Eq. (2)) iff

P F

^ pX

P F

^ ¨¨¨ ^ pX

P F

, (8)

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

326

for all units U

, . . . , U

in the ensemble U of all units.

In Eq. (8) feasibility of an aggregated schedule x

is checked by probing whether all schedules (rows)

from the respective component matrix that make up

the aggregated schedule are feasible for the respective

energy unit. This can be easily tested with the help of

the respective unit speciﬁc ﬂexibility models tM u as

described in Eq. (2).

Simulated Annealing (Kirkpatrick et al., 1983) is

an established Markov Chain Monte Carlo Methods

(MCMC) for non-linear optimization. It mimics a

physical cooling process. In general, MCMC meth-

ods are an effective tool for statistical sampling ap-

plied to optimization problems (Li et al., 2009).

Algorithm 1 shows the general process for opti-

mizing the unfavorable densities due to the folded dis-

tributions in aggregated ensemble training sets. First,

for each energy unit in the group, a speciﬁc train-

ing set is sampled from an appropriately parameter-

ized simulation model and a ﬂexibility model M

trained for units i. Each of these ﬂexibility models is

able to decide for the respective energy unit whether a

given schedule is operable or not. Next, the algorithm

is initialized with temperature ϑ, weights w for the ob-

jective and a cooling rate. While no stopping criterion

is met the following loop is executed. The training set

is mutated to generate a new offspring training set.

The mutation operator for our Simulated Annealing

is deﬁned as follows:

“ X

„ N p0, σ

‹

‚

. (9)

Mutation is done by adding a vector with normal dis-

tributed random values (with variance σ

as step size)

to a randomly chosen instance r

„ Up1, mq from X

Not necessarily all components have to be mutated

at the same time. Algorithm 1 shows a version with

only 20% of the components mutated. The feasibility

of the mutated training set element is checked with

the help of the set of ﬂexibility models tM

u. If the

mutated element is not feasible, it is rejected until a

feasible version is found. With this barrier approach

feasibility of the solution is ensured. Finally, the ob-

jective value of mutated training set is compared with

the old one and accepted (or not) after the metropolis

criterion.

5 RESULTS

To evaluate the effectiveness of our approach, we sim-

ulated ensembles of non-homogeneous micro-CHP of

Algorithm 1 : Basic scheme for the Simulated Annealing

approach for ensemble training set improvement.

sample units

build models tM

for single units

build X

and X

initialize temperature ϑ and weights w

while ϑ ă ϑ

min

repeat

Ð X

j Ð r „ Up0, mq

for c “ 1; c ă m; c++ do

if r „ Up0, 1q ď 0.2 then

j,c

Ð X

` r „ N p0, σ

end if

end for

check feasibility Eq. (8)

until mutation feasible

if e

q´EpX

ą r „ U p0, 1q then

end if

ϑ Ð coolingpϑq

end while

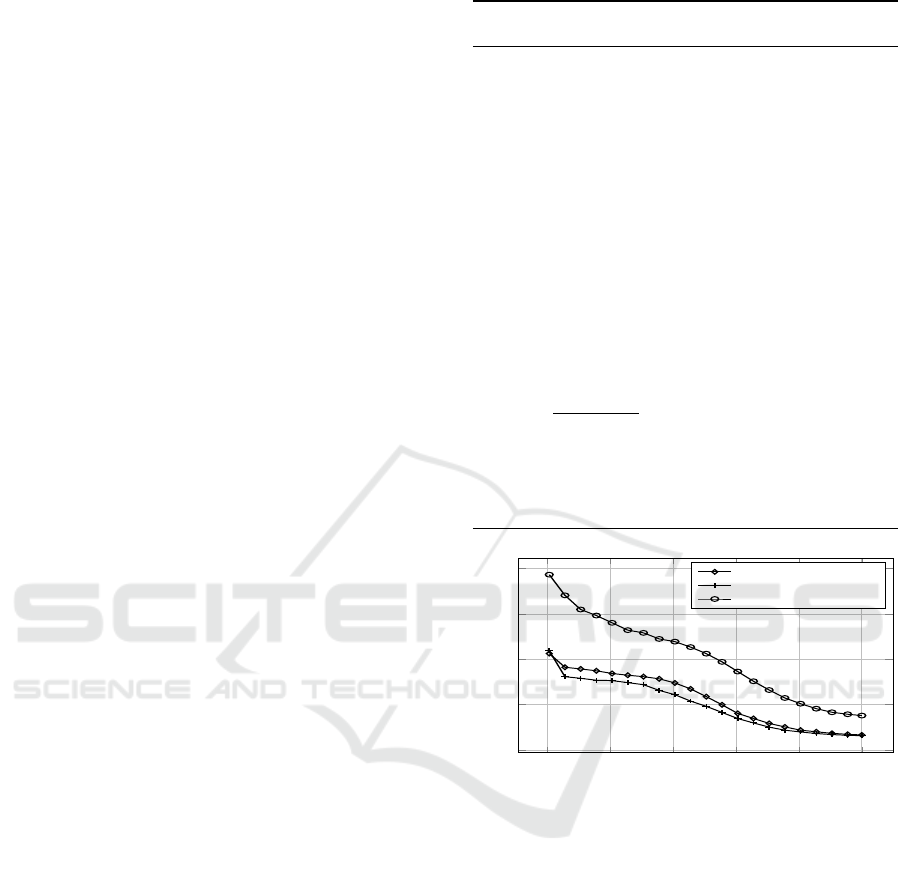
0 0.2 0.4

0.6

0.8 1

¨10

iteration

error

d “ 5, n “ 10, σ

“ 1%

d “ 5, n “ 10, σ

“ 5%

d “ 16, n “ 10, σ

“ 1%

Figure 5: Convergence of the SA approach.

different size. We tested the performance of re-

spectively two classiﬁers that make up the ﬂexibility

model (one trained with the original ensemble train-

ing set and one trained with the respective optimized

training set). Table 1 shows the result for different en-

semble sizes up to groups of 50 units. Up to 40 units

the Simulated Annealing approach works very well.

Table 1 compares for both classiﬁers the accuracy, the

sensitivity, the speciﬁcity and the miss rate respec-

tively calculated by comparing the classiﬁcation re-

sult (feasible and thus operable by the ensemble, or

not) with the simulation model (simulating whether a

schedule is really operable, or not).

The accuracy denotes the rate of correctly classi-

ﬁed schedules (feasible as well as not feasible). Af-

ter optimizing and planing the training set, the trained

classiﬁers perform almost as well as in the single unit

case (Bremer et al., 2011). In the case of 50 units

Unfolding Ensemble Training Sets for Improved Support Vector Decoders in Energy Management

327

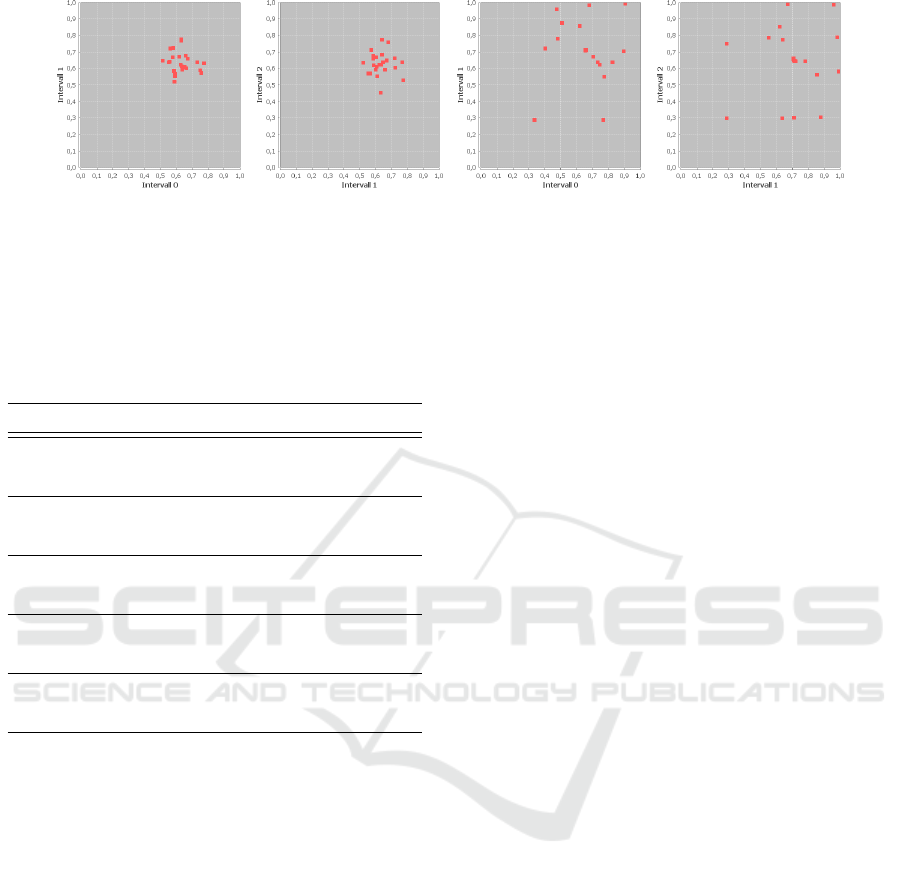
(a) (b)

Figure 6: Before-and-after test for an ensemble of 20 micro-co-generation plants with 5-dimensional schedules. (a) shows the

aggregated training set before unfolding and the improvement after (b).

Table 1: Classiﬁer performances of classiﬁers (search space

models) trained with the original training set (X

orig

) with

folded power level distributions and with the improved

training sets (X

opt

) optimized with the SA approach.

# units set accuracy sensitivity speciﬁcity miss

m “ 10

orig

0.493 0.027 0.999 0.972

opt

0.935 0.921 0.951 0.078

m “ 20

orig

0.506 0.043 1.000 0.957

opt

0.938 0.903 0.975 0.097

m “ 30

orig

0.513 0.002 0.999 0.997

opt

0.964 0.963 0.964 0.037

m “ 40

orig

0.497 0.002 1.000 0.998

opt

0.907 0.843 0.972 0.157

m “ 50

orig

0.572 0.001 1.000 0.999

opt

0.577 0.015 0.998 0.985

(or more) the improvement drops rapidly. The sen-

sitivity shows the share of correctly classiﬁed feasi-

ble schedules. The speciﬁcity, on the other hand, de-

notes the rate of correctly classiﬁed infeasible sched-

ules (compared with all schedules). This score of

course is unbeatable high for the original training set,

because with this training set the feasible region is

seriously underestimated in size (only a small, cen-

tral sub-region is learned) and thus almost never in-

feasible schedules at the boundary of the real (lots

larger) regions is falsely classiﬁed. Nevertheless, the

improved training set performs almost as good. The

miss rate shows the rate of falsely classiﬁed infea-

sible schedules which drops signiﬁcantly after op-

timizing the training set. A visual impression of

the improvement that is achieved by the optimiza-

tion of the training set can be seen in Figure 6. The

ﬁgure shows 2-dimensional intersections through 5-

dimensional schedules before and after optimization.

The convergence of the algorithms has been tested on

several scenarios. Figure 5 shows some of the results.

6 CONCLUSION AND FURTHER

WORK

Using machine learning approaches for ﬂexibility

modeling and automatically deriving decoders from

these models for efﬁcient and domain knowledge in-

dependent implementation of (distributed) optimiza-

tion methods has proven a useful tool in managing the

future smart grid. So far, these models can only be

applied to single energy units, because distributions

of power levels in the training sets of single units fold

up when aggregating them to ensemble training sets.

Thus, the training set render useless for appropriately

deriving a model for the joint ﬂexibility of a group of

energy units. We presented an approach to overcome

the problem of folded distributions when training de-

coders for ensembles of energy resources in predictive

scheduling. For this reason, we introduced an inter-

mediate step prior to model training. After aggregat-

ing schedules from training sets for the ﬂexibility of

individual energy resources (resulting in a training set

with an abnormally high density of training instances

in the middle of the feasible region), a Simulated An-

nealing step attenuates this skewed density while at

the same time maintaining the feasibility of the sched-

ules.

Future work still has to show whether the process

of correcting the training set density can be achieved

sufﬁciently fast also for short term predictive schedul-

ing. Up to now, the Simulated Annealing approach

takes up to several minutes to complete. Another

necessary improvement will distribute the training set

correction to a fully decentralized approach. Never-

theless, the results so far demonstrate the feasibility

of correcting to training set of ensembles of energy

units.

With our approach also households, hotels, small

businesses, schools or similar with an ensemble of co-

generation, heat pump, solar power, and controllable

consumers will be able to take part in agent-based

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

328

decentralized predictive scheduling for providing en-

ergy services in future smart grid architectures with-

out a need for an (expensive) individual link of each

single device in the ensemble.

REFERENCES

Abarrategui, O., Marti, J., and Gonzalez, A. (2009). Con-

structing the active european power grid. In Proceed-

ings of WCPEE09, Cairo.

Awerbuch, S. and Preston, A. M., editors (1997). The Vir-

tual Utility: Accounting, Technology & Competitive

Aspects of the Emerging Industry, volume 26 of Top-

ics in Regulatory Economics and Policy. Kluwer Aca-

demic Publishers.

Bremer, J. and Lehnhoff, S. (2017). Hybrid Multi-ensemble

Scheduling, pages 342–358. Springer International

Publishing, Cham.

Bremer, J., Rapp, B., and Sonnenschein, M. (2011). Encod-

ing distributed search spaces for virtual power plants.

In IEEE Symposium Series on Computational Intelli-

gence 2011 (SSCI 2011), Paris, France.

Bremer, J. and Sonnenschein, M. (2013a). Constraint-

handling for optimization with support vector sur-

rogate models. In Filipe, J. and Fred, A., editors,

ICAART 2013 – Proceedings of the 5th International

Conference on Agents and Artiﬁcial Intelligence, vol-

ume 2, pages 91–105, Barcelona, Spain. SciTePress.

Bremer, J. and Sonnenschein, M. (2013b). Model-based in-

tegration of constrained search spaces into distributed

planning of active power provision. Comput. Sci. Inf.

Syst., 10(4):1823–1854.

Bremer, J. and Sonnenschein, M. (2013c). Sampling the

search space of energy resources for self-organized,

agent-based planning of active power provision. In

Page, B., Fleischer, A. G., G

obel, J., and Wohlgemuth,

V., editors, 27th International Conference on Environ-

mental Informatics for Environmental Protection, En-

viroInfo 2013, pages 214–222. Shaker.

Coello Coello, C. A. (2002). Theoretical and numerical

constraint-handling techniques used with evolutionary

algorithms: a survey of the state of the art. Com-

puter Methods in Applied Mechanics and Engineer-

ing, 191(11-12):1245–1287.

Duckham, M., Kulik, L., Worboys, M., and Galton, A.

(2008). Efﬁcient generation of simple polygons for

characterizing the shape of a set of points in the plane.

Pattern Recognition, 41(10):3224 – 3236.

European Parliament & Council (2009). Directive

2009/28/ec of 23 april 2009 on the promotion of the

use of energy from renewable sources and amending

and subsequently repealing directives 2001/77/ec and

2003/30/ec.

Gieseke, F. and Kramer, O. (2013). Towards non-linear

constraint estimation for expensive optimization. In

Esparcia-Alc

azar, A., editor, Applications of Evolu-

tionary Computation, volume 7835 of LNCS, pages

459–468. Springer Berlin Heidelberg.

Hall, P. (1927). The distribution of means for samples of

size n drawn from a population in which the variate

takes values between 0 and 1, all such values being

equally probable. Biometrika, 19(3/4):pp. 240–245.

Hinrichs, C. (2014). Selbstorganisierte Einsatzplanung

dezentraler Akteure im Smart Grid. PhD thesis, Carl

von Ossietzky Universitt Oldenburg.

Hinrichs, C., Bremer, J., and Sonnenschein, M. (2013). Dis-

tributed Hybrid Constraint Handling in Large Scale

Virtual Power Plants. In IEEE PES Conference on In-

novative Smart Grid Technologies Europe (ISGT Eu-

rope 2013). IEEE Power & Energy Society.

Kamphuis, R., Warmer, C., Hommelberg, M., and Kok, K.

(2007). Massive coordination of dispersed generation

using powermatcher based software agents. In 19th

International Conference on Electricity Distribution.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. Science,

220(4598):671–680.

Kramer, O. (2010). A review of constraint-handling tech-

niques for evolution strategies. Appl. Comp. Intell.

Soft Comput., 2010:1–19.

Li, Y., Protopopescu, V. A., Arnold, N., Zhang, X., and

Gorin, A. (2009). Hybrid parallel tempering and sim-

ulated annealing method. Applied Mathematics and

Computation, 212(1):216–228.

McArthur, S., Davidson, E., Catterson, V., Dimeas, A.,

Hatziargyriou, N., Ponci, F., and Funabashi, T. (2007).

Multi-agent systems for power engineering applica-

tions – Part I: Concepts, approaches, and technical

challenges. IEEE Transactions on Power Systems,

22(4):1743–1752.

Nieße, A., Lehnhoff, S., Tr

oschel, M., Uslar, M., Wiss-

ing, C., Appelrath, H.-J., and Sonnenschein, M.

(2012). Market–based self–organized provision of ac-

tive power and ancillary services. IEEE.

Padhy, N. (2004). Unit Commitment - A Bibliographi-

cal Survey. IEEE Transactions on Power Systems,

19(2):1196–1205.

Pinto, R., Bessa, R. J., and Matos, M. A. (2017). Surrogate

model of multi-period ﬂexibility from a home energy

management system. CoRR, abs/1703.08825.

Ramchurn, S. D., Vytelingum, P., Rogers, A., and Jennings,

N. R. (2011). Agent-based homeostatic control for

green energy in the smart grid. ACM Trans. Intell.

Syst. Technol., 2(4):35:1–35:28.

Schiendorfer, A., Stegh

ofer, J.-P., and Reif, W. (2014). Syn-

thesised constraint models for distributed energy man-

agement. In Ganzha, M., Maciaszek, L. A., and Pa-

przycki, M., editors, Proceedings of the Federated

Conference on Computer Science and Information

Systems, pages 1529–1538, Warsaw, Poland.

Smith, A. and Coit, D. (1997). Handbook of Evolutionary

Computation, chapter Penalty Functions, page Section

C5.2. Oxford University Press and IOP Publishing,

Department of Industrial Engineering, University of

Pittsburgh, USA.

Sonnenschein, M., L

unsdorf, O., Bremer, J., and Tr

oschel,

M. (2014). Decentralized control of units in smart

grids for the support of renewable energy supply. En-

vironmental Impact Assessment Review, (0):–.

Tax, D. M. J. and Duin, R. P. W. (2004). Support vector data

description. Mach. Learn., 54(1):45–66.

Unfolding Ensemble Training Sets for Improved Support Vector Decoders in Energy Management

329