Searching for Effective and Efﬁcient Way of Knowledge Transfer within

an Organization

Agnieszka Kowalska-Stycze

, Krzysztof Malarz

and Kamil Paradowski

Silesian University of Technology, Faculty of Organization and Management,

ul. Roosevelta 26/28, PL-41800 Zabrze, Poland

AGH University of Science and Technology, Faculty of Physics and Applied Computer Science,

al. Mickiewicza 30, PL-30059 Krakow, Poland

Keywords:

Knowledge Transfer, Distributed Leadership, Complex Systems, Organisations as Complex Systems, Cellular

Automata.

Abstract:

In this paper three models of knowledge transfer in organization are considered. In the ﬁrst model (A) the

transfer of chunks of knowledge among agents is possible only when the sender has exactly one more chunks

of knowledge than recipient. This is not dissimilar with bounded conﬁdence model of opinion dynamics. In

the second model (B) the knowledge transfer take place when sender is “smarter” than recipient. Finally, in the

third scenario (model C) we allow for knowledge transfer also when sender posses the same or greater number

of chunks of knowledge as recipient. The simulation bases on cellular automata technique. The organization

members occupy nodes of square lattice and they interact only with their nearest neighbors. With computer

simulations we show, that the efﬁciency and the effectiveness of knowledge transfer i) for model C is better

than for model B ii) and it is worse for model A than for model B.

1 INTRODUCTION

Numerous studies show a relationship between social

interaction and knowledge transfer effectiveness and

organization performance. For example, Chen and

Huang (Chen and Huang, 2007) studied the impact

of organizational climate and organizational structure

for knowledge management from the perspective of

social interaction. The authors of Ref. (Chen and

Huang, 2007) emphasize that the competitiveness of

companies depends not only on knowledge creation,

but mainly from the knowledge diffusion and applica-

tion of knowledge in the organization. They also point

out that, when the organizational structure is less for-

mal, social interaction is more favorable for the trans-

fer and improves the process of knowledge manage-

ment. It was observed also that friendship networks

signiﬁcantly support the transfer of knowledge, be-

cause in such situation i) the enhanced cooperation,

ii) eased competition iii) and better exchange of in-

formation take place (Ingram and Roberts, 2000).

The inﬂuence of the structure of a network of

informal contacts on knowledge transfer was also

studied by the Reagans and McEvily (Reagans and

McEvily, 2003). The study was conducted at R & D

sector, which has a very horizontal organizational

structure, without a formal hierarchy and which em-

ploys mostly scientists and engineers. The authors of

Ref. (Reagans and McEvily, 2003) analyzed, among

others, such factors as: i) the ease of knowledge trans-

fer from the source to the recipient, ii) codiﬁabil-

ity (ease of availability of knowledge for others), iii)

the strength of ties (the intensity of the connections

in terms of the emotional closeness, iv) and the fre-

quency of communication). Their ﬁndings indicate

that i) both social cohesion and long range of interac-

tions facilitate the transfer of knowledge and ii) strong

ties should be used for the transfer of tacit knowledge.

All these works show the importance of social inter-

action, especially informal contacts in the process of

knowledge transfer. Moreover, Reagan and McEvily

(Reagans and McEvily, 2003) demonstrated, that both

strong ties and a dense network of contacts facilitate

knowledge transfer. Such an approach is an indication

to the simulation research and bottom-up approach,

in which relationships at the local level generate the

phenomenon on a global level (i.e. at the level of the

whole organization). Therefore we use the technique

of cellular automata (CA) to model the knowledge

transfer basing on close relationships between mem-

bers of the organization. In our research we focus

on the transfer of knowledge within the organization,

Kowalska-Stycze

n, A., Malarz, K. and Paradowski, K.

Searching for Effective and Efﬁcient Way of Knowledge Transfer within an Organization.

DOI: 10.5220/0006546701510158

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 1, pages 151-158

ISBN: 978-989-758-275-2

151

because, as postulated by Watson and Hewett (Wat-

son and Hewett, 2006), acquiring the knowledge con-

tained within the organization is the key i) to building

a competitive advantage and ii) to improve business

performance. New knowledge is created when people

communicate and share their knowledge, assimilate it

and apply it (Wah, 1999). As Davenport and Prusak

add, knowledge exists in humans and is an integral

part of human complexity and unpredictability (Dav-

enport and Prusak, 2000).

As pointed out by P

erez-Nordtvedt et al. (P

erez-

Nordtvedt et al., 2008), a complete picture of knowl-

edge transfer yield two dimensions of knowledge

transfer: the effectiveness and the efﬁciency. There-

fore, we study different ways of transfer knowledge

and we are looking for the most efﬁcient and effective

way of transferring knowledge in the organization. It

should be noted that the effectiveness is understood

as the level of adoption of knowledge by the entity

receiving (Jensen and Szulanski, 2007), and the efﬁ-

ciency is deﬁned as the speed with which the recipi-

ent acquires new knowledge (P

erez-Nordtvedt et al.,

2008).

We use agent-base modelling. Such a simula-

tion approach for the study of knowledge transfer was

used for example by (Morone and Taylor, 2004; Xuan

et al., 2011; Hirshman et al., 2011; Giacchi et al.,

2016). These studies concerned mainly the impact of

the network properties on the transfer of knowledge

within the network of organization members. Our

goal is to study how knowledge is transferred in the

organization. Based on empirical results (Boone and

Ganeshan, 2008; Alipour et al., 2011; Reagans and

McEvily, 2003) and models of (Morone and Taylor,

2004), Hirshman et al. (Hirshman et al., 2011) we

propose three versions of the knowledge transfer CA

model to examine what way of knowledge transfer in

an organization is more efﬁcient and effective. We

hope the answer to this question will provide practi-

cal guidance for managers to support the transfer of

knowledge in the organization.

In the proposed CA model the lattice fully popu-

lated by agents is used and the von Neumann neigh-

bourhood of four neighbours (as in the model of (Mo-

rone and Taylor, 2004)). This assumption reﬂects a

dense network of social interaction and strong ties

among agents. This is consistent with the research

of (Reagans and McEvily, 2003) and (Hirshman et al.,

2011), who point out, that the number of strong ties is

on average less than six.

The starting point for our research is recently pro-

posed a CA model (Kowalska-Stycze

n et al., 2017), in

which the transfer of knowledge between agents (the

receiver and sender) is blocked if a distance of their

knowledge (measured by the difference in the number

of chunks of knowledge) is larger than one. Such ap-

proach is consistent with Deffuant et al. model (Def-

fuant et al., 2000) of opinion dynamics where opin-

ion exchange among agents is possible only when

sender and recipient have similar opinions (Hegsel-

mann and Krause, 2002; Malarz, 2006; Kułakowski,

2009; Malarz et al., 2011; Malarz and Kułakowski,

2014). In addition, we propose a model in which

the knowledge transfer is possible if sender has more

chunks of knowledge than recipient and model when

knowledge exchange takes place among agents with

the same or greater numbers of chunks of knowledge:

We assume that the transferred knowledge consists of

certain chunks of knowledge. This concept was in-

spired by model of (Hirshman et al., 2011), where the

transferred knowledge consisted of certain facts (ele-

ments, pieces of knowledge) and studies of (Reagans

and McEvily, 2003), who point out that knowledge in

the ﬁrm is into areas (pieces) of expertise.

2 MODEL

In Ref. (Kowalska-Stycze

n et al., 2017) a CA to sim-

ulate the knowledge transfer within an organization

was deﬁned. To describe a CA one should deﬁne i)

a d-dimensional network, ii) the set of states of net-

work nodes iii) and the rule deﬁning the system dy-

namics. The above mentioned rule deﬁnes state of

node in discrete time t + 1 basing on this node and

its neighborhood state in time t. Here we assume

a two-dimensional square lattice with von Neumann

neighborhood, i.e. node (agent) at discrete coordinate

(x, y) ∈ N × N and 1 ≤ x, y ≤ L has only four near-

est neighbors at (x

, y

) ∈ {(x − 1, y),(x + 1, y), (x, y −

1), (x, y + 1)}. The set of states describes chunks of

knowledge possessed by the agent. Namely, the vec-

tor variable

C(x, y,t) = [c

(x, y,t), c

(x, y,t), ··· , c

(x, y,t)]

indicates if agent at time t and at the coordination

(x, y) posses k-th chunk of knowledge [c

(x, y,t) = 1]

or not [c

(x, y,t) = 0] among K chunks of knowledge

desired by organization for their members. Initially

(at t = 0), each agent has each chunk of knowledge

with probability p. Every time step t agent at (x, y)

may inherit single chunk of knowledge from one of

its randomly selected neighbor.

2.1 Model A

For model proposed in Ref. (Kowalska-Stycze

n et al.,

2017) the transfer of chunks of knowledge among

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

152

100

0 5 10 15 20 25 30

n(k)[%]

k =

(a) model A: p = 0.2

100

0 5 10 15 20 25 30

n(k)[%]

k =

100

0 5 10 15 20 25 30

n(k)[%]

k =

(e) model C: p = 0.2

100

0 2 4 6 8 10

n(k)[%]

k =

(b) model A: p = 0.5

100

0 2 4 6 8 10

n(k)[%]

k =

(d) model B: p = 0.5

100

0 2 4 6 8 10

n(k)[%]

k =

(f) model C: p = 0.5

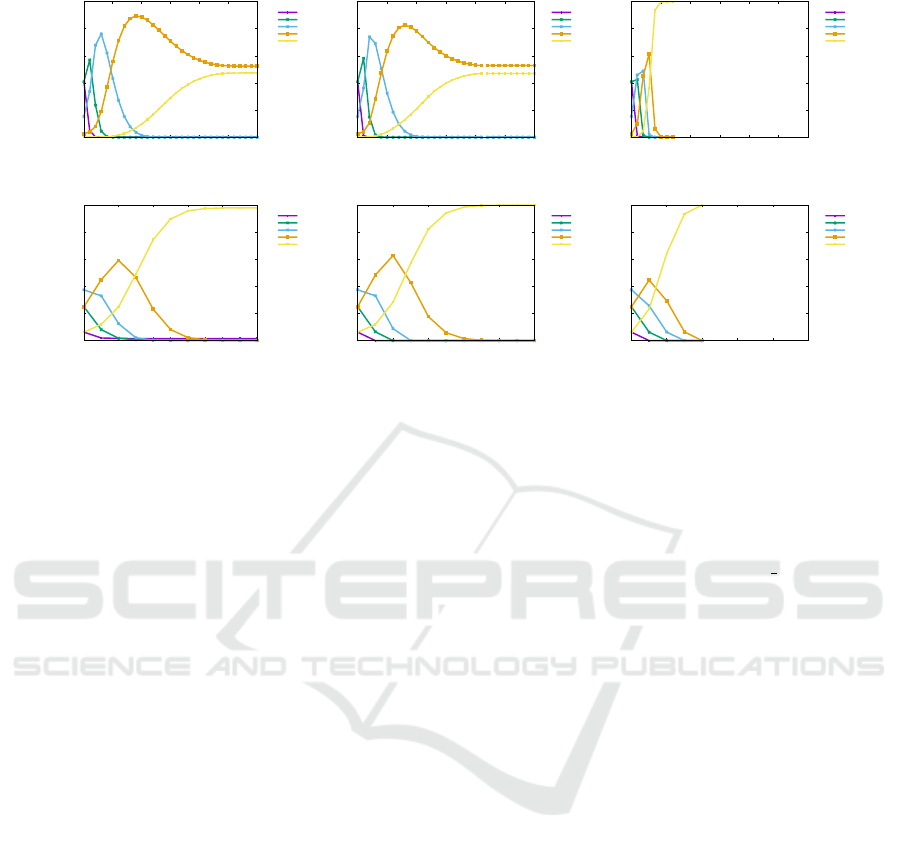
Figure 1: The time evolution of the fraction n(k) of agents having k chunks of knowledge for L = 20, K = 4 and various

initial concentration p of chunks of knowledge among agents. The results are averaged over M = 10

independent simulations.

(a)-(b) model A, (c)-(d) model B, (e)-(f) model C.

agents is possible only when the sender has exactly

one more chunks of knowledge than recipient:

(x, y,t + 1) = 1 ⇐⇒ c

(x, y,t) = 0

and c

, y

,t) = 1 and ν(x

, y

,t) = ν(x, y,t)+1,

(1)

where ν(x, y, t) and ν(x

, y

,t) are numbers of chunks

of knowledge at time t for receiver and sender of

knowledge, respectively.

2.2 Model B

As we mentioned in the Introduction, here we would

like to omit the restriction of knowledge transfer

only from senders having exactly one more chunk of

knowledge than recipient. Namely, we allow for send-

ing chunk of knowledge from neighbors at (x

, y

) to

recipient at (x,y) if sender has more chunks of knowl-

edge than recipient:

(x, y,t + 1) = 1 ⇐⇒ c

(x, y,t) = 0

and c

, y

,t) = 1 and ν(x

, y

,t) > ν(x, y, t). (2)

2.3 Model C

Finally, we modify the rule described in Sec. 2.2 in

order to allowing for transfer of chunks of knowledge

among agents with the same or grater numbers of

chunks of knowledge:

(x, y,t + 1) = 1 ⇐⇒ c

(x, y,t) = 0

and c

, y

,t) = 1 and ν(x

, y

,t) ≥ ν(x, y, t). (3)

In further part of this paper we will refer to

these three models as model A [Eq. (1)], model B

[Eq. (2)] and model C [Eq. (3)], respectively. Java

applet presenting system evolution is available at

http://www.zis.agh.edu.pl/knowledge transfer/.

3 THE DESIGN OF

EXPERIMENTS

Experiments that have been conducted were designed

to investigate which of the three models gives the

most effective and efﬁcient transfer of knowledge.

Similarly to the work (Kowalska-Stycze

n et al.,

2017), the following independent variables were cho-

sen in the designed experiments: i) maximal number

of chunks of knowledge K ii) and initial concentration

of chunks of knowledge p.

Our goal is to seek the most efﬁcient and the

most effective way to transfer knowledge. In view

of the above, we deﬁne the corresponding variables

describing these two parameters of knowledge trans-

fer. Firstly, as the dependent variable describing an

effectiveness of knowledge transfer the following pa-

rameters were adopted:

• the fraction n(k) of agents having k chunks of

knowledge,

• the fraction n(K) of agents having all chunks of

knowledge,

• the fraction f (k) of agents having k-th chunk of

knowledge c

Searching for Effective and Efﬁcient Way of Knowledge Transfer within an Organization

153

• the coverage h f i of any chunks of knowledge c

agents knowledge, i.e. the fraction of knowledge

chunks held by typical member of the organiza-

tion.

Secondly, as the dependent variable describing an ef-

ﬁciency of knowledge transfer, the time τ necessary

for reaching a stationary state was adopted.

4 RESULTS

In order to compare efﬁciency of the knowledge trans-

fer among newly proposed (Sec. 2.2 and 2.3) and

previously discussed (Sec. 2.1) models we have re-

produced some results presented in Ref. (Kowalska-

Stycze

n et al., 2017) but for ten times better statistic,

i.e. for M = 10

, where M is the number of indepen-

dent simulations used for averaging procedure. This

number of independent simulations is also applied for

simulations based on models B and C.

4.1 Time Evolution of the Fraction of

Agents Having k Chunks of

Knowledge

In Fig. 1 the time evolution of the fraction n(k) of

agents having k chunks of knowledge for L = 20,

K = 4 and p = 0.2, 0.5 and for various models are

presented. The fraction n(k) is formally deﬁned as

n(k) ≡

∑

r=1

(k)

, (4)

where N

(k) stands for the number of agents having

exactly k chunks of knowledge in r-th simulation, M

is the number of independent simulations and L is lin-

ear size of the system. For low initial concentration

of chunks of knowledge among agents (p = 0.2) the

differences between results of model A and model B

seems to be negligible, except that time τ of reach-

ing the stationary state is a little bit shorter for model

B. The same apply for p = 0.5. Here however, addi-

tionally we observe that fraction of agents possessing

less than K chunks of knowledge vanishes for long

enough simulation times. Simultaneously, the frac-

tion of agents with all chunks of knowledge saturates

at n(K) = 1 while n(K) < 1 for simulations based

on model A. These effects are enhanced when model

C is applied. Moreover, for model C the fraction

of agents with all chunks of knowledge increases to

n(K) = 1 even for low initial level (p = 0.2) of chunks

of knowledge among agents.

The effectiveness of the knowledge transfer mea-

sured by n(k) depends on p and on the method of

knowledge transfer (models A, B, C) as presented in

Fig. 1. The greater initial concentration p of chunks

of knowledge the higher the percentage n(k) of agents

having k chunks of knowledge, as can be seen by

comparing upper [Fig. 1(a, c, e), p = 0.2] and lower

[Fig. 1(b, d, f), p = 0.5] panels of Fig. 1. Furthermore,

comparing the results for model A, B and C one can

see that the knowledge transfer is most effective in the

case of the model C while it is quite similar in the case

of models A and B.

Now let us look at the efﬁciency of knowledge

transfer. In Fig. 1 the efﬁciency can be understood

as the time (number of simulation steps) required to

obtain the maximum fraction n(k) of agents having k

chunks of knowledge. In the case of the model C, the

time of the transfer of knowledge is much shorter than

for models A and B.

4.2 Time Evolution of the Fraction of

Agents Having All Chunks of

Knowledge

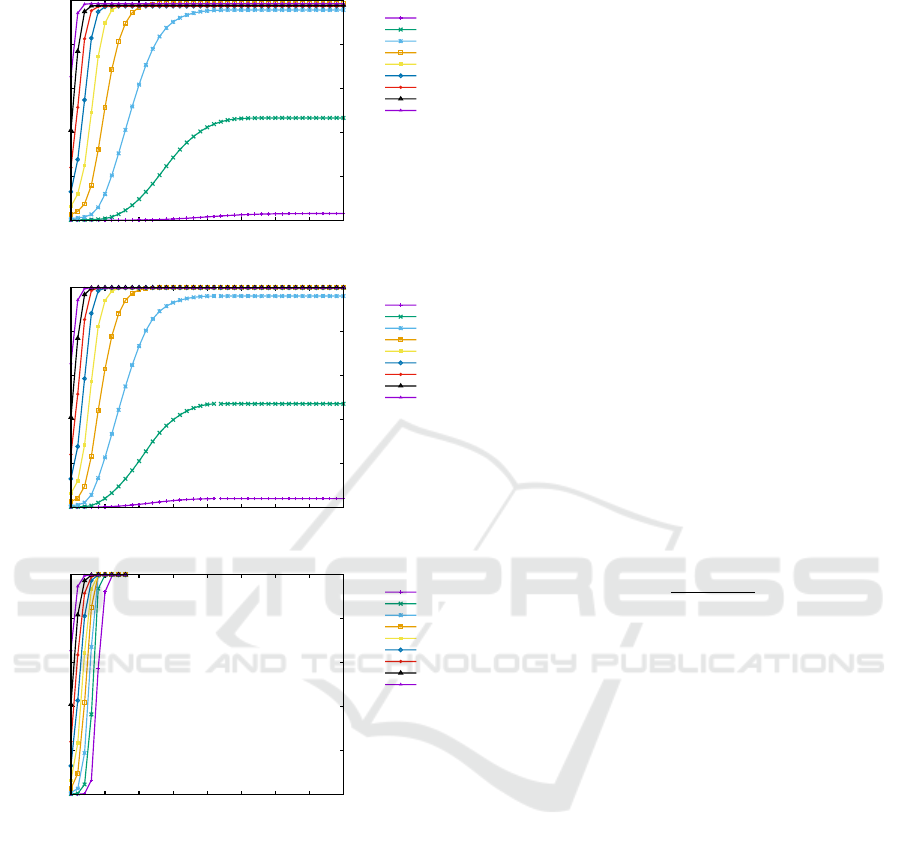
In Fig. 2 the time evolution of the fraction n(K) of

agents having total knowledge—i.e. possessing all K

chunks of knowledge (c

, c

, · · · , c

) = (1, 1, · · · , 1) is

presented. In Fig. 2(a) the data for model A are re-

produced. The data obtained for model B [Fig. 2(b)]

exhibit again shorter times of reaching the saturation

of curves n(K) with simulation steps t vs. the same

data for model A. Moreover, for model B and for ini-

tial concentrations of chunks of knowledge p > 0.3

the curves n(K) saturates at n(K) = 1 while in model

A n(K) < 1 independently on p. Finally, for model

C, these effects are strongly enhanced and for all

checked values of initial concentration of chunks of

knowledge p only several simulations steps are re-

quired to reach n(K) = 1.

As it was mentioned earlier, n(K) is also a variable

describing the effectiveness of knowledge transfer. As

can be seen in Fig. 2, the effectiveness of knowledge

transfer is greater for model A than B, but deﬁnitely

the best results gives model C. In this case, even small

values of initial fraction p cause that all the organiza-

tion members have all K required chunks of knowl-

edge.

4.3 Time Necessary for Reaching the

Stationary State

In Fig. 3 times τ necessary for reaching the stationary

state as dependent on initial concentration of chunks

of knowledge p for L = 20 and K = 4, 8 and vari-

ous models are presented. In Fig. 3(a) the results pre-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

154

0.2

0.4

0.6

0.8

0 5 10 15 20 25 30 35 40

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(a) model A

p =

n(K) [%]

0.2

0.4

0.6

0.8

0 5 10 15 20 25 30 35 40

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(b) model B

p =

n(K) [%]

0.2

0.4

0.6

0.8

0 5 10 15 20 25 30 35 40

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p =

n(K) [%]

Figure 2: The time evolution of the fraction n(K) of agents

having total knowledge—i.e. possessing all K chunks of

knowledge (c

, c

, · ·· , c

) = (1, 1, ·· · , 1) for L = 20 and

K = 4. The values of n(K) are averaged over M = 10

in-

dependent simulations.

sented in Ref. (Kowalska-Stycze

n et al., 2017) are re-

produced. The heuristic low degree polynomial ﬁt has

been added for eyes guidance as well. For model B—

when agents may receive chunks of knowledge from

“smarter” agents—we observe shorter times τ in re-

spect to results of model A for both checked values

of K. However, the characteristic of the ﬁt shapes

are roughly the same for models A and B. This sit-

uation changes qualitatively and quantitatively when

model C is applied—the obtained values of τ are

twice smaller when comparing with results for model

A and the ﬁt shape is different than for models A and

The number of simulation steps τ to obtain the

steady state, expresses the efﬁciency of knowledge

transfer. As can be seen in Fig. 3, the time of the

transfer of knowledge is shorter in the case of model B

than A, but deﬁnitely it is shortest for the model C. In

the latter case, the time τ decreases with increasing p.

The transfer of knowledge chunks among agents with

the same or greater numbers of chunks of knowledge

therefore gives the best results.

4.4 The Average Coverage of Chunks of

Knowledge in Whole Organization

In Fig. 4 the average coverage of chunks of knowl-

edge

h f i = K

−1

∑

k=1

f (k)

of agents having any chunk of knowledge c

for L =

20 and long simulations time t → ∞ and various val-

ues of K (K = 2, 3, 4, 8, 16) as dependent on initial

concentration of chunks of knowledge p is presented.

The fraction f (k) is formally deﬁned as

f (k) ≡

∑

r=1

(k)

, (5)

where F

(k) is the number of agents having k-th chunk

of knowledge [i.e. with c

(x, y,t → ∞) = 1] in r-th

simulation.

In this experiment, we can look at the effective-

ness of knowledge transfer more globally, i.e. in the

whole system (the whole organization). The more

chunks of knowledge (K) is required in the organi-

zation, the greater must be the initial concentration of

knowledge in the organization (p) to allow almost all

agents acquire the required knowledge [see Fig. 4].

Moreover, comparing the three models A, B and C—

and basing on results presented in Fig. 4—the trans-

fer of knowledge is more effective for model B than

A. A lower values of initial concentration of chunks

of knowledge p are required to ensure the global sat-

uration of skills in organization (h f i = 1) when com-

paring models B and A [cf. Fig. 4(d) and Fig. 4(b)].

For model B these values increse with the number of

chunks of knowledge K desired in the organization.

Obviously the best results, as in the previous experi-

ments, are obtained for the situation C [cf. Fig. 4(f)

and Fig. 4(d)].

As it was mentioned in Ref. (Kowalska-Stycze

et al., 2017), for model A (Sec. 2.1), “the dependence

h f i on p increases to a certain threshold values of p

[. . . ] then it decreases, and it increases again [. . . ]

Searching for Effective and Efﬁcient Way of Knowledge Transfer within an Organization

155

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

(a) model A

K =

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

(b) model B

K =

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

K =

Figure 3: The time τ necessary for reaching the stationary state as dependent on initial concentration of chunks of knowledge

p. The results are averaged over M = 10

independent simulations. The error bars are smaller than the symbols. (a) model A,

(b) model B, (c) model C.

100

0 0.2 0.4 0.6 0.8 1

K =

(a) model A

h f i [%]

100

0 0.2 0.4 0.6 0.8 1

K =

h f i [%]

100

0 0.2 0.4 0.6 0.8 1

K =

(e) model C

h f i [%]

100

0 0.2 0.4 0.6 0.8 1

K =

(b) model A

h f i [%]

100

0 0.2 0.4 0.6 0.8 1

K =

(d) model B

h f i [%]

100

0 0.2 0.4 0.6 0.8 1

K =

(f) model C

h f i [%]

Figure 4: The average coverage of chunks of knowledge h f i of agents having any chunk of knowledge c

for L = 20 and

long simulations time t → ∞ and various values of K (K = 2, 3, 4, 8, 16) as dependent on initial concentration of chunks of

knowledge p. The values of h f i are averaged over M = 10

independent simulations.

We see [. . . ], that for L = 20 and K ≥ 7 a drop in

h f i is absent.” The surprising effect of decreasing the

effectiveness of the knowledge transfer with increas-

ing the initial concentration p of chunks of knowledge

among agents for K < 7 [cf. Figs. 4(a-b)] was directly

associated with and explained by the assumed rules of

the knowledge transfer described in Ref. (Kowalska-

Stycze

n et al., 2017). In particular, for the minimal

set (K = 2) of required chunks of knowledge one may

evaluate the mean-ﬁeld-like probabilities of ﬁnding

pairs of agents allowing for knowledge transfer or

blocking it (Kowalska-Stycze

n et al., 2017). The lat-

ter vanishes for model B and for model C, what re-

sults in monotonically non-decreasing h f i vs. p de-

pendencies for model B and model C as presented

in Figs. 4(c-d) and 4(e-f). Moreover, when sending

the chunks of knowledge is not restricted only to the

“smarter” agents (model C), the quantitative differ-

ence on h f i vs. p curves for various values of K

disappears. As we can deduce from Fig. 4(e-f)—

when model C is assumed—the agents are able to ac-

quire all chunks of knowledge desired by the organi-

zation independently on the level K of the knowledge

required in the organization if only initial concen-

tration of chunks of knowledge is sufﬁciently large.

Moreover, in model C, agents will not acquire all of

K chunks of knowledge only when some chunk of

knowledge will not be available initially in the orga-

nization, i.e. when

∃k ∀x, y : c

(x, y, 0) = 0 and (x, y) ∈ N ×N, 1 ≤ x, y ≤ L.

(6)

The condition (6) is fulﬁlled with probability

∗

= 1 −



(1 − p)



, (7)

which is the probability that at least one column in

random binary matrix with K columns and L

rows

will contain only zeros when matrix elements are “1”

with probability p and “0” with probability (1 − p).

The dependencies p

∗

(p) for L = 20 and various val-

ues of K are presented in Fig. 5. As we can see, the

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

156

probabilities that some chunks of knowledge will be

initially missing in organization with L

= 400 mem-

bers are marginal if p > 2%.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.005 0.01 0.015 0.02

K =

∗

Figure 5: The dependencies p

∗

(p) [Eq. (7)] for L = 20 and

various values of K.

5 DISCUSSION AND

CONCLUSION

In this article the transfer of knowledge in an organi-

zation is studied. The goal is to ﬁnd an effective and

efﬁcient way of communicating knowledge among

members of the organization, i.e. we are searching

for models giving better efﬁciency and better effec-

tivity of knowledge transfer. Therefore, we have in-

vestigated a CA model to answer the question if dif-

ferences on the microscopic scale between the three

versions of the knowledge transfer model manifest in

differences in the efﬁciency and speed of knowledge

transfer.

Many studies show the importance of social inter-

action among organizational members in knowledge

exchange (Chen and Huang, 2007; Ibarra, 1993; Tsai,

2002). It should be noted, that these interactions be-

tween organization members are mainly informal and

these interactions are the main source of inﬂuence in

organizations (Ibarra, 1993). Therefore, the proposed

models base on informal relations between the orga-

nization members. Moreover, apart from the stock

of knowledge, the efﬁcient knowledge transfer re-

quires the strong disseminative capacity of knowledge

senders and the absorptive capacity of knowledge re-

ceivers (Tang, 2011). The abilities of people i) to

efﬁciently and effectively communicate, ii) to spread

knowledge in a way that other people can understand

information accurately, iii) and to use knowledge in

practice are very important. The lack of competence,

skills and language efﬁciency of knowledge senders

makes the transfer of their knowledge to others rather

difﬁcult (Cabrera, 2003). It should be added, that

in this knowledge transfer process, leaders also play

an important role (Girdauskiene and Savaneviciene,

2012). They become informal leaders (distributed

leadership), when leadership is understood as a com-

mon social process resulting from the interaction of

multiple entities (Uhl-Bien, 2006). In this perspec-

tive, the way of leaders interaction with others is more

important than the nature of their leadership roles, re-

sponsibilities or functions (Harris, 2012). In connec-

tion with this, we deﬁne the rule of knowledge trans-

fer as a transfer of knowledge from the people who

have more of knowledge chunks (leaders) to people

with less of knowledge chunks (followers).

In this paper we have assumed three situations in

which the sender is eligible to transfer knowledge to

the recipient:

• when the sender has exactly one more chunks of

knowledge than recipient (model A),

• when the sender has more chunks of knowledge

than recipient (model B),

• when the sender has the same or greater number

of chunks of knowledge than recipient (model C).

As we have shown, the differences between model

A and B are almost negligible (are not large), although

the model B gives a better result than model A. In

the model B, we assume that the transfer occurs when

sender has more chunks of knowledge than recipient

(i.e. when the sender generally has a greater knowl-

edge of the recipient). It seems to be better than the

assumptions in the model A, because, it seems more

natural that people with more knowledge (knowledge

leaders) share it with others. The knowledge transfer

is most effective in the model C. In this situation, the

senders are also people who have the same number of

chunks knowledge as the recipient (i.e., they may be

at a similar level of knowledge).

The simulations, for all three models, show a sig-

niﬁcant role of initial concentration of knowledge

chunks in the transfer process. Organizations should

therefore carry out training courses for their employ-

ees in order to increase the initial knowledge in the

organization. However, as it was shown earlier, the

most important is the way to knowledge transfer.

The best results are obtained when the transfer of

knowledge is possible when the recipient have the

same or lower level of knowledge from the broad-

casters (model C), because the knowledge transfer oc-

curs more frequently. Therefore, in case of sponta-

neous knowledge transfer, managers should develop

and support informal contacts between employees to

reduce the social distance between them.

Searching for Effective and Efﬁcient Way of Knowledge Transfer within an Organization

157

ACKNOWLEDGMENTS

This research was supported by National Sci-

ence Center (NCN) in Poland (grant no. UMO-

2014/15/B/HS4/04433) and partially by Polish Min-

istry of Science and Higher Education.

REFERENCES

Alipour, F., Idris, K., and Karimi, R. (2011). Knowl-

edge creation and transfer: role of learning organiza-

tion. International Journal of Business Administra-

tion, 2(3):61–67.

Boone, T. and Ganeshan, R. (2008). Knowledge acqui-

sition and transfer among engineers: Effects of net-

work structure. Managerial and Decision Economics,

29(5):459–468.

Cabrera, E. (2003). Social-psychological aspects of

knowledge-sharing in organizations. In Morley, M.,

Cross, C., Flood, P., Gubbins, C., Heraty, N., and

Sheikh, H., editors, Proceedings of 7th Conference on

International Human Resource Management. Intere-

source Group Publishing.

Chen, C. and Huang, J. (2007). How organizational climate

and structure affect knowledge management—the so-

cial interaction perspective. International Journal of

Information Management, 27(2):104–118.

Davenport, T. H. and Prusak, L. (2000). Working knowl-

edge: How organizations manage what they know.

Harvard Business School Press, Boston, MA.

Deffuant, G., Neau, D., Amblard, F., and Weisbuch, G.

(2000). Mixing beliefs among interacting agents. Ad-

vances in Complex Systems, 3(1-4):87.

Giacchi, E., La Corte, A., and Di Pietro, E. (2016). A dy-

namic and context-aware model of knowledge trans-

fer and learning using a decision making perspective.

In Mu

noz, V. M., Gusikhin, O., and Chang, V., edi-

tors, Proceedings of the 1st International Conference

on Complex Information Systems, pages 66–73. Sci-

ence and Technology Publications.

Girdauskiene, L. and Savaneviciene, A. (2012). Leadership

role implementing knowledge transfer in creative or-

ganization: how does it work? Procedia—Social and

Behavioral Sciences, 41:15–22.

Harris, A. (2012). Distributed leadership: implications for

the role of the principal. Journal of Management De-

velopment, 31(1):7–17.

Hegselmann, R. and Krause, U. (2002). Opinion dynamics

and bounded conﬁdence: models, analysis and simu-

lation. JASSS—the Journal of Artiﬁcial Societies and

Social Simulation, 5(3):2.

Hirshman, B. R., Charles, J. S., and M., C. K. (2011). Leav-

ing us in tiers: can homophily be used to generate tier-

ing effects? Computational and Mathematical Orga-

nization Theory, 17:318–343.

Ibarra, H. (1993). Network centrality, power, and innova-

tion involvement: Determinants of technical and ad-

ministrative roles. Academy of Management Journal,

36(3):471–501.

Ingram, P. and Roberts, P. (2000). Friendships among com-

petitors in the sydney hotel industry. American Jour-

nal of Sociology, 106(2):387–423.

Jensen, R. J. and Szulanski, G. (2007). Template use and

the effectiveness of knowledge transfer. Management

Science, 53(11):1716–173.

Kowalska-Stycze

n, A., Malarz, K., and Paradowski, K.

(2017). Model of knowledge transfer within an or-

ganization.

Kułakowski, K. (2009). Opinion polarization in the receip-

tacceptsample model. Physica A: Statistical Mechan-

ics and its Applications, 388(4):469–476.

Malarz, K. (2006). Truth seekers in opinion dynamics

models. International Journal of Modern Physics C,

17(10):1521–1524.

Malarz, K., Gronek, P., and Kułakowski, K. (2011). Zaller–

Deffuant model of mass opinion. JASSS—the Journal

of Artiﬁcial Societies and Social Simulation, 14(1):2.

Malarz, K. and Kułakowski, K. (2014). Mental ability and

common sense in an artiﬁcial society. Europhysics

News, 45(4):21–23.

Morone, P. and Taylor, R. (2004). Knowledge diffusion dy-

namics and network properties of face-to-face interac-

tions. Journal of Evolutionary Economics, 14(3):327–

351.

erez-Nordtvedt, L., Kedia, B. L., Datta, D. K., and

Rasheed, A. A. (2008). Effectiveness and efﬁciency of

cross-border knowledge transfer: an empirical exam-

ination. Journal of Management Studies, 45(4):714–

744.

Reagans, R. and McEvily, B. (2003). Network structure

and knowledge transfer: The effects of cohesion and

range. Administrative Science Quarterly, 48(2):240–

267.

Tang, F. (2011). Knowledge transfer in intra-organization

networks. Systems Research and Behavioral Science,

28(3):270–282.

Tsai, W. (2002). Social structure of ‘coopetition’ within

a multiunit organization: Coordination, competition,

and intra-organizational knowledge sharing. Organi-

zation Science, 13(2):179–190.

Uhl-Bien, M. (2006). Relational leadership theory: Explor-

ing the social processes of leadership and organizing.

Leadership Quarterly, 17(6):654–676.

Wah, L. (1999). Behind the buzz. Management Review,

88(4):17–26.

Watson, S. and Hewett, K. (2006). A multi-theoretical

model of knowledge transfer in organizations: De-

terminants of knowledge contribution and knowledge

reuse. Journal of Management Studies, 43(2):141–

173.

Xuan, Z., Xia, H., and Du, Y. (2011). Adjustment of

knowledge-connection structure affects the perfor-

mance of knowledge transfer. Expert Systems with

Applications, 38(12):14935–14944.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

158