Assignment-based MIP Modeling for Solving a Selling Firm mTSP
with Time Limit Constraints
Mojahid Saeed Osman
Department of Industrial Engineering, American University of Sharjah,
Sharjah, United Arab Emirates
Keywords: Multiple Traveling Salesmen, Routing, Mixed Integer Programming, Assignment.
Abstract: This paper presents a version of the multiple traveling salesmen problem with service time limit constraints
and travel times. The time required to provide merchandising service at any outlet location is predetermined
based on the customer type. The objective is to minimize the number of salesmen hired by a selling firm
while visiting and providing services to all customers without exceeding salesmen’s allowed working times.
The paper proposes an assignment-based mixed integer programming model for solving the salesmen
problem of a selling firm that applies a sub-tour elimination restriction. A case example is presented for
illustrating the applicability and suitability of the proposed approach for solving the problem tackled in this
work.
1 INTRODUCTION
Salesmen play an important role in the distribution
channel of goods to have an access to the customer
and market as primary means of selling and
distributing products and achieving selling firm’s
strategic objectives. Salesman allocation and routing
are critical tasks in sales and the distribution
management. Selling firms that distribute goods to
large number of customers must perform detailed
analysis of distribution routes and salesmen
allocation to maintain successful salesforce and
reduce the salesmen cost plus the costs for the tours.
In transportation and distribution management,
traveling salesman is a key routing function. This
function involves determining the geographic tour a
salesman will travel to visit a set of locations and
serve a number of customers. Distribution and sales
planners often face the problem of determining the
efficient way of touring individual salesmen in order
to minimize the number of salesmen who can travel
to reach all sales locations in which a set of
customers is to be accessed and served. In reality,
sales firms must determine and hire multiple
salesmen to serve their customers, as well as
determining the sequence in which customers are to
be visited in each tour to minimize the total distance
traveled.
The multiple traveling salesman problem (mTSP)
is a generalization of the traveling salesman problem
(TSP) in which more than one salesman is used
(Bektas, 2006). Given a set of customer locations,
one main office location (where m salesmen are
located), traveling times between different locations,
and time limit constraints during which the customer
location must be visited and served. The objective of
the mTSP is to determine a set of tours or routes for
visiting and serving all customers so as to minimize
the number of salesmen. The requirements on the set
of tours are: all of the tours must start and end at the
same main office location, and each customer
location must be visited exactly once by a single
salesman.
The importance of multiple traveling salesmen
problem is shown in its huge savings when the
marketing and distribution costs are reduced by
minimizing the number of salesmen used.
Therefore, in the context of sales and distribution
in supply chains, traveling salesmen is one of the
important problems in distribution and supply center
management. The multiple salesmen problem is
extended in various ways; the purpose of this paper
is to propose and apply an approach for highly
relevant extensions of the classical traveling
salesmen problem in the context of sales and
distribution management. This research is concerned
with salesmen problem of a selling firm where its
164
Osman, M.
Assignment-based MIP Modeling for Solving a Selling Firm mTSP with Time Limit Constraints.
DOI: 10.5220/0006549201640169
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 164-169
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

customers are located in cities within a certain
region. The aim is to solve this problem such that the
number of salesmen is minimized while visiting and
serving all customers and satisfying salesman
touring and working time constraints.
We primarily focus on the development of
general model to determine a touring network a
salesman would travel through multiple locations to
reach and serve set of customers in an attempt to
achieve the goal of minimizing total salesmen cost
plus the costs for the tours through minimizing the
number of salesmen used. Nevertheless, as far as the
author is aware, no published research has addressed
this problem, or proposed an approach that
optimizes the number of salesmen with respect to
their work time availability and service time limit
constraints, and incorporates a net flow formula for
solving such problem. The number of salesmen is to
be determined by the optimal solution but bounded
by a given upper bound of the number salesmen.
2 LITERATURE SURVEY
Extended literature is available about various
approaches on traveling salesman and multiple
traveling salesmen problems. These approaches
usually depend on the areas of applications.
The TSP arises in main real-world applications
including the drilling problem of printed circuit
boards (PCBs) in actual production environment
introduced by Grötschel et al. (1991), overhauling
gas turbine engines of aircrafts reported by Plante et
al. (1987), analysis of the structure of crystals
presented by Bland and Shallcross (1989),
connection of components on a computer board and
vehicle routing reported by Lenstra and Kan (1974),
and order-picking and material handling in
warehouses proposed by Ratliff and Rosenthal
(1983).
mTSP has numerous real-life applications.
Macharis and Bontekoning (2004), Wang and
Regan, (2002), and Basu et al. (2000) reported
comprehensive review on various application of
mTSP. The main applications of mTSP include
production scheduling presented by Gorenstein
(1970), Carter and Ragsdale (2002) and Tang et al.
(2000), school bus routing reported by Angel et al.
(1972), crew scheduling described by Svestka and
Huckfeldt (1973), and Lenstra and Kan (1975),
mission planning presented by Brummit and Stentz
(1998), designing system networks suggested by
Saleh and Chelouah (2004), security service
investigated by Calvo and Cordone (2003) and Kim
and Park (2004), vehicle routing (VRP) discussed by
Mole et al. (1983); Laptore et al. (1985), Ralphs,
2003), and Mitrović-Minić et al. (2004).
In the context of mathematical formulation of
TSP and mTSP, many formulations are available in
literature. Orman and Williams (2006) and O¨ncan
et al. (2009) have provided surveys on several
formulation of the problem. Among these, the
formulations proposed by Dantzig et al. (1954),
Applegate et al. (2003), Christofides et al. (1981),
Svestka and Huckfeldt (1973), Kulkarni and Bhave
(1985), and Laporte and Nobert (1980).
Beside the mathematical formulation approaches,
some authors have introduced heuristic techniques to
solve the TSP and mTSP problem. Balas and Toth
(1985), Laporte (1992), and Fischetti et al. (2002)
have presented surveys of algorithms for the
problem. A number of well-known heuristic
approaches have been developed to solve this
problem, which include the algorithms presented by
Dell’Amico and Toth (2000), Carpaneto et al.
(1995), and Fischetti and Toth (1992). However, the
best available algorithm for the symmetric TSP was
developed by Applegate et al. (2006), which is the
culmination of a line of research including Padberg
and Hong (1980), Padberg and Grötschel (1985),
Padberg and Rinaldi (1991), and Grötschel and
Holland (1991).
Furthermore, Bektas (2006) listed a number of
variations on the mTSP, instead of one depot, the
multi-depot mTSP has a set of depots, with a set of
salesmen at each depot . In one version, a salesman
returns to the same depot from which he started. In
another version, a salesman does not need to return
to the same depot from which he started but the
same number of salesmen must return as started
from a particular depot. Bektas (2006) listed another
variation that gives specifications on the number of
salesmen such as having the number of salesmen to
be a fixed number or it may be determined by the
solution but bounded by an upper bound. Bektas also
listed one more variation when the number of
salesmen is not fixed; he assumes that there may be
a fixed cost associated with activating a salesman. In
the fixed charge version of the mTSP, the overall
cost to minimize includes the fixed charges for the
salesmen plus the costs for the tours. There is a
variation of the mTSP with time limit constraints
associated with each node during which the node
must be visited by a tour.
Assignment-based MIP Modeling for Solving a Selling Firm mTSP with Time Limit Constraints
165

3 PROPOSED APPROACH –
ASSIGNMENT-BASED MIP
MODEL FOR mTSP
We have developed an assignment-based mixed
integer programming formulation for the mTSP
(AMIP-mTSP).
The proposed AMIP-mTSP formulation is based
on a graph G=(I,A), where I is the set of |I| nodes,
and A is the set of ½*|I|*|I-1| bidirectional arcs.
There is traveling time T
ij
associated with each arc i-
j and visiting node i requires service time S
j
where
both i and j ∈ I. We assume that the main office
location is node 1 and there are m salesmen at the
main office. We define a binary variable x
kij
that
takes the value 1 if salesman k is traversing arc i-j
and x
kij
takes the value 0 otherwise.
Prior to presenting the AMIP-mTSP formulation
in detail, we introduce the notation given in Table 1.
Table 1: MIP-mTSP Model Notations.
Description
I
is the set of all locations/points visited by salesmen
I

is a subset of locations/points visited by salesmen
excluding their main office (location point 1)
K
is the set of all salesmen
x
ki
j
is equal to 1 if salesman k travels form location i to j,
and 0 otherwise
(DV)*
y
k
is equal to 1 if salesman k is assigned to visit any
customer location, and 0 otherwise
(DV)*
M
is arbitrarily big number
T
ij
is the traveling time between location i and j
(IP)*
S
j
is the average service time at location j
(IP)*
H
is the maximum available working time for each
salesman
(IP)*
O
i
is the relative position of location i in set I (ex. set
[a,b,c,], O
a
=1,O
b
=2, and O
c
=3)
(IP)*
N
is the maximum number of locations that can be visited
by any salesman as number of elements/locations in a
set I.
*IP = Input Parameter ** DV = Decision Variable
The objective function and functional constraints
of the proposed AMIP-mTSP model are detailed as
follows.
Objective Function:
Min


K
k
k
y
1
(1)
Subject to:
k
I
i
kij
I
j
Myx 
 
 1 1

k  K
(2)
1
1 1

 
 
I
i
kij
K
k
x

j  I’
(3)
1
1 1

 
 
I
j
kij
K
k
x

i  I’
(4)
k
I
j
jk
yx 

2
1

k  K
(5)
k
I
i
ki
yx 

2
1

k  K
(6)
  
  

I
j
K
k
kij
I
j
K
k
kji
xx
1 11 1

i 
I
(7)
k
I
i
I
j
kijjij
HxST 
 
 1 1
)(

k  K
(8)
1
1



NxNOO
K
k
kijji

i≠j  I’
(9)
kij
x
= 0 or 1

i&j  I, and k  K
(10)
k
y
= 0 or 1

k  K
(11)
The objective function (1) minimizes the number of
salesmen hired to visit and perform merchandising
services at all customer locations. Constraint (2)
ensures that if a salesman has at least one customer
location to visit, he must be hired. Constraint (3) and
(4) state that each customer must be visited once by
a salesman coming from the company or another
customer location. Constraint (5) confirms that if a
salesman is hired, he must visit a customer location
from the main location. Constraint (6) ensures that if
a salesman is hired, he must return to the main
location from the customer location visited.
Constraint (7) imposes the net flow rule that
salesman entering each customer location must leave
it. This constraint also ensures that all salesmen who
leave the main location must return back to it.
Constraint (8) guarantees that the total time of
traveling and serving customers by each salesman
does not exceed the available working time.
Constraint (9) applies the elimination of sub tours
proposed by Miller-Tucker-Zemlin (1960).
Constraint (10) and (11) declare that the decision
variables x
kij
and y
k
are binary.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
166

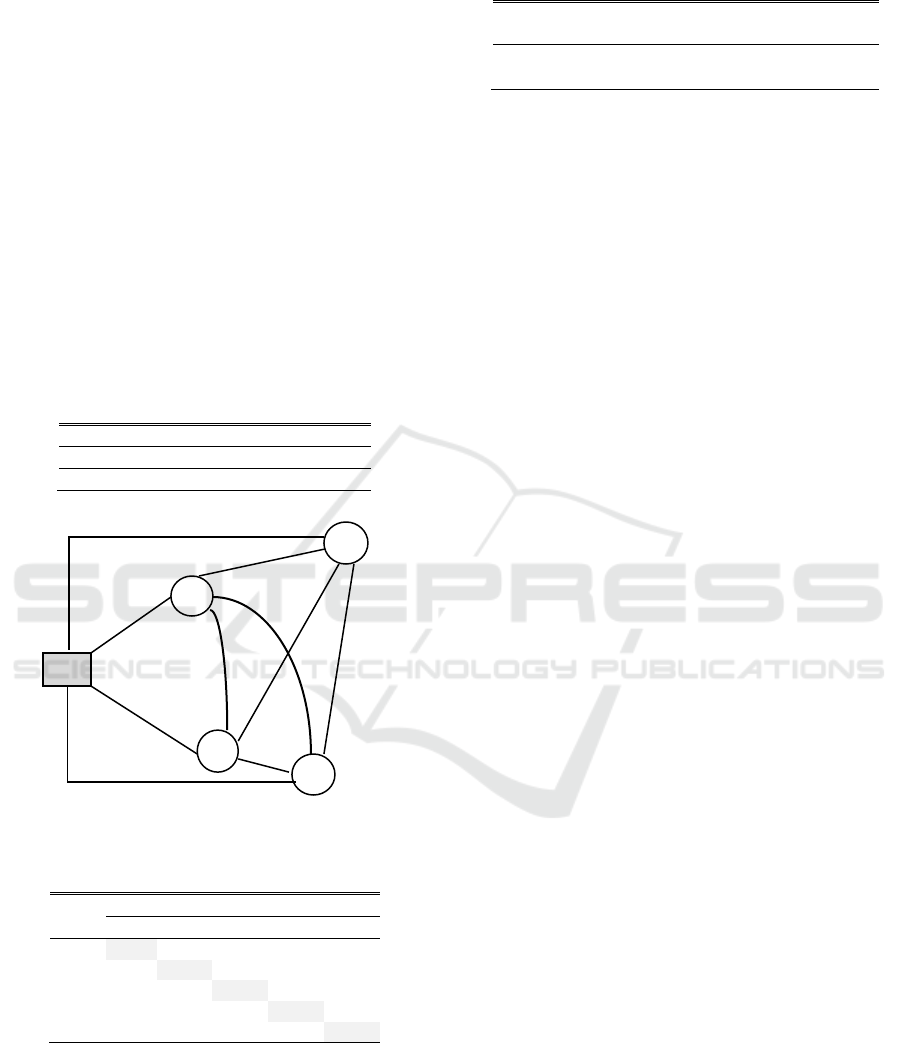
4 ILLUSTRATIVE EXAMPLE
We illustrate the proposed AMIP-mTSP approach
by solving the multiple traveling salesmen problem
shown in Figure 1. In this problem, customer
locations CL1 through CL4 are to be visited for
merchandizing services given that ML is the main
location where m salesmen are located.
The average service time in each location
including the time spent in the main office are
shown in Table 2 while the traveling times between
the five locations are given in Tables 3, and for
avoiding reflexive traveling to the same location, the
traveling times between the same locations are given
a large number, 999. In this example, we assumed
that the average available working time for each
salesman is 60 time units.
Table 2: Service times in Location j.
Locations
ML
CL1
CL2
CL3
CL4
5
10
15
20
25
Figure 1: Illustrative Example Problem Representation.
Table 3: Traveling times between location i and j.
j
i
ML
CL1
CL2
CL3
CL4
ML
999
6
8
4
3
CL1
6
999
9
2
5
CL2
8
9
999
4
7
CL3
4
2
4
999
4
CL4
3
5
7
4
999
The optimal salesman tours obtained as results of
solving the AMIP-mTSP optimization model of are
reported in Table 4. Only two salesmen are required
to visit all customer locations, each salesman k
served 2 customer locations such that each customer
is served by precisely one salesman.
Table 4: Optimal Solution for Illustrative Example.
Salesman
ID
Salesman
Tour
Total
Service time
1
ML→CL1→CL4→ML
54
2
ML→CL2→CL3→ML
56
The above illustrative example was solved using
GAMS 22.6 using the CPLEX solver. The system
used to solve the proposed model is Dell Inspiron 15
3000 Series laptop with Windows 10 and Intel(R)
Core(TM) i3 6006U CPU at 2.0 GHz processor,
4GB of RAM.
The minimum number of salesmen and their
tours for visiting all customer locations obtained as
proven optimal solution reflect the accuracy of the
proposed model formulation. AMIP-mTSP model
solved the illustrative example in approximately 114
CPU milliseconds with absolute and relative gaps of
zero. For the proposed model, the number of
constraints is 2|K|*[1+|I|)]+|I|+|I’|*[2+|I’-1|] and the
number of variables is |K|*[(|I|*|I-1|)+1], where |•|
represents the cardinality of a set. For instance, for
|I|=5, |K|=4, the number of constraints and variables
are 85 and 84 respectively. It is anticipated that
even if for moderate number of customer
locations/nodes, the proposed AMIP-mTSP model
can still yield optimal solutions in reasonable
computer CPU time and memory.
5 CONCLUSIONS
In this paper, we described the development of
mathematical formulation of an assignment-based
MIP optimization model for the mTSP with time
limit constraints. The objective of the proposed
AMIP-mTSP model is to optimize the allocation and
touring of individual salesmen for minimizing the
number of salesmen assigned to visit all sales points
and provide merchandizing service to all customers
while satisfying all the touring and allowed working
time constraints for individual salesman.
The AMIP-mTSP model provided promising
solutions; the results reveal the applicability and
suitability of the proposed AMIP-mTSP approach
for solving multiple salesmen problem with time
limit constraints for selling firms. The touring of
salesmen of a selling firm is only one application
example of a problem that can be modeled as
assignment-based mTSP with the aim of minimizing
the number of salesmen.
ML
CL3
CL1
CL2
CL4
Assignment-based MIP Modeling for Solving a Selling Firm mTSP with Time Limit Constraints
167

REFERENCES
Angel, R.D., Caudle, W.L., Noonan, R. and Whinston, A.,
1972. Computer assisted school bus scheduling.
Management Science 18: 279–88.
Applegate, D.L., Bixby, R.E., Chv´atal, V. and Cook,
W.J., 2003. Implementing the Dantzig–Fulkerson–
Johnson algorithm for large scale traveling salesman
problems. Math Program Ser B 97: 91–153.
Applegate, D. L., Bixby, R. E., Chvátal, V. and Cook, W.
J. 2006. The Traveling Salesman Problem: A
Computational Study, Princeton University Press,
ISBN 978-0-691-12993-8.
Balas, E., and Toth, P., 1985. Branch and bound methods.
The Traveling Salesman Problem: A Guided Tour of
Combinatorial Optimization, Wiley: Chichester: 361–
401.
Bland, R.E., and Shallcross, D.E., 1989. Large traveling
salesman problem arising from experiments in X-ray
crystallography: a preliminary report on computation.
Operations Research Letters 8(3): 125-128.
Basu, A., Elnagar, A., and Al-Hajj, A., 2000. Efficient
coordinated motion. Mathematical and Computer
Modelling, 31: 39–53.
Bektas, T., 2006. The multiple traveling salesman
problem: an overview of formulations and solution
procedures. OMEGA: The International Journal of
Management Science 34(3): 209-219.
Brummit, B., and Stentz, A., 1998. GRAMMPS: a
generalized mission planner for multiple mobile
robots. Proceedings of the IEEE international
conference on robotics and automation.
Calvo, R.W. and Cordone, R., 2003. A heuristic approach
to the overnight security service problem. Computers
and Operations Research 30: 1269–87.
Carpaneto, G., Dell’Amico, M. and Toth, P., 1995. Exact
solution of large-scale, asymmetric travelling salesman
problems. ACM Transactions on Mathematical
Software 21: 394–409.
Carter, A.E., and Ragsdale, C.T., 2002. Scheduling pre-
printed newspaper advertising inserts using genetic
algorithms. Omega 30: 415–21.
Christofides, N., Mingozzi, A., and Toth, P., 1981. Exact
algorithms for the vehicle routing problem, based on
spanning tree and shortest path relaxations.
Mathematical Programming 20: 255–82.
Dantzig, G.B., Fulkerson, D.R., and Johnson, S.M., 1954.
Solution of a large-scale traveling salesman problem.
Operations Research 2: 393–410.
Dell’Amico, M., and Toth, P., 2000. Algorithms and codes
for dense assignment problems: The state of the art.
Discrete Applied Mathematics 100(1-2): 17–48.
Fischetti, M., and Toth, P., 1992. An additive bounding
procedure for the asymmetric traveling salesman
problem. Mathematical Programming: Series A and B
53(2): 173–197.
Fischetti, M., Lancia, G., and Serafini, P. 2002. Exact
algorithms for minimum routing cost trees. Networks,
39(3): 161-173.
Gorenstein, S., 1970. Printing press scheduling for multi-
edition periodicals. Management Science 16(6): 373–
83.
Grötschel, M., and Holland O., 1991. Solution of Large-
scale Symmetric Traveling Salesman Problems.
Mathematical Programming 51: 141-202.
Kim, K.H., and Park, Y., 2004. A crane scheduling
method for port container terminals. European Journal
of Operational Research 156: 752–68.
Kulkarni, R.V., and Bhave, P.R., (1985). Integer
programming formulations of vehicle routing
problems. European Journal of Operational Research
20: 58–67.
Laporte, G., 1992. The vehicle routing problem: an
overview of exact and approximate algorithms.
European Journal of Operational Research 59: 345-
358.
Laporte, G., and Nobert. Y., 1980. A cutting planes
algorithm for the m-salesmen problem. Journal of the
Operational Research Society 31, 1017-1023.
Lenstra, J.K., and A.H.G. Rinnooy Kan., 1974. Some
Simple Applications of the Travelling Salesman
Problem. BW 38/74, Stichting Mathematisch Centrum,
Amsterdam.
Lenstra, J.K., and Rinnooy Kan, A.H.G., 1975. Some
simple applications of the traveling salesman problem.
Operational Research Quarterly 26:717–33.
Macharis, C., and Bontekoning, Y.M., 2004. Opportunities
for OR in intermodal freight transport research: a
review. European Journal of Operational Research
153: 400–16.
Miller, C., Tucker, A., and Zemlin, R., 1960. Integer
programming formulations and traveling salesman
problems. Journal of Association for Computing, 7:
326-329.
Mitrović-Minić, S., Krishnamurti, R., and Laporte, G.
2004. Double-horizon based heuristics for the dynamic
pickup and delivery problem with time windows.
Transportation Research 28(8): 669–85.
Mole, R.H., Johnson, D.G., and Wells, K., 1983.
Combinatorial analysis for route first-cluster second
vehicle routing. Omega 11(5), 507–12.
Orman, A.J., and Williams, H.P., 2006. A survey of
different integer programming formulations of the
travelling salesman problem. Springer: Berlin,
Heidelberg: 91–104.
O¨ncan, T., Altınel, I.K., and Laporte, G., 2009. A
comparative analysis of several asymmetric traveling
salesman problem formulations. Computers and
Operations Research 36: 637–654.
Padberg, M.W., and Hong, S., 1980. On the symmetric
travelling salesman problem: A computational study.
Mathematical Programming Study 12: 78–107.
Padberg, M.W., and Grötschel, M., 1985. Polyhedral
computations. The Traveling Salesman Problem: A
Guided Tour of Combinatorial Optimization. Wiley:
Chichester: 307–360.
Padberg, M., and Rinaldi, G., 1991. A branch-and-cut
algorithm for the resolution of largescale symmetric
traveling salesman problems. SIAM Review 33:60-100.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
168

Plante, R.D., Lowe T.J., and Chandrasekaran R., 1987.
The Product Matrix Traveling Salesman Problem: An
Application and Solution Heuristics. Operations
Research 35: 772-783.
Ralphs, T.K., 2003. Parallel branch and cut for capacitated
vehicle routing. Parallel Computing 29: 607–29.
Ratliff, H.D., and Rosenthal A.S., 1983. Order-Picking in
a Rectangular Warehouse: A Solvable Case for the
Travelling Salesman Problem. Operations Research
31: 507-521.
Saleh, H.A., and Chelouah, R. 2004. The design of the
global navigation satellite system surveying networks
using genetic algorithms. Engineering Applications of
Artificial Intelligence 17: 111–22.
Svestka, J.A., and Huckfeldt, V.E., 1973. Computational
experience with an m-salesman traveling salesman
algorithm. Management Science 19(7): 790–9.
Tang, L., Liu, J., Rong, A., and Yang, Z., 2000. A multiple
traveling salesman problem model for hot rolling
scheduling in Shangai Baoshan Iron and Steel
Complex. European Journal of Operational Research
124: 267-82.
Wang, X., and Regan, A.C., 2002. Local truckload pickup
and delivery with hard time window constraints.
Transportation Research Part B 36: 97–112.
Assignment-based MIP Modeling for Solving a Selling Firm mTSP with Time Limit Constraints
169