Game-theoretic Analysis of Air-cargo Allotment Contract

Kannapha Amaruchkul

Graduate School of Applied Statistics, National Institute of Development Administration (NIDA),

118 Serithai Road, Bangkok 10240, Thailand

Keywords:

Air-cargo, Capacity Management, Stochastic Model Applications.

Abstract:

Consider an air-cargo carrier and a freight forwarder, which may establish an allotment contract at the start

of the season. The allotment size needs to be determined, before their stochastic demands materialize. The

forwarder hopes to receive a discount rate, lower than the spot rate. The carrier hopes to increase capacity

utilization by handling not only its own direct-ship demand but also the forwarder’s demand. We formulate a

Stackelberg game, in which the carrier is the leader and offers contract parameters such as the wholesale price

and the refund rate for the unused allotment as well as the minimum allotment utilization. Given the carrier’s

offer, the forwarder decides how much to book as an allotment, in order to maximize its own expected proﬁt.

We analyze the game and identify conditions, in which an equilibrium contract coordinates the air-cargo

chain. We show that the minimum allotment utilization is needed to construct a coordinating contract. In our

numerical examples, we illustrate how to apply our approach to the case study of one of the biggest forwarders

in Thailand. The contract can improve both parties’ proﬁts, compared to the scenario without any contract,

where the forwarder purchases all capacity from the spot market.

1 INTRODUCTION

Air-cargo operations play a crucial role in the mod-

ern economy, since they improve efﬁciency in logis-

tics and increase competitive advantages. Despite the

1% world trade by volume, airfreight represents more

than 35% of global trade by value (International Air

Transport Association, 2016). Air cargo operations

generate almost 10% of the passenger airline revenue,

more than twice revenues from the ﬁrst class. Air

cargo consists of various commodity types, e.g., per-

ishable cargo, pharmaceutical products, dry ice, live

animals, electronic devices, human remains, and gold

bullion. World air-cargo is forecasted to grow over

200% over the next two decades. The largest aver-

age annual growth rate is found in Asia (Boeing Com-

pany, 2012). The air-cargo growth is partly driven by

global liberalization, cross-border e-commerce, and

the implementation of supply chain/logistics manage-

ment strategies, which emphasize on short lead times,

e.g., lean management and just-in-time (JIT) produc-

tion systems. With e-commerce boom, airfreight has

become a de facto mode of cross-border transporta-

tion, for the customer centric businesses with fast de-

livery times. A shipper can receive services directly

from an air cargo carrier or delegate to a freight for-

warder. A large portion of air cargo volume is handled

through freight forwarders.

A freight forwarder acts as an intermediary party,

who connects a shipper to an airline. It handles vari-

ous aspects of the shipping process, e.g., pickup and

delivery services, customs clearance, import and ex-

port documentation, cargo tracking and tracing. Most

forwarders do not own an airplane and obtain cargo

space on ad hoc basis or through a medium- or long-

term capacity agreement, also known as the allotment.

The carrier offers a contract to the forwarder, hoping

to increase its capacity utilization. Capacity utiliza-

tion is one of the top operational problems, faced by

the majority of the cargo carriers (Accenture, 2015).

The forwarder wants to establish the contract, in order

to receive volume discounts or lower freight charges.

Air-cargo spaces are sold in two stages: In the

ﬁrst stage which happens a few months before a sea-

son starts, carriers allocate space to forwarders ei-

ther as part of a binding contract or as part of good-

will (Billings et al., 2003). Each year comprises of

two seasons, Winter and Summer schedules, speciﬁed

by the International Air Transport Association (Slager

and Kapteijns, 2004). The allotment allows the for-

warder to achieve a more economical rate, compared

to the so-called spot rates for ad hoc shipments.

Based on its anticipated volume requirement on a

given route, the forwarder pre-books a certain amount

Amaruchkul, K.

Game-theoretic Analysis of Air-cargo Allotment Contract.

DOI: 10.5220/0006551800470058

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 47-58

ISBN: 978-989-758-285-1

of capacity at a pre-speciﬁed rate. The airline al-

locates cargo capacity on the season’s ﬂights as an

allotment. The allotment contract is established be-

fore the start of each season, whose duration ranges

from a few weeks to a year. Typically, about 50-

70% of air-cargo space is sold to forwarders through

a “hard” block space agreement (BSA) at a negoti-

ated price, a “soft” block permanent booking (PB) or

other forms of capacity purchase agreements (Sales,

2013). Carriers in North America typically allocate

a small fraction of their capacity, whereas those in

Asia Paciﬁc allocate a large fraction (Hendricks and

Elliott, 2010). After the forwarder collects and con-

solidates shipments from its customers, and the ac-

tual allotment usage becomes known, the payment is

transferred between the carrier and the forwarder. The

carrier may impose some cancellation fee for the un-

used allotment by the forwarder. However, for the

airline’s most important forwarders, the cancellation

clause is rarely enforced; these powerful forwarders

pay only for their actual allotment usages. After the

unused allotment is released by the forwarder a few

weeks before a ﬂight departure, the carrier re-sells the

remaining capacity on a free-sale or ad hoc basis to

direct shippers.

Since air-cargo capacity can be sold at different

prices to heterogeneous customers but cannot be sold

after the ﬂight departure, it is a prime candidate for

revenue management (RM) strategies. Overview of

RM theory and practice can be found in textbooks,

e.g., (Phillips, 2005), (Talluri and van Ryzin, 2004)

and (Yeoman and McMahon-Beattie, 2004), (Ingold

et al., 2000), and journal articles, e.g., (Netessine and

Shumsky, 2002), (Chiang et al., 2007) and (McGill

and van Ryzin, 1999). Despite an extensive litera-

ture on passenger RM, literature on air-cargo RM is

fairly limited. (Kasilingam, 1996) and (Billings et al.,

2003) are among the early descriptive papers that pro-

vide overview and complexity of the air-cargo RM.

(Bazaraa et al., 2001) describes the air-cargo system

in the Asia Paciﬁc. (Slager and Kapteijns, 2004) de-

scribes the implementation of air-cargo RM system at

KLM and highlight key factors that critically affect

its performance. Air-cargo RM from business per-

spective is discussed in (Becker and Dill, 2007) and

(DeLain and O’Meara, 2004). The overview and the

industry outlook of the air cargo service chain can be

found in, e.g., (Boeing Company, 2009) and (Interna-

tional Air Transport Association, 2016).

Key short-term air-cargo operations include book-

ing control (e.g., (Zhang et al., 2017), (Barz and Gart-

ner, 2016), (Levin et al., 2012) and (Amaruchkul

et al., 2007)) and shipment routing (e.g., (Prior et al.,

2004) and (Yang et al., 2006)), whereas medium-

and long-term operations include ﬂeet replacement

and capacity contract. (Yeung and He, 2012) gives

a brief survey on shipment planning and capacity

contracting in the air cargo industry. Articles on an

air cargo capacity contract are brieﬂy reviewed be-

low. With the exception of (Barz, 2007) which con-

siders risk-adverse party, the articles below assume

that the forwarder is rational, risk-neutral and maxi-

mizes its expected proﬁt. (Gupta, 2008) shows that

an efﬁcient airline-forwarder service chain can be

achieved through two ﬂexible contract schemes. In

the ﬁrst scheme, the airline imposes a ﬁxed upfront

payment for reserving an allotment, whereas in the

second scheme there is no reservation fee, but the

airline chooses the freight rate. (Amaruchkul et al.,

2011) considers the airline’s allocation problem, in

which the forwarder possesses some private informa-

tion, e.g., its customer demand and operating cost.

An optimal allotment, which maximizes the total con-

tribution of the air cargo service chain, is attainable

via a contract with an appropriate upfront and can-

cellation fees. (Hellermann, 2013) proposes an op-

tions contract, similar to supply chain contracts in,

e.g., electricity generation and semiconductor manu-

facturing, and investigates the suitability of options

contracts in the air cargo industry. Under certain

contract parameters and a suitable spot market envi-

ronment, the options contract outperforms the ﬁxed-

commitment contract. (Feng et al., 2015) proposes

the tying capacity allocation mechanism, in which

multiple routes with different capacity utilization are

included in the contract. (Tao et al., 2017) studies an

option contract to mitigate the carrier’s capacity uti-

lization risk. These papers employ a mechanism de-

sign approach and propose a contract scheme to im-

prove the air cargo service chain. Ours contributes to

this literature: We propose a different scheme, which

includes the wholesale price and the penalty cost as-

sociated with the unused allotment usage as well as

the required allotment utilization.

Our mathematical model captures important as-

pects of the allotment problem, commonly found in

practice. In our model, the size of the allotment

depends on the forwarder’s anticipated customer de-

mand. Contract terms, e.g., a freight charge and a

cancellation fee, may also affect the forwarder’s de-

cision: A deep discount or a small cancellation fee

makes the allotment more attractive, from the for-

warder’s viewpoint. On the other hand, if the penalty

fee associated with the unused allotment is very large,

or the wholesale contract price is still very high, com-

pared to the spot rate, the forwarder may not want a

large allotment or may not want to establish a con-

tract at all. The allotment affects the proﬁts of both

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

forwarder and carrier. The carrier’s revenue depends

on both the contract payment from the forwarder and

the revenue from direct shippers. At the time that the

contract is established, the direct-ship demand and the

forwarder’s demand remain unknown. The contract

parameter and the allotment need to be determined,

before demands materialize. To this end, we formu-

late a Stackelberg game, in which the carrier is the

leader and offers a set of contract parameters to the

forwarder. Based on its demand distribution and the

contract parameter, the forwarder determines the best

allotment size, which maximizes its own expected

proﬁt. Our article analyzes this sequential game of

the air-cargo allotment contract.

The rest of this article is organized as follows.

Section 2 presents the Stackelberg game, and it is an-

alyzed in Section 3. For a given contract parameter,

we solve for the forwarder’s allotment, which max-

imizes its own expected proﬁt. After obtaining the

forwarder’s best response, we solve for the equilib-

rium of the game, i.e, the optimal contract parameter

offered by the carrier. Section 4 provides some nu-

merical examples to illustrate our approach, and the

beneﬁt from the allotment contract is quantiﬁed nu-

merically. Finally, Section 5 gives a summary and a

few extensions.

2 FORMULATION

Consider an air-cargo service chain, which consists

of a freight forwarder and an air-cargo carrier en-

dowed with cargo capacity of κ. In the strategic

level, the air-cargo capacity is assumed to be a one-

dimensional quantity; in practice, the allotment agree-

ment is given in terms of weight. (In the operational

level, the forwarder is charged based on the dimen-

sional weight, which the volume is converted to a

“volume weight.” If the cargo measurements are in

centimeters, the volume weight is obtained by divid-

ing the cubic centimeters by 6000. The chargeable

weight is the higher of the gross weight (in kilograms)

and the volume weight. This article concerns with

the forwarder’s strategic decision making, not opera-

tional.) The freight forwarder wants to pre-book ca-

pacity in bulk with an airline to achieve a discount

rate, which is less than or equal to the spot rate, de-

noted by v. The carrier wants to block some space as

an allotment for the forwarder, to achieve better cargo

utilization, because its own direct-ship demand may

not be enough to ﬁll the cargo hold.

Let x be the size of the allotment, D

the random

customer demand to the forwarder, D

the direct-ship

demand to the carrier, on the given route. The se-

quence of events is as follows: Prior to the start of the

selling season, the carrier offers a wholesale price w

to the forwarder, and the forwarder determines the

size of the allotment, x. When the allotment agree-

ment is made, the random demands to both forwarder

and carrier are still unknown. Assume that the for-

warder’s demand materializes before the carrier’s de-

mand. (This is typically observed in practice, since

the forwarder spends much more effort to attract de-

mand as early as possible.) A few weeks before de-

parture, the forwarder knows its actual requirement.

The actual allotment usage is min(D

,x), and the un-

used allotment is (x−D

)

. If demand is less than the

allotment, then the forwarder can return the unwanted

space, and the airline sells the remaining capacity on

free-sale basis. The carrier may impose a penalty cost

for the unused allotment if the forwarder releases the

space after the cutoff time, usually 48 hours before

departure time. On the other hand, suppose that the

actual demand is greater than the allotment. The for-

warder books the excess demand, (D

− x)

at the

spot rate, v.

Let p

be the forwarder’s per-unit price charged

to its customer. The forwarder’s revenue from ac-

cepting its own demand D

is given as p

. Let

h be the unit penalty cost associated with the unused

allotment, (x − D)

. The unit cost could be the al-

lotment reservation fee minus the refund. The rate

of the refund might depend on how easily the carrier

could sell remaining space in the spot market. It can

also depend on the timing when the unused allotment

is released. The penalty cost could also include loss

of goodwill; if the allotment utilizations by the for-

warder are consistently low on most ﬂights, the carrier

might reduce the allotment size or terminate the allot-

ment contract in the next season. By contrast, in some

cases in which the forwarder is much more powerful

than the carrier, the unused allotment could be fully

refunded, and the unit cost would be negligible. The

forwarder’s expected contribution for an allotment x

is deﬁned as

π(x) = E[p

− w min(D

,x) (1)

− v(D

− x)

− h(x − D

)

]

= E[(p

− w)min(D

,x) (2)

+ (p

− v)(D

− x)

− h(x − D

)

]

where (2) follows from the identity min(D

,x) =

− (D

− x)

. In (1), the ﬁrst term is the for-

warder’s revenue, the second term the wholesale pay-

ment for the actual allotment usage, the third term the

forwarder’s spot purchase for the excess demand, and

the fourth term the penalty cost associated with the

unused allotment. Note that from (2), the forwarder’s

contribution margin per unit allotment is (p

− w),

Game-theoretic Analysis of Air-cargo Allotment Contract

and that associated with the spot capacity is (p

− v).

The forwarder’s margin is deﬁned as the price charged

to the customer minus the incremental cost, which is

the difference between the total cost the forwarder

would experience if it makes the commitment to its

customer and the total cost it would experience if

it does not (Phillips, 2005). For instance, the for-

warder’s incremental cost might include fuel and se-

curity surcharges, terminal handling fees, and cus-

toms clearance, which would be incurred from han-

dling one unit of cargo, as well as any commissions or

fees the forwarder would incur, assuming that the for-

warder do not pass any of these costs to its customers.

(If the forwarder directly passes on, say the fuel sur-

charge to its customer, this particular cost would not

be included in the incremental cost.)

In (1), the contract parameter w is interpreted as

the per-unit price for the actual allotment usage, and

h the per-unit penalty cost for the unused portion of

the allotment. They can be interpreted differently as

follows: The transfer payment from the forwarder to

the carrier can be written as

wmin(D

,x)+ h(x − D

)

= wx + (h − w)(x − D

)

(3)

= wx − (w − h)(x − D

)

(4)

In (3) and (4), we can interpret w as the wholesale

price for the entire allotment x, paid upfront by the

forwarder. If h = w, then the forwarder pays for the

entire allotment x at the wholesale price w upfront,

and there are no additional monetary transfers. If

h > w, then the forwarder pays for the allotment x up-

front at the wholesale price of w, and after its demand

is realized, the penalty rate of (h − w) is charged for

the unused portion of the allotment; see (3). If h < w,

then the forwarder pays for the allotment x upfront at

the wholesale price of w as before, but after its de-

mand is realized, the refund rate of (w − h) for the

unused portion of the allotment is returned from the

carrier to the forwarder; see (4). Since the air-cargo

selling season is so short that we do not need to ac-

count for monetary discount; thus, the expected proﬁt

is not affected by the timing in which the payment

is collected. Our formulation subsumes both refund

and penalty rates for the unused portion of the allot-

ment. After the forwarder’s demand D

materializes,

the forwarder pays the penalty cost to the carrier for

the unused portion of the allotment if h > w; on the

other hand, if h < w, the carrier returns the refund to

the forwarder.

In practice, the contract terms may include the

wholesale price and the penalty cost (or the refund

rate) as well as the required allotment utilization. De-

ﬁne the allotment utilization as the ratio of the ex-

pected actual allotment usage to the allotment size x:

u(x) =

E[min(D

,x)]. (5)

If the utilization is too low, in the next season, the air-

line might decrease the allotment, or increase the con-

tract rate, or impose a minimum volume requirement,

or terminate the allotment contract. Let u

∈ (0, 1) be

the required allotment utilization. In practice, the for-

warder generally needs to maintain the utilization to

be at least 60-70%.

max{π(x) : u(x) ≥ u

)}. (6)

Let Ω = (w, h,u

) be the contract parameter. After

the forwarder releases its unused allotment, the carrier

re-sells this to direct shippers. Let p

be the carrier’s

price charged to the direct customers. The carrier’s

expected proﬁt is deﬁned as:

ψ(x,Ω) = E[p

min(D

,κ− min(D

,x))

+ w min(x,D

) + h(x − D

)

] (7)

In (7), the ﬁrst term is the carrier’s revenue from sell-

ing the remaining cargo space, κ − min(D

,x), to its

own direct-ship customers, the second term the for-

warder’s payment for the actual allotment usage, and

the third term the penalty paid by the forwarder to the

carrier for the unused allotment.

Note that the carrier’s expected proﬁt depends on

both the contract parameter Ω and the forwarder’s de-

cision on the allotment x. In our Stackelberg game,

we assume that the carrier is the leader which offers

a contract parameter Ω, and the forwarder is the fol-

lower, which decides on the allotment x. Let x

∗

(Ω)

denote the forwarder’s best response to the contract

parameter Ω; i.e.,

∗

(Ω) = argmax{π(x) : 0 ≤ x ≤ u

At the equilibrium solution, the carrier anticipates

the forwarder’s best response x

∗

(Ω), and the carrier

chooses the best contract parameter Ω, which maxi-

mizes its own expected proﬁt:

max

Ω

E[p

min(D

,κ− min(x

∗

(Ω),D

))

+ w min(D

∗

(w)) + h(x

∗

(w) − D

)

] (8)

subject to: x

∗

(Ω) ≤ κ (9)

In Section 3, we will determine the equilibrium of the

game. This is sometimes referred to as the decentral-

ized chain, in which each party maximizes its own

expected proﬁt.

Finally, we consider the entire air-cargo service

chain: Suppose that the forwarder and the carrier

are owned by the same ﬁrm, called the integrator.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

This is referred to as the centralized chain. The to-

tal chain’s expected proﬁt is deﬁned as the sum of the

forwarder’s expected proﬁt and that of the carrier:

τ(x) = π(x) +ψ(x,Ω)

= E[p

+ p

min(D

,κ− min(D

,x))

− v(D

− x)

]. (10)

In (10), the ﬁrst term is the revenue from the cus-

tomers, which need dedicated services as offered

by the forwarder, the second term the revenue from

direct-ship customers, and the third term is the cost

from purchasing spot capacity for the excess de-

mand. In practice, p

≥ p

because the forwarder of-

fers value-added service, e.g., customs clearance and

door-to-door service. Eq. (10) assumes that the inte-

grator accepts all the forwarder’s demand, D

. The

integrator handles x units of the forwarder’s demand

using its own capacity and reserves the remaining ca-

pacity κ − min(x,D

) for the direct-ship customers.

The forwarder’s excess demand is handled through

the spot market. Note that in the integrator’s proﬁt,

there are no payment terms, because we assume that

the forwarder and the carrier belong to the same ﬁrm,

and their payments cancel out when we analyze the

entire service chain.

The service chain is said to be efﬁcient if the total

expected proﬁt of the chain (the integrator’s expected

proﬁt) is equal to the sum of the proﬁts of the two

parties. The contract which allows the efﬁciency to

occur is said to coordinate the service chain (Cachon,

2003). The coordinating contract is a desirable fea-

ture, since there would be no efﬁciency loss from en-

tering into the contract, and the service chain risk is

shared appropriately. In the analysis, we will ﬁnd an

equilibrium coordinating contract, if exists.

3 ANALYSIS

For each i ∈ { f ,a}, assume demand D

is a nonnega-

tive continuous random variable. Let F

be the distri-

bution function of D

the complementary cumula-

tive distribution function, F

−1

the quantile function,

and ξ

the density function.

Deﬁne υ

−1

: (0,1) → (0, ∞) as the inverse function

of the utilization function; i.e., u(x) = t if and only

if υ

−1

(t) = x. In words, υ

−1

(t) corresponds to the

allotment at which the utilization is exactly equal to t.

Lemma 1.

1. The forwarder’s constrained maximization

max{π(x) : u(x) ≥ u

}

is equivalent to

max{π(x) : x ≤ υ

−1

)}.

2. In the carrier’s problem (8), constraint (9)

∗

(Ω) ≤ κ

holds, if

≥ u(κ).

Proof. The ﬁrst derivative of the expected utilization

u(x) = E[min(D

,x)]/x with respect to the allotment

x is

(x) = −

tξ

(t)dt < 0. (11)

Eq. (11) follows from

E[min(D

,x)] =

tξ

(t)dt +x

(x) =

(t)dt.

Since u

(x) < 0, the utilization is decreasing in x. For

all x ≤ υ

−1

), u(x) ≥ u

. In particular, u(x) ≥ u

≥

u(κ) implies that x ≤ κ since u is decreasing.

It follows from Lemma 1 that the utilization constraint

imposes the upper bound υ

−1

) on the allotment

size. The utilization constraint involving the expected

value becomes a simple linear constraint x ≤ υ

−1

Theorem 1 characterizes the expected proﬁt func-

tion and derives its maximum point. The forwarder’s

best response function x

∗

(Ω) is given analytically.

Theorem 1.

1. If w ≥ v, the forwarder’s expected proﬁt is de-

creasing and maximized at x

∗

(Ω) = 0.

2. If w < v and h = 0, the forwarder’s expected proﬁt

given an allotment π(x) is increasing and maxi-

mized at x

∗

(Ω) = υ

−1

3. If w < v and h > 0, the forwarder’s expected proﬁt

is concave, unimodal and maximized at

∗

(Ω) = min{F

−1



v − w

v − w + h



, υ

−1

)}.

(12)

Proof. Using identity min(D

,x) = D

− (D

− x)

the forwarder’s expected proﬁt can be written as

E[(p

− w)D

− (v − w)(D

− w)

− h(x − D

)

For shorthand, let r = v − w. If r ≤ 0, the second

term r(D − x)

is increasing, and the forwarder’s ex-

pected proﬁt function π(x) is decreasing; thus, it is

maximized at x

∗

= 0.

Note that the ﬁrst term E[(p

− w)D

] does not

depend on the allotment. Maximizing the forwarder’s

expected proﬁt is equivalent to minimizing the “ex-

pected total cost”

η(x) = E[r(D

− x)

+ h(x − D

)

Game-theoretic Analysis of Air-cargo Allotment Contract

Its ﬁrst derivative with respect to x is

(x) = −r

(x) + hF

(x)

= −r + (r + h)F

(x).

Note that at η

(0) = −r < 0, η(x) is decreasing

when x = 0. Also, lim

x→∞

(x) = h > 0, η(x) is

increasing when x is large. Hence, η(x) and the

expected proﬁt π(x) are unimodal. Furthermore,

(x) = (r + h)ξ

(x) ≥ 0, η(x) is convex, and the for-

warder’s expected proﬁt π(x) is concave. Setting the

ﬁrst derivative to zero and invoking the ﬁrst part of

Lemma 1, we obtain the expression for the optimal

solution.

The ﬁrst part of Theorem 1 asserts that if the whole-

sale price is greater than the spot price, the forwarder

would not pre-book any allotment at all. On the other

hand, suppose that the wholesale price does not ex-

ceed the spot price. If the carrier imposes no penalty

cost associated with the unused allotment (i.e., h = 0),

the forwarders expected proﬁt is increasing, and the

forwarder would choose the largest allotment that the

carrier would allow, i.e., the upper bound υ

−1

)

given by the required allotment utilization u

. The

last part of Theorem 1 asserts that if there is a pos-

itive penalty cost (i.e., h > 0), the forwarder should

pre-book the allotment, which balances the cost as-

sociated with the unused allotment and the oppor-

tunity cost from not having enough allotment. In

the newsvendor (single-period) inventory model, the

ﬁrst is referred to as the overage, and the latter is

referred to as the underage; an optimal order quan-

tity that minimizes the expected total cost E[c

(D −

+ c

(q − D)

] is q

∗

= F

−1

/(c

+ c

)) where

(resp., c

) is the unit underage (resp., overage) cost

from ordering less (resp., more) than demand, and F

is the distribution of demand D. See a standard text-

book in operations management for the newsvendor

model; e.g., chapter 5 in (Nahmias, 2009). An opti-

mal allotment in Theorem 1 bears a striking resem-

blance to the optimal order quantity in the newsven-

dor model.

In (12), the quantity (v −w)/(v−w +h) = 1/(1 +

θ) is called the critical ratio, where θ = h/(v − w).

The penalty cost h is equal to the constant θ times the

margin difference r = (v − w). It plays an important

role in the forwarder’s allotment decision, x

∗

: The

larger the critical ratio or the smaller the constant θ,

the larger the allotment size, since the quantile F

−1

is an increasing function. In particular, if the critical

ratio is 0.5 or the constant θ = 1, then an optimal al-

lotment is exactly equal to the median demand. If the

critical ratio is greater (resp., less) than 0.5 or the con-

stant θ is less (resp., greater) than 1, then an optimal

allotment is greater (resp., less) than the median de-

mand. If the penalty cost associated with the unused

allotment, h, increases, the forwarder should decrease

the allotment size. On the other hand, the forwarder

should increase the allotment, if the margin difference

r = (v−w) increases. These sensitivity analyses make

economic sense.

In Theorem 2, we analyze the carrier’s problem

when the penalty cost h > 0 is given a priori. In

Theorem 3, we provide the analysis when there is

no penalty cost, h = 0. Depending on the market

power of the two parties, some of the contract pa-

rameters might be pre-determined a priori. For in-

stance, on the high-demand route, the carrier might be

more powerful than the forwarder, and all contract pa-

rameters (w, h,u

) = Ω can be determined by the car-

rier. On the low-demand route, the forwarder might

be more powerful, and the carrier is able to choose

only one parameter, says the wholesale price w; the

rest of the contract parameters, e.g., (h,u

), are pre-

speciﬁed a priori.

Theorem 2. Assume that the penalty cost is ﬁxed and

strictly positive, h > 0 and that the required utilization

is u

= u(κ). The carrier’s problem (8) can be re-

formulated as the allotment being the decision vari-

able:

max

x≤κ

E[p

min(D

,κ − min(x,D

))

+ ω(x)min(x, D

) + h(x − D

)

] (13)

where

ω(x) = v −

(x)

h. (14)

Further assume that the two demands D

and D

are

independent. Suppose that the ratio of the spot to the

carrier’s price is v/p

> F

(κ) and that the penalty

cost is

0 < h < [(p

− ω(κ)](1/F

(κ) − 1). (15)

Then, the carrier’s expected proﬁt is maximized at x

∗

which is the root of:

(x)[ω(x) − h − p

(κ − x)]

+ E[min(x,D

)]ω

(x) + h. (16)

Proof. Suppose that h > 0. For w ≥ v, the forwarder’s

best response is zero allotment. For w < v, ω(x) is

implicitly as

(x) =

v − ω

v − ω + h

After re-arranging and collecting terms, we obtain the

wholesale price as in (14).

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

Let ζ(x) be the objective function in (13). Note

that

(x) = (ω(x) −h)

(x) + E[min(x,D

)]ω

(x)

+ h − p

P(D

> κ − x,D

> x)

(x)[ω(x) − h − p

(κ − x)]

+ E[min(x,D

)]ω

(x) + h

where the last equation follows from the assumption

that D

and D

are independent, so P(D

> s,D

t) =

(s)

(t). Note that ω(x) is differentiable (since

the distribution is continuous), so ω

(x) is continuous,

and the ﬁrst derivative ζ

(x) is continuous. Recall that

the carrier requires that the allotment 0 < x ≤ κ. Note

that at the two end points,

(0) = v − p

(κ)

and that

(κ) =

(κ)[ω(κ)−h− p

]+E[min(x, D

)]ω

(x)+h.

If v/p

> F

(κ), then ζ

(0) > 0. Also ζ

(κ) < 0

from (15). Finally, if follows the intermediate value

theorem that there exists x

∗

which solves ζ

(x) = 0.

Note that the carrier’s constraint x ≤ κ holds, since

= u(κ); see Lemma 1.

Unless the cumulative distributions F

;i = 1,2 are

very simple, a closed-form solution to (16) does not

exist, and the equilibrium of the game needs to be

found numerically; see numerical examples in Sec-

tion 4.

Theorem 3. Suppose that h = 0 and

w = v −ε

where ε > 0 is a very small positive number. Then,

the carrier’s problem can be re-formulated as the re-

quired utilization being the decision variable:

max

≥u(κ)

E[p

min(D

,κ − min(υ

−1

),D

) (17)

+(v − ε) min(υ

−1

),D

)]

Proof. It follows from Theorem 1 that if w < v and

h = 0, then π(x) is increasing and maximized at the

upper bound on the allotment, υ

−1

). Constraint

≥ u(κ) ensures that x

∗

(Ω) ≤ κ; see Lemma 1.

Theorem 3 states that if the penalty cost is h = 0

and that the wholesale price is just below the spot

price, then the forwarder chooses the largest allotment

which satisﬁes the required utilization. In the carrier’s

problem, the required utilization becomes the only de-

cision variable.

In practice, it is uncommon to ﬁnd that an air-

line provides a full refund for the unused allotment

(thus, h = 0). To ensure its high customer service

level, the forwarder may ask for a very large allot-

ment (much greater than its anticipated customer de-

mand) and release the unwanted allotment so late that

the airline does not have enough time to re-sell it in

the spot market. To prevent the forwarder to pre-book

a large allotment, Theorem 3 suggests that the carrier

needs to impose the minimum utilization requirement

[u(x) ≥ u

] where u

≥ u(κ). This bound u

might

be tighter than u(κ) [speciﬁcally, u

> u(κ)], since

in practice the carrier might not want to allocate the

entire capacity κ as the allotment and might want to

reserve some space for the direct-ship customers.

Finally, we analyze the integrator’s problem. Let

= argmax{τ(x) : 0 ≤ x ≤ κ}

Theorem 4.

1. If v > p

, then x

= κ.

2. If v < p

, then x

is a root of

(x) − p

P(D

> x, D

> κ − x). (18)

In particular, if the two demands D

and D

are

independent, then



κ − F

−1



1 −



Proof. Using (D

− x)

= D

− min(x,D

), the inte-

grator’s expected proﬁt (10) becomes

τ(x) = (p

− v)E[D

] + φ(x) (19)

where

φ(x) = E[v min(D

,x) + p

min(D

,κ − min(D

,x))].

(20)

In (19), the ﬁrst term is constant; thus, maximizing

τ(x) is equivalent to maximizing φ(x). Note that φ(x)

is identical to the expected proﬁt in the well-known

two-class capacity allocation in the airline passenger

revenue management context; see e.g., Chapter 2 in

(Talluri and van Ryzin, 2004) and (Amaruchkul et al.,

2011). Recall in the two-class model, we need to de-

termine the booking limit x for the discount (class-2)

customers, which arrive ﬁrst, and the remaining ca-

pacity is reserved for the full-fare (class-1) customers,

which arrive last; the airline’s expected proﬁt is

E[p

min(x,D

) + p

min(D

,κ − min(x,D

))] (21)

where for i = 1,2, the parameter p

and the random

variable D

are price and demand for the class-i cus-

tomers, respectively. By comparing (20) to (21), we

clearly see that the forwarder’s demand D

is equiv-

alent to the discount-fare customer D

, and the car-

rier’s direct-ship demand D

is equivalent to the full-

fare customer D

. If v > p

, we would accept D

as much as possible, so x

= κ. On the other hand, if

Game-theoretic Analysis of Air-cargo Allotment Contract

v < p

, we need to balance between accepting D

now

or waiting for D

which arrives later. The optimality

condition is derived in e.g., Chapter 2 in (Talluri and

van Ryzin, 2004) and (Amaruchkul et al., 2011).

Recall that in the integrator’s problem (10), we accept

all of the forwarder’s demand. If the integrator’s ca-

pacity is not enough, then the spot market is used to

handle the excess demand. Thus, if the spot price is

very expensive, then the integrator would allocate all

capacity for the forwarder’s demand in order to mini-

mize the spot purchase, and no space is protected for

the direct-ship customers. On the other hand, if the

spot market is not that large, then the integrator would

protect κ − x

for the direct-ship customer which ar-

rives after the forwarder’s demand.

It follows from the optimality equation in Theo-

rem 4 that the integrator’s optimal allotment increases

when the spot price v increases, or the direct-ship

per-unit price p

decreases, or that the direct-ship de-

mand becomes smaller in the usual stochastic order-

ing sense. These directional changes make economic

sense.

Corollary 1. Suppose that h = 0 and w = v − ε. At

the equilibrium, the carrier imposes the required uti-

lization u

= x

(ε) where

(ε) =



κ − F

−1



1 −

v − ε



is the equilibrium allotment. For ε > 0, x

(ε) < x

and

lim

ε→0

(ε) = x

. (22)

Proof. The expression for the equilibrium allotment

follows immediately by observing the similarity be-

tween the carrier’s problem (17) and the integra-

tor’s problem (20). In the integrator’s problem (20),

the unit contribution from the allotment usage is v,

whereas in the game (17), the corresponding unit con-

tribution is v − ε. Since w = v − ε where ε is a small

positive number, we have that x

(ε) < x

It follows from (22) that a contract with no penalty

cost can be made as close as possible to the coordi-

nating contract. The air cargo service chain becomes

efﬁcient, in the limiting sense, when the carrier im-

poses no penalty cost.

Suppose that the carrier imposes a positive penalty

cost h > 0. When the service chain is efﬁcient, the op-

timality conditions in Theorem 1 and Theorem 4 co-

incide. If the integrator’s optimal allotment x

solves

the carrier’s problem (13), or it is the root of (14), then

there exists the equilibrium coordinating contract in

the decentralized chain, and the wholesale price satis-

ﬁes

= v − γ h (23)

where γ = F

). If γh < v < p

, then the

wholesale (23) is positive, and the allotment does not

exceed the carrier’s capacity κ. As in Theorem 2,

in most cases, the equilibrium coordinating contract

needs to be found numerically.

4 NUMERICAL EXAMPLES

We provide a numerical example to illustrate our ap-

proach of ﬁnding an equilibrium in the air-cargo con-

tract game. The forwarder’s demand is taken from one

of the leading logistics providers in Thailand. Dur-

ing 2014, the forwarder did not pre-book any allot-

ments on the route from BKK airport (Bangkok Inter-

national Airport, Thailand) to DUB airport (Dublin

Airport, Ireland). In the past, around 89% of the

forwarder’s customer demands were handled by one

of the largest Persian Gulf carriers, and the rest by

the other airlines in the spot market. Assume that

the per-unit price the forwarder charges its customer

is p

= 63 THB/kg, the per-unit price the carrier

charges its direct shippers p

= 60 THB/kg, and the

spot price v = 58 THB/kg. We need to estimate the

demand distribution from the historical data. Some

classical descriptive statistics are as follows: Mini-

mum is 2.72 (kg); maximum 1142.32, median 294.88;

mean 340.13; standard deviation 211.68; skewness

1.41; kurtosis 5.69. The coefﬁcient of variation

is 0.62; in words, the standard deviation is more

than half of the mean. The mean is greater than

the median, and skewness is positive. We ﬁt the

gamma distribution with the (shape, rate) parameter,

(α

,β

) = (2.6031,0.0077). The corresponding p-

value is 0.3390. There is insufﬁcient evidence at 0.01

level of signiﬁcance to reject the null hypothesis that

the forwarder’s demand follows the gamma distribu-

tion. Assume that the direct-ship demand also follows

the gamma distribution with the (shape, rate) param-

eter (α

,β

) = (5.76,0.01), so the expected direct-

ship demand is 576 kg, and the standard deviation is

240 kg. The carrier’s cargo capacity is assumed to

be κ = 1000.

In Examples 1–3, we assume that the required uti-

lization u

= u(κ):

= u(κ) =

E[min(D

,κ)]

= 336.48/1000 = 33.65%.

In Examples 1–2, we assume that the penalty cost is

ﬁxed at h = 56 THB/kg.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

Example 1 (Forwarder’s problem). We study the ef-

fect of the wholesale price to the forwarder’s allot-

ment decision. We consider two cases: In the ﬁrst

case, the forwarder’s expected proﬁt is concave and

unimodal and the forwarder’s decision is given in

Theorem 1, whereas in the second case, it is decreas-

ing and the forwarder’s decision is zero allotment.

Suppose that the wholesale price does not exceed

the spot price: w = 45 ≤ 58 = v. Recall the for-

warder’s expected proﬁt (1)

E[p

− w min(D

,x) − v(D

− x)

− h(x − D

)

For the ﬁrst term in (1), the forwarder’s mean demand

E[D

] is the expected value of the gamma distribu-

tion:

E[D

] =

Γ(α

)

−1

where Γ(α) is the gamma function, deﬁned by

Γ(α) =

∞

α−1

−x

dx.

For the second term in (1), we evaluate the expected

allotment usage E[min(D

,x)] using the limited ex-

pected value (LEV) function. The LEV function for

gamma random variable, Y, with the shape parame-

ter α and the scale parameter θ is

E[min(Y,x)] = αθΓ(α + 1; x/θ) + x[1 − Γ(α;x/θ]

where Γ(α;x) is the incomplete gamma function de-

ﬁned by

Γ(α;x) =

Γ(α)

α−1

−t

dt.

(For the gamma distribution, the scale parameter

is equal to the reciprocal of the rate parameter;

for instance, the scale parameter of D

is 1/β

1/0.0077 = 129.8701.) For the last two terms in (1),

we use the following

E[(D

− x)

] = E[D

] − E[min(D

,x)]

E[(x − D

)

] = x −E[min(D

,x)]

where the expected allotment usage is calculated pre-

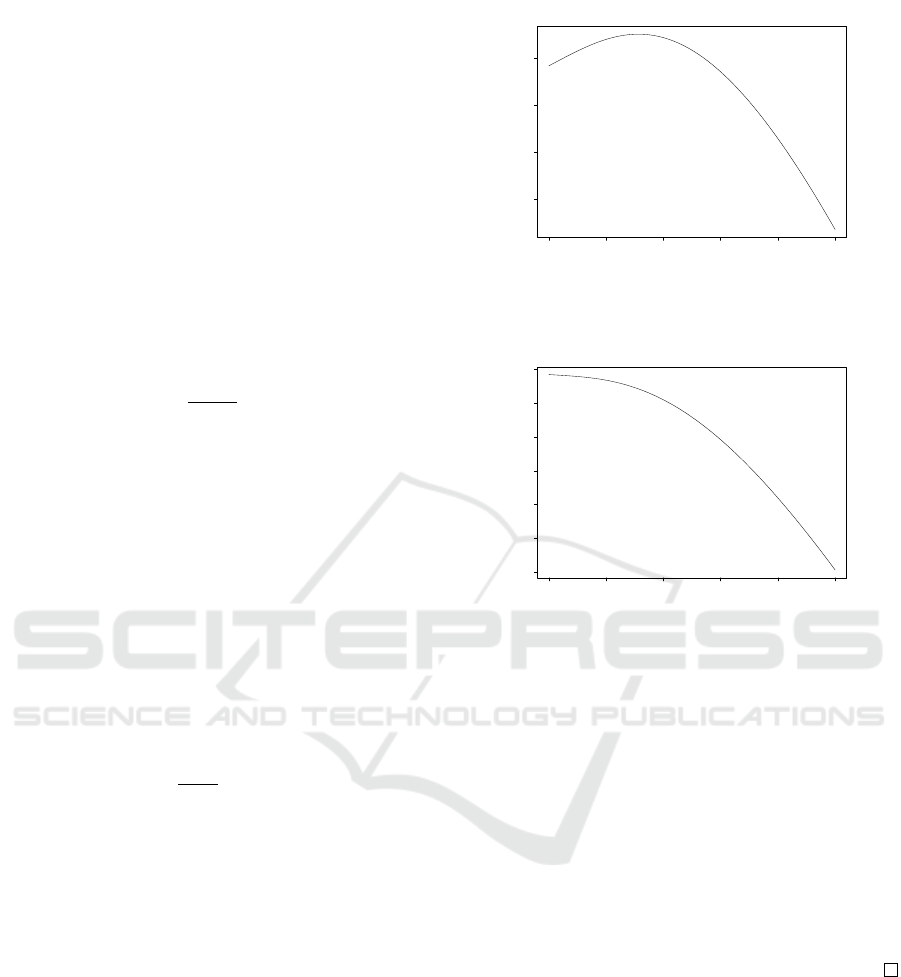
viously using the LEV function. Figure 1 shows the

forwarder’s expected proﬁt as a function of the allot-

ment, given that the carrier offers the wholesale price

of w = 45.

The case w = 45 ≤ 58 = v corresponds to the

last case in Theorem 1: The forwarder’s expected

proﬁt function is concave, unimodal and maximized

at x

∗

(45) = 156.39 ≈ 156. When the carrier offers

the per-unit price of w = 45 for the actual allotment

usage and charges the per-unit penalty of h = 56 for

0 100 200 300 400 500

−4000 −2000 0 2000

allotment

forwarder's profit

Figure 1: Forwarder’s expected proﬁt as a function of the

allotment, given that the carrier offers the wholesale price

of w = 45 ≤ 58 = v.

0 100 200 300 400 500

−10000 −8000 −6000 −4000 −2000 0 2000

allotment

forwarder's profit

Figure 2: Forwarder’s expected proﬁt as a function of the

allotment, given that the carrier offers the wholesale price

of w = 60 > 58 = v.

the unused allotment, the forwarder chooses the al-

lotment of x

∗

(45) = 156, which maximizes its own

expected proﬁt.

On the other hand, suppose that the carrier offers

the wholesale price greater than the spot price, w =

60 > 58 = v. Then, the forwarder’s expected proﬁt is

decreasing in the allotment; see Figure 2.

When the spot price is smaller than the wholesale

price, there is no need for the forwarder to pre-book

any space; the forwarder can purchase capacity at the

spot market for the consolidated cargo. This corre-

sponds to the ﬁrst case in Theorem 1.

Example 2 (Carrier’s problem). In Example 1, we

consider two cases, (w, x

∗

) = 45, 156) and (w,x

∗

) =

(60,0). In this example, the wholesale prices are var-

ied from 0 to 70, and we plot the forwarder’s best re-

sponse, i.e., the allotment which maximizes the for-

warder proﬁt function for a given wholesale price.

Figure 3 shows the forwarder’s best response as a

function of the wholesale price. The wholesale price

function ω(x) is the inverse of the forwarder’s best

response function.

After the wholesale price function ω(x) is readily

found, we are now in the position to solve for the equi-

Game-theoretic Analysis of Air-cargo Allotment Contract

0 10 20 30 40 50 60 70

0 50 100 150 200 250 300

wholesale price

forwarder's best response

Figure 3: Forwarder’s best response to the carrier’s offered

wholesale price.

librium of the Stackelberg game, x

∗

which maximizes

the carrier’s expected proﬁt (8) given the forwarder’s

best response:

max

x∈(0,κ]

E[p

min(D

,κ − min(x,D

)) (24)

+ ω(x)min(x, D

) + h(x − D

)

]

To calculate the ﬁrst term in (24), we again make use

of the LEV. For all x ≤ κ, we have that

E[min(D

,κ − min(D

,x)]

∞

E[min(D

,κ − min(t,x)]ξ

(t)dt

E[min(D

,κ − t)]ξ

(t)dt

∞

E[min(D

,κ − x)]ξ

(t)dt

E[min(D

,κ − t)]ξ

(t)dt

+ E[min(D

,κ − x)]

(x).

The carrier’s proﬁt is maximized at x

∗

= 181. From

the wholesale price function ω(x

∗

) = ω(181) = 40.

At the equilibrium, the carrier ﬁrst offers the whole-

sale price of w

∗

= 40, and the forwarder responses

with the allotment of x

∗

) = 181, which maximizes

its expected proﬁt. Recall that the penalty cost h = 56.

At an equilibrium, the contract parameter can also be

interpreted as the per-unit upfront payment w

∗

= 40

for the entire allotment, x

∗

) = 181, and a penalty

rate of h − w = 16 for the unused portion of the allot-

ment.

Recall that in 2014, the forwarder did not pre-

book any allotments on the BKK-DUB route. When

it uses only the spot market, the forwarder’s expected

proﬁt is (p

− v)E[D

] = (63 − 58)(338.0649) =

1690 THB per ﬂight. With the allotment contract, the

forwarder’s proﬁt is improved by 126.39%. Table 1

summarizes the expected proﬁts of both parties and

the total proﬁt in the service chain.

Table 1: Beneﬁt from allotment contract with

∗

)) = (40, 181).

Proﬁt

Forwarder Carrier Total

W/O contract 1690 34025 35715

W/ contract 3826 40568 44393

% ∆ 126% 19% 24%

In this numerical example, we see that the allot-

ment contract makes both parties better off. More-

over, the carrier’s cargo load factor with the contract

{E[min(D

∗

)] + E[min(D

,κ − min(D

∗

))]}

= 71.72%

whereas that without the contract (the allotment x = 0)

E[min(D

,κ)] = 60.88%.

With the allotment contract, the carrier improves its

cargo load factor by 17.8%.

Example 3 (Coordinating contract with positive

penalty cost). In the above example, the integrator’s

optimal allotment is

= F

−1

(1 − v/p

) = 778.79

and the optimal integrator’s expected proﬁt is τ(x

) =

50395.14. Note that v − γh = 58 − (24.2338)(56) =

−1299.093 < 0. The coordinating contract does

not exists in this route. The chain efﬁciency is

44393/50395.1 = 88.09%.

Suppose that on another route, the forwarder’s

demand is gamma with the parameter (α

,β

) =

(6.32,0.0077); the forwarder’s shape parameter in-

creases, so the expected demand increases from 338

to 821 kg. This route is more popular, so we assume

that prices are higher; speciﬁcally, p

= 190 and p

180. The integrator’s optimal allotment is x

= 343,

and the integrator’s optimal proﬁt is 220468.2.

Suppose the penalty cost remains h = 56.

From (23), w = v − γh = 55.7968 ≈ 56 where γ =

0.03934. However, this coordinating contract (w,x) =

(56,343) is not the equilibrium solution of the game,

which is (w,x) = (56, 335). At the equilibrium, the

proﬁts of the forwarder and carrier are 108891.6 and

111569.5, respectively, and the allotment is smaller

than the optimal allotment in the integrated chain. Al-

though the equilibrium contract does not coordinate

the chain, but the service chain efﬁciency

π(335) + ψ(335)

τ(343)

108891.6 + 111569.5

220468.2

= 99.997%

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

Table 2: Coordinating contracts with zero penalty cost.

Wholesale Proﬁt

Price Forwarder Carrier Total

30 10977 39418 50395

40 7660 42735 50395

56 2354 48042 50395

is nearly 100%. The total chain proﬁt under the equi-

librium contract is slightly smaller than the optimal

integrated proﬁt.

Suppose that the penalty cost is h = 25.5.

From (23), w = v − γh = 56.99676 = 57. This con-

tract (w,x) = (57,343) is also the equilibrium of the

game. Hence, the chain is coordinated, and the ef-

ﬁciency is exactly 100%. From practical viewpoint,

the two contracts may be selected by the carrier, since

their proﬁts are nearly identical. In the ﬁrst con-

tract, the upfront payment of (56)(335) = 18760 is

collected upfront, and there are no additional pay-

ments. In the second contract, the upfront payment

of (57)(343) = 19551 is collected upfront, and the re-

fund rate of 57 −25.5 = 31.5 for the unused portion of

the allotment is paid from the carrier to the forwarder,

after it releases the unwanted space.

Example 4 (Coordinating contract with no penalty

cost). In the limiting sense, a set of coordinating

contracts can be constructed with zero penalty cost

and the minimum utilization requirement. From

Examples 1 and 3, the integrator’s optimal proﬁt

is maximized at x

= 778.79. The forwarder’s

expected utilization at x

is E[min(D

)]/x

331.65/778.79 = 0.4258 = 42.58%. Suppose that the

carrier requires that the forwarder to maintain the ex-

pected utilization of u

= 0.4258. For any wholesale

prices less than the spot price v = 56, the forwarder’s

best response is υ

−1

) = x

; see Theorem 1. Table 2

shows the proﬁts of both parties and the total proﬁt of

the chain.

All of these contracts (with no penalty cost h = 0

and wholesale prices smaller than the spot price, w <

v = 56) coordinate the chain. This may shred some

light on why contracts, commonly found in practice,

sometimes impose no penalty for the unused portion

of the allotment but do impose the allotment utiliza-

tion. The proﬁt division between the two parties de-

pends on the wholesale price. If the carrier is very

powerful, it can offer a wholesale price just below the

spot price and takes almost all of the chain’s proﬁt.

On the other hand, if the forwarder is more power-

ful, then the wholesale price becomes smaller, and the

forwarder gains the larger portion of the the chain’s

proﬁt.

5 CONCLUDING REMARK

We consider the carrier and the forwarder, which may

enter into an allotment contract before the selling sea-

son starts. The forwarder pre-books an allotment at

some reservation fees. After the forwarder’s cus-

tomer demand materializes, the forwarder returns the

unwanted space, and some cancellation fees may be

applied. We formulate the contract design problem

as the Stackelberg game, in which the carrier is the

leader and offers a set of contract parameters. The

forwarder responses by choosing the best allotment,

which maximizes its expected proﬁt, given the con-

tract parameter the carrier proposed ﬁrst. We deter-

mine the closed-form solution for the forwarder’s best

response and give a sufﬁcient condition for the game

to possess an equilibrium. In particular, we show that

the contract, commonly found in practice, with no

penalty cost but with the utilization requirement is ef-

ﬁcient (in the limiting sense). Our numerical example

qualiﬁes the beneﬁt from the allotment contract.

A few extensions are as follows: Like many con-

sumer goods, volume discounts are commonly found

in the air cargo industry; consequently, the margin

may depend on the actual usage, and the penalty cost

may depend on the amount of the returns. The dis-

count may be applied to all the units, actually used by

the forwarder, or it may be applied only to the addi-

tional units beyond the breakpoint. The all-units case

is more common in Thailand. The contract payment

may consist of the minimum payment plus the vari-

able payment depends on the volume; for instance,

for the ﬁrst 500 kilograms, the forwarder charges a

ﬁxed payment of 51000 THB, and the variable pay-

ment is 60 THB/kilogram for each additional kilo-

gram beyond the breakpoint, 500. The variable pay-

ment is sometimes discounted. The penalty cost may

depend on not only the amount of returns but also the

timing that the unused allotment usage is released to

the carrier. It would be of practical interest to ﬁnd an

optimal allotment, when dynamic pricing is in placed.

Another extension is to consider multiple freight for-

warders. Our approach could be used to construct a

heuristic solution to the case of multiple forwarders;

would represent the sum of all forwarders’ de-

mand, and all other cost parameters would be the av-

erages of all forwarders (e.g., p

would be the average

of all forwarders’ price to their customers). More-

over, our approach could also be applied for the pas-

senger airline allotment problem. In the passenger air-

line industry, the airline usually blocks a pre-speciﬁed

number of seats to a wholesaler/agent or other airline,

which has established contracts such as interline or

codeshare agreement prior to the start of the selling

season. We hope to pursue these or related problems.

Game-theoretic Analysis of Air-cargo Allotment Contract

REFERENCES

Accenture (2015). 2015 air cargo survey: Taking off for

higher proﬁtability. Retrieved July 3, 2016 from

www.accenture.com.

Amaruchkul, K., Cooper, W., and Gupta, D. (2007). Single-

leg air-cargo revenue management. Transportation

Science, 41(4):457–469.

Amaruchkul, K., Cooper, W., and Gupta, D. (2011). A note

on air-cargo capacity contracts. Production and Oper-

ations Management, 20(1):152–162.

Barz, C. (2007). Risk-Averse Capacity Control in Revenue

Management. Springer-Verlag, Berlin.

Barz, C. and Gartner, D. (2016). Air cargo network revenue

management. Transportation Science, 50(4):1206–

1222.

Bazaraa, M., Hurley, J., Johnson, E., Nemhauser,

G., Sokol, J., Chew, E., Huang, C., Mok, I.,

Tan, K., and Teo, C. (2001). The Asia Pa-

ciﬁc air cargo system. Research Paper No: TLI-

AP/00/01. The Logistics Institute-Asia Paciﬁc. Na-

tional University of Singapore and Georgia Insti-

tute of Technology. Retrieved January 06, 2007 from

http://www.tliap.nus.edu.sg/Library/default.aspx.

Becker, B. and Dill, N. (2007). Managing the complexity

of air cargo revenue management. Journal of Revenue

and Pricing Management, 6(3):175–187.

Billings, J., Diener, A., and Yuen, B. (2003). Cargo rev-

enue optimisation. Journal of Revenue and Pricing

Management, 2(1):69–79.

Boeing Company (2009). World air cargo forecast 2014–

2015. Retrieved July 3, 2016 from www.boeing.com.

Boeing Company (2012). World air cargo forecast

2012–2013. Retrieved February 5, 2012 from

http://www.boeing.com/commercial/cargo/wacf.pdf.

Cachon, G. (2003). Supply chain coordination with con-

tracts. In de Kok, A. and Graves, S., editors, Hand-

books in Operations Research and Management Sci-

ence: Supply Chain Management. Elsevier, Amster-

dam.

Chiang, W., Chen, J., and Xu, X. (2007). An overview

of research on revenue management: Current issues

and future research. International Journal of Revenue

Management, 1(1):97–128.

DeLain, L. and O’Meara, E. (2004). Building a business

case for revenue management. Journal of Revenue and

Pricing Management, 2(4):368–377.

Feng, B., Li, Y., and Shen, H. (2015). Tying mechanism

for airlines’ air cargo capacity allocation. European

Journal of Operational Research, 244:322–330.

Gupta, D. (2008). Flexible carrier-forwarder contracts for

air cargo business. Journal of Revenue and Pricing

Management, 7(4):341–356.

Hellermann, R. (2013). Options contracts with overbook-

ing in the air cargo industry. Decision Sciences,

44(2):297–327.

Hendricks, G. and Elliott, T. (2010). Implementing

revenue management techniques in an air cargo

environment. Retrieved March 3, 2010 from

www.unisys.com/transportation/insights.

Ingold, A., McMahon-Beattie, U., and Yeoman, I. (2000).

Yield Management: Strategies for the Service Indus-

tries. South-Western Cengage Learning, Bedford

Row, London.

International Air Transport Association (2016). IATA cargo

strategy. Retrieved July 3, 2016 from www.iata.org.

Kasilingam, R. (1996). Air cargo revenue management:

Characteristics and complexities. European Journal

of Operational Research, 96(1):36–44.

Levin, Y., Nediak, M., and Topaloglu, H. (2012). Cargo

capacity management with allotments and spot market

demand. Operations Research, 60(2):351–365.

McGill, J. and van Ryzin, G. (1999). Revenue management:

Research overview and prospects. Transportation Sci-

ence, 33(2):233–256.

Nahmias, S. (2009). Production and Operations Research.

McGraw-Hill, Inc., New York.

Netessine, S. and Shumsky, R. (2002). Introduction to the

theory and practice of yield management. INFORMS

Transactions on Education, 3(1):34–44.

Phillips, R. (2005). Pricing and Revenue Optimization.

Stanford University Press, Stanford, CA.

Prior, R., Slavens, R., and Trimarco, J. (2004). Menlo

worldwide forwarding optimizes its network routing.

Interfaces, 34(1):26–38.

Sales, M. (2013). The Air Logistics Handbook: Air Freight

and the Global Supply Chain. Routledge, New York,

NY.

Slager, B. and Kapteijns, L. (2004). Implementation of

cargo revenue management at KLM. Journal of Rev-

enue and Pricing Management, 3(1):80–90.

Talluri, K. and van Ryzin, G. (2004). The Theory and Prac-

tice of Revenue Management. Kluwer Academic Pub-

lishers, Boston, Massachusetts.

Tao, Y., Chew, E., Lee, L., and Wang, L. (2017). A capacity

pricing and reservation problem under option contract

in the air cargo freight industry. Computers and In-

dustrial Engineering, 110:560–572.

Yang, S., Chen, S., and Chen, C. (2006). Air cargo ﬂeet

routing and timetable setting with multiple on-time

demands. Transportation Research Part E: Logistics

and Transportation Review, 42(5):409–430.

Yeoman, I. and McMahon-Beattie, U. (2004). Revenue

Management and Pricing: Case Studies and Appli-

cations. Thomson Learning, Bedford Row, London.

Yeung, J. and He, W. (2012). Shipment planning, capac-

ity contracting and revenue management in the air

cargo industry: A literature review. Proceedings of

the 2012 International Conference on Industrial En-

gineering and Operations Management, Istanbul, July

2012.

Zhang, C., Xie, F., Huang, K., Wu, T., and Liang, Z. (2017).

MIP models and a hybrid method for the capacitated

air-cargo network planning and scheduling problems.

Transportation Research Part E, 103:158–173.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems