
A Data Quality Dashboard for CMMS Data
Ralf Gitzel
1
, Subanatarajan Subbiah
1
and Christopher Ganz
2
1
Corporate Research Germany, ABB AG, Ladenburg, Germany
2
Global Service R&D, ABB Group, Zurich, Switzerland
Keywords: Data Quality, Reliability, CMMS, Dashboard, Case Study, Failure Data, Industrial Service.
Abstract: Reliability or survival data analysis is an important tool to estimate the life expectancy and failure behaviour
of industrial assets such as motors or pumps. One common data source is the Computerized Maintenance
Management System (CMMS) where all equipment failures are reported. However, the CMMS typically
suffers from a series of data quality problems which can distort the calculation results if not properly
addressed. In this paper, we describe the possible data quality problems in reliability data with a focus on
CMMS data. This list of problems is based on the results of six case studies conducted at our company. The
paper lists a set of metrics which can be used to judge the severity. We also show how the impact of data
quality issues can be estimated. Based on this estimate, we can calibrate a series of metrics for detecting the
problems shown.
1 INTRODUCTION
When it comes to the prediction of failures in
industrial equipment, there are two major categories
of approaches. First, one can use statistical data about
failures to do a survival analysis (Miller, 1997).
Second, one can use sensor data to detect changes to
attributes such as vibration, temperature, etc. e.g. see
(Antoni, 2006). Using sensor data to predict failures
has the advantage that it allows predictions for
individual units. The main disadvantage of sensors is
their cost and the cost of installation. This might come
as a surprise given the rise of low cost sensors,
however the special requirements of the condition
monitoring use case mainly the required accuracy and
reliability often drives up the cost. For these reasons,
using statistical data for the analysis of failure
behaviour is still appealing.
1.1 Survival Analysis of Manually
Collected Failure Data
A commonly used data source is a company’s
Computerized Maintenance Management Systems
CMMS. Organizations use a CMMS to collect all
failures reported by the operators. The maintenance
team uses the CMMS to identify and prioritize
problems that require fixing. While not primarily
intended for this purpose, the data is already collected
and accessible and thus can also be used in survival
analysis.
The typical outcome of a survival analysis is a
function called R(t), which represents the probability
for a product to still be working at a given time t. The
reliability function does not take into account the
impact of concrete events such as overstress, so any
prediction made for an individual unit is to be taken
with scepticism. Yet, R(t) is still useful for
maintenance planning, fleet-level failure forecasting
(Hines, 2008), warranty planning (Wu, 2012),
reliability optimization (Salgado, 2008), (Vadlamani,
2007), and as support for R&D (kunttu, 2012).
However, the analysis of this data is not as
straightforward as it might seem. Since the data used
was never intended for survival analysis, it suffers
from a series of data quality problems such as, but not
limited to, missing information or wrong values.
These problems can be detected with tailored metrics
and their impact on the survival analysis estimated.
1.2 Contribution and Content of This
Paper
This paper describes the latest step in our ongoing
effort to implement a comprehensive data quality
library for data related to industrial service. In our
previous work, we have presented a list of metrics
both for human-collected failure data (Gitzel, 2015)
170
Gitzel, R., Subbiah, S. and Ganz, C.
A Data Quality Dashboard for CMMS Data.
DOI: 10.5220/0006552501700177
In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 170-177
ISBN: 978-989-758-285-1
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

as well as condition monitoring sensor data (Gitzel,
2016) as well as a visualization scheme for the
metrics. In this paper, we use the results of six case
studies conducted so far to present the typical data
quality problems affecting reliability data. In this
paper, our focus is on problems which can occur in
CMMS data. Five of the case studies have been
presented previously see (Gitzel 2015). The new
study uses CMMS data from a large chemical
production plant.
After looking at related work Section 2 we briefly
explain how CMMS data can be used for survival
analysis Section 3. As our first contribution, Section
4 provides an overview of key metrics suitable for
CMMS data quality analysis. Our second
contribution Section 5 is a heuristic estimation
method to classify metric values as good, OK, or bad.
The assessment is based on the level of impact a
certain data quality problem has on the correctness of
the reliability function.
2 RELATED WORK
There is a large body of papers related to data quality.
However, there are only a few papers which look into
the data quality of data used for the purpose of
assessing the condition and residual life of industrial
equipment. Despite the fact that survival analysis is a
common approach in this context, there are barely any
papers addressing this topic.
Data Quality in general: Data quality is a topic that
has been well explored. There are many different
causes for data quality issues which can occur at
many stages of the data’s life cycle see (Hines, 2008),
(Salgado, 2008), (Gitzel, 2011), (Bertino, 2010). The
most common approach to measure data quality is to
define several dimensions of data quality, each of
which covers a series of individual metrics, (Redman,
1996), (Leo, 2002). In fact, there are many
frameworks based on this basic premise e.g. (Yang,
2006), (Bovee, 2003), see (Borek, 2014) pg. 13 for a
survey of frameworks for an exception as well as an
ISO standard (Peter, 2008). In this paper, we adopt
the commonly used dimensional structure proposed
in (Bertino, 2010).
Data Quality in reliability/survival analysis: While
the existence of data quality problems in reliability
data is generally acknowledged as seen in (Gitzel,
2011), (Bertino, 2010), (Montgomery, 2014), and
(Bendell, 1988) this is not reflected in many
published attempts to rectify these problems. Besides
our own prior work (Gitzel, 2015), (Gitzel, 2014) we
have found only a collection of best practices (IEEE,
2007) and one paper providing a series of metrics to
understand the quality of a reliability analysis’s input
data (Montgomery, 2014). A more common approach
is develop reliability-related algorithms that are able
to deal with poor data quality for a good review, see
(Wu, 2013). Very often, these algorithms use
estimates based on assumptions e.g. (Bendell. Such
an approach works well if the assumptions are
correct. In our opinion, there is not enough
understanding about reliability data to verify that the
assumptions reflect reality, especially since there are
not enough algorithms to understand to what extent
the data available is correct.
3 THE USE OF CMMS DATA IN
SURVIVAL ANALYSIS
Survival data typically consists of times to failure
TTFs calculated from field data. For example
consider Figure 1. A fleet of 2 assets each in use since
the time marked by the star has experienced 6 failures
as shown by the dots in the graph. The delta between
the failures are the TTFs in this case there are 6 TTF
values. These values can be seen as the results of a
random variable f. The probability distribution
function behind f can be estimated using the TTFs.
The reliability function as described in Section 1 is
simply the inverse of f.
Figure 1: Collecting Times to Failure TTFs.
A plant’s CMMS is a good source of data for this
calculation. However, the data format is a little more
complex, which causes a series of data quality
problems. The subset of data relevant for our analysis
is approximated by the figure below.
Unlike in the data in Figure 1, the asset data does
not contain a list of relevant failure events. Instead,
both failure events and assets are associated with
functional locations to use the SAP term. A functional
location describes a function in the plant’s production
system “main feeder pump”. Assets are concrete
instances that can be installed at the locations “pump
A Data Quality Dashboard for CMMS Data
171

XYZ”. Over time, assets can move to different
locations as they are replaced with other assets,
repaired or overhauled and installed in other places.
Thus, the connection between asset and failure is only
an indirect one. As one can imagine, this is a key
source of data quality issues in a CMMS.
Figure 2: Key CMMS Data.
4 DATA QUALITY METRICS FOR
RELIABILITY DATA
We have already discussed data quality issues
affecting survival analysis in a previous paper (Gitzel,
2015). Thus, we have by now analysed six cases from
different contexts in order to identify the data quality
problems which affect a reliability calculation. The
latest case a customer’s CMMS system has led to the
discovery of new data quality problems, many of
which are unique to CMMS data.
In this section, we present an updated list of
metrics with a focus on those suitable for CMMS
data. For each metric, we describe the problem it
measures and the formula to calculate the metric. We
also describe the impact this problem has on a
survival analysis and propose ways how to address
this problem.
4.1 Sampling
4.1.1 Sampling Size
Problem: In order for a statistical analysis to be
relevant, we need a sample of an appropriate size. The
sample size needed depends on the standard deviation
of the population. The higher the standard deviation,
the more samples we need.
Metric:
,
where SEM is the Standard error of the mean and
MTBF is the mean. See (Gitzel, 2015) for more
details on this metric.
Impact: If sample size is too small, the sample does
not represent the full population properly. The
standard error of the mean estimates the possible
effect on the MTBF, other effects depend a lot on the
distribution function underlying the failure behaviour
if any.
Suggested Remedy: The obvious way to get reliable
survival statistics is to increase the sample size.
However, in many cases this would mean waiting for
more failures to occur which is not practical.
4.1.2 Observed Time Window
Problem. Observed time to failure TTF is the key
information needed to define a Reliability function.
In most cases TTF is the time between two failures,
except for the first failure, where it is the time since
start-up of the asset. This can lead to an interesting
problem in cases where the CMMS was installed after
plant start-up, because a lot of failure events will not
be recorded in the system.
Metric. The following metric calculates how much of
the plant lifetime is covered by the observed time
window recorded in the CMMS.
,
where
is the total time of CMMS operation
and
is the total time of plant operation. So, if the
plant is 40 years old and the CMMS was only
installed 20 years ago, the observed time window
would be 0.5.
Impact: The main problem of a small observed time
window is that we do not have access to the majority
of failure information. Moreover, if the difference
between plant lifetime and observed time window is
not taken into account, wrong TTFs will be included
in the list. In the figure below, stars represent the time
when an asset was started up, circles represent
failures. To the naïve observer it might seem that
there were no failures initially with failures showing
up only recently. However, this is an artefact of the
fact that failure recording started only with the
installation of the CMMS system the dotted line
parallel to the y axis. Thus, the long initial TTF is not
correct and the problem leads to an overestimation of
reliability.
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
172
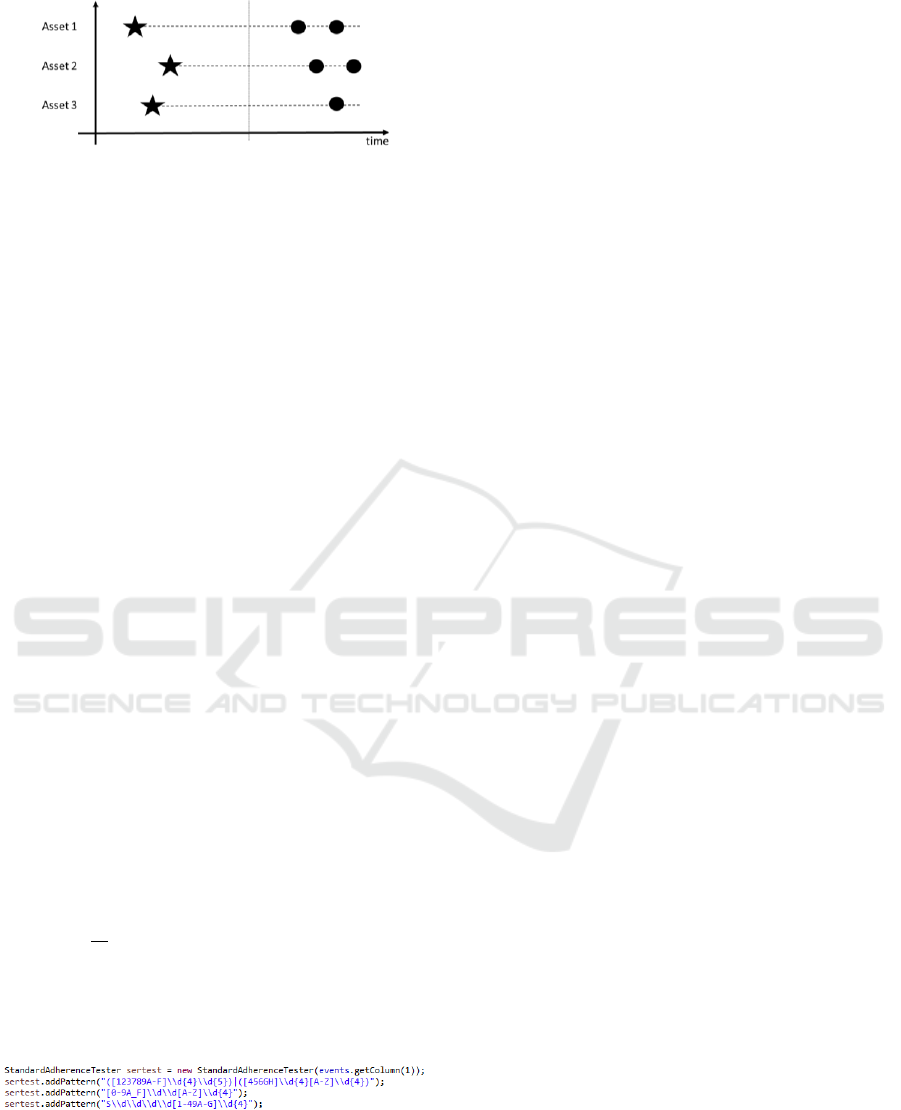
Figure 3: Effect of Observed Time Window.
Suggested Remedy: The first TTF should be
removed and a left-censored time computed from the
difference between first failure and start-up be added.
This is a partial correction which works best if there
are enough “real” TTFs to compensate.
4.2 Consistency
Data is inconsistent if different names are used for the
same element. It is also inconsistent if quantitative
information uses different units inch vs. cm or scales
hours vs. days. Inconsistency often results from
merging different data sources. There are other
inconsistencies which are typically closely related to
a particular problem instance one of which is
described below.
4.2.1 Inconsistent Names
Problem: Important elements such as assets,
functional locations or related attributes use an
inconsistent notation. For example, an asset might be
correctly identified via the serial number but when a
particular failure report uses the inventory number of
the asset to refer to it.
Metric: A metric which can heuristically identify
values which do not adhere to the agreed naming
convention can use regular expressions to see which
values do not match the pattern suggested by the
convention e.g. serial number structures, see Fig 4.
,
where n is the number of all fields using a name
and
is the number of name fields which match the
proscribed pattern.
Figure 4: Implementation of the Serial Number Consistency
Check.
Impact: Since we need to establish a link between
failure information and failures that were reported,
there needs to be a unique “key”. Otherwise, there
will be failures which cannot be assigned properly,
which a tremendous negative effect on the analysis
quality as has discussed in Section 5.2. In the case of
attribute names, we will not be able to properly build
subfleets for detailed analysis. A subfleet of all
“highly critical 3” assets will miss out all assets
labeled as “3” instead.
Suggested Remedy: Go through all identified non-
consistent values and try to change them to the correct
value. Inconsistencies can very often be resolved
through replacement rules.
4.2.2 Inconsistent Use of Functional
Locations
Problem. In a CMMS, functional locations might be
the only connection between the assets and the failure
events see Figure 2. In order for the analyst to be able
to connect a failure with an asset, the work order
reporting the failure must be connected to the right
asset. However, sometimes failures are linked to
locations higher in the hierarchy. So the best practice
might be that failures are attached to the leaves of the
functional location hierarchy e.g. pump AB.XYZ but
some failure reports might be attached to non-leave
nodes e.g. building AB instead.
Metric:
as described above see Section 4.2.1.
Impact. Failures attached to the wrong functional
locations mean that these failures are not attributed to
the assets where they occurred. This means that there
are assets with higher TTFs which leads to an
overestimation of reliability.
Suggested Remedy: Sometimes further investigation
can help to find the right functional location but in
other cases the information about the proper leaf to
use might be lost.
4.3 Free-of-Error
There are two important categories of errors we can
detect with our metrics – syntactical errors and logical
errors. Logical errors include dangling keys e.g.
failure events referring to equipment which does not
exist, non-unique keys and illogical order of dates
such as failure date before manufacturing date.
4.3.1 Logical Errors - Dangling Keys
Problem: Sometimes elements in the data reference
each other. A typical problem is a failure event
referring to an asset or functional location which does
A Data Quality Dashboard for CMMS Data
173

not exist. Also, functional locations might refer to
assets which do not exist or vice versa.
Metric: A metric which measures the percentage of
working keys can be used discover the problem of
dangling keys.
, where d is the number of dangling
keys and n is the number of all keys.
Impact: Dangling keys mean that failure events
cannot be assigned to assets or that assets cannot be
assigned to functional locations. Both cases mean that
the reliability is overestimated.
Suggested Remedy: Very often, this problem is
caused by improper subfleet selection, i.e. we have
excluded elements which should still be in the list or
we have included items which should not be in the list
and now refer to other elements outside the scope.
Thus, this problem can often be resolved by looking
at the complete data set.
4.4 Completeness
Completeness is what most people seem to associate
with data quality. Completeness metrics essentially
depend on how much data is missing. In past papers,
we have detailed different completeness metrics,
however, we feel that these are the most important
ones.
4.4.1 Data Field Completeness
Problem: For a given column/data field, the value is
missing. A missing value can be empty or is
represented by text like “N/A”, “unknown”, “nan”
etc.
Metric: The column completeness metric tracks the
percentage of values in a particular data field which
are not empty.
, where e is the number of empty
fields and n is the number of all fields of this type.
Impact: The impact of empty fields varies with the
importance of a field. If the field is critical to the
calculation, this means that one asset cannot be used,
effectively reducing the sample size. If the field is
used for subfleet building it has the same effect once
sub-fleets are used. Substitution fields might not have
an impact as long as they value they can substitute is
of OK data quality.
Suggested Remedy: Sometimes missing values can
be filled in but there is a substantial risk that we will
use data generated based on our assumptions to
confirm those assumptions. We have made some
good experiences with scenario building (Gitzel,
2015).
4.4.2 Asset-function Location Mapping
Completeness
Problem: As shown in Figure 2, the connection
between functional locations and assets might be
needed to map failure events to assets. However, a
plant is not static and assets move to different
locations. Thus, if the asset-failure mapping is not
established at the time of the recording of the failure,
we need a table which documents at what time an
asset was found at what location. Sometimes, this
mapping has gaps.
Metric: The following metric tracks how many
failure events could not be assigned due to gaps in the
asset-location mapping.
, where e is the total number of
failure events and u is the number of failure events
which could not be assigned to an asset due to a gap
in the mapping.
Impact: The impact of unassigned events in
discussed in detail in Section 5.
Suggested Remedy: Restoring this information is
quite often not possible.
4.5 Plausibility
Often, data is not obviously wrong and thus marked
by the metrics in Section 3 but seems so improbable
that we at least have to consider the possibility that it
is wrong. What is plausible or not depends on the
context but there are some example metrics that are
useful in the context of CMMS data. All plausibility
metrics have the same basic format.
, where x is the name of the metric, v
is the number of elements that violate the plausibility
assumption and n is the total number of elements.
4.5.1 Double Tap
Problem: If two failures of the same asset occur one
after another in a very short time period a day or two,
the reason could be that the asset was not repaired
properly. However, more likely, there was a second
complaint about the same problem when no action
was taken the first time. In the second case, it might
make sense to remove one of the events. Otherwise,
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
174

the reliability will be severely underestimated. The
first case might stay in the data if we consider poor
repair to be a valid cause of failures or not if we count
this as one problem that took longer to fix.
Impact: The reliability will be severely
underestimated if there are many wrong double taps.
Suggested Remedy. If you feel a double tap is not
correct, remove the second or the first event. Given
the short time difference, your choice has no major
impact.
4.5.2 Failure after Replacement
Problem: According to the data, an asset was
replaced by another one without having failed.
However, the new asset fails almost immediately
afterwards. While such a scenario is certainly
possible, there is also the possibility that a
replacement was booked but the failure event still
belongs to the previous asset. In other words, the old
asset failed and was replaced with a new unit instead
of the old asset being replaced by a unit that failed
right away.
Impact: The reliability will be underestimated.
Suggested Remedy: Clarify each event or remove
the events. Only fix this problem automatically if you
are sure that assets are normally not replaced while
still working.
5 IMPACT OF DATA QUALITY
ISSUES
Data quality issues can have a series of effects. The
reliability curve can lead to systematic over- or
underestimation a “shift” to the right or left. In more
extreme cases, the shape is changed which means the
impact for a particular time t will differ. Also, a
changed shape can change the failure rate from
increasing to decreasing or vice versa. This has a
major impact on maintenance planning which cannot
be discussed in the context of this paper.
Examining all effects and understanding their
impact in order to scale our metrics is an effort
beyond the scope of this paper. However, there is a
large group of metrics that implies that a certain piece
of data cannot be used either because it is missing or
it is wrong. In these cases, either the sample size is
reduced or failure events need to be discarded. For
both cases, we can make a good estimate on whether
the extent of the data quality problem is still
acceptable or not.
5.1 The Effect of Problems Reducing
Sample Size
Both missing and wrong data can lead to a reduction
in the number of TTFs. For example, missing subfleet
information means that certain assets cannot be
included in the calculation. Syntactically wrong start
dates mean that we cannot calculate the TTFs for that
asset.
Typically, these problems are fixed by removing
the offending elements. This removed the problem as
such but reduces the sample size and thus the sample
size metric. For this reason, we need a good measure
as to what constitutes a good sample size.
The sample size metric as proposed in this paper,
estimates the typical percentage deviation introduced
by the small sample. Thus, a metric of 75% indicates
that the actual values might be of the
calculated value. The percentage of deviation
acceptable depends on the use case. The analyst
should decide which relative deviation is still
acceptable for a particular type of analysis. If
is
the deviation that is considered to be entirely
unproblematic and
is a deviation that is still
acceptable, the following thresholds can be defined
for the metric
. These thresholds can be used for a
traffic-light design with states red (unacceptable),
green (acceptable), and yellow (insignificant).
Acceptable
Unacceptable
5.2 The Effect of Problems Leading to
Missing Failure Events
A number of data quality problems can lead to a
failure event not being assigned to an asset – either
because it cannot be assigned at all or because there
is reason to doubt the correctness of the assignment.
For example, due to the arrangement described in
Section 3, wrong or missing asset keys and wrong or
missing functional location keys mean that a given
event cannot be assigned to an asset see Section 4.4
for details.
Figure 5: Missing Failure Event.
A Data Quality Dashboard for CMMS Data
175

Furthermore, some events are lost due to a short
observation window see Section 4.1.3. Finally, failure
events which occur before the installation date and
other implausible events are most likely not correct
and should be evaluated Section 4.5.
The effect of a missing failure event is illustrated
in Figure 5. In the example, one of the events of asset
2 is missing (represented by the white circle). Thus,
instead of the correct times of failure TTF
4
and TTF
5
,
the wrong TTF
w
is added to the list. This means that
two correct TTFs are missing and one TTF that is far
too high is added by accident. Obviously, this leads
to an overestimation of reliability.
While this effect seems to suggest that unusually
high TTFs are suspicious, we cannot know which
ones are real and which ones are artefacts of missing
events. Based on our philosophy of identifying
problems and refraining from corrective actions
based on assumptions, we propose an impact
estimation heuristic. In order to identify thresholds
similar to the section above, we use a series of
simulations to determine possible data quality effects.
Due to the underlying assumptions see below, these
values should be taken as a rule of thumb and could
be refined in the future.
Our estimation is based on a series of simulations.
In each simulation we use a randomly generated
reliability curve and test the effect of missing events.
We use multiple percentages of randomly missing
events 10%, 25%, 50% and 75% and calculate an
alternative curve based on the reduced event set.
Figure 6: Typical Simulation Result.
Figure 6 shows a typical simulation result. The
black curve represents the correct reliability. The
coloured curves show the consecutive effect of
missing failure events. As expected, missing failure
events lead to an increasing overestimation of
reliability. For all our tested curves, the
overestimation is most pronounced in the middle of
the curve.
The simulation is based on a series of
assumptions. First, we need some random distribution
as a basis for our simulated curves. We follow
common practice and assume that all failure curves
follow a Weibull distribution. In order to cover a wide
range of possible scenarios, we use a series of
different shape and scale parameters selected to
represent different failure behaviours random,
increasing, decreasing, almost normally distributed
etc. Second, we assume that there is no wrong data
included in the calculation. Unrecognized wrong data
is a different issue which beyond the scope of the
metrics addressed here. Finally, for the sake of
simplicity, we assume that there will be no two
consecutive events missing. We argue that the effect
of will be more pronounced but not of a different
quality than what we see in our examples.
The overall results of the simulations are shown
in Table 1. For example, if 10% of the data is missing,
there will be a reliability overestimation anywhere
between 2.9 and 23.2 percentage points, depending
on curve shape. So, if we find a 25 percentage point
overestimation to be acceptable, we need a minimum
metric value of 75% taken from the 25% column,
since the metric is the inverse of the number of
missing events.
In this paper, we briefly outline our design
philosophy for a data quality dashboard. For a more
in-depth discussion see (Gitzel, 2015).
Table 1: Effect of missing events.
10%
25%
50%
75%
Max
23.2
23.5
47.3
71.5
Min
2.9
8.2
20
38.7
Average
7.9
15.0
30.9
53.0
6 CONCLUSIONS
Maintenance data collected in a production plant’s
information systems typically the CMMS is useful for
the analysis of asset reliability. However, various data
quality problems can impede this analysis. In this
paper we have presented a hierarchy of metrics
suitable for an assessment of the quality of CMMS
data. Based on several use cases, we have identified
relevant metrics and proposed criteria to structure
them. Finally, we have proposed heuristics needed to
decide whether a metric result is good or bad.
In our opinion, the sensitivity of survival analysis
to data quality issues is quite severe – a finding we
did not expect. To us this implies that in order for
ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems
176

survival analysis to work, we need to either come up
with good measures to ensure data quality or to find
algorithms which can correct the problems.
However, in the light of recent developments such as
Industrie 4.0 and Industrial Internet, maybe the
alternative is to primarily rely on condition
monitoring data. Of course, this means that there will
be other data quality issues to be addressed and future
research is required.
REFERENCES
R. G. Miller 1997. Survival analysis, John Wiley & Sons.
J. Antoni, J.; R. B. Randall 2006. The spectral kurtosis.
Application to the vibratory surveillance and
diagnostics of rotating machines. In Mechanical
Systems and Signal Processing.
R. Gitzel, S. Turring and S. Maczey 2015. A Data Quality
Dashboard for Reliability Data. In 2015 IEEE 17th
Conference on Business Informatics, Lisbon.
R. Gitzel 2016. Data Quality in Time Series Data - An
Experience Report. In. Proceedings of CBI 2016
Industrial Track, http.//ceur-ws.org/Vol-
1753/paper5.pdf.
IEEE 2007. IEEE Standard 493 - IEEE Recommended
Practice for the Design of Reliable Industrial and
Commercial Power Systems.
S. Kunttu, J. Kiiveri 2012. Take Advantage of
Dependability Data, maintworld, 3/2012.
J.W. Hines, A. Usynin 2008. Current Computational Trends
in Equipment Prognostics. In International Journal of
Computational Intelligence Systems.
M. Salgado, W. M. Caminhas W.M; B. R. Menezes 2008.
Computational Intelligence in Reliability and
Maintainability Engineering. In. Annual Reliability and
Maintainability Symposium - RAMS 2008.
S. Wu, A. Akbarov 2012. Forecasting warranty claims for
recently launched products. In Reliability Engineering
& System Safety.
R. Vadlamani 2007. Modified Great Deluge Algorithm
versus Other Metaheuristics in Reliability
Optimization, Computational Intelligence in Reliability
Engineering, Studies in Computational Intelligence.
R. Gitzel, C. Stich 2011. Reliability-Based Cost Prediction
and Investment Decisions in Maintenance – An
Industry Case Study, In. Proceedings of MIMAR,
Cambridge, UK.
Bertino, E.; Maurino, A.; Scannapieco, Monica 2010. Guest
Editors’ Introduction. Data Quality in the Internet Era.
In Internet Computing, IEEE.
D.P. Ballou et al. 1997. “Modeling Information
Manufacturing Systems to Determine Information
Product Quality”, Management Science.
Borek, A.; Parlikad, A. K.; Webb, J.; Woodall, P. 2014.
Total information risk management – maximizing the
value of data and information assets.
Bertino, E.; Maurino, A.; Scannapieco, M. 2010. Guest
Editors’ Introduction. Data Quality in the Internet Era.
In Internet Computing, IEEE.
Becker, D.; McMullen W.; Hetherington-Young K. 2007.
A flexible and generic data quality metamodel. In
Proceedings of International Conference on
Information Quality.
Montgomery, N.; Hodkiewicz, M. 2014. Data Fitness for
Purpose. In. Proceedings of the MIMAR Conference.
Delonga, M. Zuverlässigkeitsmanagementsystem auf Basis
von Felddaten. Universität Stuttgart.
Bendell, T. 1988. An overview of collection, analysis, and
application of reliability data in the process industries.
In Reliability, IEEE Transactions.
Redman, T.C., ed. 1996. Data Quality for the Information
Age.
Leo L. Pipino, Yang W. Lee, Richard Y. Wang 2002. “Data
Quality Assessment”, Communications of the ACM.
Bovee, M.; Srivastava, R. P.; Mak, B. 2003. A Conceptual
Framework and Belief-function Approach to Assessing
Overall Information Quality. In. International Journal
of Intelligent Systems.
Peter Benson 2008. ISO 8000 the International Standard for
Data Quality, MIT Information Quality Industry
Symposium.
Xiaojuan, Ban; Shurong, Ning; Zhaolin, Xu; Peng, Cheng
2008. Novel method for the evaluation of data quality
based on fuzzy control. In Journal of Systems
Engineering and Electronics.
Damerau, Fred J. 1964. A technique for computer detection
and correction of spelling errors. In Communications of
the ACM.
Levenshtein, Vladimir I. 1966. Binary codes capable of
correcting deletions, insertions, and reversals, In Soviet
Physics.
Bard, Gregory V. 2007. Spelling-error tolerant, order-
independent pass-phrases via the Damerau–
Levenshtein string-edit distance metric, In Proceedings
of the Fifth Australasian Symposium on ACSW.
Wu, Shaomin 2013. A review on coarse warranty data and
analysis, In. Reliability Engineering & System Safety.
Hu, X. Joan, Lawless, Jerald F. 1996. Estimation of rate and
mean functions from truncated recurrent event data. In
Journal of the American Statistical Association.
Gitzel, R. 2014. Industrial Services Analytics. Presentation
at the 1. GOR Analytics Tagung.
A Data Quality Dashboard for CMMS Data
177
