Transfer Learning to Adapt One Class SVM Detection to Additional

Features

Yongjian Xue and Pie rre Beauseroy

Institut Charles Delaunay/LM2S, UMR CNRS 6281, Universit´e de Champagne, Universit´e de Technologie de Troyes,

12, rue Marie Curie CS 42060 - 10004, Troyes Cedex, France

Keywords:

Transfer Learning, Multi-task Learning, Outliers Detection, One Class Classiﬁcation.

Abstract:

In t his paper, we use the multi-task learning idea to solve a problem of detection with one class SVM when

new sensors are added to the system. The main idea is t o adapt the detection system to the upgraded sensor

system. To solve that problem, t he kernel matrix of multi-task learning model can be divided into two parts,

one part is based on the former features and the other part is based on the new features. Typical estimation

methods can be used to ﬁ ll the corresponding new features in the old detection system, and a variable kernel is

used for the new features in order to balance the importance of the new features with the number of observed

samples. Experimental results show that it can keep the false alarm rate relatively stable and decrease the miss

alarm rate rapidly as the number of samples increases in t he target task.

1 INTRODUCTION

In real applications, many machine learning models

may not work very well due to the ideal assumption

that the training d ata and the future data are subject

to the same distribution or that they are observed in

the same feature space, which may not hold with re-

cent system that can evolve based on sen sor upgrade

or use of logical software based on sensors. Trans-

fer learning approach arose accordingly to solve that

problem, and it has received signiﬁcant attention in

recent years, which is widely studied in both supervi-

sed learning and unsuperv ised learning area (Pan and

Yang, 2 010). In this paper, we focus on using the

multi-task learning approach to solve the transfer le-

arning problem to one class classiﬁcation or outliers

detection problem, where the detection model may

experience a change due to practical reasons.

For detection, two kinds of one class supp ort vec-

tor machines are mainly used. One is proposed b y

(Tax and Duin, 1999), which aims to ﬁnd a hypersp-

here with minimal volume to enclose the data sam-

ples in feature space, the amount of data within the

hypersp here is tuned by a parameter C (noted as C-

OCSVM). Another one is introduced by (Sch¨olkopf

et al., 2001), which ﬁnds an optimal hyperplane in

feature space to separate a selected proportion of the

data samples from the origin, and the selection para-

meter is ν which gives an upper boun d on the fraction

of outliers in the training data (noted as ν-OCSVM).

It is proved that these two approaches lead to the same

solution according to (Chang and Lin, 2001), if a re-

lationship between parameters ν and C is fulﬁlled and

under build condition over the choice of the kernel.

From data driven side, we can divide the issues for

such detectio n system into two categories. One is the

transfer learning problem when the feature space re-

mains th e same meaning that the number of features is

not c hanged but are drown from a different data distri-

butions. For example, the in troduction of a detection

task for a new version of a system, or the update of a

detection a fter system maintenances with sensor up-

date. Another issue is the transfer learning problem

in different fe ature space, where we have different

number of features for the target task. For example,

in the application of fault detection for an engine sy-

stem, there are a few sensors which have already wor-

ked on an engine d ia gnosis system for much time and

every sensor gets a few data. Now due to technical

or some othe r practical needs, such as improving de-

tection performances, new senso rs are added to this

system. As far as we know, this problem has never

been tackled in the detection context using one class

SVM.

Instead of training a new detection system from

scratch, multi-task learning seems to b e an ideal mean

to adapt the former detection to an updated system,

since it uses th e assumption which is satisﬁed in

Xue, Y. and Beauseroy, P.

Transfer Learning to Adapt One Class SVM Detection to Additional Features.

DOI: 10.5220/0006553200780085

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 78-85

ISBN: 978-989-758-276-9

our context that related tasks share some co mmon

structure or similar model parameters ( Evgeniou and

Pontil, 2004), assumin g one task is the former system

and the second one is the upd a te d system. And the

idea is also used to solve one class classiﬁcation pro-

blem by (Yang et al., 2010; He et al., 2014), but both

of them are subject to the situation that the related

tasks are in the same feature space. In (Xue and Beau-

seroy, 2016), a new multi- ta sk learning model is p ro-

posed to solve the detection problem when additional

new feature is added, where it gives a good transi-

tion from the old detection system to the new mo di-

ﬁed one. However, in some cases the kernel matrix in

that model is not positive semi-deﬁnite which means

that some approximation in a semi-deﬁnite subspace

must be considered to determine the detection.

In this paper, a new approach is proposed to avoid

that issue. As is shown in section 2.2, we can divide

the kernel matrix into two part, one part is based on

the old features and the second part is based on the

new added feature. After typical estimation method is

condu c te d to ﬁll the corresponding new feature in the

old detection system in order to get a positive semi-

deﬁnite matrix, a speciﬁc variable kernel is used in the

second kernel matrix (which is base on the new fea-

ture) to co ntrol the impa ct of the new feature over the

detection according to the am ount of collected new

data.

The paper is organised as follows. I n section 2, we

propose the approac h to use multi-task lear ning idea

to solve one class SVM problems with the same fe -

atures and w ith additional new features respectively.

Then we prove the effectiveness of the proposed ap-

proach by experimental results in section 3. Finally,

we give conclusions and future work in section 4.

2 MULTI-TASK LEARNING FOR

ONE CLASS SVM

For the one class transfer learning classiﬁcation p ro-

blem, two kinds of situation might happen depending

whether the source task and the target task share the

same feature space (homogenous case) or not (hete-

rogenous case). To study the heterogenous case, we

consider th e situation of adding new feature one b y

one in target task to simulate the modiﬁcation or evo-

lution of an existing detectio n system.

2.1 Homogeneous Case

Consider the case of source task (with data set X

∈

) and target task (with data set X

∈ R

) in the

same space. For source task, a good dete ction model

can be trained based on a large number of samples

. After the maintenance or modiﬁcatio n of the sy -

stem, we have just a limited number of samples n

during a period of time. Intuitively, we may either try

to solve the proble m by considering independent se-

parated tasks or treat them together as one single task.

Inspired by references (Evgenio u and Po ntil, 2004)

and (He et al., 2014), a multi-task learning method

which trie s to ba la nce between the two extreme cases

was proposed by (Xue and Beauseroy, 2016). The de-

cision function for each task t ∈ {1, 2} (where t = 1

correspo nds to the source task and t = 2 corresponds

to the target task) is deﬁned as:

(x) = sign(hw

, φ(x)i−1), (1)

where w

is the normal vector to the decisio n hyper-

plane and φ(x) is the non-linear feature mapping. In

the chosen multi-task learning approach, the needed

vector of each task w

could be divided into two part,

one part is the common mean vector w

shared among

all the learning tasks and the oth e r part is the spec iﬁc

vector v

for a speciﬁc task.

= µw

+ (1 −µ)v

, (2)

where µ ∈ [0, 1]. When µ = 0, then w

= v

, which

correspo nds to two separated task, while µ = 1, im-

plies that w

= w

, which corresponds to one single

global task. Based on this setting, the primal one class

problem c ould be formulate d as:

min

,ξ

µ k w

(1 −µ)

∑

t=1

k v

∑

t=1

∑

i=1

s.t. hµw

+ (1 −µ)v

, φ(x

)i ≥ 1 −ξ

, ξ

≥ 0,

(3)

where t ∈ {1, 2}, x

is the ith sample from task t, ξ

is the corresponding slack variable and C is pen alty

parameter.

Based on the Lagrangian, the dual form could be

given as:

max

−

α+ α

s.t. 0 ≤α ≤C1,

(4)

where α

= [α

, ..., α

, α

, ..., α

] and



µK



(5)

is a modiﬁed Gram matrix, K

= hφ(X

), φ(X

)i,

= hφ(X

), φ(X

)i, K

= hφ(X

), φ(X

)i, which

means that we can solve the problem by classical one-

class SVM with a speciﬁc kernel (we u se Gaussian

kernel in this paper).

Accordingly, the dec ision function for the target

task c ould be deﬁned as:

(x) = sign(α



µhφ(X

), φ(x)i

hφ(X

), φ(x)i



−1). (6)

Transfer Learning to Adapt One Class SVM Detection to Additional Features

2.2 Heterogenous Case

Due to practical reasons, when new feature is added to

the old detection system, if we continue to use the old

detection system w e will not be able to take advan-

tage of the new information to improve the dete ction

performances. If we wait until we gather enough new

data to train a new dete ctor which mea ns that on one

hand we h ave to delay the beneﬁt of the update o f the

system, and on the other hand we have to g o throug h

all the hyper par ameter optimisation process which

may be time consuming. On the contrary, the multi-

task learning model should be able to take into consi-

deration the information brought by the new feature.

We introduce a former method (MT L

) and a new one

(MT L

) to tackle that problem. For both we c onsider

∈ R

be the data set o f the old de te ction system,

and X

∈ R

p+1

be the data set since new feature is

added.

2.2.1 MT L

Notice that for the formulation of multi-task learning

(4), if w e want to compute the modiﬁed Gram matrix

(5), problem h a ppens with block matrix K

because

of the different features for the source task and the tar-

get task. In the work of (Xue and Beauseroy, 2016),

named as MT L

, the new feature is ignored for com-

puting matrix K

. To some extend, it gives a bala nce

from the old detection system to the new one by tu-

ning the parameter µ with a proposed criteria. Howe-

ver, by using this method, the modiﬁed kernel matrix

is not always positive semi-deﬁnite which means that

a global optimisation solution can not b e guaranteed

with standard approach.

2.2.2 MT L

To ﬁll the corresponding new feature, some estima-

tion methods like the nearest neighbour, the imp u-

tation etc., can be used. Accordingly, we g et

{x | x

(1)

, ..., x

(p)

(p+1)

}, where

(p+1)

is the n ew fe-

ature in the old detection system estimated by using

informa tion from X

. The drawback of this method is

that when the number of samples X

for target task is

small, it is hard to give a good estimation to the new

feature in X

Once we get

∈ R

p+1

and X

∈ R

p+1

, as we

use G a ussian kernel, then the kernel matrix in (5) can

be decomposed into two par t:



µK



p+1



µK



{z }

◦





| {z }

,(7)

where ◦ is element-wise product and A

is kernel ma-

trix based on R

with the ﬁrst pth features for X

and

, A

is kernel matrix based on R

space with the

p + 1th estimated feature

(p+1)

from X

and x

(p+1)

from X

. Notice that K

is a positive semi-deﬁnite

matrix wh e n µ ∈ [0, 1], even if different kernel para-

meters are adopted for computing A

and A

We u se the Gaussian kernel that is deﬁned as:

k(x

, x

) = exp(

−x

−2σ

), (8)

where σ is the kern e l param eter. Notice that when

σ → +∞ then k(x

, x

) →1. So we propose to u se the

former σ

for R

subspace and to choose a varying

σ(n) for the new feature, where n is the numbe r of

samples. As a ﬁrst intuition, we want σ(n

) to be

large when n

is small and to be close to σ

when

is large.

By do ing this, the entries of matrix A

will tend

to be 1 when n

is small, which means th at it does

not have very important inﬂuence to th e total kernel

matrix when the estimation of the new feature ˜x

(p+1)

in X

is not very dependable. As n

becomes lar-

ger, more information is brought in from the new fea-

ture and a better estimation of ˜x

(p+1)

will be obtained,

more consideration shou ld be taken for matrix A

, so

σ decreases and it converges to the same value as σ

when n

is large enou gh.

In kernel density estimation, the optimal window

width for a standard distribution is given by (Silver-

man, 1986):

opt



d + 2



d+4

−

d+4

, (9)

where d is the number of dimensions and n is the

number of samples.

Upon above, the kernel parameter function for A

could be deﬁned as:

σ(n) = c

exp(

√

opt

, (10)

where the exponent function exp(

√

) decreases from

a large value when n is small to a small value close

to 1 when n is large, which means that we multiply

opt

by a large number at the beginning and we almost

keep h

opt

when n is large enough. The constant c

used to control the value that we want to multiply h

opt

when n is small and c

is a scale factor that makes

σ(n) converge to σ

when n is large. A few groups of

σ(n) are shown in ﬁgure 2. We name this multi-task

learning method as MT L

in this paper.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

3 EXPERIMENTS

In this section, experiments are conducted on artiﬁcial

data set. We compare the proposed method MT L

with the former one MT L

, as well as the other pos-

sible solutions: the old detection system T

based on

the old featu res, the new detection system T

based

on data when new feature is added, and the union de-

tection system T

big

which is based on the e stima te d

data

and the new obtained data X

3.1 Setup

Let y

, y

∼ N(0, 1), three features are deﬁned

as:

(1)

= y

, (11)

(2)

= 3 cos(

) + N(0, 0.05), (12)

(3)

= y

, (13)

where N(0, 0.05) is G aussian noisy. We use X

= {x |

(1)

, x

(2)

} as the data set for the old detection system

(source task), and X

= {x | x

(1)

, x

(2)

, x

(3)

} as th e data

set for the new detection system (target task). The

number of training samples is n

= 2 00, and we in-

crease n

from 5 to 400 to simulate the change of the

new detectio n system. A 3 dimensional view of the

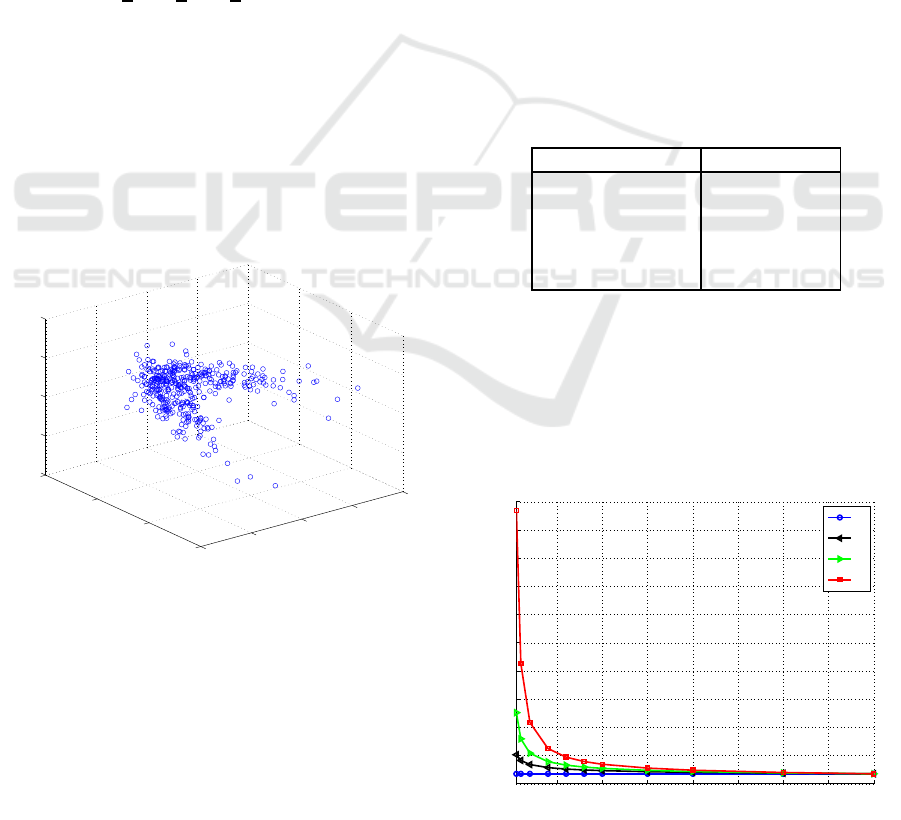
data set is shown in ﬁgure 1.

−4

−2

−4

−2

(1)

(2)

(3)

Figure 1: 3D view of the data set.

To test the performance of the detection system,

20,000 positive samples are generated from X

to test

the false alarm rate. Besides that, we use 20,000 uni-

form distribution data which cover the whole test data

set to test the performa nce of miss alarm rate. Speci-

ﬁcally, let u

(1)

, u

(2)

, u

(3)

∼U (−4, 4), three groups of

negative samples a re deﬁned as:

1. Uniform distribution for all the feature s X

negI

{x | u

(1)

, u

(2)

, u

(3)

2. Uniform d istribution only for the third dimension

negII

= {x | x

(1)

, x

(2)

, u

(3)

} to simulate the out-

liers coming from the new added feature.

3. Uniform distribution only for the ﬁrst two dimen-

sions X

negIII

= {x |u

(1)

, u

(2)

, x

(3)

} to simulate the

outliers coming from the old features.

We choose kernel p arameter σ

= 1.75 and ν =

0.1 fo r ν-OCSVM (it exits a corre sponding C for

C-OCSVM) which make the proportion of outliers

around 0.1 for the old detection system at the begin-

ning. A list of the comparison of different me thods

is shown in table 1. Where

= {x | x

(1)

, x

(2)

(3)

˜x

(3)

is the e stima ted feature (we use nearest n eighbour

method to ﬁll this new fe ature) and X

(3)

denotes

that X

without the new feature . For T

, T

and T

big

the same kernel parameter σ

is used, for MT L

the

setting is same as in (Xue and Beauseroy, 2016) and

for MT L

, σ

is used for the ﬁrst two features and a

variation of σ(n) according to (1 0) is used for the third

feature. The choice of µ for MT L

is c onducted by

the criteria proposed in (Xue and Beauseroy, 2 017).

All the results are averaged by 10 time s.

Table 1: Setting of the comparison of different methods.

Compare methods Train data sets

, X

(3)

big

, X

MT L

, X

MT L

, X

3.2 Performance with Different Kernel

Parameters

Three groups of kernel parameters σ

, σ

are ge-

nerated to test the performance o f MT L

. As shown

in ﬁgure 2, we choose c

= 1 , 3, 6 and then choo se

50 100 150 200 250 300 350 400

Figure 2: Different kernel functions.

Transfer Learning to Adapt One Class SVM Detection to Additional Features

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

False alarm rate

100

150

200

300

400

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

(a)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

(b)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

(c)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

MTL

(σ

)

(d)

Figure 3: Results of different kernel parameters for MT L

: (a) false alarm rate, (b) miss alarm rate on X

negI

(uniform data for

all features), (c) miss alarm rate on X

negII

(uniform data only for new f eature), (d) miss alarm rate on X

negIII

(uniform data

only for old features).

correspo nding c

in (10) which makes σ(400) = σ

(where σ

= 1.75 is the kernel parameter for the old

detection system).

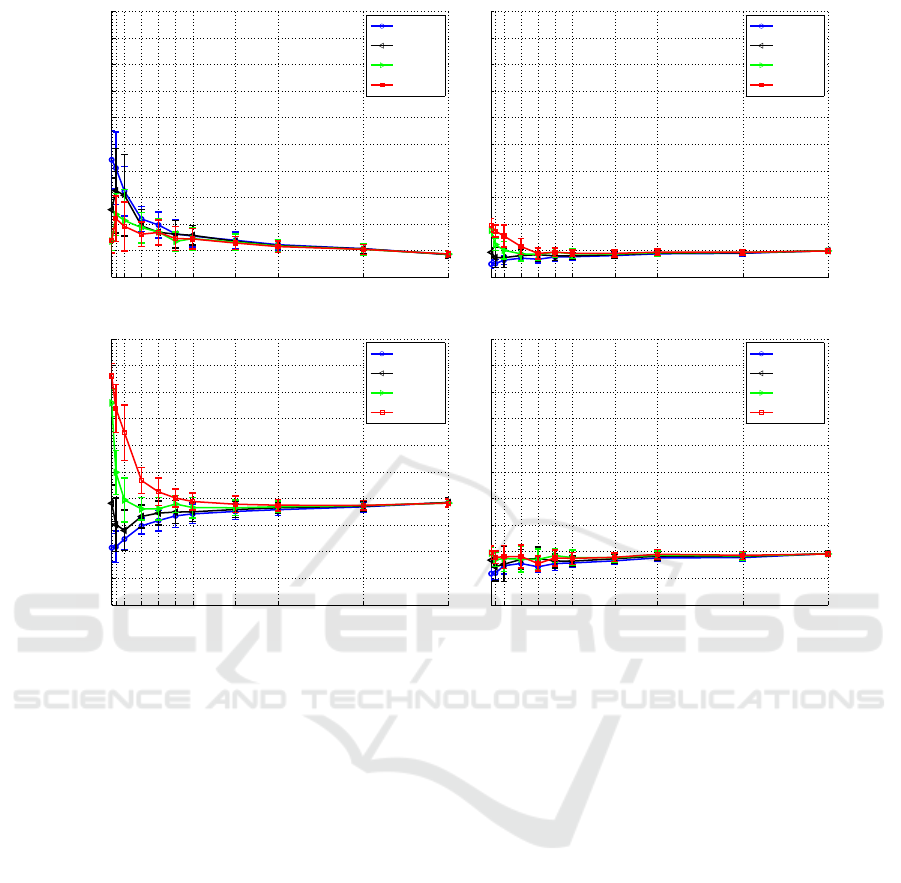
Results of MT L

are shown in ﬁgure 3 with dif-

ferent σ fo r computing A

in (7). If we use con-

stant σ

, the false alarm rate is very high whe n n

is small because of the bad estimation while lack of

samples from X

. Both the false alarm rate and the

miss alarm rate w ill become more stable as n

incre-

ases due to better estimation for ˜x

(3)

. However, with

the variation of kernel parameters σ

, σ

, when n

is small, the larger σ is, the c loser of A

is to a ma-

trix with 1 elements (that means we are using a kernel

matrix which is very close to the matrix just based

on the old features), so we increase less for the false

alarm ra te (MT L

(σ

) < MT L

(σ

) < MT L

(σ

) <

MT L

(σ

)).

As f or the miss alarm rate on X

negI

(ﬁgure 3(b))

to simulate th e outliers coming from for all features,

the method with variation kernel parameters increa-

ses a bit at the beginning and it decreases rapidly to

the same value as we use ﬁxed one. The same trend

happens for data set X

negII

(ﬁgure 3(c)) to simula te

the outliers coming from the new features except at

the beginning, where the miss alarm rate is re la tively

high, but as we increase n

, we decrease σ and the

miss alarm rate decreases rapidly to the same value

with ﬁxed σ

. This kind of trend makes meaningful

sense because when new feature is added, while n

is small, if outliers are all f rom the new feature, we

can not decide them all as negative samples, instead

we would rather keep a relative stable false alarm rate

while reduce the miss alarm rate rapidly as n

incre-

ases which means that we take the new feature’s in-

formation into consideration gradually. For the miss

alarm rate on X

negIII

(ﬁgure 3(d)), all methods keep al-

most stable which means that we do not increase the

miss ala rm rate if the outliers come from the old fea-

tures. Fro m the ab ove ana lysis, MT L

(σ

) produces

a relatively good detection model when new feature

is added, where σ

is relatively large at the beginning

and it converges to σ

at the end.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

False alarm rate

100

150

200

300

400

big

MTL

(a)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(b)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(c)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(d)

Figure 4: Compare results of different methods: (a) false alarm rate, (b) miss alarm rate on X

negI

(uniform data for all features),

negII

(uniform data only for new feature), (d) miss alarm rate on X

negIII

(uniform data only for old

features).

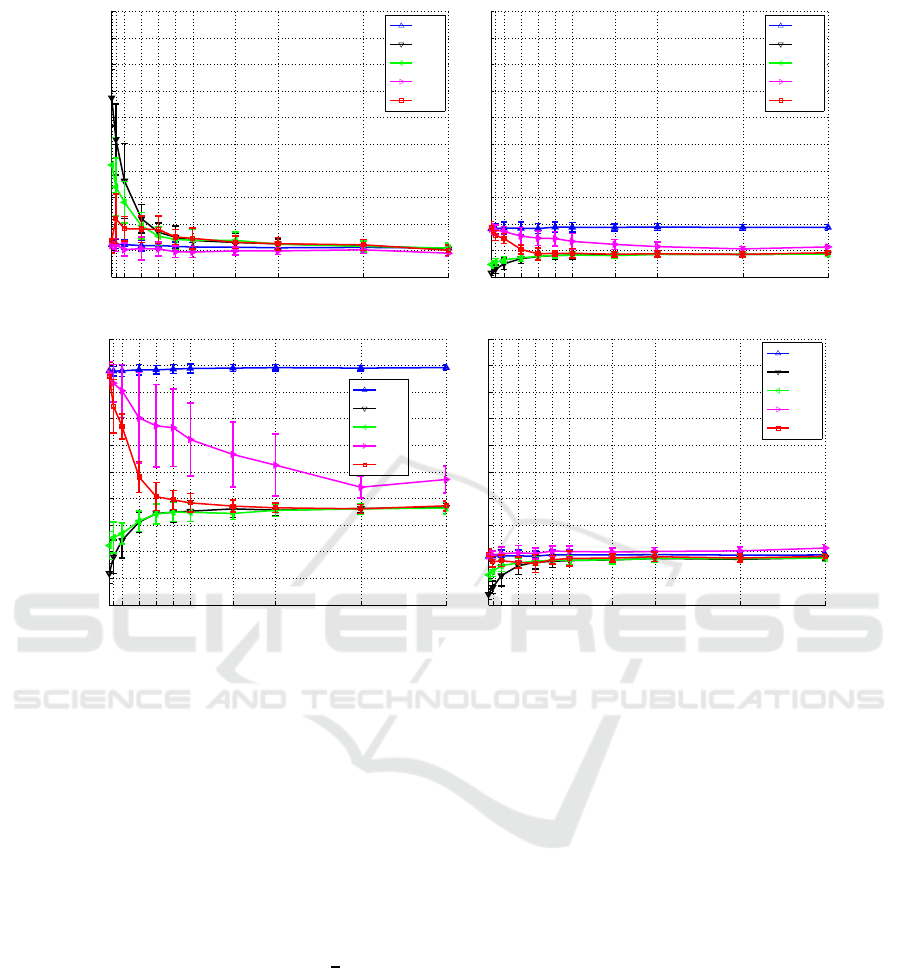
3.3 Experimental Results

We use MT L

(σ

) to compare with the other possi-

ble methods listed in table 1, results are repo rted in

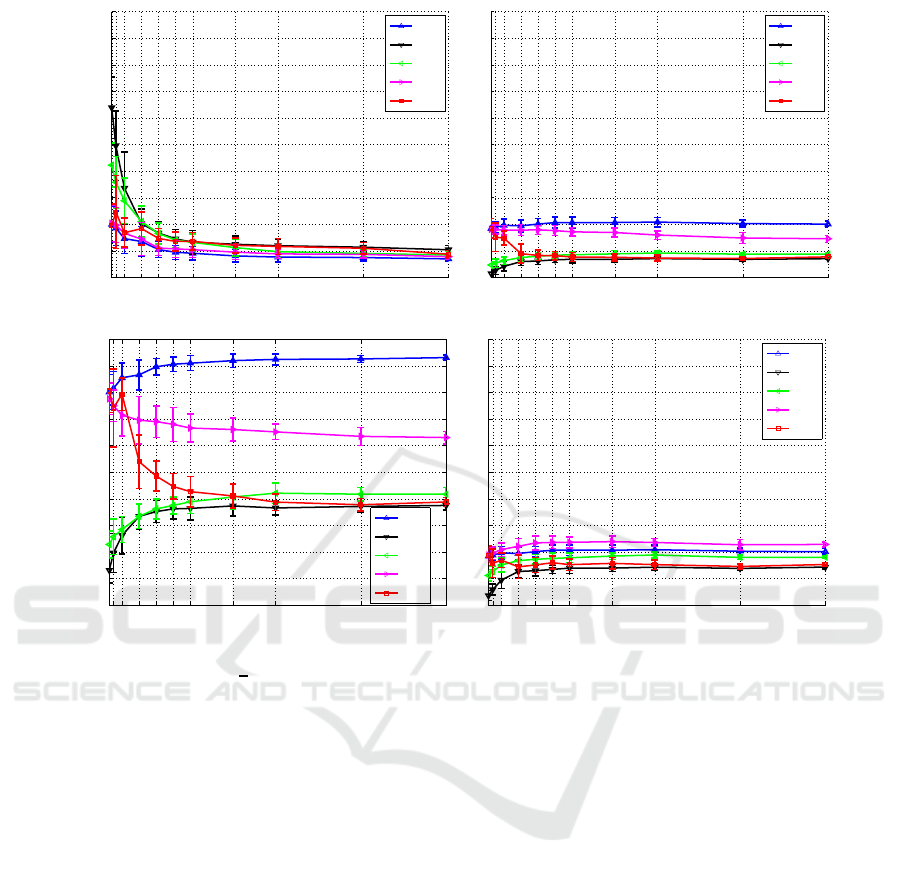
ﬁgure 4 . Besides that, in order to study the problem

that might happen is the adaptation for the old feature

space ( that means the data distribution f or the old fe-

atures may experienc e a change due to system main-

tenance or upd a te ), we give a r otation o f

to the ﬁrst

two features in X

to study the model’s performance

on this situation, and the results are shown in ﬁgure 5.

For the method T

, which is trained on the old f e a-

tures of X

and X

, the false alarm rate is almost con-

stant around 0.1, but the miss alarm ra te is the highest

one among all the other metho ds because it does not

take into consideration of the new feature.

For T

which is based only on X

since the new

feature is added, it gives very high false alarm rate

when n

is small, which means that it does not make

full use of th e infor mation from the former detection

system at the beginning, as n

increases large enough

(here n

> 1 50), it produces more stable false alarm

rate and miss alarm rate.

If we combine the estimated data set

and X

train a detection model, named as T

big

, the false alarm

rate is lower than that of T

, and the miss alarm rate

will e nd up with the same as T

. However, with a ro-

tation of the ﬁrst two features in X

, it will increase

the chance of miss alarm at the end (which is shown

in ﬁgure 5(b), 5( c) and 5(d)), because T

big

tends to in-

close all the train data set together. That means T

big

not practical when data distribution of the old features

experiences a change in the new detectio n system.

For m ulti-task learning method, both MT L

and

MT L

gives a transition from the old detection sy-

stem T

(which is just based on the old features) to the

new modiﬁed system T

(which is based on the new

data set X

since new feature is added) as n

increa-

ses. The false alarm rate of MT L

is a bit lower than

that of MT L

, and both of them are relatively stable

compare d to T

and T

big

. But for miss alarm rate, only

MT L

converges to that of T

while MT L

does not

Transfer Learning to Adapt One Class SVM Detection to Additional Features

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

False alarm rate

100

150

200

300

400

big

MTL

(a)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(b)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(c)

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Miss alarm rate

100

150

200

300

400

big

MTL

(d)

Figure 5: Compare results with

rotation in X

for the ﬁrst two features: (a) false alarm rate, (b) miss alarm rate on X

negI

(uniform data for all features), (c) miss alarm rate on X

negII

(uniform data only for new feature), (d) miss alarm rate on X

negIII

(uniform data only for old features).

as n

increases. And the general miss alarm rate of

MT L

is much lower than that of MT L

, this diffe-

rence is much la rger when there is a rotation to the

ﬁrst two features in X

(ﬁgure 5). There fore, MT L

gives a b etter transition f rom the old detection system

to the new one than MT L

, it can keep the false alarm

rate relatively stab le while decrease the miss alarm

rate rapidly to a stable value.

4 CONCLUSIONS

In this paper, a modiﬁed approach of multi-task lear-

ning method MT L

is pro posed to solve the problem

of transfe r learning to one class SVM, wh e re additio-

nal new features are added in the target task.

The idea is to decompose the kernel matrix in

multi-task learning model into two pa rts, one part is

the kernel matrix based on the old features and the ot-

her part is the kernel matrix based on the new added

features. Typical methods can b e used to estimate the

correspo nding new features in the source data set in

order to compute the kernel matrix based on the new

features. Then a variable kernel is used to balance the

importance of the new features with the number of

new samples and at last it converges to the same value

as used in the old de te ction system. Experimental re-

sults sh ow th at the proposed method ou tperforms the

former propo sed method MT L

and the other possible

approa c hes.

Future work may consider online implementation

of the proposed approach.

REFERENCES

Chang, C.-C. and Lin, C.-J. (2001). Training v-support vec-

tor classiﬁ ers: theory and algorithms. Neural compu-

tation, 13(9):2119–2147.

Evgeniou, T. and Pontil, M. (2004). Regularized multi–task

learning. In Proceedings of the tenth ACM SIGKDD

international conference on Knowledge discovery and

data mining, pages 109–117. ACM.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

He, X., Mourot, G ., Maquin, D., Ragot, J., Beauseroy,

P., Smolarz, A., and Grall-Ma¨es, E. (2014). Multi-

task learning with one-class svm. Neurocomputing,

133:416–426.

Pan, S. J. and Yang, Q. (2010). A survey on transfer lear-

ning. Knowledge and Data Engineering, IEEE Tran-

sactions on, 22(10):1345–1359.

Sch¨olkopf, B., Pl at t, J. C., Shawe-Taylor, J., Smola, A. J.,

and Williamson, R. C. (2001). Estimating the support

of a high-dimensional distribution. Neural computa-

tion, 13(7):1443–1471.

Silverman, B. W. (1986). Density estimation for statistics

and data analysis, volume 26. CRC press.

Tax, D. M. and Duin, R. P. ( 1999). Support vector domain

description. Pattern recognition letters, 20(11):1191–

1199.

Xue, Y. and Beauseroy, P. (2016). Multi-task learning for

one-class svm with additional new features. In Pattern

Recognition (ICPR), 2016 23rd International Confe-

rence on, pages 1571–1576. IEEE.

Xue, Y. and Beauseroy, P. (2017). Transfer learning for

one class svm adaptation to limited data distribution

change. Pattern recognition letters, accepted.

Yang, H., King, I., and Lyu, M. R. (2010). Multi-task lear-

ning for one-class cl assiﬁcation. In Neural Networks

(IJCNN), The 2010 International Joint Conference on,

pages 1–8. IEEE.

Transfer Learning to Adapt One Class SVM Detection to Additional Features