Image Features in Space

Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios

Marc Steven Kr¨amer, Simon Hardt and Klaus-Dieter Kuhnert

Institute of Realtime-Learning Systems, University of Siegen, Hoelderlinstr. 3, 57076 Siegen, Germany

Keywords:

Visual Odometry, Motion Estimation, Space Robotics, SIFT, SURF, BRIEF, ORB, KAZE, AKAZE, BRISK.

Abstract:

Image features are used in many computer vision applications. One important ﬁeld of use is the visual naviga-

tion. The localization of robots can be done with the help of visual odometry. To detect its surrounding, a robot

is typically equipped with different environment sensors like cameras or lidar. For such a multi sensor system

the exact pose of each sensor is very important. To test, monitor and correct these calibration parameters, the

ego-motion can be calculated separately by each sensor and compared. In this study we evaluate SIFT, SURF,

ORB, AKAZE, BRISK, BRIEF and KAZE operator for visual odometry in a space scenario. Since there was

no suitable space test data available, we have generated our own.

1 INTRODUCTION

Over the years a variety of methods and algorithms

for the detection and extraction of image features have

been developed in digital image processing and com-

puter vision. Typical application are object track-

ing, image retrieval, panorama stitching or camera

pose estimation. An important and common usage

for accurate localization, especially in the ﬁeld of mo-

bile robotics, is the visual odometry (Scaramuzza and

Fraundorfer, 2011). This is the process of ego-motion

and pose estimation for a mobile robot by analysing

the images of an attached camera.

To detect the surrounding environment, a robot

can be equipped with several sensors. These are for

example (stereo) cameras, lidar, ultrasonic or radar.

All these sensor data can be combined into a consis-

tent environment model. For this sensor registration

and fusion process, the exact positions and orienta-

tions (pose) of all sensors are extremely important.

These data is normally obtained during a calibration

of the whole system. A way to check and monitor

these parameters is based on the robots ego-motion,

which is estimated separately from the sensing data

of the different sensors. A comparison with a ground

truth, in our case a high precise ﬁbre optical inertial

measurement unit (IMU), allows to verify the proper

calibration and offers in a second step the possibil-

ity to correct it. During the motion estimation (visual

odometry) with a camera, image features are a cen-

tral aspect for calculating the pixel shifts of successive

images (Fraundorfer and Scaramuzza, 2012).

The evaluation which is published in this paper is

part of a bigger project called AVIRO, where a sensor

fusion system for space robotic is developed. There-

fore, we tested different feature algorithms for the us-

age in a space scenario.

In the literature a variety of evaluations for feature

algorithms have been published. Most of them anal-

yse different feature algorithms with a dataset pro-

posed by (Mikolajczyk and Schmid, 2003) and which

consists of images with real geometric and photo-

metric transformations. These are rotation, scale

changes, viewpoint changes, image blur or illumina-

tion changes. (Canclini et al., 2013) evaluated the

processing time, repeatability and matching accuracy

for image retrieval task. For object tracking in a

video (Sebe et al., 2002) evaluatedSIFT, SURF, ORB,

BRISK, FREAK and BRIEF. (Miksik and Mikola-

jczyk, 2012) focused in an evaluation for fast feature

matching on the speed of the matching process. After

a summary of all papers it can be said, that the ideal

operator depends on the application. This also results

from (Is¸ık, 2014).

Evaluations of features for visual odometry have

been made for typical road scenes in (Qu et al., 2016).

Also (Chien et al., 2016) investigated different feature

algorithms for visual odometry on the street and sug-

gested SURF as the best algorithm. The performance

of SIFT and SURF in case of a stereo camera was

evaluated by (Jiang et al., 2013) on a road scene in

an urban environment and by (Benseddik et al., 2014)

with a robot inside a building.

Other publications evaluated the operators with a

300

Krämer, M., Hardt, S. and Kuhnert, K-D.

Image Features in Space - Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios.

DOI: 10.5220/0006555303000308

In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 300-308

ISBN: 978-989-758-276-9

data set of plant species (Kazerouni et al., 2015) or

UAV images (Yumin et al., 2016). Especially for the

ﬁeld of space robotics, more precisely a planetary sce-

nario, (Shaw et al., 2013) tested the BRIEF algorithm

for a robust visual odometry in a sand quarry in Ox-

fordshireUK. (Maimoneet al., 2007) concluded in his

publications about visual odometry on mars rovers,

that for a robust technology, the runtime of the algo-

rithms is the bottleneck.

This paper is organized as follows: In section 2 we

describe our test data set. The recording of a real and

generation of a virtually simulated scene. After this in

section 3, the method of comparison and evaluation is

presented before we discuss the results in section 4.

Finally, the paper is concluded in section 5.

2 GENERATION OF

TESTSCENES

Research publications on feature operators are usu-

ally a comparison which is geared to the needs of the

speciﬁc application. Algorithms were applied to real

or virtual test scenes and compared to ground truth

data. This involves mainly the simple retrieval of ob-

jects or object points in two or more different images.

Here objects are everyday objects, such as a boats

(Benseddik et al., 2014), grafﬁti (Miksik and Mikola-

jczyk, 2012), trees (Is¸ık, 2014) or hands (Sebe et al.,

2002). In order to ﬁnd suitable operators e.g. for plant

recognition, a test database with many photos under

varying settings (exposure time, camera angle, lens,

digital resolution and other parameters) is created.

There are own test scenes for more speciﬁc applica-

tion areas. In the automobile sector a road scene was

recorded by a camera and the ground truth data was

extracted from an intertial measurement unit (Geiger

et al., 2013). In addition to the feature algorithms, the

quality of a visual odometry can be measured at the

same time.

The special application in the project AVIRO is

the space robotic. Thus suitable test databases were

also created for the evaluation of the feature algo-

rithms. By using features, pose changes of a robot in

(outer) space were estimated. It is therefore obvious

to generate test data for this special purpose.

So we created a simpliﬁed scenario to test the al-

gorithms for this visual odometry application. A cam-

era rotates around its own axis. During the rotation

the exact rotation angle is measured and recorded par-

allel to the video. With this relatively simple method,

several scenes were generated in a simulated virtual

and a real environment. All image data has been saved

as raw images without any compression.

2.1 Real Enviroment

AVIRO is developed in the ofﬁces and laboratories of

the University of Siegen. Therefore, a part of the test

database consists of scenes in this environment. For

the recordings the mono camera UI-5360CP from ids

imaging has been used. Figure 1 shows the used test

setup and table 1 provides information about the cam-

era.

Table 1: Technical data of the mono camera UI-5360CP

from ids imaging.

Sensor CMOS 2/3”

Resolution 2048x1088

Framerate 36Hz

A carrier board is mounted on a photo tripod on

which the camera and a ﬁber gyroscope are installed.

Above, there are additional electrical circuits which

stably produce the complex voltage supply for the

gyro system. The ﬁber gyro is the µFORS-1 model

from Northrop Grumman Litef which is also used for

aircraft navigation or rocket control. Technical data

can be found in table 2.

Figure 1: Test setup for recording data in a real environ-

ment. The photo shows the test setup for recording test

data. The used monocamera UI-5360CP is mounted on a

tripod together with a high-precision ﬁber gyro. During the

recordings the setup was rotated around the vertical axis.

Table 2: Technical Data of the ﬁber gyro µFORS-1.

Rate Bias ≤ 1

◦

Random Walk ≤ 0,1

◦

√

Gyro Range ±1000

◦

Max data rate 8kHz

During a rotation of the tripod a video stream with

a framerate of 30Hz is created by the camera. Simul-

taneously, the ﬁber gyro records the rotation at 1 kHz.

Image Features in Space - Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios

301

The camera stands directly on the vertical axis and ro-

tates without a translatory effect. Since this is a cam-

era of industrial quality, a consistent timing behaviour

can be assumed and the triggering time of each frame

is known. This results in a test dataset in which an

exact rotational position of the tripod can be assigned

to each image. This rotation angle is the ground truth

value for later evaluations.

Several test records have been created in this con-

ﬁguration. Figure 2 shows an example of four images

of the generated video sequences. It is a typical ofﬁce

environment, as it also prevails with most of all other

tests. However, this kind of test is more suitable for

mobile ground robotsand less for the use on satellites.

Therefore, further data records for the feature evalu-

ation were generated which are described in the next

section.

Figure 2: Example images of a test scene in real environ-

ment.

2.2 Simulated Environment

The planned operational environment of the ﬁnished

AVIRO system is in space. This differs signiﬁcantly

from the created test data described in the previous

section. As no suitable data was available for this test,

it had to be created. In order to obtain realistic test

data it was decided to simulate a space scene virtually

on the computer. As a tool the open source 3D ren-

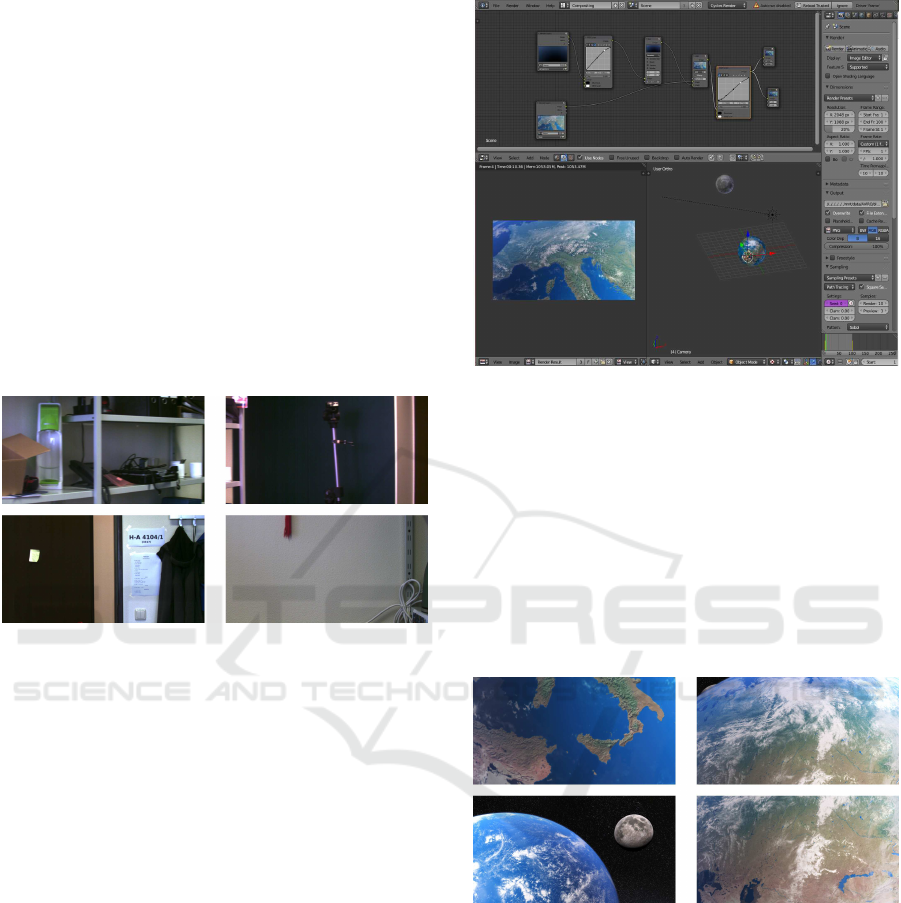
dering software Blender was used. An existing and

Creative Commons licensed space scene by Adriano

Oliveira (Oliveira, 2014) was extended with a higher

resolution texture of the Earth’s surface (see ﬁgure 3).

Figure 4 shows some rendered example images. A to-

tal of ﬁve test recordingswere made. For this purpose,

the camera was positioned in ﬁve different locations

in the virtual space environment and rotated with a

ﬁxed angle around an axis by an animation. It was

noticed that the camera is aimed at different objects

of the scene. Thus, a mixture of images of the earth’s

surface and the further space or other planets (moon)

could be generated - a simulation of conceivable

states of a satellite.

The Blender software offers the possibility to

Figure 3: Generation of the simulated virtual scene with

Blender.

specify the camera parameters with which the virtual

scene is drawn. As a result, focal length, resolution

and chip size could be adapted to the data of the real

camera (ids imaging UI-5360CP). The ground truth

data are available directly in the program, since the

camera position or, more correctly, its orientation, is

known. Here, as in the ﬁrst real scene, the camera

was rotated virtually about an axis. Thus, datasets

with image and angle pairs have been created which

are available for later tests.

Figure 4: Sample images of a test scene in a simulated vir-

tual environment.

2.2.1 Simulated Sensor Noise

The second dataset contains images generated by the

Blender software. Colors in the space scene are ideal

mapped (taking into account the illumination condi-

tions) on the resulting images. However, this does not

reﬂect the indeed real behaviour of a video camera.

The sensor noise which causes a falsiﬁcation of the

color values is as an important point not considered.

In order to include the inﬂuence of this effect, noise

was artiﬁcially added to the image data of the simu-

lated scenes in a further step. This takes place in two

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

302

stages.

The dataset contains RGB images with a color

depth of 8 bits. First, the image matrix is converted

from RGB to the HSV color model. In the HSV

color space, a uniform, random value between −15

and +15 is added to the brightness component (V).

This simulates variations in the exposure time. After

re- converting to RGB a random value between −20

and +20 is added to each component. This produces

the sensor noise in reality. For the calculation opera-

tions overﬂow or underﬂowof the 8-bit numeric space

is handled. For values < 0 the value is set to 0 or if

> 255 to 255.

3 COMPARISON OF THE

ALGORITHMS

A large number of different algorithms for feature de-

tection and description have been developed so far.

In addition it is an active research area in which new

methods are continually developed. Furthermore,

each of the algorithms can be parameterized. This

creates a lot of possible combinations and makes it

harder to choose from these the best working solution

for our project. In order to make this decision, some

test datasets were generated which have already been

described in the last sections.

3.1 Method

Each of the generated test dataset contains a sequence

of pairs consisting an image and the corresponding

camera angle. The evaluation of feature algorithms is

now based on the principle that the camera rotation

between two consecutive images is calculated (pixel

shift). This value is compared with the Ground Truth,

which is contained in the test datasets. The single

steps of this procedure are described in more detail

below. Algorithm 1 also shows the method in a com-

pact way.

The evaluation has been done on a Desktop Com-

puter with Ubuntu 14.04 LTS. The system was an

Intel(R) Core(TM) i7-4930K CPU with 3.40GHz,

12MB Cache and 64 GB RAM. The opencv version

was 3.1.0 with the related opencv

contribute package

for the non free feature algorithms and compiled with

gcc version 4.8.4.

Load Image and Rectify. The ﬁrst image is loaded.

With help of the camera parameters, which were

determined in the sensor calibration, distortions

caused by the lens can be corrected. This is not

necessary in the simulated scene and the virtual

camera.

Find Keypoints. In the image keypoints have to be

found which can be easily found again the next

consecutive image. Each feature generation al-

gorithm basically consists of two parts: the de-

tector and the descriptor. In the ﬁrst step the de-

tector is used to search for keypoints which are

very different from their surroundings. In simpli-

ﬁed terms these can be locations where for exam-

ple a bright/dark transition is located. Figure 5

shows the SIFT detector applied to a sample im-

age. Marked points are represented by small cir-

cles.

Figure 5: SIFT detector applied to a sample image. The

ﬁgure illustrates the detector of the Scale Invariant Feature

Transform (SIFT) algorithm. In the picture keypoints which

are suitable for feature operations are drawn.

Speciﬁcation of the Points by Descriptors. The

previously found points are now represented

by descriptors. A descriptor is a vector with

numbers. These are attributes that characterize

the point. For this purpose the surrounding of

the point, i.e. the neighboring pixels, are also

included. More detailed information, as an

example for the descriptor of the SIFT procedure,

can be found in (Lowe, 2004).

Load Next Image. The next image of the test dataset

is loaded and rectiﬁed. Here the camera has been

rotated by a certain angle. As with the previously

processed image, keypoints are searched and de-

scribed by descriptor vectors.

Comparison of Keypoints. The comparison be-

tween the feature vectors from the ﬁrst and the

second image (matching) follows. Figure 6 shows

this procedure using an image of the real scene.

The pixels of the feature vectors which have been

identiﬁed as equal by the matching process are

connected with lines. It can be seen that not all

lines have the same orientation.

Image Features in Space - Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios

303

The difference between the x- and y-components

of the image points of each matched point-pair is

the displacement. In ﬁgure 7 the distribution of

these is plotted. The majority of the points ac-

cumulate in a cluster, as can be seen in the his-

tograms to the right and below. Also, there are

some outliers that reﬂect the wrong lines in the

picture.

Estimate the Camera Rotation. The keypoint

matching process yields a set of keypoint pairs.

In a ﬁrst step a ﬁlter is applied to ﬁlter out some

outliers in these data. The comparison of feature

vectors provides as a result a quality value which

indicates how good the vectors ﬁt together. Based

on these values the best ﬁfty pairs are extracted.

This is shown for the previous example in bottom

image of ﬁgure 6. Now the connected lines of the

keypoints have approximately the same length

and orientation. This can be seen in plot 8.

The range in which the points are located is sig-

niﬁcantly reduced comparedto the previousdistri-

bution from 7. For the calculation of the camera

rotation we use the median of these values. This is

also shown in the whiskey boxplots on the sides.

Since the camera has only been rotated around a

single axis, the rotation of the camera can now be

calculated by means of the pixel shift (in this ex-

ample in the x-direction). The necessary camera

parameters, such as the aperture angle and focal

length, are known by the camera calibration. The

pixel shift in y-direction is 2.45 pixels which is

equivalent to 0.029

◦

. In the x-direction, there are

106.94 pixels and 1.28

◦

respectively. The low y-

deviation can be explained by sensor noise, back-

lash in the camera mounting or calibration errors.

4 EXPERIMENTAL RESULTS

Comparative tests were performed with seven fea-

ture algorithms. These are named after their ab-

breviations. Following the used algorithms are

listed. For a detailed description of the individ-

ual methods we refer to the literature.

SIFT. Scale-Invariant Feature Transform (Lowe,

2004)

SURF. Speeded Up Robust Features (Bay et al.,

2006)

BRIEF. Binary Robust Independent Elementary

Features (Calonder et al., 2010)

ORB. Oriented FAST and Rotated BRIEF

(Rublee et al., 2011)

Algorithm 1: Evaluation of feature algorithms.

Input: Data set with image and angle pairs

T = (I

,α

),(I

,α

),...,(I

,α

)

Output: Quality value s

of the feature

algorithm f

1 s

= 0

descriptors

=f.describe(f.detect(I

));

2 for i = 1 to size(T) do

3 descriptors

curr

=f.describe(f.detect(I

));

4 pairs=Best

(match(descriptors

descriptors

curr

));

5 calculate pixel shift ∆x with pairs;

6 calculate rotation angle β with ∆x;

7 s

+ |β −α

—; //sum up error

8 descriptors

= descriptors

curr

;

KAZE. KAZE-Features (Alcantarilla et al.,

2012)

AKAZE. Accelerated-KAZE Features (Pablo

Alcantarilla (Georgia Institute of Technolog),

2013)

BRISK. Binary Robust Invariant Scalable Key-

points (Leutenegger et al., 2011)

The previously generated test database is divided into

a simulated and a real environment. Therefore, the

results of the comparison are also considered sepa-

rately. Figure 9 shows consecutive images of both en-

vironments. Detected keypoints and their determined

agreement in the second picture are drawn. Totally

there are two datasets (T

, T

) in real and ﬁve (T

) in the simulated environment.

For the ﬁrst test T

, the measurement setup (see

image 1) has been rotated by 90

◦

in a time of about 20

seconds. The reference value (Ground Truth) of this

dataset was determined with a high-precision ﬁber

gyro. In the measurement results the calculated angle

from all feature algorithms deviates. After a rotation

of 87.76

◦

(reference value) the calculated values of

the algorithms are between 90.46

◦

and 91.16

◦

. The

difference between the optical methods is therefore

only 0.7

◦

. More important is the question why there

is a systematic error between all calculated values and

the reference. When examining this behavior and the

underlying calculation steps, attention is immediately

drawn to the sensor calibration of the camera.

Camera calibration is a mathematical minimiza-

tion which never provides a hundred-percent cor-

rect solution. It has been done with the checker-

board method (see (Tsai, 1986)). An opening angle

of 0.01196655

◦

per pixel in x-direction can be fol-

lowed by the camera calibration. A 90 degree rota-

tion causes a displacement of 7590 pixels (BRISK

method). Smaller deviations in the aperture angle

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

304

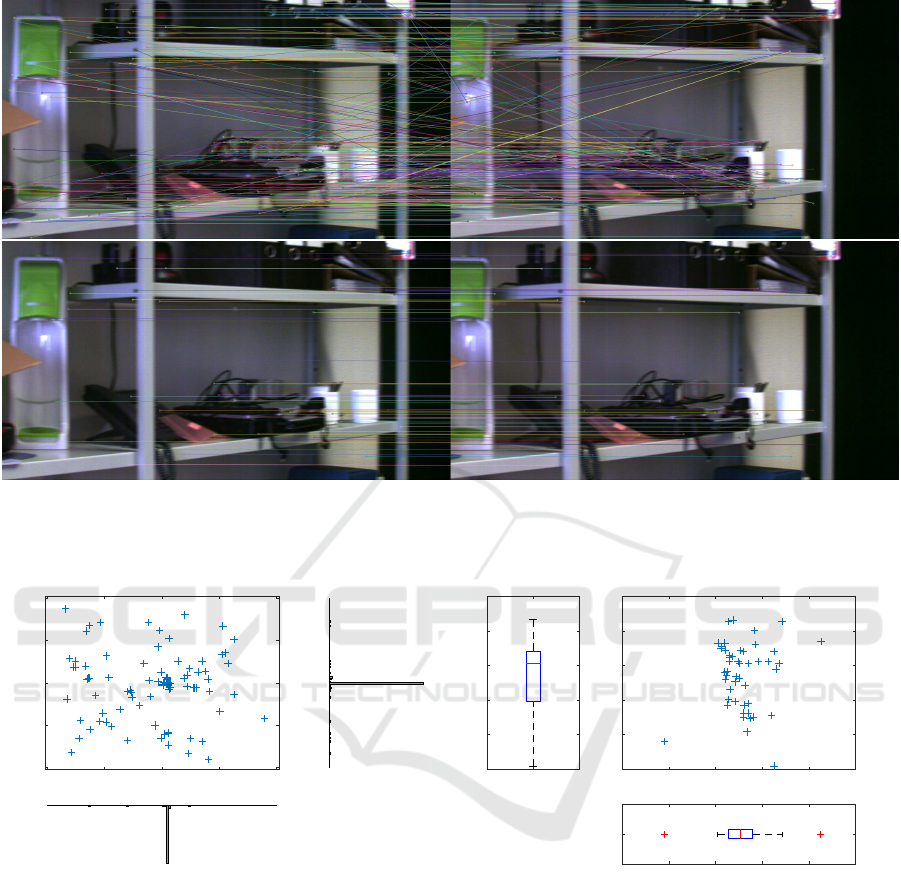
Figure 6: Finding feature point-pairs. Shown are two camera images in which the camera was rotated around an angle of a

few degrees. Keypoints detected by a feature detector are shown in the images. The lines connect points identiﬁed as being

the same in a matching process. On the top image 280 point pairs are shown. In the version below the best matching ﬁfty

pairs were extracted.

-2000 -1000 0 1000 2000

-1000

-500

500

1000

Figure 7: Feature Point Matching. The plot shows the dis-

placement of the individual pairs in the x- and y-directions

of the matching process in ﬁgure 6 on the top. On the sides

are histograms. The total of points is 280.

therefore strongly inﬂuence the ﬁnal result. In ad-

dition the correction of the lens distortion (rectiﬁcta-

tion) is added which has also been determined during

the camera calibration and can also falsify the values.

With further tests and new calibrations no signif-

icant improvement could be achieved. The key ﬁnd-

ing from these results is that the angular changes can

only be viewed at shorter intervals. This is can also

be seen in ﬁgure 10. This graph shows the error of

the calculated angle. At the top it is summed up and

on the bottom shown stepwise. The plots indicate

the error in degrees. The summed error in pixels is

95 100 105 110 115 120

-5

-4

-3

-2

-1

Figure 8: Filteredfeature points. The boxplot shows the dis-

tribution of the 50 best feature point of the data. The median

is symbolized by the red line and the blue box correspond

to the 0.25 or 0.75 quantiles. The length of the whiskers is

1.5 times the interquartile distance. Outliers are represented

by red crosses. The displacement along the x-axis reﬂects

the rotation of the camera. The y-shift would have to be 0.

However it is shifted by sensor noise or calibration errors.

230.51px where the average error per step is 2.15px.

This equals 0.02

◦

. In order to achieve a better com-

parison with the simulated test data it is important to

note that only every ﬁfth images was taken from the

30hz video stream to test the real scenes. This step

provides a rotation of about one degree per image.

Thus the average error per step is below three percent.

A summary of the individual in T

errors is pro-

Image Features in Space - Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios

305

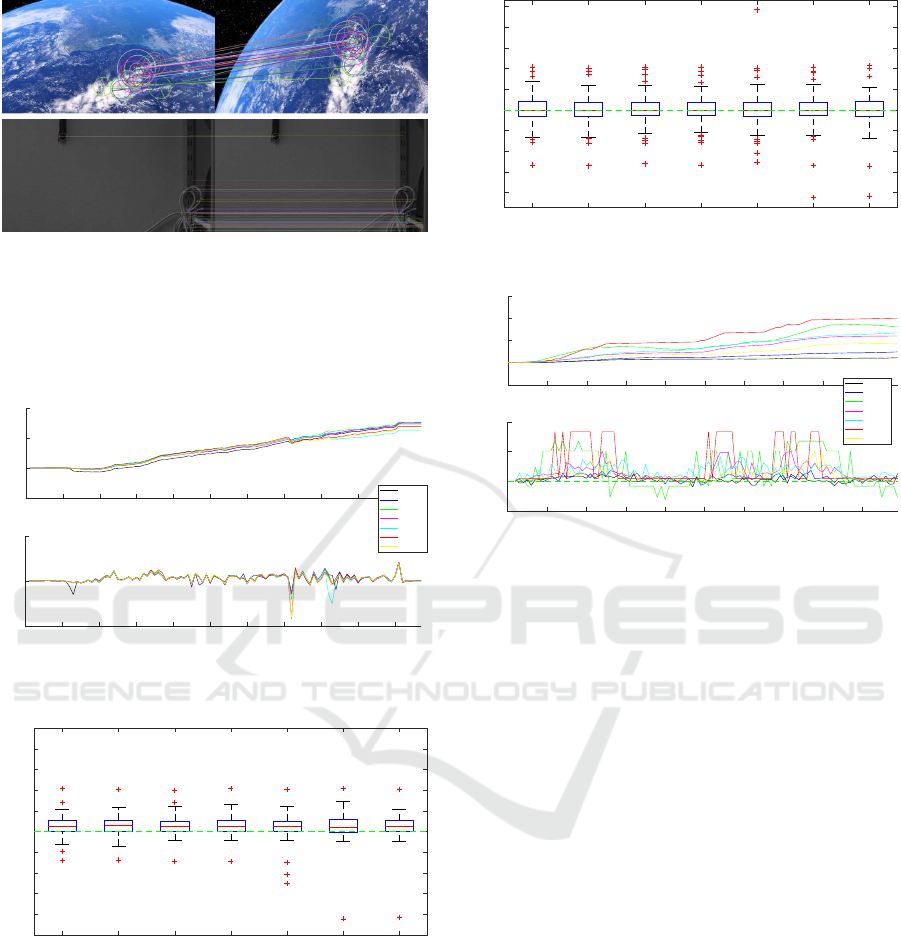
Figure 9: Feature Matching in both environment of the test

dataset. The illustrations show in each case two images of

the test dataset in the real and simulated environment. The

SIFT algorithm was applied to the images. The radius spec-

iﬁes the size of the keypoint. In addition the orientation is

indicated. Corresponding keypoints are connected with a

line.

0 10 20 30 40 50 60 70 80 90 100

step

-2

angle (°)

0 10 20 30 40 50 60 70 80 90 100

step

-0.5

0.5

angle (°)

SIFT

SURF

ORB

AKAZE

BRISK

BRIEF

KAZE

Figure 10: Errors of all feature algorithms in T

. Cumu-

lated error on the top, stepwise below.

SIFT SURF ORB AKAZE BRISK BRIEF KAZE

-0.5

-0.4

-0.3

-0.2

-0.1

0.1

0.2

0.3

0.4

0.5

angle error (°)

Figure 11: Boxplot of errors in T

. A green zero line is

indicated for better clarity.

vided by the boxplot in ﬁgure 11. Here the errors are

shown for each feature algorithm. It is easy to see that

there are no big differences between the algorithms in

this test scene.

In ﬁgure 12 the error values of both real scenes

and T

are summarized. T

is a left rotation

around 90 degrees. Scene T

is the same rotation the

other way (right) back to the initial point. This fact

explains the displacement of the median to the zero

point. Nevertheless there is no major difference be-

SIFT SURF ORB AKAZE BRISK BRIEF KAZE

angle error (°)

-0.4

-0.3

-0.2

-0.1

0.1

0.2

0.3

0.4

0.5

Figure 12: Boxplot of errors in T

and T

. A green zero

line is indicated for better clarity.

0 10 20 30 40 50 60 70 80 90

step

-0.5

0.5

1.5

angle error(°)

0 10 20 30 40 50 60 70 80 90

Schritt

-0.02

0.02

0.04

angle error (°)

SIFT

SURF

ORB

AKAZE

BRISK

BRIEF

KAZE

Figure 13: Errors of all feature algorithms in T

. Cumu-

lated error on the top, stepwise below.

tween the algorithms since the calibration effects (e.g.

lens distortion) are much stronger than the differences

of the operators.

The second tested dataset consisted of six simu-

lated scenes. In contrast to the previous real scenes

no camera calibration has to be generated here. These

parameters could be speciﬁed during the simulation

and were applied when the images were created. Fig-

ure 13 shows the summed and single errors for T

. In

the simulated scene the difference between the algo-

rithms is clearly visible. This also shows the boxplot

of this data in ﬁgure 14.

A summary of all simulated scenes T

= T

..T

shows ﬁgure 15. It can be seen that the feature algo-

rithms SIFT and SURF have the best quality. In order

to obtain a meaningful comparison value from the re-

sults of the tested feature algorithms, the error sum

was formed in each case. This is shown in table 3

for each algorithm and provides SIFT method as the

winner.

The previous tests pointed out SIFT as the most

appropriate feature algorithm. In addition to the an-

gular errors the average runtimes were also measured

during the tests. The diagram in 17 shows this. The

runtimes of the feature detectors and extractors were

determined separately. The graph shows that the cal-

culation time of the algorithms varies widely. While

the total duration of BRIEF is less than 0.1 seconds

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

306

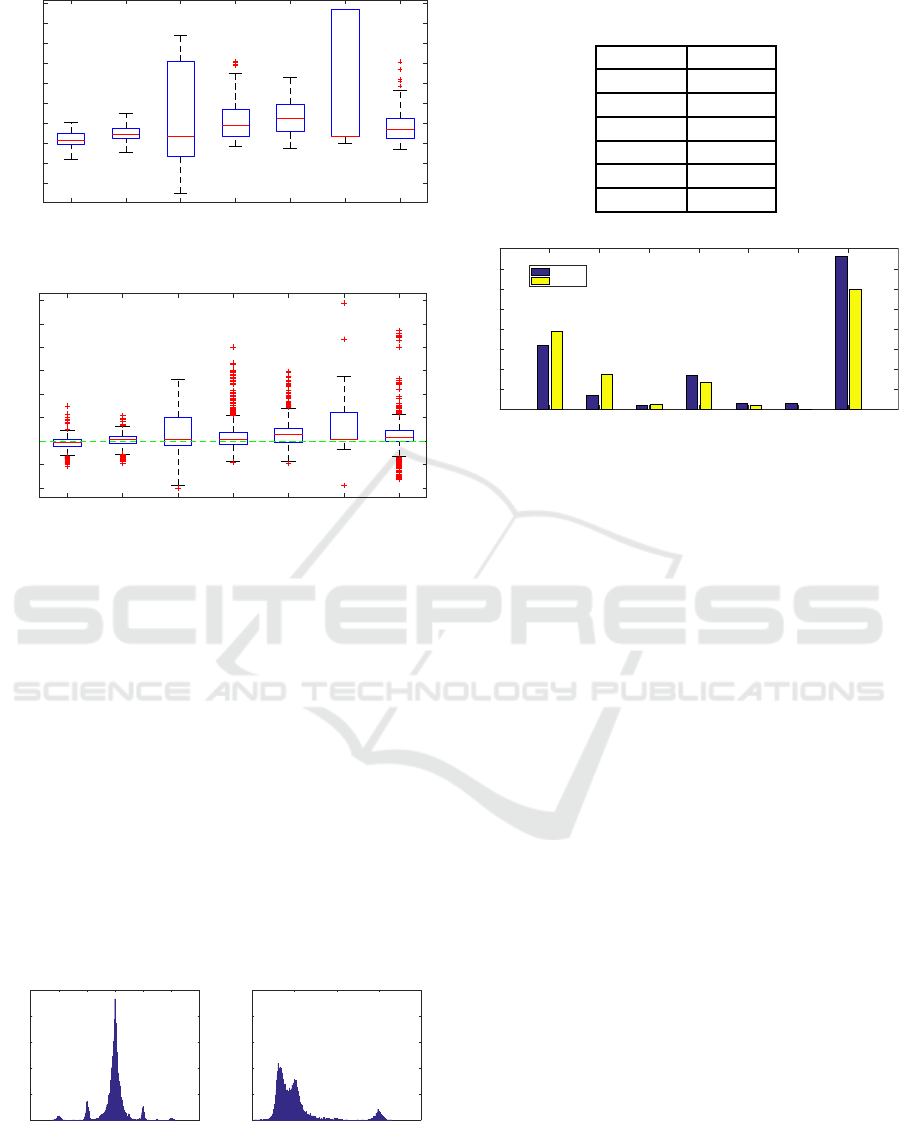
SIFT SURF ORB AKAZE BRISK BRIEF KAZE

-0.01

-0.005

0.005

0.01

0.015

0.02

0.025

0.03

0.035

angle error (°)

Figure 14: Boxplot of errors in T

. A green zero line is

indicated for better clarity.

SIFT SURF ORB AKAZE BRISK BRIEF KAZE

angle error (°)

-0.04

-0.02

0.02

0.04

0.06

0.08

0.1

0.12

Figure 15: Boxplot of errors in T

. A green zero line is

indicated for better clarity.

(0.07s detector + 0.004 s extractor), KAZE needs an

average of 2.7 seconds (1.5 s + 1.2 s) more than 30

times of the BRIEF time. The SIFT algorithm also

has a high runtime of 1.4 seconds (0.64s + 0.78s.

Another interesting evaluation of the test scenes is

the distribution of the determined pixel shift. This is

shown in ﬁgure 16. The data is based on the results of

three scenes in the simulated environment and a total

of 300 images (with 50 point pairs each) in which the

camera was rotated around the y-axis. The left plot

shows the shift on the X axis. Since this has not been

affected by the rotation the value 0px is expected. To

the right is the distribution of the y-shift. Their opti-

mal (Ground Truth) value is 15.9px. As opposed to

the normal distribution of the x-shift, this distribution

is multimodal. A possible explanation are rounding

during the scene rendering in Blender.

-3 -2 -1 0 1 2 3

x-shift (px)

100

200

300

400

500

count

15.5 16 16.5 17 17.5

y-shift(px)

100

200

300

400

500

Figure 16: Distribution of the shift in a simulated scene.

Table 3: Root Mean Square (RMS) of the feature algorithms

in the simulated scene.

SIFT 2.4359

SURF 2.7549

ORB 10.3270

AKAZE 5.3275

BRISK 5.9131

BRIEF 9.3461

KAZE 5.9881

SIFT SURF ORB AKAZE BRISK BRIEF KAZE

0.2

0.4

0.6

0.8

1.2

1.4

1.6

time (s)

Detector

Extractor

Figure 17: Runtimes of the feature algorithms.

5 CONCLUSIONS

In this paper we evaluated different feature algorithms

for the usage in a space scenario. These are namely

SIFT, SURF, ORB, AKAZE, BRISK, BRIEF and

KAZE. Since there was no test data for the special ap-

plication of space robotic available, two scenes were

created. One in our ofﬁces and the other in a virtually

generated space scene, which is a more realistic op-

erational environment. The feature algorithms have

been evaluated by a rotation of the camera. By com-

paring the estimated and ground truth angle a rank-

ing was made. In our case the scale invariant feature

transform (SIFT) algorithm provided the best results.

Since visual odometry has to be real-time capabil-

ity, we also evaluated the runtimes. The SIFT algo-

rithm has a high runtime and is thus not realizable in

realtime. Even with a smaller framerate. For this rea-

son the implementation of SIFT in our space project

AVIRO is carried out in hardware.

REFERENCES

Alcantarilla, P. F., Bartoli, A., and Davison, A. J. (2012).

Computer Vision – ECCV 2012: 12th European Con-

ference on Computer Vision, Florence, Italy, October

7-13, 2012, Proceedings, Part VI, chapter KAZE Fea-

tures, pages 214–227. Springer Berlin Heidelberg,

Berlin, Heidelberg.

Bay, H., Tuytelaars, T., and Gool, L. V. (2006). Surf:

Speeded up robust features. In Proceedings of the

ninth European Conference on Computer Vision.

Image Features in Space - Evaluation of Feature Algorithms for Motion Estimation in Space Scenarios

307

Benseddik, H. E., Djekoune, O., and Belhocine, M. (2014).

Sift and surf performance evaluation for mobile robot-

monocular visual odometry. Journal of Image and

Graphics, 2(1).

Calonder, M., Lepetit, V., Strecha, C., and Fua, P. (2010).

Computer Vision – ECCV 2010: 11th European

Conference on Computer Vision, Heraklion, Crete,

Greece, September 5-11, 2010, Proceedings, Part IV,

chapter BRIEF: Binary Robust Independent Elemen-

tary Features, pages 778–792. Springer Berlin Heidel-

berg, Berlin, Heidelberg.

Canclini, A., Cesana, M., Redondi, A., Tagliasacchi, M.,

Ascenso, J., and Cilla, R. (2013). Evaluation of low-

complexity visual feature detectors and descriptors. In

2013 18th International Conference on Digital Signal

Processing (DSP), pages 1–7.

Chien, H. J., Chuang, C. C., Chen, C. Y., and Klette, R.

(2016). When to use what feature? sift, surf, orb,

or a-kaze features for monocular visual odometry. In

2016 International Conference on Image and Vision

Computing New Zealand (IVCNZ), pages 1–6.

Fraundorfer, F. and Scaramuzza, D. (2012). Visual odom-

etry: Part ii: Matching, robustness, optimization, and

applications. IEEE Robotics & Automation Magazine,

19(2):78–90.

Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).

Vision meets robotics: The kitti dataset. International

Journal of Robotics Research (IJRR).

Is¸ık, S¸. (2014). A comparative evaluation of well-known

feature detectors and descriptors. International Jour-

nal of Applied Mathematics, Electronics and Comput-

ers, 3(1):1–6.

Jiang, Y., Xu, Y., and Liu, Y. (2013). Performance evalua-

tion of feature detection and matching in stereo visual

odometry. Neurocomputing, 120:380 – 390. Image

Feature Detection and Description.

Kazerouni, M. F., Schlemper, J., and Kuhnert, K.-D. (2015).

Comparison of modern description methods for the

recognition of 32 plant species. Signal & Image Pro-

cessing, 6(2):1.

Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).

Brisk: Binary robust invariant scalable keypoints. In

Proceedings of the 2011 International Conference on

Computer Vision, ICCV ’11, pages 2548–2555, Wash-

ington, DC, USA. IEEE Computer Society.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. In International Journal of Com-

puter Vision, pages 1–28.

Maimone, M., Cheng, Y., and Matthies, L. (2007). Two

years of visual odometry on the mars exploration

rovers. Journal of Field Robotics, 24(3):169–186.

Mikolajczyk, K. and Schmid, C. (2003). A performance

evaluation of local descriptors. In 2003 IEEE Com-

puter Society Conference on Computer Vision and

Pattern Recognition, 2003. Proceedings., volume 2,

pages II–257–II–263 vol.2.

Miksik, O. and Mikolajczyk, K. (2012). Evaluation of local

detectors and descriptors for fast feature matching. In

Pattern Recognition (ICPR), 2012 21st International

Conference on, pages 2681–2684. IEEE.

Oliveira, A. (2014). Blend swap: Earth in cycles.

https://www.blendswap.com/blends/view/52273.

Pablo Alcantarilla (Georgia Institute of Technolog), Jesus

Nuevo (TrueVision Solutions AU), A. B. (2013). Fast

explicit diffusion for accelerated features in nonlinear

scale spaces. In Proceedings of the British Machine

Vision Conference. BMVA Press.

Qu, X., Soheilian, B., Habets, E., and Paparoditis, N.

(2016). Evaluation of Sift and Surf for Vision Based

Localization. ISPRS - International Archives of the

Photogrammetry, Remote Sensing and Spatial Infor-

mation Sciences, pages 685–692.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf. In

Proceedings of the 2011 International Conference on

Computer Vision, ICCV ’11, pages 2564–2571, Wash-

ington, DC, USA. IEEE Computer Society.

Scaramuzza, D. and Fraundorfer, F. (2011). Visual odom-

etry: Part i: The ﬁrst 30 years and fundamentals.

Robotics & Automation Magazine, IEEE, 18(4):80–

92.

Sebe, N., Tian, Q., Loupias, E., Lew, M., and Huang, T.

(2002). Evaluation of Salient Point Techniques, pages

367–377. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

Shaw, A., Woods, M., Churchill, W., and Newman, P.

(2013). Robust visual odometry for space exploration.

12th Symposium on Advanced Space Technologies in

Robotics and Automation.

Tsai, R. Y. (1986). An efﬁcient and accurate camera calibra-

tion technique for 3D machine vision. In Proc. Conf.

Computer Vision and Pattern Recognition, pages 364–

374, Miami.

Yumin, T., Baowu, X., Weinan, J., and Chao, S. (2016).

Research on image feature point extraction methods of

low altitude remote sensing. In 2016 4th International

Workshop on Earth Observation and Remote Sensing

Applications (EORSA), pages 222–226.

ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods

308