Exploration Methods for Connectionist Q-learning in Bomberman

Joseph Groot Kormelink

, Madalina M. Drugan

and Marco A. Wiering

Institute of Artiﬁcial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands

ITLearns.Online, The Netherlands

Keywords:

Reinforcement Learning, Computer Games, Exploration Methods, Neural Networks.

Abstract:

In this paper, we investigate which exploration method yields the best performance in the game Bomberman.

In Bomberman the controlled agent has to kill opponents by placing bombs. The agent is represented by

a multi-layer perceptron that learns to play the game with the use of Q-learning. We introduce two novel

exploration strategies: Error-Driven-ε and Interval-Q, which base their explorative behavior on the temporal-

difference error of Q-learning. The learning capabilities of these exploration strategies are compared to ﬁve

existing methods: Random-Walk, Greedy, ε-Greedy, Diminishing ε-Greedy, and Max-Boltzmann. The results

show that the methods that combine exploration with exploitation perform much better than the Random-Walk

and Greedy strategies, which only select exploration or exploitation actions. Furthermore, the results show that

Max-Boltzmann exploration performs the best in overall from the different techniques. The Error-Driven-ε

exploration strategy also performs very well, but suffers from an unstable learning behavior.

1 INTRODUCTION

Reinforcement learning (RL) methods are computa-

tional methods that allow an agent to learn from its in-

teraction with a speciﬁc environment. After perceiv-

ing the current state, the agent reasons about which

action to select in order to obtain most rewards in the

future. Reinforcement learning has been widely ap-

plied to games (Mnih et al., 2013; Shantia et al., 2011;

Bom et al., 2013; Szita, 2012). To deal with the large

state spaces involved in many games, often a multi-

layer perceptron is used to store the value function of

the agent, where the value function forms the basis of

most RL research. An aspect which has received little

attention from the research community is the question

which exploration strategy is most useful in combi-

nation with connectionist Q-learning to learn to play

games.

We use Q-learning (Watkins and Dayan, 1992)

with a multi-layer perceptron to let an agent learn to

play the game Bomberman. Bomberman is a strategic

maze game where the player must kill other players

to become the winner. The player controls one of the

Bombermen players and must, by means of placing

bombs, kill the other players. To get to the other play-

ers, one ﬁrst removes a set of walls by placing bombs.

Afterwards, the agent needs to navigate to its oppo-

nents and trap them by strategically placing bombs.

The player wins the game if all opponents have died

due to exploding bombs in their vicinity.

We study how different exploration strategies per-

form when combined with connectionist Q-learning

for learning to play Bomberman. We introduce

two novel exploration strategies: Error-Driven-ε and

Interval-Q, which use the TD-error of Q-learning to

change their explorative behavior. These exploration

strategies will be compared to ﬁve existing tech-

niques: Random-Walk, Greedy, ε-Greedy, Diminish-

ing ε-Greedy and Max-Boltzmann. The agent plays

a huge number of games against three ﬁxed oppo-

nents that use the same behavior to measure its perfor-

mance. For this, the average amount of points gath-

ered by the adaptive agent is measured together with

its win rate over time. The results show that the meth-

ods that only rely on exploration (Random-Walk) or

exploitation (Greedy) perform much worse than all

other methods. Furthermore, Max-Boltzmann ob-

tains the best results in overall, although the proposed

Error-Driven-ε strategy performs best during the ﬁrst

800,000 training games out of a total of 1,000,000

games. The problem of Error-Driven-ε is that it can

become unstable, which negatively affects its perfor-

mance when trained for longer times.

In Section 2, we describe the implementation of

the game together with the used state representation

for the adaptive agent and the implemented ﬁxed be-

Kormelink, J., Drugan, M. and Wiering, M.

Exploration Methods for Connectionist Q-learning in Bomberman.

DOI: 10.5220/0006556403550362

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 355-362

ISBN: 978-989-758-275-2

355

Figure 1: Starting position of all Bombermen. Brown walls

are breakable, grey walls are unbreakable. The 7 × 7 grid

is surrounded by another unbreakable wall, which is not

shown here.

havior of the opponent agents. In Section 3, we ex-

plain reinforcement learning algorithms and in Sec-

tion 4 we present the different exploration methods

that are compared. Section 5 describes the experimen-

tal setup and the results, and the paper is concluded in

Section 6.

2 BOMBERMAN

Bomberman is a strategic maze-based video game de-

veloped by Hudson Soft in 1983. The goal is to ﬁnish

some assignment by means of placing bombs. We fo-

cus on the multi-player variant of Bomberman where

the goal is to kill other players and be the last man

standing. At the beginning of the game all four play-

ers start in opposing corners of the grid, see Figure

1. The Bombermen have 6 possible moves they can

take to transition through the game: up, down, left,

right, wait, place bomb. The grid is ﬁlled with two

types of obstacles: breakable and not breakable. Be-

fore the player can kill its opponents, the player needs

to pave a path through the grid. Since the grid is ﬁlled

with obstacles at the start of the game, players need

to break destructible objects in order to reach other

players.

We have developed a framework that implements

Bomberman in a discrete manner on a 7 ×7 grid. The

amount of states can be approximately computed in

the following way. There are 42 positions (including

death) for four agents, two different states for the 28

breakable walls (empty, standing), and two states for

40 positions that determine if there is a bomb at a po-

sition or not. This results in 42

× 2

≈ 10

different states.

Every Bomberman is controlled by an agent. The

game state is sent to the agents, which then deter-

mine their next moves. After the actions have been

executed, the consequences of the actions are com-

municated to the agents in the form of rewards. The

actions are executed simultaneously so that no agent

has an advantage. After a bomb has been placed it

will wait 5 time-steps before it explodes. If a bomb

explodes all hits with players and breakable walls are

calculated. An agent or wall is hit, if it either horizon-

tally or vertically no more than 2 cells away from the

position of the bomb. Players are allowed to occupy

the same position or to move through each other. A

turn (or time-step) therefore consists of: determining

the actions, executing the actions and then calculat-

ing hits. If there is a hit with a breakable wall, the

wall vanishes. If a bomb explosion hits a player, the

player dies. If all players die simultaneously, no one

wins. As the game progresses, agents gain more free-

dom due to the vanishing walls. Therefore, the agents

can walk around for a long time, which poses prob-

lems because the game can last for inﬁnity. After 150

time-steps, additional bombs are placed at random lo-

cations and the amount of bombs placed afterwards

increases every time-step. This leads ﬁnally to very

harsh game dynamics, in which it is impossible for all

Bombermen to stay alive for a long time.

State Representation. The game state is trans-

formed into an input vector for the learning agent,

which will be used by the multi-layer perceptron

(MLP) to learn the utility (value) of performing each

possible action. The game environment is divided in

7 × 7 grid cells, where every cell represents a posi-

tion. The agent can fully observe the environment.

Therefore for each cell 4 values are computed:

• Free, breakable, obstructed cell (1, 0, -1)

• Position contains the player (1, 0)

• Position contains an opponent (1, 0)

• Danger level of position (-1 ≤ danger ≤ 1)

Danger is measured as

Time passed

Time needed to explode

, where a

bomb takes 5 time-steps after it is placed until it ex-

plodes. The danger value is negative if the bomb

has been placed by the player and positive if it has

been placed by an opponent (or environment). In this

way, the agent can learn to distinct between danger

areas caused by a bomb it placed itself or caused by a

bomb placed by an opponent (or the environment af-

ter 150 time-steps). The state representation contain-

ing 49 ×4 = 196 inputs is sent to the MLP, which will

be trained using Q-learning as described in Section 3.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

356

Opponents. To evaluate how well the different

methods can learn to play the game, we use a ﬁxed

opponent strategy against which the adaptive agent

plays. For this we implemented a hard coded oppo-

nent algorithm, which generates the ﬁxed behavior of

the three opponent agents. The opponent algorithm

consists of 3 elements, see Algorithm 1, which will

now be described.

1) The agent always searches for cover in the

neighbourhood of a bomb. In Algorithm 1, we can

see this in the ﬁrst conditional statement. The agent

searches for cover by calculating the utility of every

action. It does this by iterating through all bombs that

are within hit-range of the Bomberman. If a Bomber-

man is within hit-range of a bomb, a utility value is

calculated for every action. We separate the x- and

y-axis in the distance and utility calculations. There-

fore, actions that make sure the Bomberman and the

bomb are no longer on the same x and y axis get

a higher utility. Finally, the action with the highest

utility gets selected, if there are bombs in the agent’s

vicinity.

2) Next to not getting hit by exploding bombs, it

is important that the agent destroys breakable walls

with its bombs. If an agent is surrounded by 3 walls

(including the boundaries not visible in Figure 1), it

will place a bomb. If the agent is surrounded by 3

walls, there has to be at least one breakable wall. The

combination of placing bombs when surrounded by

walls and searching for cover in the neighbourhood

of bombs works well, because it shows incentive of

opening up paths while staying clear of bombs.

3) If there are no bombs and not enough walls the

algorithm produces random behaviour. When it per-

forms a random action, it might very well be possible

that the action is placing a bomb, after which the agent

might search for cover again. This algorithm is called

semi-random because the behaviour is mostly guided,

but random at times. Note that the opponent’s behav-

ior is fairly simple, because it does not place bombs

near other players, but still challenging, because of

their bomb-cover behavior.

3 REINFORCEMENT LEARNING

Reinforcement learning (Sutton and Barto, 2015) is a

type of machine learning that allows agents to auto-

matically learn the optimal behaviour from its inter-

action with an environment. Each time-step the agent

receives the state information from the environment

and selects an action from its action space depend-

ing on the learned value function and the exploration

strategy that is being followed. After executing an ac-

Algorithm 1: Semi-Random Opponent.

possibleA = ReturnPossibleActions(player)

bombList = SurroundingBombs(player)

if bombList.NotEmpty() then

utilityList[] = possibleA.Size()

for a : possibleA do

for bomb : BombList do

possiblePos = MakeAction(a, player)

curUtility = Dist(bomb, possiblePos)

utilityList[a] += curUtility

end for

bestUtility = IndexMax(utilityList)

return(possibleA[bestUtility])

end if

SBT (ob j) = SurroundedByT hreeWalls(ob j)

if SBT (player) == T RUE then

return(placeBomb)

end if

return(RandomAction())

tion the agent receives a reward, which is a numerical

representation of the direct consequence of the action

it executed. The difference between the received re-

ward plus the next value for the best action and the

actual value for the current state is the TD-error. The

goal of learning is to minimize the TD-error, so the

agent can predict the consequences of its actions and

select the actions that lead to the highest expected sum

of future rewards.

A Markov Decision Process (MDP) is a model

for fully-observable sequential decision making prob-

lems in stochastic environments. S is a ﬁnite set of

states, where s

∈ S is the state at time-step t. A is

a ﬁnite set of actions, where a

∈ A is the action ex-

ecuted at time-step t. The reward function R(s,a, s

)

denotes the expected reward when transitioning from

state s to state s

after executing action a. The reward

at time-step t is denoted with r

. The transition func-

tion P(s, a,s

) gives the probability of ending up in

state s

after selecting action a in state s. The discount

factor γ ∈ [0, 1] assigns a lower importance to future

rewards for optimal decision making.

Tabular Q-learning. The policy of an agent is a

mapping between states and actions. Learning the

optimal policy of an agent is done using Q-learning

(Watkins and Dayan, 1992). For every state-action

pair a Q-value Q(s,a) denotes the expected sum of

rewards obtained after performing action a in state s.

Q-learning updates the Q-function using the informa-

tion obtained after selecting an action (s

, a

, r

, s

t+1

)

using the following update rule:

Exploration Methods for Connectionist Q-learning in Bomberman

357

Q(s

) = Q(s

) + αδ

(1)

with:

= r

+ γmax

Q(s

t+1

,a) − Q(s

) (2)

In equation 1, δ

is the temporal-difference error

(TD-error) of Q-learning computed with equation 2.

The learning rate 0 < α ≤ 1 is used to regulate how

fast the Q-value is pushed in a certain direction. When

the next-state s

t+1

is an absorbing ﬁnal state, then the

Q-values for all actions in such a state are set to 0 in

equation 2. Furthermore, when a game ends, then a

new game is started. Q-learning is an off-policy al-

gorithm, which means that it learns independently of

the agent’s selected next action induced by its explo-

ration policy. If the agent would try out all actions

in all states an inﬁnite amount of times, Q-learning

with lookup tables converges to the optimal policy for

ﬁnite MDPs.

Multi-layer Perceptron. A problem is that large

state spaces require a lot of memory, since every state

uses its own Q-value for every action. When using

lookup tables, Q-learning needs to explore all actions

in all states before being able to infer which action is

best in a speciﬁc state.

To solve these issues regarding space and time

complexity, the agent uses an MLP. An MLP is a feed-

forward neural network that maps an input vector that

represents the state, to an output vector, that repre-

sents the Q-values for all actions. The MLP consists

of a single hidden-layer in which the sigmoid func-

tion is used as activation function. The MLP uses a

linear output function for the output units, so it can

also predict values outside of the [0,1] range. As in-

put the complete game state representation containing

196 features, as described in Section 2, is presented

to the MLP. The output of the MLP is a vector with

6 values, where every value represents a Q-value for

a corresponding action. The MLP is initialized ran-

domly, which means that it needs to learn what Q-

values correspond to the state-action pairs. We do

this by backpropagating the TD-error computed with

equation 2 through the MLP to update the weights in

order to decrease the TD-error for action a

in state s

After training, The MLP computes the appropriate Q-

values for a speciﬁc state without storing all different

Q-values for all states.

Reward Function. We transform action conse-

quences into something that Q-learning can use to

learn the Q-function by giving in-game events a nu-

merical reward. For learning the optimal behavior,

the rewards of different objectives should be set care-

fully so that maximizing the obtained rewards results

in the desired behavior. The used in-game events and

rewards for Bomberman are shown in Table 1.

Table 1: Reward Function.

Event Reward

Kill a player 100

Break a wall 30

Perform action -1

Perform impossible action -2

Die -300

These rewards have been carefully chosen to

clearly distinct between good and bad actions. Dy-

ing is represented by a very negative reward. The re-

ward of killing a player is attributed to the player that

actually placed the involved bomb. The rest of the re-

wards promote active behaviour. No reward is given

to ﬁnally winning the game (when all other players

died). In order to maximize the total reward intake,

the agent should learn not to die, and kill as many op-

ponents and break most walls with its bombs. In the

experiments, a discount factor of 0.95 is used.

4 EXPLORATION METHODS

Q-learning with a multi-layer perceptron allows the

agent to approximate the sum of received rewards af-

ter selecting an action in a particular state. If the agent

always selects the action with the highest Q-value in

a state, the agent never explores the consequences of

other possible actions in that state, and, consequently,

it does not learn the optimal Q-function and policy.

On the other hand, if the agent selects many explo-

ration actions, the agent performs randomly. The

problem of optimally balancing exploration and ex-

ploitation is known as the exploration / exploitation

dilemma (Thrun, 1992). There are many different ex-

ploration methods, and in this paper we introduce two

novel exploration strategies that we compare with 5

existing exploration methods. The best performing

method is the method that gathers the most points (re-

wards) and obtains the highest ﬁnal win rate.

4.1 Existing Exploration Strategies

We will now describe 5 different existing strate-

gies for determining which action to select given a

state and the current Q-function. The ﬁrst method,

Random-Walk, does not use the Q-function at all. The

second method, Greedy, never selects exploration ac-

tions. The other three exploration strategies balance

exploration with exploitation by using the Q-function

and randomness in the action selection.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

358

Random-Walk exploration executes a randomly

chosen action every time-step. This method produces

completely random behaviour, and is therefore good

as a simple baseline algorithm to compare other meth-

ods to. Because Q-learning is an off-policy algorithm,

for a ﬁnite MDP it can still learn the optimal policy

when only selecting random actions due to the use of

the max-operator in equation 2.

Greedy method is the complete opposite of the

Random-Walk exploration strategy. This method as-

sumes the current Q-function is highly accurate and

therefore every action is based on exploitation. The

agent always takes the action with the highest Q-

value, because it assumes that this is the best action.

Greedy tries to solve some problems of Random-

Walk in the game Bomberman: if the agent dies con-

stantly in the early game, the agent will not get to ex-

plore the later part of the game. This could be solved

by taking no bad actions and this could be achieved by

only taking actions with the highest Q-value, although

this requires the Q-function to be very accurate, which

in general it will not be. Because this method never

selects exploration actions, it can often not be used for

learning the optimal policy.

ε-Greedy exploration is one of the most used and

simplest methods that trades off exploration with ex-

ploitation. It uses the parameter ε to determine what

percentage of the actions is randomly selected. The

parameter falls in the range 0 ≤ ε ≤ 1, where 0 trans-

lates to no exploration and 1 to only exploration. The

action with the highest Q-value is chosen with proba-

bility 1− ε and a random action is selected otherwise.

The MLP is initialized randomly; at the start of learn-

ing, the Q-function is not a good approximation of the

obtained sum of rewards. Greedy could repetitively

take a speciﬁc sub-optimal action in a state; ε-Greedy

solves this problem by exploring the effects of differ-

ent actions.

Diminishing ε-Greedy. ε-Greedy explores with the

same amount in the beginning as in the end of a sim-

ulation. We however assume the agent is improv-

ing its behaviour and thus over time needs less ex-

ploration. Diminishing ε-Greedy uses a decreasing

value for ε, so the agent uses less exploration if the

agent played more games. The exploration value

is then curExplore = ε ∗ (1 −

currentGen

totalGens

). The algo-

rithm also incorporates a minimal exploration value,

i.e. curExplore = 0.05, to make sure the agent keeps

exploring in the long run. totalGens stands for the

amount of generations, where one generation means

training for 10,000 games in our experiments.

Max-Boltzmann. One drawback of the different ε-

Greedy methods is that all exploration actions are

chosen randomly, which means that the second best

action is chosen as likely as the worst action. The

Boltzmann exploration method solves this problem by

assigning a probability to all actions, ranking best to

worst. This method was shown to perform best in a

comparison between four different exploration strate-

gies for maze-navigation problems (Tijsma et al.,

2016).

The probabilities are assigned using a Boltzmann

distribution function. The probability π(s,a) for se-

lecting action a in state s is:

π(s,a) =

Q(s,a)/T

∑

|A|

Q(s,a

)/T

(3)

Where |A| is the amount of possible actions and T

is the temperature parameter. A high T translates to a

lot of exploration.

Max-Boltzmann (Wiering, 1999) exploration

combines ε-Greedy exploration with Boltzmann ex-

ploration. It selects the greedy action with probability

1 − ε and otherwise the action will be chosen accord-

ing to the Boltzmann distribution. By introducing an-

other hyperparameter, the exploration behavior can be

better controlled than with ε-greedy exploration. This

is at the cost of more experimentation time, however.

4.2 Novel Exploration Strategies

We will now introduce two novel exploration meth-

ods, which use the obtained TD-errors from equation

2 to control their behavior.

The error-Driven-ε exploration tries to resolve

the problem of Diminishing ε-Greedy for which it is

necessary to specify beforehand how much the agent

explores over time. To solve this problem, Error-

Driven-ε bases the exploration rate ε on the difference

in average obtained TD-errors between the previous

two generations during which 10,000 training games

were played. During the ﬁrst 2 generations, ε-greedy

is used, because there is no error information avail-

able in the beginning of learning. Afterwards, ε is

computed with:

ε = max((1 −

min(err

g−1

,err

g−2

)

max(err

g−1

,err

g−2

)

),minExp) (4)

Where g is the current generation number and the

error is calculated as the average of all TD-Errors

of 10,000 played games during a generation. The

method also uses a minimal amount of exploration

to ensure that some exploration is always performed.

Exploration Methods for Connectionist Q-learning in Bomberman

359

The idea of this algorithm, is that when the TD-

errors stay approximately the same over time, the Q-

function has more or less converged so that the min-

imum and maximum of the average TD-errors of the

two previous generations are about the same. In this

case, the algorithm will use the minimum value for ε.

On the other hand, if the TD-errors are decreasing (or

ﬂuctuating), more exploration will be used.

Interval-Q is a novel exploration strategy that

uses the error range of the Q-value estimates next to

the prediction of the Q-values. This method is based

on Kaelbling’s Interval Estimation (Kaelbling, 1993),

where conﬁdence intervals were computed for solving

a multi-armed bandit problems with a ﬁnite number

of actions. Kaelbling’s Interval Estimation is used to

assess how reliable a Q-value is by learning the con-

ﬁdence interval (or value range) for an action. Hence,

we create an MLP with 12 output units instead of 6

as in the other methods. The ﬁrst 6 outputs represent

the Q-values and the other 6 outputs represent the ex-

pected absolute TD-error, where the TD-error is com-

puted with equation 2.

In this method, the action is selected that has the

highest upper conﬁdence value in the Q-value esti-

mate. We calculate the upper conﬁdence by adding

|T D − error| to the Q-value for an action a in state

s. Finally, because the MLP is randomly initialized

and has to learn the Q-values and expected absolute

TD-errors, the method selects a random action with

probability ε. The pseudo-code of this method is

shown in Algorithm 2.

Algorithm 2: Interval-Q(ε).

rand = RandomValue(0,1)

if rand < ε then

return(RandomMove())

end if

state = GetState()

qValues = GetQValues(state)

range = GetErrorRange(state)

maxReach = −∞

bestAction = NULL

for (action : Actions) do

reach = qValues[action] +

range[action]

if reach > maxReach then

maxReach = reach

bestAction = action

end if

end for

return(bestAction)

5 EXPERIMENTS AND RESULTS

We evaluated the seven discussed exploration meth-

ods in combination with an MLP and Q-learning.

Every method is trained for 100 generations, where

a generation consists of 10,000 training games and

100 testing games. During the test games learning

is disabled and the agent does not use any explo-

ration actions. An entire simulation consists of 100

generations of training (1,000,000 training games and

10,000 test games), which requires around one day of

computation time on a common CPU. The results are

obtained by running 20 simulations per method and

taking the average scores. For every algorithm we ex-

amine what percentage of the games the method wins,

and how many points it gathers. The amount of gath-

ered points is the average sum of rewards obtained

while playing 100 test games.

We use a single hidden-layer MLP with 100 hid-

den nodes and 6 output nodes (except for the MLP

for Interval-Q that uses 12 output nodes). The MLP is

initialized randomly with weight values between -0.5

and 0.5. After running multiple preliminary experi-

ments, 100 hidden units were found to be sufﬁcient to

produce intelligent behaviour for a grid size of 7 × 7.

We also experimented with different amounts of hid-

den units, but removing units decreased the perfor-

mance and increasing the number of hidden units only

added computational time without a performance in-

crease. Adding more hidden layers has also been in-

vestigated, but this also did not improve the perfor-

mance at the cost of more computational power.

Hyperparameters. To ﬁnd the best hyperparame-

ters preliminary experiments have been performed.

Because the large amount of time to perform a sim-

ulation of 1,000,000 training games, we could not

speciﬁcally ﬁne-tune all the parameters of the dif-

ferent methods. In the experiments, all MLPs were

trained with a learning rate of 0.0001. Table 2 shows

the exploration parameters for all methods, where ε

equals the exploration chance, min-ε is the minimal

exploration chance and T denotes the Temperature.

The different algorithms use different amounts of tun-

able parameters (from 0 to 3).

Table 2: The parameter settings in training.

Settings ε min-ε T

Random-Walk / / /

Greedy / / /

ε-Greedy 0.3 / /

Error-Driven-ε / 0.05 /

Interval-Q 0.2 / /

Diminishing ε-Greedy 0.3→0.05 0.05 /

Max-Boltzmann 0.3 / 200→1

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

360

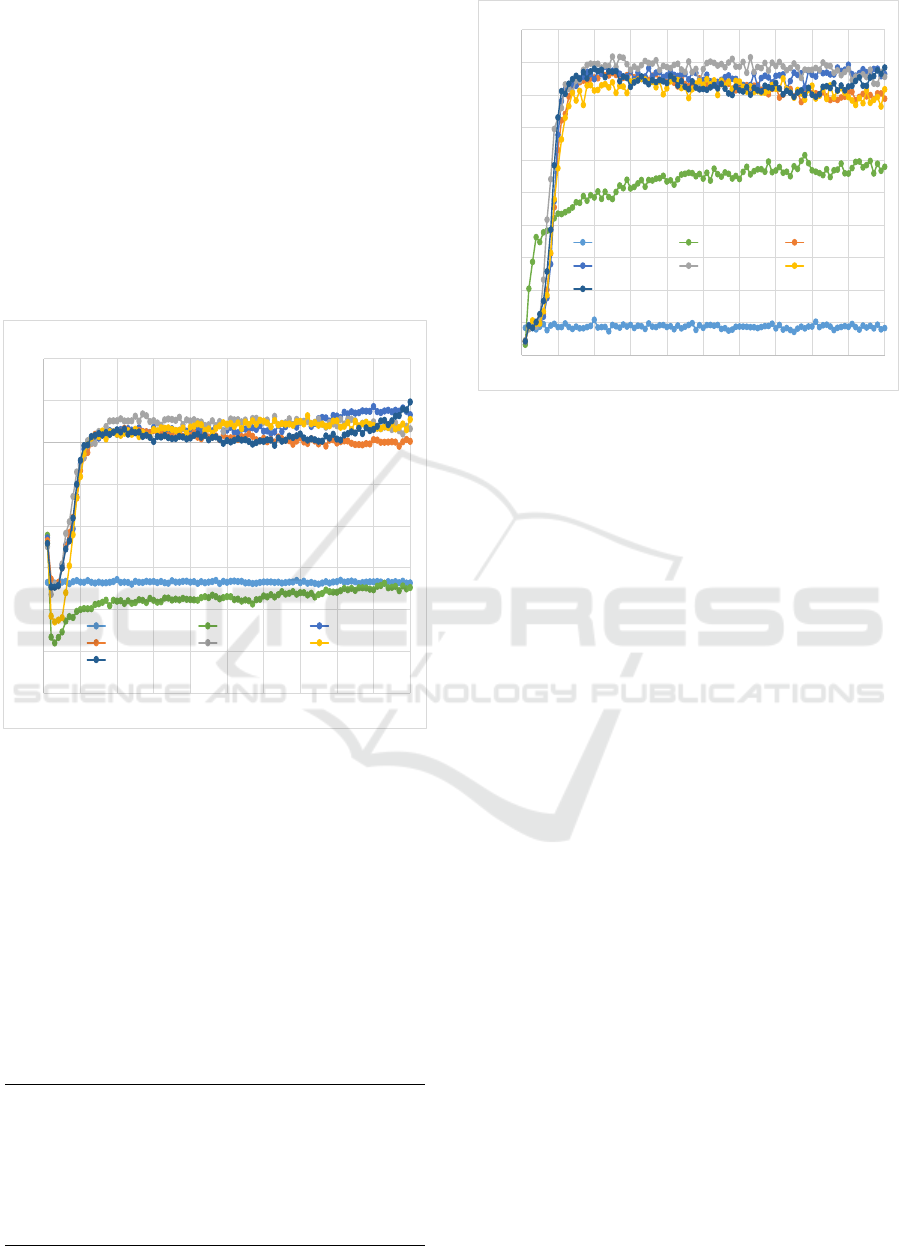
Results. Figure 2 shows the win rate of the different

exploration methods over time. We note that there is

a big difference between the methods that use an ex-

ploration/exploitation trade-off and the methods that

do not (Greedy, Random-walk). The different explo-

ration strategies obtain quite good performances, al-

though they do not improve much after 20 genera-

tions. Error-Driven-ε outperforms all other methods

for the ﬁrst 80 generations (800,000 games), but even-

tually gets surpassed by Diminishing ε-Greedy and

Max-Boltzmann. The reason is that Error-Driven-ε

can become unstable which results in a decreasing

performance.

-600

-500

-400

-300

-200

-100

100

200

0 10 20 30 40 50 60 70 80 90 100

Points

Generations Of Training

Exploration Method Performance Points

RandomWalk Greedy Diminishing ε-Greedy

ε-Greedy Error-Driven-ε Interval-Q

Max-Boltzmann

Figure 2: Win rate of the exploration methods, where a

generation consist of 10,000 training games and 100 test-

ing games. The results are averaged over 20 simulations.

Table 3 shows the mean percentage of the games

that were won and the standard error over the last

100 test games during the last generation. The re-

sults are averaged over 20 simulations. It can be seen

that Max-Boltzmann performs the best, while Error-

Driven-ε and Diminishing ε-Greedy perform second

Table 3: Mean and standard error of the win rate over the

last 100 games. The results are averaged over 20 simula-

tions.

Method Mean win rate SE

Max-Boltzmann 0.88 0.015

Error-Driven-ε 0.86 0.026

Diminishing ε-Greedy 0.86 0.022

Interval-Q 0.82 0.027

ε-Greedy 0.79 0.014

Greedy 0.58 0.033

Random-Walk 0.08 0.006

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0 10 20 30 40 50 60 70 80 90 100

Winrate

Generations Of Training

Exploration Method Performance Win Rate

RandomWalk Greedy ε-Greedy

Diminishing ε-Greedy Error-Driven-ε Interval-Q

Max-Boltzmann

Figure 3: Points gathered by the methods, where a genera-

tion consist of 10,000 training games and 100 testing games.

The results are averaged over 20 simulations.

best. It is quite surprising that ε-Greedy performs

much worse and comes on the 5-th place, only before

the Random-Walk and Greedy methods.

Figure 3 shows for every method the average

amount of points it gathered. The two methods with-

out exploration/exploitation trade-off converge to a

low value, while the other methods perform much

better. All methods with the exploration/exploitation

trade-off initially follow a similar learning curve, af-

ter which Error-Driven-ε performs the best for around

50 generations. In the end Max-Boltzmann performs

best after increasing its performance a lot during the

last 10 generations. This is caused by the decreasing

temperature, which goes ﬁnally to a value of 1. More

generations may help this method to increase its per-

formance even further, which does not seem to be the

case for the other algorithms.

Table 4 shows the average amount of points gath-

ered and the standard error for every exploration

method. These data were also gathered over the last

100 games. The table shows that Max-Boltzmann

performs signiﬁcantly (p < 0.001) better than the

other methods, scoring on average 30 points more

than the second best method, Diminishing ε-Greedy.

Again ε-Greedy comes on the 5-th place.

5.1 Discussion

After training all methods for a long time, Max-

Boltzmann performs best. In the end, Max-

Boltzmann gathers on average 30 points more than the

second best method, Diminishing ε-Greedy, and has a

2% higher win rate. Especially the high amount of

Exploration Methods for Connectionist Q-learning in Bomberman

361

Table 4: Mean and standard error of the gathered amount

of points over the last 100 games. The results are averaged

over 20 simulations.

Method Mean points SE

Max-Boltzmann 96 1.3

Diminishing ε-Greedy 66 1.1

Interval-Q 55 1

Error-Driven-ε 32 1.5

ε-Greedy 3 1.2

Random-Walk -336 0.2

Greedy -346 1.1

points is important, because the learning algorithms

try to maximize the discounted sum of rewards that

relates to the amount of obtained points. A high win

rate does not always correspond to a high amount of

points, which becomes clear when comparing Greedy

to Random-Walk. Greedy has a much higher win rate

than Random-Walk whereas it gathers less points.

In the ﬁrst 60 generations the temperature of Max-

Boltzmann is relatively high, which produces approx-

imately equal behaviour to ε-Greedy. During the last

10 generations the exploration gets more guided re-

sulting in an signiﬁcantly increasing average amount

of points. Error-Driven-ε exploration outperforms

all other methods in the 10-70 generations interval.

However this method produces unstable behaviour,

which is most likely caused by the way the explo-

ration rate is computed from the average TD-errors

over generations.

We can conclude that Max-Boltzmann performs

better than the other methods. The only problem with

Max-Boltzmann is that it takes a lot of time before

it outperforms the other methods. In Figures 2 and

3, we can see that only in the last 10 generations

Max-Boltzmann starts to outperform the other meth-

ods. More careful tuning of the hyperparameters of

this method may result in even better performances.

Looking at the results, it is clear that the trade-

off between exploration and exploitation is im-

portant. All methods that actualize this explo-

ration/exploitation trade-off perform signiﬁcantly bet-

ter than the methods that use only exploration or ex-

ploitation. The Greedy algorithm learns a locally op-

timal policy in which it does not get destroyed easily.

The Random-Walk policy performs many stupid ex-

ploration actions, and is killed very quickly. There-

fore, the Random-Walk method never learns to play

the whole game.

6 CONCLUSIONS

This paper examined exploration methods in connec-

tionist reinforcement learning in Bomberman. We

have explored multiple exploration methods and can

conclude that Max-Boltzmann outperforms the other

methods on both win rate and points gathered. The

only aspect where Max-Boltzmann is being out-

performed, is the learning curve. Error-Driven-ε

learns faster, but produces unstable behaviour. Max-

Boltzmann takes longer to reach a high performance

than some other methods, but it is possible that there

exist better temperature-annealing schemes for this

method. The results also demonstrated that the com-

monly used ε-Greedy exploration strategy is easily

outperformed by other methods.

In future work, we want to examine how well the

different exploration methods perform for learning to

play other games. Furthermore, we want to carefully

analyze the reasons why Error-Driven-ε becomes un-

stable and change the method to solve this.

REFERENCES

Bom, L., Henken, R., and Wiering, M. (2013). Reinforce-

ment learning to train Ms. Pac-Man using higher-order

action-relative inputs. In 2013 IEEE Symposium on

Adaptive Dynamic Programming and Reinforcement

Learning (ADPRL), pages 156–163.

Kaelbling, L. (1993). Learning in Embedded Systems. A

Bradford book. MIT Press.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. CoRR, abs/1312.5602.

Shantia, A., Begue, E., and Wiering, M. (2011). Con-

nectionist reinforcement learning for intelligent unit

micro management in starcraft. In Neural Networks

(IJCNN), The 2011 International Joint Conference on,

pages 1794–1801. IEEE.

Sutton, R. S. and Barto, A. G. (2015). Reinforcement Learn-

ing : An Introduction. Bradford Books, Cambridge.

Szita, I. (2012). Reinforcement learning in games. In Wier-

ing, M. and van Otterlo, M., editors, Reinforcement

Learning: State-of-the-Art, pages 539–577. Springer

Berlin Heidelberg.

Thrun, S. (1992). Efﬁcient exploration in reinforce-

ment learning. Technical Report CMU-CS-92-102,

Carnegie-Mellon University.

Tijsma, A. D., Drugan, M. M., and Wiering, M. A. (2016).

Comparing exploration strategies for Q-learning in

random stochastic mazes. In 2016 IEEE Symposium

on Adaptive Dynamic Programming and Reinforce-

ment Learning (ADPRL), pages 1–8.

Watkins, C. J. C. H. and Dayan, P. (1992). Technical note:

Q-learning. Machine Learning, 8(3):279.

Wiering, M. A. (1999). Explorations in efﬁcient reinforce-

ment learning. PhD thesis, University of Amsterdam.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

362