Actor-Critic Reinforcement Learning with Neural Networks in

Continuous Games

Gabriel Leuenberger and Marco A. Wiering

Institute of Artiﬁcial Intelligence and Cognitive Engineering, University of Groningen, The Netherlands

Keywords:

Reinforcement Learning, Continuous Actions, Multi-Layer Perceptrons, Computer Games, Actor-Critic

Methods.

Abstract:

Reinforcement learning agents with artiﬁcial neural networks have previously been shown to acquire human

level dexterity in discrete video game environments where only the current state of the game and a reward are

given at each time step. A harder problem than discrete environments is posed by continuous environments

where the states, observations, and actions are continuous, which is what this paper focuses on. The algorithm

called the Continuous Actor-Critic Learning Automaton (CACLA) is applied to a 2D aerial combat simulation

environment, which consists of continuous state and action spaces. The Actor and the Critic both employ

multilayer perceptrons. For our game environment it is shown: 1) The exploration of CACLA’s action space

strongly improves when Gaussian noise is replaced by an Ornstein-Uhlenbeck process. 2) A novel Monte

Carlo variant of CACLA is introduced which turns out to be inferior to the original CACLA. 3) From the latter

new insights are obtained that lead to a novel algorithm that is a modiﬁed version of CACLA. It relies on a

third multilayer perceptron to estimate the absolute error of the critic which is used to correct the learning rule

of the Actor. The Corrected CACLA is able to outperform the original CACLA algorithm.

1 INTRODUCTION

Succeeding in game environments that were origi-

nally designed to be played by humans without prior

knowledge of the game requires algorithms to be able

to autonomously learn to perceive and to act with high

dexterity, aimed at maximizing the total reward. Such

basic abilities are essential to the construction of an-

imal or human like artiﬁcial intelligence. Previous

work has demonstrated the applicability of artiﬁcial

neural networks to games (Tesauro, 1995; Bom et al.,

2013; Mnih et al., 2013). Instead of discrete actions

that are analogous to button presses we use contin-

uous actions that have to be used to move the con-

trol surfaces of an airplane within our 2D aerial com-

bat game environment that involves linear and angular

momentum.

The aim of this work is not to engineer algorithms

for realistic battles, but to research basic reinforce-

ment learning (RL) algorithms such as the Continu-

ous Actor Critic Learning Automaton (CACLA) (van

Hasselt and Wiering, 2007) that learn from scratch

in continuous state-action environments. For this the

aerial combat environment seems well suited since

it provides a larger diversity of challenges than for

instance the pole balancing task that was originally

used. For work that is specialized on fully realis-

tic aerial combat see the recently developed Genetic

Fuzzy based algorithms that seem to be invincible for

human experts (Ernest et al., 2016).

In section 2 we give a short background on

reinforcement learning and CACLA. We describe

the Ornstein-Uhlenbeck process that can be used to

strongly improve the exploration of possible action

sequences and a novel Monte Carlo version of CA-

CLA that memorizes the current episode is intro-

duced. We then introduce a novel version of CACLA,

Corrected CACLA, that corrects the learning rule of

its Actor based on a third MLP that estimates the ab-

solute TD-error. In section 3 we give a description of

our aerial combat environment and describe the ex-

perimental setup. Section 4 presents the results. The

conclusion is given in section 5.

2 REINFORCEMENT LEARNING

At every time-step t the agent receives a state or ob-

servation s

from its environment. It then outputs an

action a

that inﬂuences the next state of the environ-

Leuenberger, G. and Wiering, M.

Actor-Critic Reinforcement Learning with Neural Networks in Continuous Games.

DOI: 10.5220/0006556500530060

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 53-60

ISBN: 978-989-758-275-2

ment and obtains a reward r

t+1

. The agent starts as

a blank slate, not knowing its environment. It should

then learn to succeed in its environment by interact-

ing with it over many time steps. The quantity that

the agent has to aim at increasing is typically a dis-

counted sum over future rewards called the return R

that is deﬁned as follows:

:= r

t+1

+ γ R

t+1

T −t

∑

i=1

i−1

t+i

(1)

where γ ∈[0, 1] is the discount factor and T is the time

at which the current episode ends. For an extensive in-

troduction to reinforcement learning (RL), see (Sutton

and Barto, 1998; Wiering and Van Otterlo, 2012).

One could use unsupervised or semi-supervised

learning techniques in order to let the agent construct

an internal model of the environment, that could then

be used for planning. However this paper focuses

on simpler algorithms called model-free RL methods.

It is useful to ﬁrst optimize model-free RL methods

in order to show the capabilities that more advanced

methods should possess before having learned their

model as well as the least amount of dexterity that

they should be able to achieve.

In a Markov decision process (MDP) an observa-

tion can be interpreted as a state of the environment

where the probability distribution over the possible

next states depends solely on the current state and

action, not on the previous ones. This means that it

is sufﬁcient for the agent to choose an action solely

based on its current observation. The aerial combat

environment that is used in this paper is close to an

MDP, therefore we use algorithms that act solely on

their current observation or state.

A function that estimates the Return based on the

current state is called a Value function:

(s) := E[R

= s]

If the function additionally takes into account a pos-

sible next action, it is called a Q-function:

(s, a) := E[R

= s, a

= a]

Such estimates can be provided by function approx-

imators such as a multilayer perceptron (MLP) that

is trained through backpropagation (Rumelhart et al.,

1988) to approximate for instance the target r

t+1

γ V

t+1

), that is a closer approximation of the return.

If the Q-function is directly used to evaluate and select

the optimal next action, this is called an off-policy al-

gorithm, e.g., Q-learning (Watkins and Dayan, 1992;

Mnih et al., 2013).

A function that outputs an action based on the

current state is called a policy π(s) and can also be

implemented as an MLP. Such parametrized policies

can be used within on-policy algorithms, which facil-

itates the action selection in continuous action envi-

ronments among other advantages. The on-policy al-

gorithm used in this paper is an Actor-Critic method

(Barto, 1984) that uses both a value function imple-

mented as an MLP, called ’Critic’, as well as a policy

implemented as a second MLP, called ’Actor’. This

algorithm is explained in more detail in the following

section.

2.1 Continuous ACLA

The Continuous Actor Critic Learning Automaton

(CACLA) (van Hasselt and Wiering, 2007) is an

Actor-Critic method which is simpler and can be more

effective than the Continuous Actor Critic (Prokhorov

and Wunsch, 1997). Like other temporal difference

learning algorithms CACLA uses r

t+1

+ γ V

t+1

) in

every time step as a target to be approximated by the

Critic.

CACLA performs the action that the Actor out-

puts with the addition of random noise that enables

the exploration of deviating actions. In our environ-

ment the actions are elements of [0, 1]

. The temporal

difference error δ

is deﬁned as:

:= r

t+1

+ γ V

t+1

) −V

) (2)

In CACLA the Actor π

is trained during time step

t + 1 only if δ

> 0. Once the Critic reached a high

accuracy, a positive δ

indicates that the latest per-

formed action a

= π

) + g

led to a larger value

at time t + 1 than was expected at time t (where g

the noise sampled at time t). In a deterministic setting

this improvement could be due to the added noise that

randomly led to a superior action. Thus the Actor π

is trained using a

as its target to be approximated.

In the original CACLA paper the added noise was

white Gaussian noise with a standard deviation of

0.1. In this paper an improved type of noise will be

used, called the Ornstein-Uhlenbeck process, that is

explained in the following section.

2.2 Ornstein-Uhlenbeck Process

In a continuous environment such the one used here,

the action sequence produced by an optimal policy is

expected to be strongly serially correlated, meaning

that actions tend to be similar to their preceding ac-

tions. White Gaussian noise however consists of se-

rially uncorrelated samples of the same normal dis-

tribution. Adding such noise leads to an inefﬁcient

exploration of possible actions as the probability dis-

tribution over explored action sequences favours se-

rially uncorrelated sequences rather than more real-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

istic, serially correlated sequences. One way to in-

crease the efﬁciency of exploration is simply to add

reverberation to the noise, thus making it serially cor-

related. White Gaussian noise with reverberation is

equivalent to the Ornstein-Uhlenbeck process (Uhlen-

beck and Ornstein, 1930), which is the velocity of a

Brownian particle with momentum and drag. In dis-

crete time and without the need to incorporate physi-

cal quantities it can be written in its simplest form as

Gaussian noise with a decay factor κ ∈ [0, 1] for the

reverberation:

= κz

t−1

+ g

(3)

The Ornstein-Uhlenbeck process (OUP) has re-

cently been applied in RL algorithms other than CA-

CLA (Lillicrap et al., 2015). In section 4.1 of this

paper the performances resulting from the different

noise types are compared for CACLA.

2.3 Monte Carlo CACLA

A further possibility to improve CACLA’s perfor-

mance, unrelated to the described exploration noise,

is to let it record all of its observations, rewards, and

actions within an episode. At the end of an episode,

in our case lasting less than 1000 time steps, this

recorded data is used to compute the exact returns R

for each time step within the episode. The recorded

observations can then be used as the input objects in a

training set, where the Critic is trained with the target

and if R

−V

) > 0 then the Actor is trained as

well with the target a

. We call this novel algorithm

Monte Carlo (MC) CACLA, and it is based on Monte

Carlo (MC) learning as an alternative to temporal dif-

ference (TD) learning (Sutton and Barto, 1998).

As later shown in section 4.2 the performance

of MC-CACLA is worse than the performance of

the original CACLA. We theorize about the possible

cause and ﬁnd the same problem in the original CA-

CLA but to a lesser degree. The new insights led us

to a corrected version of CACLA that is described in

the following subsection.

2.4 Corrected CACLA

Consider a reward r

t+1

that is given as a spike in

time, i.e., the reward is an outlier compared to the re-

wards of its adjacent/ambient time steps. In CACLA

the Critic takes the current sensory input and outputs

) that is an approximation of r

t+1

+ γ V

t+1

). If

the Critic is unable to reach sufﬁcient precision to dis-

criminate this time step with the spike from its ambi-

ent time steps then its approximation will be blurred

in time. This imprecision can cause the TD-error δ

(equation 2) to be negative in all ambient time steps

within the range of the blur around a positive reward

spike, or vice versa; to be positive in all ambient time

steps within the range of the blur around a negative

reward spike as illustrated in Figure 1. In such a case

the positive TD-error is not indicative of the previous

actions having been better than expected. The orig-

inal CACLA does not make a distinction and learns

the previous actions regardlessly. These might be the

very actions that led to the negative reward spike by

crashing the airplane. This is a weakness of CACLA

that can be corrected to some extent by the following

algorithm.

Besides the Actor and the Critic our Corrected

CACLA uses a third MLP D

with the same inputs,

and the same number of hidden neurons. Its only out-

put neuron uses a linear activation function. Like the

Critic it is trained at every time-step, but its target to

be approximated is log(|δ

|+ε) with as input the state

vector s

. The output of this MLP can be interpreted

as a prediction and thus as an expected value:

(s) = E[log(|δ

|+ ε)|s

= s]

where ε is a small positive constant that is added to

avoid the computation of log(0). We have set the pa-

rameter ε to 10

−5

. With Jensen’s inequality (Jensen

and Valdemar, 1906) a lower bound for the value of

the absolute TD-error can be obtained:

E[|δ

||s

= s] ≥ exp(D

)) −ε

estimates the logarithm of |δ

| instead of |δ

| it-

self. This allows for an increased accuracy across a

wider range of orders of magnitude and also lowers

the impact of the spike on the training of D

. The

advantage was conﬁrmed by an increased ﬂight per-

formance during preliminary tests.

If D

learns to predict a high value of the TD-error

for an area of the state-space, this indicates that in

this area the absolute TD-error has been repeated on

a regular basis and is thus not due to an improved ac-

tion but due to an inaccuracy of the Critic. Hence we

modify CACLA’s learning rule in the following way.

In the original CACLA algorithm the Actor is trained

on the last action only if δ

> 0. In the Corrected CA-

CLA algorithm the same rule is used, except that this

condition is substituted by δ

> E[|δ

|], where the lat-

ter value is the output of the third MLP. Note that this

rule only improves the performance around negative

reward spikes, thus potentially improving the ﬂight

safety. The experiments that were conducted to assess

the performance of this novel algorithm are described

in the following section.

Actor-Critic Reinforcement Learning with Neural Networks in Continuous Games

Figure 1: Illustration of the TD-error due to the temporal

blur Critic. The TD-error is the difference between the

green and the red line. The blue line represents the func-

tion used in the Corrected CACLA to estimate the absolute

TD-error. The negative reward spike extends far beyond the

lower border of the image.

3 EXPERIMENTS

3.1 Aerial Combat Environment

In order to compare the different algorithms against

each other we use a competitive environment. We

only deal with the case where two agents compete

against each other with both of them controlling one

airplane each, thus there are no other airplanes besides

these two. The environment is sequential but divided

into episodes. An episode ends either after a player

was eliminated or a time limit of 800 time steps has

been reached. A player can be eliminated either by

crashing into the ground, by crashing into the oppo-

nent, or getting hit by ﬁve bullets. The starting coor-

dinates and attitude angles of the airplanes are chosen

at random, afterwards the game is deterministic until

the end of the episode.

The space is two-dimensional where the ﬁrst di-

mension represents the altitude and the second dimen-

sion is circular. The ground is horizontal and ﬂat with

gravity pulling towards it. The altitude has no upper

limitation, except for a drop in atmospheric pressure.

The airplanes have linear momentum as well as an-

gular momentum that have to be inﬂuenced through

aerodynamic forces acting on the wings and the con-

trol surfaces. If the incoming air hits the wing at an

angle larger than 15 degrees then the plane stalls, i.e.,

it loses lift. This creates the challenge of producing

a maximal lateral acceleration without overstepping

the stalling angle when ﬂying a curve. Neither the at-

titude angle nor the angular speed of the plane are di-

rectly controlled by the agent. The agent has to learn

to control these through the angle of the elevator and

the throttle which are both continuous. Additionally it

is required to adapt to the ﬂight dynamics that change

with the altitude, since lift and drag are scaled propor-

tionally to the atmospheric pressure that drops expo-

nentially in relation to the altitude. The third output

of the agent triggers the ﬁxed forward facing gun that

can only give off four consecutive shots before over-

heating and having to cool down.

The parameters of the ﬂight physics are chosen

such that looping is possible at high speeds, spin-

ning is possible at low speeds, and hovering is pos-

sible at low altitudes only. The ratio of the size of

the airplanes to the circumference of the circular di-

mension and the drop in pressure are chosen such that

the entire game can be viewed comfortably within

a 1000×1000 pixel window. A sequence of clipped

screenshots is shown in Figure 2.

In order to save computational power we do not

use the pixels as the sensory input for the agents. For

agents that learn directly from pixels see (Koutn

ık

et al., 2013; Mnih et al., 2013). The sensory input

we used, consists of information that would typically

be available to a pilot either through their ﬂight in-

struments or by direct observation. We list all of

the inputs of one agent here. the directions are two-

dimensional unit vectors and are calculated from the

perspective of one airplane. The scalars are scaled

such that their maxima are of the zeroth order of mag-

nitude. The ﬁnal used inputs are:

• Direction to the horizon and its angular speed

• Altitude and the rate of climb

• Absolute air speed and the acceleration vector

• Distance to the opponent and its rate of change

• Inverse distance to the opponent (apparent size)

• Direction to the opponent and its angular speed

• The orientation of the opponent

• The temperature of the guns

All of the vector components together with the

scalars yield a total of 17 continuous inputs. These

sensory inputs make the states of the environment

fully observable with the exception of the bullets that

are invisible to the agents. The environment is thus a

partially observable MDP but remains close to a fully

observable MDP.

During every time step a reward is given that is

proportional to the altitude of the plane and reaches

0.1 at an altitude of 1000 pixels. This reward speeds

up the process of learning to ﬂy during the initial

stages of training. A reward spike of -25 is given for

being eliminated and reward spikes of +5 are given

when a bullet hits the opponent.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Figure 2: A sequence with two agents on a collision course

while attempting to ﬁre bullets at each other. They avoid the

collision in the last moment.

The goal of designing this environment was not

to construct a fully realistic simulator. For a more

complex and fully realistic aerial combat simulation

environment see AFSIM (Zeh and Birkmire, 2014) as

used in (Ernest et al., 2016).

3.2 Experimental Setup

To tune the hyperparameters we performed prelimi-

nary experiments. In all of the following experiments

each MLP consists of 17 input neurons and 100 hid-

den neurons with sigmoid activation functions. The

output layer of the Critic consists of one neuron with a

linear activation function. The output layer of the Ac-

tor consists of three neurons with sigmoid activation

functions. All of the MLPs are trained with a learning

rate of 0.001. The discount factor γ is always set to

0.99. All of the experiments are divided into epochs

of which each one consists of 300 episodes of which

the last 80 episodes are used for measurements. Dur-

ing these measurements the noise is deactivated and

the total reward is averaged over the 80 episodes to

produce one data point.

As explained in section 2.2 we run CACLA with

the Gaussian noise g

for exploration and compare it

to a second CACLA where g

is replaced by the OUP

. We compare the two algorithms by letting them

compete against each other. g

does not have the same

standard deviation as z

. In order to show that the dif-

ference in performance is not primarily caused by the

differing standard deviations we run a second experi-

ment where g

is replaced by g

that is scaled with the

factor

−2

√

1 −κ

which gives it the same standard de-

viation as z

. The following two equations summarize

the relations between the three applied noise signals:

:= κz

t−1

+ g

, g

:= g

−2

1 −κ

(4)

The reverberation decay factor κ is set to 0.9 because

it seemed to perform best in our environment.

The experiments to compare the noise types are

run for 40 epochs each. During this time the standard

deviation of g

is decreased exponentially from 0.2

to 0.02. The experiment is repeated ten times with

different random initializations of the MLP weights,

amounting to a total of 120,000 episodes. This entire

experiment is conducted once to compare z

to g

and

a second time to compare z

to g

. The results of these

comparisons are reported in section 4.1.

Since the OUP strongly increases the perfor-

mance, all of the algorithms used in all of the follow-

ing experiments employ the OUP with κ = 0.9.

Monte Carlo CACLA (MC-CACLA), as de-

scribed in section 2.3, is obtained by substituting CA-

CLA’s return-approximation r

t+1

+γ V

t+1

) with the

true return R

. The training is then conducted at the

end of each episode using the recorded observations

and rewards. The competitions between CACLA and

MC-CACLA are also 40 epochs long with the noise

dropping from a standard deviation of 0.2 down to

0.02. It is also repeated for ten different random ini-

tializations of the MLPs. A second experiment is con-

ducted with settings that require more training time

but allow for a higher ﬁnal performance. Each exper-

iment lasts 80 epochs while the standard deviation of

the noise is decreased from 0.5 to 0.01. The experi-

ment is repeated for ﬁve different random initializa-

tions. The results of these experiments are reported in

section 4.2.

The Corrected CACLA, as described in section

2.4, is also tested by letting it compete against the

original CACLA. Each experiment lasts 80 epochs

while the standard deviation of the noise is decreased

from 0.5 to 0.01. The experiment is repeated for ten

different random initializations. The results of these

experiments are reported in section 4.3.

4 RESULTS

The results of the experiments are presented as graphs

in the next subsections. Each ﬁgure represents a com-

petition between two algorithms which inﬂuence each

other’s performance. If for instance the ﬁrst algorithm

always crashes its airplane soon, then the episodes

will on average last for a shorter amount of time

which will cause the second algorithm to have a lower

score as well. The scores of different ﬁgures should

thus not be directly compared to each other while the

scores of the different algorithms within the same ﬁg-

ure should be compared.

4.1 Ornstein-Uhlenbeck Process

In Figure 3 it can be seen that CACLA with OUP-

based exploration signiﬁcantly outperforms CACLA

that uses the original Gaussian exploration. For this

Gaussian exploration the signal g

from equation 3.1

Actor-Critic Reinforcement Learning with Neural Networks in Continuous Games

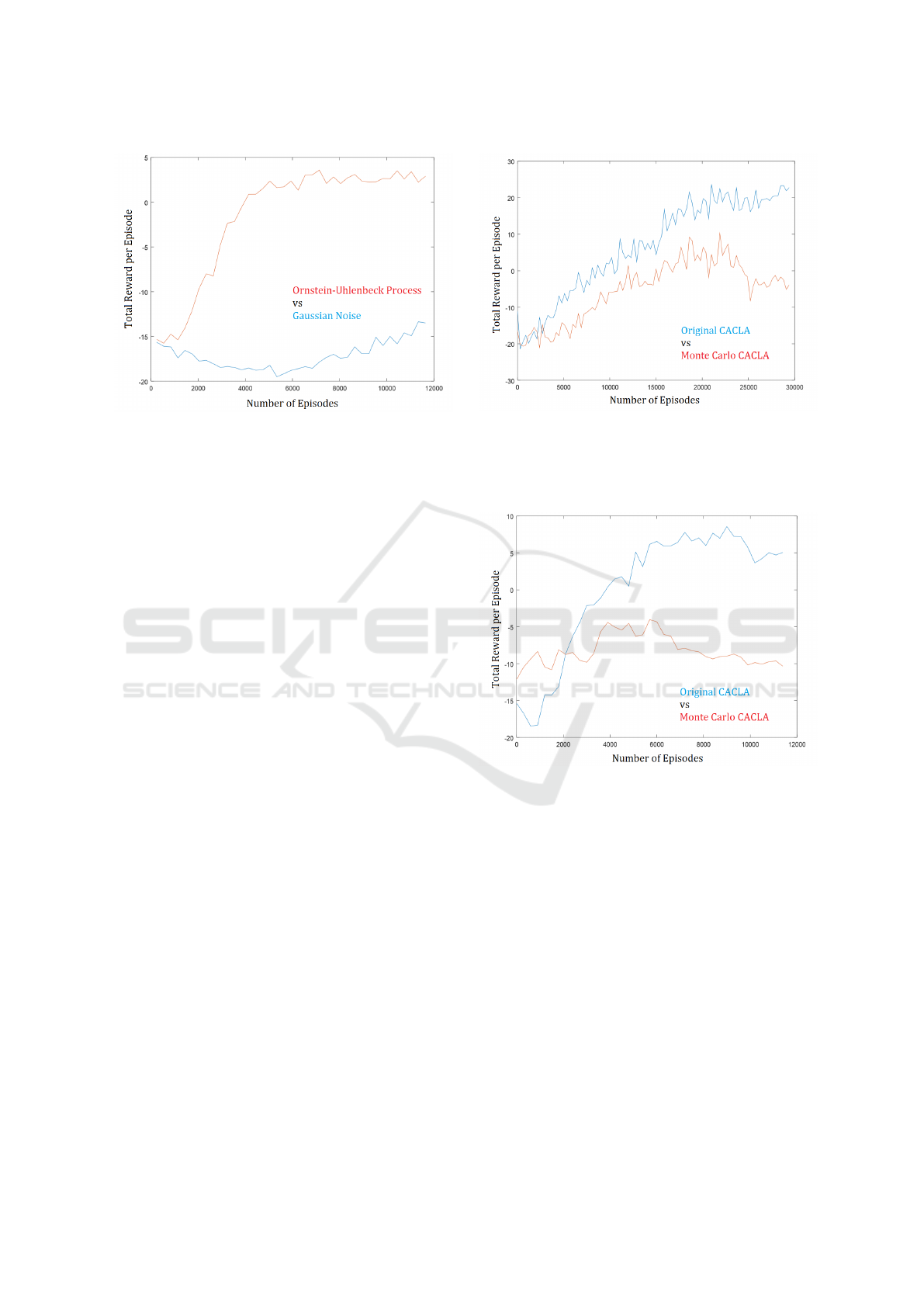
Figure 3: Results of the competition between CACLA with

Gaussian exploration (g

) and CACLA with OUP-based ex-

ploration (z

). The graphs are averaged over ten different

random initializations. The standard deviation of the noise

was gradually decreased from 0.2 to 0.02.

was used. The signal g

is scaled such that it has the

same standard deviation as the signal z

. An identical

experiment was conducted where the raw g

was used

instead of g

. The result of this experiment is very

similar and thus not reported in this paper.

It can be seen that the total reward of CACLA with

Gaussian exploration decreases initially. This could

be due to more frequent eliminations through the im-

proving marksmanship of CACLA with OUP-based

exploration. By letting experiments run for a longer

time it can be observed that CACLA with Gaussian

exploration is able to converge to a similar ﬁnal per-

formance as CACLA with OUP-based exploration.

However, CACLA with Gaussian exploration would

take an order of magnitude more time to do so.

Due to the strong result, all of the algorithms in

the following sections were designed with the OUP-

based exploration.

4.2 Monte Carlo CACLA

In Figure 4 and Figure 5, it can be seen that the

original CACLA strongly outperforms MC-CACLA

with the exception of the ﬁrst 2000 episodes. Since

the MC-CACLA uses more memory and uses the ac-

curate Return R

, one would intuitively expect MC-

CACLA to be superior. One reason of its worse

performance is that Monte Carlo learning techniques

have a larger variance in their updates than TD-

learning algorithms. Another reason could be the

spiking rewards that produce a Return that locally re-

sembles a step-function over time. The Critic, ap-

proximating this stepping Return, might not be sufﬁ-

ciently precise to discriminate between the surround-

Figure 4: Results of the competition between the Monte

Carlo version of CACLA and the original CACLA. The

graphs are averaged over ﬁve different random initializa-

tions. The standard deviation of the noise g

was gradually

decreased from 0.5 to 0.01.

Figure 5: Results of the competition between the Monte

Carlo version of CACLA and the original CACLA. The

graphs are averaged over ten different random initializa-

tions. The standard deviation of the noise g

was gradually

decreased from 0.2 to 0.02.

ing time steps before and after the reward spike. This

would lead to positive or negative differences between

the Value and the Return. This would then disturb

the Actor’s learning rule that relies on the difference

−V

). This problem of the algorithm was then

looked for in the original CACLA as well. The prob-

lem was found to be theoretically possible in the orig-

inal CACLA (described in section 2.4), but in a more

benign way, the deviation of the Critic around a spike

would be smaller in the original CACLA. In section

2.4 a possible solution to this problem was described.

The following section presents the results of this so-

lution.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Figure 6: Results of the competition between the Corrected

CACLA and the original CACLA algorithm. The graphs

are averaged over ten different random initializations. The

standard deviation of the noise g

was gradually decreased

from 0.5 to 0.01.

4.3 Corrected CACLA

In Figure 6, it can be seen that the Corrected CA-

CLA on average outperforms the original CACLA.

The averages of the total rewards from the ﬁrst un-

til the last episode were compared. The Corrected

CACLA algorithm performed better for ten out of ten

random initializations which resulted in a p-value of

−10

. The strongest difference in performance is be-

tween the 5000th and the 10,000th episode. Towards

the end of the graph the two algorithms converge to-

wards the same strategy and the same performance.

The Corrected CACLA algorithm is constructed such

that it has an advantage when there are negative re-

ward spikes as explained in section 2.4. This advan-

tage is conﬁrmed by these results. Later, once the

agents learned to increase their ﬂight safety such that

there are less negative reward spikes, the Corrected

CACLA loses its advantage. This advantage might

prevail in a different environment where the negative

reward spikes do not disappear over time.

5 CONCLUSIONS

All of the algorithms were tested by competing in our

aerial combat environment. Our results show that sub-

stituting the original Gaussian noise in CACLA with

the OUP leads to a strongly improved exploration of

actions and better performance of the algorithm. This

improvement is to be expected in environments where

the optimal action sequences are temporally corre-

lated, which is typical for continuous environments.

The results also showed that MC-CACLA performs

worse than the original CACLA algorithm. More

work on a Monte Carlo version of CACLA would

need to be done. One possible cause of the poor per-

formance is that the temporal inaccuracy of the Critic

disturbs the learning rule of the Actor. The same prob-

lem was found in the original CACLA but to a much

lesser degree. This problem appears when spiking re-

wards are given. We solved this problem in CACLA

by adding a third MLP that is used to predict the log-

arithm of the absolute error of the Critic. The learn-

ing rule of the Actor was then adapted such that it is

trained only when the TD-error is larger than the es-

timated absolute error of the Critic. This algorithm

was described in detail in section 2.4. The results

show that this approach can indeed improve the per-

formance over the original CACLA algorithm. This

result is remarkable because the Actor in the Cor-

rected CACLA is trained less often than in the original

CACLA. However our Corrected CACLA likely only

has an advantage in environments where negative re-

ward spikes occur.

In future research a similar algorithm could be

developed that also improves CACLA’s performance

when there are mostly positive reward spikes. Fur-

thermore, extending these algorithms by a learnable

model that is used to plan ahead at multiple temporal

resolutions could strongly improve the ﬁnal perfor-

mance of agents in this aerial combat environment.

This is left as future research.

REFERENCES

Barto, A. (1984). Neuron-like adaptive elements that can

solve difﬁcult learning control-problems. Behavioural

Processes, 9(1).

Bom, L., Henken, R., and Wiering, M. (2013). Rein-

forcement learning to train Ms. Pac-Man using higher-

order action-relative inputs. In Proceedings of IEEE

International Symposium on Adaptive Dynamic Pro-

gramming and Reinforcement Learning : ADPRL.

Ernest, N., Carroll, D., Schumacher, C., Clark, M., Cohen,

K., and Lee, G. (2016). Genetic fuzzy based artiﬁcial

intelligence for unmanned combat aerial vehicle con-

trol in simulated air combat missions. J Def Manag,

6(144):2167–0374.

Jensen, J. and Valdemar, L. (1906). Sur les fonctions con-

vexes et les in

egalit

es entre les valeurs moyennes.

Acta mathematica, 30(1):175–193.

Koutn

ık, J., Cuccu, G., Schmidhuber, J., and Gomez, F.

(2013). Evolving large-scale neural networks for

vision-based reinforcement learning. In Proceedings

of the 15th annual conference on Genetic and evolu-

tionary computation, pages 1061–1068. ACM.

Lillicrap, T., Hunt, J., Pritzel, A., Heess, N., Erez, T., Tassa,

Y., Silver, D., and Wierstra, D. (2015). Continu-

Actor-Critic Reinforcement Learning with Neural Networks in Continuous Games

ous control with deep reinforcement learning. arXiv

preprint arXiv:1509.02971.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312.5602.

Prokhorov, D. and Wunsch, D. (1997). Adaptive critic

designs. IEEE transactions on Neural Networks,

8(5):997–1007.

Rumelhart, D., Hinton, G., and Williams, R. (1988). Learn-

ing representations by back-propagating errors. Cog-

nitive modeling, 5(3):1.

Sutton, R. and Barto, A. (1998). Reinforcement learning:

An introduction, volume 1. MIT press Cambridge.

Tesauro, G. (1995). Temporal difference learning and TD-

gammon. Communications of the ACM, 38(3):58–68.

Uhlenbeck, G. and Ornstein, L. (1930). On the theory of

the brownian motion. Physical review, 36(5):823.

van Hasselt, H. and Wiering, M. (2007). Reinforcement

learning in continuous action spaces. In Approximate

Dynamic Programming and Reinforcement Learning,

2007. ADPRL 2007. IEEE International Symposium

on, pages 272–279.

Watkins, C. and Dayan, P. (1992). Q-learning. Machine

learning, 8(3):279–292.

Wiering, M. and Van Otterlo, M. (2012). Reinforcement

Learning State-of-the-Art, volume 12. Springer.

Zeh, J. and Birkmire, B. (2014). Advanced framework for

simulation, integration and modeling (AFSIM) ver-

sion 1.8 overview. Wright Patterson Air Force Base,

OH: Air Force Research Laboratory, Aerospace Sys-

tems.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence