
Occlusion-robust Detector Trained with Occluded Pedestrians
Zhixin Guo, Wenzhi Liao, Peter Veelaert and Wilfried Philips
Ghent University-IMEC, Sint-Pietersnieuwstraat 41, Gent 9000, Belgium
Keywords:
Pedestrian Detection, Occlusion Handling, Adaboost, Integral Channel Features.
Abstract:
Pedestrian detection has achieved a remarkable progress in recent years, but challenges remain especially when
occlusion happens. Intuitively, occluded pedestrian samples contain some characteristic occlusion appearance
features that can help to improve detection. However, we have observed that most existing approaches inten-
tionally avoid using samples of occluded pedestrians during the training stage. This is because such samples
will introduce unreliable information, which affects the learning of model parameters and thus results in dra-
matic performance decline. In this paper, we propose a new framework for pedestrian detection. The proposed
method exploits the use of occluded pedestrian samples to learn more robust features for discriminating pedes-
trians, and enables better performances on pedestrian detection, especially for the occluded pedestrians (which
always happens in many real applications). Compared to some recent detectors on Caltech Pedestrian dataset,
with our proposed method, detection miss rate for occluded pedestrians are significantly reduced.
1 INTRODUCTION
Pedestrian detection is a key problem in computer vi-
sion and has numerous applications including video
surveillance, self-driving vehicles and robotics. Many
tasks such as pedestrian tracking and semantic under-
standing rely heavily on the performance of pedes-
trian detectors. Although it has been intensively stud-
ied during the past several decades, occlusion remains
challenging.
Because of the significant success of the
deformable part-based models (DPM) approach
(Felzenszwalb et al., 2010), many researchers work
on this model to overcome the occlusion issues.
Instead of conventionally treating pedestrians as a
whole object (Dalal and Triggs, 2005), DPM models
separate a pedestrian into different body parts. The
occluded parts can then be handled properly and the
influence of changed appearance caused by occlusion
is eliminated. But this requires an accurate estimation
of the visibility of different body parts (Wang et al.,
2009; Ouyang et al., 2016), which makes the training
of DPM models delicate and complex. Besides, the
high computation cost of training a set of detectors
from different body parts and fusion of their detection
scores further increase the difficulties of this kind of
methods.
Through observation of the Caltech Pedestrian
dataset (Dollar et al., 2012), Dollar et al. indicate that
most occluded pedestrians have a limited number of
occlusion types (7 types account for 97% of all occlu-
sions in the dataset). Inspired by this discovery, some
researchers train a set of occlusion-specific models to
improve the detection of occluded pedestrians (Math-
ias et al., 2013). However, this method suffers from
similar problems as the DPM based methods. Train-
ing distinct detectors for different occlusion patterns
is not only costly, but also difficultbecause of the need
for a sufficient number of specific occluded pedestrian
samples. In addition, a proper method to merge the re-
sults of distinct detectors is also needed, because the
occlusion pattern is unknown during detection.
In summary, most current approaches do not use
occluded pedestrians during the training stage, be-
cause detectors cannot distinguish a real pedestrian
from the occluding object, which results in learn-
ing wrong parameters and causes a significant per-
formance drop. Some methods (Wojek et al., 2011;
Mathias et al., 2013) introduce occluded pedestrians
into the training procedure, but these samples are clas-
sified into different occlusion patterns and only the
visible regions are actually used when training the
occlusion-specific detectors.
Inspired by the idea that some valuable appear-
ance characteristics in occluded pedestrian samples
could be used to enhance the detector’s occlusion-
handling performance, we propose a new framework
that makes full advantage of the occlusion informa-
tion for training. The main contributions of this pa-
per are as follows. 1) We exploit occluded pedestrian
86
Guo, Z., Liao, W., Veelaert, P. and Philips, W.
Occlusion-robust Detector Trained with Occluded Pedestrians.
DOI: 10.5220/0006569200860094
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 86-94
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

samples into the training stage to further improve the
detection performances. 2) We propose a new fea-
ture selection strategy based on the occlusion distri-
bution of the training samples. Experimental results
on the Caltech Pedestrian dataset demonstrate that the
detection performance of our approach significantly
exceeds the performance of some existing methods.
The rest of the paper is organized as follows. Af-
ter reviewing the related work in Section 2, we in-
troduce the baseline ACF detector and our proposed
method in Section 3 and Section 4 respectively. Sec-
tion 5 shows the experimental results. The conclusion
is drawn in Section 6.
2 RELATED WORK
Over the past decades a great effort has been made
to improve the pedestrian detection performance. In
this section, we first discuss the development of the
boosted detection framework on which we base our
work, and then review the state-of-the-art occlusion-
handling methods.
In 2004, Viola and Jones (Viola and Jones, 2004)
pioneered a detection architecture that computed fea-
tures very efficiently with integral images. Adaboost
(Friedman et al., 2000) was used to train a cascade of
decision trees, and a sliding window strategy was em-
ployed to search each potential region of the image.
This successful structure was then combined with
some more powerful features. Dalal and Triggs (Dalal
and Triggs, 2005) proposed the histogram of oriented
gradient (HOG) feature which since then has been
widely used. Some researchers combined HOG with
additional features (Walk et al., 2010; Wang et al.,
2009), while the integral channel features (ICF) pro-
posed by Dollar et al. (Doll´ar et al., 2009) showed ex-
cellent discriminative power. In the ICF detector, the
VJ boosted structure (Viola and Jones, 2004) is used
to select appropriate ICF features and train powerful
classifiers. Inspired by the ICF architecture, a vari-
ety of improvements have been made to achieve bet-
ter performance as well as efficiency. FPDW (Doll´ar
et al., 2010) detector is proposed to accelerate the
detection by estimating some features across differ-
ent image scales, instead of computing them explic-
itly. Benenson et al. (Benenson et al., 2012) move
this estimation from the detection to the training stage
and further improve efficiency. To strengthen the rep-
resentation ability of features, SquaresChnFtrs (Be-
nenson et al., 2013) uses all sizes of square fea-
ture pools instead of random rectangular pools and
get better performance. More recently, Dollar et al.
(Doll´ar et al., 2014) proposes the ACF detector, which
far outperforms contemporary detectors. Based on
ACF, LDCF (Nam et al., 2014) demonstrates that
decorrelation of local feature information is helpful.
Some recent work continues to improve the detec-
tion performance by generalizing more powerful fea-
tures (Zhang et al., 2015), exploring the model capac-
ity (Ohn-Bar and Trivedi, 2016) or combining detec-
tors with deep Convolutional Neural Network (CNN)
models (Angelova et al., 2015).
For occlusion-handling, it is natural to first es-
timate the visibility of pedestrian body parts, and
then handle the visible and occluded parts separately.
Wang et al. (Wang et al., 2009) propose to use the
response of HOG features of the global detector to
estimate the occlusion likelihood map. The final de-
cision is made by applying the pre-trained part detec-
tors on the fully visible regions. To further explore
the visibility correlations of body parts, Ouyang et
al. (Ouyang et al., 2016) employ a deep network,
which supplements the DPM detection results. In
(Enzweiler et al., 2010), Enzweiler et al. obtain the
degree of visibility by examining occlusion discon-
tinuities extracted from additional depth and motion
information.
Since it is rather hard to ensure the accuracy of
visibility estimation, some researchers turn to the
training of a set of distinct detectors for different oc-
clusion patterns. In (Wojek et al., 2011), a full-body
DPM detector and six part-based detectors, at low and
high resolution, are trained and combined to make the
final decision. While in (Mathias et al., 2013), Math-
ias et al. train a more exhaustive set of ICF detectors
(16 different occlusion patterns). By biased feature
selection and reusing trained detectors, the training
cost can be 10 times lower compared to conventional
brute-force training. Besides single-person models,
some multi-person occlusion patterns are investigated
to handle occlusion in crowded street scenes. Tang et
al. (Tang et al., 2014) make use of the characteristic
appearance pattern of person-person occlusion, and
train a double-person detector for occluded pedestrian
pairs in the crowd. A similar model is proposed in
(Ouyang and Wang, 2013b) where the authors use
a probabilistic framework instead of Non-maximum
Suppression (NMS) to deal with strong overlaps.
Enlightened by the ideas in (Tang et al., 2014)
and (Ouyang and Wang, 2013b) that occlusion can
be used as valuable information rather than as a dis-
traction, we propose a new framework for pedestrian
detection. This method explicitly makes use of the
occluded pedestrian samples, which may contain use-
ful occlusion appearance information, but are mostly
discarded by existing methods.
Occlusion-robust Detector Trained with Occluded Pedestrians
87

3 BASELINE DETECTOR AND
DATASET
3.1 Aggregate Channel Feature (ACF)
Detector
ACF (Doll´ar et al., 2014) employs a boosting struc-
ture that greedily minimizes a loss function for the
final decision rule
F(x) =
∑
t
α
t
f
t
(x), (1)
where the strong classifier F(x) is a weighted sum
of t weak classifiers f
t
(x). α
t
denotes the weight of
each weak classifier, and x ∈ R
K
is the feature vec-
tor. In ACF, the channel features (Doll´ar et al., 2009)
are used, including 6 histogram of oriented gradient
channels, 1 gradient magnitude channel and 3 LUV
colour channels. A given image is transformed into
10 channels of per-pixel feature maps. Given an input
feature x ∈ R
K
, a decision tree acts as a weak classifier
and outputs the confidence score f
t
(x).
A weak decision tree is built during each iteration
of the training procedure. At each non-leaf node of
the tree, a binary decision stump will be learned. The
main task of training a decision stump is selecting
one feature from a set of candidate features (pixels)
and exhaustively searching its optimal threshold val-
ues. The feature (with its corresponding threshold)
which leads to the smallest classification error will be
selected. The classification error at one stump is a
weighted summation of the misclassified samples:
ε =
∑
ω
i
1
{ f (x
i
)6=y
i
}
, (2)
where 1
{...}
is the indicator operator. f(x
i
) and y
i
indi-
cate the classification result and true class of the input
feature x
i
respectively. ω
i
is the weight of each train-
ing sample. Given a feature index k ∈ {1,2,..., K},
the classification error of a given feature is:
ε
(k)
=
∑
x
i
[k]≤τ
ω
i
1
{y
i
=+p}
+
∑
x
i
[k]>τ
ω
i
1
{y
i
=−p}
, (3)
where x
i
[k] indicates the kth feature of the sample x
i
.
ε
(k)
indicates the classification error when selecting
the kth feature and threshold τ. p is a polarity element
{±1}. By greedily learning all the stumps, a decision
tree is built. The default ACF detector is composed of
4096 such trees with a maximum depth of 5.
The above training structure has been proved to
be very effective for non-occluded pedestrians. How-
ever, during the selection of optimal features, only the
classification error is taken into consideration. This
sole judgement standard makes the selection suscep-
tible to noisy image patches, and in particular, to the
Figure 1: Caltech Pedestrian Dataset.
occlusion of pedestrian samples. In the following sec-
tion we will propose a more robust feature selection
strategy that better exploits the occluded pedestrian
samples.
3.2 Caltech Pedestrian Dataset
In our experiments, we use the Caltech Pedestrian
dataset (Dollar et al., 2012), which is currently one of
the most popular pedestrian detection benchmarks. It
consists of 250k labeled frames with 350k annotated
bounding boxes. In particular, each partially occluded
pedestrian is annotated with two bounding boxes (see
Fig. 1), which indicate the full body (in green) and
the visible part (in yellow) respectively. This visible
region information will be used for the training with
occluded pedestrians in Section 4.3.
4 PROPOSED METHOD
This section details our proposed method on how
to introduce the occluded pedestrian samples into
the training stage and improve the detection perfor-
mances of the occluded pedestrians. Specifically, we
first assume that all the training samples have the
same known occlusion region (Fig. 2(a)) in Section
4.1, then we extend this assumption to a more real-
istic situation and propose a biased feature selection
strategy in Section 4.2. Last but not least, we apply
the proposed feature selection strategy to the real sit-
uation and propose a new training structure for the
occluded pedestrians in Section 4.3.
In ACF detector, the final decision is made by a
combination of weak classifier results. Each weak
classifier will read several pixels from the feature map
(Fig. 2(b)). The keyinsight of this paper is that we can
improve the detection by controlling the feature selec-
tion procedure during the training of decision trees.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
88

(a) (b)
Figure 2: Pedestrian samples are manually occluded in the
top-left corner with non-person image patches randomly cut
from negative samples. Some features in the occlusion re-
gion (marked as red) are selected by weak classifiers but
they are not reliable.
To simplify this problem, a default setting of the
ACF detector is applied to demonstrate the validity of
our proposed method, while a more exhaustive explo-
ration of the detector and the best performance can be
found in Section 5.
4.1 Simple Situation: Known
Occlusions
We start with the very simple case, where we assume
that all samples have the same occlusion region in the
top-left corner (the occlusion region occupies 1/4 of
the image area, see Fig. 2(a)). This is the easiest case
to handle because we are certain that features that are
located in the occluded region do not represent char-
acteristics of pedestrians. Thus if the features selected
by weak classifiers are in the top-left corner of the fea-
ture map (red pixels in Fig. 2(b)), they must be unre-
liable. What we need to do is to just restrict the loca-
tions of features, forbidding the selection of features
in the occlusion region.
We simulate this simple case by covering all
the training samples (including positive and negative
samples) with non-pedestrian image patches in the
top-left corner. These image patches are randomly
cut from the negativesamples. In Fig. 3(a) we can see
the feature distribution of the model trained by our
manually occluded samples. As expected, although
the detector selects most of the features from the non-
occluded region, a few features from the top-left cor-
ner are also used. Therefore, we also train a new
model in which we forbid the selection of features
in the top-left corner. In Fig. 4, simple and *simple
indicate the performance of the original ACF model
and the new ACF model without using the features of
occluded regions, while *simple outperforms simple
both in the reasonable and the partial occlusion cases.
Therefore, we can improve the detection by avoid-
ing the selection of unreliable features during the
training stage. We may presume the features in the
top-left corner to be unreliable because all samples
have the same occlusion in that area. However, for
more complex situations, it will be more difficult to
judge the reliability of a feature.
4.2 Complex Situation: Training with
Sample Mixtures
Now we assume a more complex and realistic situ-
ation that only 20% of the samples are occluded in
the top-left corner. The features in the occluded re-
gion can no longer be discarded directly because they
undergo a little influence from the occlusion but still
represent some pedestrian characteristics. Therefore,
instead of judging a feature only by the classification
error (as explained in Section 3.1), we need an ad-
ditional selection criterion that takes into account the
occlusion probability of a feature during the training
stage. In short, if two features from the input feature
map have very similar classification errors, we prefer
the one that has lower occlusion probability. There-
fore, we propose a new method to select features, of
which a new cost function ε
′
(k)
(feature k is selected)
can be defined:
ε
′
(k)
= ε
(k)
(1+ γ
(k)
) (4)
γ
(k)
= θ∗ (N
occ
(k)
/N
pos
(k)
) (5)
where ε
(k)
indicates the classification error defined in
Eq. (3), γ
(k)
represents the occlusion cost coefficient
of feature k, which increases its classification error ac-
cording to its occlusion probability N
occ
(k)
/N
pos
(k)
. N
pos
(k)
indicates the number of positive samples in the cur-
rent node, while N
occ
(k)
indicates the number of samples
that have an occlusion in the location of feature k. θ
acts as a constant weight to control the impact of the
occlusion cost. To ensure that the classification error
is always the prior consideration, we set the θ value
much smaller than 1 (In this paper we have made mul-
tiple experiments and finally set 1/25 as the θ value.
A bigger θ will overweight the occlusion probabil-
ity and sacrifice some very discriminative features)
so that a feature with low occlusion probability will
be preferred to a feature that is barely better but has
much higher occlusion probability. Hence a feature is
selected according to the new classification cost:
k = argmin ε
′
(k)
(6)
In this part N
occ
(k)
/N
pos
(k)
equals 0.2 and 0 for fea-
tures in the occlusion and non-occlusion regions, re-
spectively. Fig. 3(b) shows a biased feature selection
Occlusion-robust Detector Trained with Occluded Pedestrians
89

(a) Simple situation: avoid se-
lecting features in the occlusion
region
(b) Complex situation: features
in the occlusion region are as-
signed bigger classification cost
which lower the probability of
being selected
(c) Real situation: the combi-
nation of the new classification
cost with occlusion distribution
map makes the feature selection
more biased on low probability
occlusion regions
Figure 3: Distribution of the feature selection rate in trained models. Features in the brighter area are more likely to be
selected.
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
50.88% Simple
41.75% *Simple
31.17% Complex
29.96% *Complex
29.05% ACF
31.21% ACF+occ
29.32% *ACF+occ
(a) Reasonable
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
68.31% Simple
59.13% *Simple
52.85% Complex
46.61% *Complex
46.53% ACF
45.64% ACF+occ
43.42% *ACF+occ
(b) Partial occlusion
Figure 4: Performance of models trained in different situations. (a) Reasonable: less than 35% occluded pedestrians (including
full-visible ones) (b) Partial occlusion: less than 35% occluded pedestrians (excluding full-visible ones).
of the modified model that fewer features in the top-
left corner are selected. In Fig. 4, we use complex and
*complex to indicate the performances of the original
model (trained with original feature selection strategy
of Eq. (3)) and the modified model (trained with the
proposed feature selection strategy of Eq. (4) and (5)),
respectively. The modified model *complex shows
an improvement from 31.17% to 29.96% (lower log-
average miss rate indicates better performance) in
the reasonable case (Fig. 4(a)) and an improvement
from 52.85% to 46.61% in the partial occlusion case
(Fig. 4(b)). In addition, we can find that the mod-
ified model *complex has achieved comparable per-
formance to that of the default ACF model trained
with non-occlusion pedestrian samples (29.05% and
46.53%).
So far we have only focused on the manually spec-
ified occluded samples whose occlusion regions are
fixed. For real pedestrian samples, we need to han-
dle the occlusion which may occur in any part of a
person.
4.3 Real Situation
Now we propose a new method to take advantage of
the real occluded pedestrian samples during the train-
ing stage. This method is based on the new feature
selection strategy proposed in Section 4.2, where the
occlusion probabilityof a feature is taken into account
by introducing a modified cost function (Eq. (4) and
(5)). Unlike the manually occluded samples used in
Section 4.1 and 4.2, the occlusion regions of real sam-
ples are unfixed. Therefore, the occlusion probability
of feature k N
occ
(k)
/N
pos
(k)
in Eq. (5) is no longer a con-
stant. We will estimate it by calculating the occlusion
distribution map of the training samples.
We create a binary 16×32 pixel occlusion mask
map for each occluded pedestrian sample marked
with visible bounding boxes. By averaging all the
marked samples, we obtain an occlusion distribution
map in Fig. 5(a). From the map we notice that the oc-
clusion distribution is not uniform. The lower part of
a pedestrian is more likely to be occluded while the
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
90

(a) Occlusion distribution map. Brighter
region indicates higher occlusion proba-
bility
Ftr X1
Ftr X2 Ftr X3
+1 -1 +1 -1
Ftr X1
Ftr X3
Ftr X2
Ftr X1
Ftr X3'
Ftr X2'
(b) feature X2 and X3 selected by orignial training procedure are replaced
by X2’ and X3’ according to the occlusion probability distribution in each
decision node
Figure 5: Proposed method.
head region suffers the least from occlusion. This re-
sult conforms with our common sense that the head
region is often the most visible part, because most ob-
stacles are located on the ground.
Fig. 5(b) shows how our proposed method impacts
the selection of features. Under the original feature
selection strategy (Eq. (3)), feature X1, X2 and X3
are selected by the weak classifier. Then we calculate
the occlusion distribution map of each splitting node
and employ Eq. (4)-(6) to select more robust features.
For example, feature X2 is replaced by a more reli-
able feature X2’ which is less likely to be occluded
according to the occlusion distribution map. In Fig.
3(c), we see that with the proposed method, the new
model is more biased to select the features from the
region with low occlusion probability (for example,
the head region).
Fig. 4 clearly shows how our proposed method
improves the detection of occluded pedestrians. We
first introduce occluded pedestrian samples and train
the ACF+occ model, which shows an improvement of
the average miss-rate from 46.53% to 45.64% for the
partial occlusion cases (Fig. 4(b)). This demonstrates
that the introduction of occluded samples in the train-
ing process improves the detection of occluded pedes-
trians. Unsurprisingly, there is also a reduction of
performance in the reasonable case (Fig. 4(a)). How-
ever, when we use our method to train the *ACF+occ
model, there is further improvement in both the rea-
sonable and partial occlusion cases. *ACF+occ suc-
cessfully eliminates the impact of occlusion samples
and achieves a performance comparable to the default
ACF model for the reasonable case, while in partial
occlusion case the average miss rate further reduces
to 43.42%.
5 OPTIMAL TRAINING AND
MORE EXPERIMENTS
Now that we have proposed a new method of uti-
lizing occluded pedestrian samples, in this section
we demonstrate its effectiveness with several experi-
ments. The experiments are divided into two parts. In
the first part, we exhaustively explore the potential of
ACF models and obtain our best detector trained with
non-occlusion pedestrian samples. In the second part,
we further improve the performance by introducing
occluded pedestrians and training them with the pro-
posed method. The evaluation results under different
test cases of the Caltech dataset show performances
that are better than some state-of-the-art methods.
In both parts of the experiments, we double the
default model size to 41×100 pixels, which results in
a richer feature of 32×64 pixels per channel. Pos-
itive samples in most experiments are obtained by
sampling the Caltech video data with a skipping step
equal to 10, while a smaller skipping step (more dense
sampling) is also used in some cases. We employ
some of the modifications proposed in (Ohn-Bar and
Trivedi, 2016): a scaling (factor 1.1) is used to aug-
ment the number of positive samples by 3 (scaling
in horizontal, vertical and both directions), while the
randomness handling is also employed to make the
Occlusion-robust Detector Trained with Occluded Pedestrians
91
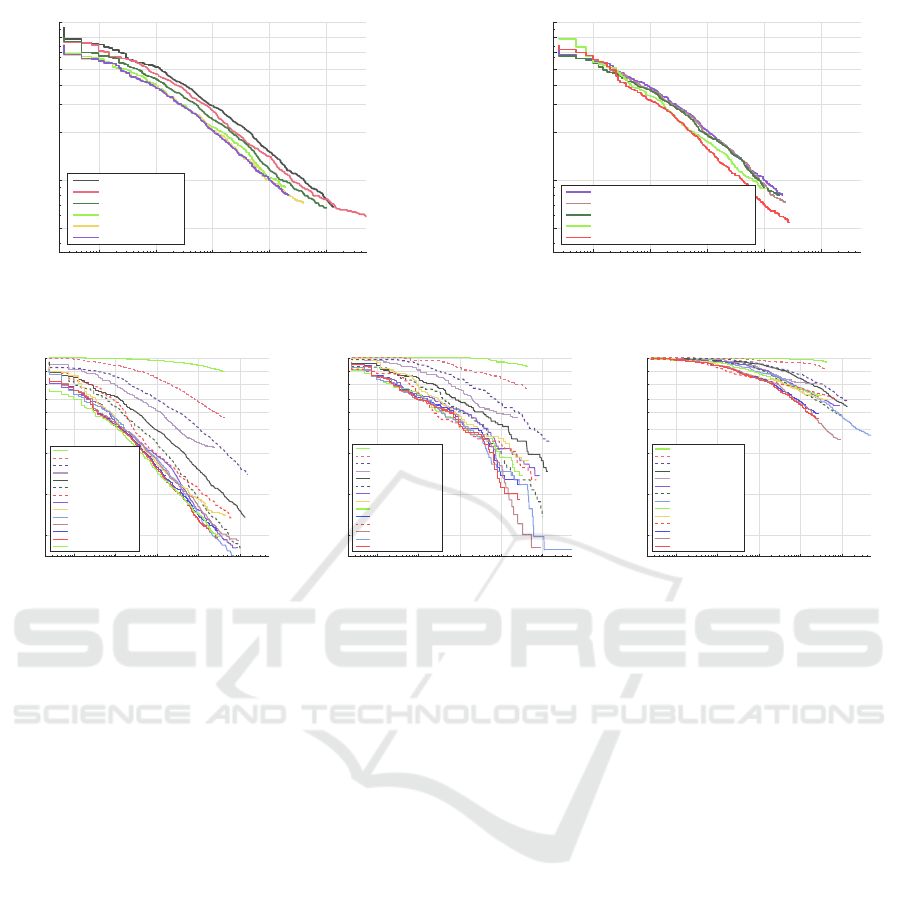
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
29.05% ACF
26.39% D3N50
23.87% D4N80
21.39% D5N120
20.56% D7N350
20.25% D6N200
(a)
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
20.25% D6N200
19.80% D6N200-rmUpperWindow
19.32% D6N200-rmEst
17.35% D6N200-LDCF
15.68% IACF-NonOcc
(b)
Figure 6: Performance of models trained with fully visible pedestrian samples.
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
94.73% VJ
68.46% HOG
48.68% Franken
39.32% JointDeep
29.05% ACF
21.89% SpatialPooling+
20.86% TA-CNN
17.71% ACF++
17.32% CCF+CF
17.10% Checkerboards+
17.04% IACF-Occ
15.68% IACF-NonOcc
15.09% proposed
14.98% LDCF++
(a)
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
98.67% VJ
84.47% HOG
67.57% Franken
56.82% JointDeep
48.53% ACF
39.25% SpatialPooling+
38.40% ACF++
37.69% CCF+CF
33.11% LDCF++
32.90% IACF-NonOcc
32.80% TA-CNN
32.59% IACF-Occ
31.31% Checkerboards+
30.56% proposed
(b)
10
-3
10
-2
10
-1
10
0
10
1
false positives per image
.05
.10
.20
.30
.40
.50
.64
.80
1
miss rate
98.78% VJ
95.97% HOG
88.82% Franken
86.58% ACF
81.88% JointDeep
79.51% ACF++
78.25% SpatialPooling+
77.93% Checkerboards+
75.74% LDCF++
72.68% CCF+CF
70.35% TA-CNN
68.47% IACF-NonOcc
68.41% IACF-Occ
66.78% proposed
(c)
Figure 7: Comparison with state-of-the-art methods in reasonable, partial occlusion and heavy occlusion cases.
results more reliable.
5.1 Training with Non-occlusion
Samples
We investigate the optimal training parameters by
gradually increasing the maximum depth of the de-
cision trees. For larger model capacity (deeper trees),
a bigger collection of training samples is needed to
explore the full potential of the model.
We start our experiment with a tree depth equal
to 3 and gradually increase the depth to 7 with more
training samples (see Fig. 6(a)). At the start, we train
a maximum depth 3 model with 50k negativesamples,
named D3N50 (D indicates the maximum depth while
N indicates negative samples of the model), which al-
ready outperforms the ACF detector trained with de-
fault settings (maximum depth 5 with 50k negative
samples). We conduct multiple experiments to find
the optimal data size under a maximum tree depth.
When additional data does not lead to an obvious im-
provement, we consider the model to be saturated. In
this way, tree depths from 3 to 7 are evaluated with
50k, 80k, 120k, 200k and 350k negative samples re-
spectively. For deeper trees (depth 6 and 7), more
dense sampling with a skipping step of 4 is employed
to enlarge the number of positive samples.
In Fig. 6(a) we observe a quick saturation of per-
formance: when the maximum depth reaches 6, addi-
tional data seems to help little, even with deeper trees.
Thus we fix D6N200 as our baseline setting and fur-
ther improve it in Fig. 6(b).
Since the Caltech dataset is captured in the real
world, some prior knowledge of the situation can
be used. Instead of exhaustively searching the im-
age with sliding windows, we remove those can-
didates from the upper 1/3 of the image, which
obviously reduces the calculation and avoids some
false positive detections in the non-pedestrian regions
(D6N200-rmUpperWindow). Furthermore, we obtain
D6N200-LDCF and D6N200-rmEst by employing
feature decorrelation filtering (Nam et al., 2014) and
removing feature estimation as suggested in (Ohn-Bar
and Trivedi, 2016). With all the above modifications,
we obtain our best performance detector trained only
with non-occlusion samples named IACF-NonOcc
(improved ACF detector trained with non-occlusion
samples), which is comparable with the state-of-
the-art ACF based method LDCF++ (Ohn-Bar and
Trivedi, 2016), see Fig. 7(a)).
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
92

Figure 8: Detection results of IACF-NonOcc (first row) and proposed (second row) on Caltech Pedestrain dataset. For
comparison both the detectors are kept with same number of false positives, while the proposed model successfully recognised
more occluded pedestrians.
5.2 Training with Occluded Samples
In Fig. 7, we evaluate the performance of our models:
IACF-NonOcc, IACF-Occ and proposed by compar-
ing with some state-of-the-art methods. The IACF-
NonOcc is trained only with full-visible pedestrian
samples, as explained in Section 5.1. Then we in-
troduce occluded pedestrian samples into the train-
ing stage and obtain IACF-Occ. In order to show
the influence of the occluded samples, all the param-
eters and modifications of IACF-NonOcc are kept un-
changed. At last, we achieve the best performance by
employing our new training method proposed in Sec-
tion 4 and get proposed.
The methods we use as comparison include VJ
(Viola and Jones, 2004), HOG (Dalal and Triggs,
2005), Franken (Mathias et al., 2013), JointDeep
(Ouyang and Wang, 2013a), ACF (Doll´ar et al.,
2014), SpatialPooling+(Paisitkriangkraiet al., 2016),
TA-CNN (Tian et al., 2015), ACF++ (Ohn-Bar and
Trivedi, 2016), LDCF++ (Ohn-Bar and Trivedi,
2016), CCF+CF (Yang et al., 2015) and Checker-
boards+ (Zhang et al., 2015). We obtain the detec-
tion results of the above methods from the website of
Caltech Pedestrian dataset.
In the commonly used Reasonable case (Fig.
7(a)), unsurprisingly, we observe an obvious perfor-
mance decline of nearly 2% (15.68% to 17.04%) after
we introduce the occluded samples during the train-
ing stage (IACF-Occ), while the proposed method
(proposed) successfully eliminates this drop and even
slightly outperforms the baseline IACF-NonOcc (it
reaches 15.09% compared with 15.68%).
The occlusion test cases represent the strong oc-
clusion handling ability of our proposed model. In the
partial occlusion case (Fig. 7(b)), the introduction of
occluded samples slightly improves the performance
from 32.90% to 32.59%, while the proposed model
further obtains the best result of 30.56%. More im-
pressive results appear in the heavy occlusion case
(Fig. 7(c)), which achieves a significant improvement
of nearly 10% (from 75.74% to 66.78%) over the
state-of-the-art ACF based model LDCF++, while the
efficiency remains the same (only the selected fea-
tures and thresholds are changed during detection).
Some results of the Caltech Pedestrian dataset are
presented in Fig. 8. We observe a more robust detec-
tion of occluded pedestrians with our method.
6 CONCLUSIONS
This study proposes a novel method to take full ad-
vantage of the occluded samples in pedestrian detec-
tion. By employing a biased feature selection strategy,
the proposed detector shows a significantly enhanced
occlusion handling ability.
Since the occlusion distribution map is built on the
Caltech Pedestrian dataset, we plan to test its general-
ization property in other datasets in our future work.
But as explained in Section 4.3, this occlusion distri-
bution conforms with the real situation that the lower
part of a pedestrian is more likely to be occluded.
Therefore, there is reason to believe our method could
maintain similar occlusion handling abilities in other
datasets of urban situations. What is more, we expect
to use our training method in deeper models with a
larger size of data to achieve a further improvement.
Occlusion-robust Detector Trained with Occluded Pedestrians
93

REFERENCES
Angelova, A., Krizhevsky, A., Vanhoucke, V., Ogale, A. S.,
and Ferguson, D. (2015). Real-time pedestrian detec-
tion with deep network cascades. In BMVC, pages
32–1.
Benenson, R., Mathias, M., Timofte, R., and Van Gool, L.
(2012). Pedestrian detection at 100 frames per second.
In Computer Vision and Pattern Recognition (CVPR),
2012 IEEE Conference on, pages 2903–2910. IEEE.
Benenson, R., Mathias, M., Tuytelaars, T., and Van Gool, L.
(2013). Seeking the strongest rigid detector. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 3666–3673.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Computer Vision and
Pattern Recognition, 2005. CVPR 2005. IEEE Com-
puter Society Conference on, volume 1, pages 886–
893. IEEE.
Doll´ar, P., Appel, R., Belongie, S., and Perona, P. (2014).
Fast feature pyramids for object detection. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 36(8):1532–1545.
Doll´ar, P., Belongie, S. J., and Perona, P. (2010). The fastest
pedestrian detector in the west. In BMVC, volume 2,
page 7.
Doll´ar, P., Tu, Z., Perona, P., and Belongie, S. (2009). Inte-
gral channel features.
Dollar, P., Wojek, C., Schiele, B., and Perona, P. (2012).
Pedestrian detection: An evaluation of the state of the
art. IEEE transactions on pattern analysis and ma-
chine intelligence, 34(4):743–761.
Enzweiler, M., Eigenstetter, A., Schiele, B., and Gavrila,
D. M. (2010). Multi-cue pedestrian classification with
partial occlusion handling. In Computer vision and
pattern recognition (CVPR), 2010 IEEE Conference
on, pages 990–997. IEEE.
Felzenszwalb, P. F., Girshick, R. B., McAllester, D., and
Ramanan, D. (2010). Object detection with discrim-
inatively trained part-based models. IEEE transac-
tions on pattern analysis and machine intelligence,
32(9):1627–1645.
Friedman, J., Hastie, T., Tibshirani, R., et al. (2000). Addi-
tive logistic regression: a statistical view of boosting
(with discussion and a rejoinder by the authors). The
annals of statistics, 28(2):337–407.
Mathias, M., Benenson, R., Timofte, R., and Van Gool, L.
(2013). Handling occlusions with franken-classifiers.
In Proceedings of the IEEE International Conference
on Computer Vision, pages 1505–1512.
Nam, W., Doll´ar, P., and Han, J. H. (2014). Local decorre-
lation for improved detection. Eprint Arxiv.
Ohn-Bar, E. and Trivedi, M. M. (2016). To boost or not to
boost? on the limits of boosted trees for object detec-
tion. In Pattern Recognition (ICPR), 2016 23rd Inter-
national Conference on, pages 3350–3355. IEEE.
Ouyang, W. and Wang, X. (2013a). Joint deep learning
for pedestrian detection. In Proceedings of the IEEE
International Conference on Computer Vision, pages
2056–2063.
Ouyang, W. and Wang, X. (2013b). Single-pedestrian de-
tection aided by multi-pedestrian detection. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 3198–3205.
Ouyang, W., Zeng, X., and Wang, X. (2016). Partial oc-
clusion handling in pedestrian detection with a deep
model. IEEE Transactions on Circuits and Systems
for Video Technology, 26(11):2123–2137.
Paisitkriangkrai, S., Shen, C., and van den Hengel, A.
(2016). Pedestrian detection with spatially pooled fea-
tures and structured ensemble learning. IEEE trans-
actions on pattern analysis and machine intelligence,
38(6):1243–1257.
Tang, S., Andriluka, M., and Schiele, B. (2014). Detection
and tracking of occluded people. International Jour-
nal of Computer Vision, 110(1):58–69.
Tian, Y., Luo, P., Wang, X., and Tang, X. (2015). Pedes-
trian detection aided by deep learning semantic tasks.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 5079–5087.
Viola, P. and Jones, M. J. (2004). Robust real-time face
detection. International journal of computer vision,
57(2):137–154.
Walk, S., Majer, N., Schindler, K., and Schiele, B. (2010).
New features and insights for pedestrian detection.
In Computer vision and pattern recognition (CVPR),
2010 IEEE conference on, pages 1030–1037. IEEE.
Wang, X., Han, T. X., and Yan, S. (2009). An hog-lbp
human detector with partial occlusion handling. In
Computer Vision, 2009 IEEE 12th International Con-
ference on, pages 32–39. IEEE.
Wojek, C., Walk, S., Roth, S., and Schiele, B. (2011).
Monocular 3d scene understanding with explicit oc-
clusion reasoning. In Computer Vision and Pat-
tern Recognition (CVPR), 2011 IEEE Conference on,
pages 1993–2000. IEEE.
Yang, B., Yan, J., Lei, Z., and Li, S. Z. (2015). Convolu-
tional channel features. In Proceedings of the IEEE in-
ternational conference on computer vision, pages 82–
90.
Zhang, S., Benenson, R., and Schiele, B. (2015). Filtered
channel features for pedestrian detection. In Computer
Vision and Pattern Recognition (CVPR), 2015 IEEE
Conference on, pages 1751–1760. IEEE.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
94
