
Agent-based Simulation Model Embedded
Accounting’s Purchase Method; Analysis on the Systemic Risk
of Mergers and Acquisitions between Financial Institutions
Hidenori Kato
1
, Yuichi Sei
2
, Yasuyuki Tahara
2
and Akihiko Ohsuga
2
1
Faculty of Informatics and Engineering, The University of Electro-Communications, Tokyo, Japan
2
Graduate School of Informatics and Engineering, The University of Electro-Communications, Tokyo, Japan
Keywords: Systemic Risk, Merger, Inter-bank Transaction, Marketable Assets, Agent Simulation, Purchase Method.
Abstract: The aim of the present study is to evaluate systemic risks due to merger between financial institutions by
manipulating the decline rate of marketable asset price. An agent-based simulation platform with purchase
method of international financial reporting standards (IFRS) is developed and analyses the influence of the
goodwill (Noren), produced by mergers between financial institutions. The research reveals the following two
points: (1) the decline rate of marketable asset price determines the number of bankruptcies, (2) when market
value asset price plumps sharply, the effect of merger is small.
1 INTRODUCTION
The most severe impacts of the financial crisis from
2007 to 2009 arose immediately after the failure of
Lehman Brothers on September 15, 2008 (Acharya,
2012). As failures of financial institutions may affect
market functions, the global financial crisis has
precipitated an increasing appreciation of the need for
a systemic perspective toward financial stability
(Arinaminpathy, 2012). This is called “systemic
risk”, which is a possibility that an event at an indivi-
dual company level could trigger severe instability or
collapse an entire industry or economy. In the several
past years, many studies have examined systemic
risk, especially in EU countries and the U.S.A.
In Japan, major financial institutions had to merge
to prevent systemic risk from increasing. Regional
economies are shrinking with declining population. In
January 2017, Japan’s Mie Bank and Daisan Bank
said they had agreed to consolidate their operations,
in an attempt to boost their competitiveness and deal
with demographic challenges (Nikkei, 2017). In
addition, Sumitomo Mitsui Financial Group and
Resona Holdings were finalizing an arrangement to
consolidate group regional banks in March 2017.
Earnings reveal the plight of Japan’s regional banks.
Net profit dropped on the year in the April-December
period for 60 of 82 listed regional banks (Nikkei,
2017).
One of the previous researches has suggested that
mergers between financial institutions have proved
disadvantageous (Hashimoto, 2015). This model
applied therein uses simplified balance sheet and
some regulations. However, it is better to consider
goodwill account separately after implementation of
mergers. In this paper, we deal with mergers between
financial institutions to investigate the possibilities of
systemic risk due to financial crisis. The issue
mentioned above is to analyse impacts of mergers
between banks. Therefore, we introduce to our model
the purchase method defined in international financial
reporting standards and use the same modelling
framework as Kikuchi’s model (Kikuchi et al., 2016).
The goal of this article is to analyse systemic risk
change due to mergers between financial institutions.
By introducing purchase method, we can deal cases
where the purchase amount is larger than the assets of
a merged company. In addition, systemic risks are
examined by changing the decline rate of marketable
asset price.
2 RELATED RESEARCH
2.1 Interbank Network
Financial institutions such as banks and securities
companies conduct various transactions in the
168
Kato, H., Sei, Y., Tahara, Y. and Ohsuga, A.
Agent-based Simulation Model Embedded Accounting’s Purchase Method; Analysis on the Systemic Risk of Mergers and Acquisitions between Financial Institutions.
DOI: 10.5220/0006569701680175
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 1, pages 168-175
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

interbank network. When one bank is insolvent, the
stability of banking system is affected in various ways
depending on the patterns of payment across locations
(Freixas et al, 2000). Freixas et al. (2000) investigates
the ability of the banking system to withstand the
insolvency of one bank and whether the closure of
one bank generates a chain reaction on the rest of the
system.
Degryse and Nguyen (2007) investigates the
evolution and determinants of contagion risk for the
Belgian banking system over the period 1993-2002,
using detailed information on aggregate interbank
exposures of individual banks. They examine large
bilateral interbank exposures, and cross-border
interbank exposures. They find that a change from a
complete structure toward a “multiple-money-center”
structure, which is called core-periphery network, has
decreased the risk and impact of contagion. In
addition, an increase in the relative importance of
cross-border interbank exposures has lowered local
contagion risk.
May and Arinaminpathy (2010) explores that
some simple mathematical figure for banking system
with emphasis on the interplay between the
characteristics of individual banks and the overall
dynamical behaviour system.
2.2 Systemic Modelling
Another area of applied research that bears on the
issue of systemic risk is related to agent-based
simulation.
Maeno et al. (2012) presents a computer
simulation model to analyse the risk of transmission
of financial distress in a bank credit network and the
knock-on defaults of banks. They find that the
number of defaults is determined by the bank credit
network, the balance sheet of banks including equity
capital ratio, and the capital surcharge on big banks.
Some researchers have challenged to introduce
interbank-network into agent-based modelling. These
researches investigate stress tolerance of the banking
system. The propagation of bankruptcy in financial
institutions is as shown in the figure below (Fig.1):
Figure 1: Propagation of failures of financial institutions.
Hashimoto and Kurahashi (2015) proposes an
indicator of systemic risk by gauging the risk of
failure. It establishes the interbank market of Erodos-
Renyi network. Each agent has a simplified balance
sheet. They find that central bank financing may
spread a chain of failures of financial institutions.
As a related work, Kikuchi et al. proposes new
agent-based simulation model. Kikuchi’s group
develops an agent-based simulation platform and then
examines how current systemic management
regulations cause bankruptcies. They analyse how the
borrowing and lending banks and the borrowers go
bankrupt in the chain via interbank network. In the
research, each financial institution has a simplified
balance sheet as shown in Figure 2.
Figure 2: Balance sheet in Kikuchi model.
In previous studies, researchers explored how the
prevention of propagation of failures was possible. In
these studies they focus on balance sheets of the
financial institutions and investigate the effects on the
propagation of failure (May and Arinaminpathy,
2010). Another area of applied research related to
systemic risk has examined agent-based simulation
(Kikuchi et al., 2016).
Extensive effort has been dedicated to
documenting the negative effects on go-bankrupt-in-
chain in the market. Little attention has been paid to
positive value such as goodwill (Noren in Japanese)
brought about by merger and acquisition; this is the
focus of attention in this paper.
3 DEFINITION
This study is modelled from the method proposed by
Kikuchi et al. (2016), which has been used to test the
effects of Basel Capital Account in the market. We
explain agent-based-model with goodwill (Noren)
item included in the balance sheet to investigate the
impacts on the inter-bank market.
Agent-based Simulation Model Embedded Accounting’s Purchase Method; Analysis on the Systemic Risk of Mergers and Acquisitions
between Financial Institutions
169

3.1 Balance Sheet
Balance sheet is a financial statement that
summarizes a company’s assets, liabilities and
shareholders’ equity at a specific point in time (Saito,
2014). In this study, we use the same modelling
framework as Kikuchi’s model (Kikuchi et al., 2016).
The difference from previous studies is the item of
“goodwill”. Goodwill is an intangible asset that arises
as a result of the acquisition of one company by
another for a premium value (Saito, 2014). Goodwill
is considered an intangible asset because it is not a
physical asset. Therefore, goodwill account can be
found in the assets portion of a company’s balance
sheet (Saito, 2014). If goodwill is not introduced,
corporate mergers cannot be evaluated properly,
because we cannot add revenue of fixed asset.
In this research, we introduce goodwill upon
merger of financial institutions. Each financial
institution has a simplified balance sheet in Figure 3.
Figure 3: Balance sheet in our model.
3.2 Merger of Financial Institutions
A merger is a deal to unite two existing companies
into one new company (Saito, 2014). There are two
types of mergers.
First, we explain an absorption-type merger.
When two or more entities are combined into an
existing company, it is known as a merger through
absorption. In this type of merger, only one entity
survives after the merger, while the rest of all cease
to exist.
Second, we explain a consolidation-type merger.
When two or more companies fuse to give birth to a
new company, it is known as a merger through
consolidation. This implies that all the companies to
the merger are dissolved, i.e. they lose their identities
and a new company is established.
In our study, we only deal with an absorption-type
merger.
3.3 Accounting Used in Mergers
In terms of accounting processing, there are two kinds
of account items of transaction, “acquisition” and
“affiliated company accounted for by the equity-
method”. It is necessary for each merger case to apply
appropriate accounting treatment. “Acquisition” is
account for the purchase method. On the other hand,
“affiliated company accounted for by the equity-
method” is account for pooling of interest method. In
Japan, “pooling of interest method” has been
abolished, so we use purchase method in this study.
3.4 Bankruptcy Mechanisms
In the proposed model herein, bankruptcy factors of
financial institutions are as follows: 1) excessive debt
2) decrease of capital adequacy ratio to below a
certain value and 3) lack of funds after funding to
continue procurement. The first factor resembles the
one handled by the model of May and Arinaminpathy
(May and Arinaminpathy, 2010). The second factor
means that minimum capital ratio is required. The
third factor describes a situation where a company
cannot cover its lack of funds in the short-term money
market.
4 THE MODEL IN THIS STUDY
4.1 Outline
Each agent has its own balance sheet. Marketable
asset price follows the transition of probability differ-
rence equation. We analogize a network to a complete
graph. Each financial institution updates its balance
sheet when an agent completes a trade with another.
The goal of this study is to analyse systemic risk
change due to mergers between financial institutions.
By introducing purchase method, we can deal cases
where the purchase amount is larger than the assets of
a merged company. In addition, systemic risks are
examined by changing the decline rate of marketable
asset price.
4.2 Agents
We use the same modelling framework as the one in
(Kikuchi et al., 2016), whereby each bank has a
simplified balance sheet. Each balance sheet consists
of the following factors. Compared with Kikuchi’s
model, our model has two more parameters,
combination by purchase and goodwill, as shown in
Table 1.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
170

Table 1: Balance sheet items of banks.
Parameter
Label
1) Marketable Asset
2) Non-Marketable Asset
3) Debt
4) Equity
5) Deposit facilities
6) Short-term investment
7) Short-term funding
8) Combination by purchase
9) Goodwill
Financing gap is then defined as below:
(1)
Surplus/Shortage institutions are defined as below:
{
|
}
(2)
{
|
}
(3)
Note that the status of each bank remains unchanged
from first step to final step.
We also define unrealized profit or loss (
),
capital adequacy ratio (
), income profit (
) and
ROE (
):
(4)
(5)
Where and denote the rate of return for
marketable and non-marketable assets respectively.
Marketable assets are then defined as below:
(6)
is the market price of marketable assets in step t.
Next, we explain the process of a merger between
randomly chosen two banks before trading on the
interbank network. A bank with more assets acquires
another bank with smaller assets. The purchase price
of banks and the goodwill value are defined as
follows.
First, we examine whether one bank can buy the
other by the total capital amount.
(7)
If the bank cannot acquire the other, the model
will choose another combination of banks.
When an acquisition is confirmed as executable,
our model determines the amount of goodwill. We
define as Marketable asset price of acquisition j:
, Non-marketable asset of acquisition
j:
, debt of acquisition j:
Then the amount of goodwill (
) shall be
determined as follows.
(8)
In addition, our model defines minimum capital
adequacy ratio (CAR-
). It is the lowest level
of the bank’s capital ratio to be an eligible borrower.
4.3 Network
We use the same modelling framework as the one
proposed by Kikuchi et al. (2016). Bank
engages
in short-term investment and funding with other
financial institutions
(9)
and tries to eliminate its funding gap. Then,
is the
adjacency matrix of the I/B network.
4.4 Financial Behaviour
First, a shortage institution
issues financing orders
to surplus institutions
Additionally,
places an order to all surplus
institutions in the interbank network by evenly
splitting the amount of its financial gap.
checks the
financial condition of
and the amount available for
lending to it to judge the feasibility of the loan to
.
4.5 The Effects of Bankruptcy
4.5.1 Individual Bankruptcy
If the capital ratio is equal to or less than the threshold
value, or, if the funding gap is not filled,
shall be
deemed “bankrupt” in our model.
Additionally, banks became bankrupt by either
the above criteria through the same step is defined as
. Thus the following case is defined as “multiple
simultaneous collapse”:
(10)
4.5.2 Chain Reaction Collapse
If financial institution
experiences bankruptcy,
financial institutions
that are involved in short-
term operations with
end up with uncollectible
Agent-based Simulation Model Embedded Accounting’s Purchase Method; Analysis on the Systemic Risk of Mergers and Acquisitions
between Financial Institutions
171
funds from these investments. In this model
uncollectible funds by the transactions with
are
deducted from
capital.
(11)
If the following conditions are satisfied, some
of
banks suffer bankruptcy. In this way a chain
reaction collapse occurs.
(12)
5 ANALYSIS OF MODEL
BEHABIOR
5.1 Price Time Series of Marketable
Assets
Market price provides the basis for the time series of
marketable assets used in the simulation, and is
calculated using the following discretized stochastic
differential equation (Luenberger, 1997).
(13)
Where t is time step(t=-m+1, … ,0,1,…,T ),
j: is trail number,
is price of marketable
asset(j times, step t)(
=100),
is risk free rate[%],
is volatility [%], and . In this simulation,
we set 1 step = 1 day = 1/250 year and
125 (assuming 6 month is the budget-
closing period for a bank account). Additionally,
taking into account long-term government bond yield
levels and stock markets in each country:
sample paths are generated and
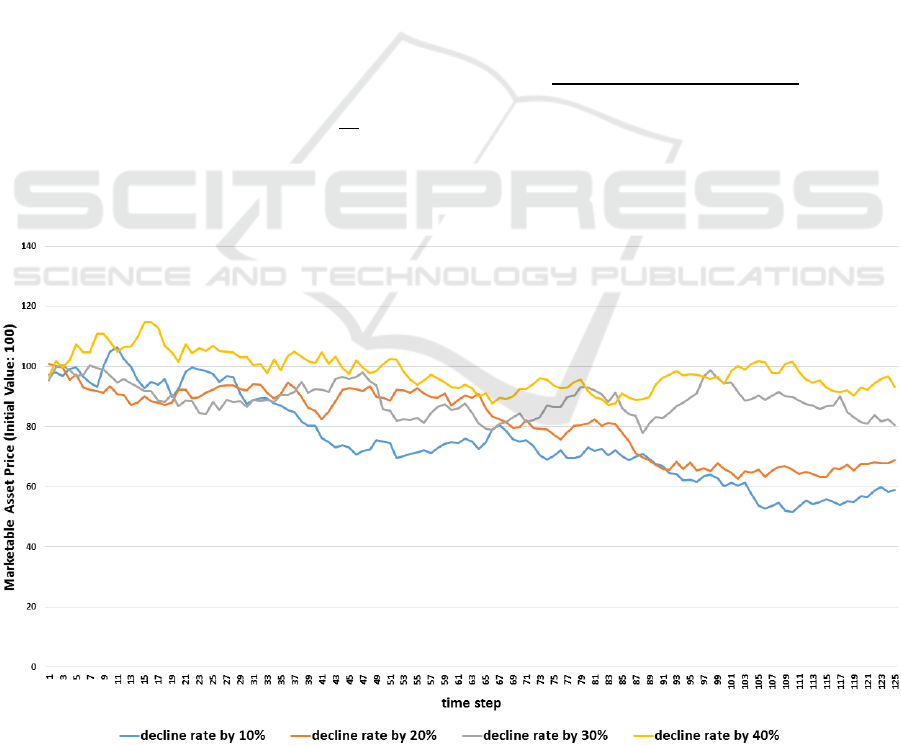
we adopt marketable asset price decline rate by 10%,
20%, 30% and 40% from the initial value.
5.2 Common Setting
The common setting of parameters is shown in the
simulation Figure 5. There are 20 financial
institutions in total, and I/B network is a complete
graph. In terms of financing gap, since surplus
institutions outnumber shortage institutions, surplus
institutions are subjected to the following adjustment:
(14)
Moreover, following assumption is made:
Figure 4: Price time series of marketable assets employed in this simulation totalled 1,000 trials and we adopted the decline
rate by 10%, 20%, 30% and 40% prices from the initial value.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
172

5.3 Check the Model
When marketable asset price fall by 40%, we carry
out one set simulation shown in the Figure 5. Figure
7 shows the number of remaining banks. In this
experiment, 6 out of 20 banks remain in the final step.
In this experiment, continuous failure has occurred at
the
step and involving 10 banks’ continuous
bankruptcy has occurred at the
step. This chain
collapse is similar to the previous study. One
bankruptcy causes another, which leads to still others.
Some banks cannot keep capital and this brings
further bankruptcy. As a result, a chain of bank
failures occurs.
Figure 5: Parameter set used for this simulation.
Figure 6: Parameter rationale.
5.4 Impact Analysis by Bank Merger
We use the same modelling framework as in the
Kikuchi’s model (Kikuchi et al., 2016), and expand it
to introduce bank mergers by purchase method. We
investigate the impact of mergers between banks
amid declining marketable asset prices. We assume 4
patterns of decline rate of marketable asset price. It is
a pattern that falls by 10%, 20%, 30%, 40%
respectively from initial price. Simulation is carried
out 100 times and the average number of bankruptcy
banks is compared with the decline rate of asset price.
Figure 7: Changes in the number of remaining banks in individual trials.
Agent-based Simulation Model Embedded Accounting’s Purchase Method; Analysis on the Systemic Risk of Mergers and Acquisitions
between Financial Institutions
173
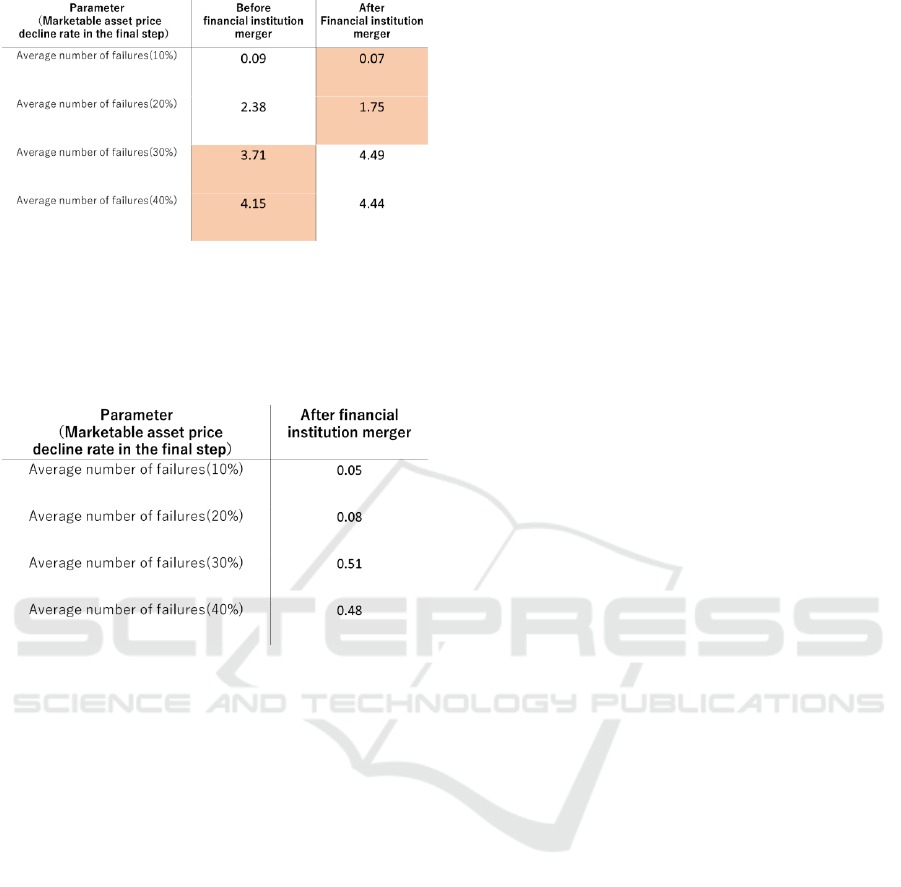
Figure 8: Changes in the average number of bank failures.
The data in Figure 8 shows that when the decline
rate of asset price is low, it is very effective for
financial system to implement a merger and that when
the decline rate of asset price is high, it is not effective.
Figure 9: Number of bank failures by 4 falling asset price
patterns.
Figure 9 shows the average number of failures of
integrated banks. When the decline rate of marketable
asset price is 20%, such bank failure is 0.08. At this
time, it turns out that integrated banks hardly go
bankrupt. However, when it declines more than 30%,
there is a higher possibility that integrated banks will
collapse.
6 DISCUSSION
We discuss the results of the experiment. First, the
number of bankruptcies of financial institutions
increase due to decline in marketable asset price.
From Figure 8, it is found that the higher the decline
rate of asset price becomes, the larger the number of
failures is examined when banks merged. The factor
of the increase in the number of failures is a
deterioration in the capital ratio. It is because some
banks cannot raise funds due to worsening capital
ratio rate, even if banks conduct merger.
Next, we discuss Figure 9. When the decline rate
of asset price is high, half of banks go bankrupt. There
is almost no improvement in the capital adequacy
ratio due to merger.
On the other hand, when the decline rate of asset
price is low, it is better for bank to implement a
merger. Figure 6 shows that the number of failures is
greatly reduced due to merger. By strengthening
capital, the number of financial institutions of going
bankrupt declines. In other words, as shown in Figure
7, the decline rate of asset price is less than 20%, the
banks hardly go bankrupt. A possible contributor to
this finding may have been amount of capital. Banks
after merger have more capital than other banks.
7 CONCLUSION
The main purpose of this study is to examine whether
goodwill brought about by the merger and acquisition
prevents the go-bankrupt-in-chain in the interbank
market.
The most important finding of this study is that if
the marketable value asset prices plummet sharply,
the effect of merger is small.
Another key finding is that the decline rate of
marketable asset price determines bankruptcies.
The data in Figure 8 shows that the number of
failures has been greatly reduced due to merger.
When the decline rate of asset price is low, it is better
for bank to implement merger.
The results of this study imply that by
strengthening capital, a possibility of financial
institutions of going bankrupt declines.
In addition, as shown in Figure 9, if the decline
rate of asset price is less than 20%, banks have hardly
go bankrupt. A possible contributor to this finding
may have been amount of capital. Banks after merger
have more capital than other banks.
We examine the effects of goodwill (Noren) that
have received very little attention in the literature.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Numbers JP16K12411, JP17H04705.
REFERENCES
Acharya, V., Engle, R. and Richardson, M. (2012). Capital
shortfall: A new approach to ranking and regulating
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
174

systemic risks. The American Economic Review, Vol.
102, No. 3, pp.59-64.
Arinaminpathy, N., Kapadia S. and May R. (2012). Size
and complexity in model financial systems. Proceed-
ings of the National Academy of Sciences of the United
States of America, Vol.109, No.45, pp.338-pp.343
Common challenges spur merger of Japan’s Mie bank,
Daisan bank (2017). NIKKEI ASIAN REVIEW,
http://asia.nikkei.com/Business/Deals/Common-challe
nges-spur-merger-of-Japan-s-Mie-Bank-Daisan-Bank.
Degryse, H. and Nguyen, G. (2007). Interbank exposures:
an empirical examination of contagion risk in the
Belgian banking system. International Journal of
Central Banking, Vol.3, No.2, pp.123-171
Freixas, X., Parigi, B. and Rochet, J.C. (2000). Systemic
Risk, interbank relations, and liquidity provision by the
central Bank. Journal of Money, Credit, and Banking,
Vol.32, No.3, pp. 611-638.
Hashimoto, M. and Kurahashi S. (2015). The analysis of
Systemic Risk Index effects under Inter-bank
transactional network. Joint Agent Workshop &
Symposium 2015 (JAWS2015), pp.108-115.
Japan’s regional bank consolidation gains momentum
(2017). Nikkei Asian Review, http://asia.nikkei.com/
Business/Trends/Japan-s-regional-bank-consolidation-
gains-momentum.
Kikuchi, T., Kunigami, M., Yamada, T., Takahashi, H. and
Terano, T. (2016). Agent-based simulation analysis on
investment behaviours of financial firms related to
bankruptcy propagations and financial regulations. The
Japanese Society for Artificial Intelligence, Vol.31,
No.6, ppAG_G1-11.
Luenberger, D.G. (1997). Invest Science. Oxford
University Press.
Maeno, Y., Morinaga, S., Matsushima, H., and Amaya, K.,
(2012). Risk of the collapse of a bank credit network.
The Japanese Society for Artificial Intelligence, Vol.27,
No.6, pp.338-346.
May, R. and Arinaminpathy, N. (2010). Systemic risk: the
dynamics of model banking system. J.R. Soc. Interface,
Vol.7, No.46, pp.823-838.
Saito, S. (2014). Financial Accounting. Yuhikaku
Publishing, pp.11-24, Tokyo, 4
th
edition.
Agent-based Simulation Model Embedded Accounting’s Purchase Method; Analysis on the Systemic Risk of Mergers and Acquisitions
between Financial Institutions
175
