
Density-based Clustering using Automatic Density Peak Detection
Huanqian Yan, Yonggang Lu and Heng Ma
School of Information Science and Engineering, Lanzhou University, Lanzhou, Gansu 730000, China
Keywords: Clustering, Pattern Recognition, Decision Graph, Image Segmentation.
Abstract: Clustering is an important unsupervised machine learning method which has played an important role in
various fields. Density-based clustering methods are capable of dealing with clusters of different sizes and
shapes. As suggested by Alex Rodriguez et al. in a paper published in Science in 2014, the 2D decision
graph of the estimated density value versus the minimum distance from the points with higher density
values for all the data points can be used to identify the cluster centroids. However, there lack automatic
methods for the determination of the cluster centroids from the decision graph. In this work, a novel
statistic-based method is designed to identify the cluster centroids automatically from the decision graph. So
the number of clusters is also automatically determined. Experiments on several synthetic and real-world
datasets show the superiority of the proposed method in centroid identification from the datasets with
various distributions and dimensionalities. Furthermore, it is also shown that the proposed method can be
effectively applied to image segmentation.
1 INTRODUCTION
Clustering is the process of grouping a set of data
objects into multiple groups or clusters so that
objects within a cluster have high similarity, but are
very dissimilar to objects in other clusters.
Dissimilarities or similarities are assessed based on
the attribute values describing the objects using
certain distance measures (Law, Urtasun, and Zemel,
2017). Clustering is an important technique for
exploratory data analysis, and has been studied for
many years. It has been shown to be useful in many
practical domains such as data classification and
image processing (Piotr, 2012).
Clustering is generally considered as a difficult
problem because the optimal number of clusters
cannot be easily determined and clusters may have
different distributions, shapes and sizes (Lu and
Wan, 2012). It has been shown that clustering is a
nonconvex, discrete optimization problem. Due to
the existence of many local minima, there is
typically no way to find a globally minimal solution
without trying all possible partitions (Kleinberg,
2003). Although many heuristic methods have been
developed, most of them are not generic enough and
can only be used for particular clustering problems.
Most clustering algorithms are based on two popular
techniques known as hierarchical and partitional
clustering. The partitional clustering algorithms
include square-error-based clustering methods,
density-based clustering methods, distribution-based
clustering methods and so on.
For hierarchical methods, they can be classified
as being either agglomerative or divisive, based on
how the hierarchical decomposition of the given set
of data objects is formed (Grant and Flynn, 2016;
Charikar and Chatziafratis, 2017). Hierarchical
clustering methods don’t need some strict initial
conditions, but they suffer from the mechanism that
a previous merge or split cannot be changed during
the following process.
For square-error-based clustering methods, such
as k-means (Wagstaff et al., 2001), k-medoids
(Kaufman and Rousseeuw, 2009), and affinity
propagation (Frey and Dueck, 2007; Serdah and
Ashour, 2016). An objective function, typically the
sum of the distance to a set of putative cluster
centers, is optimized until the best cluster center
candidates are found (Serdah and Ashour, 2016;
Ward, 1963; Hoppner, 1999; Jain, 2010). However,
for k-means and k-medoids, because a data point is
always assigned to the nearest center, they cannot be
used to detect non-globular clusters (Jain, 2010). For
affinity propagation method, with an improper initial
exemplar preference, it may fail to work properly.
Most square-error-based methods are greedy
Yan, H., Lu, Y. and Ma, H.
Density-based Clustering using Automatic Density Peak Detection.
DOI: 10.5220/0006572300950102
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 95-102
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
95

algorithms that depend on initial conditions and may
converge to suboptimal solutions.
Unlike square-error-based clustering, density-
based clustering can detect clusters with arbitrary
shapes or sizes. The most popular density-based
clustering methods include DBSCAN (Ester et al.,
1996), mean-shift (Fukunaga et al., 1975), OPTICS
(Campello et al., 2015), and DENCLUE (Campello
et al., 2015), etc. A drawback of these methods is
that the parameter setting is not a straightforward
task that user has to take care of. An excellent
density-based clustering method published in
Science in 2014 is proposed by Alex Rodriguez et
al. (Rodriguez and Laio, 2014). The method is called
Clustering by Fast Search and Find of Density Peaks
(CFSFDP). It is based on the simple idea that a
cluster centroid has a higher density value than its
neighbors and is far away from the other objects
with higher density values. CFSFDP can predict the
number of clusters by identifying the cluster
centroids in a 2D decision graph whose axes are the
density value and the minimum distance from the
points with higher density values respectively. But
the cluster cendroids in the decision graph must be
manually decided.
To address this issue, we propose a novel
clustering method called Automatic Density Peak
Detection (ADPD) in this paper. A new outlier
detection method is designed to identify the cluster
centroids automatically from the decision graph
using a statistical-based nonparametric density
estimation. This method can identify clusters with
arbitrary shapes or sizes and can determine the
number of clusters automatically.
The rest of the paper is organized as follows. The
original CFSFDP method
is introduced in Section 2.
The proposed ADPD algorithm is described in
Section 3. The experimental results are presented in
Section 4. And conclusions are drawn in Section 5.
2 THE CFSFDP METHOD
The CFSFDP method (Rodriguez and Laio, 2014)
generates clusters by assigning data points to the
same cluster as its nearest neighbor with higher
density after cluster centroids are selected by users.
A heuristic method named decision graph is
designed to select these centroids. For each data
point , two important indicators are considered in
the decision graph: local density
, and the
minimum distance
from points of higher density
values. Their definitions are:
Local Density
: The local density
of point
is defined as
(1)
where
is a kernel function,
is the distance
between point and point , and
is the cutoff
distance threshold. In the CFSFDP method,
is a
parameter which needs to be determined manually.
In our experiments, the Gaussian kernel function is
used. So the local density
is defined as:
.
Minimum Distance
: The minimum distance
of point is measured by computing the
minimum distance between the point and any other
points of higher density values:
(2)
The value
is much larger than the typical
distances between nearest neighbours if the
of
point i is a local or global maximum density value.
This observation, which is the core of the algorithm,
is illustrated by an example in Figure 1. Figure 1A
shows 30 points from two normal distributions.
Figure 1B is the decision graph which shows the plot
of
as a function of
for each point. From the
decision graph, the two points having high local
density values and large minimum distances can be
easily identified. The two points are identified as
cluster centroids, which are shown as filled triangle
or square in both Figure 1A and Figure 1B.
Figure 1: (A) Points distribution in a 2D space. (B)
Decision graph for the data in (A).
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
96
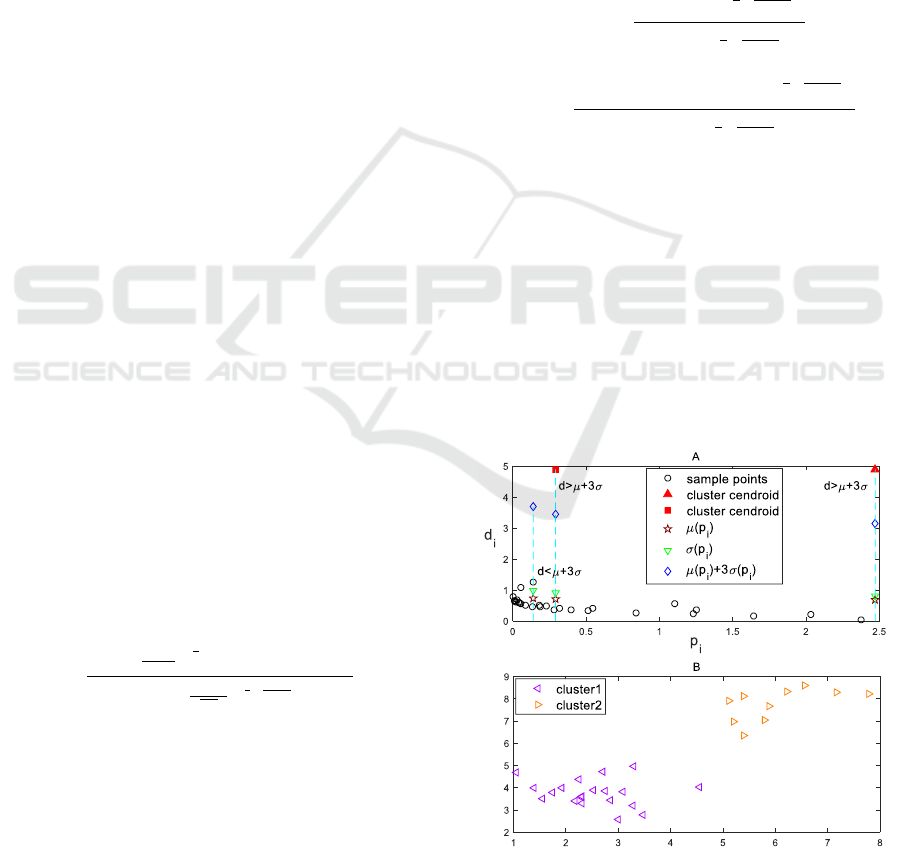
3 IDENTIFYING CENTROIDS
FROM THE DECISION GRAPH
AUTOMATICALLY
As shown in Figure 1B, the cluster cendroids are
usually the points that have large
values and
relatively high
values, a simple threshold-based
method suggested by Alex Rodriguez et al.
(Rodriguez and Laio, 2014)
for selecting the cluster
centroids is to use the following formula:
(3)
where the threshold parameter
has to be
decided by users. The drawbacks of the method are
that it does not use the distribution information of
the points in the decision graph and the parameter
can not be easily determined for different
datasets.
To deal with the drawbacks of the above method,
a statistic-based method for selecting the cluster
centroids is developed based on the following
observation: the value
is much larger than the
typical distances between nearest neighbors if the
point is a point having local or global maximum
density value. Thus, an important feature for
identifying a cluster cendroid is that its
value is
anomalously large. So, in our method, cluster
cendroids are identified using a specially designed
outlier detection method which contains mainly
three steps: firstly, the probability density
in the decision graph at a specific density value
and an arbitrary distance value is estimated;
secondly, the expectation value and the variance of
the distance are computed at the specific
value
using the probability density
; thirdly, the
cluster cendroids are identified using the expectation
value and the variance of the distance .
Two-dimensional Gaussian function is used to
estimate the probability density at the specific
in
the decision graph, which is given by:
(4)
where the is the total number of the data points,
and are the 2D kernel widths. The denominator
is a normalization factor which is used to ensure that
.
The selection of the values for the 2D kernel
widths and are important. It is found that and
can be estimated using the standard deviations of
and
of all the data points:
(5)
The selection of the parameters and will be
discussed in Subsection 4.2.
Using the probability density defined in (4), the
expectation value and the variance of the distance
at the specific
can be computed using:
(6)
(7)
By substituting (4) into (6) and (7), it follows
that:
(8)
(9)
Using (8) and (9), the expectation value and the
variance at the specific
can be easily computed
using the summation instead of the integration in (6)
and (7). Then, the outliers are identified using the
following threshold:
(10)
For any point i, if its minimum distance
, it is identified as an outlier, and thus is
used as a cluster cendroid in our experiments.
The process and result of identifying the cluster
centroids using the proposed method is shown in
Figure 2, where the data is from the Figure 1A.
Figure 2: (A) The process of identifying cluster centroids
in the decision graph. (B) The result of clustering,
different colors correspond to different clusters.
Density-based Clustering using Automatic Density Peak Detection
97

Using the threshold defined in (10), two points
represented as filled triangle and square are
identified as the cluster centroids.
4 EXPERIMENTAL RESULTS
There are six synthetic datasets and eight real-world
datasets used in the experiments. Two synthetic
datasets, called Dataset A and Dataset B generated
by ourselves, are shown in Figure 3, where different
colors represent different classes. The other four
synthetic datasets, including Aggregation, Flame,
Spiral, and R15, are downloaded from the internet,
which are shown in Table 1. Eight UCI real-world
datasets, including Iris, Breast cancer (Wisconsin),
Glass Identification, Wine Quality-red, Liver
Disorders, Seeds, Banknote authentication, Ecoli,
are also shown in Table 1.
Figure 3: Dataset A: Three 2D normal distributions with
the same size centered at ,
and . Dataset B: Four 2D normal distributions
with different size: , , centered at ;
, , centered at ; , ,
centered at and , , centered at
.
4.1 Evaluation Criterion
Because for all the datasets, ground truth cluster
labels are available, the Fowlkes-Mallows index
(FM-index) is used to evaluate the clustering result
(Fowlkes and Mallows, 1983), which is defined as:
(11)
where TP is the number of true positives, FP is the
number of false positives, and FN is the number of
false negatives. A higher value for the FM-index
indicates a greater similarity between the clusters
and the ground truth.
4.2 Parameter Selection
In the CFSFDP method, the parameter
must be
determined before computing the density values. It
can be chosen under the condition that the average
number of neighbors is around 1% to 2% of the total
number of the points, as suggested by Alex
Rodriguez et al (Rodriguez and Laio, 2014). In our
experiments, it is found that 4% is a better choice.
So, in our experiments, the parameter
is
determined with the condition that the average
number of neighbors is around 4% of the total
number of the points.
In our method, the parameters
and
defined in
(5) have to be determined. To decide the value of
,
we first set
=0.5, then different values of
are used
to compute
and identify the cluster centroids.
The clustering results of three datasets including Iris,
Seeds and Dataset B are shown in Figure 4A when
different
values are used. It can be seen from
Figure 4A that the clustering results are not sensitive
Table 1: Details of datasets in our experiments.
Dataset
N
a
D
b
M
c
Source
Aggregation
788
2
7
http://cs.joensuu.fi/sipu/datasets/
Flame
240
2
2
http://cs.joensuu.fi/sipu/datasets/
R15
600
2
15
http://cs.joensuu.fi/sipu/datasets/
Spiral
312
2
3
http://cs.joensuu.fi/sipu/datasets/
Iris
150
4
3
http://archive.ics.uci.edu/ml/datasets/
Seeds
210
7
3
http://archive.ics.uci.edu/ml/datasets/
Ecoli
336
8
8
http://archive.ics.uci.edu/ml/datasets/
Wine Quality-red
1599
12
6
http://archive.ics.uci.edu/ml/datasets/
Liver Disorders
345
7
2
http://archive.ics.uci.edu/ml/datasets/
Glass Identification
214
9
7
http://archive.ics.uci.edu/ml/datasets/
Banknote authentication
1372
4
2
http://archive.ics.uci.edu/ml/datasets/
Breast cancer (Wisconsin)
699
9
2
http://archive.ics.uci.edu/ml/datasets/
a
The number of the data points
b
The number of features
c
The actual number of the clusters
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
98

to the selection of the parameter . So, in our
experiments, the parameter
is set to 0.5.
To determine the parameter
, the parameter
is
set to 0.5, and different values of
are used in our
experiments. The clustering results produced with
different
values are shown in Figure 4B. It is
found that good clustering results with FM-
index>0.7 can be produced within a relatively wide
range of the parameter
, while
=0.5 is a relatively
good choice. So, the parameter
=0.5 is selected in
our experiments.
Figure 4: The FM-indices of the clustering results
produced with (A) different values and (B) different
values.
4.3 Comparison of the Clustering
Results
In order to evaluate the statistic-based centroid
identification method in ADPD algorithm, it is
compared with the simple threshold-based CFSFDP
method proposed by Alex Rodriguez et al
(Rodriguez and Laio, 2014). First, the percentile-
based method is used to select the centroids for
CFSFDP, the f-th percentile value from the set
is used to determine
the threshold
. The three datasets, including Iris,
Seeds and Dataset B, are also used in the
experiments. The clustering results under different
values for the three datasets are shown in Figure 5.
From Figure 5, it can be found that f = 1 is a
good choice. So the 1st percentile from the set
is used as the threshold
for the percentile-based method.
The comparison of the FM-indices of the
clustering results for the percentile-based method
and the proposed ADPD method are shown in Table
2 for different datasets. As shown in Table 2,
compared with the percentile-based method, the
ADPD method has produced better results for 11
datasets out of the total 14 datasets.
Our method ADPD only has a worse result for
the Banknote authentication dataset. From the results
of the two method, it is found that accurate
identification for cluster centroids is important.
Automatic threshold-based methods, such as the
percentile-based method, cannot always work well
for different datasets.
Figure 5: The FM-indices of the clustering results
produced with different f values.
Table 2: The FM-indices and the number of clusters produced by the percentile-based method and our method on 14
different datasets.
Dataset
Percentile-based method
ADPD
FM-index
#Clusters
FM-index
#Clusters
Dataset A
0.854
6
0.964
3
Dataset B
0.777
10
0.996
7
Aggregation
0.800
8
0.937
6
Flame
0.865
3
0.994
3
R15
0.374
6
0.993
15
Spiral
0.919
4
1
3
Iris
0.771
2
0.771
2
Seeds
0.809
3
0.809
3
Ecoli
0.544
4
0.672
5
Wine Quality-red
0.380
16
0.508
9
Liver Disorders
0.523
4
0.689
9
Glass Identification
0.480
3
0.544
5
Banknote authentication
0.550
14
0.513
35
Breast cancer (Wisconsin)
0.402
7
0.719
2
Density-based Clustering using Automatic Density Peak Detection
99

To further evaluate the effectiveness of our
method, it is also compared with the CFSFDP
method using manual parameter selection, in which
different
values are tuned for different datasets.
A lot of values of the parameter
are tried for
each dataset and the best one is used in the
experiments for the manual CFSFDP method. The
FM-indices of the clustering results and the number
of clusters are recorded in Table 3.
As is shown in Table 3, the method ADPD has
similar performance as the manual method. The
proposed ADPD method and the manual CFSFDP
method has the same results for 8 datasets out of the
total 14 datasets, noticing that the ADPD method
uses fixed parameters for all the datasets while the
manual method use different tuned parameters for
different datasets. Furthermore, the ADPD method
has produced the best results for 4 datasets which all
have complex distribution or high dimensions, while
the manual CFSFDP method has produced the best
results for only 2 datasets. For dataset Banknote
authentication, the ADPD fails to produce a
satisfying result. To study the special case, the
decision graph for the Banknote authentication
dataset is shown in Figure 6 from which it is found
that it is difficult to identify the centroids from the
decision graph, which may be why APDP does not
perform well.
In addition, from analysis of the results of
Dataset B, Flame, and Glass Identification, it is
found that the centroids located at the area of low
density points or isolated points can not be identified
by the simple threshold-based methods. So for some
unbalanced datasets, the threshold-based method
may produce bad results.
Figure 6: The decision graph for Banknote authentication.
From both Table 2 and Table 3, it can be seen
that the proposed ADPD method can produce better
results compared to the percentile-based CFSFDP
method, and can produce competitive results
compared to the manual CFSFDP method which
needs manual tuning of the parameters.
4.4 Application on Image Segmentation
Image segmentation is the decomposition of a gray
level or color image into homogeneous tiles. It is
arguably the most important low-level vision task.
Homogeneity is usually defined as similarity in pixel
values, so clustering algorithms can be used for
image segmentation. In our experiments, the
proposed ADPD method and the percentile-based
CFSFDP method are used to do automatic image
segmentation for two color images named City and
Flower, which have 30000 and 31440 pixels
respectively. In the experiments, only the RGB
values of each pixel are used as features for both
methods. The results of the image segmentation are
shown in Figure 7.
Table 3: The FM-indices and the number of clusters produced by the manual method and our method on 14 different
datasets.
Dataset
Manual method
ADPD
FM-index
#Clusters
FM-index
#Clusters
Dataset A
0.964
3
0.964
3
Dataset B
0.993
4
0.996
7
Aggregation
0.937
6
0.937
6
Flame
1
2
0.994
3
R15
0.993
15
0.993
15
Spiral
1
3
1
3
Iris
0.771
2
0.771
2
Seeds
0.809
3
0.809
3
Ecoli
0.649
2
0.672
5
Wine Quality-red
0.508
3
0.508
9
Liver Disorders
0.526
3
0.689
9
Glass Identification
0.537
2
0.544
5
Banknote authentication
0.693
3
0.513
35
Breast cancer (Wisconsin)
0.719
2
0.719
2
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
100

Figure 7: The image segmentation results by the percentile-based method (middle) and our ADPD method (right) for the
color image Flower and City.
As shown from the Figure 7, the first column on
the left are the original images, the middle column
shows the segmentation produced by the percentile-
based CFSFDP method, and the last column on the
right shows the segmentation produced by the
proposed ADPD method. The first row contains the
results for the Flower image, and the second row
contains the results for the City image. For the
Flower image, the percentile-based CFSFDP method
produces 315 clusters, while the ADPD method
produces 280 clusters. For the City image, the
percentile-based CFSFDP method produces 300
clusters, while the ADPD method produces 280
clusters. So, the percentile-based CFSFDP method
produces more clusters than the proposed ADPD
method for both images.
From the segmentation results in Figure 7, it can
be seen that the proposed ADPD method can
identify good homogenous segmented regions, such
as sky, clouds, walls, roofs, cars, flowers, stamens,
etc. The percentile-based CFSFDP method can also
identify homogenous segmented regions, but it fails
to identify the clouds, cars, and stamens. So,
although the percentile-based CFSFDP method
produces more clusters, it identifies fewer details of
the images compared to the ADPD method. It can be
seen that with the proposed automatic centroid
identification in the ADPD method, good image
segmentation can be produced with only the RGB
features.
5 CONCLUSIONS
In this paper, a novel clustering method is proposed
based on a statistical-based automatic centroid
identification from the decision graph. It is shown
that the proposed ADPD method can deal with
datasets of various distributions and dimensionalities,
and the proposed statistical-based centroid
identification is better than the simple threshold-
based centroid identification. Besides, the ADPD
method can also be used for image segmentation
effectively. In future work, we plan to improve the
ADPD method to estimate the number of clusters
more accurately with advanced density estimation.
ACKNOWLEDGEMENTS
This work is supported by the National Natural
Science Foundation of China (Grants No. 61272213)
and the Fundamental Research Funds for the Central
Universities (Grants No.lzujbky-2016-k07).
REFERENCES
Law, M. T., Urtasun, R., and Zemel, R. S., 2017. Deep
spectral clustering learning. In International
Conference on Machine Learning , pp. 1985-1994.
Lu, Y., and Wan, Y., 2012. Clustering by Sorting Potential
Values (CSPV): A novel potential-based clustering
method. Pattern Recognition, 45(9), pp. 3512-3522.
Piotr, K., 2012. The complete gradient clustering
algorithm: properties in practical applications. Journal
of Applied Statistics, 39(6), pp. 1211-1224.
Kleinberg, J., 2003. An impossibility theorem for
clustering. Advances in neural information processing
systems, pp. 463-470.
Grant, J., and Flynn, P., 2016. Hierarchical Clustering in
Face Similarity Score Space. arXiv preprint
arXiv:1605.06052.
Density-based Clustering using Automatic Density Peak Detection
101

Charikar, M., and Chatziafratis, V., 2017. Approximate
hierarchical clustering via sparsest cut and spreading
metrics. In Proceedings of the Twenty-Eighth Annual
ACM-SIAM Symposium on Discrete Algorithms .
Society for Industrial and Applied Mathematics, pp.
841-854.
Wagstaff, K., Cardie, C., Rogers, S., and Schrödl, S., 2001.
Constrained k-means clustering with background
knowledge. In ICML, pp. 577-584.
Kaufman, L., and Rousseeuw, P. J., 2009. Finding groups
in data: an introduction to cluster analysis (Vol. 344).
John Wiley & Sons.
Frey, B.J. and Dueck, D., 2007. Clustering by passing
messages between data points. science, 315(5814), pp.
972-976.
Serdah, A. M., and Ashour, W. M., 2016. Clustering large-
scale data based on modified affinity propagation
algorithm. Journal of Artificial Intelligence and Soft
Computing Research, 6(1), 23-33.
Ward Jr, J.H., 1963. Hierarchical grouping to optimize an
objective function.Journal of the American statistical
association, 58(301), pp. 236-244.
Höppner, F., 1999. Fuzzy cluster analysis: methods for
classification, data analysis and image recognition.
John Wiley & Sons.
Jain, A.K., 2010. Data clustering: 50 years beyond K-
means. Pattern recognition letters, 31(8), pp. 651-666.
Ester, M., Kriegel, H. P., Sander, J., and Xu, X, 1996. A
density-based algorithm for discovering clusters in
large spatial databases with noise. In Kdd (Vol. 96, No.
34, pp. 226-231).
Fukunaga, K. and Hostetler, L., 1975. The estimation of
the gradient of a density function, with applications in
pattern recognition. IEEE Transactions on information
theory, 21(1), pp. 32-40.
Campello, R. J. G. B., Moulavi, D., Zimek, A., and Sander,
J. 2015. Hierarchical density estimates for data
clustering, visualization, and outlier detection. Acm
Transactions on Knowledge Discovery from
Data,10(1), 5.
Rodriguez, A. and Laio, A., 2014. Clustering by fast
search and find of density peaks. Science, 344(6191),
pp. 1492-1496.
Fowlkes, E. B., and Mallows, C. L.,1983. A method for
comparing two hierarchical clusterings. Journal of the
American statistical association,78(383), 553-569.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
102
