Deep Reinforcement Learning for Advanced Energy Management of

Hybrid Electric Vehicles

Roman Liessner, Christian Schroer, Ansgar Dietermann and Bernard B

aker

Dresden Institute of Automobile Engineering, TU Dresden, George-B

ahr-Straße 1c, 01069 Dresden, Germany

Keywords:

Energy Management, Deep Learning, Reinforcement Learning, Hybrid Electric Vehicle.

Abstract:

Machine Learning seizes a substantial role in the development of future low-emission automobiles, as man-

ufacturers are increasingly reaching limits with traditional engineering methods. Apart from autonomous

driving, recent advances in reinforcement learning also offer great beneﬁt for solving complex parameteriza-

tion tasks. In this paper, deep reinforcement learning is used for the derivation of efﬁcient operating strategies

for hybrid electric vehicles. There, for achieving fuel efﬁcient solutions, a wide range of potential driving

and trafﬁc scenarios have to be anticipated where intelligent and adaptive processes could bring signiﬁcant

improvements. The underlying research proves the ability of a reinforcement learning agent to learn nearly-

optimal operating strategies without any prior route-information and offers great potential for the inclusion of

further variables into the optimization process.

1 INTRODUCTION

Today, automobile manufacturers are confronted with

major demands regarding the development of new

drive trains. On the one hand, strict legislation and

regulation requiring overall and continuous reduction

of fuel consumption and emission levels of new ve-

hicles. On the other hand, rising customer demands

concerning vehicle dynamics, overall comfort and af-

fordability. While purely electric vehicles often lack

larger operation ranges and are still rather expensive

due to high costs for production and development, hy-

brid electric vehicles (HEV) offer a good compromise

to combine the beneﬁts of conventional combustion

engines and novel electric motors.

The use of an electric machine (EM) as a supple-

mentary motor increases the degree of freedom of the

driving unit and a so-called operating strategy has to

be applied for the efﬁcient coordination of both en-

ergy converters. Ideally, a variety of factors with ef-

fect on fuel consumption are taken into account by

such a strategy. These factors range from the driver’s

inﬂuence through different driving styles and habits,

environmental conditions like trafﬁc, route and road

information up to internal state information of the ve-

hicle like fuel and battery levels. In general, these

factors can be seen as highly stochastic, intercorre-

lated and dependent on the individual situation. For

example, the driving style of a sporty driver operat-

ing a sports car in a large city is signiﬁcantly different

from the driving style of the same driver in an all-

terrain vehicle in the mountains.

These scenarios are captured in velocity proﬁles,

so-called driving cycles, which are not only used for

calibration but also for certiﬁcation of new vehicles.

Formerly, emission levels were derived purely from

deterministic cycles (e.g. “New European Driving

Cycle”) for which an efﬁcient strategy could specif-

ically be optimized. Nevertheless, the ability of these

synthetic cycles to represent reality can and should be

questioned as the variety of potential driving scenar-

ios in real-world trafﬁc is huge. For that reason, fu-

ture certiﬁcation tests (Real Driving Emissions) (Eu-

ropean Commission, 2017) will be performed directly

on the road rather than in fully controlled testing

environments which poses major challenges for the

manufacturers. Therefore, traditional approaches for

the derivation of operating strategies with ﬁxed rule-

based strategies seem outdated, especially with inclu-

sion of diverse driver, route and vehicle information.

In order to bring signiﬁcant fuel and energy savings

beyond certiﬁcation procedures to the actual customer

with every-day use of the vehicle, new and innovative

approaches are required for the energy management

of HEVs.

In recent years, machine learning has increasingly

gained momentum in the engineering context where

highly non-linear problems have to be solved and

Liessner, R., Schroer, C., Dietermann, A. and Bäker, B.

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles.

DOI: 10.5220/0006573000610072

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 2, pages 61-72

ISBN: 978-989-758-275-2

greater abstraction levels reduce valuable informa-

tion. Reinforcement learning (RL) in particular of-

fers signiﬁcant beneﬁt for planning and optimiza-

tion tasks, mostly because an agent learns model-

free, with great efﬁciency and through direct interac-

tion with its environment. In contrast to traditional

RL methods, which were bound to rather small and

lowdimensional problems, the combination of RL and

neural networks, called deep reinforcement learning,

allows the application in very complex domains with

highdimensional sensory input. In the context of au-

tonomous driving for example, RL can play a vital

role in ﬁne-grained control of the vehicle in challeng-

ing environments (Mirzaei and Givargis, 2017)(Chae

et al., 2017). Next to that, the energy management

of modern vehicles appears to be a problem where

state-of-the-art machine learning could dramatically

improve current technology, bringing signiﬁcant ben-

eﬁts to customers and the environment.

The main contributions of this paper are: (1) Deriva-

tion of a deep reinforcement learning framework ca-

pable of learning nearly-optimal operating strategies

(2) The use of stochastic driver models for improved

state generalization and preventing the strategy from

overﬁtting. (3) Inclusion of the battery temperature

with additional power limitation in to the optimiza-

tion process.

The paper is structured into six sections. Section

2 establishes the fundamentals of hybrid vehicles, en-

ergy management and reinforcement learning. Sec-

tion 3 introduces related work and a concrete formu-

lation of the problem. In Section 4, the experimen-

tal setup for solving the energy management problem

with RL is described, for which the results will be

shown in section 5. Section 6 concludes the paper

and gives a prospect of potential future work.

2 BACKGROUND

2.1 Hybrid Electric Vehicles

The term ‘hybrid vehicle’ is classiﬁed by the UN

as vehicles which have at least two energy stor-

ages and two energy converters for locomotion (UN-

ECE Transport Division, 2005). Today, the most

widely spread implementation is the combination of

a conventional internal combustion engine (ICE) with

an electric machine. Biggest advantage of this com-

bination is the ability to exploit vehicle deceleration

for recuperation, meaning the conversion of braking

energy into electric energy for recharging the elec-

tric energy storage. With the EM assisting the ICE

in times of high loads up to 30% of fuel could be

saved, especially in urban environments, where the

efﬁciency of vehicles operated solely by ICE is typ-

ically rather low (Guzzella and Sciarretta, 2013).

If the combustion engine and the electric machine are

both directly connected to the driving axle of the hy-

brid vehicle they form a parallel power train structure

where the EM can be switched on and off as desired.

The basic architecture of parallel hybrid drive train

structures is shown in Figure 1.

gearbox

rear axle

CRS

, trq

CRS

Fuel

rear wheels

Clutch

Figure 1: Structural scheme of a parallel mild hybrid.

Hybrid vehicles with a parallel power train are of-

ten designed as mild hybrids, meaning that the EM

has a comparatively low power output against the

ICE. In this case, the EM is mainly used for recuper-

ation of braking energy and short-term support of the

combustion engine in periods of high load. In con-

trast to plug-in hybrids, mild hybrids do not offer the

opportunity to charge the electric storage externally

and the entirety of the energy used for support of the

ICE has to be gained from recuperation. Deliberately,

purely electric driving with only the EM operated for

locomotion of the vehicle is not intended (Guzzella

and Sciarretta, 2013). Mild hybrids can be seen as

a compromise between vehicles operated by a single

combustion engine and full hybrids with the ability to

drive fully electric for long routes, saving costs in the

development and production of the vehicle as well as

operational costs for fuel and energy.

2.2 Operating Strategy

Mainly, the control of HEVs can be split into two

levels. The component level (low-level), which

controls the components of the driving unit with

traditional feedback-control procedures, and the

supervisory level (high-level) for monitoring and

control of any power ﬂow within the vehicle. Latter

one will also process any kind of vehicle and driving

information (speed, torque, acceleration, slope), and

thus can be described as the energy management

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

system (EMS). Primary goal of the EMS is deriving

optimal control signals for the low-level in order to

achieve best possible energy efﬁciency (Onori et al.,

2016). The energy management is embedded in an

overall operating strategy of the vehicle which, next

to fuel saving, could also include any other aspects

like vehicle dynamics or driving comfort as well

as certain technical goals. For example, limitations

of the maximum battery power could be desired in

order to avoid damage or to extend the lifetime of the

component.

Most derivation processes for energy management

start with model-based simulations. Deriving an

optimal strategy can then be described as a multi-goal

optimization process. Various methods exist for

solving this problem. On the one hand, global

optimization methods like dynamic programming

(DP) (Kirschbaum et al., 2002) which offer the

chance to determine optimal solutions for any given

driving cycle. However, since these methods require

full knowledge of the route in advance and are

computationally very expensive, the application in

the vehicle for online control seams infeasible. In

practice DP mostly serves for academic validation

of other procedures. On the other hand there are

local optimization methods like the Equivalent

Consumption Minimization Strategy (ECMS) where

fuel and electric energy used for driving is balanced

through a weighting factor (Chasse and Sciarretta,

2011). Nevertheless, selection of an appropriate

factor requires further effort for optimization with

ECMS since it heavily depends on the state of the

route being driven and the habits of the driver.

Further details to traditional optimization methods

for operating strategies can be found in (Guzzella and

Sciarretta, 2013).

For adaptability towards different driver types,

more innovative approaches are required. Next to

stochastic dynamic programming shown in (Leroy

et al., 2012) and (Tate et al., 2008), machine learn-

ing and especially reinforcement learning offer good

concepts for the efﬁcient inclusion of speciﬁc driving

and driver information into the optimization process

of operating strategies for hybrid vehicles.

2.3 Reinforcement Learning

The basic idea of reinforcement learning algorithms is

strongly geared towards how humans or animals learn

and can be described as a learning process by trial and

error. The interactive nature makes RL particularly

interesting for learning problems with no existing set

of structured and labeled training examples.

Figure 2: Scheme of the typical agent-environment-

interaction for reinforcement learning (Sutton and Barto,

2012).

The fundamental structure of any RL algorithm is

shown in Figure 2 and can be described as a structured

interaction of an agent with its environment. At every

discrete timestep t the agent is presented with a state

from the environment for which he must choose an

action a

. The agent determines his actions based on

an internal policy π which maps an action to every

observable state:

π : s ← a (1)

For every chosen action the agent receives a re-

ward r

t+1

and a new state s

t+1

. Goal of any RL al-

gorithm is for the agent to adjust his policy in such a

way that his return g

, which is given as the weighted

sum of the temporal rewards

∞

∑

k=0

t+k+1

(2)

is maximized at any given timestep. The discount

factor γ ∈ [0, 1) indicates the relevance of future re-

wards. In general, the agents policy can be either

stochastic or deterministic, latter will further be de-

noted with µ. In order for the agent to learn an op-

timal policy π

∗

which maximizes his return in the

given environment, the problem statement has to ful-

ﬁll the Markov-Property, meaning that at any point

of time all of the environments historic state infor-

mation is captured in the current state s

and so any

following state and future rewards solely depend on

and the agents chosen action a

. A process sat-

isfying the Markov-Property can be described as a

Markov-Decision-Process (MDP) (Puterman, 2010).

Since complete satisfaction of this condition for real-

world problems is often unfeasible, a good approxi-

mation of an MDP is often sufﬁcient for the applica-

bility of reinforcement learning.

Different approaches exist for solving an MDP

with RL, one of which is the concept of Temporal-

Difference (TD) Learning. Here, the agent maintains

an estimate of the achievable return which can itera-

tively be updated based on the truth found in the ac-

tually experienced state sequences and the received

rewards during the interaction with the environment.

One proven way of solving an MDP with TD-methods

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles

Figure 3: Basic structure of the DDPG actor-critic agent. Actor with parameters θ

, state s as input and action based on

deterministic policy µ as output. Critic taking both state and chosen action of the actor as input and giving out an according

Q-Value, based on parameters θ

. Update signal for higher rewards for actor as policy gradient, derived with the chain-rule

of both networks (Timothy P. Lillicrap et al., 2015).

is Q-Learning where the agent estimates a Q-Value

for every possible action, indicating the achievable fu-

ture return when this action is chosen. After every

interaction with the environment, an iterative update

of the current estimation for the chosen action can be

made by

Q(s

, a

) ← Q(s

, a

) + α [ ˜y

− Q(s

, a

)] (3)

with

˜y



t+1

+ γ max

t+1

Q(s

t+1

, a

t+1

)



(4)

With a sufﬁciently small learning rate α, the iterative

updates of the agents estimations are proven to con-

verge towards the real Q-Values of the MDP. Knowl-

edge of the Q-Values automatically results in follow-

ing the optimal policy if the agent in every state picks

the action with the highest Q-Value:

∗

(s) = argmax

Q(s, a) (5)

which ultimately maximizes his return. Even

though Q-Learning has proven to be very effective

for rather small and low-dimensional control tasks,

the need for discrete state and actions spaces limits

the number of application options for real-world opti-

mization problems.

2.4 Deep Reinforcement Learning

Deep reinforcement learning, as a combination of

deep learning with artiﬁcial neural networks and the

interactive learning structure of RL, has gained much

attention in recent years. As the foundation of al-

most any major progress in artiﬁcial intelligence in

the past decade, neural networks offer the essentials

to make RL valuable for a whole new range of highdi-

mensional real-world optimization problems. Hence,

deep neural networks can be deployed as non-linear

function approximators with trainable parameters θ

in the context of Q-learning, resulting in the Deep Q-

Network (DQN) algorithm (Volodymyr Mnih et al.,

2013). Instead of iteratively updating running esti-

mates of the actions Q-values, the DQN is trained to

output the correct values for any given state by mini-

mizing the loss:

L(θ

) =



− Q(s

, a

| θ

)



(6)

with



t+1

+ γ max

t+1

Q(s

t+1

, a

t+1

| θ

)



(7)

For what was always believed to be inherently unsta-

ble, (Mnih et al., 2015) show effective learning of the

DQN by introducing two main features: training of

the network with uncorrelated minibatches of the past

- called experience replay - and deriving target val-

ues y

with a separate network with parameters θ

called the target network. In this manner, a DQN-

agent could be trained to achieve human level per-

formance in many games of an Atari 2600 emulator

only receiving unprocessed pixels as state-input and

the raw score as a reward.

The processing of highdimensional state-vectors

can be seen as a signiﬁcant advantage for many en-

gineering tasks where often data gathered from a

large number of sensors has to be ﬁltered elaborately

for the use with conventional optimization methods.

However, for many control tasks even bigger advan-

tages are believed to arise from the use of continu-

ous control parameters in order to avoid quality lim-

iting discretization errors. Plain Deep-Q-Networks

do not offer the chance of continuous output param-

eters. Thus, numerous evolutions of DQN have been

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

proposed in the last years, mostly categorized as pol-

icy gradient algorithms like the Deep Deterministic

Policy Gradient (DDPG) (Timothy P. Lillicrap et al.,

2015) or Trust Region Policy Optimization (TRPO)

(John Schulman et al., 2015). A continuous variant of

DQN is proposed in (Shixiang Gu et al., 2016) with

the Normalized Advantage Function. Continuous pol-

icy gradient methods use an actor-critic architecture

where an actor represents a currently followed policy

with output of continuous action variables which are

then evaluated by a second part called the critic. In

case of DDPG both actor and critic are presented as

deep neural networks, where the actor performance

is evaluated through a deterministic policy gradient

(David Silver et al., 2014) derived from the critic as a

DQN. The DDPG architecture is shown in Figure 3.

3 REINFORCEMENT LEARNING

FOR HEV CALIBRATION

3.1 Related Work

Compared to traditional and most commonly used

methods for deriving efﬁcient operating strategies in

the automotive industry like DP, ECMS or fuzzy ap-

proaches, machine learning and in particular rein-

forcement learning present new opportunities with

signiﬁcant advantages. Most of all the agent would

not require any prior information about the course of

the route in order to decrease fuel consumption since

he is fully trained to do so with only current state in-

formation.

In (X. Lin et al., 2014) a RL agent is given control

over particular parameters of the control unit within

the model of a HEV. Given a discrete state consisting

of power demand, vehicle speed, and battery charg-

ing state the agent was able to determine a strategy

to regulate battery output voltage and gear transla-

tion resulting in fuel savings up to 42%. In (C. Liu

and Y. L. Murphey, 2014) the discrete state space of

the constrained optimization is extended with speciﬁc

trip information like the remaining traveling distance,

which made the operating strategy even more efﬁ-

cient. In both cases traditional Q-learning methods

were used for optimization which require discretiza-

tion of the generally continuous state and control pa-

rameters within the vehicle.

Preliminary investigations (Patrick Wappler,

2016) have proven the high quality of the gained

solutions of classic RL algorithms. The discrete

representation of the results in a Q-table would also

allow a straight forward approach for the integration

in common energy management systems of HEV.

However, the well-known curse of dimensionality

exponentially increases the size of the table with in-

clusion of further variables which limits the problem

to rather small state and action spaces in order to deal

with restrictions concerning memory and computing

time. Additionally, without the use of approximation

or interpolation methods the agent is unable to value

any state he has not processed during training. With

severely different driving scenarios occuring in the

real world considering trafﬁc or driving styles, the

derivation of a fully complete discrete representation

is unfeasible. A rough discretization excludes valu-

able information within the optimization problem

and limits the achievable fuel savings.

3.2 Problem Formulation

The central goal of the energy management is ﬁnding

a control signal action(t) for the minimization of the

fuel consumption m

Fuel

during a drive of time t

≤ t ≤

, expressed as the minimization of an integral value

J =

˙m

Fuel

(action(t), t)dt (8)

wherein ˙m

Fuel

describes the fuel mass ﬂow rate.

The minimization of J is subject to physical limita-

tions concerning performance measures, limitations

of the energy storage and variance of the charging

state of the battery (SOC). Thus, the energy man-

agement optimization problem is a temporally limited

optimization problem with secondary and boundary

conditions (Onori et al., 2016).

3.2.1 Boundary Conditions

Unlike plug-in hybrids, mild hybrids can not be

charged externally so they must be operated in a

charge-conserving way. Hence a boundary condition

can be stated:

SOC(t

) = SOC

target

(9)

which also allows for comparison of different so-

lutions with an optimal solution found by dynamic

programming. A desired target value could be:

SOC

target

= SOC(t

) (10)

maintaining the initial charging state of the bat-

tery at the beginning of the driving cycle. How-

ever, for practical application a hard constraint does

not seem necessary and ranging the terminal charging

state SOC(t

) between threshold values is acceptable.

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles

With a sufﬁciently small range, a deviation to the tar-

get value does not lead to interference of the vehicles

functionality (Onori et al., 2016).

3.2.2 Secondary Conditions

Secondary conditions of the optimization problem

can be stated for the state variables of the HEV as well

as the control parameters. Limiting state variables

like the SOC and the battery temperature ϑ

bat

ensure

safe use of the components, operation in regions of

high efﬁciency and extended lifetime. Limitations of

the control variables arise from physical limits of ac-

tuators and maximum performance (or power output

P) of engines and battery.

Thus, it can be stated:

SOC

min

≤ SOC(t) ≤ SOC

max

bat,min

≤ P

bat

(t) ≤ P

bat,max

bat,min

≤ ϑ

bat

(t) ≤ ϑ

bat,max

Trq

x,min

≤ Trq

(t) ≤ Trq

x,max

x,min

≤ n

(t) ≤ n

x,max

(11)

for

x = ICE, EM

where n and Trq denote rotational speeds and

torque of the EM and ICE. The notations (·)

min

and

(·)

max

represent the minimum and maximum of the

respective entries at every point of time.

4 REINFORCEMENT LEARNING

SETUP

The use of deep reinforcement learning requires the

statement of the problem as the typical interaction of

an agent with his environment. Concerning the energy

management problem of HEV, the agent can be cho-

sen to represent the control unit of the vehicle. Then

the environment can include any outside part of the

world containing information for the derivation of an

efﬁcient operating strategy. Here the environment is

assembled by two models, one of the vehicle and one

of the driver.

4.1 Vehicle Model

The mild hybrid power train, which is used for the

vehicle model, is brieﬂy described in section 2.2 and

shown in Figure 1. Both energy converters are located

on the crank shaft of the driving unit where the torque

is split according to the operating strategy and physi-

cal limitations. The ICE gets fuel from a fuel tank and

the EM is supplied with electric energy from a battery.

The same battery stores the recuperated energy from

vehicle deceleration, downhill driving or load point

shifting of the combustion engine.

Since targets concerning speed and acceleration

are speciﬁed by driving cycles, the vehicle model is

orientated backwards with power demands calculated

from the wheels to the driving unit with each inter-

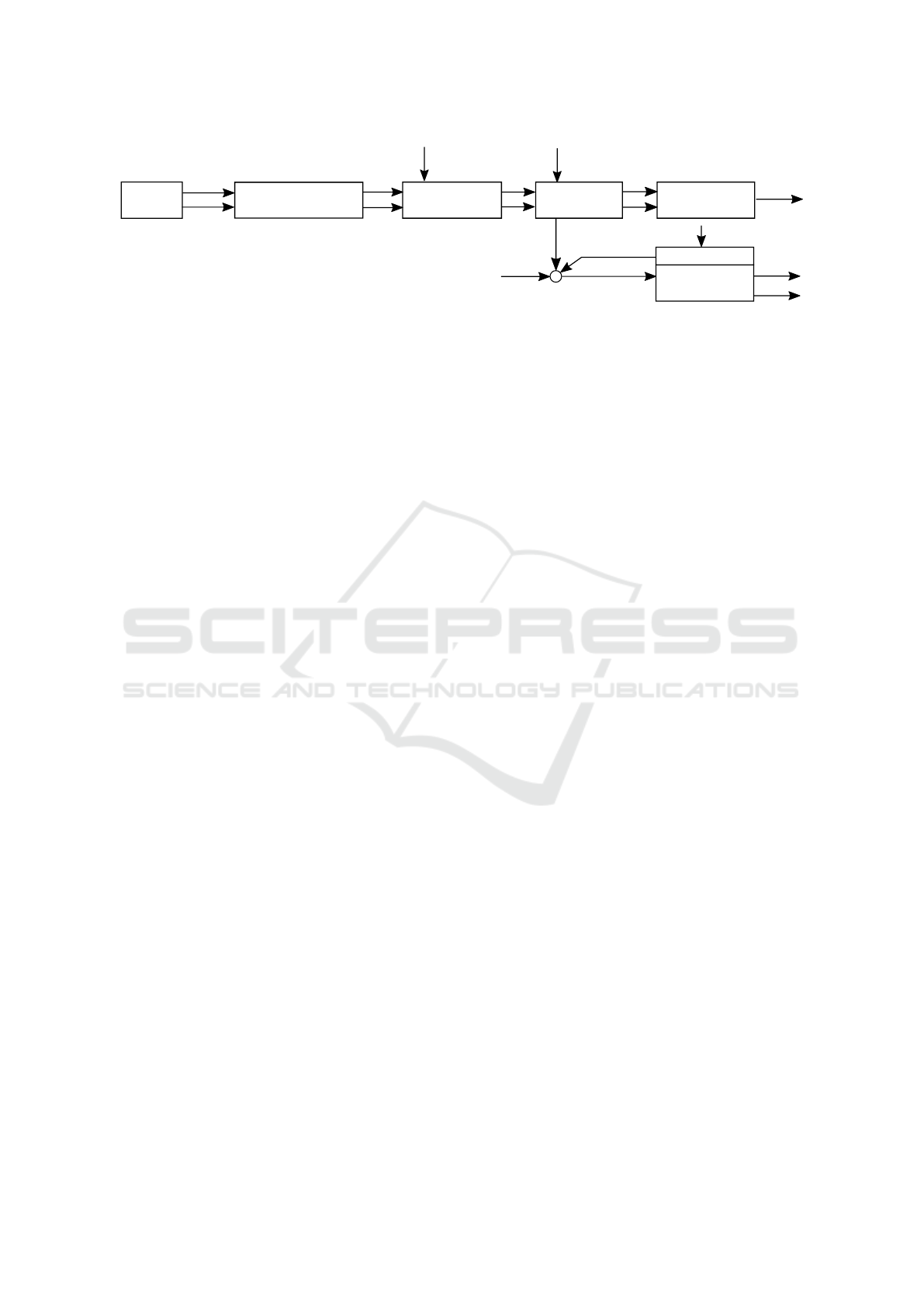
mediate component modelled individually. Figure 4

shows the signal ﬂow of the vehicle model as a block

diagram.

4.1.1 Vehicle Dynamics

With a predetermined speed v

veh

and slope δ

veh

from

the driving cycle and the vehicle parameters par

veh

the required power for the vehicle P

veh

can be deter-

mined by approximating the driving resistance caused

by rolling friction and aerodynamic drag (Guzzella

and Sciarretta, 2013):

veh

= f (v

veh

, δ

veh

, par

veh

) (12)

With the addition of the dynamic rolling radius of

the wheel r, the required torque Trq

whl

and the rota-

tional speed at the wheels n

whl

can be calculated to:

Trq

whl

veh

· r

veh

(13)

whl

veh

2π · r

(14)

4.1.2 Consumption Model

An analytical description of chemical processes

within the combustion engine is barely possible,

hence the fuel consumption of the ICE was modelled

empirically based on measured data from a power

train test bench. With input of the speed and torque

at the wheels, the selected gear G as well as the

electric power of the electric motor P

EM,el

(derived

by the chosen action of the agent), the model deter-

mines a fuel volume m

Fuel

consumed in a time span

of ∆t = 1s:

Fuel

= f (n

whl

, Trq

whl

, G, P

EM,el

) (15)

4.1.3 Electric Motor Model

The model of the EM determines the losses due to the

conversion between electric and mechanical power.

Based on the efﬁciency for a given crankshaft speed

crs

and the direction of the conversion, the empirical

model outputs the power after losses:

mech

= f (n

crs

, P

) (16)

= f (n

crs

, P

mech

) (17)

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

Driving

cycle

Motor

EM,el

aux

velocity

slope

Trq

crs

Trq

ice

Gear

Trq

EM,target

Fuel

SOC

bat

ICE

Differential &

gearbox

Driving resistance

& wheel

Battery

Cooling

cool,el

Trq

whl

ice

Control

Figure 4: Signal ﬂow diagram of the HEV model.

4.1.4 Battery Model

For the calculation of change in charging state, the

battery was modelled as an equivalent two terminal

network with simpliﬁcation of the underlying physics

of batteries. With neglection of any effect of tempera-

ture or loading cycles for the batteries capacitance, the

change of charging state was purely determined from

the previous state and any required power output from

the battery, composing of the power for operation of

the EM as well as any auxiliary users (e.g. the cooling

system):

SOC

t+1

= f (SOC

, P

bat

) (18)

For results shown in section 5.4, a temperature

model of the battery was implemented approximating

the change of temperature due to the power output and

the cooling control signal Cool

Control

bat,t+1

= f (ϑ

bat,t

, P

bat

,Cool

Control

) (19)

The utilization of the cooling system causes an ad-

ditional power consumption P

cool,el

4.2 Driver Model

The driver is implemented as driving cycles imply-

ing speciﬁc velocity procedures the vehicle drives

through simulatively. Next to standard procedures

for the determination of emission levels, cycles gen-

erated by a stochastic driver model from (Liessner

et al., 2017) are used for a more realistic reproduc-

tion of real-world trafﬁc scenarios. Hereby, diverse

characteristics can be considered within those cycles

like different market features, speciﬁc driving styles

and habits or trafﬁc situations at different points dur-

ing the day. The tuning of operating strategies to-

wards special features in real-world driving scenarios

can be seen as a major beneﬁt for customers concern-

ing fuel efﬁciency of their vehicles since it can be as-

sumed that e.g. an operating strategy derived with eu-

ropean driving data will not work as efﬁcient in India

or China.

4.3 States, Actions and Reward

4.3.1 States

At each timestep during simulative driving the envi-

ronment provides a state vector for the agent consti-

tuting the current internal state of the vehicle. Here,

the state vector is deﬁned by:

= (n

whl

, M

whl

, SOC, ϑ

bat

, G) (20)

In the case of the underlying vehicle model not

taking into account the battery temperature and the

according power limit, ϑ

bat

can be rejected from the

state vector. In this form the environmental state com-

plies with the Markov-Property in terms of any fol-

lowing state of the environment (vehicle model) being

only dependent on the current state and the chosen ac-

tion by the agent. Hence reinforcement learning can

be utilized to solve the underlying control problem.

4.3.2 Actions

For any given state the agent has to choose an action

which he considers optimal for the maximization of

his return. For the energy management problem ac-

tions can include any parameterizable metric with an

effect on fuel and energy efﬁciency. Commonly pa-

rameterized metrics in the optimization of operating

strategies are the split of torque between the electric

motor and the combustion engine, the choice of the

gear or the management of the battery temperature.

Here we only consider the choice of power output

for the electric motor as an action controlled by the

RL agent. Choice of gear and temperature regula-

tion are implemented as heuristics. As mentioned,

the electric motor is subject to multiple restrictions

concerning the maximum possible power output. Not

only is this limited by the current crankshaft speed

but also - if considered by the model - by the maxi-

mum power output of the battery regarding its temper-

ature. In contrast to discrete Q-tables, where the use

of certain actions in speciﬁc states can be restricted

by assigning extremely low Q-values, a continuous

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles

output of neural networks can hardly be limited with-

out any additional feedback signal which the network

can learn to cope with. Hence the selectable action of

the agent was implemented as a percent value of the

current maximally applicable torque with the output

layer of the neural network as a tanh-layer restricting

the action to a

∈ [−1, 1]. The applicable power of the

electric motor is then determined by:

(

· P

EM,max

f or a

≥ 0

· P

EM,min

f or a

< 0

(21)

where the agent can choose to operate the EM ei-

ther as a motor or a generator respectively by choos-

ing positive or negative action values.

4.3.3 Reward

Since the main goal of the operating strategy is min-

imizing fuel consumption but the RL agent aims at

maximizing his return, a common practice is to state

the reward with a negative sign. Here the agents re-

ward based on his selected action is deﬁned as the

negative total energy usage per timestep by:

= −(E

che

+ κE

) (22)

with

che

= m

Fuel

· ρ

Fuel

· H

Fuel

(23)

and

= P

bat

· ∆t (24)

where the agent not only gets incentivized to min-

imize fuel consumption but to do so with the least

amount of electric energy as possible. Thereby E

is weighted by a factor κ = f (SOC) which rates the

cost of electric energy proportionally to the deviation

of the SOC to a target value SOC

target

. In doing so, the

agent should learn to balance his SOC over the course

of a driving cycle as described in section 3.2.1.

4.4 Training

With the stated RL speciﬁc formulation, a DDPG

algorithm was implemented for solving the energy

management problem. With a lower computational

cost than TRPO and a straight forward implementa-

tion, DDPG has proven its usability and sample ef-

ﬁciency in other implementations (Duan Yan et al.,

2016). Additionally, the actor critic architecture of-

fers a good approach for possible application in real-

world vehicle-hardware with rather low computa-

tional capabilities, since the resulting operating strat-

egy is captured in a single neural network.

Training was conducted for one speciﬁc driving

cycle which could include any type of information

about driving styles or trafﬁc situations. The current

operating strategy was evaluated every 5 episodes on

that speciﬁc cycle to track the learning progress. In

training episodes however, as mentioned, the agent

was confronted with a unique stochastic cycle based

on the original one in order to prevent the strategy

from overﬁtting to a speciﬁc velocity procedure. At

the same time, the length of the stochastic cycles

was varied in every episode. In order to increase the

amount of possible states which the network is con-

fronted with during training, the initial values of the

network were varied each training episode on a ran-

dom basis and within deﬁned bounds. For evaluation

the SOC and ϑ

bat

were always initialized to 50% and

◦

C in order to the track learning progress.

For general exploration of the state space, as

in (Timothy P. Lillicrap et al., 2015), an Ornstein-

Uhlenbeck-Process (Borodin and Salminen, 1996)

was used for adding noise to the chosen actions of

the agent. The exploration noise was slowly decayed

over the ﬁrst 1000 training episodes.

The training procedure of DDPG is shown as

pseudocode in algorithm 1.

Algorithm 1: Pseudocode for DDPG.

1: initialize networks

2: initialize replay buffer

3: for episode = 1,M do

4: initialize exploration process

5: observe initial state s

6: for t=1,T do

7: choose action a

with actor and add noise

8: execute a

9: observe r

t+1

and s

t+1

10: store [s

, a

, r

t+1

, s

t+1

] in buffer

11: choose minibatch from buffer

12: update critic with loss L from minibatch

13: update actor with policy gradient

14: update target networks

4.5 Hyperparameters

Similar to the original architecture, both actor and

critic were implemented as deep neural networks with

2 hidden layers each with 400 and 300 neurons and

Rectiﬁed-Linear-Unit activation. The actor receives

a standardized state vector and outputs a continuous

action as described. The critic additionally takes in

the actions into the second layer of the network and

outputs a continuous Q-Value through linear activa-

tion. An Adam-optimizer was chosen for the update-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

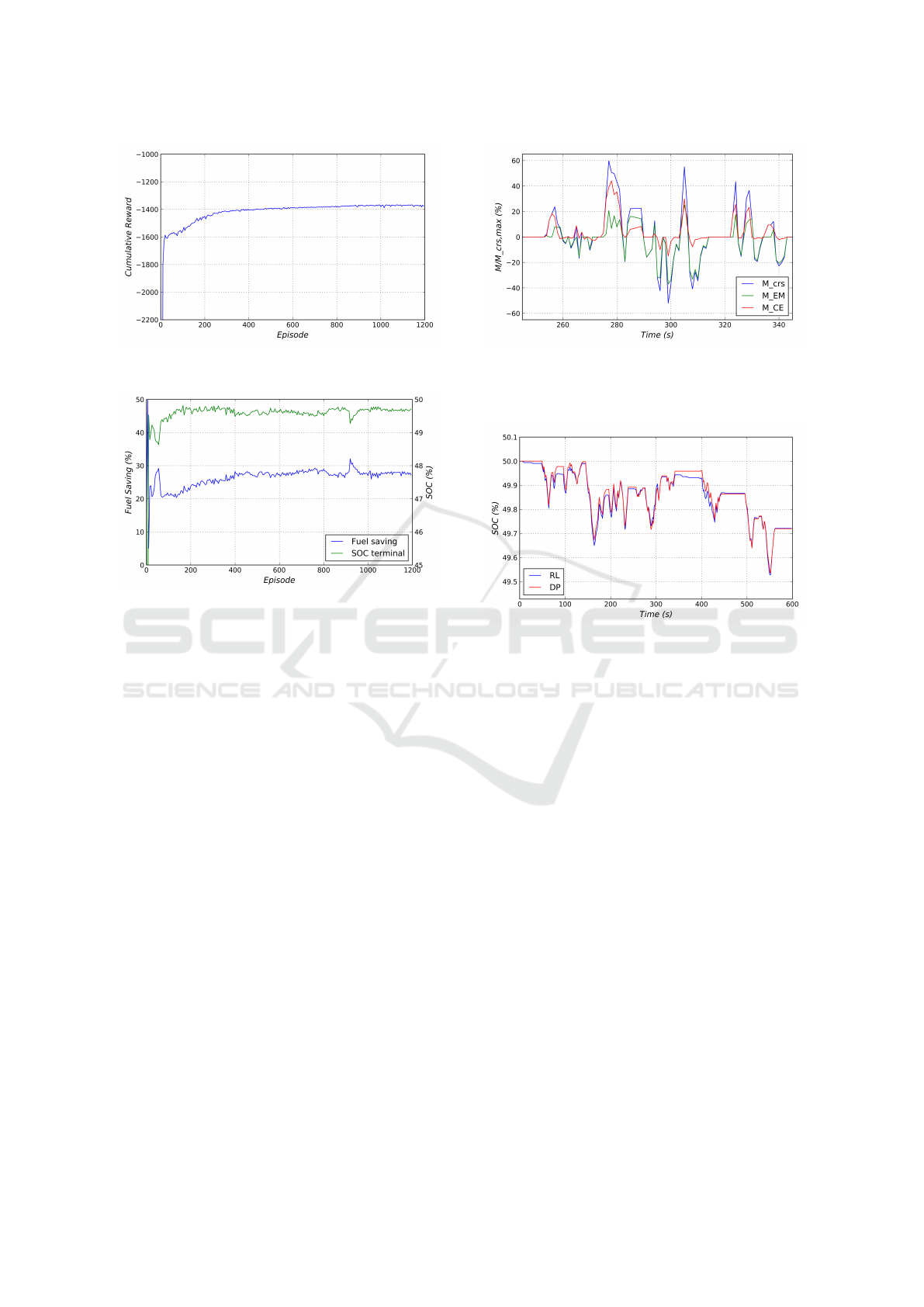
Figure 5: Cumulative reward (return) of the agent during

training process for the New-York-City-Cycle.

Figure 6: Fuel saving in % compared to driving solely with

the combustion engine (blue) and terminal battery charging

state (green) during the training process for the New-York-

City-Cycle.

process of the neural networks with a learning rate of

−5

for the critic and 10

−4

for the actor. The replay

buffer for sampling minibatches was initialized to a

size of 10

where in every timestep a minibatch size

of 32 was sampled to update the critic network.

For the training process a discount factor of γ = 0

was chosen, thus the agent optimized his strategy only

towards local rewards. However, since the reward

function contains a dynamic weighting factor depen-

dent on the current charging state, the agent has turned

out to adapt his strategy rather long-sighted. That way

signiﬁcantly better results were achieved compared to

discounts γ > 0.

5 RESULTS

5.1 Learning

Figure 5 and 6 show exemplary training progress

for simulative driving of the New-York-City-Cycle

(NYCC), a characteristic cycle for low speed city

driving with many start-stop maneuvers. As shown,

the agent continuously increases his cumulative re-

Figure 7: Excerpt of the split of overall torque (blue) be-

tween the combustion engine (red) and the electric mo-

tor (green) for the New-York-City-Cycle, controlled by the

fully trained agent.

Figure 8: Comparison of battery loading trajectories for the

New-York-City-Cycle with the strategy learned by the RL

agent (blue) and the optimal strategy derived by Dynamic

Programming (red).

ward - the return - with progressive training. In do-

ing so, according to the reward function, the resulting

energy consumption is decreased consistently with a

constant fuel saving of over 20% compared to driv-

ing with the combustion engine only, established very

early in the training process. With the resulting bat-

tery charge at the terminal state of an episode very

close to the initial value of 50%, the SOC can be

described as balanced. In a low speed environment

where the rather low-powered electric motor can be

used very effectively, a positive deviation of the bat-

tery charge throughout the cycle can well be expected

for any efﬁcient operating strategy. Since the agent

did not have any hard constraint towards the charging

state but was only implicitly incentivized through the

reward function, he is free to make any compromise

between the use of chemical or electric energy which

he considers most efﬁcient.

Figure 7 shows an excerpt from the resulting strat-

egy for the NYCC in terms of split of torque between

the combustion engine and the electric motor which

the agent establishes with the choice of his actions. As

shown, the agent fully learns to use moments of vehi-

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles

cle deceleration for recharging the battery with recu-

perational energy by choosing actions a < 0 which

runs the electric motor in generator-mode. Mention-

able is that after 20 episodes of training the level of

this behavior is already nearly as sophisticated as af-

ter 1000 episodes of simulative driving.

It is recalled that the results for purely determin-

istic cycles only serve evaluation purposes. Since the

agent is trained with random cycles similar to the one

he is being evaluated on, he is able to deal with high

amounts of stochasticity concerning the velocity pro-

ﬁle of the drive and will control the electric motor just

as efﬁcient. Due to the lack of space this can not be

fully presented here and will be brieﬂy covered in sec-

tion 5.3.

In general, training the agent for a variety of dif-

ferent driving cycles is exceptionally stable. For driv-

ing proﬁles including rather high velocity and accel-

eration rates the learning rate of the actor network had

to be adjusted occasionally, since the unavoidable in-

crease of the reward magnitude through higher mo-

mentary fuel consumptions leads to bigger gradients

in the beginning of the training, where the neural net-

works are initialized with outputs close to zero and

the loss increases accordingly. Clipping the rewards

or gradients to certain maximum values would be a

considerable option to avoid this, though useful infor-

mation about the fuel consumption might be excluded

at a later point in the training.

5.2 Quality Analysis

For analyzing the quality of the operating strategy

learned by the agent, a comparison was made to a

strategy derived by dynamic programming with dis-

crete state and action spaces. With full knowledge

of the cycle in advance, the result of DP can be seen

as the globally optimal solution even though a small

error will be unavoidable through the use of discrete

parameters.

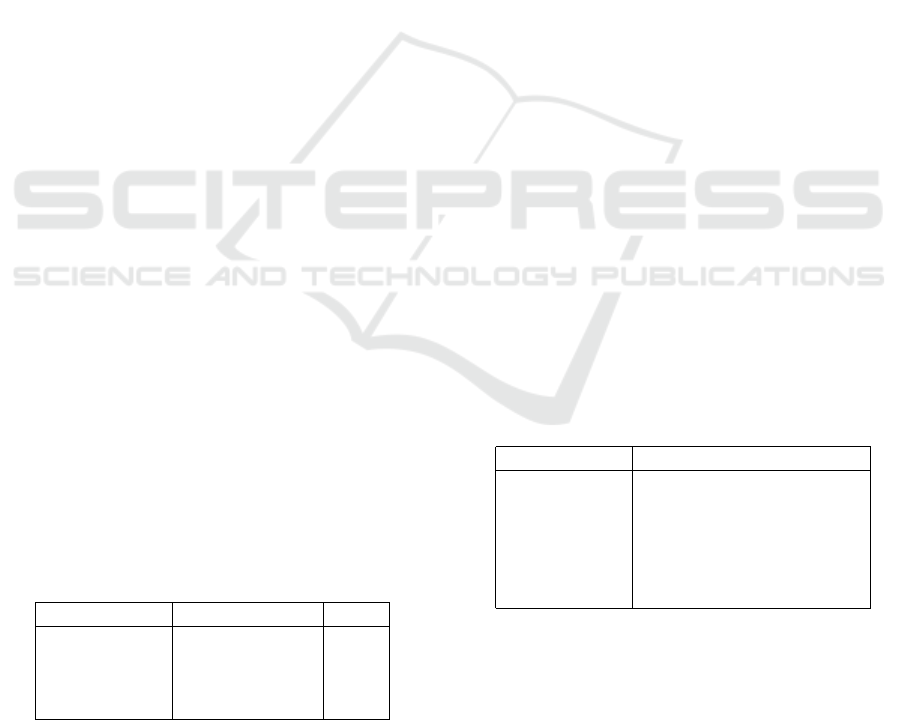
Table 1: Comparison of fuel savings for the strategy derived

by the RL agent and a global optimum computed with DP

in contrast to driving with ICE only.

Driving Cycle RL DP ∆

NYCC 28.6% 29.5% 0.9%

WLTP 16.0% 16.3% 0.3%

US06 10.8% 11.2% 0.4%

FTP75 20.1% 20.7% 0.6%

Table 1 shows the resulting fuel savings for 4 dif-

ferent velocity proﬁles typically used in calibration

and certiﬁcation processes. The DP results are based

on the terminal SOC of the RL strategy in order to as-

sure comparability. As seen, only small deviations oc-

cur, where the optimal strategy achieves less than 1%

more savings in fuel which makes the strategy learned

by the agent nearly-optimal. A comparison of both

battery charging trajectories resulting from the operat-

ing strategy for the NYCC is shown in Figure 8, con-

ﬁrming that the agent’s strategy converges towards a

global optimum and does not get stuck in a poor local

optimum throughout the training process. In contrast

to DP, the RL agent does not need any prior informa-

tion about the driving route and he is trained to control

the EM optimally with only momentary state infor-

mation provided by the vehicle environment. A local

strategy optimization with nearly globally optimal so-

lutions can be seen as a major advantage of deep rein-

forcement learning over any other traditional method

for the derivation of operating strategies for HEVs.

5.3 Stochastic Cycles

As mentioned, in every episode of the training process

the agent is confronted with a different stochastic ve-

locity proﬁle with the same characteristics concerning

speed and acceleration as the one he will be evalu-

ated on. Next to preventing overﬁtting, this is mainly

aimed at increasing the agent’s ability to general-

ize his strategy towards potentially unknown states

and driving proﬁles. Where traditional RL methods

with discrete parameters require tedious approxima-

tion methods, generalizing knowledge is a major ad-

vantage of deep RL obtained through the use of neural

networks.

Table 2: Comparison of a strategy trained with stochastic

velocity proﬁles and the other trained solely deterministi-

cally. Results are shown as the deviation of fuel saving in

% compared to a global optimal solution computed by dy-

namic programming.

Driving Cycle Stochastic Deterministic

NYCC 1.6% 1.5%

Rand

NYCC,1

0.95% 3.1%

Rand

NYCC,2

1.5% 6.6%

Rand

NYCC,3

1.7% 2.5%

Rand

NYCC,4

1.4% 3.1%

Rand

NYCC,5

1.6% 3.2%

Table 2 shows a comparison of two strategies, one

trained with stochastic cycles based on the NYCC,

the other trained purely with the deterministic NYCC

which was repeatedly driven through simulatively.

Where the deterministically derived strategy performs

good on the original NYCC, it is shown that for any

other stochastic velocity proﬁle similar to the origi-

nal NYCC the strategy performs signiﬁcantly worse

which clearly indicates overﬁtting. The stochastically

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

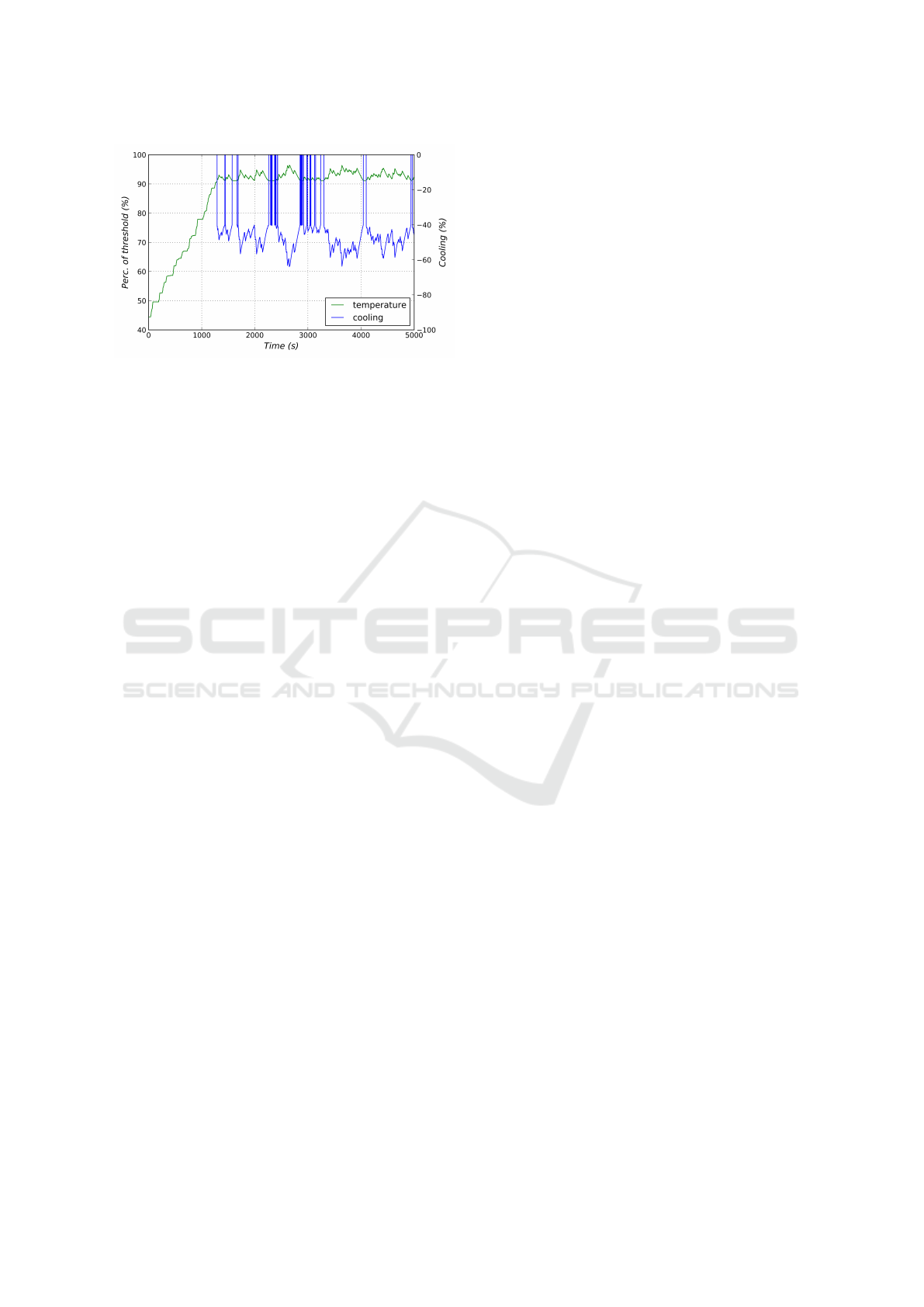
Figure 9: Battery temperature relative to the threshold for

power limitation (green) together with the control of cool-

ing power (blue) for simulative driving of a 5.000s long

stochastic cycle based on NYCC with the operating strat-

egy learned by the agent.

trained strategy in contrast shows constantly good

results for any driven route similar to the original

NYCC with a deviation to the global optimal solution

of only 0.9 − 1.7%. Additionally, stochastic cycles

could include any type of further information about

driving habits or trafﬁc scenarios which neural net-

works could easily take into account for the operating

strategy. This results in a much more accurate illustra-

tion of realistic trafﬁc potentially leading to increased

fuel savings and emission reduction in the actual oper-

ation of the vehicle rather than deriving approximate

values on a test bench which could hardly be achieved

in the real-world.

5.4 Inclusion of Temperature

Information

As mentioned, for this paper a temperature approx-

imation of the battery was included into the vehicle

model combined with a power restriction to prevent

damage from overheating. Additionally, a cooling

mechanism of the battery was implemented with a

heuristic used for control. Figure 9 shows an exem-

plary development of the battery temperature for sim-

ulative driving of a 5000 s stochastic cycle, which the

agent has optimized his strategy for. As it shows, the

agent has learned to control the EM in such a man-

ner that the temperature level of the battery remains

below a threshold value over which the maximum

power output of the battery would be restricted and

the agent could not use the full potential of the elec-

tric motor. Additionally, a clear tendency can be seen

to keep the temperature level close to the threshold

level of the cooling heuristic, around 91%, in order to

decrease the additional use of battery power for the

cooling system. With the additional boundary con-

dition implemented implicitly into the vehicle model

and the agent not receiving any explicit information

except the resulting reward based solely on the en-

ergy consumption, the agent still found nearly optimal

solutions to the energy management problem. Here

the major potential of deep reinforcement learning

can be seen compared to traditional methods for the

derivation of operating strategies with discrete vari-

ables as additional optimization goals can be imple-

mented into the training process without any signiﬁ-

cant extra cost or loss in quality.

6 CONCLUSION

The energy management of hybrid electric vehicles

poses major challenges for automobile manufacturers

where traditional approaches show many deﬁciencies

in processing additional information concerning real-

world driving scenarios. In this paper, a deep rein-

forcement learning framework has been derived that

offers great potential for solving many of those prob-

lems. It has been shown that a deep RL agent is ca-

pable of achieving nearly-optimal fuel consumption

results with a locally trained strategy which can be ap-

plied online in the vehicle. In contrast to dynamic pro-

gramming, no prior knowledge of the driving route is

necessary and the training with stochastic driving cy-

cles allows for greater generalization to variously dif-

ferent velocity proﬁles. Additionally, deep reinforce-

ment learning allows the efﬁcient inclusion of further

optimization criteria.

Another advantage can be seen in the potential

adaptability of the agent which would be able to learn

from real driving data even during direct usage of the

vehicle. A conceivable result would be an intelli-

gent energy management system constantly adapting

to speciﬁc driving habits, typically driven routes or

other desirable characteristics of the vehicle owner or

driver.

Future work can build up on the presented re-

sults and the arising potential for further improve-

ment. This includes a broader examination of the

agents capabilities of online generalization and adapt-

ability, simulating alternating trafﬁc scenarios or dif-

ferent driving habits while constantly updating the

agents strategy. Furthermore, a big ﬁeld of research

arises from the integration of additional vehicle or fu-

ture route information, e.g. from navigation data. A

predictive strategy offers great potential for further re-

duction of fuel consumption and emission-levels.

In a next step, the algorithm could be applied on

a power train test bench for assessing and reﬁning the

results learned with the simulation model. Similarly,

the transfer into the real vehicle would be feasible.

Deep Reinforcement Learning for Advanced Energy Management of Hybrid Electric Vehicles

REFERENCES

Borodin, A. N. and Salminen, P. (1996). Ornstein-

uhlenbeck process. In Borodin, A. N. and Salminen,

P., editors, Handbook of Brownian Motion — Facts

and Formulae, pages 412–448. Birkh

auser Basel,

Basel.

C. Liu and Y. L. Murphey (2014). Power management

for plug-in hybrid electric vehicles using reinforce-

ment learning with trip information. In 2014 IEEE

Transportation Electriﬁcation Conference and Expo

(ITEC), pages 1–6.

Chae, H., Kang, C. M., Kim, B., Kim, J., Chung, C. C., and

Choi, J. W. (2017). Autonomous braking system via

deep reinforcement learning. CoRR, abs/1702.02302.

Chasse, A. and Sciarretta, A. (2011). Supervisory control

of hybrid powertrains: An experimental benchmark of

ofﬂine optimization and online energy management.

Control Engineering Practice, 19(11):1253–1265.

David Silver, Guy Lever, Nicolas Heess, Thomas Degris,

Daan Wierstra, and Martin Riedmiller (2014). Deter-

ministic policy gradient algorithms. In Tony Jebara

and Eric P. Xing, editors, Proceedings of the 31st In-

ternational Conference on Machine Learning (ICML-

14), pages 387–395. JMLR Workshop and Conference

Proceedings.

Duan Yan, Chen Xi, Houthooft Rein, Schulman John, and

Abbeel Pieter (2016). Benchmarking deep reinforce-

ment learning for continuous control. International

Conference on Machine Learning, 2016:1329–1338.

European Commission (2017). Draft regulation: real-

driving emissions in the euro 6 regulation on emis-

sions from light passenger and commercial vehicles.

Guzzella, L. and Sciarretta, A. (2013). Vehicle propulsion

systems: Introduction to modeling and optimization.

Springer, Heidelberg, 3rd ed. edition.

John Schulman, Sergey Levine, Philipp Moritz,

Michael I. Jordan, and Pieter Abbeel (2015).

Trust region policy optimization. CoRR.

Kirschbaum, F., Back, M., and Hart, M. (2002). Determina-

tion of the fuel-optimal trajectory for a vehicle along a

known route. IFAC Proceedings Volumes, 35(1):235–

239.

Leroy, T., Malaize, J., and Corde, G. (2012). Towards

real-time optimal energy management of hev pow-

ertrains using stochastic dynamic programming. In

2012 IEEE Vehicle Power and Propulsion Conference,

pages 383–388. IEEE.

Liessner, R., Dietermann, A., B

aker, B., and L

upkes, K.

(2017). Generation of replacement vehicle speed cy-

cles based on extensive customer data by means of

markov models and threshold accepting. SAE Inter-

national Journal of Alternative Powertrains, 6(1).

Mirzaei, H. and Givargis, T. (2017). Fine-grained ac-

celeration control for autonomous intersection man-

agement using deep reinforcement learning. CoRR,

abs/1705.10432.

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Ve-

ness, J., Bellemare, M. G., Graves, A., Riedmiller,

M., Fidjeland, A. K., Ostrovski, G., Petersen, S.,

Beattie, C., Sadik, A., Antonoglou, I., King, H., Ku-

maran, D., Wierstra, D., Legg, S., and Hassabis, D.

(2015). Human-level control through deep reinforce-

ment learning. Nature, 518(7540):529–533.

Onori, S., Serrao, L., and Rizzoni, G. (op. 2016). Hy-

brid electric vehicles: Energy management strategies.

Springer, London.

Patrick Wappler (2016). Applikation von hybridfahrzeu-

gen auf basis k

unstlicher intelligenz. Master’s the-

sis, Technische Universit

at Dresden, Lehrstuhl f

Fahrzeugmechatronik.

Puterman, M. L. (dr. 2010). Markov decision processes:

Discrete stochastic dynamic programming. Wiley Se-

ries in Probability and Statistics. John Wiley & Sons,

Hoboken, [dodr.] edition.

Shixiang Gu, Timothy P. Lillicrap, Ilya Sutskever,

and Sergey Levine (2016). Continuous deep q-

learning with model-based acceleration. CoRR,

abs/1603.00748.

Sutton, R. S. and Barto, A. G. (2012). Introduction to rein-

forcement learning. MIT Press, 2 edition.

Tate, E. D., Grizzle, J. W., and Peng, H. (2008). Shortest

path stochastic control for hybrid electric vehicles. In-

ternational Journal of Robust and Nonlinear Control,

18(14):1409–1429.

Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel,

Nicolas Heess, Tom Erez, Yuval Tassa, David Silver,

and Daan Wierstra (2015). Continuous control with

deep reinforcement learning. CoRR, abs/1509.02971.

UNECE Transport Division (2005). Vehicle regulations:

Regulation no. 101, revision 2,.

Volodymyr Mnih, Koray Kavukcuoglu, David Silver,

Alex Graves, Ioannis Antonoglou, Daan Wierstra, and

Martin Riedmiller (2013). Playing atari with deep re-

inforcement learning. In NIPS Deep Learning Work-

shop.

X. Lin, Y. Wang, P. Bogdan, N. Chang, and M. Pedram

(2014). Reinforcement learning based power manage-

ment for hybrid electric vehicles. In 2014 IEEE/ACM

International Conference on Computer-Aided Design

(ICCAD), pages 33–38.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence