
Towards Domain-independent Biases for Action Selection in Robotic
Task-planning under Uncertainty
Juan Carlos Sabor
´
ıo
1
and Joachim Hertzberg
1,2
1
Institute of Computer Science, University of Osnabr
¨
uck, Wachsbleiche 27, Osnabr
¨
uck, Germany
2
DFKI Robotics Innovation Center (Osnabr
¨
uck), Albert-Einstein-Straße 1, Osnabr
¨
uck, Germany
Keywords:
Action Selection, Monte-Carlo Planning, Planning under Uncertainty.
Abstract:
Task-planning algorithms for robots must quickly select actions with high reward prospects despite the
huge variability of their domains, and accounting for the high cost of performing the wrong action in the
“real-world”. In response we propose an action selection method based on reward-shaping, for planning in
(PO)MDP’s, that adds an informed action-selection bias but depends almost exclusively on a clear specifica-
tion of the goal. Combined with a derived rollout policy for MCTS planners, we show promising results in
relatively large domains of interest to robotics.
1 INTRODUCTION
Planning under uncertainty requires computing val-
ues for states and actions, that reflect a combination
of some form of utility or reward and their probabil-
ity. These planning problems are often modelled as
Markov Decision Processes (MDP’s) or Partially Ob-
servable MDP’s (POMDP’s), and solved using many
well known methods among which Monte-Carlo Tree
Search (MCTS) is a popular choice, especially in the
online planning community. The modern standard
for MCTS is UCT (Kocsis and Szepesv
´
ari, 2006),
which uses the UCB1 formula (Auer et al., 2002)
in search trees, thus guaranteeing asymptotic conver-
gence and solutions that minimize regret. Recently
POMCP (Silver and Veness, 2010), an extension of
UCT for partially observable domains, has become
somewhat of a reference point for POMDP planning
and contributed to the consolidation of Monte-Carlo
algorithms as a more efficient alternative to traditional
POMDP solvers.
Despite these advances, transferring these meth-
ods to online planning in robots and other simi-
lar agents is not easy. The onboard hardware of
robots imposes severe limitations on computational
resources, and the high variability and uncertainty
of domains of interest still render most of these al-
gorithms inadequate for fast, online planning. Plan-
ning in the “real-world” introduces additional con-
siderations that are often overlooked in maze prob-
lems and other game-like domains: not only is their
state-complexity different, but there is also a certain
amount of consistency and regularity that may be ex-
ploited.
We argue that several simplifications and assump-
tions are not only possible, but necessary, in order
to achieve satisficing behavior in such domains. One
such simplification is quickly focusing on promising
states, and avoiding less promising ones. We have
developed these ideas while trying to provide a for-
mal interpretation of the intuitive concept of “rele-
vance”, which in planning terms may be seen as a reli-
able (albeit imperfect) attentional filter guiding action
selection, which may offer an intuitive way of han-
dling problems with high dimensionality. Planning
algorithms should be able to quickly identify promis-
ing (high expected value) states and focus on getting
there. State values represent a weighted average of
future rewards, so the problem reduces to quickly lo-
cating these sources of future rewards. One relatively
simple idea is preferring actions that lead to subgoals
(subsets of some terminal state) while avoiding those
that don’t, and encouraging these actions by provid-
ing additional, positive rewards. Achieving a subgoal
objectively brings the agent a step closer to achieving
a larger goal, and so we use this idea to formalize a
metric of state to goal proximity.
In this paper we propose partial goal satisfaction
as a way to compute the proximity of states to goals
and provide a reward bonus in action selection, which
easily becomes an action selection policy for Monte-
Carlo rollouts. This is by no means a complete so-
Saborío, J. and Hertzberg, J.
Towards Domain-independent Biases for Action Selection in Robotic Task-planning under Uncertainty.
DOI: 10.5220/0006578500850093
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 85-93
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
85

lution to online planning onboard robots, but rather a
contribution towards the improvement of action selec-
tion in planning algorithms, when information about
the goal is available. The intended effect is planning
more efficiently in domains with many states and ac-
tions.
Alternative, well-known approaches for address-
ing large planning spaces include value approxima-
tion and state aggregation, but these work under the
assumption that there are large groups of states that
can be clustered together (due to similarity or other
reasons) using fixed criteria. At the moment we are
interested in how agents may use knowledge of their
goal(s) to improve their action selection criteria, in
particular by focusing on only a few good alternatives
when many options are available, as is the case of do-
mains with high variability and large branching factor.
In the following sections we discuss previous re-
lated work, and proceed to explain our proposal. We
provide two case studies and an analysis of exper-
imental results, as well as conclusions and future
work.
2 NOTATION
Unless otherwise specified, S and A are finite sets of
states and actions respectively and T (s,a,s
0
) is the
probability of reaching state s
0
when executing a in s,
which yields a real-valued reward R(s,a,s
0
). An MDP
is the tuple hS,A,T,Ri, with discount factor γ. Un-
der partial observability, an agent receives an obser-
vation ω ∈ Ω with probability O(s, a,ω) = p(ω|s,a)
and maintains an internal belief state b ∈ B, where
b(s) is the probability of s being the current state. A
POMDP is therefore hS, A,T,R,Ω,Oi. The sequence
h
t
= (a
0
,ω
1
,. .. ,a
t−1
,ω
t
) is the history at time t.
The common notation for planning in POMDP’s
uses belief states, or probability distributions over the
entire state space. That is, policies are given in terms
of beliefs. In this paper, however, we present our ac-
tion selection bias in terms of fully observable states
and states with mixed observability (states that con-
tain both fully and partially observable features). Our
experimental setup uses states sampled from a belief
state approximator. Future work includes extending
these definitions to more general cases, such as belief
states.
3 RELATED WORK
Our work centers on improving the performance of
action selection for (PO)MDP planning algorithms,
relying mostly on UCT (Kocsis and Szepesv
´
ari, 2006)
and its POMDP extension, POMCP (Silver and Ve-
ness, 2010). Unlike more traditional POMDP algo-
rithms that approximate the belief space using vector
sets, POMCP uses Monte-Carlo Tree Search (MCTS)
and approximates the current belief state using an un-
weighted particle filter. Because this is a key improve-
ment of the Monte-Carlo family of algorithms, this
paper focuses on states with partially observable ele-
ments instead of belief states. The concept of mixed
observability has produced positive results even out-
side of MCTS algorithms (Ong et al., 2010). Alter-
natively, MCTS algorithms have also been used for
belief selection in POMDP’s (Somani et al., 2013).
Existing approaches addressing the state-space
complexity involve clustering states and generalizing
state or belief values (Pineau et al., 2003), (Pineau
et al., 2006), function approximation (Sutton and
Barto, 2012) and random forest model learning (Hes-
ter and Stone, 2013). Our main critique of these meth-
ods for online task planning is that they have fixed
aggregation criteria that do not respond to the con-
nection between states and goals. For instance, states
could be clustered together depending on context so
their shared values reflect the agent’s current goals.
Other approaches generate abstractions for plan-
ning and learning over hierarchies of actions (Sut-
ton et al., 1999), (Dietterich, 2000). The drawback
is that relatively detailed, prior knowledge of the do-
main is required to manually create these hierarchies,
although recent work suggests a possible way to build
them automatically (Konidaris, 2016).
Planning algorithms for (PO)MDP’s overlap with
reinforcement learning (RL) methods, with the differ-
ence that in RL the agent must find an optimal pol-
icy while discovering and learning the transition dy-
namics. Reward shaping is commonly used in RL to
improve performance by simply giving additional re-
wards for certain preferred actions. This generates an
MDP with a different reward distribution and there-
fore different convergence properties, but potential-
based reward shaping (PBRS) has been shown to pre-
serve policy optimality (Ng et al., 1999). A study of
PBRS in the context of online POMDP planning can
be found in (Eck et al., 2016).
Building on these arguments, the work presented
in this paper reflects our efforts to provide a general-
purpose, PBRS bias for action selection in planning
tasks of interest to robotics, in order to address the
complexity of planning in domains with large vari-
ability, where states or beliefs may not always be eas-
ily aggregated.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
86

4 MEASURING GOAL
PROXIMITY
The main challenge for efficient planning is quickly
separating good or promising states from bad or un-
wanted states. Even domains without clearly speci-
fied goals (eg. pure RL tasks) have terminal states
or conditions that establish what must be accom-
plished and what subgoals the agent should pursue.
In robotics, it is reasonable to assume planning agents
are somewhat informed and aware of at least part of
their goal(s). If no goals are known, the robot should
find one. Any sufficiently detailed state description
(eg. features needed for planning) provides informa-
tion to compute, for any given state, some numerical
score representing how many features in the terminal
state have already been accomplished. The larger this
number is, the closer this state is to being a terminal or
a goal state. We call this idea partial goal satisfaction
(PGS), formalized in equation 1.
PGS is simple to implement in fully observable
domains, but due to the uncertainty of observations,
estimating this number might be challenging in par-
tially observable domains. Fully observable features
can be easily counted in meaningful ways (eq. 2).
For partially observable features, information gather-
ing actions should increase the probability that their
current, estimated value is correct, thus also affecting
the probability of an agent being in some given state
(b(s)). In other words, collecting information about
a given set of partially-observable features yields a
better estimate of the world’s current, true state. The
simplest, most general approach is therefore measur-
ing some form of uncertainty or entropy and provid-
ing rewards as this uncertainty is reduced (eq. 3). Let
s ∈ S be a state, decomposed into countable discrete
features s
i
, G
+
be the set containing the observable
features present in the goal, G
−
the set of observ-
able restrictions, ∆(s) the set of states reachable from
s (similar to the transitive closure of T (s,·)) and G
p
the set of partially or non-observable elements, then:
pgs(s) =
∑
s
i
/∈G
p
v(s
i
) +
∑
s
j
∈G
p
w(s
j
) (1)
where:
v(s
i
) =
1 iff s
i
∈ G
+
x ∈ (0, 1) iff ∃s
0
∈ ∆(s) s.t.:
s
0
k
∈ s
0
∧ s
0
k
∈ G
+
0 iff s
i
/∈ {G
+
∩ G
−
}
−1 iff s
i
∈ G
−
(2)
and
w(s
j
) =
(
0 iff H(s
j
) 6 T
H
−1 otherwise
(3)
This means the different features in each state are
evaluated depending on whether they are partially ob-
servable (s
j
∈ G
p
) or not. Positive, observable fea-
tures add points and negative features deduct points.
State changes that lead to a positive feature (s
0
k
∈ G
+
)
in a future state (s
0
∈ ∆(s)) yield a fraction of a point
and help implicitly define subgoals (eg. interacting
with an object referenced in the goal, such as picking
up the coffee cup that goes on the table), and if no
relevant features are present no points are awarded or
taken. Partially observable features are scored based
on their entropy, punishing features or states with
high entropy. Whenever enough information is gath-
ered and the entropy is reduced below some threshold
T
H
, this punishment is removed. This encourages the
agent to quickly get rid of this penalty by executing
a number of information gathering actions, which in
turn may lead to discovering new reward sources (eg.
interacting with relevant but previously unrecognized
elements). In principle any combination of the indi-
vidual elements in the goal may be considered a sub-
goal for scoring purposes, and only completing all of
them simultaneously yields the total, problem-defined
terminal reward.
PGS may be useful in different contexts, but it is
intended as an optimistic value initialization method
that allows an agent to exploit nearby opportunities if
available. Directly applying PGS on some planning
problems that appear relatively simple, such as some
particular blocks world configurations, may not yield
the desired results. As explained below, PGS is in-
tended to be used within the context of Monte-Carlo
or similar search algorithms, where the optimistic as-
sumptions of PGS will eventually be corrected (if
they’re wrong) and the problem solved properly.
4.1 PGS in Reward Shaping
Reward shaping, commonly used to improve the per-
formance of (PO)MDP algorithms and RL problems,
works by adding a small, additional reward to some
state transitions. These additional rewards often come
from an in-depth analysis of the structure of the prob-
lem and provide some form of heuristic bias in action
selection. The new reward structure defines a decision
process with additional reward sources, implicitly in-
troducing subgoals the agent may achieve in order to
get closer to the final goal. In our case, instead of
providing explicit, domain dependent knowledge to
shape rewards, we use the PGS function to encourage
the agent to pursue courses of action leading to the
completion of subgoals.
Towards Domain-independent Biases for Action Selection in Robotic Task-planning under Uncertainty
87

Reward shaping substitutes the usual reward func-
tion in an MDP with:
R(s,a, s
0
) + F(s,a,s
0
) (4)
where R is the problem-defined reward distribu-
tion and F is a reward bonus. If F has the form
F(s,a,s
0
) = γφ(s
0
) − φ(s) (5)
then it is a potential function and eq. 4 is potential-
based. We now define φ(s) for PGS as
φ(s) = αpgs(s) (6)
where α a scaling factor. Because most (PO)MDP
algorithms already use γ to refer to the discount fac-
tor, from now on we will refer to γ
PGS
when in the
context of PBRS. In practice, transitions to states that
are closer to a subgoal (positive reward source) will
produce a positive difference, transitions to states that
are farther from subgoals generate a negative differ-
ence, and other transitions cancel each other out. Nor-
mally reward shaping functions are highly domain-
dependent and specific for particular problems. PGS
manages to attain simplicity and generality, possibly
requiring only minor details for implementation, but
with values coming from knowledge about goals al-
ways available to the agent or robot.
4.2 PGS as a Rollout Policy
The MCTS family of MDP and POMDP algorithms
works by sampling sequences of states from a prob-
abilistic transition model. A tree of states (or in the
case of POMCP a tree of histories) is progressively
expanded and the average returns and visit counts are
maintained per tree node. When enough statistics are
available (eg. all known successors of a state have
been visited) the UCB1 rule is used to select an action.
When a new state is discovered, a rollout or random
simulation is performed and its outcome used as an
initial value estimation. Rollout policies are therefore
largely responsible for the performance of MCTS on-
line planning algorithms. Using PGS as a rollout pol-
icy, the agent quickly focuses on actions that directly
contribute to the completion of (sub)goals and, like-
wise, avoids undesirable actions. Selecting actions
that maximize state-to-goal proximity can implicitly
summarize a very rich array of knowledge and heuris-
tics, that must otherwise be given explicitly. To the
best of our knowledge, the effect of evaluating goal
proximity within the context of Monte-Carlo rollouts
hasn’t yet been systematically studied.
Using PGS as a rollout policy (eq. 7) is very sim-
ple: given a state s and available actions a ∈ A, select
the state s
0
← (s, a) that satisfies the largest amount of
subgoals. Ties are broken randomly.
A(s) = arg max
a
pgs(s
0
← (s,a)) (7)
Because PGS is computed as a difference between
the current and previous states (eq. 5), when γ
PGS
= 1
only newly completed subgoals produce positive val-
ues. For example imagine a robot tasked with col-
lecting and delivering a cup of coffee: during plan-
ning, standing next to the cup offers the possibility
of picking it up, satisfying a subgoal that yields a re-
ward bonus, therefore becoming the preferred action
of the rollout policy. Once holding it, dropping the
cup in any place other than the correct location re-
verts this condition and produces a negative reward,
meaning it will never be chosen in a rollout (albeit
eventually during simulation, if all actions are system-
atically sampled). MCTS recommends an action only
after arbitrarily many simulations have been carried
out, but starting out with the (seemingly) right action
greatly improves performance. Unlike with PGS, im-
proved rollout policies often consist of manually de-
signed heuristics and explicit preferred actions.
5 RESULTS
We tested PGS in two well-known and commonly
used benchmark problems: the taxi domain, which
defines a fully observable MDP and Rocksample, a
POMDP that scales to very large state spaces. For the
former we implemented our own version of UCT, and
for the latter we modified the POMCP source code.
All tests ran on a desktop workstation with an Intel
i7-4790 CPU, 20 GB RAM and Debian GNU/Linux.
The challenge for robot planning under uncer-
tainty is achieving good performance within a finite
horizon, fast enough, even in large problems. These
two scenarios show the performance of PGS using
limited resources (very few Monte-Carlo simulations)
and how it scales in considerably large versions of
Rocksample.
5.1 Taxi Domain
The taxi domain, first proposed in (Dietterich, 2000),
is a simple, fully-observable MDP often used to test
planning and learning algorithms. The taxi agent
moves in any of four directions in a 5 × 5 grid and
must pick up a passenger located in one of four possi-
ble depots, and bring it to another depot. A slight vari-
ation is the “fickle taxi” in which movement is non-
deterministic: with a small probability (eg. p = 0.1)
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
88

the taxi will end up East or West of its intended direc-
tion. Possible actions are moving North, East, South
or West, collecting a passenger when standing on the
same grid cell or dropping the passenger (when car-
rying one). Rewards are −1 for each regular move,
−10 for dropping the passenger in the wrong location
and 20 for delivering a passenger correctly, which also
terminates the episode. We chose one instance of the
taxi domain and obtained the total discounted reward
of its optimal policy, 8.652, in order to compare it
with the experimental results. This particular config-
uration and in general the taxi domain are illustrated
in figure 1, where the dark cell at the top left corner is
the goal depot where the passenger must be dropped.
The walls shown in the picture are also included in the
experiment which means the agent’s movement is re-
stricted, in cells next to walls, to only open, adjacent
cells.
Figure 1: The taxi domain.
PGS in the taxi domain is easy to formalize as all
elements are fully observable. We simply award 0.25
points for picking up the right passenger and 1 point
for dropping it at the correct depot (G
+
). There are
no restrictions (G
−
=
/
0). The terminal state reward is
preserved but the rest rely on PGS, using γ
PGS
= 1 and
α = 10 to reflect the punishment for illegally dropping
a passenger. Finally, a discount factor of γ = 0.95 and
search depth of 90 steps were used within UCT. It is
common to allow the taxi to start only over a depot,
but in our experiments it could be anywhere on the
grid. We ran UCT with PGS rewards and PGS rollout
policy in both (regular and fickle) versions of the taxi
domain, and obtained the average discounted rewards
and running times over 1000 runs. Table 1 shows the
result of repeated runs on the fixed task (fig. 1) and a
set of randomly generated episodes (randomized ori-
gin and destination depots, and taxi starting location)
using 1024 simulations.
Results are especially promising when we con-
sider the total discounted reward of the optimal policy
in the fixed (non fickle) task (8.652). Restricting the
amount of computation to only 256 simulations per
move (≈ 1.6 s. per episode), the PGS-based planner
Table 1: Performance in the taxi domain after 1000 runs
with 1024 simulations.
Transition Episodes Avg. Return Time
Normal
Fixed 6.161 3.049
Random 4.257 3.531
Fickle
Fixed 3.275 4.410
Random 2.138 4.176
achieved an average discounted reward of 5.089. On
random tasks it is important to mention that episodes
were terminated after 5 s., but their (negative) reward
still averaged.
Averaging performance, especially with stochas-
tic methods, hides some additional, interesting details
of particularly good runs. We ran a separate batch of
1000 episodes using 1024 simulations, of which 616
finished in 2 s. or less and 797 in 3 s. or less. In
these runs the mean discounted reward was particu-
larly high and the statistical mode was, also for the
entire set, the optimal discounted reward (8.652). Re-
sults are shown in table 2.
Table 2: Discounted rewards with 1024 simulations and
limited runtime.
Time (s.) Count Mean Min Mode
6 2 616 7.499 3.523 8.652
6 3 797 7.125 1.97 8.652
Interestingly, it seems that when given more time
(or simulations), a larger number of unsuccessful runs
appear (therefore reducing the minimum and average
returns). This could be due to the fact that, being
somewhat greedy, UCT can sometimes enter loops
when attempting to solve simple discrete mazes. At a
certain distance (sufficiently far from a reward source)
all possible next states (eg. cells in the maze) ap-
pear equally good (or bad) at first and their action val-
ues might be very similar or even the same. Given
more time, this type of repetitive behavior results in
very long policies with extremely low returns. With
enough planning time (convergence in RL and MCTS
methods is, after all, guaranteed after asymptotically
many iterations), the agent might be able to break
out of this loop, locate the goal and improve its pol-
icy. This is precisely the reason for introducing ad-
ditional reward sources, but we are interested in find-
ing reasonably good solutions as quick as possible.
The taxi domain is an interesting benchmark because,
despite being extremely simplified in terms of tasks
and actions, there are many “empty” cells that create
large groups of very similar states. In richer domains
with more features, where naive planning algorithms
may require systematic deliberation and long run-
times, PGS shows very promising results (eg. Rock-
Towards Domain-independent Biases for Action Selection in Robotic Task-planning under Uncertainty
89

sample in next subsection).
Our main motivation for speeding up MDP plan-
ning is transferring these methods to robotic task
planning, so we are particularly interested in main-
taining good levels of performance and not necessar-
ily optimizing indefinitely. This means, in practice,
we are aiming at solving (parts of) complex domains
within a few seconds and not necessarily millisec-
onds. Despite being essentially a toy problem because
of its size and full observability, the taxi domain is
a abstraction of a common manipulation task (nav-
igating, collecting, delivering) and our results show
PGS succeeds in achieving good levels of perfor-
mance with very limited time, planning directly on
an unfactored MDP.
5.2 Rocksample
Rocksample, originally found in (Smith and Sim-
mons, 2004), is a commonly used problem that sim-
ulates a Mars rover tasked with collecting valuable
rocks. This problem corresponds to a POMDP in
which the location of the agent and the rocks are
known, but the value of these rocks is initially un-
known and must be determined by the use of a noisy
sensor that returns one of two observations, good or
bad, with a given reliability. Rocksample[n,k] defines
an n× n grid with k rocks, where the agent may move
in any of four directions, sample a rock if standing
directly on top of it, or use the sensor on any rock
(action check
i
for rock i) for a total of 5 + k actions
(see fig. 2). Rewards are 10 for sampling good rocks,
−10 for sampling bad rocks, 10 for exiting (East)
and −100 for leaving the grid in any other direction
(Smith and Simmons, 2004). We used POMCP as a
POMDP solver (Silver and Veness, 2010), but modi-
fied it to test our proposal.
POMCP is a particularly fast POMDP solver
mainly due to two reasons: it uses an unweighted
particle filter to approximate the belief state, avoiding
costly belief updates, and it expands a tree of histories
instead of states, circumventing the curse of dimen-
sionality. Within POMCP, instead of a belief state the
agent receives a state sampled from the particle filter,
which corresponds to a state with mixed observability.
This way we were able to test our methodology within
a POMDP solver, albeit relying on states that contain
partially observable features (thus, not directly intro-
ducing preference over beliefs). In addition, POMCP
uses slightly enhanced rocksample states, where the
probability that a rock is good is updated directly af-
ter every corresponding check action, using the sen-
sor efficiency and the previous likelihood. We defined
C = G
+
∩ G
−
to be the set of collected rocks, and G
p
Figure 2: Special layout for Rocksample[11,11].
the remaining rocks. Scoring function v(s
i
) returns
1 for good rocks with good observations (G
+
) and
−1 for bad rocks (G
−
). Function w(s
j
) returns −1
if H
b
(p
r
) > 0.5, that is, if the binary entropy of rock
r (s
j
) is higher than 0.5. POMCP comes with a pre-
ferred actions policy, which uses manually encoded
heuristics such as “head North if there are rocks with
more positive observations” or “check rocks that have
been measured less than five times and have less than
two positive observations”. Clearly, PGS succeeds in
avoiding this level of over specification.
We used γ
PGS
= 1 and α = 10 (to reflect the dif-
ference in rewards received when sampling good and
bad rocks). This scoring function deducts points for
undesirable states (eg. collecting bad rocks, high en-
tropy for any rock) and only adds points when collect-
ing good rocks, but further negative points are with-
drawn once the knowledge about any particular rock
increases (i.e. entropy < 0.5). In practice this means
that during rollouts check will be preferred if it re-
duces entropy for some rock, that sample will be pre-
ferred when standing over a promising rock, and that
otherwise movement actions will be considered.
We compared three different policies: uniformly
random with legal moves (“legal” in POMCP), ex-
plicit preferred actions (“smart” in POMCP) and our
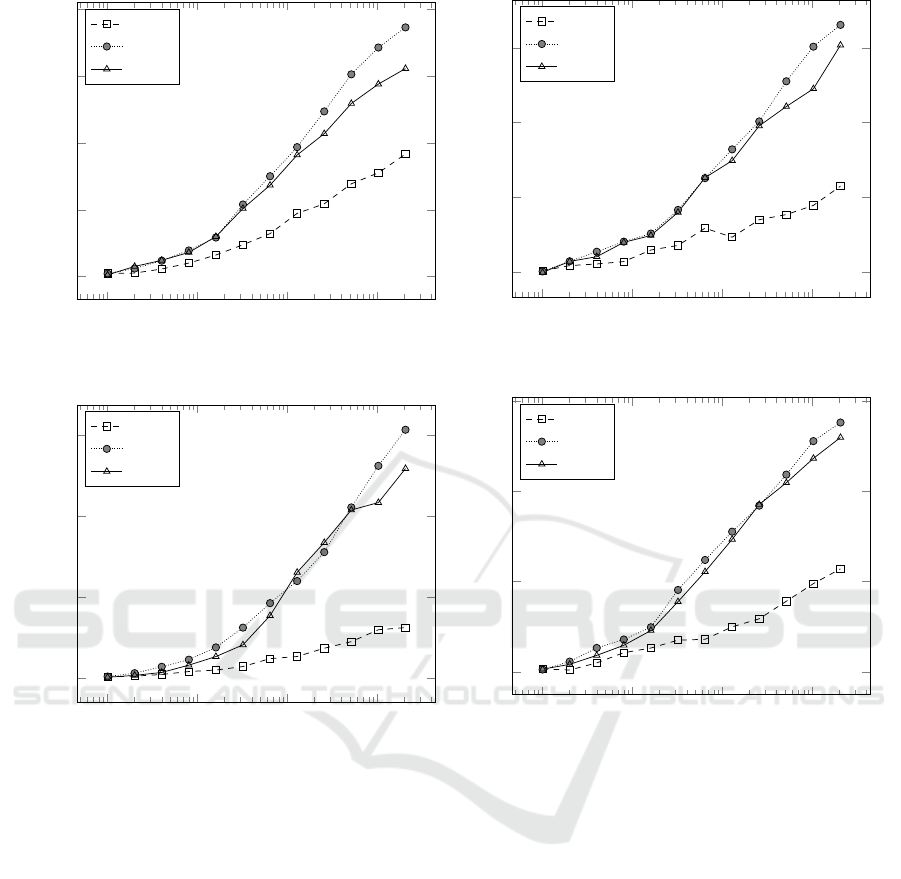
own, “PGS”. Figure 3 shows the discounted rewards
averaged over 1000 runs for all three policies in rock-
sample [11, 11], [15,15], and the large [25, 25] and
[25,12], with up to 2048 Monte-Carlo simulations per
move.
PGS clearly outperforms the legal policy and is
only slightly outmatched by the smart policy. This
difference however reduces as the problem size in-
creases, particularly in [25,25], a very large problem
for rocksample standards and in [25, 12], an equally
large grid but with fewer reward sources. Estimat-
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
90
10
0
10
1
10
2
10
3
0
5
10
15
20
Simulations
Avg. Discounted Reward
Legal
Smart
PGS
(a) [11,11]
10
0
10
1
10
2
10
3
0
5
10
15
Simulations
Avg. Discounted Reward
Legal
Smart
PGS
(b) [15,15]
10
0
10
1
10
2
10
3
0
5
10
15
Simulations
Avg. Discounted Reward
Legal
Smart
PGS
(c) [25,25]
10
0
10
1
10
2
10
3
0
5
10
15
Simulations
Avg. Discounted Reward
Legal
Smart
PGS
(d) [25,12]
Figure 3: Performance in Rocksample.
ing the PGS value of derived states for every action
in our rollout policy may be somewhat computation-
ally expensive, particularly when all or many actions
are available, since it trades off simulations for run-
time. Results show, however, this pays off compared
to the random policy: with ≈ 2.5 seconds of com-
putation in rocksample[25,12], the legal rollout pol-
icy achieves a discounted reward of 5.713 with 2048
simulations, whereas PGS collects 7.35 with only 128
simulations. A faster implementation for planning on-
board robots might be necessary, but also a shallower
planning depth may be used (the experiments used a
depth of 90 steps). Additionally, extensions for es-
timating the goal proximity of beliefs and not only
sampled states (which POMCP does) might be help-
ful.
6 CONCLUSIONS & DISCUSSION
Our experimental results show that PGS is useful
to improve the performance of planning in large
(PO)MDP’s, despite its simplicity and even consider-
ing the contributions of algorithms such as POMCP,
that handle large state spaces relatively well. Plan-
ning directly over beliefs might be useful for prob-
lems with extreme uncertainty, and where many
uncertainty-reducing actions may be necessary as is
the case of many robotic planning domains. In fully
observable problems such as the Taxi domain, PGS
achieved a level of performance that seems unattain-
able for a uniformly random policy.
In domains with partial and mixed observabil-
ity and particularly in problems with scarce reward
sources, PGS easily outperformed the uniformly ran-
Towards Domain-independent Biases for Action Selection in Robotic Task-planning under Uncertainty
91

dom policy. In these scenarios, such policies scale
poorly and domain knowledge becomes necessary to
achieve good performance. We showed that with
barely any domain-dependent knowledge, PGS can be
competitive with a manually designed, action selec-
tion policy with very detailed, heuristic knowledge.
This type of domain-independent bias is essential for
planning and acting in complex domains.
In general we can identify three main approaches
for speeding up planning in large stochastic domains:
1) Action hierarchies that produce smaller, abstract
MDP’s and then transfer these solutions to the base
MDP. 2) State abstractions that group states together
so their values are shared and the values of unknown
states, approximated. 3) PBRS, that forces an agent to
focus on good action prospects, avoiding potentially
costly choices. It seems that for planning domains
with high variability it would be difficult to efficiently
generate state or action abstractions in advance, and
the planner might have to traverse many unique states
anyway. Our PGS methodology addresses this issue
by attempting to quickly identify reward sources and
back propagate scaled partial rewards, using as lit-
tle domain knowledge as possible but exploiting an
agent’s knowledge of its own goals. All of the afore-
mentioned techniques are either strongly domain de-
pendent or use fixed criteria to generate groups or cat-
egories.
As previously stated, this work is only part of our
efforts to introduce the notion of relevance in task
planning. Future work includes expanding the for-
mal definition of goal proximity for beliefs, and de-
signing dynamic value approximation and/or state ag-
gregation methods derived from this methodology. In
order to transfer these methods to real-world robotic
tasks, some form of state aggregation or abstraction
will be required to map continuous to discrete state
representations and to correctly recognize or disre-
gard states with relevant or irrelevant information, re-
spectively. We argue that states should, similar to
PGS, be grouped based on criteria derived from the
goal.
When thinking about planning and decision prob-
lems it is normal to refer to state spaces and the num-
ber of states as a measure of their complexity. If
we were to compare most MDP benchmark problems
with real-world, robotic planning problems, we find
that the former often have combinatorial complexity
just as games do. We could potentially generate all
possible states and therefore, find arbitrarily complex
policies. This idea does not transfer well to planning
with robots in the “real world”, where the number of
states may be unknown and, potentially, much larger
than a game. Despite these differences, we under-
stand intuitively that some problems can be solved
quickly in some level of abstraction and their solu-
tions transferred back to the original domain. So if
state complexity does not necessarily represent how
complex problems are: how should the complexity of
planning problems be estimated? Certainly problems
with many states look more complex when only their
computational complexity is considered, often a func-
tion of the number of states. But more accurately, and
because planning problems include not only a domain
but also goals, some intrinsic relationship between the
values of states and their distance to the goal (or sub-
goals) must be considered. A good planning algo-
rithm should efficiently identify the gaps in between
state values in order to quickly tell apart good states
from bad states. These values come uniquely from
perceived (or simulated) rewards. Because the value
of a state is the average discounted return of its chil-
dren, it might be hard to differentiate between promis-
ing states early on, when the agent is simply too far
from any source of reward. Conversely, if the agent
always starts next to its goal, the problem should be
trivial to solve regardless of the number of possible
states. By designing planning algorithms that exploit
these observations, we expect to improve the perfor-
mance of online planning in robots and other agents,
despite the apparent complexity of “real-world” do-
mains.
ACKNOWLEDGEMENTS
This work is supported by a DAAD research grant.
REFERENCES
Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem. Ma-
chine Learning, 47(2):235–256.
Dietterich, T. G. (2000). Hierarchical reinforcement learn-
ing with the maxq value function decomposition.
Journal of Artificial Intelligence Research, 13:227–
303.
Eck, A., Soh, L.-K., Devlin, S., and Kudenko, D. (2016).
Potential-based reward shaping for finite horizon on-
line pomdp planning. Autonomous Agents and Multi-
Agent Systems, 30(3):403–445.
Hester, T. and Stone, P. (2013). TEXPLORE: Real-time
sample-efficient reinforcement learning for robots.
Machine Learning, 90(3).
Kocsis, L. and Szepesv
´
ari, C. (2006). Bandit based monte-
carlo planning. In In: ECML-06. Number 4212 in
LNCS, pages 282–293. Springer.
Konidaris, G. (2016). Constructing abstraction hierarchies
using a skill-symbol loop. In Proceedings of the
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
92

Twenty-Fifth International Joint Conference on Arti-
ficial Intelligence, IJCAI 2016, New York, NY, USA,
9-15 July 2016, pages 1648–1654.
Ng, A. Y., Harada, D., and Russell, S. (1999). Policy invari-
ance under reward transformations: Theory and appli-
cation to reward shaping. In In Proceedings of the Six-
teenth International Conference on Machine Learn-
ing, pages 278–287. Morgan Kaufmann.
Ong, S. C. W., Png, S. W., Hsu, D., and Lee, W. S. (2010).
Planning under uncertainty for robotic tasks with
mixed observability. Int. J. Rob. Res., 29(8):1053–
1068.
Pineau, J., Gordon, G., and Thrun, S. (2003). Policy-
contingent abstraction for robust robot control. In Pro-
ceedings of the Nineteenth Conference on Uncertainty
in Artificial Intelligence, UAI’03, pages 477–484, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
Pineau, J., Gordon, G. J., and Thrun, S. (2006). Anytime
point-based approximations for large POMDPs. Jour-
nal of Artificial Intelligence Research, 27:335–380.
Silver, D. and Veness, J. (2010). Monte-Carlo Planning in
Large POMDPs. In In Advances in Neural Informa-
tion Processing Systems 23, pages 2164–2172.
Smith, T. and Simmons, R. (2004). Heuristic Search Value
Iteration for POMDPs. In Proceedings of the 20th
Conference on Uncertainty in Artificial Intelligence,
UAI ’04, pages 520–527, Arlington, Virginia, United
States. AUAI Press.
Somani, A., Ye, N., Hsu, D., and Lee, W. S. (2013).
Despot: Online pomdp planning with regularization.
In Burges, C. J. C., Bottou, L., Welling, M., Ghahra-
mani, Z., and Weinberger, K. Q., editors, Advances
in Neural Information Processing Systems 26, pages
1772–1780. Curran Associates, Inc.
Sutton, R., Precup, D., and Singh, S. (1999). Between mdps
and semi-mdps: A framework for temporal abstrac-
tion in reinforcement learning. Artificial Intelligence,
112:181–211.
Sutton, R. S. and Barto, A. G. (2012). Reinforcement Learn-
ing: An Introduction. MIT Press, Cambridge, MA,
USA, 2nd edition. (to be published).
Towards Domain-independent Biases for Action Selection in Robotic Task-planning under Uncertainty
93
