Notes on Expected Computational Cost of Classifiers Cascade:
A Geometric View
Dariusz Sychel, Przemysław Kle¸sk and Aneta Bera
Faculty of Computer Science and Information Technology, West Pomeranian University of Technology,
ul.
˙
Zołnierska 49, 71-210 Szczecin, Poland
Keywords:
Cascade of Clasifier, Detection, Expected Number of Features.
Abstract:
A cascade of classifiers, working within a detection procedure, extracts and uses different number of features
depending on the window under analysis. Windows with background regions can be typically recognized as
negative with just a few features, whereas windows with target objects (or resembling them) might require
thousands of features. The central point of attention for this paper is a quantity that describes the average
computational cost of an operating cascade, namely — the expected value of the number of features the cascade
uses. This quantity can be calculated explicitly knowing the probability distribution underlying the data and
the properties of a particular cascade (detection and false alarm rates of its stages), or it can be accurately
estimated knowing just the latter. We show three purely geometric examples that demonstrate how training a
cascade with sensitivity / FAR constraints imposed per each stage can lead to non-optimality in terms of the
computational cost. We do not propose a particular algorithm to overcome the pitfalls of stage-wise training,
instead, we sketch an intuition showing that non-greedy approaches can improve the resulting cascades.
1 INTRODUCTION
The idea of classifiers cascade was originally presen-
ted by Viola and Jones in (Viola and Jones, 2001).
The main motivation behind that idea is an observa-
tion that negative windows constitute a vast majority
of all windows during a detection procedure. Regard-
less of the task (face detection, pedestrian detection,
etc.) it is roughly fair to say that the negatives are pre-
sent in at least 99.99% of all windows. For example
in face detection, several face windows are typically
detected among the total of 10
5
or even 10
6
windows,
depending on the settings (image resolution, number
of scans, detection window sizes and shifts). There-
fore, the classifier working as the detector should vary
the computational efforts applied to particular win-
dows. Windows with background regions or obvious
non-targets can be rejected as negatives based on the
information from just a few features. On the other
hand, more promising windows (with target objects
or resembling such) can be analyzed gradually using
more and more features, even up to thousands of fe-
atures. The above operation process is achieved by
dividing the overall detector into a certain number of
stages. The features are then extracted in increasing
portions, stage after stage. If some stage returns a ne-
gative response then the further calculations are sup-
pressed and the analyzed window becomes classified
as a negative. If all stages are passed through with a
positive response then the analyzed window becomes
classified as a positive.
Originally, Viola and Jones (Viola and Jones,
2001; Viola and Jones, 2004) proposed to use
Haar-like features, loosely connected to Haar wave-
lets (Papageorgiou et al., 1998), within a cascade.
This was done also for computational reasons, be-
cause the extraction of Haar-like features can be ea-
sily speeded up by integral images (Crow, 1984).
Each stage of Viola and Jones’ cascade was a strong
classifier (an ensemble of week classifiers) trained
by the AdaBoost algorithm (Friedman et al., 2000;
Freund and Schapire, 1996). The weak classifiers
were decision stumps based on single features yiel-
ding the smallest classification errors. Successive
strong classifiers included into the cascade were trai-
ned on a data subset that was classified as positive in
the previous stage. Thereby, each subsequent classi-
fier faces a tougher task, since it has to deal with less
obvious data examples (lying closer to the decision
boundary), and therefore requires more features.
As Viola and Jones noted themselves, training a
cascade is a difficult combinatorial optimization pro-
Sychel, D., Kl ˛esk, P. and Bera, A.
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View.
DOI: 10.5220/0006585301030114
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 103-114
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
103

blem which involves the following crucial parame-
ters: number of cascade stages, number of features
per stage and selection of those features, decision
thresholds per stage. It is worth to remark that this
problem has not been ultimately solved yet. The way
Viola and Jones decided to tackle it was by impo-
sing the final accuracy requirements the whole cas-
cade should meet in order to be accepted by the user.
These requirements are defined by a pair of numbers:
the wanted minimum detection rate (sensitivity) and
the allowed maximum false alarm rate (FAR). Due to
the probabilistic properties of the cascade structure,
one can apply the geometric mean and translate the
final requirements onto another pair of numbers: the
stage requirements. If each stage satisfies such requi-
rements then the whole cascade also satisfies the final
requirements.
Many improvements to cascade training has been
introduced over the years in the literature (Gama and
Brazdil, 2000; Bourdev and Brandt, 2005; Pham and
Cham, 2007; Li and Zhang, 2013; Vallez et al., 2015),
most of them trying out different feature selection al-
gorithms or subsampling methods. One should re-
mark however that in many of these works the main
optimization process is still guided by the stage requi-
rements for the predefined number of stages. Also, a
certain disorientation in the research arises due to un-
clear optimization criterions. One may wonder whet-
her a cascade should: (1) maximize accuracy, (2)
maximize AUC, (3) maximize sensitivity while sa-
tisfying a certain FAR, (4) minimize FAR while sa-
tisfying a certain sensitivity, (5) minimize its training
time, (6) minimize the expected number of features
used per window during detection, or perhaps still so-
mething else. Very often, the proposed algorithms are
driven by some mixture of these criterions based on
suitably formulated Lagrangians (Saberian and Vas-
concelos, 2014; Shen et al., 2010; Shen et al., 2013).
It can be noted that cascade performance is di-
rectly dependent on the average number of features
used per window regardless of the learning method,
therefore there is a direct connection between the ex-
pected value of features and detection time.
1.1 Motivation
In this paper we concentrate on the expected num-
ber of features used by a cascade. We do not attempt
at providing a new training algorithm that shall opti-
mize this quantity directly. Instead, we intend to give
the reader a geometric intuition on what pitfalls the
stage-wise training can fall into. We show three ge-
ometric examples (“cuboid in the corner”, “3D cube
trap”, “chessboard trap”) which demonstrate optimal
cascades in terms of the above expectation and sub-
optimal ones resulting from the stage-wise training.
Although the examples are arranged ‘manually’, they
may reflect situations (or variations) present in real
data sets.
1.2 Notation
Throughout the paper we use the following notation:
• K — number of cascade stages
• (n
1
,n
2
,...,n
K
) — number of features used on
each stage,
• (d
1
,d
2
,. ..,d
K
) — sensitivities per stage (de-
tection rates),
• (a
1
,a
2
,. ..,a
K
) — FAR values per stage (alarms),
• p — true probability of the positive class
(unknown in practice),
• 1 − p — true probability of the negative class
(unknown in practice),
• D — required sensitivity (for entire cascade),
• A — required FAR (for entire cascade),
• d
min
= D
1/K
— sensitivity required per stage,
• a
max
= A
1/K
— FAR required per stage.
For clarity, we explain that given a data pair (x, y)
where x is the vector of features and y ∈ {−,+} is the
corresponding class label, the probabilistic meaning
of d
k
and a
k
is as follows:
d
k
= P(F
k
(x)= + |y=+, F
1
(x)=···=F
k−1
(x) = +),
(1)
a
k
= 1−P(F
k
(x)= − |y=−, F
1
(x)=···=F
k−1
(x)=−),
(2)
where F
k
(x) denotes the response of k-th stage.
2 EXPECTED NUMBER OF
FEATURES
In this section we give two exact approaches and one
approximate approach allowing to calculate the ex-
pected number of features used by a cascade.
2.1 Expected Value — Definition-based
Approach
A cascade stops operating after a certain number of
stages. It does not stop in the middle of a stage.
Therefore the possible outcomes of the random va-
riable of interest, describing the disjoint events, are:
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
104

n
1
, n
1
+ n
2
, . . . , n
1
+ n
2
+ ··· + n
K
. Hence, by the
definition of expected value, the expected number of
features can be calculated as follows:
E(n) =
K
∑
k=1
k
∑
i=1
n
i
!
p
k−1
∏
i=1
d
i
!
· (1 − d
k
)
[k<K]
+(1 − p)
k−1
∏
i=1
a
i
!
· (1 − a
k
)
[k<K]
!
(3)
where [·] is an indicator function.
2.2 Expected Value — Incremental
Approach
By grouping the terms in (3) according to n
k
the fol-
lowing alternative formula can be derived:
E(n) =
K
∑
k=1
n
k
p
k−1
∏
i=1
d
i
· +(1 − p)
k−1
∏
i=1
a
i
!
(4)
From now on we shall be using expression (4),
being simpler than (3).
2.3 Remarks
Obviously, in practical applications the true proba-
bility distribution underlying the data is unknown.
Since the probability p of the positive class is very
small (as already said, typically p < 10
−4
), the ex-
pected value can be accurately approximated using
only the summands related to the negative class as fol-
lows:
E(n) ≈
K
∑
k=1
n
k
k−1
∏
i=1
a
i
. (5)
It is also interesting to remark that in the original
paper (Viola and Jones, 2004) the authors propose an
incorrect formula to estimate the expected number of
features, namely:
E
VJ
(n) =
K
∑
k=1
n
k
k−1
∏
i=1
r
i
, (6)
where r
i
represents the “positive rate” of i-th stage.
This is equivalent to
E
VJ
(n) =
K
∑
k=1
n
k
k−1
∏
i=1
(pd
i
+ (1 − p)a
i
). (7)
Please note that by multiplying positive rates of sta-
ges, one obtains mixed terms of form d
i
·a
j
that do not
have any probabilistic sense. For example for k = 3
the product under summation becomes
(pd
1
+ (1 − p)a
1
)(pd
2
+ (1 − p)a
2
),
with the terms d
1
a
2
and a
1
d
2
having no sense, be-
cause the same data point x does not change its class
label while traveling along the cascade.
3 EXAMPLE 1: “CUBOID IN THE
CORNER”
Consider a data distribution contained in the
n-dimensional unit cube with the positive class, being
a cuboid, placed in one of the cube’s corners. The
probability distribution over the entire problem dom-
ain (x
1
,. ..,x
n
) ∈ [0,1]
n
is uniform. The positive class
is represented by the set:
P = {(x
1
,. ..,x
n
) ∈ [0,1]
n
: 0 ≤ x
i
≤ w
i
},
where 0 < w
1
≤ w
2
≤ ... ≤ w
n
≤ 1 are widhts of the
cuboid (set up non-decreasingly). The negative class
is the complement:
N = [0, 1]
n
\ P.
The problem is deterministic — the classes can be se-
parated unambiguously.
For our mathematical purposes we shall now con-
sider an idealistic variant of the cascade training algo-
rithm that works directly on the continuous distribu-
tion rather than on a finite data set.
Suppose the number of stages K and the final re-
quirements D, A (sensitivity, FAR) for the entire cas-
cade have been imposed. Each stage of the cascade
shall be formed by a group of splits orthogonal to the
axes (similar to decision stumps). The intersection
implied by the splits shall indicate the region of po-
sitive response for the given stage. Splits are added
successively, using one feature at a time. The follo-
wing pseudocode serves as a sketch of the above pro-
cedure.
Algorithm 1: Viola Jones-style cascade training based on
stage-wise sensitivity / FAR requirements (for the purposes
of Example 1).
procedure TRAINCASCADEVJSTYLE(D, A, K)
d
min
:= D
1/K
, a
max
:= A
1/K
,
for k := 1,.. ., K do
n
k
:= 0, d
k
:= 0, a
k
:= 1
while (d
k
< d
min
or a
k
> a
max
) do
find feature x
i
and split position s
i
(along x
i
) that minimize classifica-
tion error within the remaining data
region
add the split (x
i
,s
i
) to the current stage
n
k
:= n
k
+ 1
calculate d
k
, a
k
end while
end for
end procedure
Let us consider the case of D = 1 (hence also
d
min
= 1). It is possible to see that this condition im-
plies the following two consequences:
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View
105

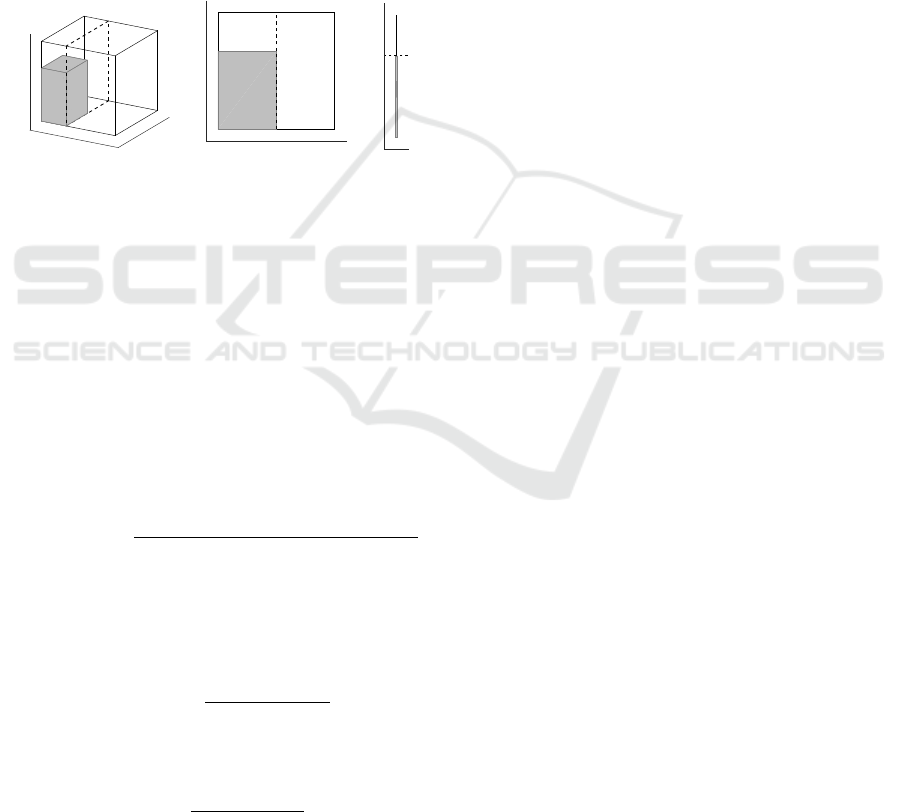
1. splits must be taken at positions s
i
exactly equal
to w
i
,
2. successive selected features shall correspond to
their natural ordering x
1
,x
2
,. ...
The reason behind the first consequence is that for
s
i
< w
i
the 100% sensitivity cannot be achieved, whe-
reas for s
i
> w
i
the FAR shall be increased unneces-
sarily. The reason behind the second consequence is
that widths of the positive cuboid have been set up in
non-decreasing order (w
1
≤ w
2
≤ ... ≤ w
n
). There-
fore, a split on x
i
taken before a split on x
j
with i > j
would result in a greater FAR (and thereby would not
minimize the error). Fig. 1 illustrates the data distri-
bution and optimal splits for the Example 1 and n = 3.
x
1
x
2
x
3
w
1
w
2
w
3
x
2
x
3
w
2
w
3
x
3
w
3
Figure 1: Example 1 “cuboid in the corner”: illustration for
n = 3.
3.1 FAR Formula for “cuboid in the
corner”
For further analysis of Example 1 we provide a useful
formula for the false alarm rate. It assumes the opti-
mal s
i
= w
i
and expresses the FAR resulting from m
new splits (i.e. using of m new features) provided that
m
0
splits have already been done so far. Therefore the
number m
0
can be treated as an offset value.
FAR(m; m
0
) =
m
0
+m
∏
k=1+m
0
w
k
!
· 1 −
n
∏
k=1+m
0
+m
w
k
!
1 −
n
∏
k=1+m
0
w
k
(8)
For example, if n = 3 and 1 initial split is to be made
the resulting FAR becomes equal to:
FAR(1; 0) =
w
1
(1 − w
2
· w
3
)
1 − w
1
· w
2
· w
3
Then, once the first split becomes fixed, and e.g. two
new splits are to made, the FAR becomes:
FAR(2; 1) =
w
2
· w
3
(1 − 1)
1 − w
2
· w
3
= 0.
The 1 − 1 value appearing in the numerator results
from the empty product
∏
3
k=1+1+2
w
k
equal to 1 by
the definition.
Formula (8) lets us note again that features for the
splits must be selected in their natural order. If the
algorithm used some different order then it is easy to
see that both factors in the numerator of (8) would
increase while the denominator remains constant.
We remark that the following property is satis-
fied by the formula (8) for any natural numbers
m
0
,m
1
,m
2
:
FAR(m
1
+m
2
;m
0
)=FAR(m
1
;m
0
)·FAR(m
2
;m
0
+m
1
).
(9)
It means that the FAR value can be calculated ‘in
portions’ and can be interpreted as follows. Taking
m
1
+ m
2
new splits after m
0
splits have been made is
equivalent to taking first m
1
splits and then m
2
new
splits (once the m
0
+ m
1
former splits are fixed).
3.2 Optimal Cascades for “cuboid in the
corner”
We are now going to look for optimal cascades for
our “cuboid in the corner” example, imposing diffe-
rent K values. Two approaches shall be presented. In
the first approach, exact solutions will be shown using
some combinatorics and an exhaustive search. In the
second, approximate solutions will be provided by a
numerical technique.
Let n
∗
be the optimal number of features sufficient
to achieve the imposed FAR value A.
n
∗
= min{m : FAR(m; 0) ≤ A}
We note that it is possible that Algorithm 1, training
the cascade, may find
N = n
1
+ ···n
K
> n
∗
features. The overhead can be caused by the fact that
all the stages must achieve the (d
min
,a
max
) require-
ments.
3.2.1 Exhaustive Combinatorial Search
First of all it is important to realize that the number of
possible different cascades is

n
∗
− 1
K − 1

. (10)
We provide two explanations for this fact.
Explanation 1: Each stage must contain at least one
weak classifier. Cascades ending with zeros in the
sequence (n
1
,. ..,n
k
) can be omitted from conside-
rations. Such cascade would have a larger E(n) va-
lue than the cascades not ending with zeros but still
using n
∗
features. Formula (10) can be interpreted
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
106

as the number of ways one can place stage separa-
tors within a string 2,3,...,n
∗
that represents feature
indexes (note that the first features is obligatory reser-
ved for the first stage). For example, if n
∗
= 7 and
K = 3 then a possible cascade one can build is e.g.:
2,3, 4,5,6,7 → 1|2,3|4,5,6,7 →
(n
1
, n
2
, n
3
)
(1, 2, 4)
.
Explanation 2: Consider a mapping from the set of
weak classifiers (for particular features) to the set of
cascade stages:
{1,2,...,n
∗
} → {1,2,...,K}
If the restriction that each stage must have at least
one classifier is omitted for a moment then the num-
ber of possible mappings is equal to number of n
∗
-
element combinations with repetitions of the set of K
elements:

n
∗
+K−1
n
∗

. The fact of taking into account
the mentioned restriction can be represented by sub-
stituting n
∗
:= n
∗
−K (since K classifiers, 1 per stage,
are fixed in the cascade from the start). This leads to
the following number of cascades

n
∗
− K +K − 1
n
∗
− K

=

n
∗
− 1
n
∗
− K

=

n
∗
− 1
K − 1

,
which is equal to (10). The coding of the exam-
ple cascade (n
1
,n
2
,n
3
) = (1,2, 4) from the previous
explanation can be now represented by the follo-
wing string representing a combination with repeti-
tions ∗| ∗ ∗|∗ ∗∗ ∗.
Algorithm 2 : Exhaustive combinatorial search for opti-
mal cascade (for the purposes of Example 1).
procedure EXHAUSTIVECASCADES(D, A, K, N)
E
∗
:= ∞  best expectation so far
(n
∗
1
,. ..,n
∗
K
) := null  best cascade so far
c := (1,.. ., N −K)  initial combination
while true do
decode c onto (n
1
,. ..,n
K
)
calculate (d
1
,. ..,d
K
) and (a
1
,. ..,a
K
)
if
∏
K
k=1
d
k
≥ D and
∏
K
k=1
a
k
≤ A then
calculate E according to (5)
if E < E
∗
then
E
∗
:= E
(n
∗
1
,. ..,n
∗
K
) := (n
1
,. ..,n
K
)
end if
end if
c :=NEXTCOMBINATION(c, N − 1)
end while
return (n
∗
1
,. ..,n
∗
K
), E
∗
end procedure
The NEXTCOMBINATION(·) represents a combi-
natorial iterating routine available in most program-
ming environments
1
. The initial combination (wit-
hout repetitions) becomes decoded onto the cascade
(N − K + 1, 1,1, .. ., 1), the next combination onto
(N − K, 2,1, .. ., 1), and the loop continues until the
last cascade (1,1,1,...,N − K + 1).
Below, we report the results of experiments pertai-
ning to Example 1 for the number of dimensions (fea-
tures): n = 30 and n = 50. In both cases we set up the
following arithmetic progression for the widths of po-
sitive cuboid in the corner: w
1
= 0.8, ∆ = (1 − w
1
)/n
and w
k
= w
1
+ (k − 1)∆.
Experiments for n = 30: The results presented in
Table 1 compare the cascades obtained via Algo-
rithm 1 (VJ-style cascade training) against the casca-
des from Algorithm 2 (combinatorial exhaustive se-
arch). The implementations were done in Wolfram
Mathematica 10.4
2
. While calculating false alarm ra-
tes a
k
, formula (8) was applied in both implemen-
tations. The total of all features in a cascade —
N = n
1
+ ··· + n
K
, obtained from the first algorithm,
was used as an input to the second algorithm. We re-
mark that the probability of the positive class in this
experiment is p =
∏
n
k=1
w
k
≈ 0.035633. This proba-
bility together with (d
k
) and (a
k
) sequences allowed
to calculate exact expected values E(n).
As one can note all cascades obtained by the
VJ-style algorithm (guided by stage requirements)
have worse expected values E(n) than the cascades
obtained by the exhaustive combinatorial search. The
latter cascades use the same number of features (de-
noted by N), but distribute them differently. The next
table (Table 2) illustrates the fact that in two cases the
number N can be still slightly decreased to N
∗
and the
final requirements are still satisfied by cascades found
via exhaustive search. Obviously, E(n) values are si-
multaneously improved as well.
Experiments for n = 50: Due to n = 50, the pro-
bability of the positive class for this experiment is
p =
∏
n
k=1
w
k
≈ 0.00415707. As in the previous ex-
periment we report two analogical tables. Table 3
confronts VJ-style cascades against the optimal ones
(using the same totals N). Table 4 indicates improved
totals N
∗
and the corresponding optimal cascades.
3.2.2 Approximate Numerical Technique
The difficulty in direct optimization of the expected
value E(n) lies in two facts: (i) the total of features at
1
In our implementation we apply the NextKSubset[·]
procedure from Wolfram Mathematica 10.4.
2
Time results are reported for Intel Xeon CPU E3-
1505M 2.8 GHz, 4 cores / 8 threads.
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View
107

Table 1: Example 1 “cuboid in the corner” (n = 30): VJ-style cascades vs optimal cascades found by exhaustive search.
no. K A
resulting cascade
(VJ-style algorithm) N E(n)
optimal cascade
(exhaustive search) E(n) no. of cascades search time [s]
1 2 10
−2
(12,11) 23 13.2884 (7,16) 10.9849 22 0.016
2 2 10
−3
(18,10) 28 18.6085 (8,20) 12.2173 27 0.016
3 3 10
−2
(8,9,7) 24 10.3641 (4,6,14) 8.74884 253 0.094
4 3 10
−3
(12,11,5) 28 13.5038 (4,7,17) 9.29271 351 0.141
5 4 10
−2
(6,6,6,5) 25 8.78596 (3,4,6,10) 7.62453 1540 0.516
6 4 10
−3
(9,9,7,4) 29 11.2031 (3,4,7,15) 8.21372 3276 1.188
Table 2: Example 1 “cuboid in the corner” (n = 30): improved totals of features N
∗
.
no. N N
∗
optimal cascade
(exhaustive search, using N
∗
E(n) no. of cascades search time [s]
3 24 23 (4,6,13) 8.59409 231 0.078
6 29 28 (3,4,7,14) 8.12233 2925 1.016
Table 3: Example 1 “cuboid in the corner” (n = 50): VJ-style cascades vs optimal cascades found by exhaustive search.
no. K A
resulting cascade
(VJ-style algorithm) N E(n)
optimal cascade
(exhaustive search) E(n) no. of cascades search time [s]
1 5 10
−2
(5,5,6,6,7) 29 7.98656 (2,3,4,7,13) 7.08589 20475 7.281
2 5 10
−3
(7,8,9,10,8) 42 9.62653 (2,3,5, 9,23) 7.61736 101270 44.766
3 6 10
−2
(4,4,5,5,6,6) 30 7.38845 (2,2, 3,4, 7,12) 6.72574 118755 44.453
4 6 10
−3
(6,7,8,8,8,6) 43 8.94712 (2,3, 3,5, 9,21) 7.12384 850668 387.328
Table 4: Example 1 “cuboid in the corner” (n = 50): improved totals of features N
∗
.
no. N N
∗
optimal cascade
(exhaustive search, using N
∗
E(n) no. of cascades search time [s]
1 29 27 (2,3,4,6,12) 6.97378 14950 5.125
2 42 41 (2,3,5,9,22) 7.58432 91390 39.281
3 30 27 (2,2,3,4,6,10) 6.59502 65780 23.093
4 43 41 (2,3,3,5,9,19) 7.0788 658008 289.906
Table 5: Resulting cascades found numerically via continuous approximate expectations (4) and (5).
n K A
optimal cascade
(exhaustive search)
resulting cascade
for approximate criterion (4)
(NMinimize[·]) time [s]
resulting cascade
for approximate criterion (5)
(NMinimize[·]) time [s]
30 2 10
−2
(7,16) (7,16) 0.609 (7,16) 0.620
30 2 10
−3
(8,20) (8,20) 0.625 (8,20) 0.625
30 3 10
−2
(4,6,14) (4,6,14) 2.688 (4,6, 14) 2.797
30 3 10
−3
(4,7,17) (4,7,17) 2.750 (4,7, 17) 2.800
30 4 10
−2
(3,4,6,10) (3,4,6,10) 6.484 (3,4,6,10) 6.422
30 4 10
−3
(3,4,7,15) (3,4,7,15) 6.781 (3,4,7,15) 6.703
50 5 10
−2
(2,3,4,7,13) (2,3,4,7,13) 18.953 (2,3, 4,7, 13) 20.001
50 5 10
−3
(2,3,5,9,23) (2,3,5,9,23) 19.313 (2,3, 5,9, 23) 19.578
50 6 10
−2
(2,2,3,4,7,12) (2,2,3,4,7,12) 26.141 (2, 2,3, 4,7,12) 26.875
50 6 10
−3
(2,3,3,5,9,21) (2,3,4,5,9,20) 26.922 (2, 3,4, 5,9,20) 27.297
disposal gets combinatorially distributed among the
(n
1
,. ..,n
K
) counts, (ii) the dependency of false alarm
rates a
k
on n
k
counts is in general unknown, and ob-
viously not continuous.
In this section we present a technique, tailored to
the “cuboid in the corner” example, that allows to find
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
108

optimal cascades via direct numerical optimization.
This is achieved by a trick introducing a continuous
approximate variant of formula (8) for FAR(m;m
0
).
In consequence, this further allows for continuous va-
riants of formulas (4) and (5) for E(n).
First, let us write down an equivalent representa-
tion of (8) as follows.
FAR(m; m
0
) =
n
∏
k=1
w
[1+m
0
≤k]·[k≤m
0
+m]
k
1 −
n
∏
k=1
w
[1+m
0
+m≤k]·[k≤n]
k
!
.
1 −
n
∏
k=1
w
[1+m
0
≤k]·[k≤n]
k
!
. (11)
Note that all the products iterate now from k = 1
to k = n but the actual restrictions on k indexes are
moved to exponents in the form of suitable indicator
functions.
Consider the sigmoid function φ
β
(x) =
1
1+e
−βx
with β parameterizing its steepness. Now, the key
trick we apply is that indicator functions can be ap-
proximated by the sigmoid function for sufficiently
large β in the following manner:
[a ≤ b] ≈ φ
β
(b − a +
1
2
). (12)
The
1
2
is added because the inequality a ≤ b is not
strict. Taking advantage of the trick we write down
the following approximate version of the FAR for-
mula:
FAR(m; m
0
) ≈
n
∏
k=1
w
φ
β
(k−1+m
0
+
1
2
)φ
β
(m
0
+m−k+
1
2
)
k
1−
n
∏
k=1
w
[1+m
0
+m≤k]·[k≤n]
k
!
.
1 −
n
∏
k=1
w
[1+m
0
≤k]·[k≤n]
k
!
. (13)
The right-hand-side of (13) can be now plugged into
the expectation formulas (4) or (5), and the numerical
optimization can be carried out directly.
Table 5 reports cascades found numerically using
Wolfram Mathematica’s NMinimize[·] procedure
performing an optimization with constraints. The
constraints in our case were: n
1
+ ··· + n
K
= N and
n
k
∈ N. The steepness parameter β was set to 10.0.
The table shows that except for a single case, the nu-
merical procedure found exactly the same cascades as
the exhaustive combinatorial search.
4 EXAMPLE 2: “3D CUBE TRAP”
In this section we present the second geometric ex-
ample, demonstrating the non-optimality of the stan-
dard VJ approach. The example is exactly three-
dimensional. The domain is constituted by a cube
that contains positive, negative and mixed regions in-
side of it, as depicted in Fig. 2. By mixed regions we
mean the regions that cannot be separated by splits
orthogonal to axes in the given space.
Figure 2: Example 2 “3D cube trap”: visualization.
In this example the probability distribution in the
cube is not uniform. From now on, we shall write
µ(P
i
) or µ(N
i
) to denote the probability measure lying
in the given region. In the example, the following par-
ticular values are imposed (but variations are possible
without damaging the conclusions):
p = µ(P) = 0.01,
1 − p = µ(N) = 0.99,
µ(P
1
) = 0.98 µ(P),
µ(P
1
) = µ(P
2
) = µ(P
3
) = 0.002 µ(P),
µ(P
4
) = 0.006 µ(P),
µ(P
5
) = µ(P
6
) = 0.004 µ(P),
µ(N
0
) = 0.975 µ(N),
µ(N
1
) = 0.002 µ(N),
µ(N
2
) = 0.001 µ(N),
µ(N
3
) = µ(N
4
) = 0.011 µ(N).
Similarly as in the first example, the decision
stumps are used as weak classifiers within the cascade
training, but as a simplification suppose the splits can
be carried out only along the borders of P
i
, N
i
regions.
We impose the following sensitivity / FAR
constraints for the entire cascade: D = 0.9,
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View
109

A = 0.02, K = 2. This results in d
min
≈ 0.9486833,
a
max
≈ 0.1414214 serving as the per-stage require-
ments.
Description of the Resulting VJ-style Cascade
Stage 1: The feature x
3
is selected because of the
large probability measure within the N
0
region. Re-
gions lying above N
0
become labeled by the classifier
as positives, whereas N
0
itself becomes labeled as ne-
gative. Other choices will significantly increase FAR
or decrease sensitivity forcing the use of another fea-
ture. Because all P
i
regions are classified as positives
then d
1
= 1 and a
1
= 0.025.
Stage 2: At this stage we can either: (i) cut the cube
orthogonally to x
1
, x
2
, (ii) try using x
3
again, or (iii)
use some combination of two features. After the re-
jection of N
0
region, the remaining measure of negati-
ves will be equal 0.025 due to the cascade properties.
Suppose the x
3
feature is selected again. By that
we do not increase the number of features used so far.
The classifiers labels the following regions as posi-
tive: P
0
,P
3
,P
5
,P
6
,N
3
,N
4
, the remaining ones become
labeled as negatives. The following results are obtai-
ned.
d
2
=
0.98 + 2 · 0.004 + 0.002
1
= 0.99 > d
min
,
a
2
=
2 · 0.011
0.025
= 0.88 > a
max
,
a
1
· a
2
> A.
Both the final and the per-stage requirements are not
satisfied.
Suppose the x
1
feature is selected. The
following regions will be marked as positives:
P
0
,P
2
,P
4
,P
6
,N
2
,N
4
, other as negatives.
d
2
= 0.9992 > d
min
,
a
2
= 0.48 > a
max
,
a
1
· a
2
< A.
Suppose the x
2
feature is selected. In this case, the
results are be identical to the ones for x
1
, because of
the symmetry in the cube.
In both last cases the final requirements for FAR
and sensitivity are satisfied and the learning process
could be completed. However, the per-stage requi-
rement for FAR is not met (a
2
> a
max
). Therefore,
the algorithm following strictly the per-stage require-
ments will have to add one more feature.
Suppose the pair of features x
1
,x
2
is selected. If
we want to minimize FAR, the following regions will
be marked as positives: P
0
,P
4
,N
2
, other as negatives.
Even if some different weights are assigned to each
weak classifier, this will increase sensitivity at the ex-
pense of FAR. The results for this case are:
d
2
= 0.986 > d
min
,
a
2
= 0.04 < a
max
,
d
1
· d
2
> D,
a
1
· a
2
< A.
At this point the learning process will be completed,
since both final and per-stage requirements are satis-
fied.
Suppose the pair of features x
1
,x
3
is selected (the
option x
2
,x
3
is symmetrical). If we want to minimize
FAR, the following regions will be marked as positi-
ves: P
0
,P
6
,N
4
, other as negatives.
d
2
= 0.984 > d
min
,
a
2
= 0.44 > a
max
.
This combination does not meet the per-stage requi-
rements.
To summarize, we remark that fulfilling the per-
stage requirements implies the need an additional fe-
ature. As a result, the final cascade with (n
1
,n
2
) =
(1,2) was achieved, using x
3
(stage 1) and x
1
,x
2
(stage 2). Instead, the genuinely optimal cascade
should be (n
1
,n
2
) = (1,1), using x
3
(stage 1) and
either x
1
or x
2
(stage 2).
Let us now calculate the expected number of
features for the cascade falling into the trap and com-
pare it against an expectation for a cascade omitting it.
Expected Number of Features for the VJ-style
Cascade
E(n) = n
1
+ n
2
(pd
1
+ (1 − p)a
1
)
= 1 + 2(0.01 ·1.0 + 0.99 ·0.025)
= 1.0695
Expected Number of Features for a Cascade
Omitting the Trap
E(n) = n
1
+ n
2
(pd
1
+ (1 − p)a
1
)
= 1 + 1(0.01 ·1.0 + 0.99 ·0.025)
= 1.0348
5 EXAMPLE 3: “CHESSBOARD
TRAP”
In this section we consider the last geometric exam-
ple. The input domain is again constituted by a cube,
this time n-dimensional, but the majority of decision
boundaries is visible in the the x
1
, x
2
subspace, as il-
lustrated in Fig. 3.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
110

x
1
x
2
P
1
, N
1
,
N
1
N
1
N
2
P
2
N
2
N
4
N
4
P
3
, N
3
Figure 3: Example 3 “chessboard trap”: visualization of x
1
,
x
2
subspace.
The set of positives is defined as follows:
P =P
1
∪ P
2
∪ P
3
,
P
1
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
: 0 ≤ x
1
,x
2
<
1
3
and 0 ≤ x
3
< 1 − ε
o
,
P
2
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
:
1
3
≤ x
1
,x
2
<
2
3
o
,
P
3
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
:
2
3
≤ x
1
,x
2
≤ 1
and chess(x
3
,. ..,x
n
;8) = 1
o
,
where:
chess(z
1
,. ..,z
q
;m) = (bz
1
· mc +. .. +bz
q
· mc) mod 2.
The negative set is [0,1]
n
\ P, but for clarity we define
it explicitly as follows:
N =N
1
∪ N
1,ε
∪ N
2
∪ N
3
∪ N
4
,
N
1
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
: 0 ≤ x
1
<
1
3
and
1
3
≤ x
2
≤ 1
o
,
N
1,ε
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
: ≤ x
1
,x
2
<
1
3
and 1 − ε ≤ x
3
≤ 1
o
,
N
2
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
:
1
3
≤ x
1
<
2
3
and (0 ≤ x
2
<
1
3
or
2
3
≤ x
2
≤ 1)
o
N
3
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
:
2
3
≤ x
1
,x
2
≤ 1
and chess(x
3
,. ..,x
n
;8) = 0
o
N
4
=
n
(x
1
,. ..,x
n
) ∈ [0,1]
n
:
2
3
≤ x
1
≤ 1
and 0 ≤ x
2
<
2
3
o
Once again suppose that splits orthogonal to axes
shall be carried out. As the reader may recognize,
the arrangement of the example allows to: isolate P
2
using just two features (x
1
and x
2
), isolate P
1
using
three features (x
1
, x
2
and x
3
), but in order to per-
fectly isolate P
3
all n features must per force be used.
This is caused by the fact that positives within P
3
to-
gether with negatives within N
3
are entangled in a
chessboard pattern defined on all remaining variables
x
3
,. ..,x
n
. This sets the trap that the greedy stage-wise
cascade training can fall into.
The probability measures are distributed as descri-
bed below (variations are possible) with two parame-
ters ε and α that we shall discuss later on:
p = µ(P) = 0.01,
1 − p = µ(N) = 0.99,
µ(P
1
) = 0.05 µ(P),
µ(P
2
) = 0.85 µ(P),
µ(P
3
) = 0.10 µ(P),
µ(N
1
∪ N
1,ε
) = 0.9 µ(N),
µ(N
1,ε
) = ε 0.9 µ(N),
µ(N
2
∪ N
3
∪ N
4
) = 0.1 µ(N),
with µ(N
3
) = α 0.1 µ(N) (e.g. α ≥ 0.9).
Please note that we impose a large α fraction, so that
the chessboard region encapsulates the large part of
the 0.1µ(N) negatives probability measure remaining
outside of N
1
and N
1,ε
.
Algorithm 3 presents the pseudocode of a cascade
training algorithm suited to the mathematical proper-
ties of the considered example. Again, the training
is guided by the stage-wise sensitivity / FAR require-
ments (VJ-style). At each stage, the algorithm succes-
sively tries out more complex classifiers based on ort-
hogonal splits. It iterates first over single features,
then pairs of features, then triples, and so forth. For
a fixed combination of features, the algorithm con-
structs a decision tree which can apply any number
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View
111

of splits (but using only the given features) in order to
minimize the classification error. In particular, the cu-
boids isolated by the splits can be labeled arbitrarily
as fits. When a certain combination of features allows
to satisfy stage requirements d
min
and a
max
, the algo-
rithm ceases searching further and the current cascade
stage becomes closed.
Algorithm 3: Viola Jones-style cascade training based on
stage-wise sensitivity / FAR requirements (for the purposes
of Example 3).
procedure TRAINCASCADEVJSTYLE(D, A, K)
d
min
:= D
1/K
, a
max
:= A
1/K
,
for k := 1,.. ., K do
n
k
:= 0, d
k
:= 0, a
k
:= 1
for d := 1,...,n do
for all feature combinations x
i
1
,. ..,x
i
d
of length d (1 ≤ i
1
< ··· < i
d
≤ n) do
build the decision tree using
features x
i
1
,. ..,x
i
d
that
minimizes classification error
(any number of splits allowed)
calculate d
k
,a
k
for the tree
memorize the tree if it is better than
the best tree so far (for curred d)
end for
if (d
k
≥ d
min
and a
k
≤ a
max
) then
use the best tree for current stage
n
k
:= d
jump out of this loop
end if
end for
end for
end procedure
Suppose the following requirements for the entire
cascade have been imposed: K = 2, D = 0.9025,
A = 0.01. This implies: d
min
= D
1/K
= 0.95,
a
max
= A
1/K
= 0.1.
Description of the Resulting VJ-style Cascade
Stage 1: It is possible to see that the single feature x
1
will turn out to be sufficient, producing the following
classifier for the first stage:
F
1
(x) =
(
−1, for 0 ≤ x
1
<
1
3
;
1, otherwise.
We obtain d
1
= 0.95 and a
1
= 0.1 for this classifier,
which satisfies stage requirements. Therefore, n
1
= 1.
Stage 2: We will now prove that, perforce, all the
remaining features shall be required for the second
stage. The reasoning is as follows. To satisfy stage re-
quirements the next classifier should perfectly isolate
the P
2
region (computationally cheap because only
one new feature x
2
is added) but also some fragment,
say β ∈ (0,1), from the P
3
region. In order to achieve
d
2
≥ d
min
, the following condition must be met
µ(P
2
) + β µ(P
3
)
µ(P
2
) + µ(P
3
)
≥ d
min
,
which yields β > 0.525. Note that if one does not ap-
ply all n − 2 remaining features (x
3
,. ..,x
n
), but only
some subset of them, then the chessboard pattern can
never be perfectly recognized (that is why the chess-
board is convenient for this example). In turn, when
some non-perfect split is made, such that the β· µ(P
3
)
measure is kept at one side then it simultaneously in-
troduces β · α · µ(N
3
) of false alarms. In other words,
the following condition:
β α 0.1µ(N)
0.1µ(N)
≤ a
max
,
yields α ≤ 0.1/0.525 which is not allowed according
to former settings (α ≥ 0.9). Therefore, all the re-
maining features x
3
,. ..,x
n
and x
2
are required and the
classifier for the second stage is
F
2
(x) =









1, for
1
3
≤ x
1
,x
2
<
2
3
;
1, for
2
3
≤ x
1
,x
2
≤ 1
and chess(x
3
,. ..,x
n
;8) = 1;
−1, otherwise;
yielding d
2
= 1,a
2
= 0.0
Let us now calculate explicitly the expected
number of features for the cascade falling into the
chessboard trap and compare it against an expectation
for a cascade omitting it.
Expected Number of Features for the VJ-style
Cascade
E(n) = n
1
+ n
2
(pd
1
+ (1 − p)a
1
)
= 1 + (n −1)(0.01 · 0.95 +0.99 · 0.1)
= 1 + 0.1085(n −1)
Expected Number of Features for a Cascade Omit-
ting the Trap
To omit the trap it is sufficient to classify the whole
chessboard region P
3
∪ N
3
as negative at stage one.
This could be achieved for example by the following
cascade.
F
1
(x) =





1, for 0 ≤ x
1
,x
2
<
1
3
;
1, for
2
3
≤ x
1
,x
2
≤ 1;
−1, otherwise.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
112

F
2
(x) =





−1, for 0 ≤ x
1
,x
2
<
1
3
and x
3
≥ 1 − ε;
1, otherwise.
Hence, for stage 1 we have: n
1
= 2, d
1
= 0.9, a
1
=
ε 0.9. Whereas, for stage 2 we have: n
2
= 1 because
x
3
is the only new variable, d
2
= 1, a
2
= 0. We remark
that cutting of the ε-region is required if
ε 0.9µ(N)
µ(N)
> A,
which yields ε > 0.01.
The expected number of features for the above
cascade is
E(n) = n
1
+ n
2
(pd
1
+ (1 − p)a
1
)
= 2 + 1(0.01 ·0.9 + 0.99ε ·0.9)
= 2.009 + 0.891ε
=
|ε:=0.02
2.02682.
Comparing the two cascades we see that the se-
cond one becomes better if
1 + 0.1085(n − 1) > 2.02682,
which happens whenever the number of features (di-
mensions) is n ≥ 11.
6 CONCLUSIONS
We have provided three geometric examples demon-
strating how training a cascade with sensitivity / FAR
constraints imposed per each stage can lead to non-
optimality in the cascade computational cost — more
precisely, in the expected number of features E(n) the
cascade uses while performing a detection procedure.
We are aware that the constructed examples are
artificial and motivated by certain mathematical pur-
poses. Yet, similar properties or variations can be ea-
sily met in real-world data. By generalizing the dis-
advantages of the stage-wise training pointed out by
our examples, the following two conclusions can be
formulated.
1. A stage satisfying the (d
min
,a
max
) requirements is
in some cases closed prematurely, which may re-
sult in a greater number of new features required
by the stages to follow. Investing more features
in such a stage (though not greedy) can in some
cases be beneficial, lowering the final E(n) value.
2. There exist many cases where a stage can be clo-
sed without actually satisfying the (d
min
,a
max
) re-
quirements, and still the final requirements for the
entire cascade can be met.
The conclusions above can help to avoid the pitfalls
caused by the greedy approach guided by the stage-
wise constraints.
In our further research we plan to design specific
cascade training algorithms based partially on search
methods and keeping track of more than one cascade
in runtime. Let us briefly sketch this idea hereby.
Training a cascade can be brought to a graph sear-
ching process with nodes representing cascade stages
with slightly different counts of features. For exam-
ple, in the simplest case one could consider three no-
des per each stage: a node using exactly the number of
features suggested by the traditional approach, a node
with one feature more (this worsens the expected va-
lue of features up to the current stage but improves
the sensitivity / FAR properties), and a node with one
feature less (this improves the expected value but wor-
sens the sensitivity / FAR properties). By tracing the
‘evolution’ of such additional nodes further on one
may hope to discover cascades with improved overall
expected values of features.
ACKNOWLEDGEMENTS
This work was financed by the National
Science Centre, Poland. Research project
no.: 2016/21/B/ST6/01495.
REFERENCES
Bourdev, L. and Brandt, J. (2005). Robust Object De-
tection via Soft Cascade. In Proceedings of the 2005
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition (CVPR’05) - Volume 2 -
Volume 02, CVPR ’05, pages 236–243. IEEE Compu-
ter Society.
Crow, F. C. (1984). Summed-area Tables for Texture Map-
ping. SIGGRAPH Comput. Graph., 18(3):207–212.
Freund, Y. and Schapire, R. (1996). Experiments with a
new boosting algorithm. In Machine Learning: Pro-
ceedings of the Thirteenth International Conference,
pages 148–156. Morgan Kaufman.
Friedman, J., Hastie, T., and Tibshirani, R. (2000). Additive
logistic regression: a statistical view of boosting. The
Annals of Statistics, 28(2):337–407.
Gama, J. and Brazdil, P. (2000). Cascade Generalization.
Machine Learning, 41(3):315–343.
Li, J. and Zhang, Y. (2013). Learning SURF Cascade for
Fast and Accurate Object Detection. In Proceedings
of the 2013 IEEE Conference on Computer Vision and
Pattern Recognition, CVPR ’13, pages 3468–3475.
IEEE Computer Society.
Papageorgiou, C. P., Oren, M., and Poggio, T. (1998). A
general framework for object detection. In Computer
Notes on Expected Computational Cost of Classifiers Cascade: A Geometric View
113

Vision, 1998. Sixth International Conference on, pa-
ges 555–562.
Pham, M. and Cham, T. (2007). Fast training and selection
of Haar features using statistics in boosting-based face
detection. In Computer Vision, 2007. ICCV 2007.
IEEE 11th International Conference on, pages 1–7.
Saberian, M. and Vasconcelos, N. (2014). Boosting Algo-
rithms for Detector Cascade Learning. Journal of Ma-
chine Learning Research, 15:2569–2605.
Shen, C., Wang, P., Paisitkriangkrai, S., and van den Hen-
gel, A. (2013). Training Effective Node Classifiers for
Cascade Classification. International Journal of Com-
puter Vision, 103(3):326–347.
Shen, C., Wang, P., and van den Hengel, A. (2010).
Optimally Training a Cascade Classifier. CoRR,
abs/1008.3742.
Vallez, N., Deniz, O., and Bueno, G. (2015). Sample se-
lection for training cascade detectors. PLos ONE, 10.
Viola, P. and Jones, M. (2001). Rapid Object Detection
using a Boosted Cascade of Simple Features. In Con-
ference on Computer Vision and Pattern Recognition
(CVPR’2001), pages 511–518. IEEE.
Viola, P. and Jones, M. (2004). Robust Real-time Face
Detection. International Journal of Computer Vision,
57(2):137–154.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
114